A NumericalInvestigation for a Class of Transient-State Variable Coefficient DCR Equations
Abstract
1. Introduction
2. The Governing Equation, Initial and Boundary Conditions
3. Derivation of an Integral Equation
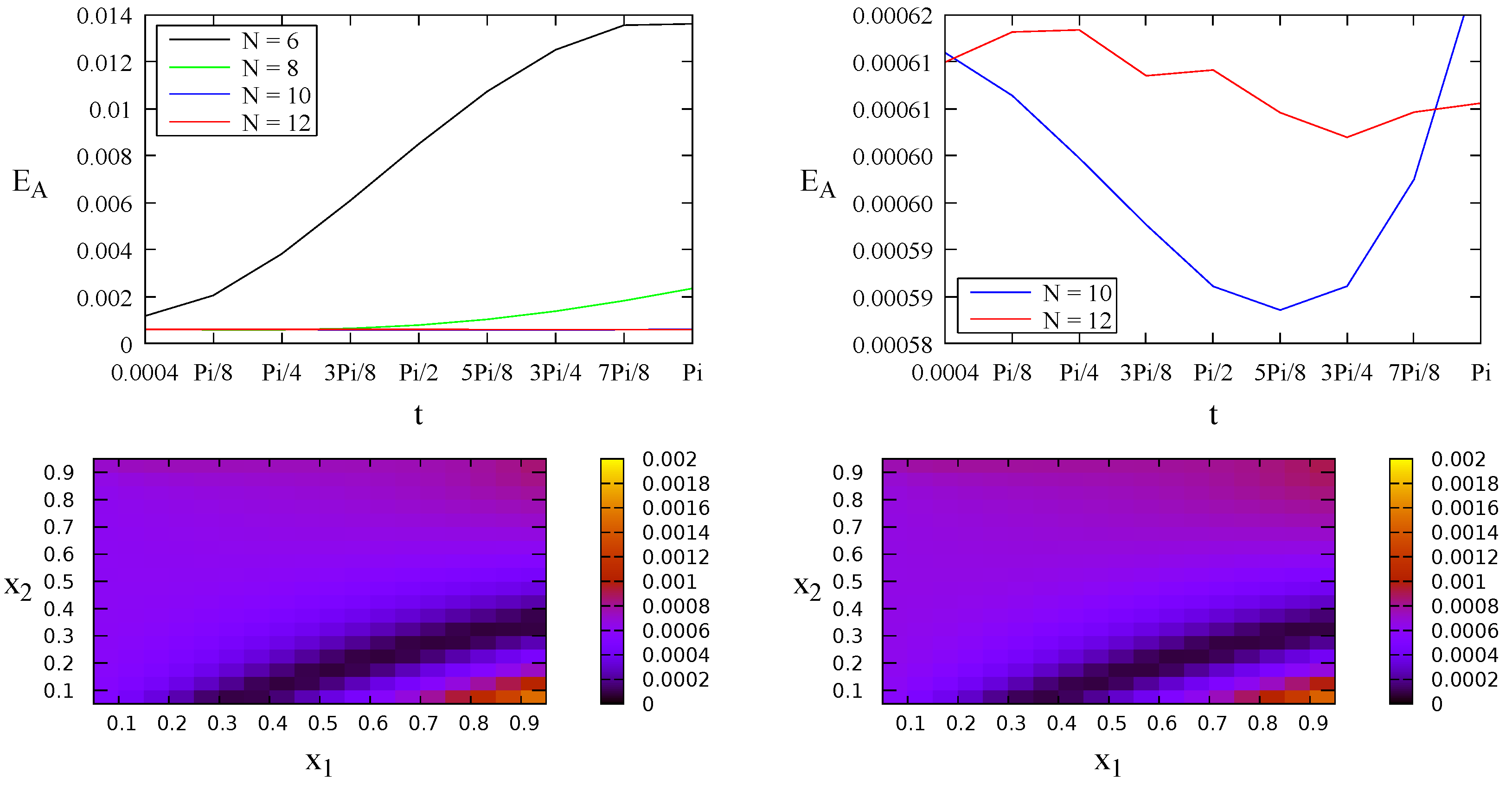
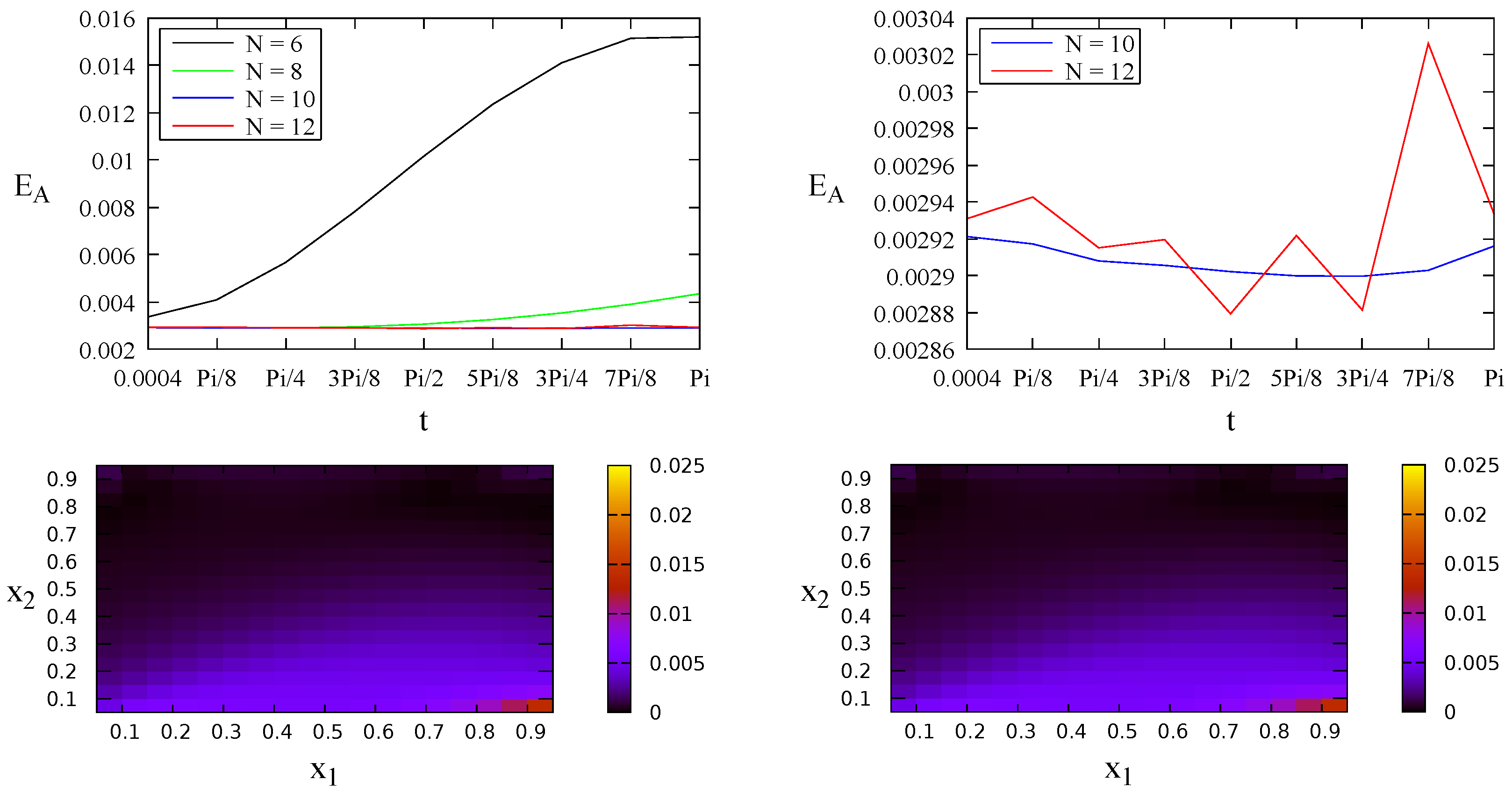
4. Numerical Examples
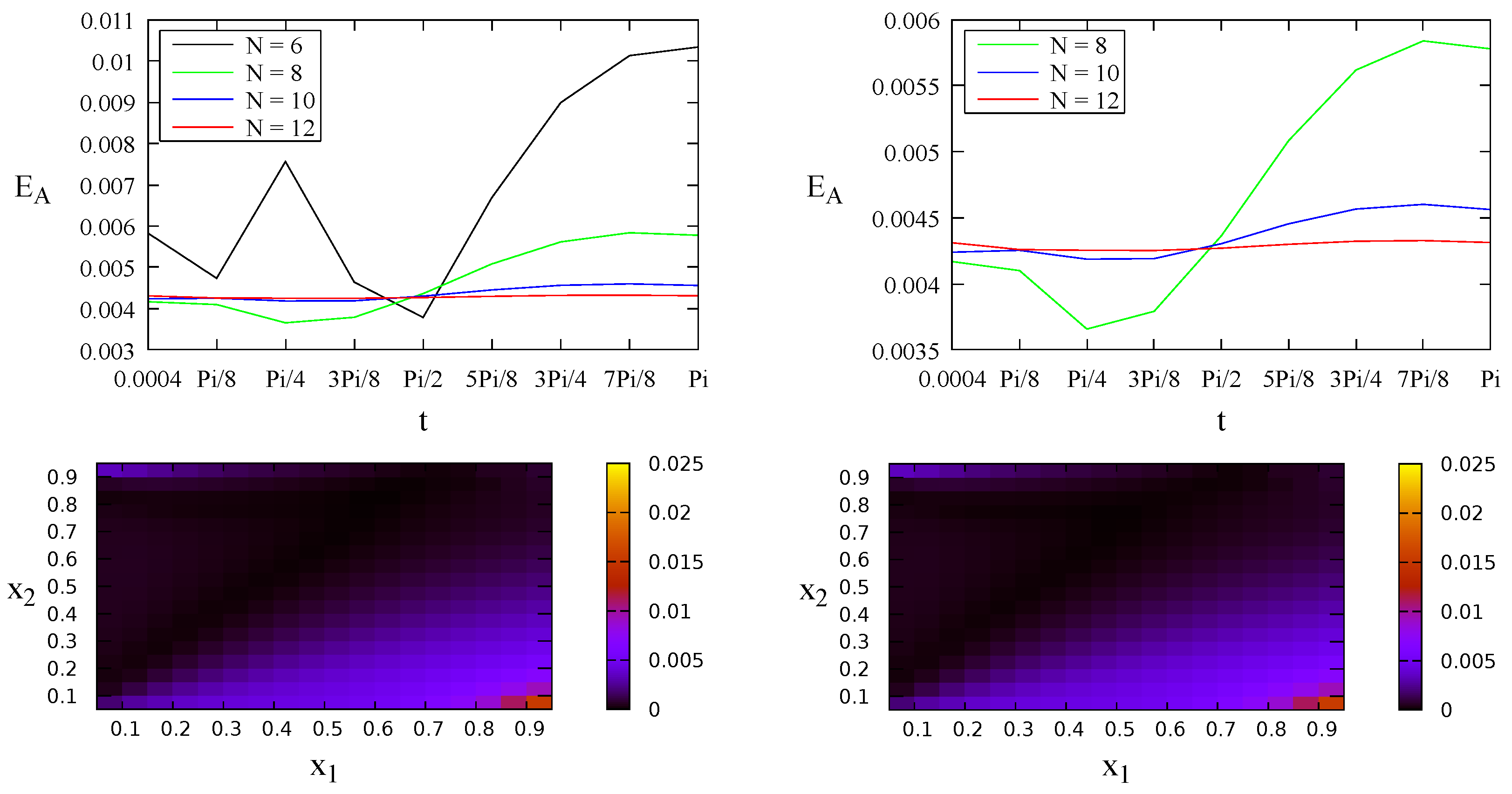
4.1. A Test Problem
| F is given on side AB, BC, CD |
| c is given on side AD |
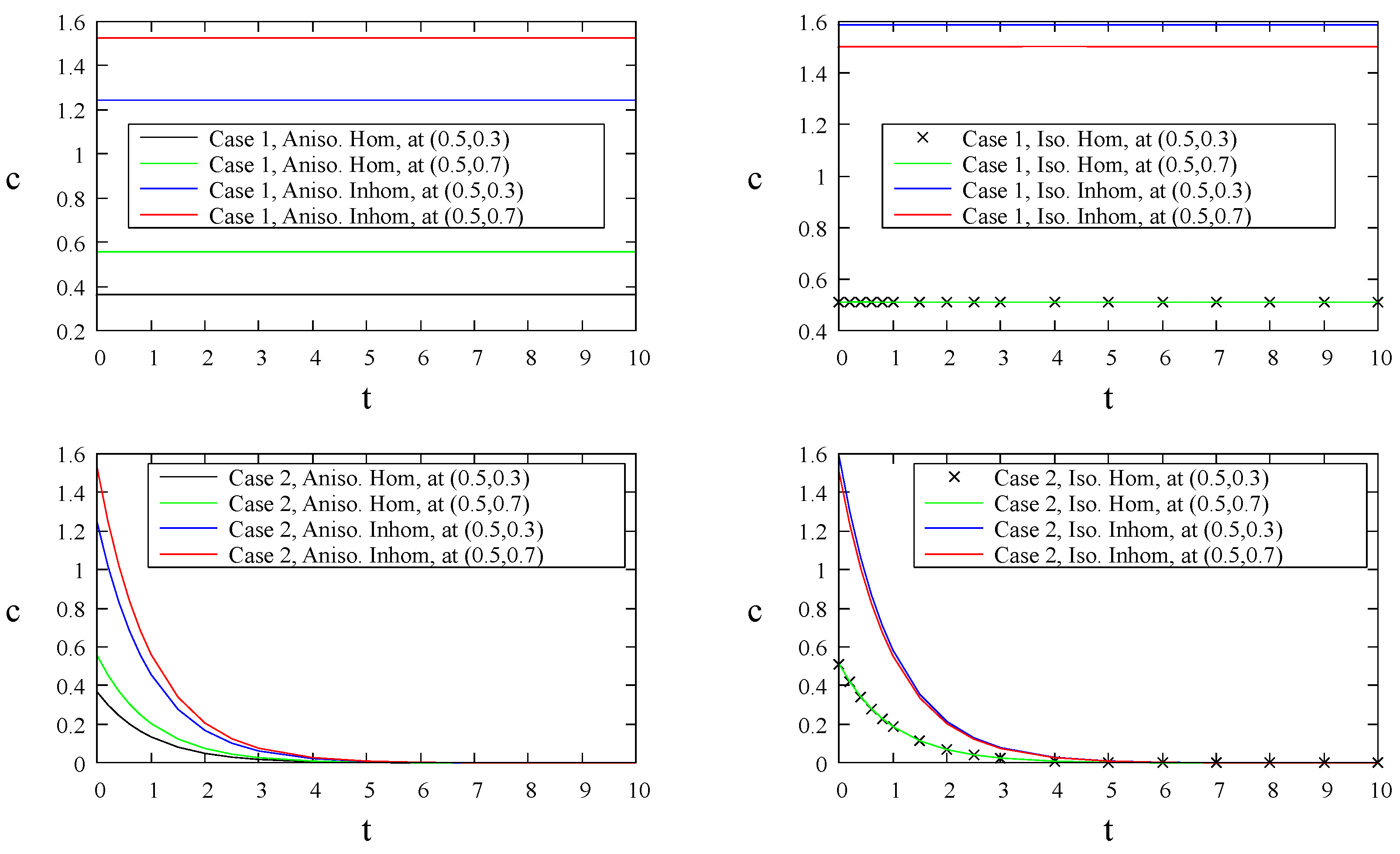
- Case 1:
- Case 2:
- Case 3:
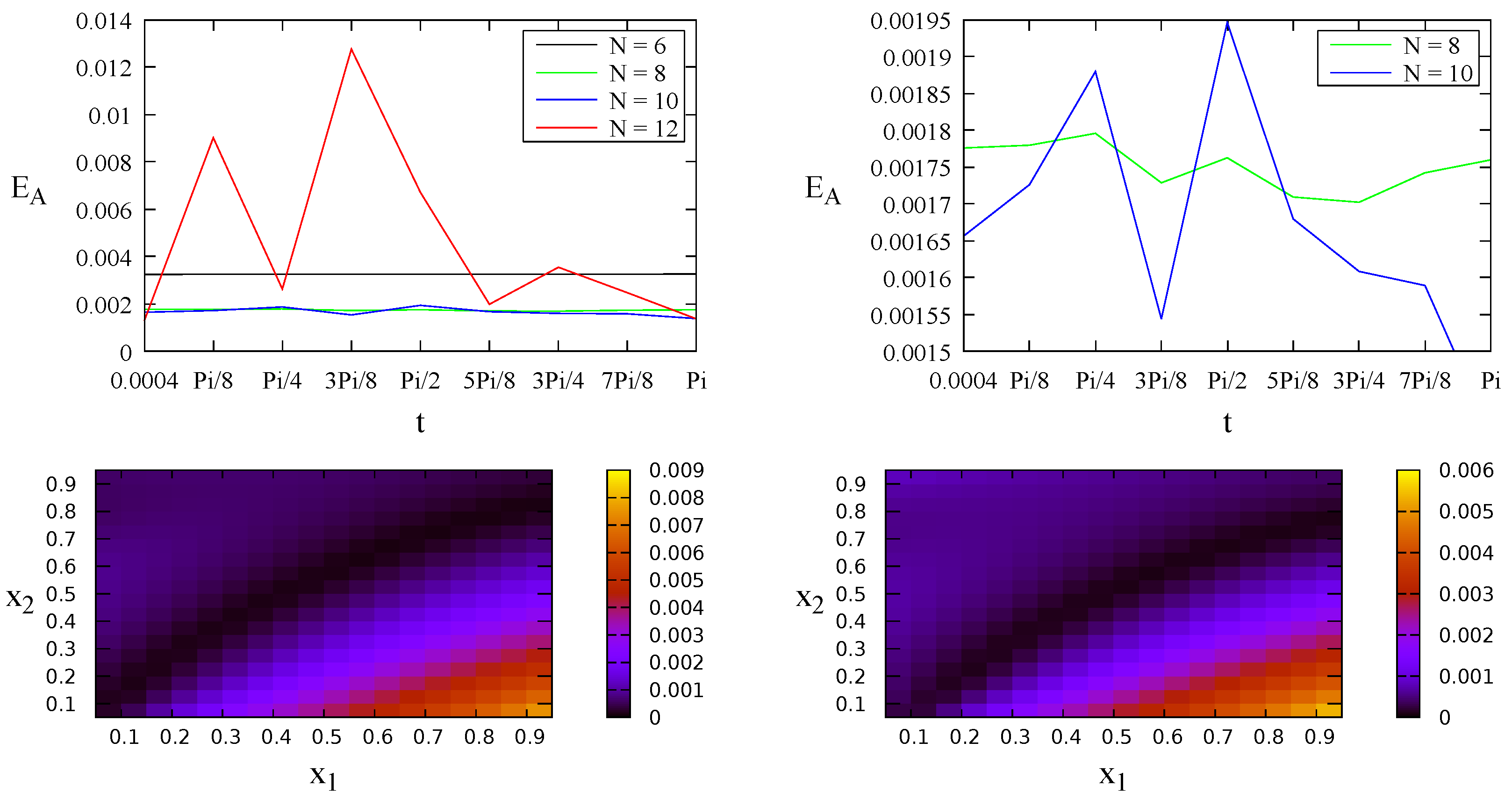
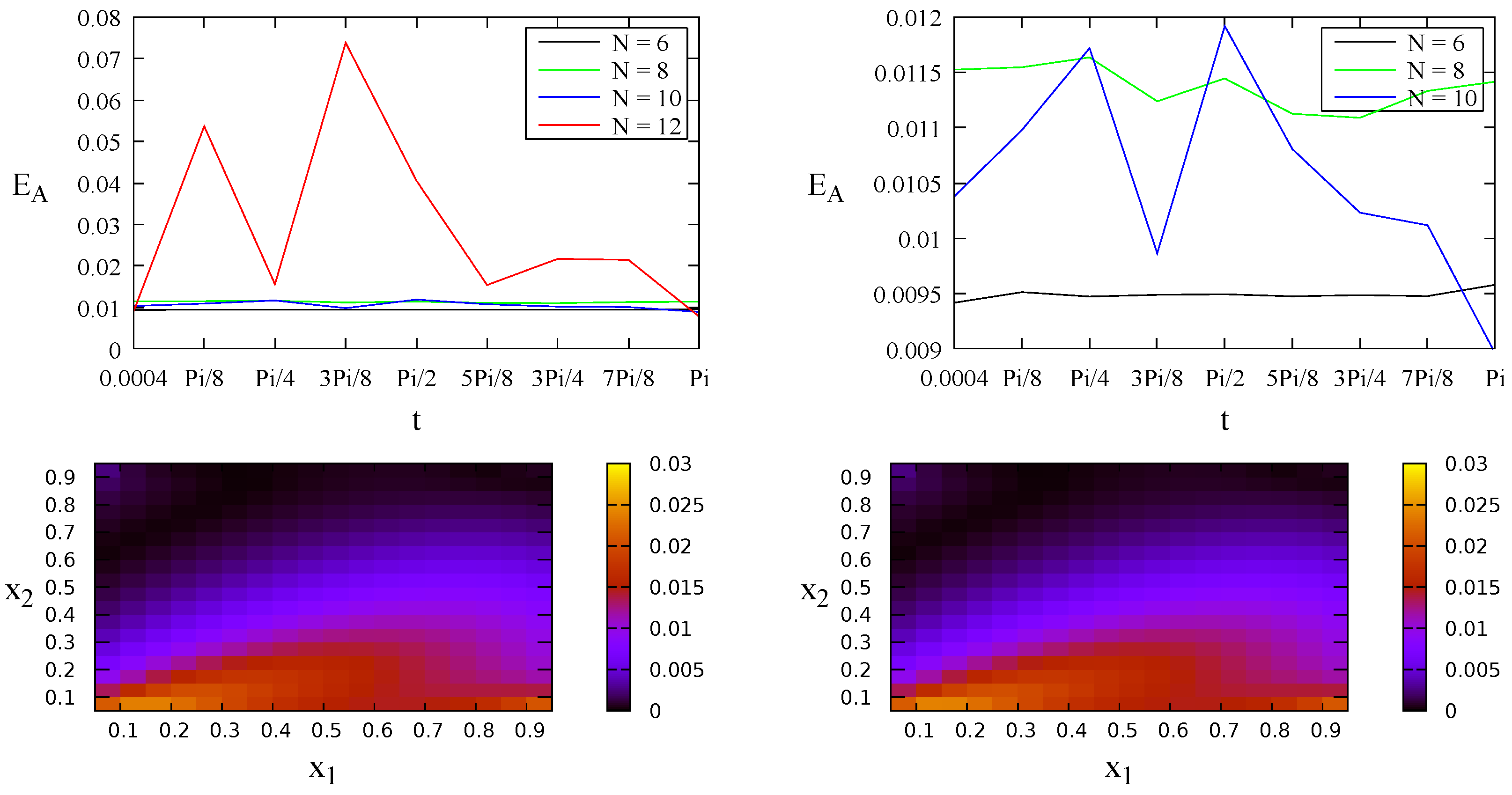
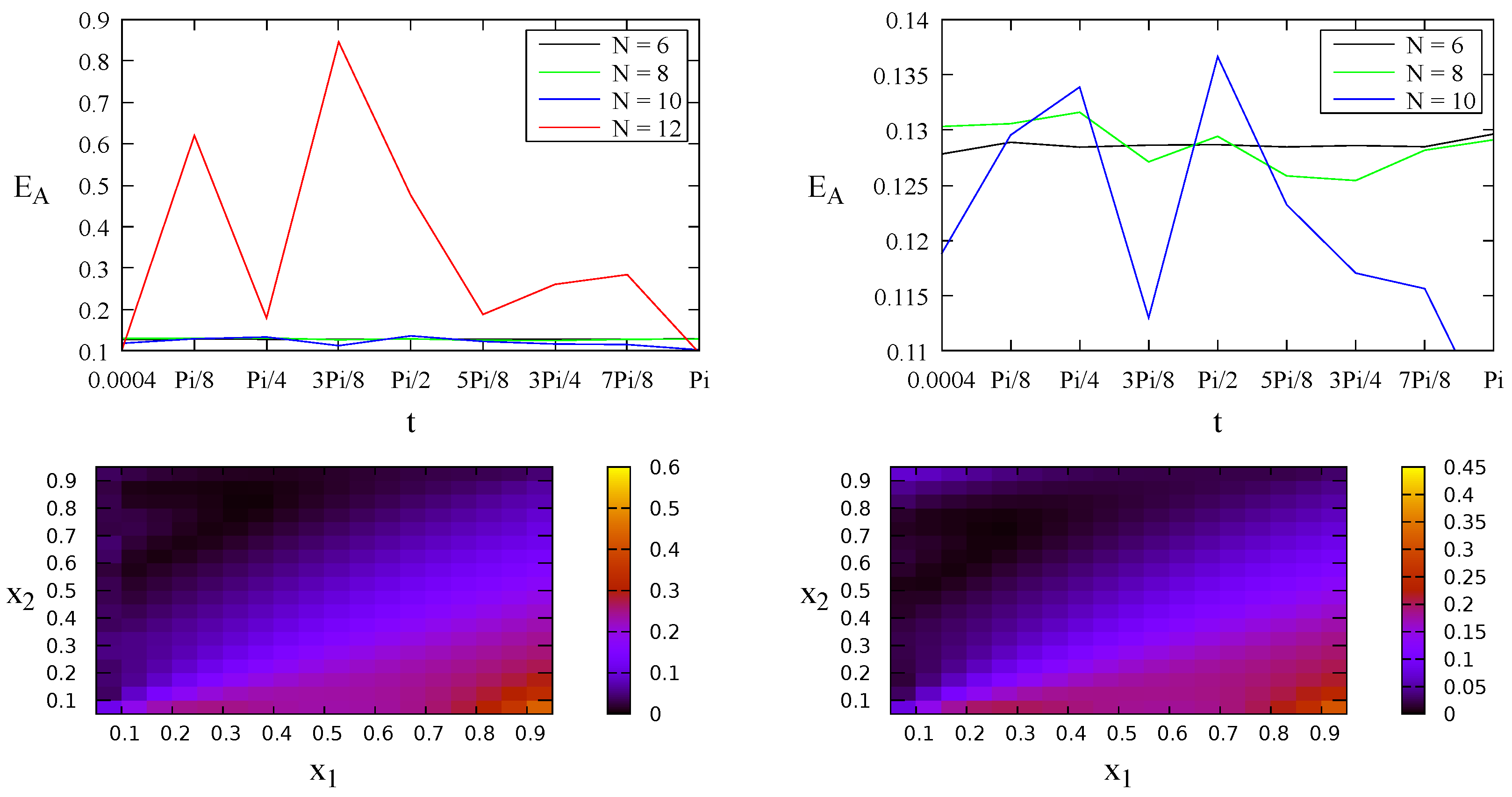
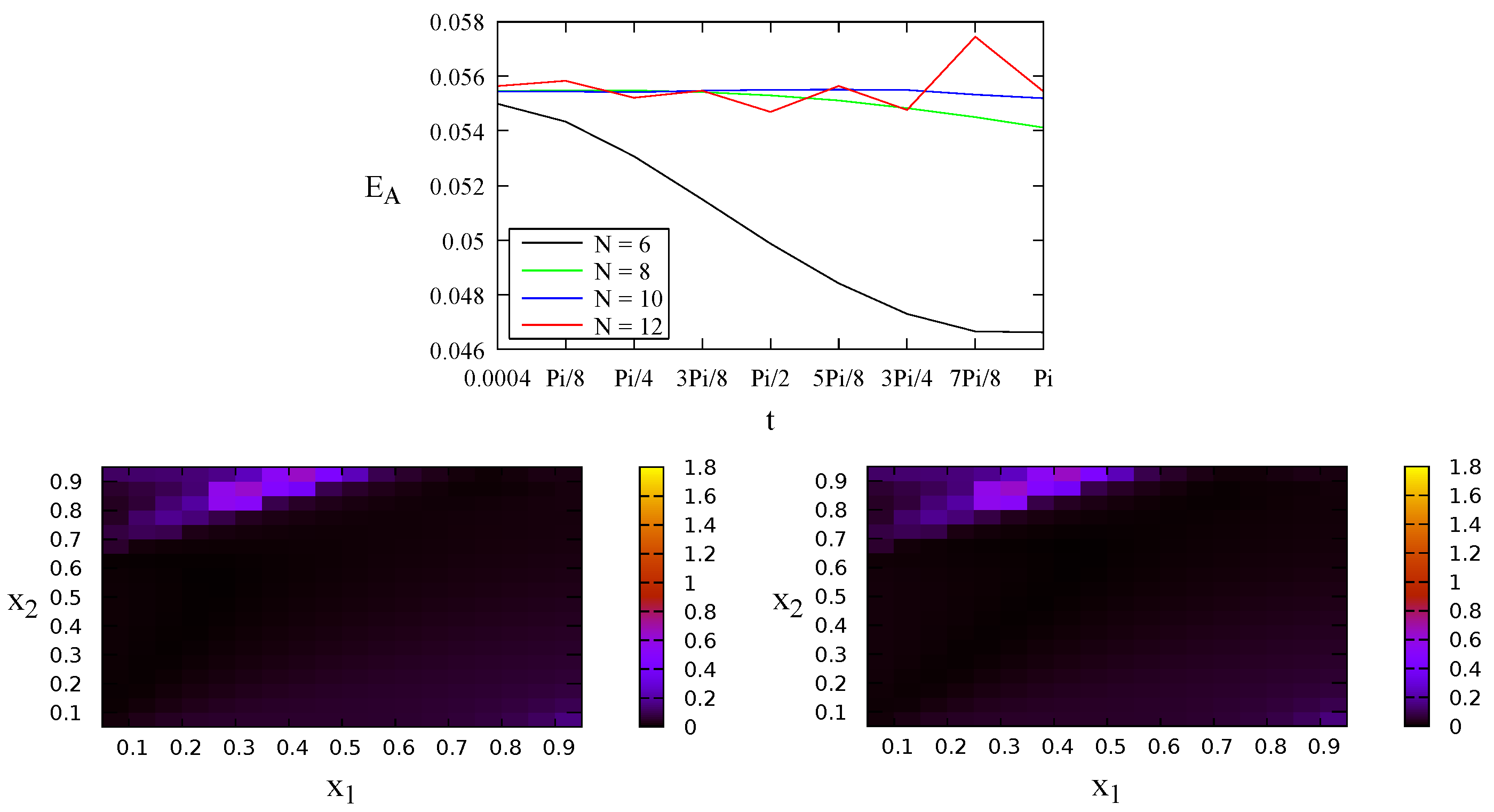
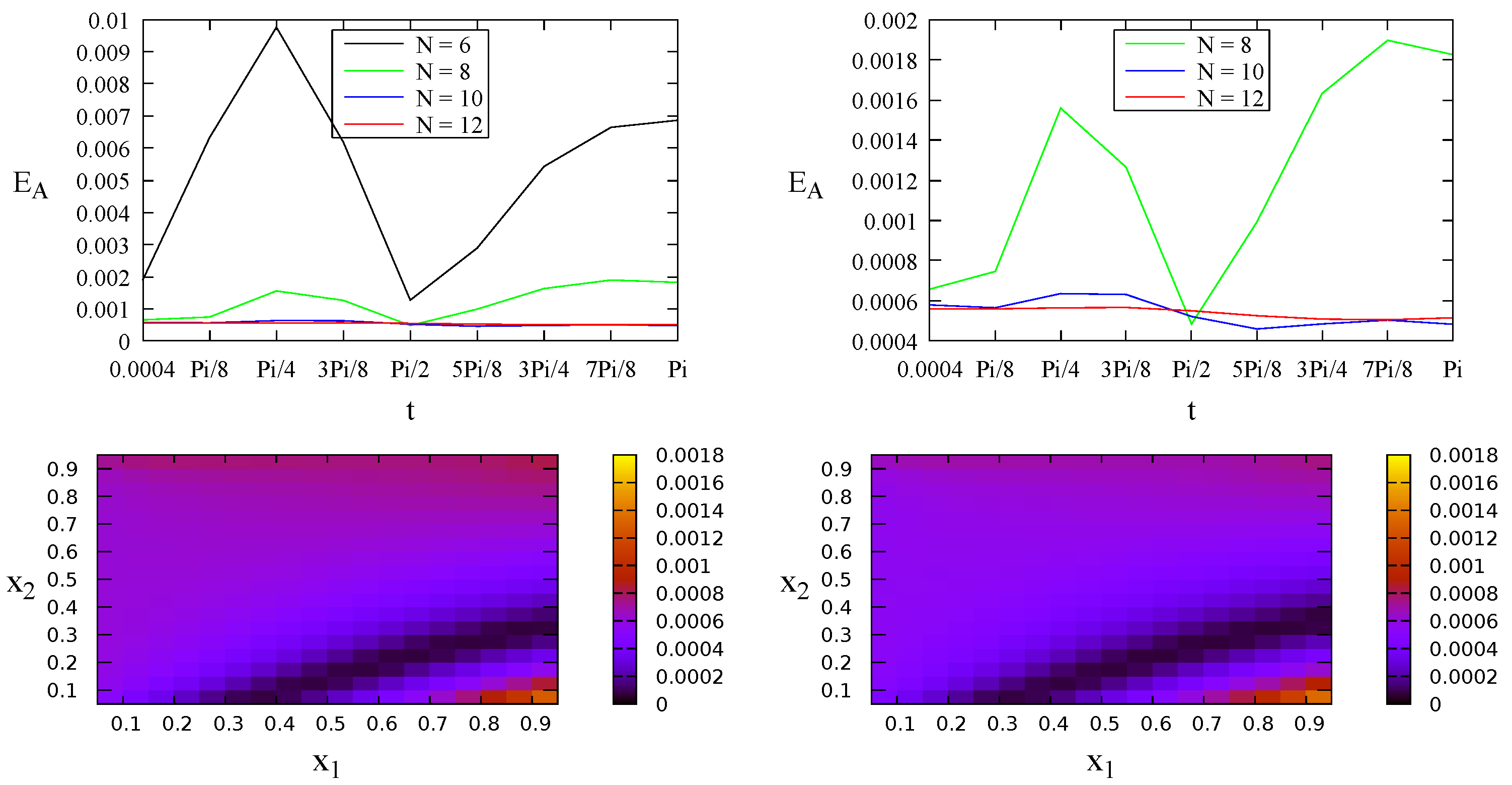
4.2. A Problem without Analytical Solution
| on side AB |
| on side BC |
| on side CD |
| on side AD |
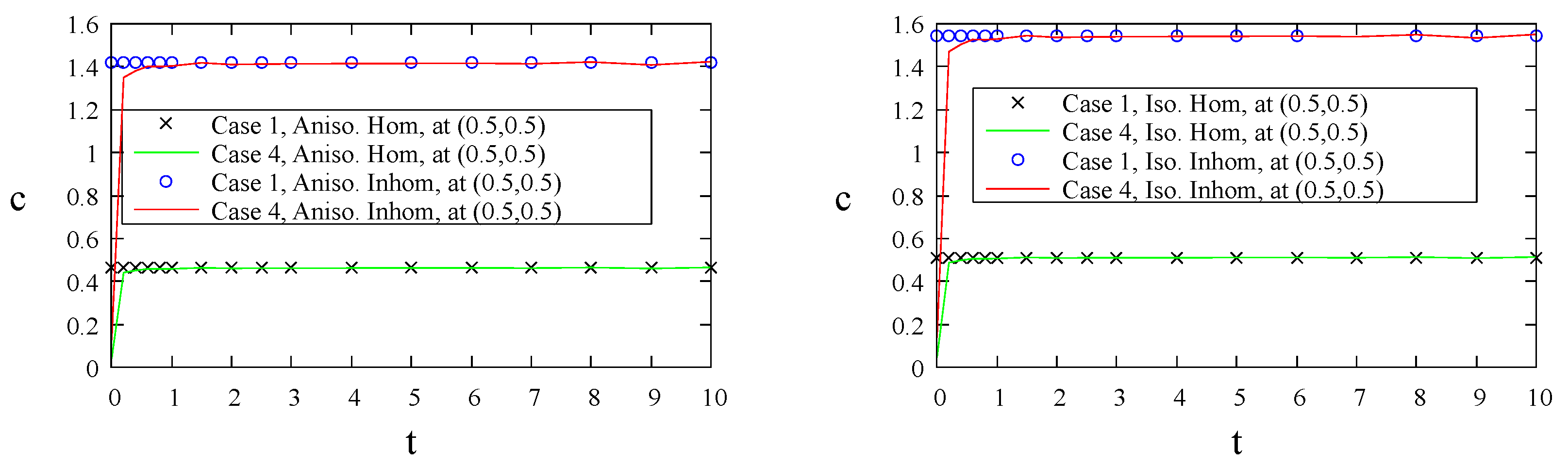
| Case 1: | |
| Case 2: | |
| Case 3: | |
| Case 4: |
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FGM | Functionally Graded Material |
| BEM | Boundary Element Method |
| LT | Laplace Transform |
| DCR | Diffusion Convection Reaction |
List of Symbols
| c | concentration |
| spatial variable | |
| t | temporal variable |
| diffusivity | |
| velocity | |
| k | reaction coefficient |
| rate of change of the concentration | |
| partial derivative with respect to and t, respectively | |
| the spatial domain and its boundary, respectively | |
| F | flux |
| h | gradation function |
| constant diffusivity | |
| constant velocity | |
| constant reaction coefficient | |
| constant rate of change of the concentration | |
| transformation function | |
| constant parameter | |
| the Laplace transform of a dependent variable | |
| s | variable of the Laplace transform |
| the fundamental solutions | |
| variable of the fundamental solutions | |
| parameters of the fundamental solutions | |
| vectors for the fundamental solutions | |
| length of the vectors , respectively | |
| parameters of the Stehfest formula |
References
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NY, USA, 1993. [Google Scholar]
- Charbeneau, R.J.; Sherif, S.A. Groundwater Hydraulics and Pollutant Transport. Appl. Mech. Rev. 2002, 55, B38–B39. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. Transient Two-Phase Flow in Porous Media: A Literature Review and Engineering Application in Geotechnics. Geotechnics 2022, 2, 32–90. [Google Scholar] [CrossRef]
- Fendoglu, H.; Bozkaya, C.; Tezer-Sezgin, M. DBEM and DRBEM solutions to 2D transient convection-diffusion-reaction type equations. Eng. Anal. Bound. Elem. 2018, 93, 124–134. [Google Scholar] [CrossRef]
- Wang, X.; Ang, W.-T. A complex variable boundary element method for solving a steady-state advection–diffusion–reaction equation. Appl. Math. Comput. 2018, 321, 731–744. [Google Scholar] [CrossRef]
- Sheu, T.W.H.; Wang, S.K.; Lin, R.K. An Implicit Scheme for Solving the Convection–Diffusion–Reaction Equation in Two Dimensions. J. Comput. Phys. 2000, 164, 123–142. [Google Scholar] [CrossRef]
- Xu, M. A modified finite volume method for convection-diffusion-reaction problems. Int. J. Heat Mass Transf. 2018, 117, 658–668. [Google Scholar] [CrossRef]
- AL-Bayati, S.A.; Wrobel, L.C. Radial integration boundary element method for two-dimensional non-homogeneous convection–diffusion–reaction problems with variable source term. Eng. Anal. Bound. Elem. 2019, 101, 89–101. [Google Scholar] [CrossRef]
- Samec, N.; Škerget, L. Integral formulation of a diffusive–convective transport equation for reacting flows. Eng. Anal. Bound. Elem. 2004, 28, 1055–1060. [Google Scholar] [CrossRef]
- Rocca, A.L.; Rosales, A.H.; Power, H. Radial basis function Hermite collocation approach for the solution of time dependent convection–diffusion problems. Eng. Anal. Bound. Elem. 2005, 29, 359–370. [Google Scholar] [CrossRef]
- AL-Bayati, S.A.; Wrobel, L.C. The dual reciprocity boundary element formulation for convection-diffusion-reaction problems with variable velocity field using different radial basis functions. Int. J. Mech. Sci. 2018, 145, 367–377. [Google Scholar] [CrossRef]
- AL-Bayati, S.A.; Wrobel, L.C. A novel dual reciprocity boundary element formulation for two-dimensional transient convection–diffusion–reaction problems with variable velocity. Eng. Anal. Bound. Elem. 2018, 94, 60–68. [Google Scholar] [CrossRef]
- Hernandez-Martinez, E.; Puebla, H.; Valdes-Parada, F.; Alvarez-Ramirez, J. Nonstandard finite difference schemes based on Green’s function formulations for reaction–diffusion–convection systems. Chem. Eng. Sci. 2013, 94, 245–255. [Google Scholar] [CrossRef]
- Azis, M.I. Standard-BEM solutions to two types of anisotropic-diffusion convection reaction equations with variable coefficients. Eng. Anal. Bound. Elem. 2019, 105, 87–93. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M. Comparison of different numerical Laplace inversion methods for engineering applications. Appl. Math. Comput. 2007, 189, 1966–1981. [Google Scholar] [CrossRef]

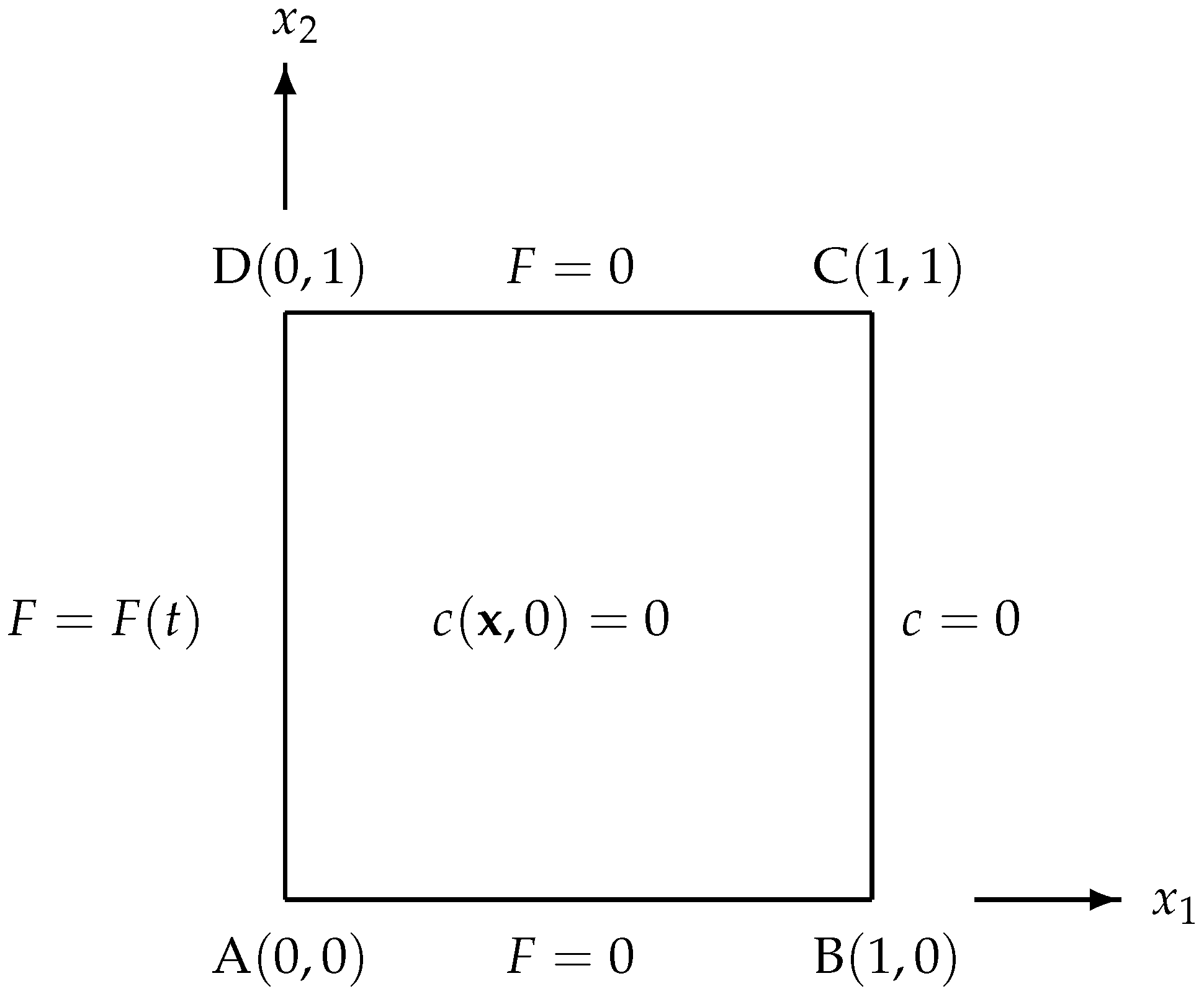


| 1 | ||||
| 366 | 1279 | |||
| 16,394/3 | −46,871/3 | 82,663/3 | ||
| 810 | −43,130/3 | 505,465/6 | −1,579,685/6 | |
| 18,730 | −236,957.5 | 1,324,138.7 | ||
| −35,840/3 | 1,127,735/3 | −58,375,583/15 | ||
| 8960/3 | −1,020,215/3 | 21,159,859/3 | ||
| 16,4062.5 | −8,005,336.5 | |||
| −32,812.5 | 5,552,830.5 | |||
| −215,5507.2 | ||||
| 359,251.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azis, M.I. A NumericalInvestigation for a Class of Transient-State Variable Coefficient DCR Equations. Mathematics 2023, 11, 2091. https://doi.org/10.3390/math11092091
Azis MI. A NumericalInvestigation for a Class of Transient-State Variable Coefficient DCR Equations. Mathematics. 2023; 11(9):2091. https://doi.org/10.3390/math11092091
Chicago/Turabian StyleAzis, Mohammad Ivan. 2023. "A NumericalInvestigation for a Class of Transient-State Variable Coefficient DCR Equations" Mathematics 11, no. 9: 2091. https://doi.org/10.3390/math11092091
APA StyleAzis, M. I. (2023). A NumericalInvestigation for a Class of Transient-State Variable Coefficient DCR Equations. Mathematics, 11(9), 2091. https://doi.org/10.3390/math11092091







