MHD Thermal and Solutal Stratified Stagnation Flow of Tangent Hyperbolic Fluid Induced by Stretching Cylinder with Dual Convection
Abstract
:1. Introduction
- Stagnation-point flow analysis for hyperbolic tangent fluid;
- Stratification phenomenon impacts on flow field with a stretched cylinder;
- Joule heating, thermal radiation, and heat source effect on the temperature profile;
- Mixed convection effect on velocity and temperature field.
2. Mathematical Formulation
3. Method of Solution
4. Results and Discussion
4.1. Discussion of Momentum Profiles
4.2. Discussion of Temperature Profiles
4.3. Discussion of Concentration Profiles
4.4. The Behavior of Surface Drag Coefficient, Nusselt Number, Sherwood Number, and Related Parameters
5. Conclusions
- For small values of the porosity parameter , the velocity pattern of the fluid decreases. It is found that the velocity reduces with , and thus the thickness of the momentum’s boundary layer is reduced. The cause behind this physical phenomenon is the pores of the porous material that reduces the velocity.
- For increases in the curvature parameter , the fluid temperature rises. Our observation indicates that the surface area of the contact decreases and the resistance provided by the cylindrical surface also decreases for greater values of the curvature parameter . Particle velocities rise as a result of this. The increased velocity is directly influenced by the kinetic energy. A higher kinetic energy is associated with a higher velocity. Higher temperatures are the outcome of a high average velocity value.
- The fluid features change from shear thinning to shear thickening as the power law index rises, and hence the fluid motion slows down. A boost in the local Weissenberg number appears to result in a decrease in the fluid velocity profiles. Since the local Weissenberg number is directly proportional to relaxation time, the internal resistance increases, and thus that velocity profiles exhibit a decreasing pattern. On the other hand, concentration and temperature profiles slightly increase.
- The conventional potential difference is diminished when the thermal stratification and the solutal stratification parameter are improved, causing the fluid temperature and concentration to decline, respectively, and when the Prandtl number rises, the fluid temperature decreases. Additionally, the effect of the Eckert number has a proportional relationship with the temperature profile.
- Higher values of the buoyancy parameter improve the velocity distribution. Physically, the buoyancy force increases with a significant increase of , hence causing the velocity to be higher. The temperature and concentration profiles show a declining pattern for higher values of .
- The local skin friction coefficient increases with the heat generation/absorption parameter and the local Nusselt number shows the opposite pattern for this parameter. The local Sherwood number has a rich profile for high values of the Schmidt number .
- Profile for the local skin friction coefficient is observed as high for the plate in comparison to the cylindrical surface; meanwhile, the reverse is true for the local Nusselt and Sherwood numbers.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Velocity ratio parameter | |
| Body force (kg m/) | |
| Temperature-dependent constants (K) | |
| Concentration-dependent constants | |
| Heat capacity at constant pressure (J/K) | |
| Hartmann number | |
| Schmidt number | |
| Dimensionless fluid velocity | |
| Identity tensor | |
| Curvature parameter | |
| Permeability of the medium () | |
| Radiation parameter | |
| Characteristic length (m) | |
| Cauchy stress tensor (N/) | |
| Power law index | |
| Pressure (N/) | |
| Prandtl number | |
| Radius of the cylindrical surface (m) | |
| Local Reynold number | |
| Solutal stratification parameter | |
| Thermal stratification parameter | |
| Reference temperature (K) | |
| Reference concentration | |
| Velocity components (m/s) | |
| Reference velocity (m/s) | |
| Local thermal Grashof number | |
| Local concentration Grashof number | |
| Mass diffusivity | |
| Mean absorption coefficient | |
| Cylindrical coordinates (m) | |
| Ratio of buoyancy forces | |
| Velocity vector (m/s) | |
| Parameter for heat generation/absorption | |
| Greek Symbols | |
| Dynamic viscosity (kg/m s) | |
| Infinite shear rate viscosity (kg/m s) | |
| Extra stress tensor (N/) | |
| Fluid density (kg/) | |
| Fluid electrical conductivity (K3A2/kg m3) | |
| Fluid temperature (K) | |
| Fluid concentration | |
| Kinematic viscosity () | |
| Porosity parameter | |
| Zero shear rate viscosity (kg/m s) | |
| Second invariant strain tensor | |
| Shear rate () | |
| Shear stress (N/) | |
| Similarity variable | |
| Stream function | |
| Local Weissenberg number | |
| Time-dependent material constant (s) | |
| Thermal conductivity (W/m K) | |
| Mixed convection parameter | |
| Stefan–Boltzmann constant | |
| Thermal expansion coefficient | |
| Concentration expansion coefficient | |
References
- Nadeem, S.; Hussain, A.; Khan, M. HAM solutions for boundary layer flow in the region of the stagnation point towards a stretching sheet. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 475–481. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Stagnation-point flow over a stretching/shrinking in a nanofluid. Nanoscale Res. Lett. 2011, 6, 623. [Google Scholar] [CrossRef] [PubMed]
- Pal, D.; Mandal, G. Mixed convection-radiation on stagnation point flow of nanofluid over a stretching/shrinking sheet in a porous medium with heat generation and viscous dissipation. J. Pet. Sci. Eng. 2015, 126, 16–25. [Google Scholar] [CrossRef]
- Zaimi, K.; Ishak, A. Stagnation-point flow towards a stretching vertical sheet with slip effects. Mathematics 2016, 4, 27. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A. Stagnation point flow of hyperbolic tangent fluid with Soret-Dufour effects. Results Phys. 2017, 7, 2711–2717. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Alsaedi, A. Activation energy impact in nonlinear radiative stagnation point flow of cross nanofluid. Int. Commun. Heat Mass Transf. 2018, 91, 216–224. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Rashidi, M.M.; Hafidzuddin, E.H.; Wahi, N. Magnetohydrodynamics (MHD) stagnation point flow past a shrinking/stretching surface with double stratification effect in a porous medium. J. Therm. Anal. Calorim. 2019, 139, 3635–3648. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Eslami, F.; Mehmandoust, B. Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches. Comput. Math. Appl. 2019, 77, 662–692. [Google Scholar] [CrossRef]
- Adigun, J.A.; Adeniyan, A.; Abiala, I.O. Stagnation point MHD slip-flow of viscoelastic nanomaterial over a stretched inclined cylindrical surface in a porous medium with dual stratification. Int. Commun. Heat Mass Transf. 2021, 126, 105479. [Google Scholar] [CrossRef]
- Arshad, K.; Ashraf, M. MHD stagnation point flow of hyperbolic tangent fluid with viscos dissipation and chemical reaction. J. Sci. Arts 2021, 21, 569–588. [Google Scholar] [CrossRef]
- Ali, F.; Reddy, C.S.; Zaib, A. 3D flow of MHD tangent hyperbloic nanoliquid with the combined effect of soret and dufour effect past a heated convective stretching sheet. Int. J. Hydrol. 2022, 6, 108–116. [Google Scholar] [CrossRef]
- Babu, B.H.; Rao, P.S.; Varma, S.V.K. Heat and Mass Transfer on Unsteady Magnetohydrodynamics (MHD) Convective Flow of Casson Hybrid Nanofluid Over a Permeable Media with Ramped Wall Temperature. J. Nanofluids 2022, 11, 552–562. [Google Scholar] [CrossRef]
- Venkateswarlu, S.; Varma, S.V.K.; Durga Prasad, P. MHD Flow of MoS2 and MgO water-based nanofluid through porous medium over a stretching surface with Cattaneo-Christov heat flux model and convective boundary condition. Int. J. Ambient. Energy 2022, 43, 2940–2949. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Ishak, A. Mixed convection flow along a stretching cylinder in a thermally stratified medium. J. Appl. Math. 2012, 2012, 491695. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, T.; Shehzad, S.A.; Alsaedi, A. Thermal and concentration stratifications effects in radiative flow of Jeffrey fluid over a stretching sheet. PLoS ONE 2014, 9, e107858. [Google Scholar] [CrossRef]
- Malik, M.Y.; Salahuddin, T.; Hussain, A.; Bilal, S. MHD flow of tangent hyperbolic fluid over a stretching cylinder: Using Keller box method. J. Magn. Magn. Mater. 2015, 395, 271–276. [Google Scholar] [CrossRef]
- Rehman, K.U.; Qaiser, A.; Malik, M.Y.; Ali, U. Numerical communication for MHD thermally stratified dual convection flow of Casson fluid yields by stretching cylinder. Chin. J. Phys. 2017, 55, 1605–1614. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D. Effects of thermal and solutal stratification on Jeffrey magneto-nanofluid along an inclined stretching cylinder with thermal radiation and heat generation/absorption. Int. J. Mech. Sci. 2017, 131, 317–324. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, A.; Salahuddin, T.; Ali, S. Chemically reactive flow of hyperbolic tangent fluid flow having thermal radiation and double stratification embedded in porous medium. Ain Shams Eng. J. 2021, 12, 3209–3216. [Google Scholar] [CrossRef]
- Faisal, M.; Asogwa, K.K.; Alessa, N.; Loganathan, K. Nonlinear Radiative Nanofluidic Hydrothermal Unsteady Bidirectional Transport with Thermal/Mass Convection Aspects. Symmetry 2022, 14, 2609. [Google Scholar] [CrossRef]
- Miansari, M.; Darvishi, M.R.; Toghraie, D.; Barnoon, P.; Shirzad, M.; Alizadeh, A.A. Numerical investigation of grooves effects on the thermal performance of helically grooved shell and coil tube heat exchanger. Chin. J. Chem. Eng. 2022, 44, 424–434. [Google Scholar] [CrossRef]
- Kayikci, S.; Eswaramoorthi, S.; Postalcioglu, S.; Loganathan, K. Thermal analysis of radiative water-and glycerin-based carbon nanotubes past a Riga plate with stratification and non-Fourier heat flux theory. J. Therm. Anal. Calorim. 2023, 148, 533–549. [Google Scholar] [CrossRef]
- Nadeem, S.; Maraj, E.N. The mathematical analysis for peristaltic flow of hyperbolic tangent fluid in a curved channel. Commun. Theor. Phys. 2013, 59, 729. [Google Scholar] [CrossRef]
- Naseer, M.; Malik, M.Y.; Nadeem, S.; Rehman, A. The boundary layer flow of hyperbolic tangent fluid over a vertical exponentially stretching cylinder. Alex. Eng. J. 2014, 53, 747–750. [Google Scholar] [CrossRef]
- Salahuddin, T.; Malik, M.Y.; Hussain, A.; Awais, M.; Khan, I.; Khan, M. Analysis of tangent hyperbolic nanofluid impinging on a stretching cylinder near the stagnation point. Results Phys. 2017, 7, 426–434. [Google Scholar] [CrossRef]
- Rehman, K.U.; Alshomrani, A.S.; Malik, M.Y.; Zehra, I.; Naseer, M. Thermo-physical aspects in tangent hyperbolic fluid flow regime: A short communication. Case Stud. Therm. Eng. 2018, 12, 203–212. [Google Scholar] [CrossRef]
- Rao, M.V.S.; Gangadhar, K.; Lorenzini, G.A. Computational analysis for boundary layer flow of magneto hydrodynamic tangent hyperbolic fluid of heat and mass transfer past a stretching cylinder with suction/injection using spectral relaxation method. Math. Model. Eng. Probl. 2019, 6, 38–46. [Google Scholar] [CrossRef]
- Saidulu, N.; Gangaiah, T.; Lakshmi, A.V. Radiation effect on MHD flow of a tangent hyperbolic nanofluid over an inclined exponentially stretching sheet. Int. J. Fluid Mech. Res. 2019, 46, 277–293. [Google Scholar] [CrossRef]
- Ali, A.; Hussain, R.; Maroof, M. Inclined hydromagnetic impact on tangent hyperbolic fluid flow over a vertical stretched sheet. AIP Adv. 2019, 9, 125022. [Google Scholar] [CrossRef]
- Bilal, S.; Shah, Z.; Kumam, P.; Thounthong, P. Mathematical and Engineering Aspects of Chemically Reactive Tangent Hyperbolic Nanofluid over a Cone and Plate with Mixed Convection. Math. Probl. Eng. 2020, 2020, 9090185. [Google Scholar] [CrossRef]
- Salahuddin, T.; Tanveer, A.; Malik, M.Y. Homogeneous–heterogeneous reaction effects in flow of tangent hyperbolic fluid on a stretching cylinder. Can. J. Phys. 2020, 98, 125–129. [Google Scholar] [CrossRef]
- Jat, K.; Sharma, K. Unsteady MHD flow of Tangent Hyperbolic Nanofluid over an Inclined Stretching Sheet and Heat Transfer Analysis. NanoWorld J. 2022, 8 (Suppl. S1), S104–S110. [Google Scholar] [CrossRef]
- Patil, P.M.; Roy, S.; Chamkha, A.J. Mixed convection flow over a vertical power-law stretching sheet. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 445–458. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Mixed convection stagnation-point flow on vertical stretching sheet with external magnetic field. Appl. Math. Mech. 2014, 35, 155–166. [Google Scholar] [CrossRef]
- Kumar, G.K.; Gireesha, B.J.; Manjunatha, S.; Rudraswamy, N.G. Effect of nonlinear thermal radiation on double-diffusive mixed convection boundary layer flow of viscoelastic nanofluid over a stretching sheet. Int. J. Mech. Mater. Eng. 2017, 12, 18. [Google Scholar] [CrossRef]
- Abdul Halim, N.; Mohd Noor, N.F. Mixed convection flow of Powell–Eyring nanofluid near a stagnation point along a vertical stretching sheet. Mathematics 2021, 9, 364. [Google Scholar] [CrossRef]
- Barnoon, P. Numerical assessment of heat transfer and mixing quality of a hybrid nanofluid in a microchannel equipped with a dual mixer. Int. J. 2021, 12, 100111. [Google Scholar] [CrossRef]
- Babu, B.; Srinivasa Rao, P.; Varma, S.V.K. Hall and ion-slip effects on MHD free convection flow of rotating Jeffrey fluid over an infinite vertical porous surface. Heat Transf. 2021, 50, 1776–1798. [Google Scholar] [CrossRef]
- Saeed, A.; Algehyne, E.A.; Aldhabani, M.S.; Dawar, A.; Kumam, P.; Kumam, W. Mixed convective flow of a magnetohydrodynamic Casson fluid through a permeable stretching sheet with first-order chemical reaction. PLoS ONE 2022, 17, e0265238. [Google Scholar] [CrossRef]
- Ullah, Z.; Zaman, G. Lie group analysis of magnetohydrodynamic tangent hyperbolic fluid flow towards a stretching sheet with slip conditions. Heliyon 2017, 3, e00443. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical solutions of magnetohydrodynamic boundary layer flow of tangent hyperbolic fluid towards a stretching sheet. Indian J. Phys. 2013, 87, 1121–1124. [Google Scholar] [CrossRef]


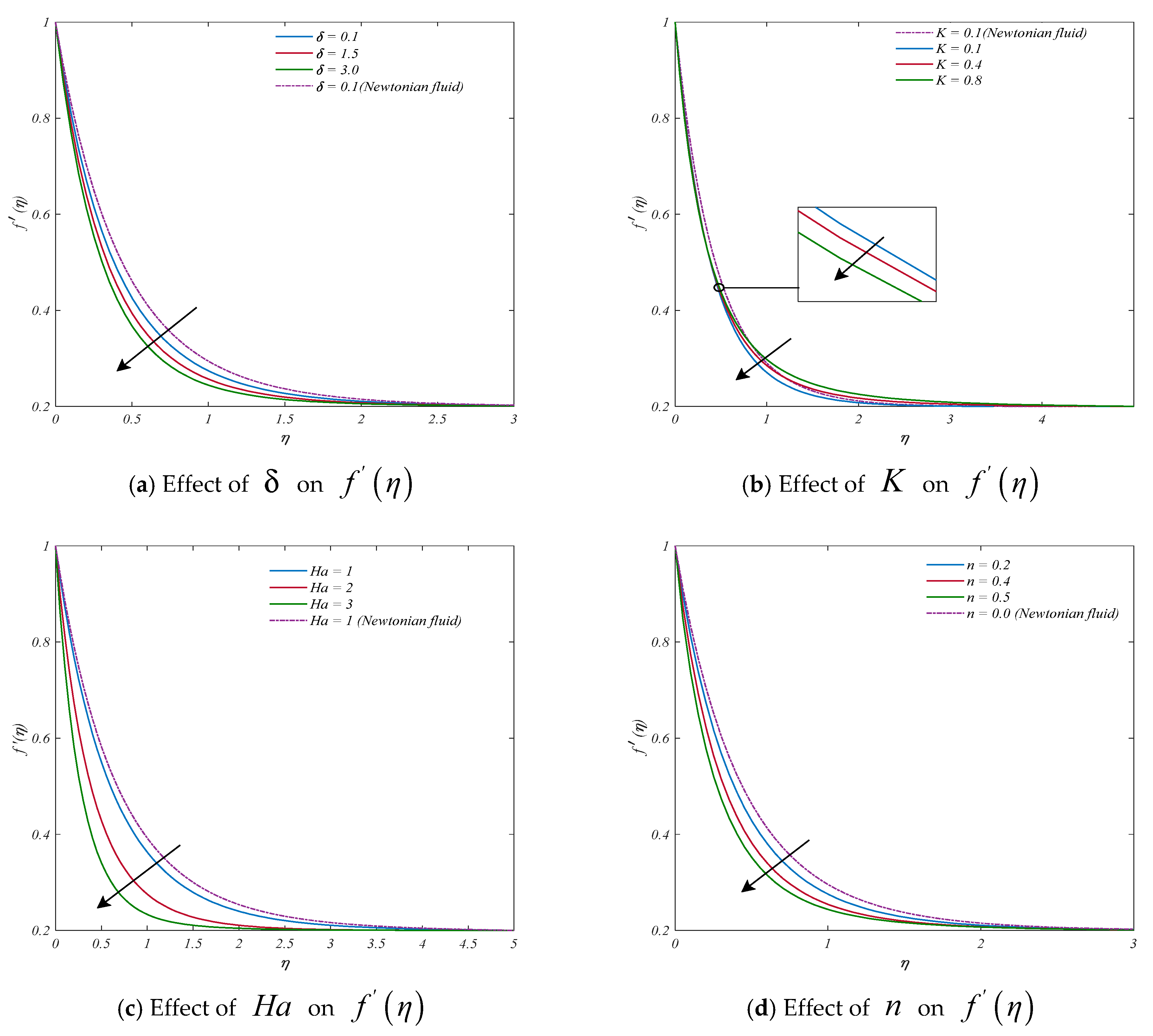












| Present Outcomes | Rehman et al. [26] | Akbar et al. [41] | |||
|---|---|---|---|---|---|
| RK 4 | Bvp5c | ||||
| 0 | 0 | −1.000000 | −1.0000 | −1.0000 | −1.00000 |
| 0 | 0.3 | −1.000000 | −1.0000 | −1.0000 | −1.00000 |
| 0 | 0.5 | −1.000000 | −1.0000 | −1.0000 | −1.00000 |
| 0.1 | 0 | −0.948942 | −0.9482 | −0.9491 | −0.94868 |
| 0.1 | 0.3 | −0.925459 | −0.9244 | −0.9432 | −0.94248 |
| 0.1 | 0.5 | −0.909298 | −0.9087 | −0.9380 | −0.93826 |
| 0.2 | 0 | −0.894632 | −0.8937 | −0.8944 | −0.89442 |
| 0.2 | 0.3 | −0.840709 | −0.8398 | −0.8805 | −0.88023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choudhary, S.; Choudhary, P.; Alessa, N.; Loganathan, K. MHD Thermal and Solutal Stratified Stagnation Flow of Tangent Hyperbolic Fluid Induced by Stretching Cylinder with Dual Convection. Mathematics 2023, 11, 2182. https://doi.org/10.3390/math11092182
Choudhary S, Choudhary P, Alessa N, Loganathan K. MHD Thermal and Solutal Stratified Stagnation Flow of Tangent Hyperbolic Fluid Induced by Stretching Cylinder with Dual Convection. Mathematics. 2023; 11(9):2182. https://doi.org/10.3390/math11092182
Chicago/Turabian StyleChoudhary, Sushila, Prasun Choudhary, Nazek Alessa, and Karuppusamy Loganathan. 2023. "MHD Thermal and Solutal Stratified Stagnation Flow of Tangent Hyperbolic Fluid Induced by Stretching Cylinder with Dual Convection" Mathematics 11, no. 9: 2182. https://doi.org/10.3390/math11092182
APA StyleChoudhary, S., Choudhary, P., Alessa, N., & Loganathan, K. (2023). MHD Thermal and Solutal Stratified Stagnation Flow of Tangent Hyperbolic Fluid Induced by Stretching Cylinder with Dual Convection. Mathematics, 11(9), 2182. https://doi.org/10.3390/math11092182







