Partial Slip Effects for Thermally Radiative Convective Nanofluid Flow
Abstract
1. Introduction
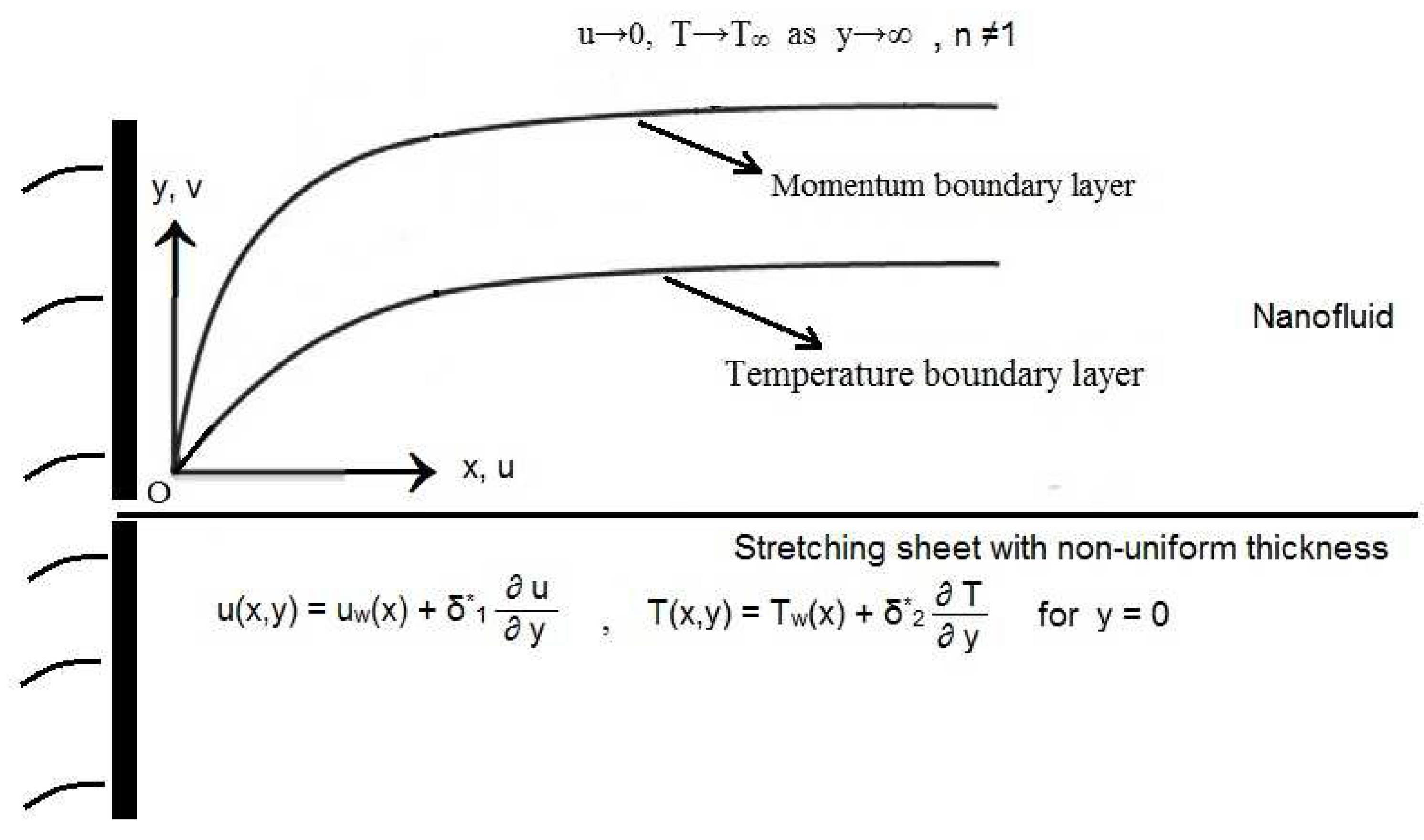
2. Theoretical Approach
2.1. Equations of Motion
2.2. Steps of the Modified Optimal Homotopy Asymptotic Method (OHAM)
3. Heat and Mass Transfer Problem by the Modified OHAM
4. Numerical Results and Discussion
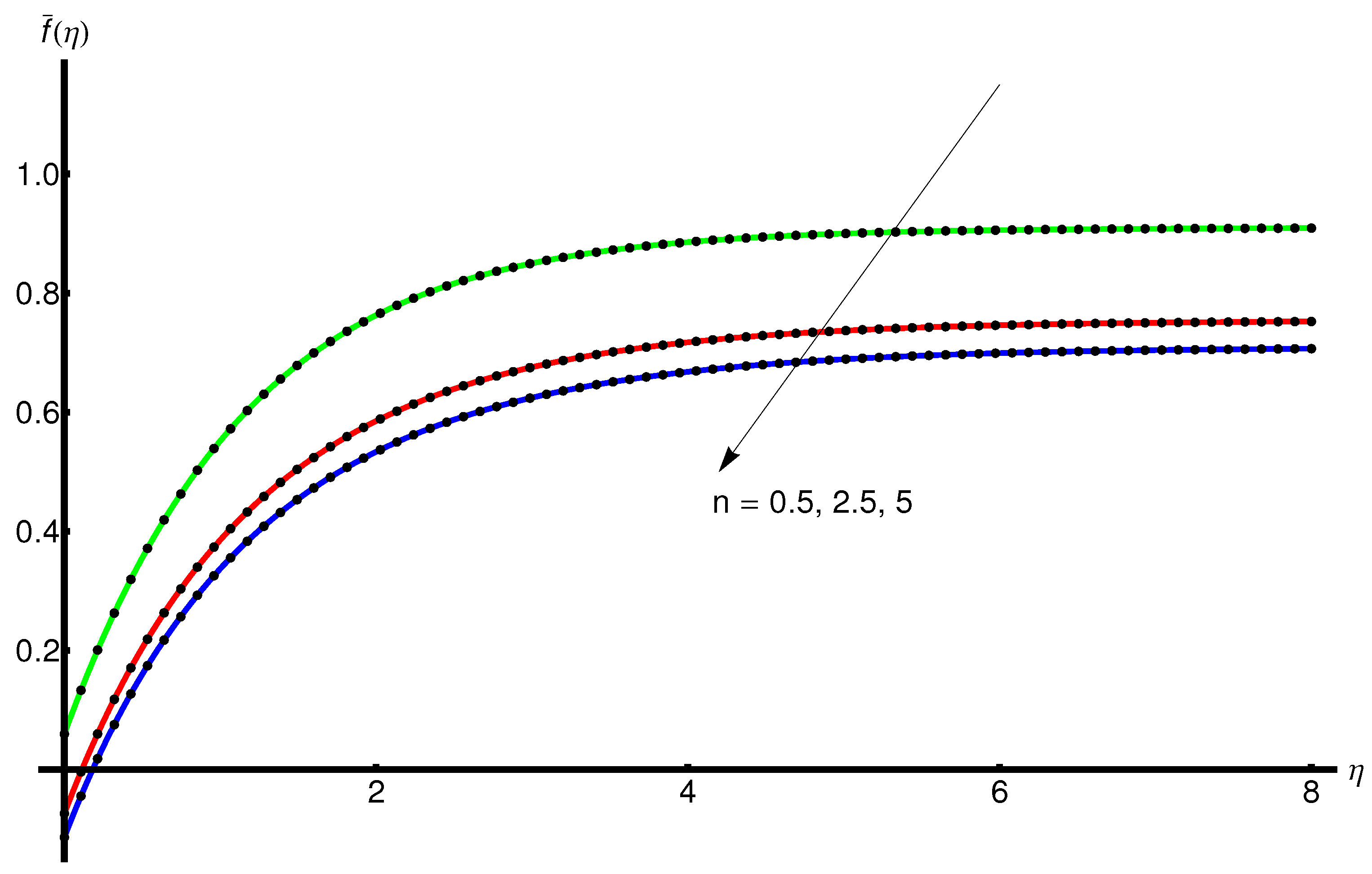
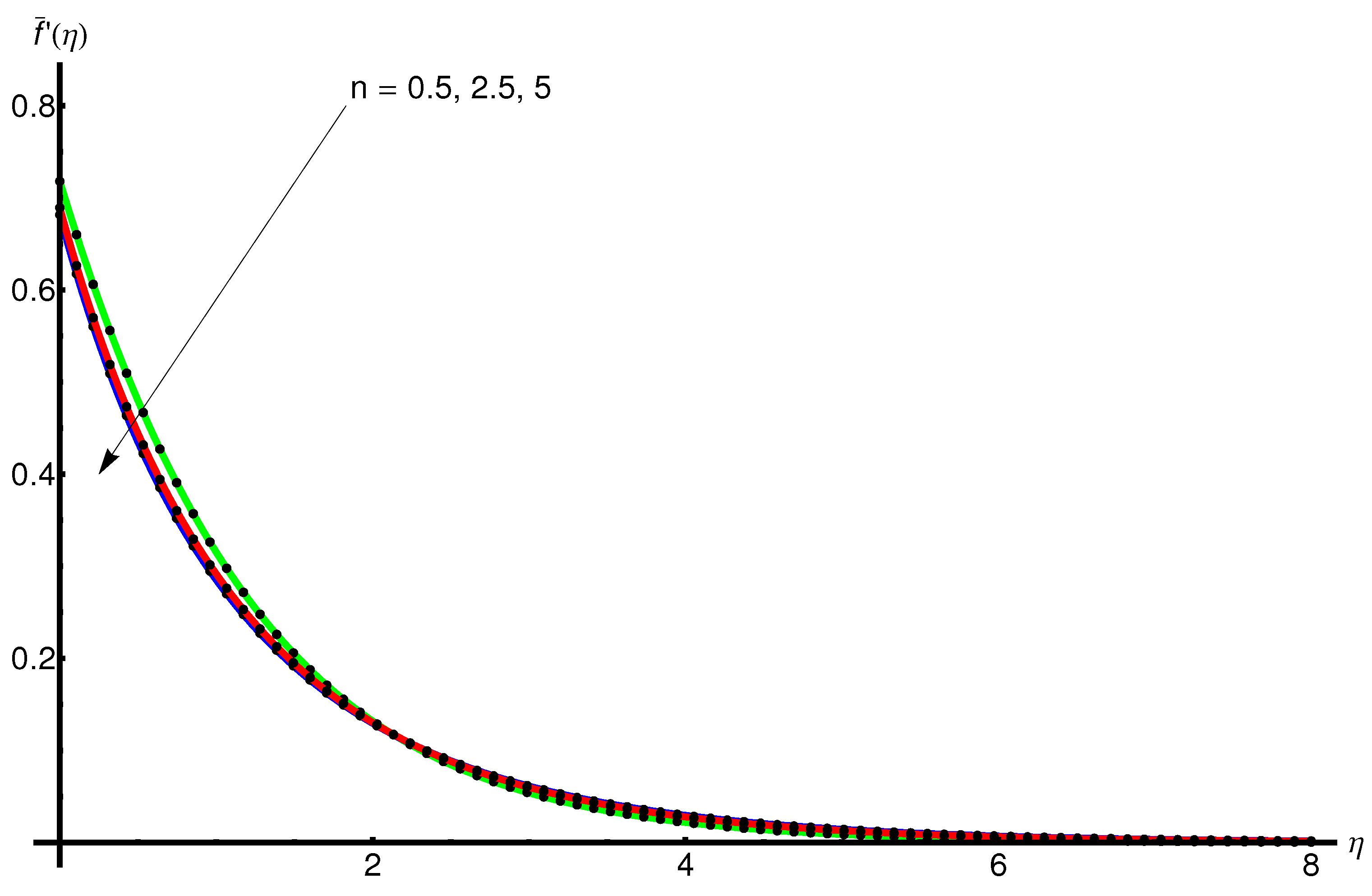
4.1. Influence of the Parameter n
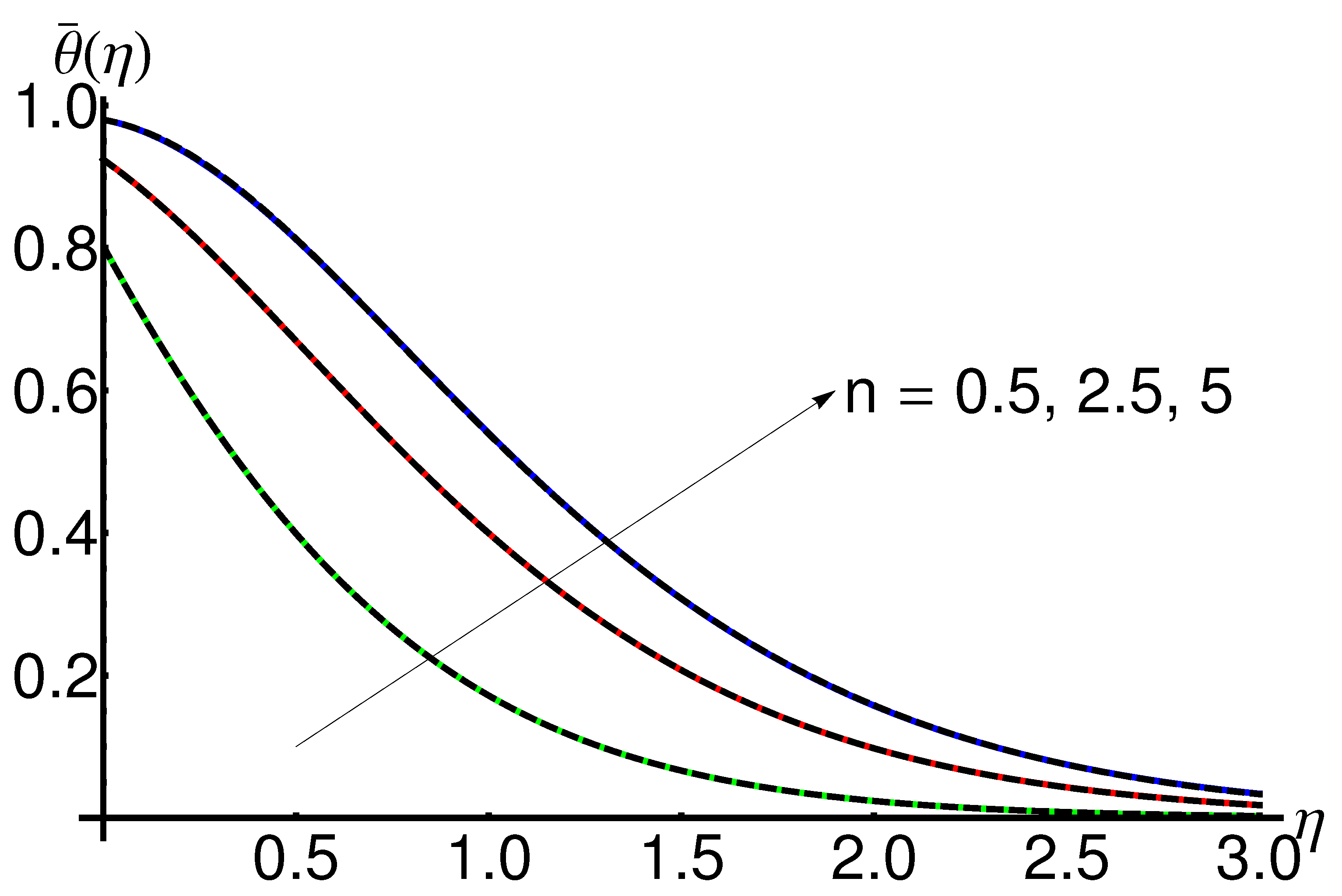
4.2. Influence of the Wall Thickness Parameter
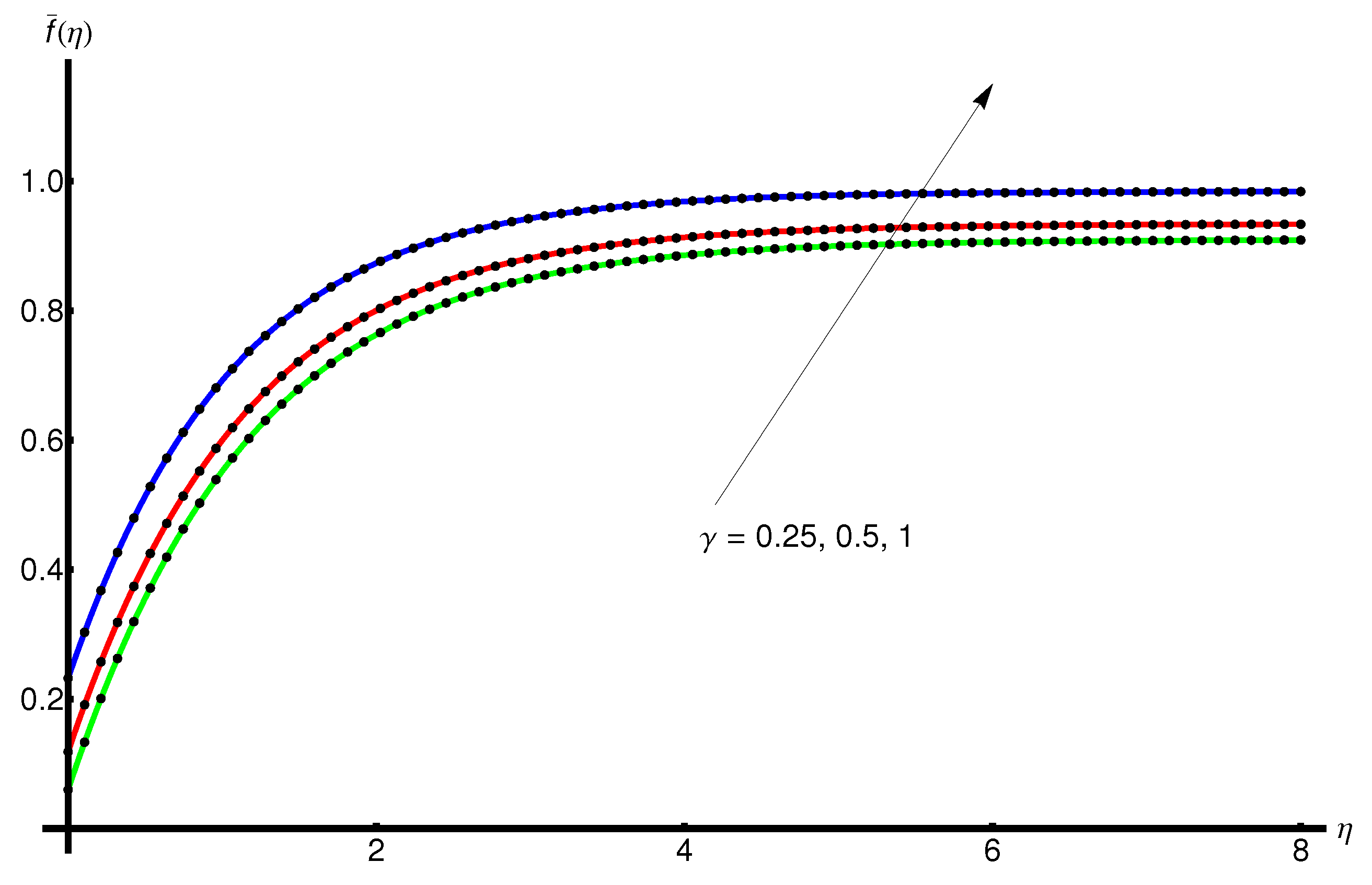
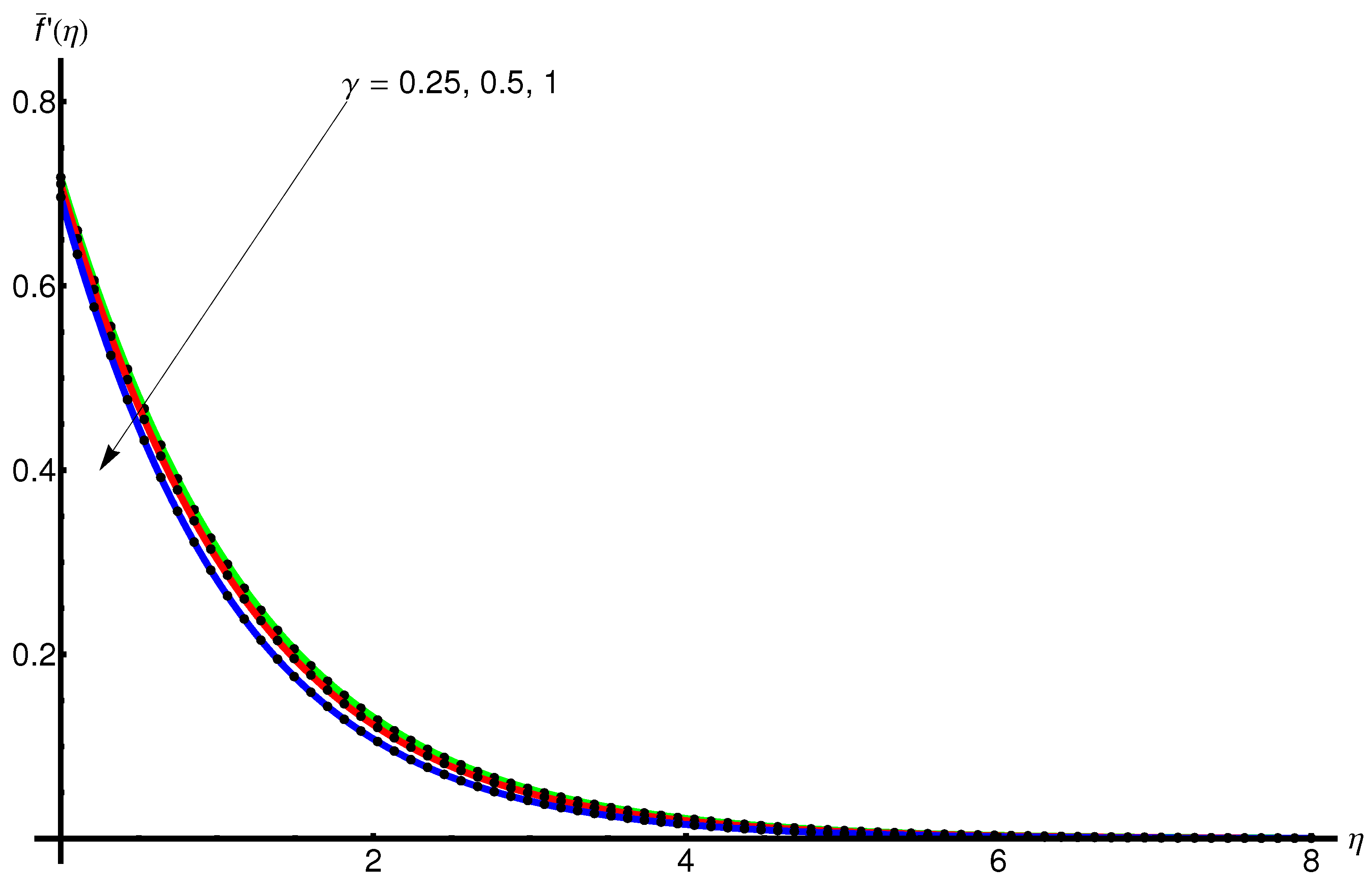
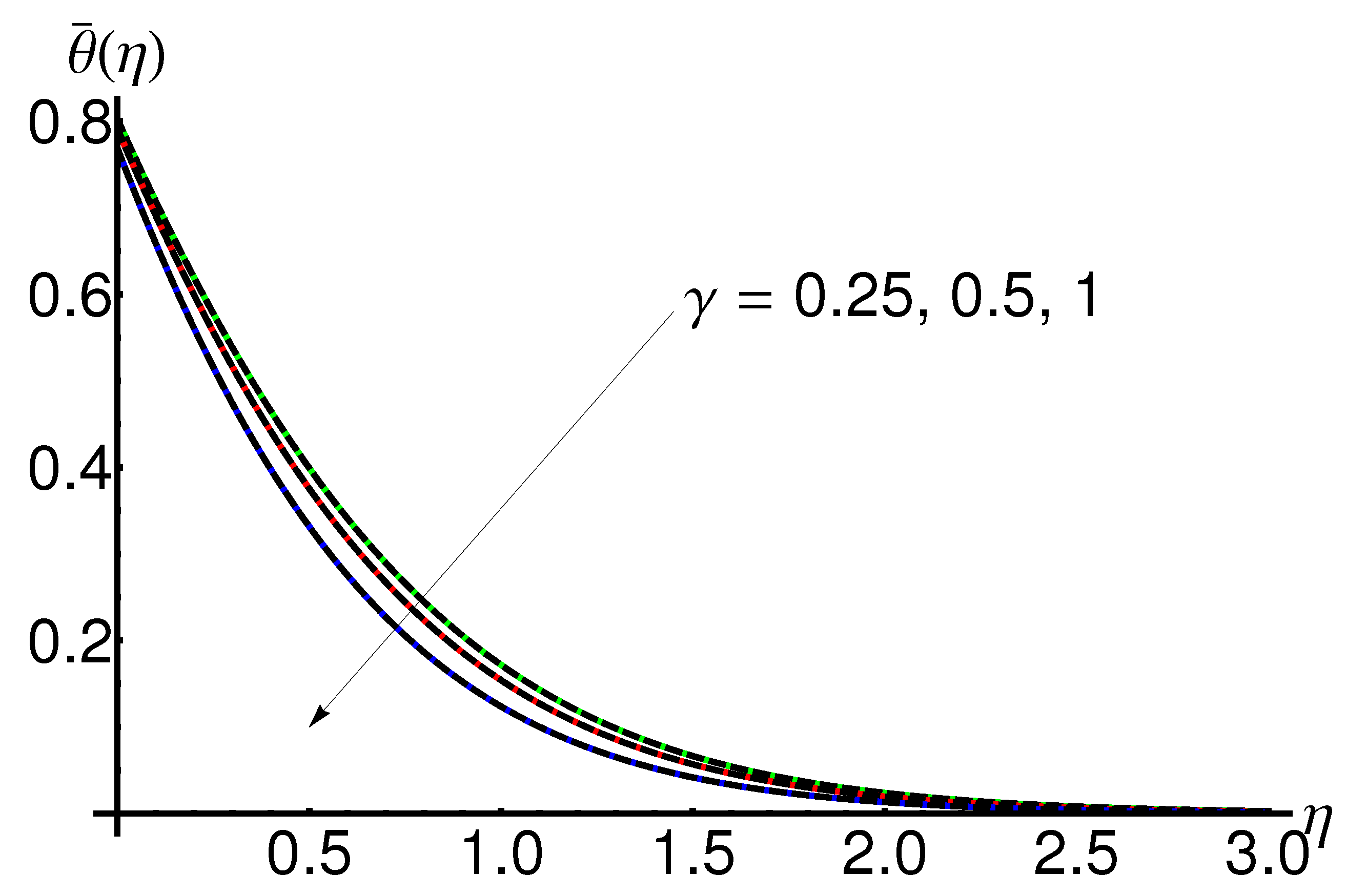
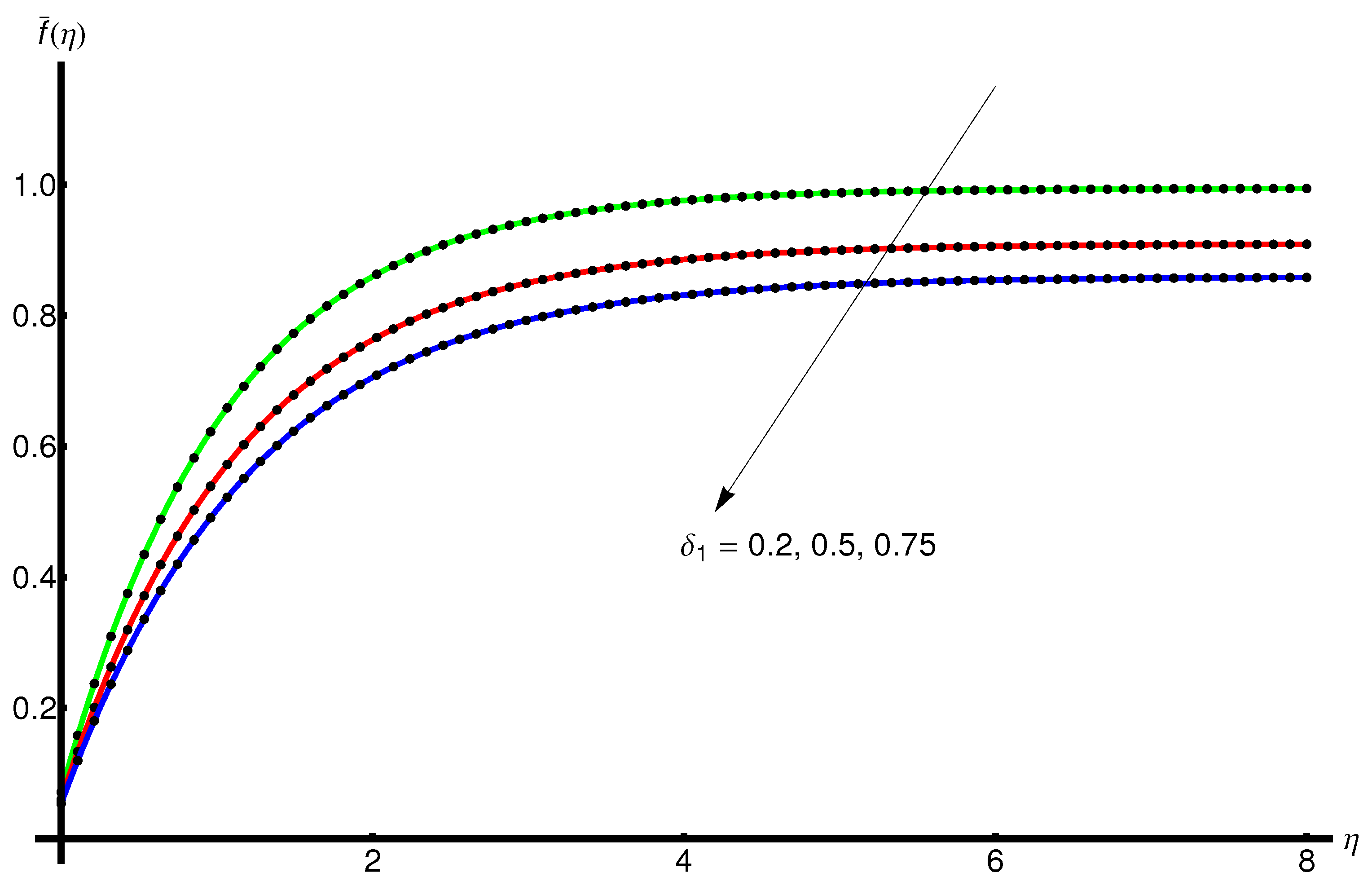
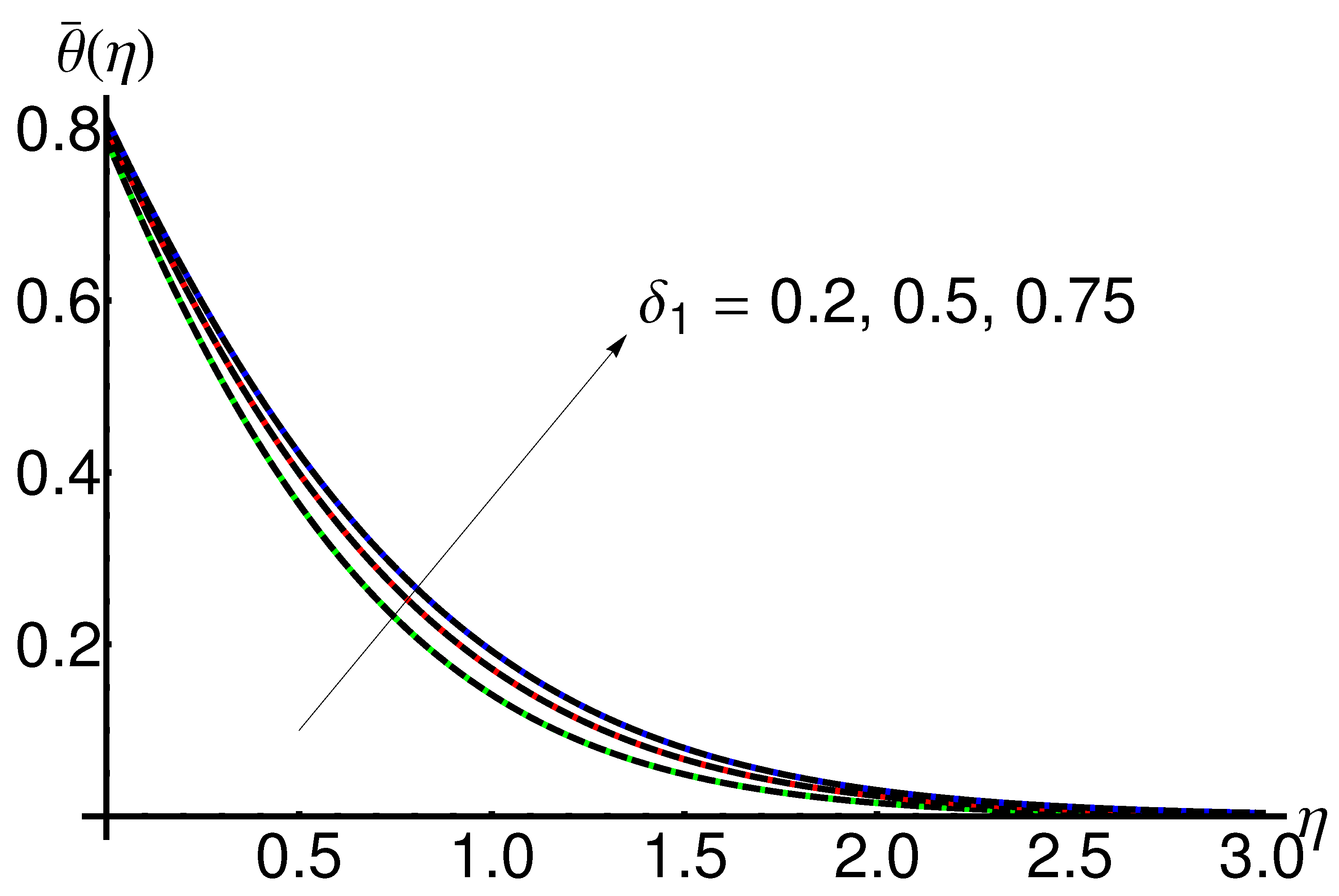
4.3. Influence of the Slip Parameter

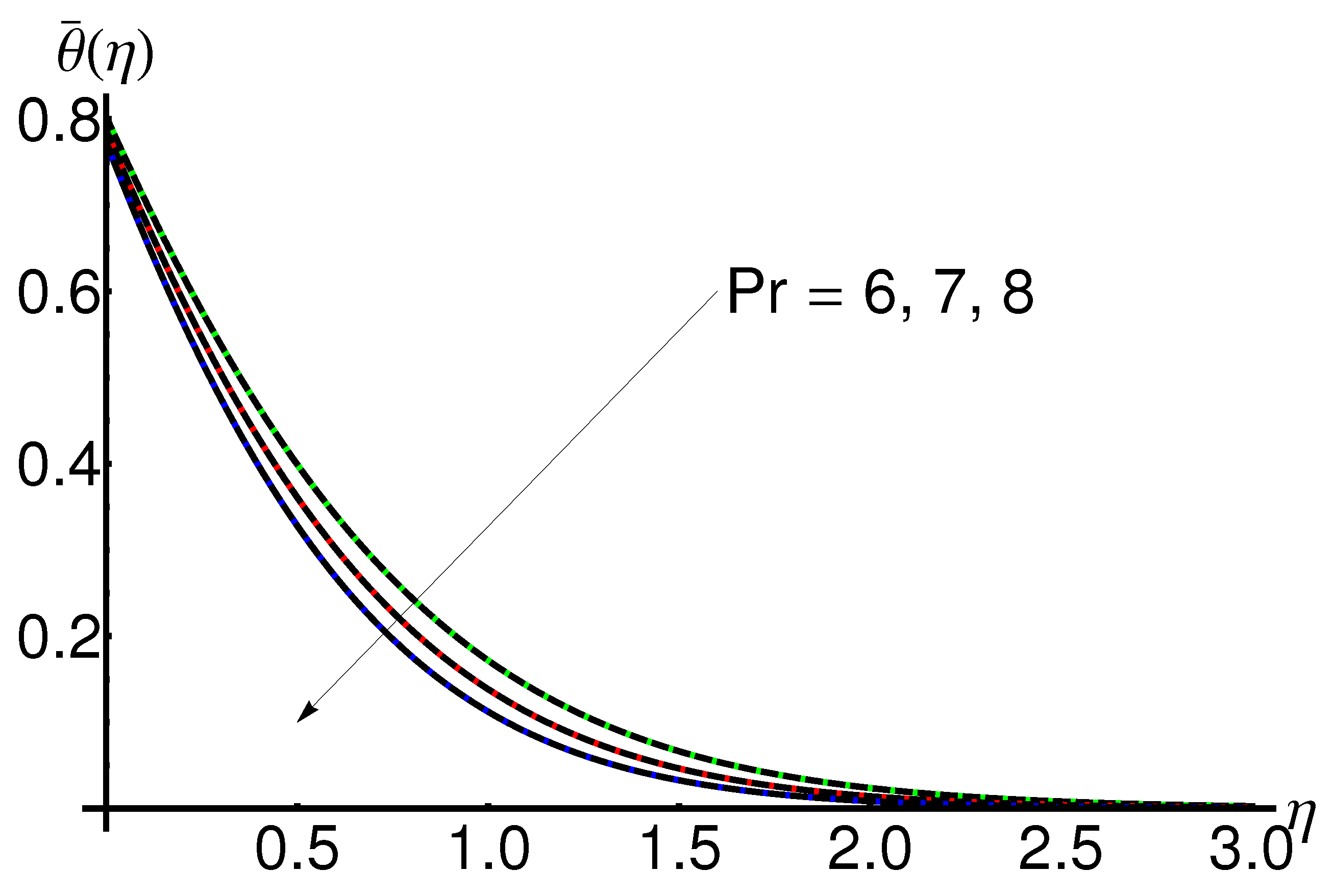
4.4. Influence of the Prandtl Number
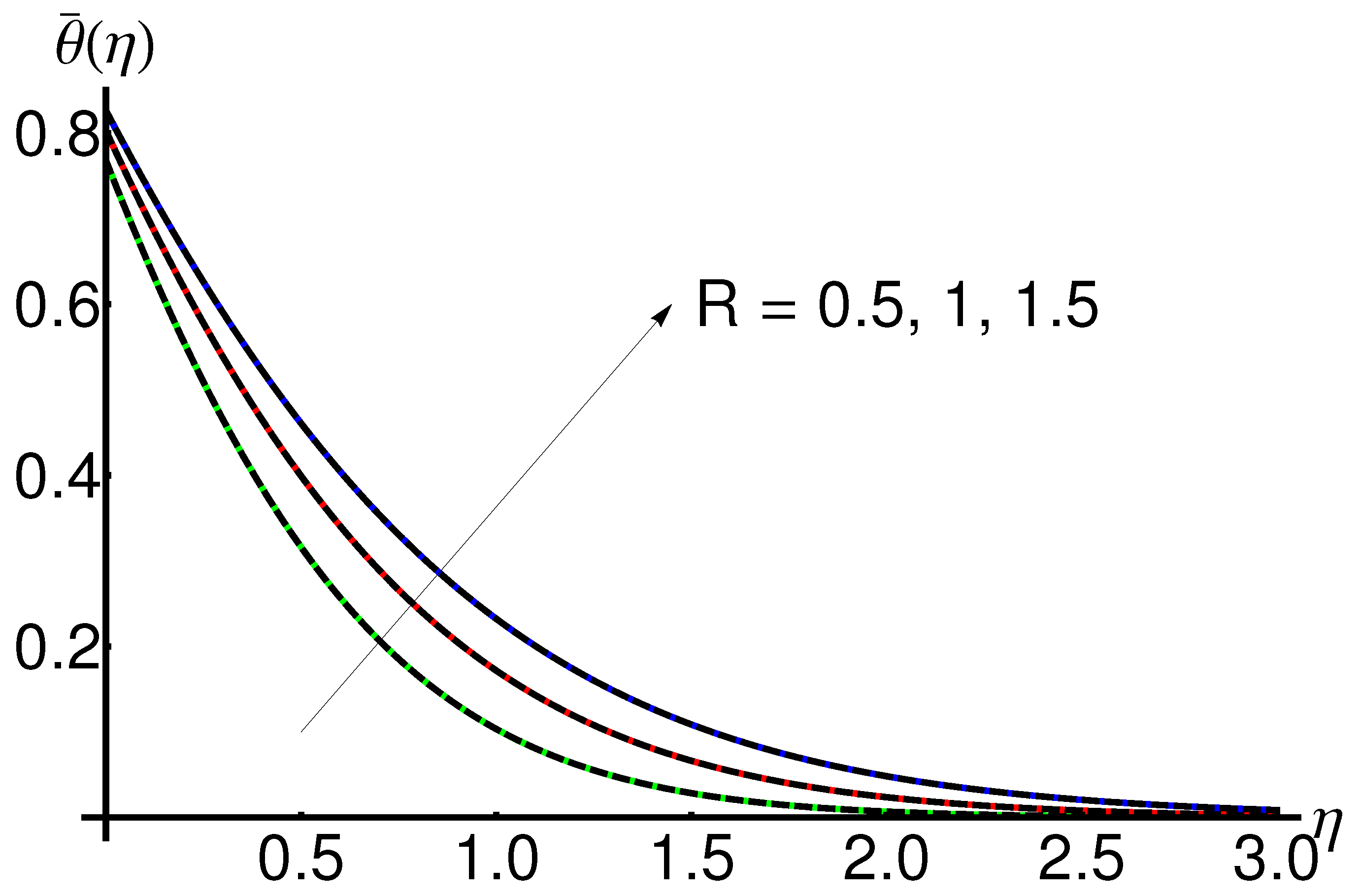
4.5. Influence of the Radiation Parameter R
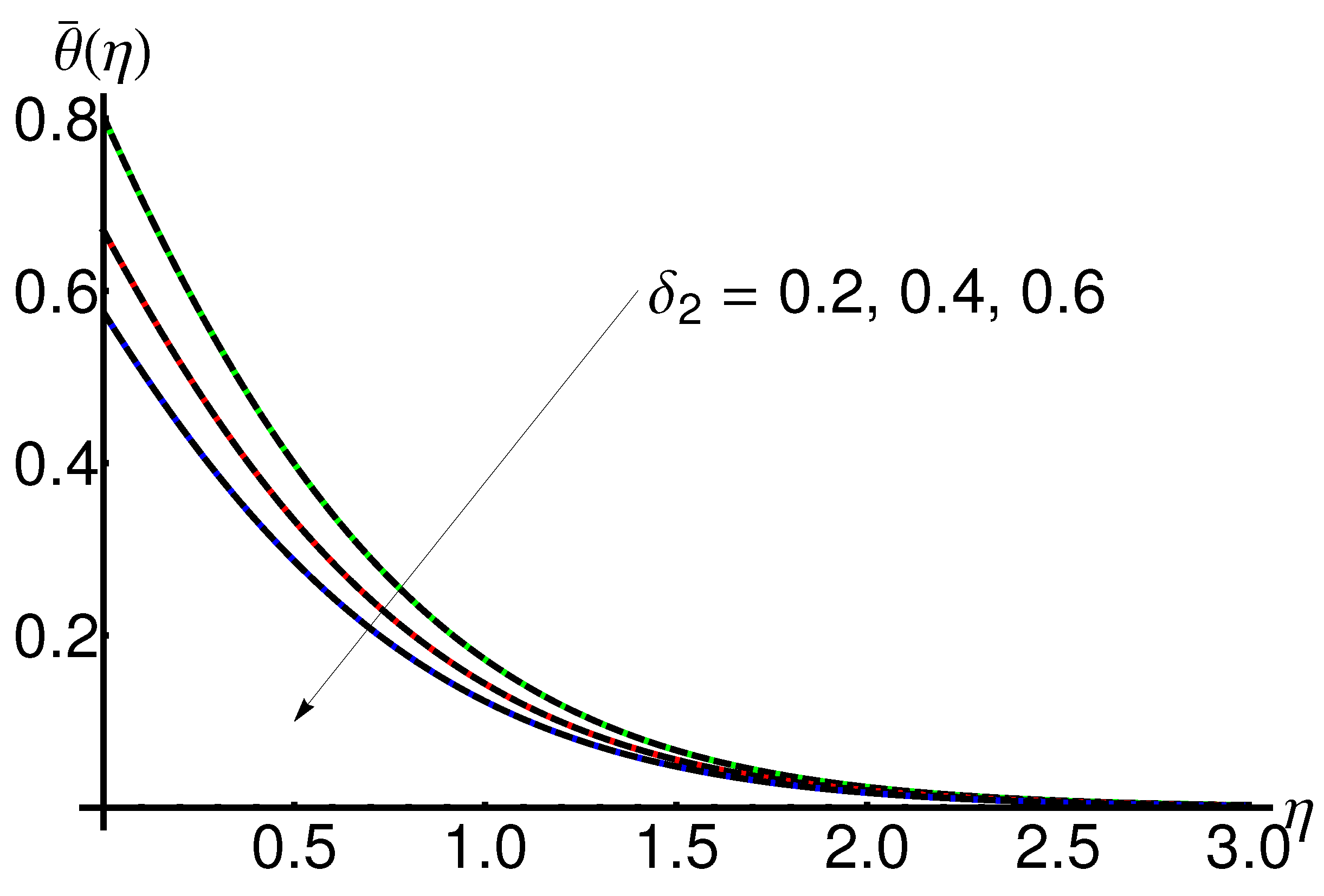
4.6. Influence of the Slip Thermal Parameter
4.7. OHAM Solutions versus Iterative Solutions
5. Conclusions
- The effect of the increasing n enhances the stretching velocity and implies the elevation of the velocity boundary layer. Moreover, the temperature of the base fluid increases with n, leading the thickness of the thermal layer to increase;
- If the wall thickness parameter increases, then the flow characteristics are considerably reduced and the temperature gradient is lowered;
- An increase in the radiation parameter R causes an increase in the thickness of the thermal boundary layer supplying more heat to the base fluid;
- An increase in the dimensionless temperature jump parameter generates a high surface temperature, decreasing fluid conductance and increasing the thickness of the temperature profile;
- The influence of Prandtl number on the temperature field in the presence/absence of joule heating is significant. The temperature and thermal boundary layer thickness were found to decrease;
- An increase in the velocity slip parameter implies a decrease in the boundary layer thickness, and a decrease in variation in the thermal boundary layer thickness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature/Notation
| Symbols | Names |
| u, | Velocity components |
| x, | Cartesian coordinates |
| n | the velocity power index parameter |
| Non-uniform permeability | |
| Coefficient related to non-uniform permeability | |
| Velocity at the wall | |
| Wall temperature | |
| Environment temperature | |
| , | Reference velocity and reference temperature |
| A | Coefficient related to stretching sheet |
| Kinematical viscosity | |
| T | Temperature of the fluid |
| k | Thermal conductivity |
| Thermal diffusivity of the nanofluid | |
| Specific heat capacitance | |
| Dimensional velocity slip parameter | |
| Dimensional temperature jump parameter | |
| b | the Maxwell’s reflection coefficient |
| c | the thermal accommodation coefficient |
| the ratio of specific heats | |
| , | the mean free paths |
| Radiative heat flux | |
| the Stefan-Boltzmann constant | |
| the mean absorption coefficient | |
| Prandtl number | |
| R | Radiation parameter |
| the wall thickness parameter | |
| the dimensionless velocity slip parameter | |
| the dimensionless temperature jump parameter | |
| Reynolds number | |
| Independent dimensionless variable | |
| Stream function | |
| Temperature | |
| , | approximate analytical solution by means of the |
| modified Optimal Homotopy Asymptotic Method, called OHAM solutions |
Appendix A
References
- Vishalakshi, A.B.; Maranna, T.; Shettar Mahabaleshwar, U.; Laroze, D. An Effect of MHD on Non–Newtonian Fluid Flow over a Porous Stretching/Shrinking Sheet with Heat Transfer. Appl. Sci. 2022, 12, 4937. [Google Scholar] [CrossRef]
- Maranna, T.; Sneha, K.N.; Mahabaleshwar, U.S.; Sarris, I.E.; Karakasidis, T.E. An Effect of Radiation and MHD Newtonian Fluid over a Stretching/Shrinking Sheet with CNTs and Mass Transpiration. Appl. Sci. 2022, 12, 5466. [Google Scholar] [CrossRef]
- Sarma, S.; Ahmed, N. Thermal Diffusion Effect on Unsteady MHD Free Convective Flow Past a Semi- Infinite Exponentially Accelerated Vertical Plate in a Porous Medium. Can. J. Phys. 2022, 100, 437–451. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Anusha, T.; Laroze, D.; Said, N.M.; Sharifpur, M. An MHD Flow of Non–Newtonian Fluid Due to a Porous Stretching/Shrinking Sheet with Mass Transfer. Sustainability 2022, 14, 7020. [Google Scholar] [CrossRef]
- Akhtar, S.; Almutairi, S.; Nadeem, S. Impact of heat and mass transfer on the Peristaltic flow of non-Newtonian Casson fluid inside an elliptic conduit: Exact solutions through novel technique. Chin. J. Phys. 2022, 78, 194–206. [Google Scholar] [CrossRef]
- Safdar, M.; Ijaz Khan, M.; Khan, R.A.; Taj, S.; Abbas, F.; Elattar, S.; Galal, A.M. Analytic solutions for the MHD flow and heat transfer in a thin liquid film over an unsteady stretching surface with Lie symmetry and homotopy analysis method. Waves Random Complex Media 2022, 33, 442–460. [Google Scholar] [CrossRef]
- Krishna, M.V. Analytical study of chemical reaction, Soret, Hall and ion slip effects on MHD flow past an infinite rotating vertical porous plate. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Reddy, Y.D.; Mebarek-Oudina, F.; Goud, B.S.; Ismail, A.I. Radiation, Velocity and Thermal Slips Effect Toward MHD Boundary Layer Flow Through Heat and Mass Transport of Williamson Nanofluid with Porous Medium. Arab. J. Sci. Eng. 2022, 47, 16355–16369. [Google Scholar] [CrossRef]
- Abbas, A.; Jeelani, M.B.; Alharthi, N.H. Darcy-Forchheimer Relation Influence on MHD Dissipative Third-Grade Fluid Flow and Heat Transfer in Porous Medium with Joule Heating Effects: A Numerical Approach. Processes 2022, 10, 906. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A.; Asker, H.G. Fluid flow over a vertical stretching surface within a porous medium filled by a nanofluid containing gyrotactic microorganisms. Eur. Phys. J. Plus 2022, 137, 541. [Google Scholar] [CrossRef]
- Nuwairan, M.A.; Hafeez, A.; Khalid, A.; Syed, A. Heat generation/absorption effects on radiative stagnation point flow of Maxwell nanofluid by a rotating disk influenced by activation energy. Case Stud. Therm. Eng. 2022, 35, 102047. [Google Scholar] [CrossRef]
- Abbas, N.; UrRehman, K.; Shatanawi, W.; Malik, M.Y. Numerical study of heat transfer in hybrid nanofluid flow over permeable nonlinear stretching curved surface with thermal slip. Int. Commun. Heat Mass Transf. 2022, 135, 106107. [Google Scholar] [CrossRef]
- Hossein, S.; Ahmadi, N.; Jabbary, A. Effects of applying brand-new designs on the performance of PEM fuel cell and water flooding phenomena. Iran. J. Chem. Chem. Eng. 2022, 41, 618–634. [Google Scholar]
- Aziz, T.; Aziz, A.; Shams, M.; Bahaidarah, H.M.S.; Alie, H. Entropy analysis with the Cattaneo-Christov heat flux model for the Powell-Eyring nanofluid flow over a stretching surface. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Jena, S.; Mishra, S.R.; Aghaeiboorkheili, M.; Pattnaik, P.K.; Muduli, K. Impact of Newtonian heating on the conducting Casson fluid flow past a stretching cylinder. J. Interdiscip. Math. 2022, 25, 2401–2416. [Google Scholar] [CrossRef]
- Sultana, U.; Mushtaq, M.; Muhammad, T. Numerical simulation for stagnation-point flow of nanofluid over a spiraling disk through porous media. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Gul, T.; Saeed, A. Nonlinear mixed convection couple stress tri-hybrid nanofluids flow in a Darcy-Forchheimer porous medium over a nonlinear stretching surface. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Khan, M.R.; Algarni, S.; Alqahtani, T.; Alsallami, S.A.M.; Saeed, T.; Galal, A.M. Numerical analysis of a time-dependent aligned MHD boundary layer flow of a hybrid nanofluid over a porous radiated stretching/shrinking surface. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Rasool, G.; Shah, N.A.; El-Zahar, E.R.; Wakif, A. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Reddy, P.B.A.; Jakeer, S.; Basha, H.T.; Reddy, S.R.; Kumar, T.M. Multi-layer artificial neural network modeling of entropy generation on MHD stagnation point flow of Cross-nanofluid. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Fadaei, M.; Izadi, M.; Assareh, E.; Ershadi, A. Melting process of PCM with Carreau—Yasuda non-Newtonian behavior in a shell and tube heat exchanger occupied by anisotropic porous medium. Int. J. Numer. Heat Fluid Flow 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Wang, J.; Mustafa, Z.; Siddique, I.; Ajmal, M.; Jaradat, M.M.M.; Rehman, S.U.; Ali, B.; Muhammad Ali, H. Computational Analysis for Bioconvection of Microorganisms in Prandtl Nanofluid Darcy-Forchheimer Flow across an Inclined Sheet. Nanomaterials 2022, 12, 1791. [Google Scholar] [CrossRef] [PubMed]
- Abdal, S.; Siddique, I.; Din, I.S.U.; Ahmadian, A.; Hussain, S.; Salimi, M. Significance of magnetohydrodynamic Williamson Sutterby nanofluid due to a rotating cone with bioconvection and anisotropic slip. J. Appl. Math. Mech. 2022, 102, e202100503. [Google Scholar] [CrossRef]
- Wahid, N.S.; Arifin, N.; Khashi’Ie, N.S.; Pop, I.; Bachok, N.; Hafidzuddin, M.E.H. Hybrid nanofluid stagnation point flow past a slip shrinking Riga plate. Chin. J. Phys. 2022, 78, 180–193. [Google Scholar] [CrossRef]
- Meenakumari, R.; Lakshminarayana, P. MHD 3D flow of powell eyring fluid over a bidirectional non-linear stretching surface with temperature dependent conductivity and heat absorption/generation. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 236, 2580–2588. [Google Scholar] [CrossRef]
- Alharbi, K.A.M.; Khan, M.R.; Ould Sidi, M.; Algelany, A.M.; Elattar, S.; Ahammad, N.A. Investigation of hydromagnetic bioconvection flow of Oldroyd-B nanofluid past a porous stretching surface. Biomass Convers. Biorefin. 2022, 13, 4331–4342. [Google Scholar] [CrossRef]
- Krishna, M.; Vajravelu, K. Rotating MHD flow of second grade fluid through porous medium between two vertical plates with chemical reaction, radiation absorption, Hall, and ion slip impacts. Biomass Convers. Biorefin. 2022. [Google Scholar] [CrossRef]
- Tayebi, T. Analysis of the local non-equilibria on the heat transfer and entropy generation during thermal natural convection in a non-Darcy porous medium. Int. Commun. Heat Mass Transf. 2022, 135, 106133. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Stability Analysis of Unsteady Hybrid Nanofluid Flow over the Falkner-Skan Wedge. Nanomaterials 2022, 12, 1771. [Google Scholar] [CrossRef]
- Jha, B.; Samaila, G. Similarity solution for boundary layer flow near a moving vertical porous plate with combined effects of nonlinear thermal radiation and suction/injection having convective surface boundary condition. Proc. Inst. Mech. Eng. J. Mech. Eng. Sci. 2022, 236, 8926–8934. [Google Scholar] [CrossRef]
- Meena, O.P.; Janapatla, P. Mixed convection flow over a vertical cone saturated porous medium with double dispersion effect. Appl. Math. Comput. 2022, 430, 127072. [Google Scholar] [CrossRef]
- Naseem, T.; Fatima, U.; Munir, M.; Shahzad, A.; Kausar, N.; Nisar, K.S.; Saleel, C.A.; Abbas, M. Joule heating and viscous dissipation effects in hydromagnetized boundary layer flow with variable temperature. Case Stud. Therm. Eng. 2022, 35, 102083. [Google Scholar] [CrossRef]
- Veeram, G.; Poojitha, P.; Katta, H.; Hemalatha, S.; Babu, M.J.; Raju, C.S.; Shah, N.A.; Yook, S.J. Simulation of Dissipative Hybrid Nanofluid (PEG-Water + ZrO2 + MgO) Flow by a Curved Shrinking Sheet with Thermal Radiation and Higher Order Chemical Reaction. Mathematics 2022, 10, 1706. [Google Scholar] [CrossRef]
- Kumar, G.V.; Rehman, K.U.; Kumar, R.V.M.S.S.K.; Shatanawi, W. Unsteady magnetohydrodynamic nanofluid flow over a permeable exponentially surface manifested with non-uniform heat source/sink effects. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Rooman, M.; Jan, M.A.; Shah, Z.; Vrinceanu, N.; Bou, S.F.; Iqbal, S.; Deebani, W. Entropy Optimization on Axisymmetric Darcy-Forchheimer Powell-Eyring Nanofluid over a Horizontally Stretching Cylinder with Viscous Dissipation Effect. Coatings 2022, 12, 749. [Google Scholar] [CrossRef]
- Goud, B.S.; Reddy, Y.D.; Mishra, S. Joule heating and thermal radiation impact on MHD boundary layer Nanofluid flow along an exponentially stretching surface with thermal stratified medium. Proc. Inst. Mech. Eng. J. Nanomater. Nanoeng. Nanosyst. 2022, 23977914221100961. [Google Scholar] [CrossRef]
- Manvi, B.; Tawade, J.; Biradar, M.; Noeiaghdam, S.; Fernandez-Gamiz, U.; Govindan, V. The effects of MHD radiating and non-uniform heat source/sink with heating on the momentum and heat transfer of Eyring-Powell fluid over a stretching. Results Eng. 2022, 14, 100435. [Google Scholar] [CrossRef]
- Ali, A.; Khan, H.S.; Saleem, S.; Hussan, M. EMHD Nanofluid Flow with Radiation and Variable Heat Flux Effects along a Slandering Stretching Sheet. Nanomaterials 2022, 12, 3872. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. The Optimal Homotopy Asymptotic Method—Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Marinca, V.; Ene, R.D.; Marinca, B.; Negrea, R. Different approximations to the solution of upper-convected Maxwell fluid over a porous stretching plate. Abstr. Appl. Anal. 2014, 2014, 139314. [Google Scholar] [CrossRef]
- Ene, R.D.; Marinca, V. Approximate solutions for steady boundary layer MHD viscous flow and radiative heat transfer over an exponentially porous stretching sheet. Appl. Math. Comput. 2015, 269, 389–401. [Google Scholar] [CrossRef]
- Ene, R.D.; Szabo, M.A.; Danoiu, S. Viscous flow and heat transfer over a permeable shrinking sheet with partial slip. Mater. Plast. 2015, 52, 408–412. [Google Scholar]
- Marinca, V.; Ene, R.D. Dual approximate solutions of the unsteady viscous flow over a shrinking cylinder with Optimal Homotopy Asymptotic Method. Adv. Math. Phys. 2014, 2014, 417643. [Google Scholar] [CrossRef]
- Ene, R.D.; Pop, N. Dual approximate solutions for the chemically reactive solute transfer in a viscous fluid flow. Waves Random Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Ene, R.D.; Petrisor, C. Some mathematical approaches on the viscous flow problem on a continuous stretching surface: Nonlinear stability and dual approximate analytic solutions. AIP Conf. Proc. 2020, 2293, 350004. [Google Scholar]
- Devi, S.P.A.; Thiyagarajan, M. Steady nonlinear hydromagnetic flow and heat transfer over a stretching surface of variable temperature. Heat Mass Transf. 2006, 42, 671–677. [Google Scholar] [CrossRef]
- Sulochana, C.; Sandeep, N. Dual Solutions for Radiative MHD Forced Convective Flow of a Nanofluid over a Slendering Stretching Sheet in Porous Medium. J. Nav. Archit. Mar. Eng. 2015, 12, 115–124. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer Properties; John Wiley and Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef]

| n | |||||
|---|---|---|---|---|---|
| 0.5 | 0.25 | 0.2 | −0.7333855928 | −0.7333855918 | 10 |
| 0.5 | 0.25 | 0.5 | −0.5639692215 | −0.5639692205 | 10 |
| 0.5 | 0.25 | 0.75 | −0.4764796954 | −0.4764796944 | 10 |
| 0.5 | 0.5 | 0.5 | −0.5784360410 | −0.5784360310 | 10 |
| 0.5 | 1 | 0.5 | −0.6070808644 | −0.6070808634 | 10 |
| 2.5 | 0.25 | 0.5 | −0.6216320348 | −0.6216320248 | 10 |
| 5 | 0.25 | 0.5 | −0.6367180731 | −0.6367180631 | 10 |
| n | R | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.25 | 0.5 | 1 | 6 | 0.2 | −0.9865380801 | −0.9865379801 | 10 |
| 0.5 | 0.25 | 0.5 | 1 | 7 | 0.2 | −1.0639948406 | −1.0639947406 | 10 |
| 0.5 | 0.25 | 0.5 | 1 | 8 | 0.2 | −1.1340917886 | −1.1340916886 | 10 |
| 0.5 | 0.25 | 0.5 | 0.5 | 6 | 0.2 | −1.1604012664 | −1.1604012564 | 10 |
| 0.5 | 0.25 | 0.5 | 1 | 6 | 0.2 | −0.9865380801 | −0.9865379801 | 10 |
| 0.5 | 0.25 | 0.5 | 1.5 | 6 | 0.2 | −0.8681344977 | −0.8681344877 | 10 |
| 0.5 | 0.25 | 0.5 | 1 | 6 | 0.2 | −0.9865380801 | −0.9865379801 | 10 |
| 0.5 | 0.25 | 0.5 | 1 | 6 | 0.4 | −0.8239638179 | −0.8239637179 | 10 |
| 0.5 | 0.25 | 0.5 | 1 | 6 | 0.6 | −0.7073908656 | −0.7073907656 | 10 |
| 2.5 | 0.25 | 0.5 | 1 | 6 | 0.2 | −0.3797410596 | −0.3885966996 | 8.855639 |
| 5 | 0.25 | 0.5 | 1 | 6 | 0.2 | −0.0997737511 | −0.0997737411 | 10 |
| 0.5 | 0.5 | 0.5 | 1 | 6 | 0.2 | −1.0438247676 | −1.0438246676 | 10 |
| 0.5 | 1 | 0.5 | 1 | 6 | 0.2 | −1.1564371927 | −1.1564370927 | 10 |
| 0.5 | 0.25 | 0.2 | 1 | 6 | 0.2 | −1.0625520610 | −1.0625520510 | 10 |
| 0.5 | 0.25 | 0.75 | 1 | 6 | 0.2 | −0.9401404517 | −0.9401403517 | 10 |
| 0 | 0.0598346157 | 0.7180153892 | 0.8026923839 |
| 0.25 | 0.2226712355 | 0.5883987717 | 0.5777496315 |
| 0.5 | 0.3557863062 | 0.4798072617 | 0.3992585355 |
| 0.75 | 0.4641079810 | 0.3896154306 | 0.2660675341 |
| 1 | 0.5519132878 | 0.3152605148 | 0.1718011819 |
| 1.25 | 0.6228576040 | 0.2543456969 | 0.1079932864 |
| 1.5 | 0.6800247596 | 0.2047029048 | 0.0663727087 |
| 1.75 | 0.7259884392 | 0.1644214653 | 0.0400386110 |
| 2 | 0.7628774926 | 0.1318523678 | 0.0237854503 |
| 2.25 | 0.7924400119 | 0.1055954914 | 0.0139544082 |
| 2.5 | 0.8161029111 | 0.0844773589 | 0.0081040406 |
| 2.75 | 0.8350253351 | 0.0675246921 | 0.0046679539 |
| 3 | 0.8501452478 | 0.0539367909 | 0.0026710288 |
| 0 | 0.0598346158 | 0.7180153897 | 0.8026925039 |
| 0.25 | 0.2226712379 | 0.5883987726 | 0.5777441370 |
| 0.5 | 0.3557863072 | 0.4798072319 | 0.3992654139 |
| 0.75 | 0.4641079768 | 0.3896154196 | 0.2660663722 |
| 1 | 0.5519132871 | 0.3152605436 | 0.1717963676 |
| 1.25 | 0.6228576084 | 0.2543457448 | 0.1079934516 |
| 1.5 | 0.6800247641 | 0.2047028870 | 0.0663767004 |
| 1.75 | 0.7259884379 | 0.1644214414 | 0.0400411532 |
| 2 | 0.7628774882 | 0.1318523684 | 0.0237837569 |
| 2.25 | 0.7924400080 | 0.1055954999 | 0.0139493825 |
| 2.5 | 0.8161029111 | 0.0844773812 | 0.0080983796 |
| 2.75 | 0.8350253396 | 0.0675247036 | 0.0046641177 |
| 3 | 0.8501452547 | 0.0539367945 | 0.0026702523 |
| 0 | 4.166664 | 5.000001 | 1.200000 |
| 0.25 | 2.338812 | 8.500138 | 5.494534 |
| 0.5 | 9.967847 | 2.982538 | 6.878355 |
| 0.75 | 4.282139 | 1.095087 | 1.161948 |
| 1 | 6.948758 | 2.880794 | 4.814365 |
| 1.25 | 4.403408 | 4.789489 | 1.652118 |
| 1.5 | 4.521325 | 1.783327 | 3.991710 |
| 1.75 | 1.352115 | 2.390061 | 2.542265 |
| 2 | 4.420232 | 6.084595 | 1.693424 |
| 2.25 | 3.888561 | 8.512293 | 5.025664 |
| 2.5 | 2.571165 | 2.233086 | 5.660951 |
| 2.75 | 4.493213 | 1.154742 | 3.836207 |
| 3 | 6.906006 | 3.618723 | 7.764704 |
| n | |||||
|---|---|---|---|---|---|
| 0.5 | 0.25 | 0.2 | 0.9946172010 | 0.9946172997 | |
| 0.5 | 0.25 | 0.5 | 0.9097559921 | 0.9097561021 | |
| 0.5 | 0.25 | 0.75 | 0.8592107287 | 0.8592108288 | |
| 0.5 | 0.5 | 0.5 | 0.934115512 | 0.93411561078 | |
| 0.5 | 1 | 0.5 | 0.984325561 | 0.98432566179 | |
| 2.5 | 0.25 | 0.5 | 0.754168409 | 0.75416850866 | |
| 5 | 0.25 | 0.5 | 0.709166712 | 0.70916736175 | 6.496262 |
| n | R | ||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 0.25 | 0.2 | 5.485739 | 1 | 6 | 0.2 | 1.079470 |
| 0.5 | 0.25 | 0.5 | 5.503738 | 1 | 6 | 0.2 | 4.737834 |
| 1 | 7 | 0.2 | 9.489441 | ||||
| 1 | 8 | 0.2 | 1.914615 | ||||
| 0.5 | 6 | 0.2 | 3.598609 | ||||
| 1.5 | 6 | 0.2 | 3.601433 | ||||
| 1 | 6 | 0.4 | 2.265013 | ||||
| 1 | 6 | 0.6 | 1.504156 | ||||
| 0.5 | 0.25 | 0.75 | 2.848927 | 1 | 6 | 0.2 | 1.139814 |
| 0.5 | 0.5 | 0.5 | 1.486587 | 1 | 6 | 0.2 | 1.787740 |
| 0.5 | 1 | 0.5 | 7.256022 | 1 | 6 | 0.2 | 2.676813 |
| 2.5 | 0.25 | 0.5 | 2.500198 | 1 | 6 | 0.2 | 1.100465 |
| 5 | 0.25 | 0.5 | 3.167293 | 1 | 6 | 0.2 | 8.243077 |
| 0 | 0.0598346157 | 0.0598346158 | 0.0598346157 |
| 2/5 | 0.3057767212 | 0.3057767284 | 0.3057767378 |
| 4/5 | 0.4831846866 | 0.4831846939 | 0.4831857409 |
| 6/5 | 0.6098618368 | 0.6098618446 | 0.6098707988 |
| 8/5 | 0.6996261828 | 0.6996261750 | 0.6996239146 |
| 2 | 0.7628775161 | 0.7628774882 | 0.7625577448 |
| 12/5 | 0.8072661326 | 0.8072660955 | 0.8051757704 |
| 14/5 | 0.8383269730 | 0.8383269310 | 0.8300974997 |
| 16/5 | 0.8600170821 | 0.8600170260 | 0.8362170948 |
| 18/5 | 0.8751415873 | 0.8751415052 | 0.8221825663 |
| 4 | 0.8856771883 | 0.8856770760 | 0.8010064019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ene, R.-D.; Pop, N.; Badarau, R. Partial Slip Effects for Thermally Radiative Convective Nanofluid Flow. Mathematics 2023, 11, 2199. https://doi.org/10.3390/math11092199
Ene R-D, Pop N, Badarau R. Partial Slip Effects for Thermally Radiative Convective Nanofluid Flow. Mathematics. 2023; 11(9):2199. https://doi.org/10.3390/math11092199
Chicago/Turabian StyleEne, Remus-Daniel, Nicolina Pop, and Rodica Badarau. 2023. "Partial Slip Effects for Thermally Radiative Convective Nanofluid Flow" Mathematics 11, no. 9: 2199. https://doi.org/10.3390/math11092199
APA StyleEne, R.-D., Pop, N., & Badarau, R. (2023). Partial Slip Effects for Thermally Radiative Convective Nanofluid Flow. Mathematics, 11(9), 2199. https://doi.org/10.3390/math11092199