Abstract
In this study, a hybrid Chebyshev pseudo-spectral finite-difference time-domain (CPS-FDTD) algorithm is proposed for simulating 2D acoustic wave propagation in heterogeneous media, which is different from the other traditional numerical schemes such as finite element and finite difference. This proposed hybrid method integrates the efficiency of the FDTD approach in the time domain and the high accuracy of the CPS technique in the spatial domain. We present the calculation formulas of this novel approach and conduct simulation experiments to test it. The biconjugate gradient is solved by combining the large symmetric sparse systems stabilized algorithm with an incomplete LU factorization. Three numerical experiments are further presented to illustrate the accuracy, efficiency, and flexibility of the hybrid CPS-FDTD algorithm.
Keywords:
acoustic wave propagation; heterogenous medium; Chebyshev pseudo-spectral method; finite-difference time-domain method; hybrid technique MSC:
86A15
1. Introduction
Accurate acoustic wave propagation is a highly challenging computational problem that is crucial to acoustic modeling, imaging, and inversion. To solve the time-domain or frequency-domain acoustic wave equation in a heterogeneous medium, it is necessary to apply numerical modeling techniques, such as the finite-difference time-domain (FDTD) method [1,2,3,4,5], finite-difference frequency-domain (FDFD) [6,7], finite-element time-domain (FETD) [8,9,10,11], finite-element frequency-domain (FEFD) [12], pseudo-spectral time-domain (PSTD) [13,14,15], and spectral-element time-domain (SETD) methods [16,17,18]. The FDTD method is the most popular numerical scheme for simulating acoustic wave propagation. However, numerical dispersion for wave propagation problems is a common problem in numerical simulations, such as the traditional FDTD method and the boundary element method.
The pseudo-spectral (PS) method is a popular numerical approach for solving ordinary differential equations (ODE) or partial differential equations (PDE) because of its high-order accuracy [19]. This method typically uses a set of orthogonal basis functions to calculate the derivatives in PDEs [20]. The Fourier pseudo-spectral (FPS) technique can be explained as the utilization of discrete Fourier series on uniform spatial grids, implicitly assuming periodic behavior [21]. However, it is difficult to implement free boundary surfaces or absorbing boundary conditions in this FPS approach. The Chebyshev pseudo-spectral (CPS) scheme can be explained as the realization of spatial, physical fields using Chebyshev polynomials defined in the interval [–1,1]. The main advantage of this technique is that an elegant formulation of boundary conditions (free surface or absorbing) can be formulated by defining the so-called characteristic variables. The main difference with any previous methods is that the displacement field and the geophysical parameters are defined on the irregular Chebyshev collocation points. The CPS method has attracted widespread attention in numerical modeling for magnetotelluric forward problems [22]. The existing literature on 2D CPS acoustic wave modeling essentially belongs to the FPS technique, which is transformed between physical and spectral spaces by FFT techniques or the cosine transforms [23].
In this study, a hybrid CPS-FDTD scheme is developed for simulating general acoustic wave propagation, which is different from traditional numerical methods such as FDTD. For this time-dependent partial differential equation, the CPS scheme is used in the spatial domain, while the finite-difference (FD) scheme is adopted in the time domain. The CPS scheme requires fewer grid points than other numerical methods to achieve the same accuracy in the spatial domain. We then deduce that the hybrid CPS-FDTD algorithm will give more accurate approximate results than the traditional FDTD approach, especially in dealing with 3D acoustic wave propagation.
The organization of this study is arranged as follows: In Section 2, the initial boundary value problem of the acoustic wave equation in a 2D medium is introduced. Section 3 presents the method of the hybrid CPS-FDTD scheme for acoustic wave propagation. Numerical experiments for acoustic wave propagation are presented in Section 4. The discussions and conclusions of this study are contained in Section 5 and Section 6, respectively.
2. Statement of the Geophysical Problem
The 2D acoustic wave equation can be written as
we choose the initial conditions:
and the Dirichlet boundary conditions:
where represents the acoustic velocity and represents the motivated source function; , , , , and represent known functions, while the displacement function u is unknown.
3. Methodology
3.1. Discretization Scheme in the Spatial Domain
The Gauss–Chebyshev–Lobatto (GCL) points can be applied for forming unevenly spaced meshes [24,25]. The GCL points for polynomial expansion can be given by
For 2D problems in the spatial domain, the GCL points can be obtained by
3.2. Chebyshev Differentiation Matrix in the Spatial Domain
The elements in the first-order Chebyshev differentiation matrix are given by
where
and
Usually, the diagonal components of can be simplified as follows [26]
3.3. CPS-FDTD Algorithm for 2D Acoustic Wave Equation
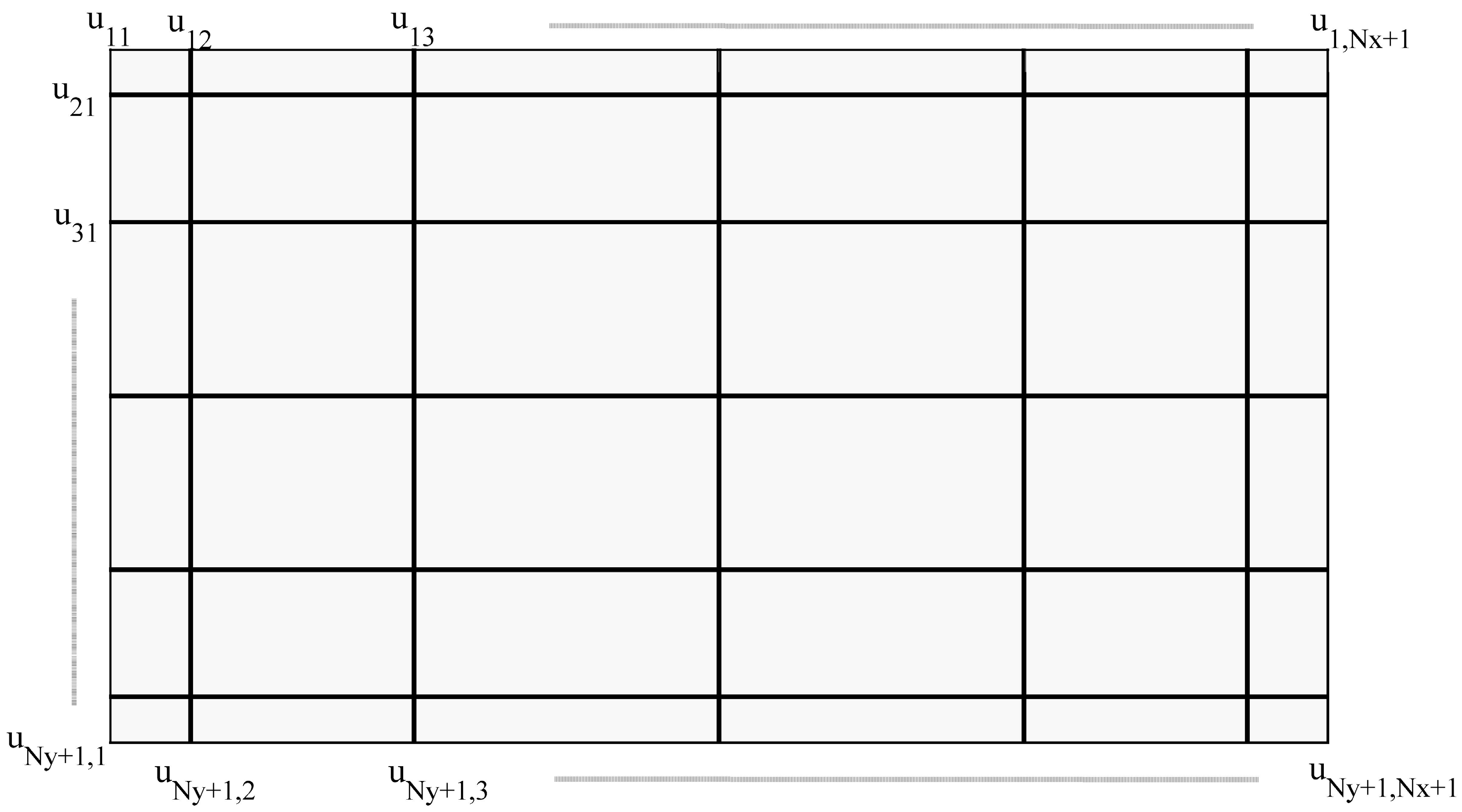
To solve the acoustic wave problem with the hybrid CPS-FDTD algorithm, we will divide the whole computational domain into rectangular cells (Figure 1). The total mesh nodes are . Meanwhile, the physical rectangular domain can be discretized with GCL points. The real points can be transformed as follows:
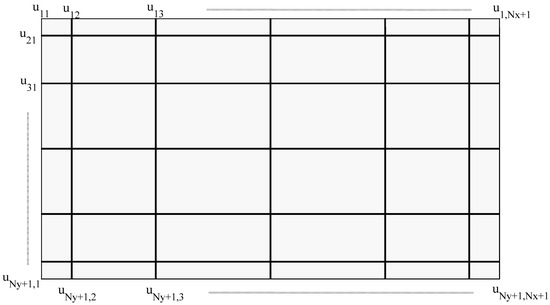
Figure 1.
2D computational spatial domain discretized by GCL points.
The solution vector u should be rewritten in a one-dimensional vector by
and the wave velocity should be rewritten by
The discretization of Equation (1) in the spatial domain for all non-boundary nodes with the CPS scheme can be written as
and the discretization of Equation (1) in the time domain by the FDTD scheme [27,28,29] can be written by
Therefore, the discretization of Equation (1) can be written as
or
where I represents an identity matrix, and V indicates the discrete wave velocity. To reduce computer memory and computational costs, we need to introduce artificial boundaries to limit the scope of the research area [30,31,32]. Therefore, an artificial boundary condition is needed to absorb the energy of the reflections from these artificial boundaries. In this article, we use techniques based on the one-way equation to achieve absorbing boundary conditions, such as [33]
Using finite-difference approximation, the discretization of the one-way wave equation can be written as
Combining the boundary conditions, the initial conditions, and the source function, the discrete equation system can be assembled as follows:
where K is the system matrix, which contains acoustic velocity parameters . p represents the column vector, which is interrelated to the given source function, the initial conditions, and the absorbing boundary conditions. The matrix K is unsymmetrical and non-sparse. Therefore, the computational time and the memory spent on solving this large linear system equations of the hybrid CPS-FDTD scheme should be longer and larger than that of the FDTD approach.
4. Numerical Experiments
4.1. Example 1
First, to test the accuracy of the hybrid CPS-FDTD method, the acoustic wave equation in a homogeneous medium will be solved. The physical domain is designed as a square computational domain with . The exact solution of the initial boundary problem for this acoustic wave can be expressed as . The initial boundary conditions are picked to satisfy the exact solution. The variations of acoustic velocities in the spatial domain are . In addition, the motivated source function can be derived from
It is noted that this acoustic wave problem has a homogeneous boundary condition, which can be easily implemented in computer code. To solve this example, the square computational domain is discretized using the GCL technique. The number of GCL points in both the x-axis and y-axis is designed as 41.
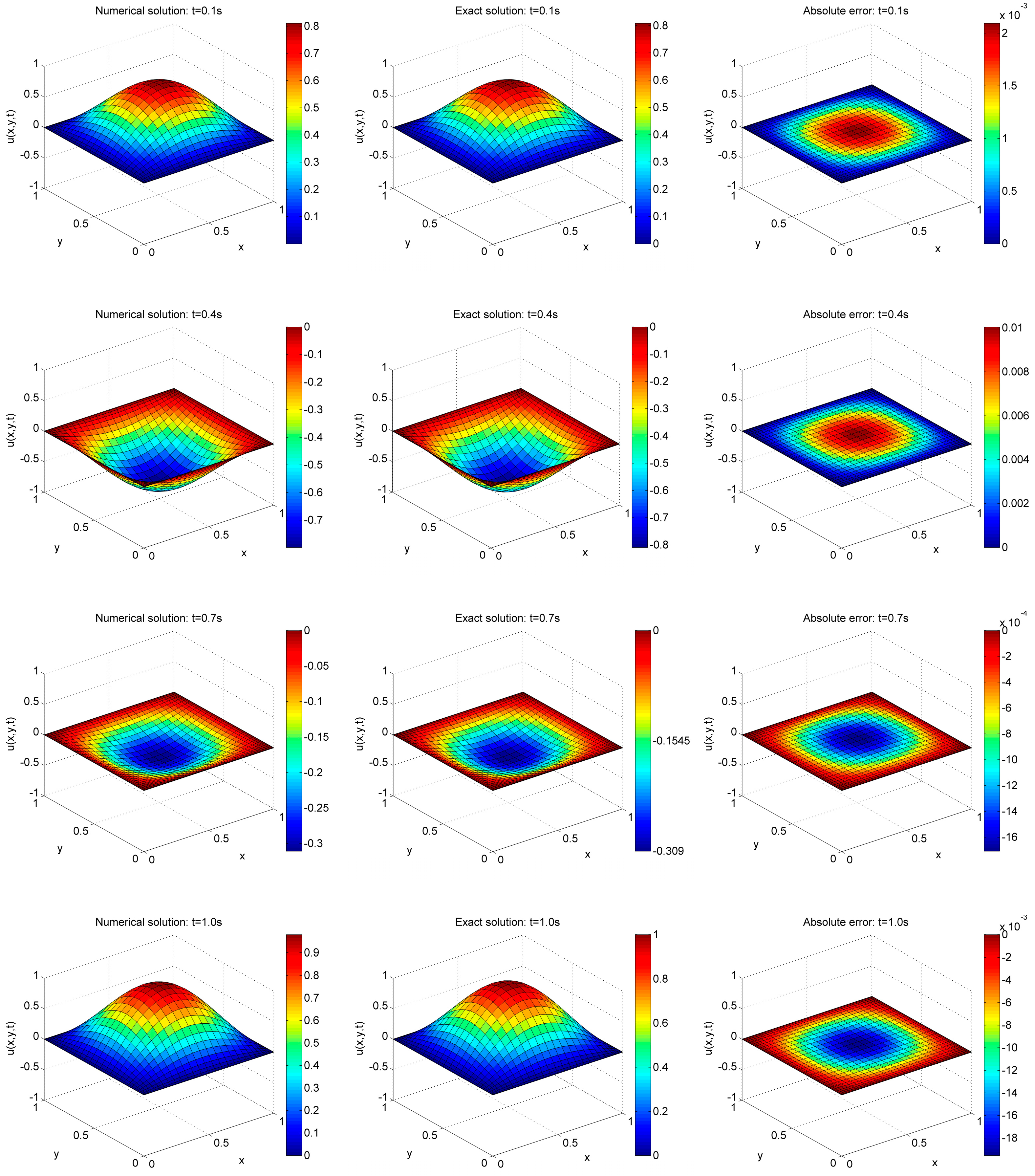
To test the hybrid CPS-FDTD numerical approach, the time step is fixed as s. Numerical solutions and exact solutions of this example are shown in Figure 2. The numerical solutions agree well with the exact solutions, which proves that the hybrid CPS-FDTD scheme is stable.
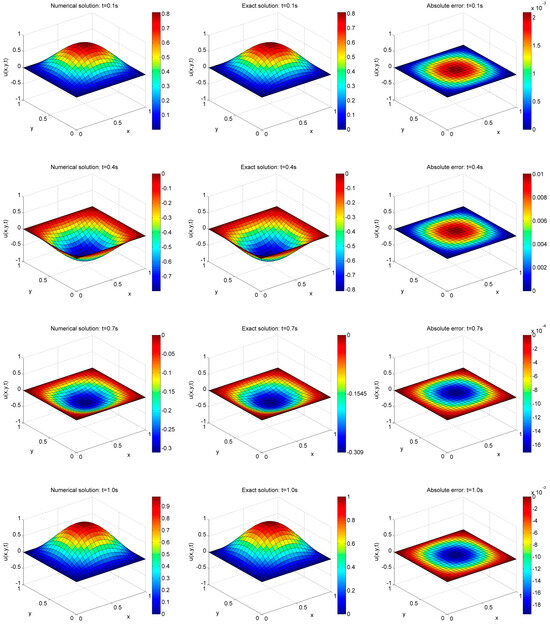
Figure 2.
Comparison of the hybrid CPS-FDTD numerical solutions and the exact solutions, for example, 1 with t = 0.1 s, 0.4 s, 0.7 s, and 1.0 s.
4.2. Example 2
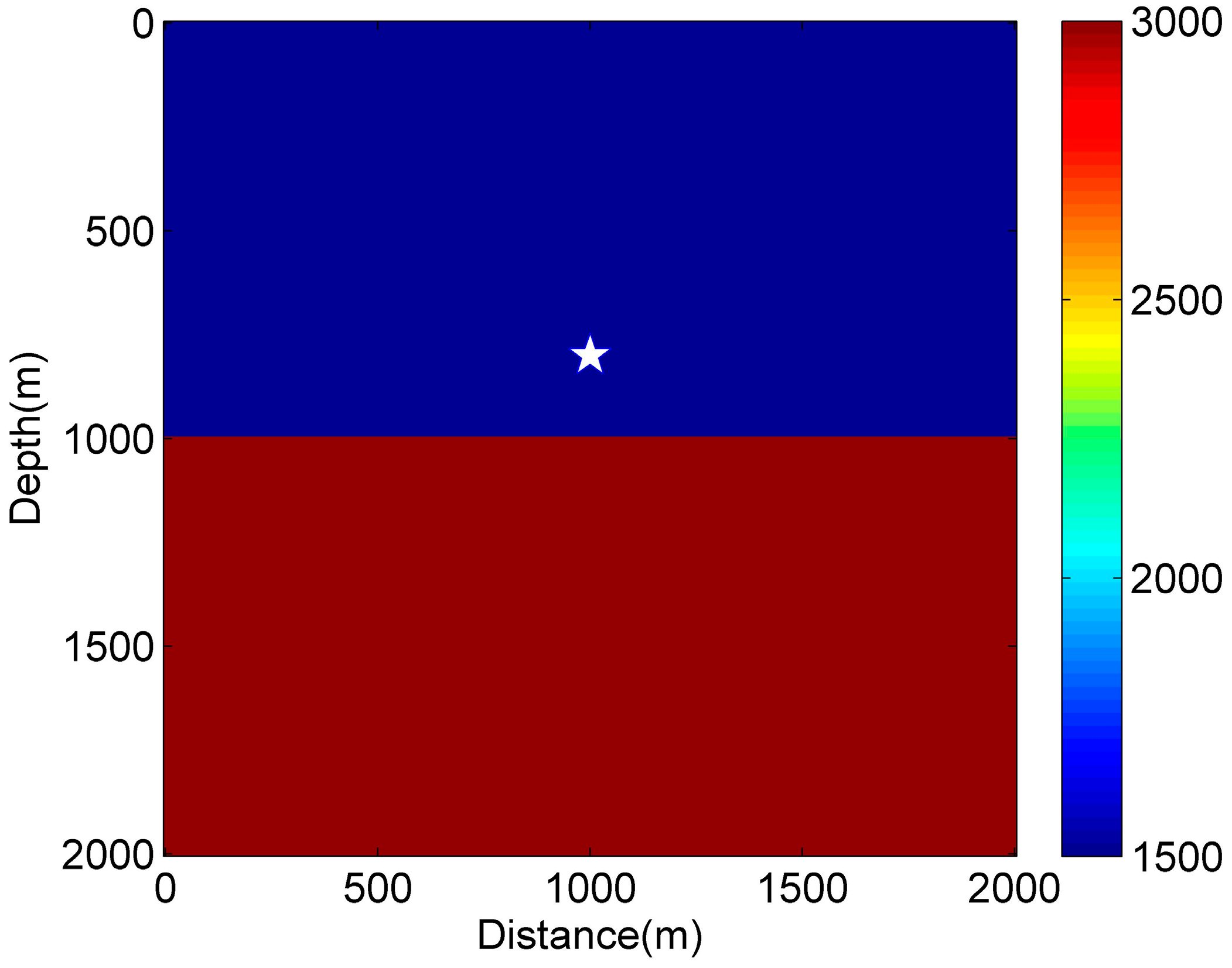
The acoustic wave equation is simulated in a homogenous subsurface medium in example 1. In this example, we compute 2D acoustic wave propagation in a two-layer acoustic velocity model. The acoustic velocity in the first layer and second layer is designed as v = 1500 m/s and v = 3000 m/s, respectively. The computational domain is designed as (Figure 3). In this numerical simulation, the Ricker wavelet source signal is motivated by its mathematical expression:
where is the peak frequency, which is set as Hz. is the temporal delay time with s and is the Dirac delta function. We use the hybrid CPS-FDTD approach to discretize the computational domain with 101 GCL points on the x-axis and y-axis with the time step ms.
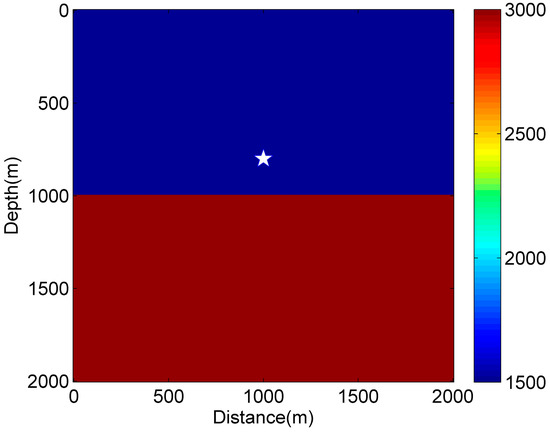
Figure 3.
A two-layer velocity model simulated by the hybrid CPS-FDTD method. The white star symbol represents the Ricker wavelet source located at (1000 m, 800 m).
To simplify the treatment of 2D boundary conditions, zero-value boundary conditions can be implemented in example 1. However, it should be pointed out that this zero-value boundary condition is inappropriate for acoustic wave propagation. In this numerical example, we apply the Clayton–Enquist absorbing boundary conditions [33] to simulate 2D acoustic wave propagation. The forward algorithm is coded in MATLAB (R2023a), and the subroutine is given in Appendix A.
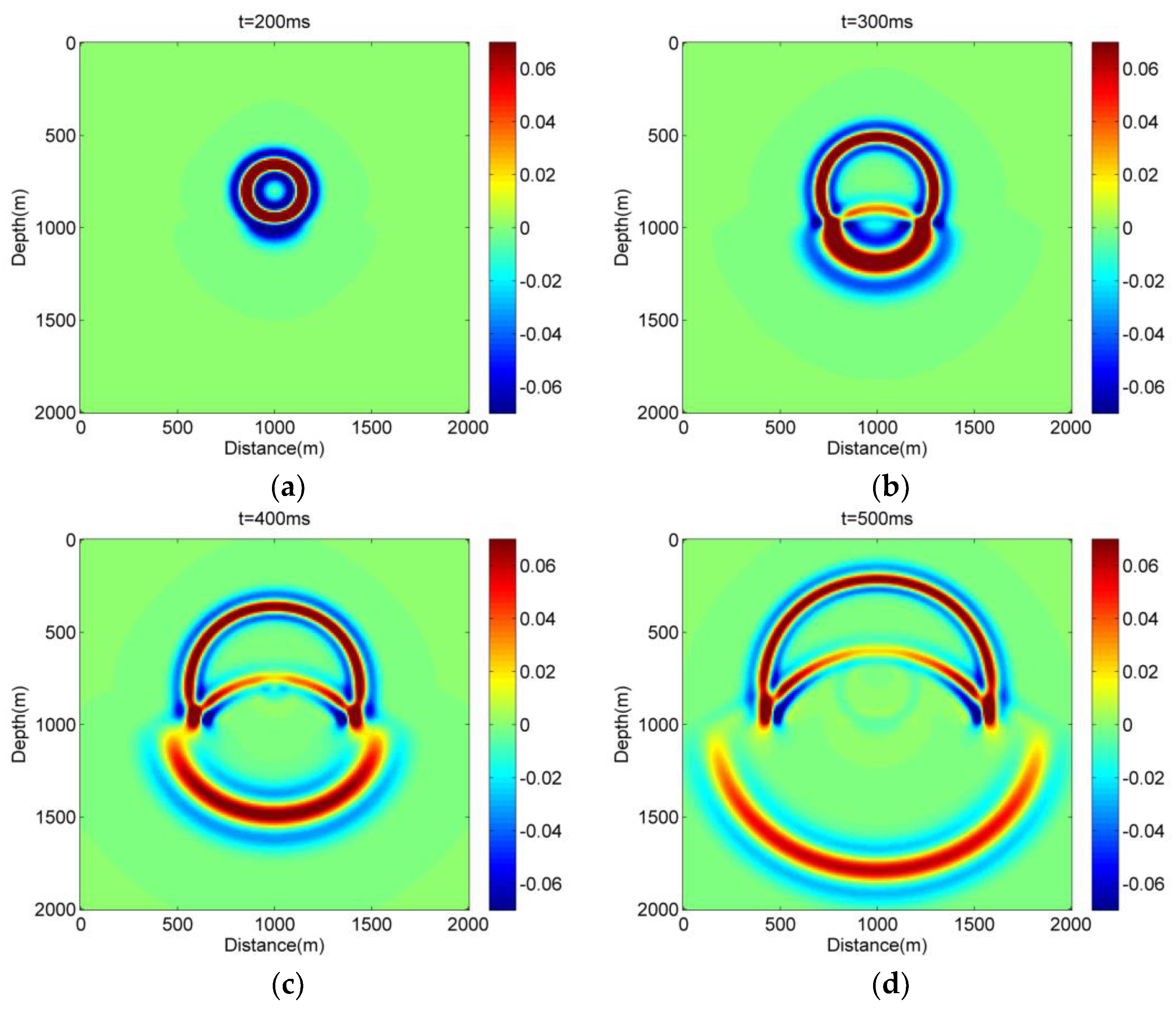
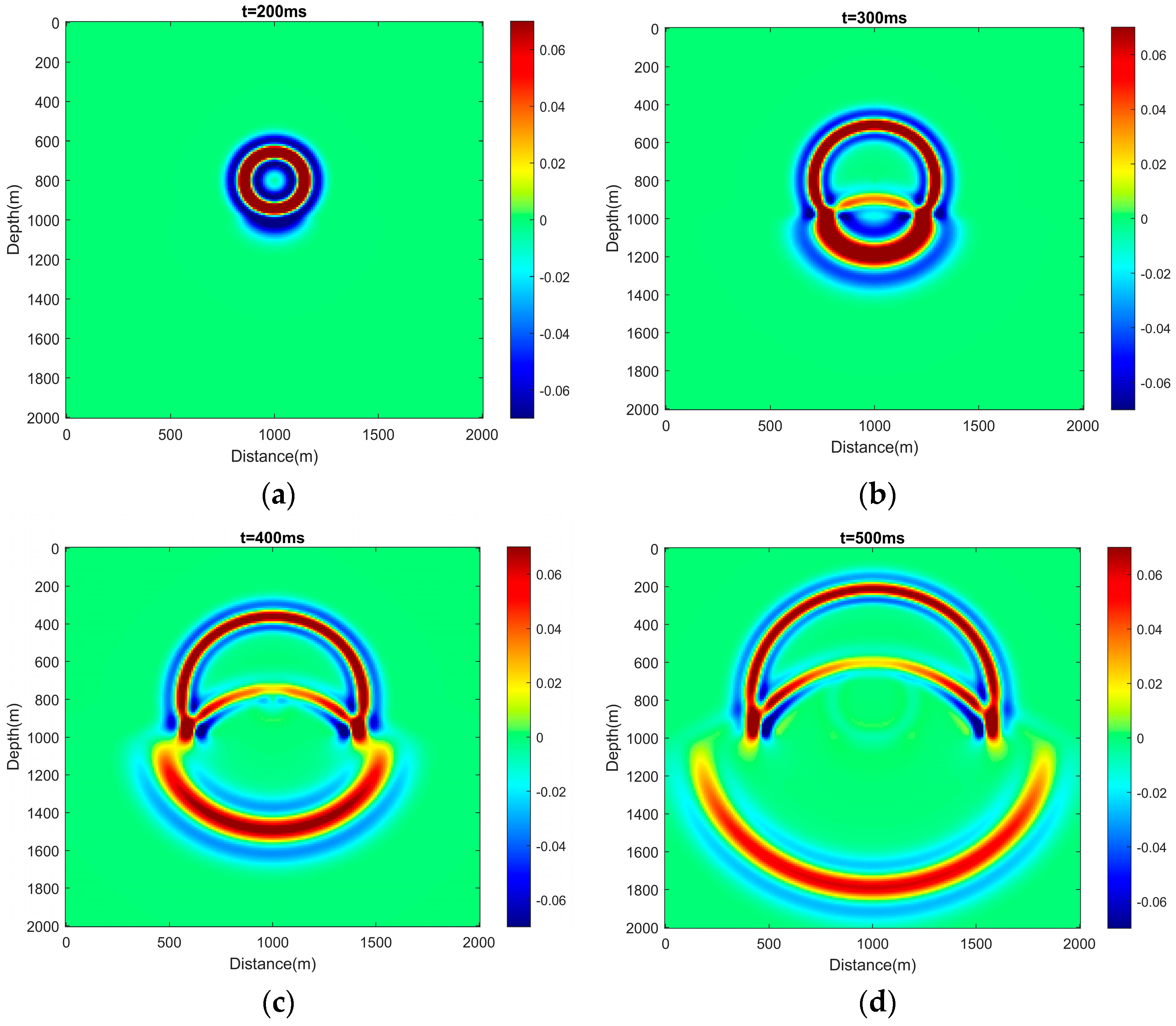
The acoustic wave propagation processes can be displayed at different times with t = 200 ms, 300 ms, 400 ms, and 500 ms (Figure 4). The wavefront is approximated to be a circle at t = 200 ms, shown in Figure 4a, in which acoustic wave propagation only exits in the first layer medium, and its wavefront generates a standard circle. With increasing time, the reflected acoustic wave can be found near the interface of the two-layer velocity model. For example, when the simulation time t is equal to 300 ms, the wavefront exhibits a moderate wave reflection on the interface shown in Figure 4b. Due to the constant velocity in each layer medium, both the refracted wavefront and reflected wavefront will generate approximate circles in the different layers. Meanwhile, when simulation time t is equal to 400 ms, both the refracted and reflected acoustic wave propagation will form standard circle wavefronts (Figure 4c). Figure 4d shows that when the wavefront encounters the left boundary and right boundary of the computational domain, there is a noticeable reflected acoustic wave at t = 500 ms.
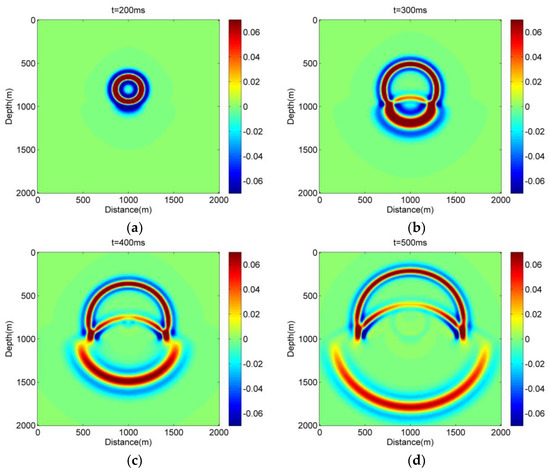
Figure 4.
Snapshots of wavefields simulated by the hybrid CPS-FDTD algorithm for the two-layer velocity model in Figure 3. (a) t = 200 ms, (b) t = 300 ms, (c) t = 400 ms, and (d) t = 500 ms.
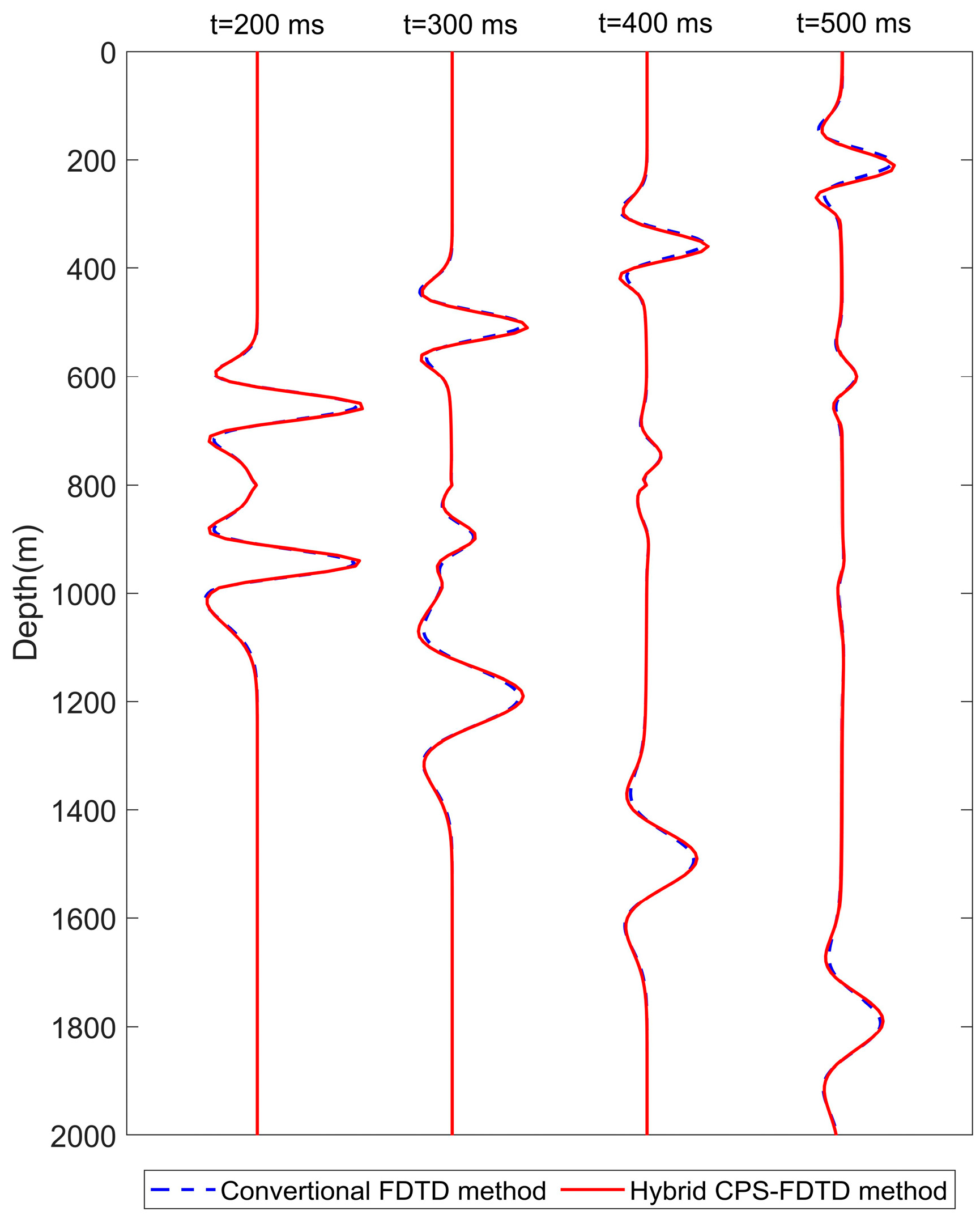
We further compare the simulation of acoustic wave propagation in this two-layer velocity model with that of the standard FDTD method [1], in which the FD approach is used both in the time domain and in the spatial domain. The 2D acoustic wave propagation process is displayed at different times t = 200 ms, 300 ms, 400 ms, and 500 ms in Figure 5, which shows that numerical solutions to our hybrid CPS-FDTD approach have a good agreement with the standard FDTD results. The wavefields computed by the CPS-FDTD algorithm (blue solid line) and the conventional FDTD method (red dashed line) at x = 1000 m are plotted in Figure 6. It shows that both the CPS-FDTD algorithm and conventional FDTD methods can achieve high accuracy, but our hybrid CPS-FDTD has less dispersion.
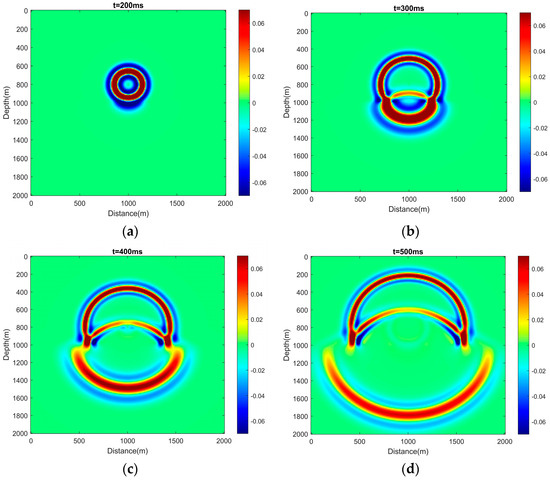
Figure 5.
Snapshots of wavefields simulated by the conditional FDTD algorithm for the two-layer velocity model in Figure 3. (a) t = 200 ms, (b) t = 300 ms, (c) t = 400 ms, and (d) t = 500 ms.
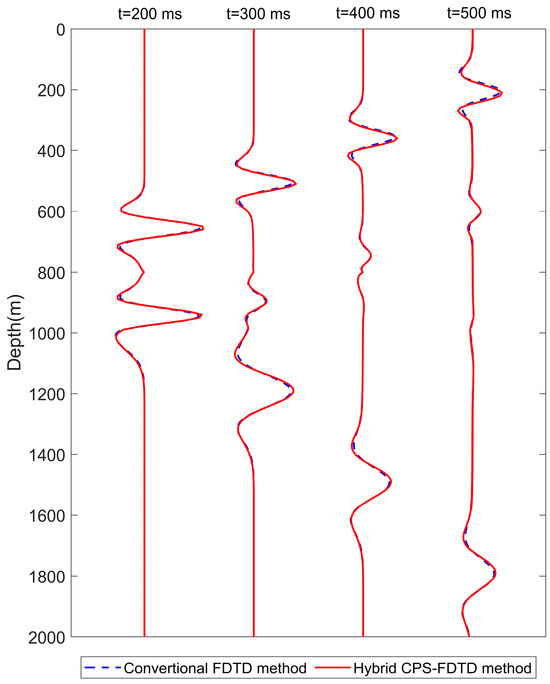
Figure 6.
Comparison of the amplitudes of wavefields simulated by the hybrid CPS-FDTD algorithm and the conventional FDTD method. The wavefields are sampled at x = 1000 m for t = 200 ms, t = 300 ms, t = 400 ms and t = 500 ms.
4.3. Example 3
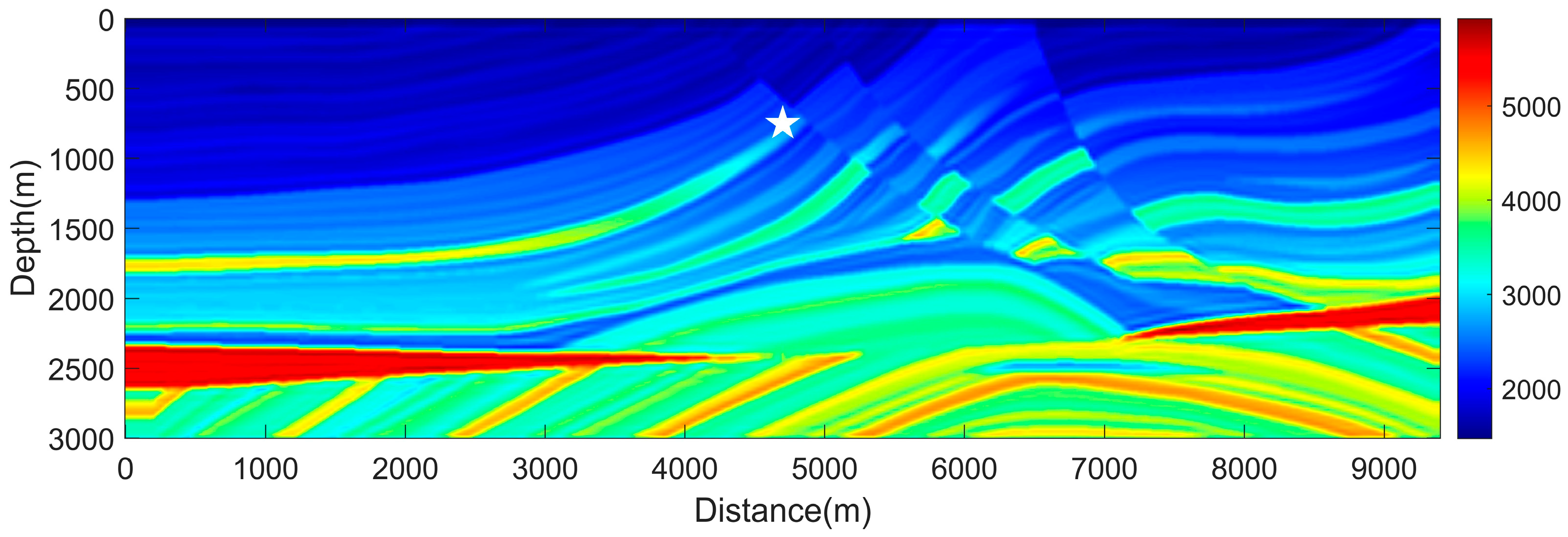
To benchmark the flexibility for the complicated subsurface geological medium of the hybrid CPS-FDTD method, we choose the Marmousi acoustic velocity model. The minimum velocity is 1500 m/s, and the maximum velocity is 6000 m/s (Figure 7). The Ricker wavelet signal source is motivated with a peak frequency of 10 Hz, and the temporal delay time is designed as s. Meanwhile, the Ricker source is placed at (4700 m, 750 m). For this numerical simulation, the discretization of the computational domain with 201 GCL points in the x-axis and y-axis defines a rectangular domain .
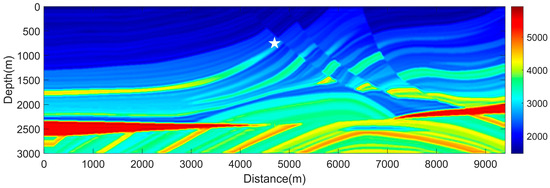
Figure 7.
Marmousi velocity model defined a 9400 m 3000 m rectangular computational domain. The minimum velocity is 1500 m/s, and the maximum velocity is 6000 m/s. The white star symbol represents the Ricker wavelet source, which is placed at (4700 m, 750 m).
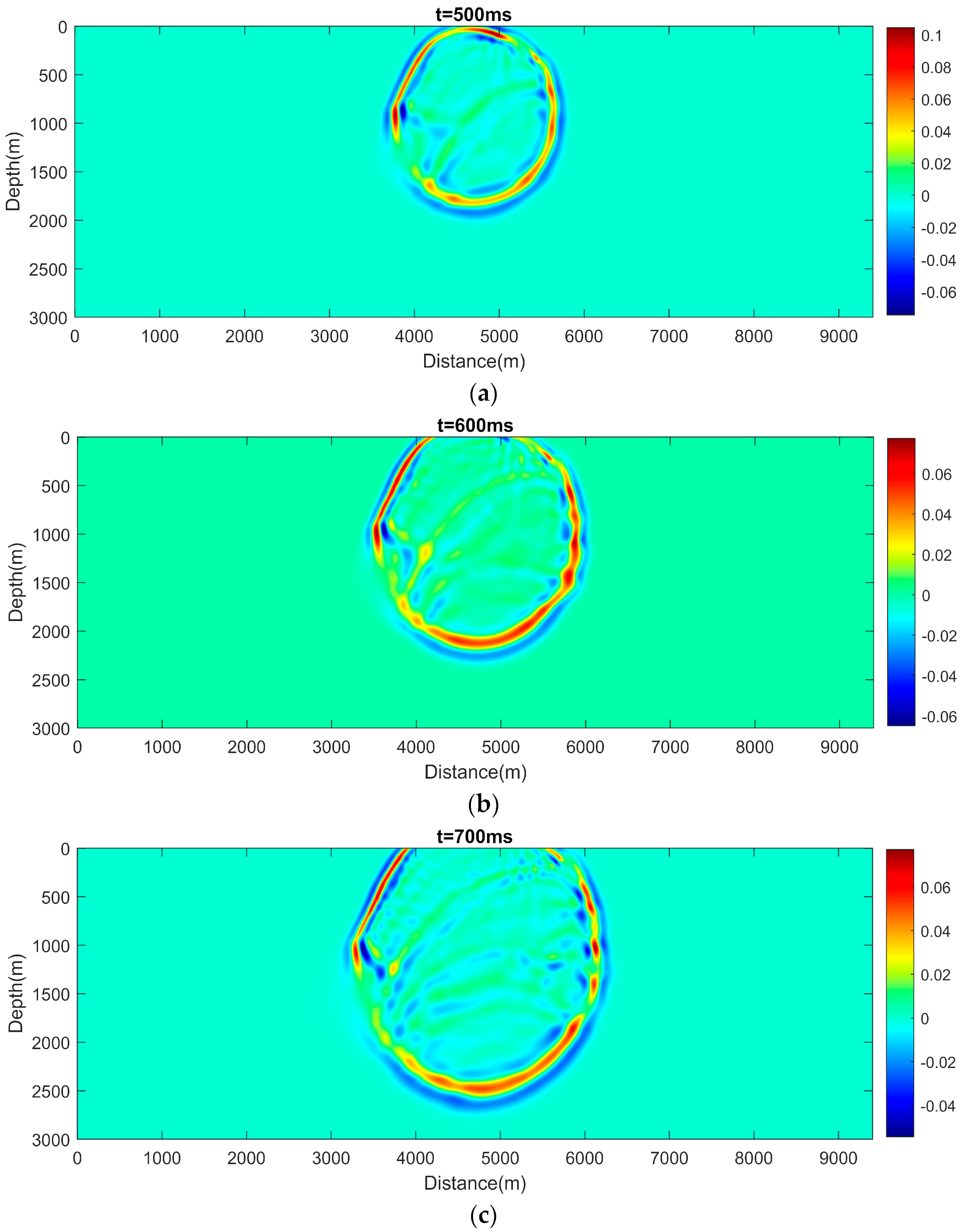
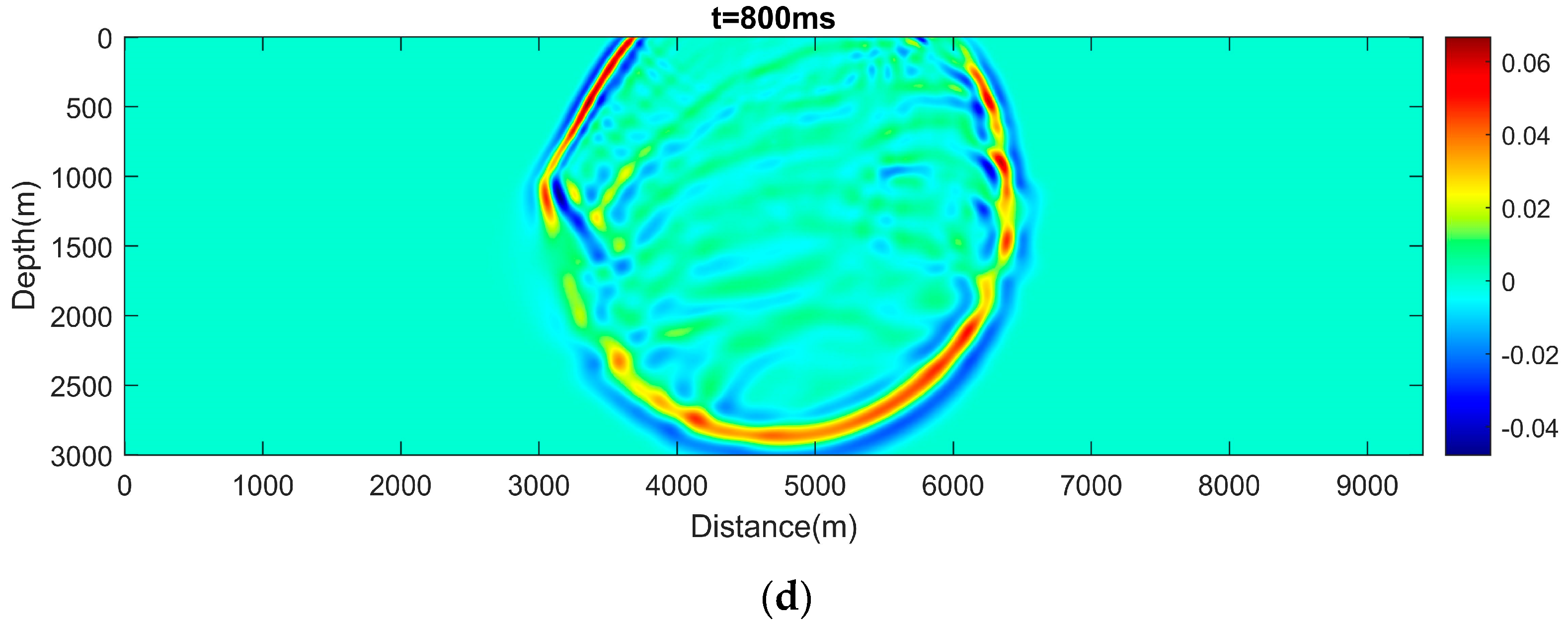
We choose the time step ms. The 2D acoustic wave propagation process is displayed at different times with t = 500 ms, 600 ms, 700 ms, and 800 ms in Figure 8, which has a good agreement with the acoustic velocity parameters of the Marmousi model. For example, we can observe visible reflections and weak dispersion at points where velocity changes rapidly. The forward algorithm is coded in MATLAB (R2023a), and the subroutine is given in Appendix A.
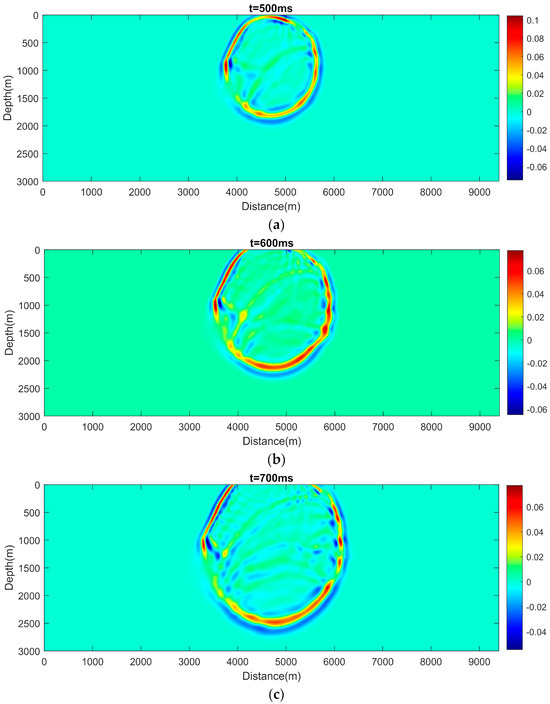
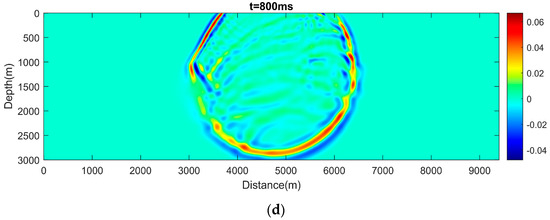
Figure 8.
Snapshots of wavefields obtained by the hybrid CPS-FDTD algorithm for the Marmousi velocity model in Figure 7. (a) t = 500 ms, (b) t = 600 ms, (c) t = 700 ms and (d) t = 800 ms.
5. Discussion
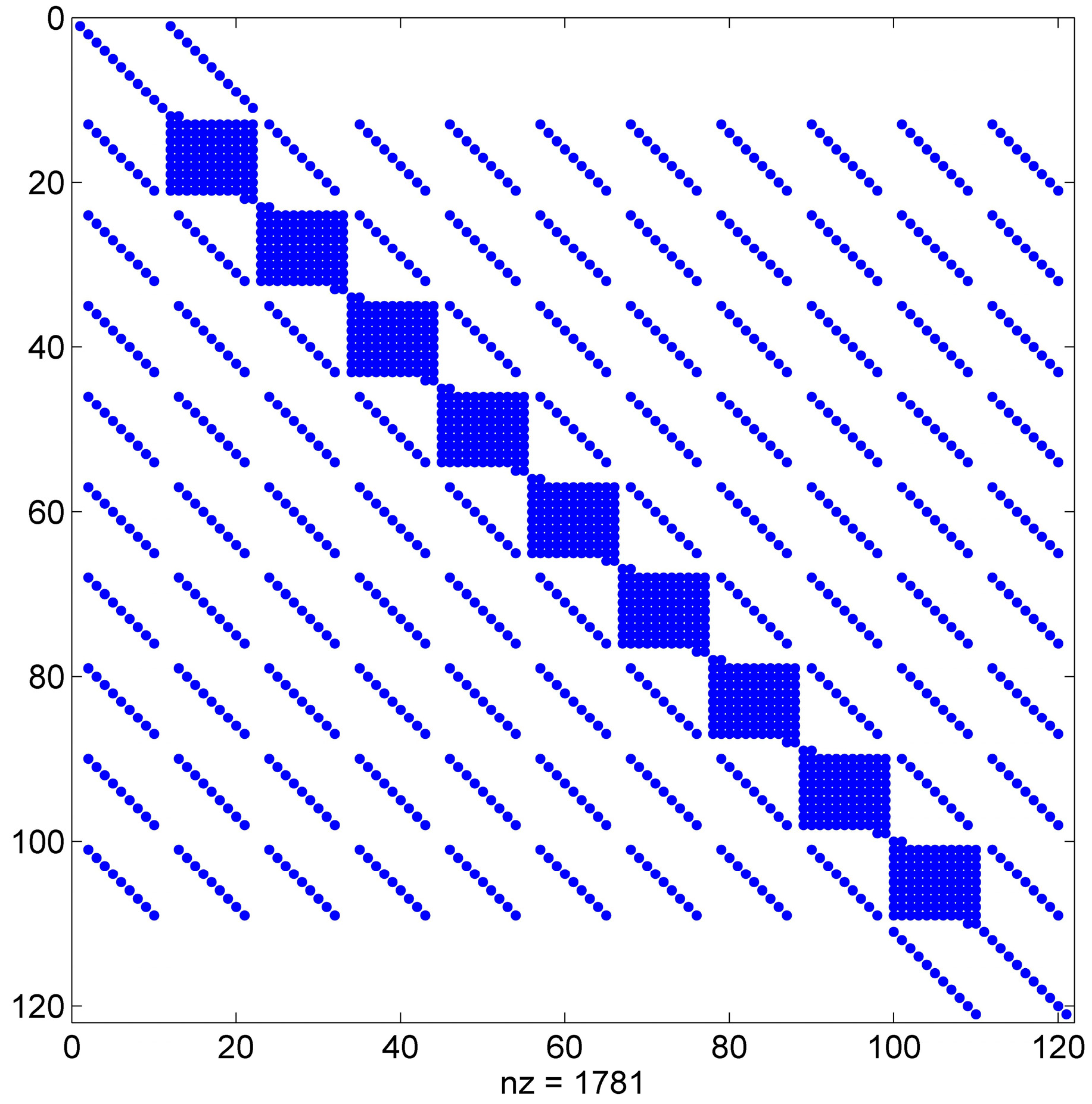
The coefficient matrix K in Equation (29) is a non-sparse, unsymmetric matrix. Figure 9 shows the sparse elements distribution of the coefficient matrix for a 10 × 10 grid (just for illustration purposes). The condition number of matrix K is approximately equal to 1010. Then, Equation (29) is considered an ill-conditioned problem. Therefore, the linear equation generated by the hybrid CPS-FDTD approach can be solved using Krylov-type iterative methods because the direct solution requires a lot of memory and computation. The convergence of Krylov-type methods depends on the number of conditions in the coefficient matrix and the clustering property of the eigenvalues. Meanwhile, the appropriate pre-conditioners, such as LU factorizations, can also significantly improve the speed of convergence.
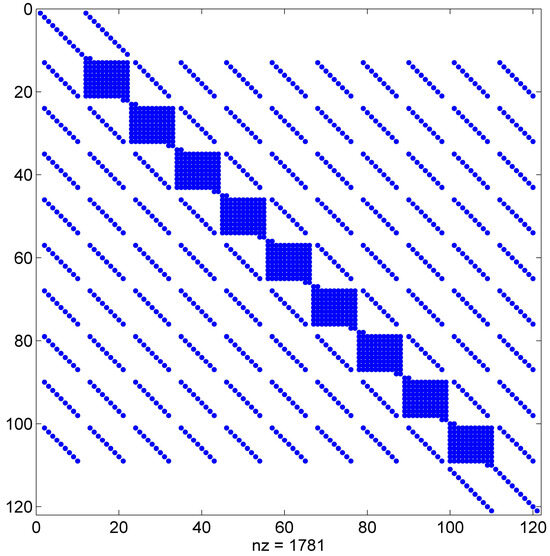
Figure 9.
Schematic diagram of nonzero elements generated by the CPS scheme.
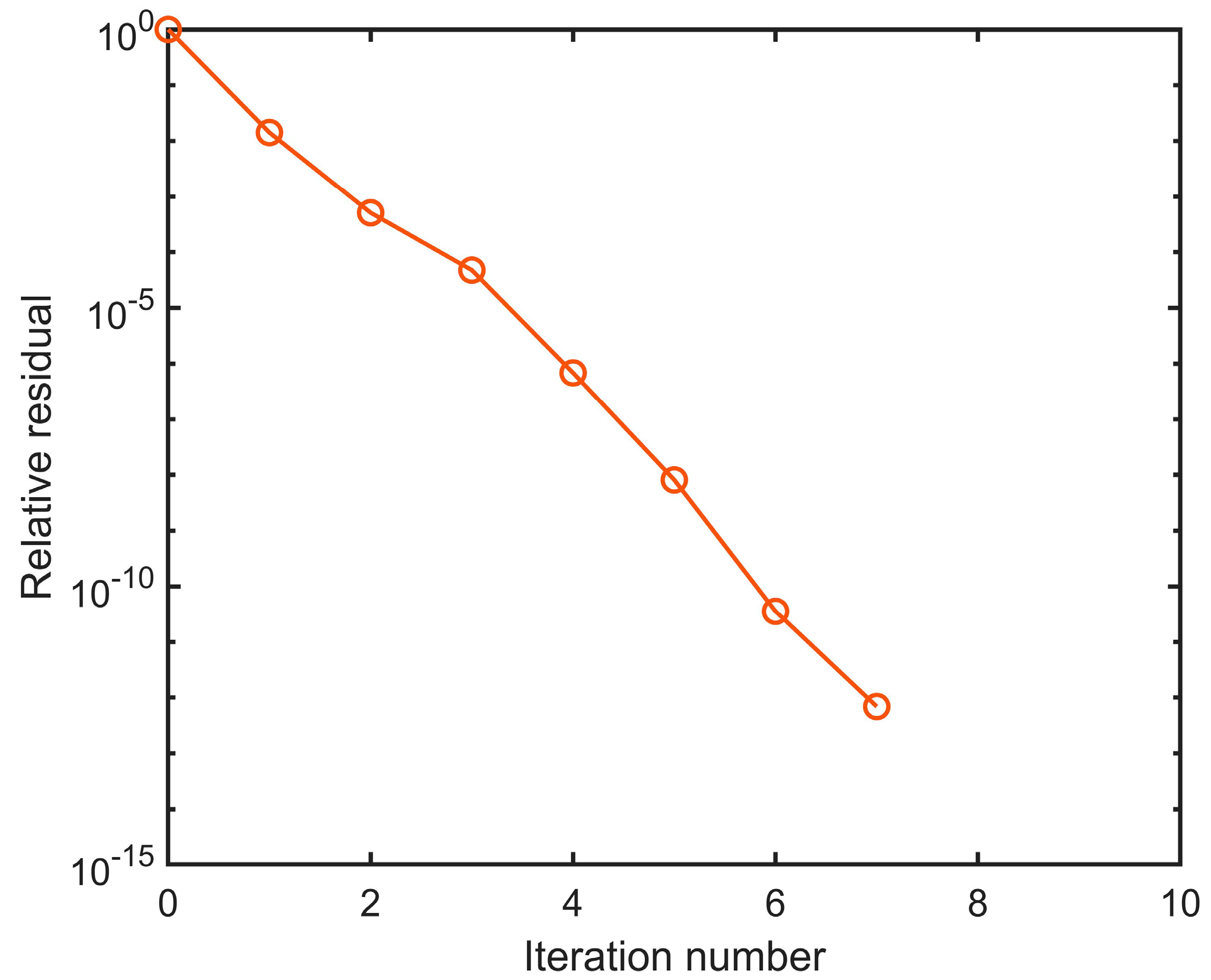
For the numerical simulations of the two-layer acoustic velocity model shown in Figure 3, the computer time is only 1.8 s in the ILU-BICGSTAB iterative method for the discrete elements of 100 × 100 in the space domain. Figure 10 shows the convergence curve and total number of the ILU-BICGSTAB iterative method, suggesting that the relative residual is reduced with the iteration number. The computational time is mainly consumed by the solution of Equation (29).
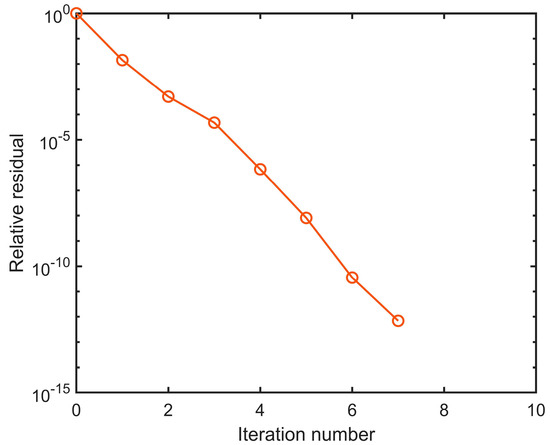
Figure 10.
Convergence curve and total number of the ILU-BICGSTAB iteration for forward equation system.
From the previous discussion, it can be seen that the proposed algorithm in this article will undoubtedly be applied to numerical simulation in seismic wave and geothermal fields.
6. Conclusions
In this study, a hybrid CPS-FDTD scheme has been proposed for the first time to simulate 2D acoustic wave propagation. We present the calculation formulas of this new approach. We also show several application examples to verify the effectiveness and high accuracy of this method. All mathematical formulas of the forward modeling algorithm are presented and coded in MATLAB.
In the proposed hybrid numerical method, the CPS mesh and the FDTD grid are non-overlapping. Acoustic wave propagation problems have been analyzed, and numerical examples demonstrate the accuracy and flexibility. It is different from the conventional FD approach in the spatial domain, which leads to a linear equation with a symmetrical and sparse matrix. Our CPS scheme can lead to a linear equation with a non-sparse and unsymmetrical matrix. Therefore, the computational time and the computer memory spent on solving the CPS linear system equations in the proposed method should be higher than that of the conventional FD method.
Author Contributions
Conceptualization, X.T. and Y.S.; formal analysis, X.T.; funding acquisition, Y.S.; methodology, X.T. and Y.S.; project administration, Y.S.; visualization, X.T.; supervision, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was partly supported by the National Natural Science Foundation of China (grant Nos. 42274083 and 41974049) and partly by the Hunan National Natural Science Foundation (grant No. 2023JJ30659).
Data Availability Statement
Data associated with this research are available and can be obtained by contacting the corresponding author.
Acknowledgments
The authors would like to thank Dawei Gao, who checked the numerical results of this study.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
Appendix A. MATLAB Program for 2D Acoustic Modelling
function [p_num] = Chebyshev_Forward(a,b,c,d,Nx,Nz,v,source)
%Input arguments
%a: Minimum value in x-direction of the computation domain
%b: Maximum value in x-direction of the computation domain
%c: Minimum value in z-direction of the computation domain
%d: Maximum value in z-direction of the computation domain
%dx: Number of elements in x-direction
%dz: Number of elements in x-direction
%v: The velocity matrix
%source: The location of Ricker source
%Output argument
%p_num: Displacement
[Dx,xi] = cheb(Nx);
Dx = Dx/((b − a)/2);
[Dz,eta] = cheb(Nz);
Dz = Dz/((d − c)/2);
x = (a + b)/2 + xi*(b − a)/2;
z = (c + d)/2 + eta*(d − c)/2;
% Source information
T = 1.0;
dt = 1e-3;
N = round(T/dt);
f = 10;
t0 = 0.1;
xs = source(1);
zs = source(2);
% Medium infromation
v_new = reshape(v,(Nx + 1)*(Nz + 1),1);
for i = 1:(Nx + 1)*(Nz + 1)
V(:,i) = v_new;
end
p2 = zeros(Nz + 1,Nx + 1);
p1 = zeros(Nz + 1,Nx + 1);
p0 = zeros(Nz + 1,Nx + 1);
% Chebyshev differentiation matrix
Dx2 = Dx^2;
I1 = eye(Nz + 1);
Lx = kron(Dx2,I1);
Dz2 = Dz^2;
I2 = eye(Nx + 1);
Lz = kron(I2,Dz2);
Lxz = Lx + Lz;
for k = 1:N
t = k*dt;
p1(zs,xs) = ricker(f,t,t0);
I = eye((Nx + 1)*(Nz + 1));
L = I/dt/dt − V.*V.*Lxz;
P = (2/dt/dt)*reshape(p1,(Nz + 1)*(Nx + 1),1) −...
(1/dt/dt)*reshape(p0,(Nz + 1)*(Nx + 1),1);
% Clayton-Enquist absorbing boundary
for i = 1:Nz + 1
for j = 1:Nx + 1
s = (j − 1)*(Nz + 1) + i;
pp1 = reshape(p1,(Nz + 1)*(Nx + 1),1);
if(j == 1)
L(s,:) = 0;
L(s,s) = 1/dt + v(i,j)/(x(j + 1) − x(j));
L(s,s + Nz + 1) = −(v(i,j)/(x(j + 1) − x(j)));
P(s,1) = pp1(s)/dt;
elseif(j == Nx + 1)
L(s,:) = 0;
L(s,s) = 1/dt + v(i,j)/(x(j) − x(j−1));
L(s,s − Nz − 1) = −(v(i,j)/(x(j) − x(j−1)));
P(s,1) = pp1(s)/dt;
elseif(i == 1)
L(s,:) = 0;
L(s,s) = 1/dt + v(i,j)/(z(i + 1) − z(i));
L(s,s + 1) = −(v(i,j)/(z(i + 1) − z(i)));
P(s,1) = pp1(s)/dt;
elseif(i == Nz + 1)
L(s,:) = 0;
L(s,s) = 1/dt + v(i,j)/(z(i) − z(i − 1));
L(s,s−1) = −(v(i,j)/(z(i) − z(i − 1)));
P(s,1) = pp1(s)/dt;
end
end
end
p_new = L\P;
p2 = reshape(p_new,Nz + 1,Nx + 1);
p_num(:,:,k) = p2;
p0 = p1;
p1 = p2;
xx = a:0.01*(b − a)/Nx:b;
zz = c:0.01*(d − c)/Nz:d;
[xi,zi] = meshgrid(xx,zz);
p2_new = interp2(x,z,p2,xi,zi,‘spline’);
imagesc(xi(1,:),zi(:,1),p2_new);
caxis([−0.07 0.07])
colorbar;
title([‘Numerical solution: t=’,num2str(1000*k*dt),‘ms’]);
xlabel(‘Distance(m)’);
ylabel(‘Depth(m)’);
drawnow;
pause(0.1);
end
References
- Cordova, L.J.; Rojas, O.; Otero, B.; Castillo, J. Compact finite difference modeling of 2-D acoustic wave propagation. J. Comput. Appl. Math. 2016, 295, 83–91. [Google Scholar] [CrossRef]
- Liao, W.; Yong, P.; Dastour, H.; Huang, J. Efficient and accurate numerical simulation of acoustic wave propagation in a 2D heterogeneous media. Appl. Math. Comput. 2018, 321, 385–400. [Google Scholar] [CrossRef]
- Solano-Feo, F.; Guevara-Jordan, J.M.; Rojas, O.; Otero, B.; Rodriguez, R. A new mimetic scheme for the acoustic wave equation. J. Comput. Appl. Math. 2016, 295, 2–12. [Google Scholar] [CrossRef]
- Malkoti, A.; Vedanti, N.; Tiwari, R.K. A highly efficient implicit finite difference scheme for acoustic wave propagation. J. Appl. Geophys. 2019, 161, 204–215. [Google Scholar] [CrossRef]
- Wang, E.; Liu, Y.; Sen, M.K. Effective finite-difference modelling methods with 2-D acoustic wave equation using a combination of cross and rhombus stencils. Geophys. J. Int. 2016, 206, 1933–1958. [Google Scholar] [CrossRef]
- Lei, W.; Liu, Y.; Li, G.; Zhu, S.; Chen, G.; Li, C. 2D frequency-domain finite-difference acoustic wave modeling using optimized perfectly matched layers. Geophysics 2023, 88, F1–F13. [Google Scholar] [CrossRef]
- Xu, W.; Gao, J. Adaptive 9-point frequency-domain finite difference scheme for wavefield modeling of 2D acoustic wave equation. J. Geophys. Eng. 2018, 15, 1432–1445. [Google Scholar] [CrossRef]
- Aimakov, N.; Tanner, G.; Chronopoulos, D. A wave finite element approach for modelling wave transmission through laminated plate junctions. Sci. Rep. 2022, 1852, 937–951. [Google Scholar] [CrossRef]
- Gao, K.; Fu, S.; Chung, E.T. A high-order multiscale finite-element method for time-domain acoustic-wave modeling. J. Comput. Phys. 2018, 360, 120–136. [Google Scholar] [CrossRef]
- Hermann, V.; Kaser, M.; Castro, C.E. Non-conforming hybrid meshes for efficient 2-D wave propagation using the Discontinuous Galerkin Method. Geophys. J. Int. 2011, 184, 746–758. [Google Scholar] [CrossRef]
- Moczo, P.; Kristek, J.; Galis, M.; Chaljub, E.; Etienne, V. 3-D finite-difference, finite-element, discontinuous-Galerkin and spectral-element schemes analysed for their accuracy with respect to P-wave to S-wave speed ratio. Geophys. J. Int. 2011, 187, 1645–1667. [Google Scholar] [CrossRef]
- Reboul, S.; Perrey-Debain, E.; Zerbib, N.; Moreau, S. A 2D frequency-domain finite element formulation for solving the wave equation in the presence of rotating obstacles. Wave Motion 2023, 121, 103171. [Google Scholar] [CrossRef]
- Fornberg, B. The pseudospectral method: Comparisons with finite difference for the elastic wave equation. Geophysics 1987, 52, 483–501. [Google Scholar] [CrossRef]
- Liu, Q.H. The pseudospectral time-domain (PSTD) algorithm for acoustic waves in absorptive media. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 1044–1055. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Wise, E.S.; Kuklis, F.; Jaros, J.; Cox, B.T. Nonlinear ultrasound simulation in an axisymmetric coordinate system using a k-space pseudospectral method. J. Acoust. Soc. Am. 2020, 148, 2288–2300. [Google Scholar] [CrossRef] [PubMed]
- Komatitsch, D.; Tromp, J. Introduction to the spectral element method for three-dimensional seismic wave propagation. Geophys. J. Int. 1999, 139, 806–822. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation. Geophys. J. Int. 2002, 149, 390–412. [Google Scholar] [CrossRef]
- Zhu, C.; Qin, G.; Zhang, J. Implicit Chebyshev spectral element method for acoustics wave equations. Finite Elem. Anal. Des. 2011, 47, 184–194. [Google Scholar] [CrossRef]
- Zou, P.; Cheng, J. Pseudo-spectral method using rotated staggered grid for elastic wave propagation in 3D arbitrary anisotropic media. Geophys. Prospect. 2018, 66, 47–61. [Google Scholar] [CrossRef]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Kosloff, D.D.; Baysal, E. Forward modeling by a Fourier method. Geophysics 1982, 47, 1402–1412. [Google Scholar] [CrossRef]
- Tong, X.; Sun, Y.; Guo, R. A Chebyshev pseudo-spectral approach for simulating magnetotelluric TM-mode responses on 2D structures. J. Appl. Geophys. 2020, 179, 104085. [Google Scholar] [CrossRef]
- Raggio, G. A pseudo spectral Chebyshev scheme for forward acoustic modeling. ZAMM J. Appl. Math. Mech. 1986, 66, 545–553. [Google Scholar] [CrossRef]
- Eisinberg, A.; Fedele, G. Discrete orthogonal polynomials on Gauss-Lobatto Chebyshev nodes. J. Approx. Theory 2007, 144, 238–246. [Google Scholar] [CrossRef]
- Odeyemi, T.; Mohammadian, A.; Seidou, O. Application of the Chebyshev pseudospectral method to van der Waals fluids. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3499–3507. [Google Scholar] [CrossRef]
- Baltensperger, R.; Berrut, J.P. The errors in calculating the pseudospectral differentiation matrices for Chebyshev-Gauss_Lobatto points. Comput. Math. Appl. 1999, 37, 41–48. [Google Scholar] [CrossRef]
- Jiwari, R.; Pandit, S.; Mittal, R.C. A differential quadrature algorithm to solve the two dimensional linear hyperbolic telegraph equation with Dirichlet and Neumann boundary conditions. Appl. Math. Comput. 2012, 218, 7279–7294. [Google Scholar] [CrossRef]
- Kumar, V.; Jiwari, R.; Gupta, R.K. Numerical simulation of two dimensional quasilinear hyperbolic equations by polynomial differential quadrature method. Eng. Comput. 2013, 30, 892–909. [Google Scholar] [CrossRef]
- Pandit, S.; Kunar, M.; Tiwari, S. Numerical Simulation of Second-Order One Dimensional Hyperbolic Telegraph Equation. Comput. Phys. Commun. 2015, 187, 83–90. [Google Scholar] [CrossRef]
- Gao, Y.; Song, H.; Zhang, J.; Yao, Z. Comparison of artificial absorbing boundaries for acoustic wave equation modelling. Explor. Geophys. 2017, 48, 76–93. [Google Scholar] [CrossRef]
- Liu, Y.; Sen, M.K. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation. Geophysics 2010, 75, A1–A6. [Google Scholar] [CrossRef]
- Narayannan, T.V.; Yoder, P.D. Perfectly matched layer boundary conditions for quantum phase space transport. Phys. Lett. A 2007, 367, 288–290. [Google Scholar] [CrossRef]
- Clayton, R.; Engquist, B. Absorbing boundary conditions for acoustic and elastic wave equations. Bull. Seism. Soc. Am. 1977, 67, 1529–1540. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).