On the Bessel Solution of Kepler’s Equation
Abstract
1. Introduction
2. Bessel’ Solution of Elliptic Kepler’s Equation
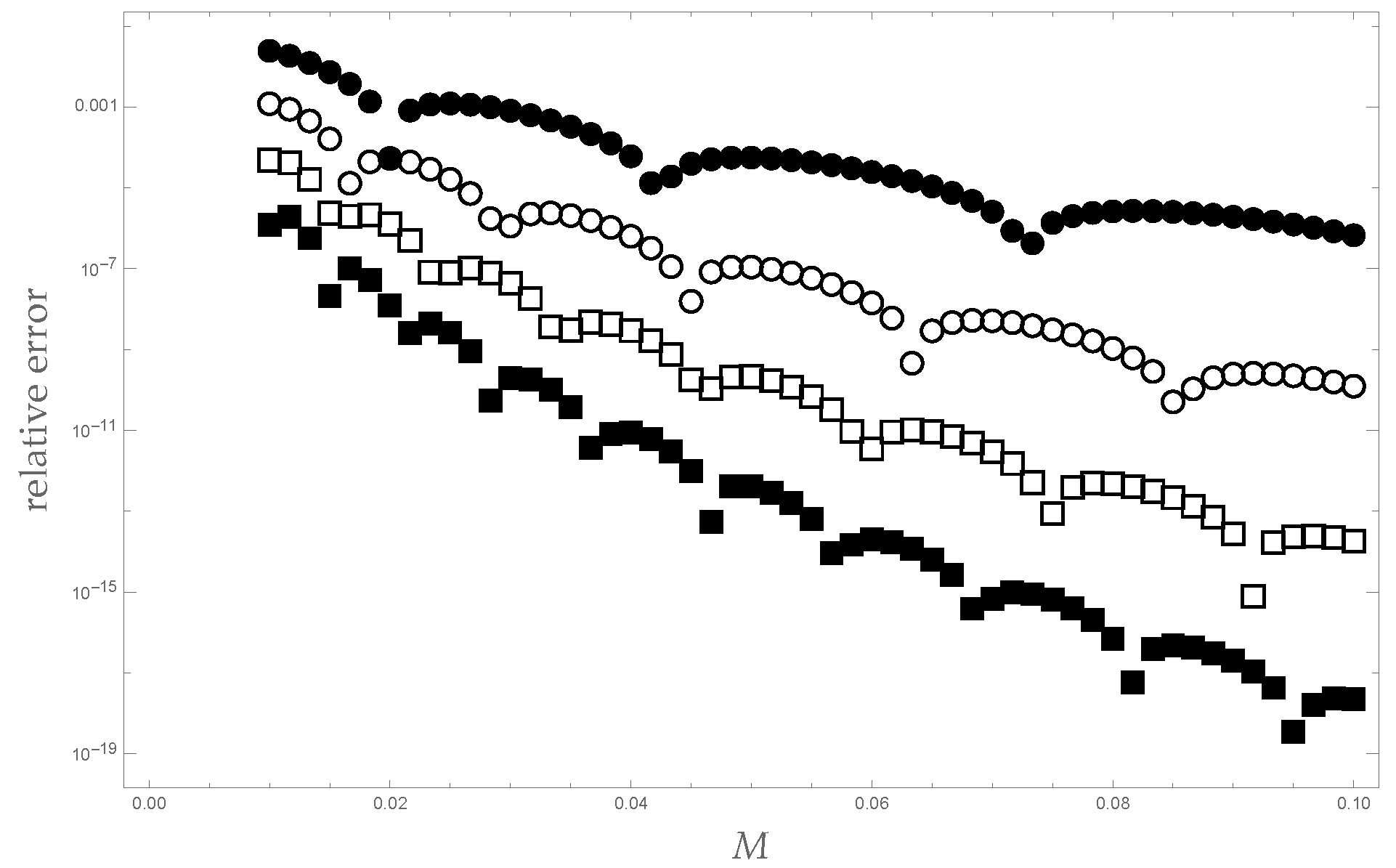
3. A Constructive Proof That Is a Stieltjes Series
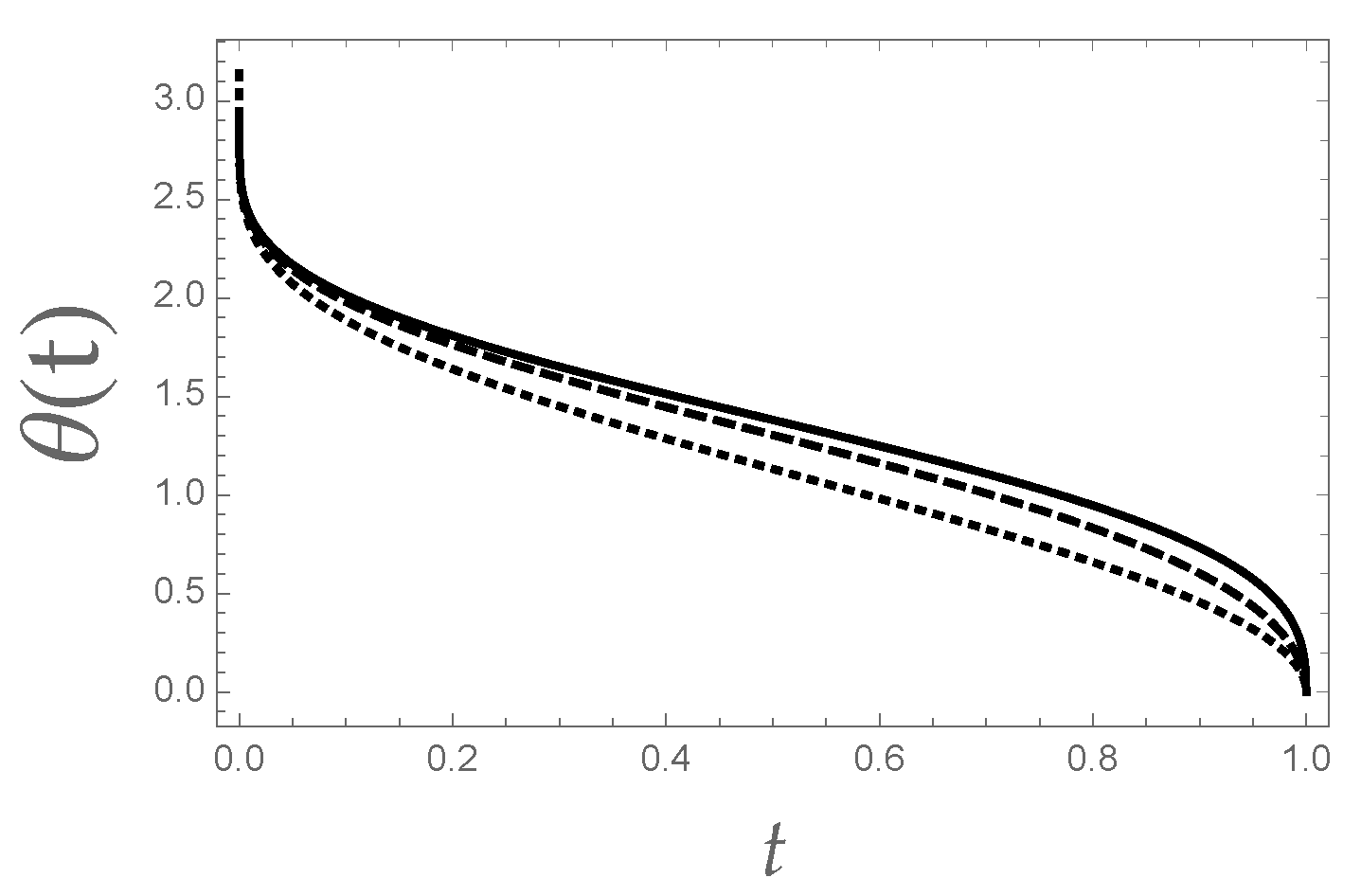
4. A New Integral Representation of KE’s Solution
5. Discussions
6. Conclusions
In common with almost any scientific problem which achieves a certain longevity and whose literature exceeds a certain critical mass, the Kepler problem has acquired luster and allure for the modern practitioner. Any new technique for the treatment of trascendental equations should be applied to this illustrious case; any new insight, however slight, lets its conceiver join an eminent list of contributors.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Colwell, P. Solving Kepler’s Equation Over Three Centuries; Willmann-Bell: Richmond, VA, USA, 1993. [Google Scholar]
- Ibrahim, R.; Saleh, A.R. Re-evaluation solution methods for Kepler’s equation of an elliptical orbit. Iraqi J. Sci. 2019, 60, 2269–2279. [Google Scholar] [CrossRef]
- Calvo, M.; Elipe, A.; Montijano, J.; Rández, L. A monotonic starter for solving the hyperbolic Kepler equation by Newton method. Celest. Mech. Dyn. Astron. 2019, 131, 18. [Google Scholar] [CrossRef]
- Tommasini, D.; Olivieri, D. Fast switch and spline scheme for accurate inversion of nonlinear functions: The new first choice solution to Kepler’s equation. Appl. Math. Comput. 2020, 364, 124677. [Google Scholar] [CrossRef]
- Abubekerov, M.K.; Gostev, N.Y. Solution of Kepler’s Equation with Machine Precision. Astron. Rep. 2020, 64, 1060–1066. [Google Scholar] [CrossRef]
- Sacchetti, A. Francesco Carlini: Kepler’s equation and the asymptotic solution to singular differential equations. Hist. Math. 2020, 53, 1–32. [Google Scholar] [CrossRef]
- Tommasini, D.; Olivieri, D. Fast Switch and Spline Function Inversion Algorithm with Multistep Optimization and k-Vector Search for Solving Kepler’s Equation in Celestial Mechanics. Mathematics 2020, 8, 2017. [Google Scholar] [CrossRef]
- Zechmeister, M. Solving Kepler’ss equation with CORDIC double iterations. Mon. Not. R. Astron. Soc. 2021, 500, 109–117. [Google Scholar] [CrossRef]
- González-Gaxiola, O.; Hernández-Linares, S. An Efficient Iterative Method for Solving the Elliptical Kepler’s Equation. Int. J. Appl. Comput. Math. 2021, 7, 42. [Google Scholar] [CrossRef]
- Tommasini, D. Bivariate Infinite Series Solution of Kepler’s Equation. Mathematics 2021, 9, 785. [Google Scholar] [CrossRef]
- Philcox, O.H.E.; Goodman, J.; Slepian, Z. Kepler’s Goat Herd: An exact solution to Kepler’s equation for elliptical orbits. Mon. Not. R. Astron. Soc. 2021, 506, 6111–6116. [Google Scholar] [CrossRef]
- Tommasini, D.; Olivieri, D. Two fast and accurate routines for solving the elliptic Kepler equation for all values of the eccentricity and mean anomaly. Astron. Astrophys. 2022, 658, A196. [Google Scholar] [CrossRef]
- Zhang, R.; Bian, S.; Li, H. Symbolic iteration method based on computer algebra analysis for Kepler’s equation. Sci. Rep. 2022, 12, 2957. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zhou, Y.; Lim, C.W.; Zhong, H. A new solution approach via analytical approximation of the elliptic Kepler equation. Acta Astronaut. 2023, 202, 303–310. [Google Scholar] [CrossRef]
- Vavrukh, M.; Dzikovskyi, D.; Stelmakh, O. Analytical images of Kepler’s equation solutions and their applications. Math. Model. Comput. 2023, 10, 351–358. [Google Scholar] [CrossRef]
- Calvo, M.; Elipe, A.; Rández, L. On the integral solution of elliptic Kepler’s equation. Celest. Mech. Dyn. Astron. 2023, 135, 26. [Google Scholar] [CrossRef]
- Brown, M.T. An improved cubic approximation for K epler’s equation. Mon. Not. R. Astron. Soc. 2023, 525, 57–66. [Google Scholar] [CrossRef]
- Kapteyn, W. Researches sur les functions de Fourier-Bessel. Ann. Sci. L’Ecole Norm. Sup. Ser. 1893, 3, 91–122. [Google Scholar]
- Dominici, D. A new Kapteyn series. Integral Transform. Spec. Funct. 2007, 18, 409–418. [Google Scholar] [CrossRef]
- Lerche, I.; Tautz, R. A note on summation of kapteyn series in astrophysical problems. Astrophys. J. 2007, 665, 1288–1291. [Google Scholar] [CrossRef]
- Pogány, T.K. Convergence of generalized Kapteyn expansion. Appl. Math. Comput. 2007, 190, 1844–1847. [Google Scholar] [CrossRef]
- Lerche, I.; Tautz, R. Kapteyn series arising in radiation problems. J. Phys. A Math. Theor. 2008, 41, 035202. [Google Scholar] [CrossRef]
- Lerche, I.; Tautz, R.; Citrin, D. Terahertz-sideband spectra involving Kapteyn series. J. Phys. A Math. Theor. 2009, 42, 365206. [Google Scholar] [CrossRef]
- Eisinberg, A.; Fedele, G.; Ferrise, A.; Frascino, D. On an integral representation of a class of Kapteyn (Fourier-Bessel) series: Kepler’s equation, radiation problems and Meissel’s expansion. Appl. Math. Lett. 2010, 23, 1331–1335. [Google Scholar] [CrossRef]
- Tautz, R.C.; Lerche, I.; Dominici, D. Methods for summing general Kapteyn series. J. Phys. A Math. Theor. 2011, 44, 385202. [Google Scholar] [CrossRef]
- Baricz, A.; Jankov, D.; Pogány, T.K. Integral representation of first kind Kapteyn series. J. Math. Phys. 2011, 52, 043518. [Google Scholar] [CrossRef]
- Nikishov, A.I. Kapteyn series and photon emission. Bull. Lebedev Phys. Inst. 2014, 41, 332–338. [Google Scholar] [CrossRef]
- Baricz, A.; Masirevic, D.J.; Pogány, T.K. Kapteyn Series. Lect. Notes Math. 2017, 2207, 87–111. [Google Scholar]
- Xue, X.; Li, Z.; Man, Y.; Xing, S.; Liu, Y.; Li, B.; Wu, Q. Improved Massive MIMO RZF Precoding Algorithm Based on Truncated Kapteyn Series Expansion. Information 2019, 10, 136. [Google Scholar] [CrossRef]
- Bornemann, F. A Jentzsch-Theorem for Kapteyn, Neumann and General Dirichlet Series. Comput. Methods Funct. Theory 2023, 23, 723–739. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Baker, G.A., Jr.; Graves-Morris, P. Padé Approximants, 2nd ed.; Cambridge U. P.: Cambridge, UK, 1996. [Google Scholar]
- Widder, D.V. The Stieltjes transform. Trans. Am. Math. Soc. 1938, 43, 7–60. [Google Scholar] [CrossRef]
- Brezinski, C. Extrapolation algorithms and Padé approximations: A historical survey. Appl. Numer. Math. 1996, 20, 299–318. [Google Scholar] [CrossRef]
- Orlando, F.; Farina, C.; Zarro, C.; Terra, P. Kepler’s equation and some of its pearls. Am. J. Phys. 2018, 86, 11. [Google Scholar] [CrossRef]
- Watson, G.N. A Treatise on the Theory of Bessel Functions; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Caliceti, E.; Meyer-Hermann, M.; Ribeca, P.; Surzhykov, A.; Jentschura, U.D. From useful algorithms for slowly convergent series to physical predictions based on divergent perturbative expansions. Phys. Rep. 2007, 446, 1–96. [Google Scholar] [CrossRef]
- Allen, G.D.; Chui, C.K.; Madych, W.R.; Narcowich, F.J.; Smith, P.W. Padé approximation of Stieltjes series. J. Approx. Theory 1975, 14, 302–316. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Olde Daalhuis, A.B.; Lozier, D.W.; Schneider, B.I.; Boisvert, R.F.; Clark, C.W.; Miller, B.R.; Saunders, B.V.; Cohl, H.S.; McClain, M.A. (Eds.) NIST Digital Library of Mathematical Functions; Release 1.1.3 of 2021-09-15; NIST: Gaithersburg, MD, USA, 2022. [Google Scholar]
- Watson, G.N. Bessel functions and Kapteyn series. Proc. Lond. Math. Soc. 1917, 16, 150–174. [Google Scholar] [CrossRef]
- Siegel, K.M. An inequality involving Bessel functions of argument nearly equal to their order. Proc. Am. Math. Soc. 1953, 4, 858–859. [Google Scholar] [CrossRef]
- Farnocchia, D.; Cioci, D.B.; Milani, A. Robust resolution of Kepler’s equation in all eccentricity regimes. Celest. Mech. Dyn. Astron. 2013, 116, 21–34. [Google Scholar] [CrossRef]
- Bender, C.M.; Weniger, E.J. Numerical evidence that the perturbation expansion for a non-Hermitian -symmetric Hamiltonian is Stieltjes. J. Math. Phys. 2001, 42, 2167–2183. [Google Scholar] [CrossRef]
- Grecchi, V.; Maioli, M.; Martinez, A. Padé summability of the cubic oscillator. J. Phys. A 2009, 42, 425208. [Google Scholar] [CrossRef]
- Levin, D. Development of non-linear transformations for improving convergence of sequences. Int. J. Comput. Math. B 1973, 3, 371–388. [Google Scholar] [CrossRef]
- Weniger, E.J. Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series. Comput. Phys. Rep. 1989, 10, 189–371. [Google Scholar] [CrossRef]
- Borghi, R.; Weniger, E.J. Convergence analysis of the summation of the factorially divergent Euler series by Padé approximants and the delta transformation. Appl. Numer. Math. 2015, 94, 149–178. [Google Scholar] [CrossRef]
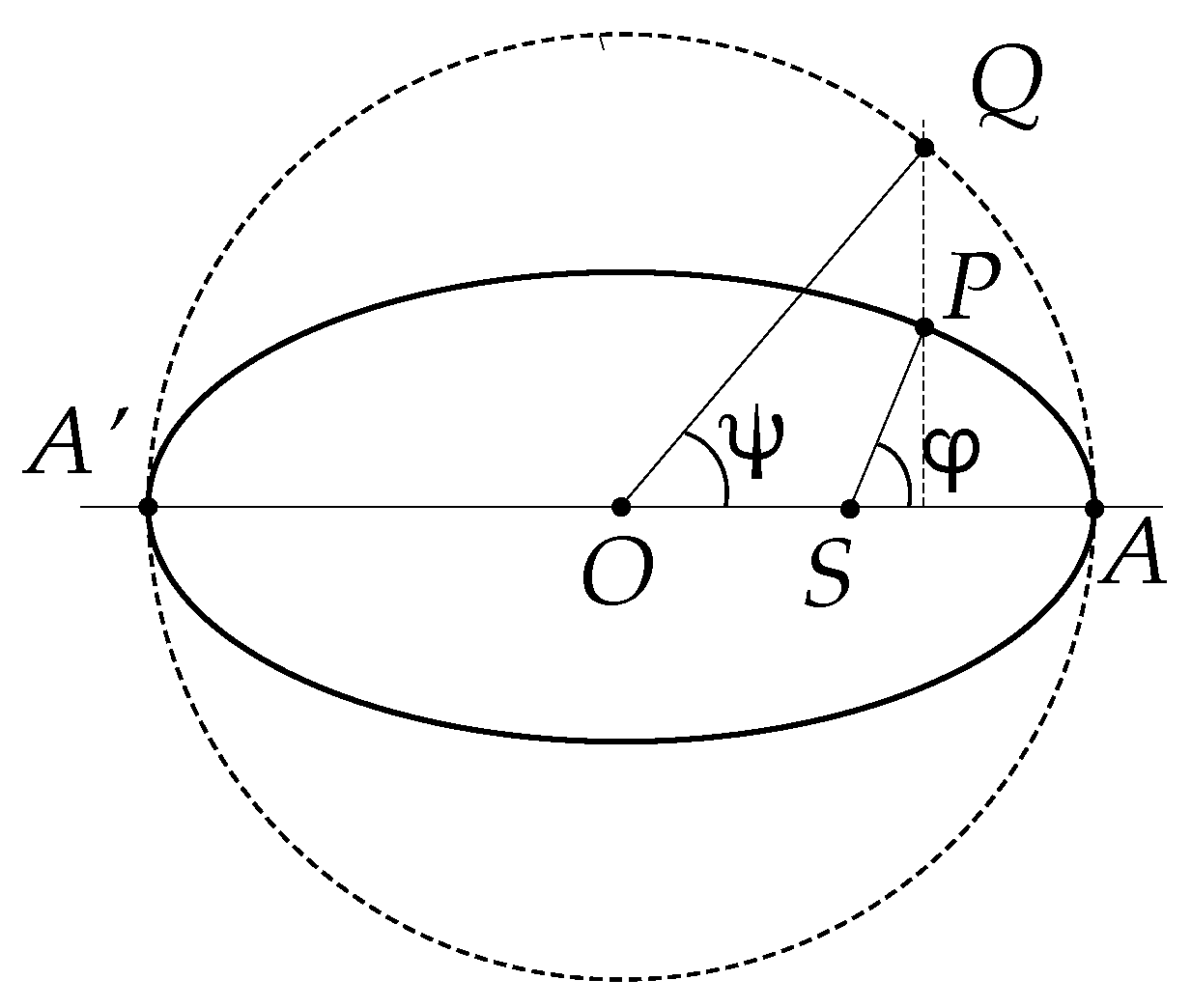

| Order | Partial Sum Sequence | Weniger -Transformation |
|---|---|---|
| 1 | 2.02 + 3.51 i | 0.112240 + 1.211289 i |
| 10 | (4.4 − 10 i) | −1.003096 + 1.238166 i |
| 20 | (−3.1 + 32 i) | −1.001839 + 1.238763 i |
| 30 | (7.7 + 10 i) | −1.001838 + 1.238765 i |
| … | … | … |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borghi, R. On the Bessel Solution of Kepler’s Equation. Mathematics 2024, 12, 154. https://doi.org/10.3390/math12010154
Borghi R. On the Bessel Solution of Kepler’s Equation. Mathematics. 2024; 12(1):154. https://doi.org/10.3390/math12010154
Chicago/Turabian StyleBorghi, Riccardo. 2024. "On the Bessel Solution of Kepler’s Equation" Mathematics 12, no. 1: 154. https://doi.org/10.3390/math12010154
APA StyleBorghi, R. (2024). On the Bessel Solution of Kepler’s Equation. Mathematics, 12(1), 154. https://doi.org/10.3390/math12010154






