New One-Parameter Over-Dispersed Discrete Distribution and Its Application to the Nonnegative Integer-Valued Autoregressive Model of Order One
Abstract
:1. Introduction
2. Poisson New X-Lindley Distribution
2.1. The Poisson New X-Lindley Distribution and Its Statistical Properties
2.2. Moments, Skewness, and Kurtosis
3. Estimation of Parameters
3.1. Maximum Likelihood Estimation
3.2. Method of Moments
3.3. Least Squares and Weighted Least Squares Estimation
3.4. Simulation Study
4. The INAR(1) Process with PNXL Innovations
4.1. Estimation of INAR(1)PNXL Process
4.1.1. Conditional Maximum Likelihood
4.1.2. Yule–Walker
4.1.3. Conditional Least Squares
4.2. Simulation of INAR(1)PNXL Process
5. Data Analysis
5.1. Corn Borer Data
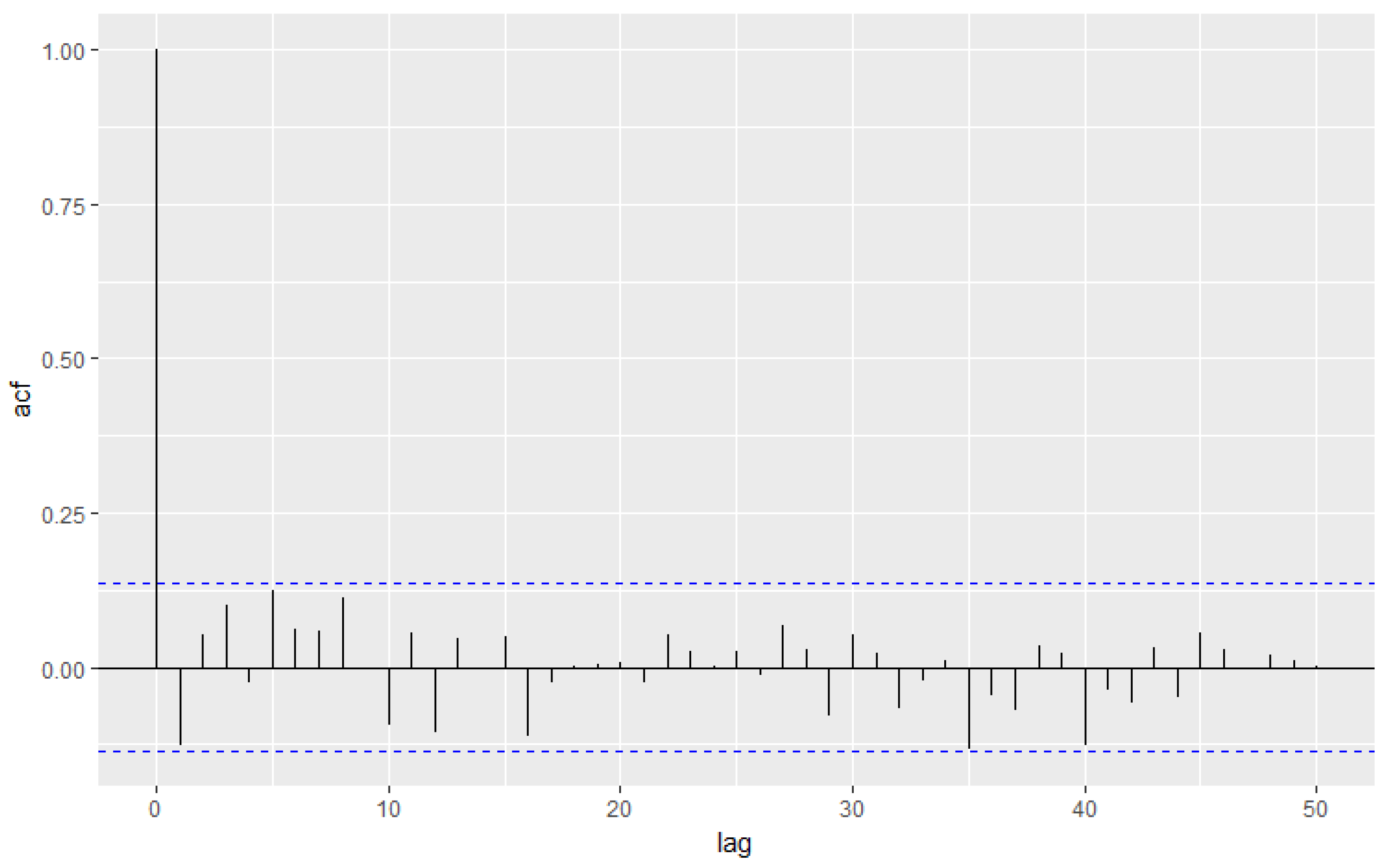
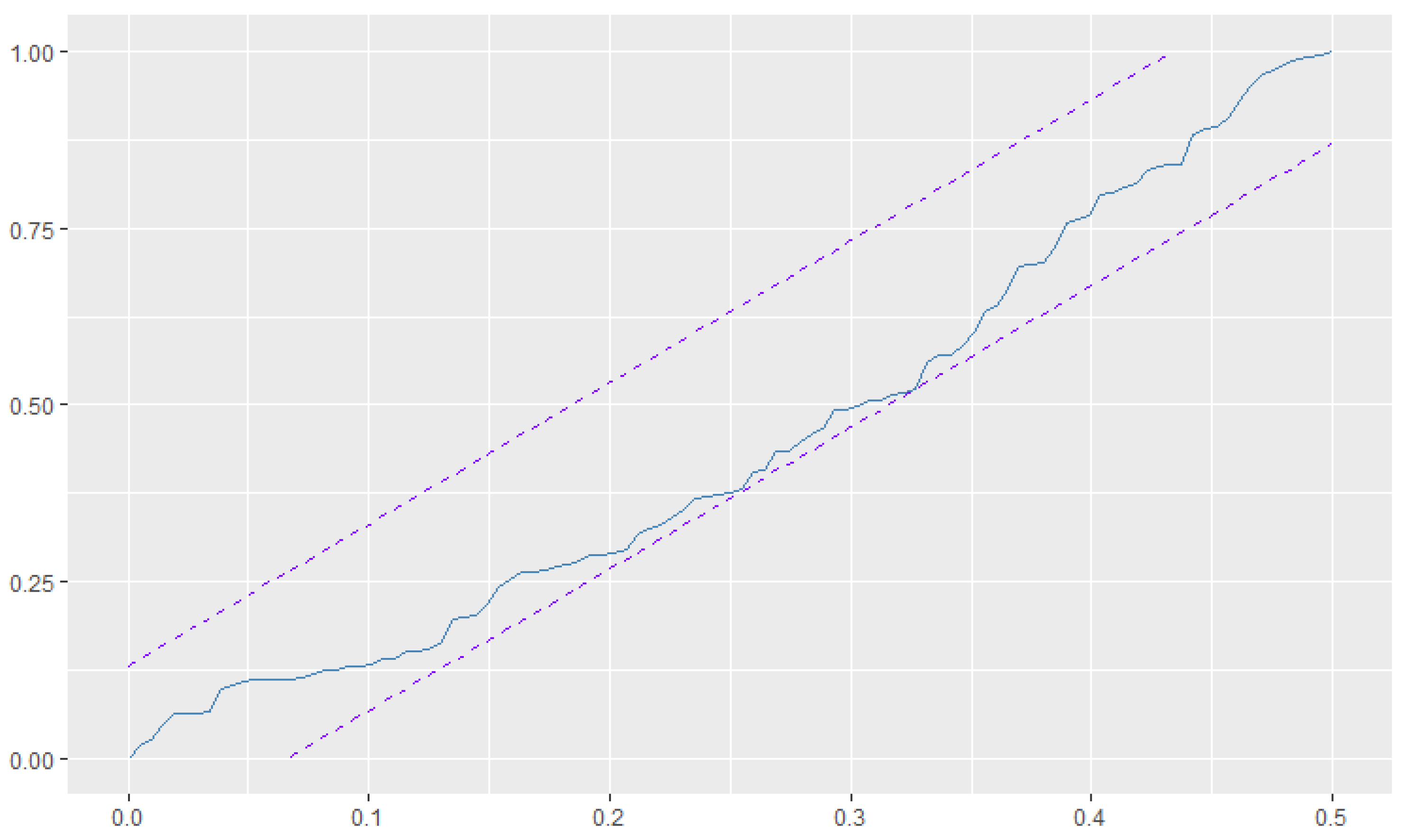
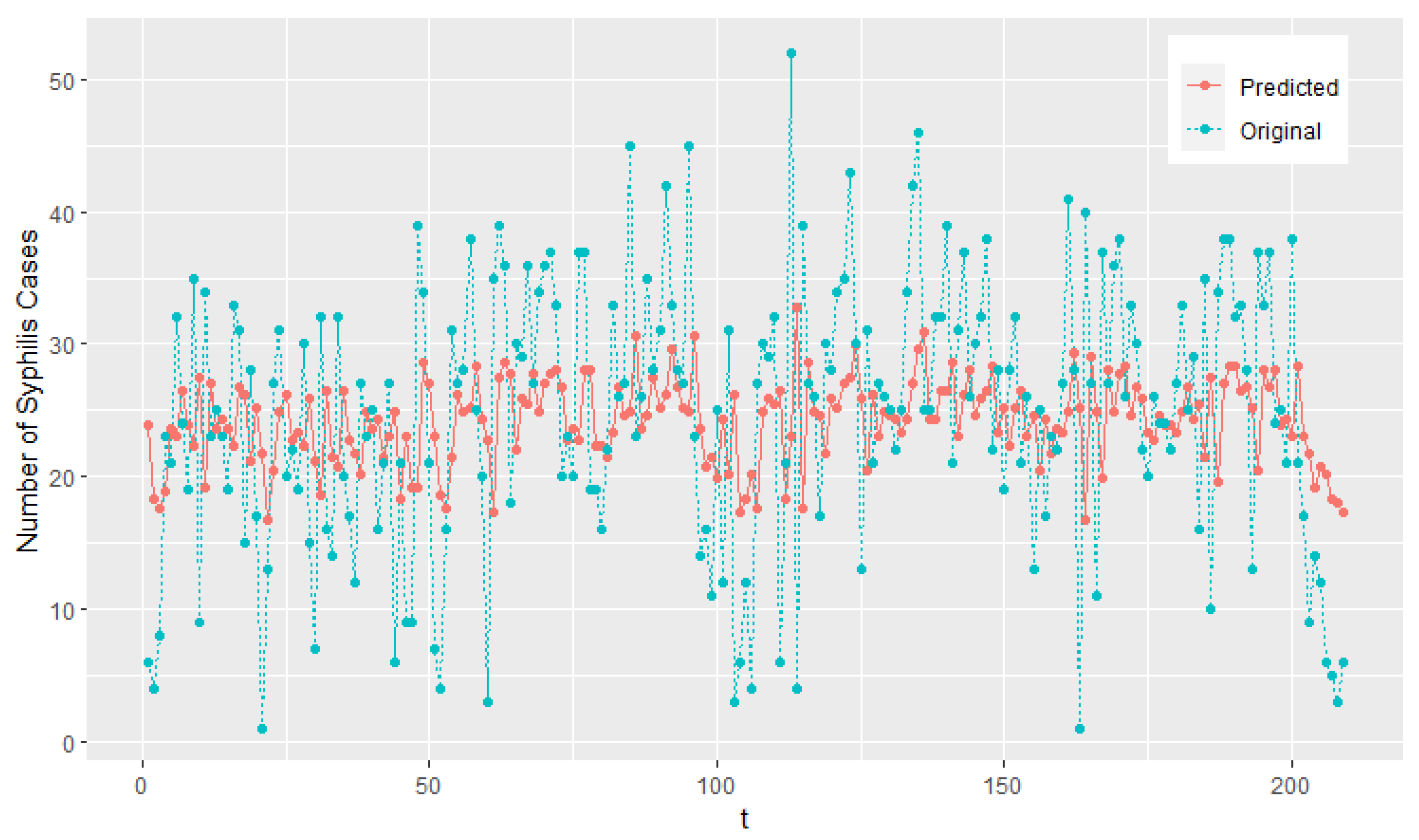
5.2. Weekly Number of Syphilis Cases Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bliss, C.I.; Fisher, R.A. Fitting the negative binomial distribution to biological data. Biometrics 1953, 9, 176–200. [Google Scholar] [CrossRef]
- Bereta, E.M.; Louzanda, F.; Franco, M.A. The Poisson-Weibull distribution. Adv. Appl. Stat. 2011, 22, 107–118. [Google Scholar]
- Sellers, K.F.; Borle, S.; Shmueli, G. The COM-Poisson model for count data: A survey of methods and applications. Appl. Stoch. Model. Bus. Ind. 2012, 28, 104–116. [Google Scholar] [CrossRef]
- Abd El-Monsef, M.; Sohsah, N. Poisson–transmuted Lindley distribution. J. Adv. Math. 2016, 11, 5631–5638. [Google Scholar] [CrossRef]
- Bhati, D.; Kumawat, P.; Gómez-Déniz, E. A new count model generated from mixed Poisson transmuted exponential family with an application to health care data. Commun. Stat. Theory Methods 2017, 46, 11060–11076. [Google Scholar] [CrossRef]
- Grine, R.; Zeghdoudi, H. On Poisson quasi-Lindley distribution and its applications. J. Mod. Appl. Stat. Methods 2017, 16, 21. [Google Scholar] [CrossRef]
- Altun, E. A new one-parameter discrete distribution with associated regression and integer-valued autoregressive models. Math. Slovaca 2020, 70, 979–994. [Google Scholar] [CrossRef]
- Altun, E.; Cordeiro, G.M.; Ristić, M.M. An one-parameter compounding discrete distribution. J. Appl. Stat. 2022, 49, 1935–1956. [Google Scholar] [CrossRef]
- Maya, R.; Chesneau, C.; Krishna, A.; Irshad, M.R. Poisson Extended Exponential Distribution with Associated INAR(1) Process and Applications. Stats 2022, 5, 755–772. [Google Scholar] [CrossRef]
- Irshad, M.; D’cruz, V.; Maya, R.; Mamode Khan, N. Inferential properties with a novel two parameter Poisson generalized Lindley distribution with regression and application to INAR(1) process. J. Biopharm. Stat. 2023, 33, 335–356. [Google Scholar] [CrossRef]
- Al-Osh, M.A.; Alzaid, A.A. First-order integer-valued autoregressive (INAR(1)) process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Aghababaei Jazi, M.; Jones, G.; Lai, C.D. Integer valued AR(1) with geometric innovations. J. Iran. Stat. Soc. 2012, 11, 173–190. [Google Scholar]
- Eliwa, M.S.; Altun, E.; El-Dawoody, M.; El-Morshedy, M. A new three-parameter discrete distribution with associated INAR(1) process and applications. IEEE Access 2020, 8, 91150–91162. [Google Scholar] [CrossRef]
- Huang, J.; Zhu, F. A new first-order integer-valued autoregressive model with Bell innovations. Entropy 2021, 23, 713. [Google Scholar] [CrossRef] [PubMed]
- Altun, E.; El-Morshedy, M.; Eliwa, M. A study on discrete Bilal distribution with properties and applications on integer valued autoregressive process. REVSTAT-Stat. J. 2022, 20, 501–528. [Google Scholar]
- Lívio, T.; Khan, N.M.; Bourguignon, M.; Bakouch, H.S. An INAR(1) model with Poisson–Lindley innovations. Econ. Bull. 2018, 38, 1505–1513. [Google Scholar]
- Altun, E. A new generalization of geometric distribution with properties and applications. Commun. Stat. Simul. Comput. 2020, 49, 793–807. [Google Scholar] [CrossRef]
- Altun, E.; Bhati, D.; Khan, N.M. A new approach to model the counts of earthquakes: INARPQX(1) process. SN Appl. Sci. 2021, 3, 1–17. [Google Scholar] [CrossRef]
- Irshad, M.R.; Chesneau, C.; D’cruz, V.; Maya, R. Discrete pseudo Lindley distribution: Properties, estimation and application on INAR(1) process. Math. Comput. Appl. 2021, 26, 76. [Google Scholar] [CrossRef]
- Altun, E.; Khan, N.M. Modelling with the novel INAR(1)-PTE process. Methodol. Comput. Appl. Probab. 2022, 24, 1–17. [Google Scholar] [CrossRef]
- Nawel, K.; Gemeay, A.M.; Zeghdoudi, H.; Karakaya, K.; Alshangiti, A.M.; Bakr, M.; Balogun, O.S.; Muse, A.H.; Hussam, E. Modelling Voltage Real Dataset by a New Version of Lindley Distribution. IEEE Access 2023, 11, 67220–67229. [Google Scholar]
- Beghriche, A.; Zeghdoudi, H.; Raman, V.; Chouia, S. New polynomial exponential distribution: Properties and applications. Stat. Transit. New Ser. 2022, 23, 95–112. [Google Scholar] [CrossRef]
- Weiß, C.H. An Introduction to Discrete-Valued Time Series; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Bodhisuwan, W.; Sangpoom, S. The discrete weighted Lindley distribution. In Proceedings of the 2016 12th International Conference on Mathematics, Statistics, and Their Applications, ICMSA, Banda Aceh, Indonesia, 4–6 October 2016. [Google Scholar]
- Krishna, H.; Pundir, P.S. Discrete Burr and discrete Pareto distributions. Stat. Methodol. 2009, 6, 177–188. [Google Scholar] [CrossRef]
- Jazi, M.A.; Lai, C.D.; Alamatsaz, M.H. A discrete inverse Weibull distribution and estimation of its parameters. Stat. Methodol. 2010, 7, 121–132. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chakravarty, D. A Discrete Gumbel Distribution. arXiv 2014, arXiv:1410.7568. [Google Scholar]
- Hussain, T.; Ahmad, M. Discrete inverse Rayleigh distribution. Pak. J. Stat. 2014, 30, 203–222. [Google Scholar]
- Para, B.A.; Jan, T.R. Discrete version of log-logistic distribution and its applications in genetics. Int. J. Mod. Math. Sci. 2016, 14, 407–422. [Google Scholar]
- McKenzie, E. Some simple models for discrete variate time series 1. J. Am. Water Resour. Assoc. 1985, 21, 645–650. [Google Scholar] [CrossRef]
- Jazi, M.A.; Jones, G.; Lai, C.D. First-order integer valued AR processes with zero inflated Poisson innovations. J. Time Ser. Anal. 2012, 33, 954–963. [Google Scholar] [CrossRef]


| n | MLE | MME | LSE | WLSE | ||||
|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |
| = 0.5 | ||||||||
| 50 | 0.065 | 0.004 | 0.067 | 0.004 | 0.141 | 0.020 | 0.158 | 0.025 |
| 100 | 0.055 | 0.003 | 0.052 | 0.003 | 0.127 | 0.016 | 0.161 | 0.026 |
| 200 | 0.044 | 0.002 | 0.044 | 0.002 | 0.126 | 0.016 | 0.165 | 0.027 |
| 250 | 0.008 | 0.000 | 0.005 | 0.000 | 0.085 | 0.007 | 0.145 | 0.021 |
| 500 | 0.004 | 0.000 | 0.002 | 0.000 | 0.103 | 0.011 | 0.052 | 0.020 |
| = 0.3 | ||||||||
| 50 | 0.034 | 0.001 | 0.037 | 0.001 | 0.087 | 0.008 | 0.074 | 0.006 |
| 100 | 0.013 | 0.000 | 0.015 | 0.000 | 0.058 | 0.003 | 0.059 | 0.004 |
| 200 | 0.008 | 0.000 | 0.008 | 0.000 | 0.050 | 0.003 | 0.060 | 0.004 |
| 250 | 0.007 | 0.000 | 0.008 | 0.000 | 0.032 | 0.001 | 0.045 | 0.002 |
| 500 | 0.001 | 0.000 | 0.001 | 0.000 | 0.003 | 0.001 | 0.035 | 0.001 |
| = 1.2 | ||||||||
| 50 | 0.107 | 0.011 | 0.108 | 0.012 | 0.511 | 0.261 | 0.635 | 0.403 |
| 100 | 0.048 | 0.002 | 0.046 | 0.002 | 0.485 | 0.235 | 0.611 | 0.373 |
| 200 | 0.046 | 0.002 | 0.046 | 0.002 | 0.485 | 0.235 | 0.642 | 0.412 |
| 250 | 0.007 | 0.005 | 0.006 | 0.000 | 0.471 | 0.222 | 0.645 | 0.416 |
| 500 | 0.004 | 0.000 | 0.006 | 0.001 | 0.483 | 0.234 | 0.560 | 0.314 |
| = 1.5 | ||||||||
| 50 | 0.055 | 0.003 | 0.052 | 0.003 | 0.684 | 0.468 | 0.897 | 0.804 |
| 100 | 0.030 | 0.001 | 0.029 | 0.001 | 0.677 | 0.458 | 0.868 | 0.754 |
| 200 | 0.025 | 0.001 | 0.026 | 0.001 | 0.689 | 0.475 | 0.880 | 0.775 |
| 250 | 0.021 | 0.000 | 0.025 | 0.001 | 0.699 | 0.489 | 0.864 | 0.747 |
| 500 | 0.020 | 0.000 | 0.021 | 0.002 | 0.666 | 0.444 | 0.889 | 0.790 |
| Parameter | n | = 0.4 and = 0.8 | |||||
|---|---|---|---|---|---|---|---|
| CML | CLS | YW | |||||
| Bias | MSE | Bias | MSE | Bias | MSE | ||
| 50 | 0.063 | 0.006 | 0.109 | 0.019 | 0.110 | 0.020 | |
| 100 | 0.044 | 0.003 | 0.080 | 0.010 | 0.081 | 0.010 | |
| 200 | 0.032 | 0.002 | 0.054 | 0.005 | 0.053 | 0.005 | |
| 250 | 0.029 | 0.001 | 0.049 | 0.004 | 0.049 | 0.004 | |
| 500 | 0.019 | 0.001 | 0.035 | 0.002 | 0.035 | 0.002 | |
| 50 | 0.130 | 0.029 | 0.164 | 0.044 | 0.162 | 0.043 | |
| 100 | 0.094 | 0.015 | 0.122 | 0.025 | 0.122 | 0.025 | |
| 200 | 0.063 | 0.007 | 0.084 | 0.012 | 0.083 | 0.012 | |
| 250 | 0.058 | 0.005 | 0.078 | 0.010 | 0.078 | 0.010 | |
| 500 | 0.041 | 0.003 | 0.056 | 0.005 | 0.056 | 0.005 | |
| = 0.8 and = 3 | |||||||
| 50 | 0.041 | 0.003 | 0.098 | 0.017 | 0.105 | 0.019 | |
| 100 | 0.028 | 0.001 | 0.061 | 0.007 | 0.065 | 0.008 | |
| 200 | 0.022 | 0.001 | 0.047 | 0.004 | 0.049 | 0.004 | |
| 250 | 0.018 | 0.001 | 0.036 | 0.002 | 0.036 | 0.002 | |
| 500 | 0.012 | 0.000 | 0.025 | 0.001 | 0.025 | 0.001 | |
| 50 | 0.745 | 0.978 | 1.024 | 1.722 | 1.008 | 1.691 | |
| 100 | 0.512 | 0.455 | 0.764 | 0.923 | 0.761 | 0.925 | |
| 200 | 0.391 | 0.241 | 0.648 | 0.652 | 0.655 | 0.665 | |
| 250 | 0.299 | 0.148 | 0.499 | 0.405 | 0.500 | 0.407 | |
| 500 | 0.212 | 0.070 | 0.377 | 0.223 | 0.377 | 0.222 | |
| Statistic | PNXL | DIW | DG | DLL | DB | DIR | DBL | DP | CMP | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.012 | 0.345 | 3.106 | 1.943 | 2.357 | 0.320 | 0.657 | 0.329 | 0.672 | ||
| 0.111 | 0.043 | 0.367 | 0.188 | 0.366 | 0.042 | 0.019 | 0.034 | 0.090 | ||
| 95% CI | lower | 0.794 | 0.261 | 2.388 | 1.575 | 1.641 | 0.237 | 0.620 | 0.263 | 0.496 |
| upper | 1.230 | 0.429 | 3.825 | 2.311 | 3.073 | 0.402 | 0.693 | 0.395 | 0.847 | |
| - | 1.541 | 0.407 | 1.401 | 0.519 | - | - | - | 0.107 | ||
| - | 0.156 | 0.029 | 0.121 | 0.051 | - | - | - | 0.116 | ||
| 95% CI | lower | - | 1.235 | 0.349 | 1.163 | 0.419 | - | - | - | 0.121 |
| upper | - | 1.847 | 0.464 | 1.638 | 0.619 | - | - | - | 0.334 | |
| X | Of | PNXL | DIW | DG | DLL | DB | DIR | DBL | DP | CMP |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 43 | 45.355 | 41.370 | 28.553 | 41.032 | 43.836 | 38.352 | 32.734 | 64.447 | 44.995 |
| 1 | 35 | 30.088 | 41.850 | 37.861 | 38.938 | 39.601 | 51.874 | 39.586 | 20.149 | 30.221 |
| 2 | 17 | 18.705 | 15.420 | 25.585 | 17.775 | 15.622 | 15.489 | 24.277 | 9.686 | 18.855 |
| 3 | 11 | 11.161 | 7.170 | 12.852 | 8.432 | 7.206 | 6.028 | 12.508 | 5.647 | 11.266 |
| 4 | 5 | 6.474 | 3.940 | 5.700 | 4.485 | 3.910 | 2.905 | 5.970 | 3.681 | 6.529 |
| 5 | 4 | 3.678 | 2.420 | 2.402 | 2.630 | 2.376 | 1.610 | 2.738 | 2.580 | 3.695 |
| 6 | 1 | 2.057 | 1.610 | 0.991 | 1.663 | 1.563 | 0.981 | 1.227 | 1.904 | 2.051 |
| 7 | 2 | 1.136 | 1.130 | 0.405 | 1.115 | 1.089 | 0.641 | 0.542 | 1.461 | 1.120 |
| 8 | 2 | 1.347 | 5.090 | 5.651 | 3.930 | 4.798 | 2.120 | 0.420 | 10.446 | 1.271 |
| Total | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 |
| - | - | - | - | - | - | - | - | - | ||
| 200.432 | 204.810 | 231.191 | 202.630 | 204.293 | 208.440 | 204.675 | 220.618 | 200.415 | ||
| AIC | 402.863 | 413.621 | 430.382 | 409.261 | 412.587 | 418.881 | 411.351 | 443.236 | 404.830 | |
| BIC | 405.651 | 419.195 | 435.957 | 414.836 | 418.162 | 421.668 | 414.138 | 446.024 | 410.405 | |
| 1.115 | 5.511 | 7.615 | 1.311 | 2.674 | 14.295 | 6.996 | 30.518 | 1.063 | ||
| df | 3 | 3 | 2 | 2 | 2 | 3 | 3 | 3 | 2 | |
| p-value | 0.774 | 0.138 | 0.022 | 0.519 | 0.263 | 0.003 | 0.072 | 0.000 | 0.588 | |
| Model | Parameters | Estimate | S.E. | AIC | BIC | DI | ||
|---|---|---|---|---|---|---|---|---|
| INAR(1)PNXL | 0.316 | 0.034 | 1660.869 | 1667.554 | 23.943 | 255.917 | 10.689 | |
| 0.092 | 0.007 | |||||||
| INAR(1)P | 0.148 | 0.026 | 2016.534 | 2023.224 | 25.349 | 25.349 | 1.000 | |
| 21.063 | 0.709 | |||||||
| INAR(1)G | 0.347 | 0.032 | 1686.428 | 1693.112 | 23.895 | 252.431 | 10.564 | |
| 0.058 | 0.005 | |||||||
| INAR(1)PWE | 0.058 | 0.159 | 1688.428 | 1698.455 | 24.990 | 369.211 | 14.774 | |
| 0.060 | 2.883 | |||||||
| 0.347 | 0.032 | |||||||
| INAR(1)ZIP | 20.552 | 0.595 | 1732.296 | 1742.323 | 25.332 | 58.543 | 2.307 | |
| 0.113 | 0.024 | |||||||
| 0.262 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irshad, M.R.; Aswathy, S.; Maya, R.; Nadarajah, S. New One-Parameter Over-Dispersed Discrete Distribution and Its Application to the Nonnegative Integer-Valued Autoregressive Model of Order One. Mathematics 2024, 12, 81. https://doi.org/10.3390/math12010081
Irshad MR, Aswathy S, Maya R, Nadarajah S. New One-Parameter Over-Dispersed Discrete Distribution and Its Application to the Nonnegative Integer-Valued Autoregressive Model of Order One. Mathematics. 2024; 12(1):81. https://doi.org/10.3390/math12010081
Chicago/Turabian StyleIrshad, Muhammed Rasheed, Sreedeviamma Aswathy, Radhakumari Maya, and Saralees Nadarajah. 2024. "New One-Parameter Over-Dispersed Discrete Distribution and Its Application to the Nonnegative Integer-Valued Autoregressive Model of Order One" Mathematics 12, no. 1: 81. https://doi.org/10.3390/math12010081
APA StyleIrshad, M. R., Aswathy, S., Maya, R., & Nadarajah, S. (2024). New One-Parameter Over-Dispersed Discrete Distribution and Its Application to the Nonnegative Integer-Valued Autoregressive Model of Order One. Mathematics, 12(1), 81. https://doi.org/10.3390/math12010081





