Asymptotic Analysis of an Elastic Layer under Light Fluid Loading
Abstract
1. Introduction
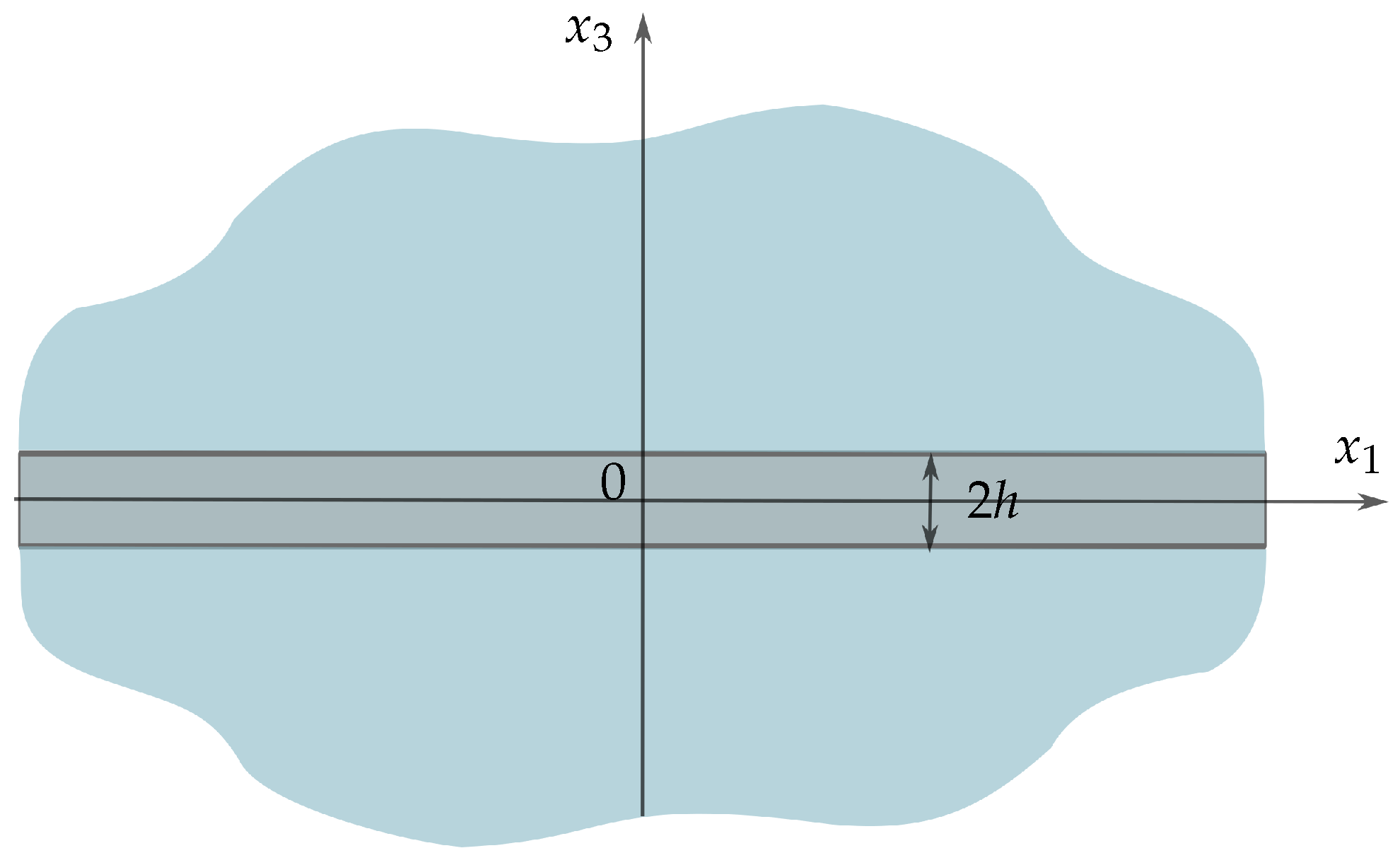
2. Governing Equations
3. Asymptotic Analysis of the Dispersion Relation
4. Asymptotic Models
4.1. Scaling
4.2. Leading-Order Approximation
4.3. First-Order Approximation
4.4. Asymptotically Consistent Equations
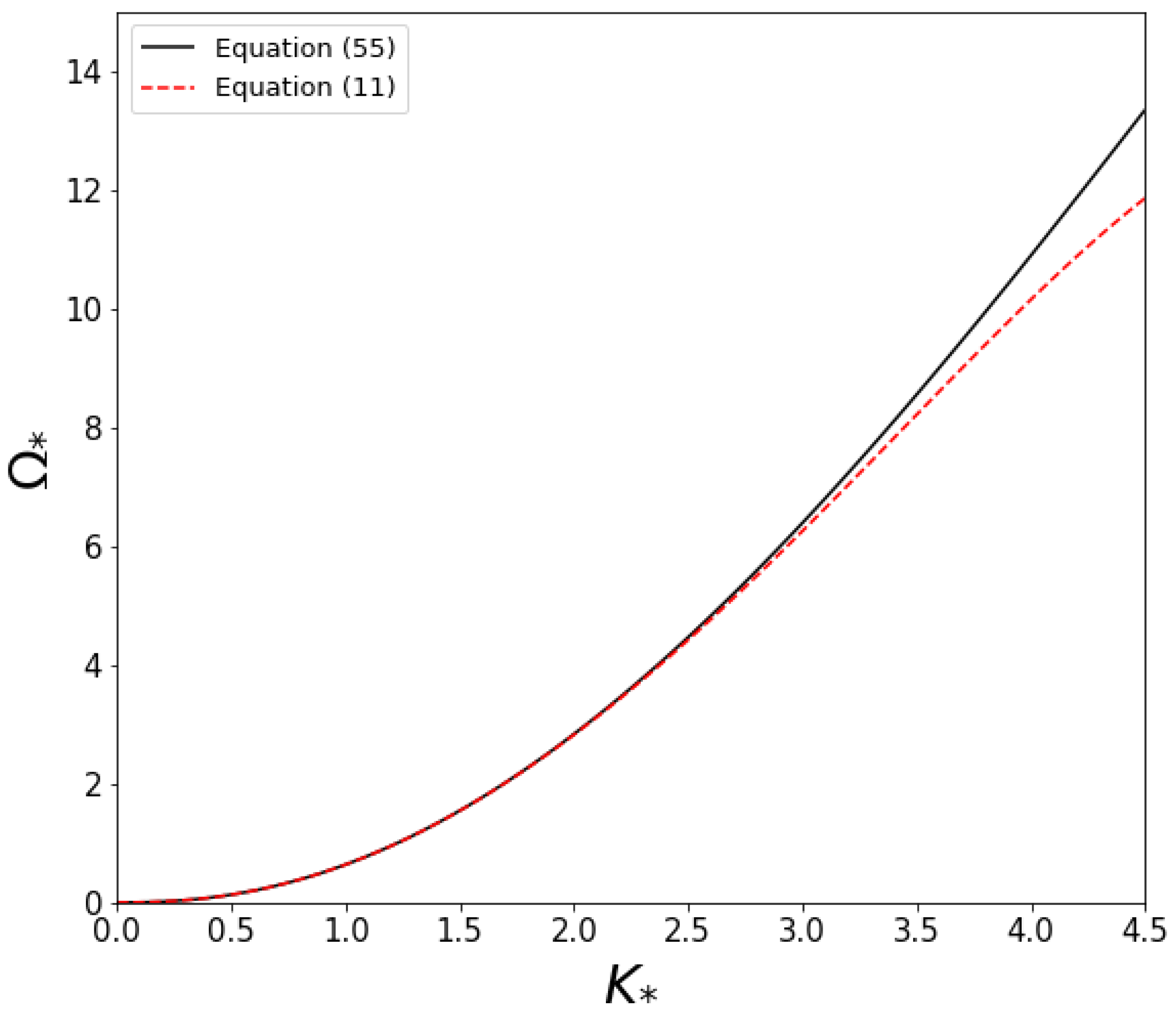
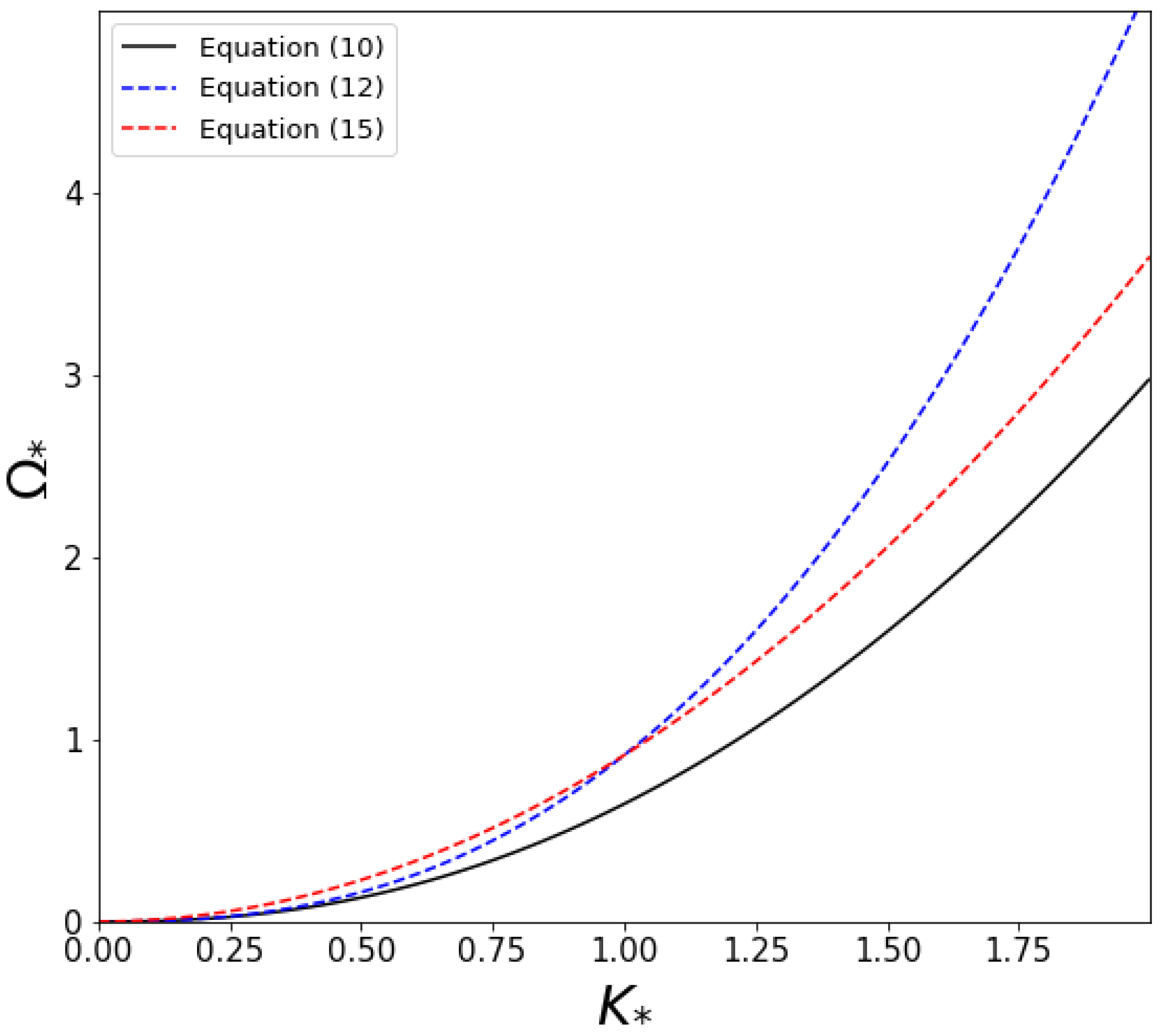
4.5. Comparison of Dispersion Relations
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rayleigh, J.W.S.B. The Theory of Sound; Macmillan: New York, NY, USA, 1896; Volume 2. [Google Scholar]
- Crighton, D. The 1988 Rayleigh medal lecture: Fluid loading—The interaction between sound and vibration. J. Sound Vib. 1989, 133, 1–27. [Google Scholar] [CrossRef]
- Crighton, D.G.; Dowling, A.P.; Ffowcs-Williams, J.; Heckl, M.; Leppington, F.; Bartram, J.F. Modern Methods in Analytical Acoustics Lecture Notes; Springer: London, UK, 1992. [Google Scholar]
- Junger, M.C.; Feit, D. Sound, Structures, and Their Interaction; MIT Press: Cambridge, MA, USA, 1986; Volume 225. [Google Scholar]
- Norris, A.N.; Rebinsky, D.A. Acoustic coupling to membrane waves on elastic shells. J. Acoust. Soc. Am. 1994, 95, 1809–1829. [Google Scholar] [CrossRef]
- Blonigen, F.J.; Marston, P.L. Leaky helical flexural wave scattering contributions from tilted cylindrical shells: Ray theory and wave-vector anisotropy. J. Acoust. Soc. Am. 2001, 110, 1764–1769. [Google Scholar] [CrossRef]
- Caresta, M.; Kessissoglou, N.J. Structural and acoustic responses of a fluid-loaded cylindrical hull with structural discontinuities. Appl. Acoust. 2009, 70, 954–963. [Google Scholar] [CrossRef]
- Titovich, A.S.; Norris, A.N. Acoustic scattering from an infinitely long cylindrical shell with an internal mass attached by multiple axisymmetrically distributed stiffeners. J. Sound Vib. 2015, 338, 134–153. [Google Scholar] [CrossRef]
- Ruotolo, R. A comparison of some thin shell theories used for the dynamic analysis of stiffened cylinders. J. Sound Vib. 2001, 243, 847–860. [Google Scholar] [CrossRef]
- Homm, A.; Ehrlich, J.; Peine, H.; Wiesner, H. Experimental and numerical investigation of a complex submerged structure. Part I: Modal analysis. Acta Acust. United Acust. 2003, 89, 61–70. [Google Scholar]
- Forrest, J.A. Measured dynamics of a thin cylindrical shell subject to axial excitation. In Proceedings of the Acoustics 2005, Busselton, WA, Australia, 9–11 November 2005; pp. 9–11. [Google Scholar]
- Slepyan, L.; Sorokin, S. Analysis of structural-acoustic coupling problems by a two-level boundary integral method: Part 1: A general formulation and test problems. J. Sound Vib. 1995, 184, 195–211. [Google Scholar] [CrossRef]
- Cole, J.E., III. Vibrations of a framed cylindrical shell submerged in and filled with acoustic fluids: Spectral solution. Comput. Struct. 1997, 65, 385–393. [Google Scholar] [CrossRef]
- Liu, C.H.; Chen, P.T. Numerical analysis of immersed finite cylindrical shells using a coupled BEM/FEM and spatial spectrum approach. Appl. Acoust. 2009, 70, 256–266. [Google Scholar] [CrossRef]
- Johansson, M.; Folkow, P.D.; Hägglund, A.; Olsson, P. Approximate boundary conditions for a fluid-loaded elastic plate. J. Acoust. Soc. Am. 2005, 118, 3436–3446. [Google Scholar] [CrossRef]
- Belov, A.; Kaplunov, J.; Nolde, E. A refined asymptotic model of fluid-structure interaction in scattering by elastic shells. Flow Turbul. Combust. 1998, 61, 255–267. [Google Scholar] [CrossRef]
- Kaplunov, J.; Prikazchikova, L.; Shamsi, S. A hierarchy of asymptotic models for a fluid-loaded elastic layer. Math. Mech. Solids 2023, 29, 560–576. [Google Scholar] [CrossRef]
- Kaplunov, J.D.; Kossovitch, L.Y.; Nolde, E. Dynamics of Thin Walled Elastic Bodies; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Talmant, M.; Überall, H.; Miller, R.D.; Werby, M.F.; Dickey, J. Lamb waves and fluid-borne waves on water-loaded, air-filled thin spherical shells. J. Acoust. Soc. Am. 1989, 86, 278–289. [Google Scholar] [CrossRef]
- Yücel, H.; Ege, N.; Erbaş, B.; Kaplunov, J. A revisit to the plane problem for low-frequency acoustic scattering by an elastic cylindrical shell. Math. Mech. Solids 2024. [Google Scholar] [CrossRef]
- Craster, R. The light fluid loading limit for fluid/solid interactions. Eur. J. Appl. Math. 1997, 8, 485–505. [Google Scholar] [CrossRef]
- Sorokin, S.V. Analysis of wave propagation in sandwich plates with and without heavy fluid loading. J. Sound Vib. 2004, 271, 1039–1062. [Google Scholar] [CrossRef]
- Sorokin, S.V. Vibrations of and sound radiation from sandwich plates in heavy fluid loading conditions. Compos. Struct. 2000, 48, 219–230. [Google Scholar] [CrossRef]
- Chapman, C.J.; Sorokin, S.V. The forced vibration of an elastic plate under significant fluid loading. J. Sound Vib. 2005, 281, 719–741. [Google Scholar] [CrossRef]
- Kaplunov, J.; Markushevich, D. Plane vibrations and radiation of an elastic layer lying on a liquid half-space. Wave Motion 1993, 17, 199–211. [Google Scholar] [CrossRef]
- Howe, M.S. Acoustics of Fluid-Structure Interactions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nakayama, Y. Introduction to Fluid Mechanics; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Kaplunov, J.; Prikazchikova, L.; Shamsi, S. Dispersion of the Bending Wave in a Fluid-loaded Elastic Layer. In Advances in Solid and Fracture Mechanics: A Liber Amicorum to Celebrate the Birthday of Nikita Morozov; Springer: Berlin/Heidelberg, Germany, 2022; pp. 127–134. [Google Scholar]
- Goldenveizer, A.; Kaplunov, J.; Nolde, E. On Timoshenko-Reissner type theories of plates and shells. Int. J. Solids Struct. 1993, 30, 675–694. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamsi, S.; Prikazchikova, L. Asymptotic Analysis of an Elastic Layer under Light Fluid Loading. Mathematics 2024, 12, 1465. https://doi.org/10.3390/math12101465
Shamsi S, Prikazchikova L. Asymptotic Analysis of an Elastic Layer under Light Fluid Loading. Mathematics. 2024; 12(10):1465. https://doi.org/10.3390/math12101465
Chicago/Turabian StyleShamsi, Sheeru, and Ludmila Prikazchikova. 2024. "Asymptotic Analysis of an Elastic Layer under Light Fluid Loading" Mathematics 12, no. 10: 1465. https://doi.org/10.3390/math12101465
APA StyleShamsi, S., & Prikazchikova, L. (2024). Asymptotic Analysis of an Elastic Layer under Light Fluid Loading. Mathematics, 12(10), 1465. https://doi.org/10.3390/math12101465