Deformation Prediction Model of Existing Tunnel Structures with Equivalent Layered Method–Peck Coupled under Multiple Factors
Abstract
:1. Introduction
2. Calculation Method
2.1. Peck Model for Predicting Settlement of Existing Tunnel Structures in Under-Tunnel Excavation
2.2. Theory of Multi-Level Equivalent Layer Method Conversion
2.3. Structural Deformation Prediction Model for Existing Tunnels When Layer Method–Peck Coupling Is Used
2.3.1. Equivalent Transformation of the Rock Layer Method for Multifactors
2.3.2. Modification of Peck’s Prediction Model under Multifactorial
3. Results and Discussion
3.1. Project Examples and Parameter Values
- (1)
- Calculation of Equivalent Modulus of Elasticity and Density Parameters for Existing Tunnels
- (2)
- Parameters related to equivalent rock transformation in cross tunnels
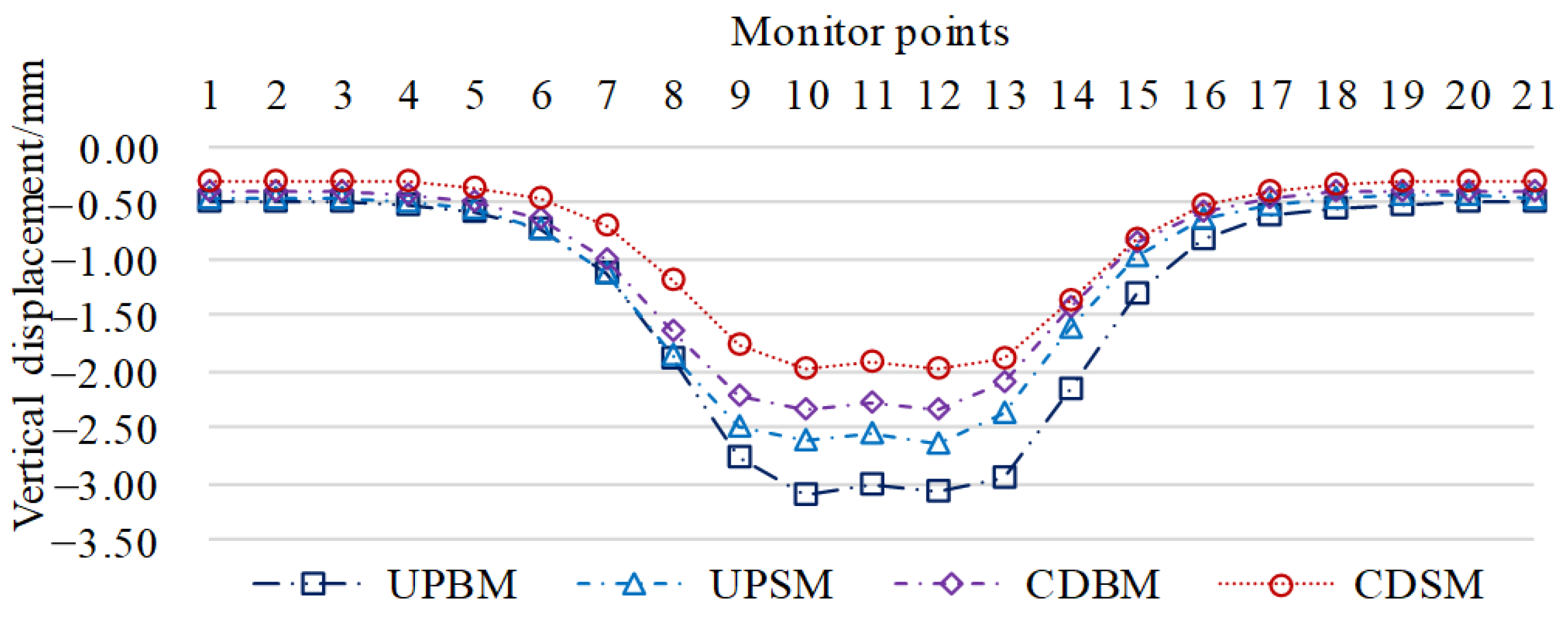
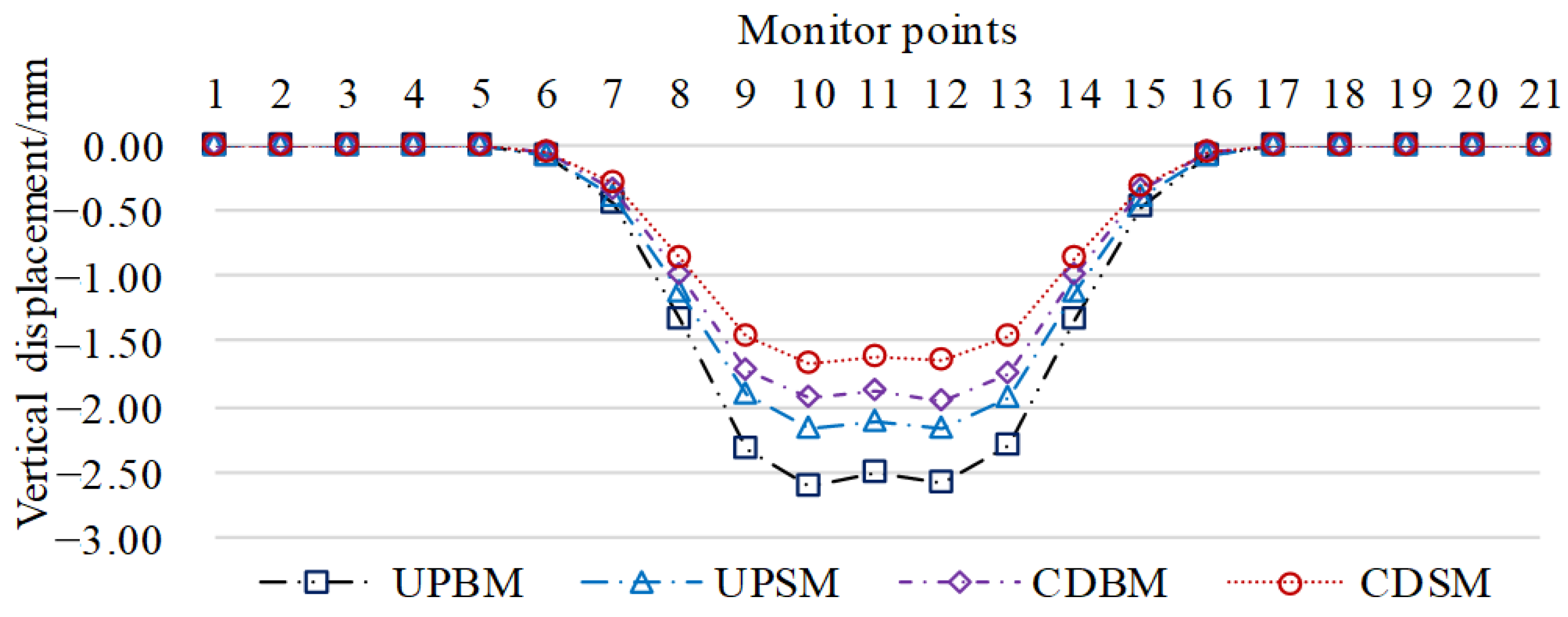
3.2. Theoretical Calculation Results
3.3. Comparison and Optimization
- (1)
- Comparison and optimization of numerical and theoretical calculations
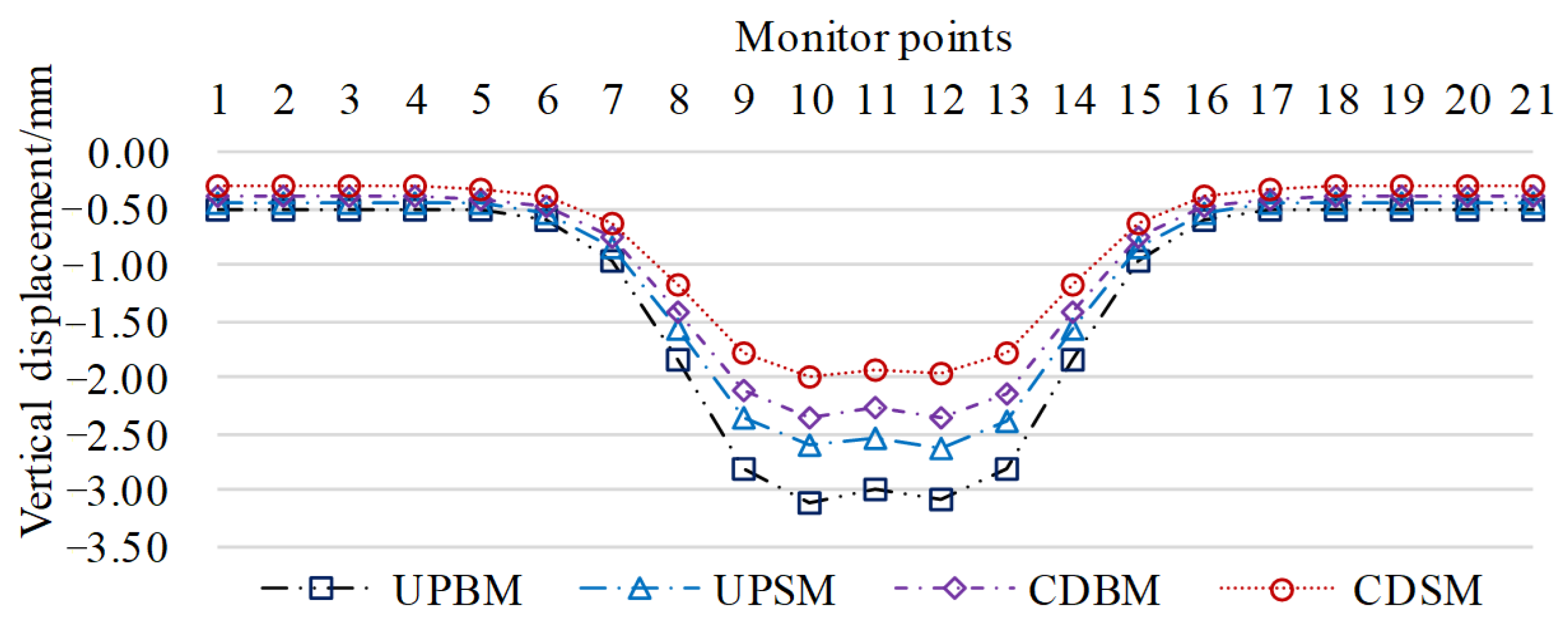
- (2)
- Monitoring data and theoretical calculations compared to verify
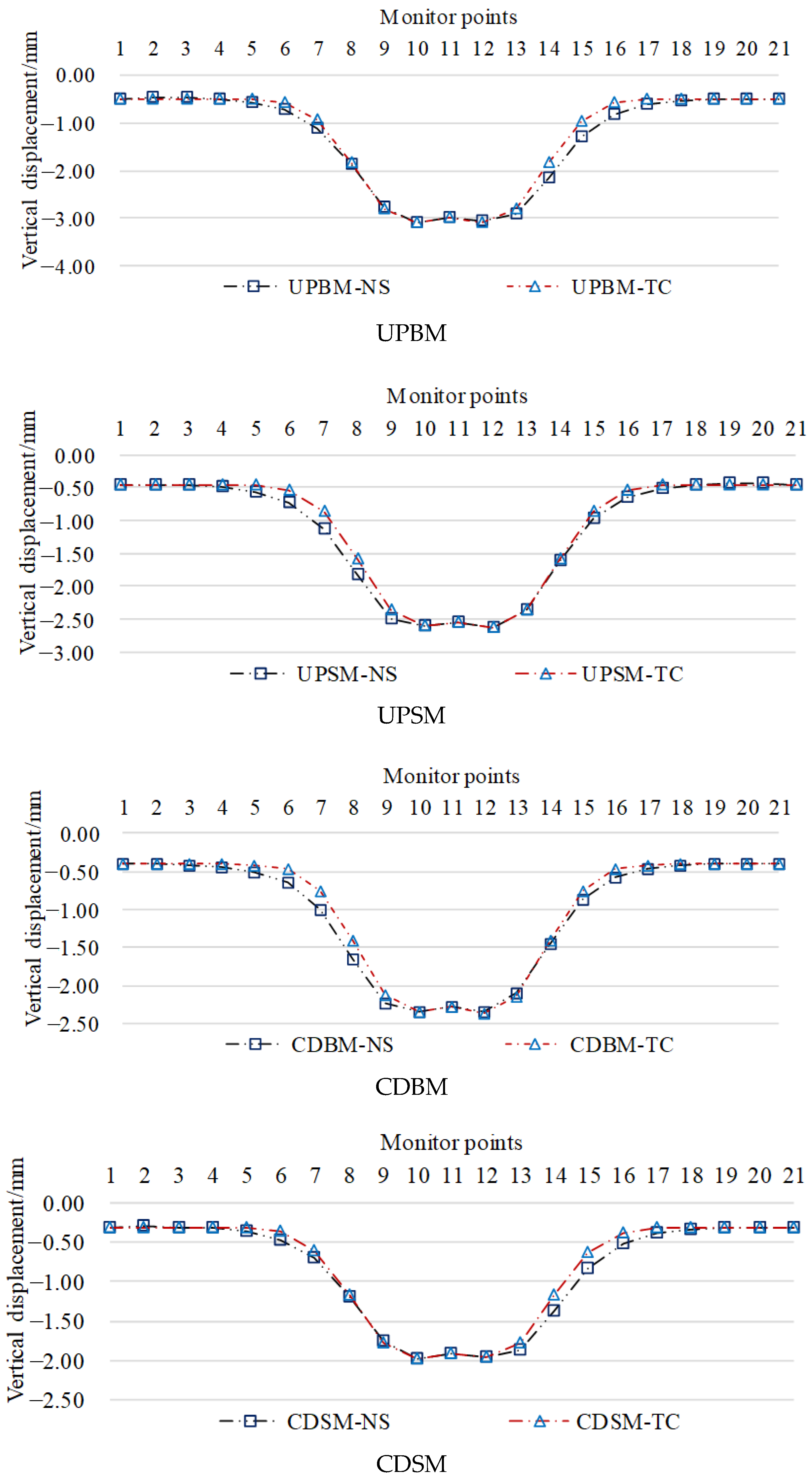
- (3)
- Limitations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Z.-L.; Chen, J.-Y.; Liu, H.; Zhang, Z.-F. Present status and development trends of underground space in Chinese cities: Evaluation and analysis. Tunn. Undergr. Space Technol. 2018, 71, 253–270. [Google Scholar] [CrossRef]
- Liu, S.-C.; Peng, F.-L.; Qiao, Y.-K.; Dong, Y.-H. Quantitative evaluation of the contribution of underground space to urban resilience: A case study in China. Undergr. Space 2024, 17, 1–24. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, X.; Zeng, K.; Zhang, X.; Zhou, M.; Du, J. Centrifuge modelling of tunnelling below existing twin tunnels with different types of support. Undergr. Space 2022, 7, 1125–1138. [Google Scholar] [CrossRef]
- Deng, H.-S.; Fu, H.-L.; Yue, S.; Huang, Z.; Zhao, Y.-Y. Ground loss model for analyzing shield tunneling-induced surface settlement along curve sections. Tunn. Undergr. Space Technol. 2022, 119, 104250. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, M.; Wang, B.; Zhang, K.; Li, Y.; Liu, Z. Numerical study on the effects of wetting–drying cycles on the failure characteristics of tunnels excavated in gypsiferous strata based on discrete element method. Bull. Eng. Geol. Environ. 2023, 82, 368. [Google Scholar] [CrossRef]
- Wu, L.; He, K.; Guo, L.; Zhang, J.; Sun, L.; Jia, Y. Research on the excavation stability evaluation method of Chaqishan ancient landslide in China. Eng. Fail. Anal. 2022, 141, 106664. [Google Scholar] [CrossRef]
- Zheng, G.; Yang, X.; Zhou, H.; Du, Y.; Sun, J.; Yu, X. A simplified prediction method for evaluating tunnel displacement induced by laterally adjacent excavations. Comput. Geotech. 2018, 95, 119–128. [Google Scholar] [CrossRef]
- Sun, H.; Chen, Y.; Zhang, J.; Kuang, T. Analytical investigation of tunnel deformation caused by circular foundation pit excavation. Comput. Geotech. 2019, 106, 193–198. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, R.; Wu, H.; Meng, F. A simplified method for estimating the longitudinal and circumferential behaviors of the shield-driven tunnel adjacent to a braced excavation. Comput. Geotech. 2020, 123, 103595. [Google Scholar] [CrossRef]
- Chen, F.Y.; Wang, L.; Zhang, W.G. Reliability assessment on stability of tunnelling perpendicularly beneath an existing tunnel considering spatial variabilities of rock mass properties. Tunn. Undergr. Space Technol. 2019, 88, 276–289. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, P.; Wu, H.; Wang, Z.; Zhong, Z. Prediction of shield tunneling-induced ground settlement using machine learning techniques. Front. Struct. Civ. Eng. 2019, 13, 1363–1378. [Google Scholar] [CrossRef]
- Cheng, L.Y.; Ariaratnam, S.T.; Chen, S.X. Analytical Solution for Predicting Ground Deformation Associated with Pipe Jacking. J. Pipeline Syst. Eng. Pract. 2017, 8, 04017008. [Google Scholar] [CrossRef]
- Choo, C.S.; Ong, D.E.L. Assessment of non-linear rock strength parameters for the estimation of pipe-jacking forces. Part 2. Numerical modeling. Eng. Geol. 2020, 265, 105405. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, H.; Miao, L.; Gong, C. Predictive model for the surface settlement caused by the excavation of twin tunnels. Tunn. Undergr. Space Technol. 2021, 114, 104014. [Google Scholar] [CrossRef]
- Kong, F.; Lu, D.; Du, X.; Li, X.; Su, C. Analytical solution of stress and displacement for a circular underwater shallow tunnel based on a unified stress function. Ocean Eng. 2021, 219, 108352. [Google Scholar] [CrossRef]
- Mair, R.J.; Taylor, R.N.; Bracegirdle, A. Subsurface settlement profiles above tunnels in clays. Geotechnique 1993, 43, 315–320. [Google Scholar] [CrossRef]
- Lin, C.G.; Huang, M.S. Tunnelling-induced response of a jointed pipeline and its equivalence to a continuous structure. Soils Found. 2019, 59, 828–839. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, Y.; Liu, Z.; Miao, L. Theoretical prediction model for deformations caused by construction of new tunnels undercrossing existing tunnels based on the equivalent layered method. Comput. Geotech. 2020, 123, 103565. [Google Scholar] [CrossRef]
- Vorster TE, B.; Klar, A.; Soga, K.; Mair, R.J. Estimating the effects of tunneling on existing pipelines. J. Geotech. Geoenviron. Eng. 2005, 131, 1399–1410. [Google Scholar] [CrossRef]
- Marshall, A.M.; Klar, A.; Mair, R.J. Tunneling beneath Buried Pipes: View of Soil Strain and Its Effect on Pipeline Behavior. J. Geotech. Geoenviron. Eng. 2010, 136, 1664–1672. [Google Scholar] [CrossRef]
- Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Geotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Verruijt, A.; Booker, J.R. Surface settlements due to deformation of a tunnel in an elastic half plane. Geotechnique 1996, 46, 753–756. [Google Scholar] [CrossRef]
- Loganathan, N.; Poulos, H.G. Analytical Prediction for Tunneling-Induced Ground Movements in Clays. J. Geotech. Geoenviron. Eng. 1998, 124, 846–856. [Google Scholar] [CrossRef]
- Li, P.; Du, S.; Wang, Y.; Zhao, H.; Shen, S. Timoshenko beam solution for the response of existing tunnels because of tunneling underneath. Int. J. Numer. Anal. Methods Géoméch. 2016, 40, 766–784. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Z.; Zhang, R.; Han, Y.; Wang, Z.; Wang, S. Effects of Undercrossing Tunneling on Existing Shield Tunnels. Int. J. Géoméch. 2021, 21, 04021131. [Google Scholar] [CrossRef]
- Shi, J.; Liu, G.; Huang, P.; Ng, C.W.W. Interaction between a large-scale triangular excavation and adjacent structures in Shanghai soft clay. Tunn. Undergr. Space Technol. 2015, 50, 282–295. [Google Scholar] [CrossRef]
- Jiang, D.; Li, Y.; Fei, Q.; Wu, S. Prediction of uncertain elastic parameters of a braided composite. Compos. Struct. 2015, 126, 123–131. [Google Scholar] [CrossRef]
- Avramidis, I.; Morfidis, K. Bending of beams on three-parameter elastic foundation. Int. J. Solids Struct. 2006, 43, 357–375. [Google Scholar] [CrossRef]
- Hong, T.; Teng, J.G.; Luo, Y.F. Axisymmetric shells and plates on tensionless elastic foundations. Int. J. Solids Struct. 1999, 36, 5277–5300. [Google Scholar] [CrossRef]
- Wang, L.L.; Ishihara, T. A study of the effects of foundation uplift on the seismic loading of wind turbine tower and shallow foundation using a new dynamic Winkler model. Eng. Struct. 2020, 219, 110745. [Google Scholar] [CrossRef]
- Klar, A.; Vorster, T.E.B.; Soga, K.; Mair, R.J. Soil–Pipe interaction due to tunnelling: Comparison between Winkler and elastic continuum solutions. Geotechnique 2005, 55, 461–466. [Google Scholar] [CrossRef]
- Liu, D.; Tian, C.; Wang, F.; Hu, Q.; Zuo, J. Longitudinal structural deformation mechanism of shield tunnel linings considering shearing dislocation of circumferential joints. Comput. Geotech. 2021, 139, 104384. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Huang, M.S. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Comput. Geotech. 2014, 56, 121–132. [Google Scholar] [CrossRef]
- Xu, Q.; Lei, S.; Zhu, Y.; Zhao, W.; Wang, C.; Wang, D. Theoretical Prediction Model for Surface Settlement Caused by the Excavation of New Tunnels Undercrossing Existing Tunnels Based on Modified Stochastic Medium Theory. KSCE J. Civ. Eng. 2022, 26, 4136–4145. [Google Scholar] [CrossRef]
- Xu, Q.; Zhu, Y.; Lei, S.; Fan, H.; Wang, D.; Ma, K.; Fang, Z. A Simplified 3D Theoretical Model for Calculating the Surface Settlement Induced by Tunnel Undercrossing Excavation. Int. J. Géoméch. 2023, 23, 04023185. [Google Scholar] [CrossRef]
- Zhou, Z.; Zheng, Y.; Hu, J.; Yang, H.; Gong, C. Deformation analysis of shield undercrossing and vertical paralleling excavation with existing tunnel in composite stratum. J. Cent. South Univ. 2023, 30, 3127–3144. [Google Scholar] [CrossRef]
- Li, Y.; Huang, C.; Lu, H.; Mou, C. Investigation of the Influence Area of the Excavation of a Double-Line Highway Tunnel under an Existing Railway Tunnel. Appl. Sci. 2024, 14, 290. [Google Scholar] [CrossRef]
- Li, Y.; Huang, C.; Lu, H.; Mou, C. Investigation on the Mechanical Characteristics of the Excavation of a Double-Line Highway Tunnel Underpass Existing Railway Tunnel under the Influence of Dynamic and Static Load. Appl. Sci. 2024, 14, 3242. [Google Scholar] [CrossRef]
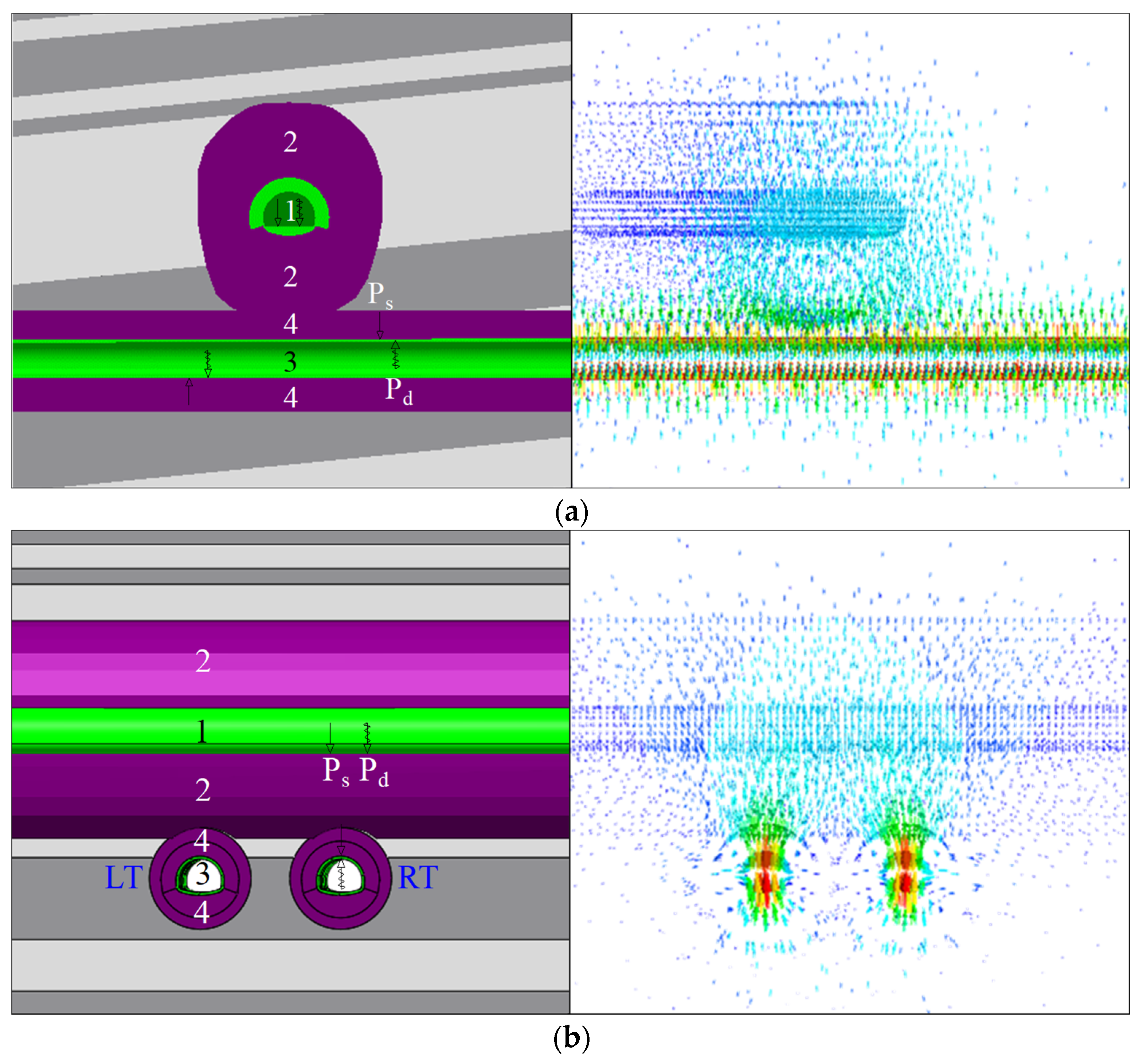
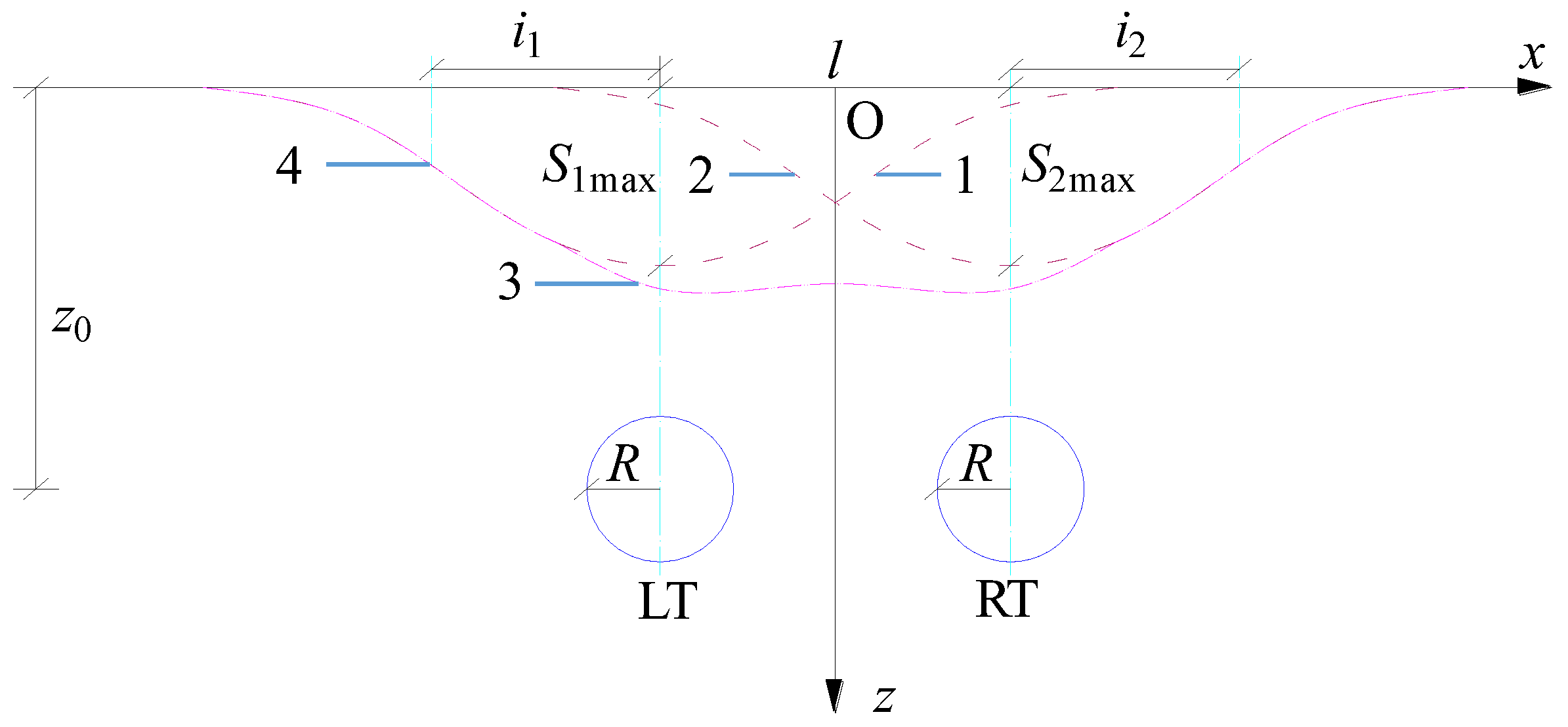

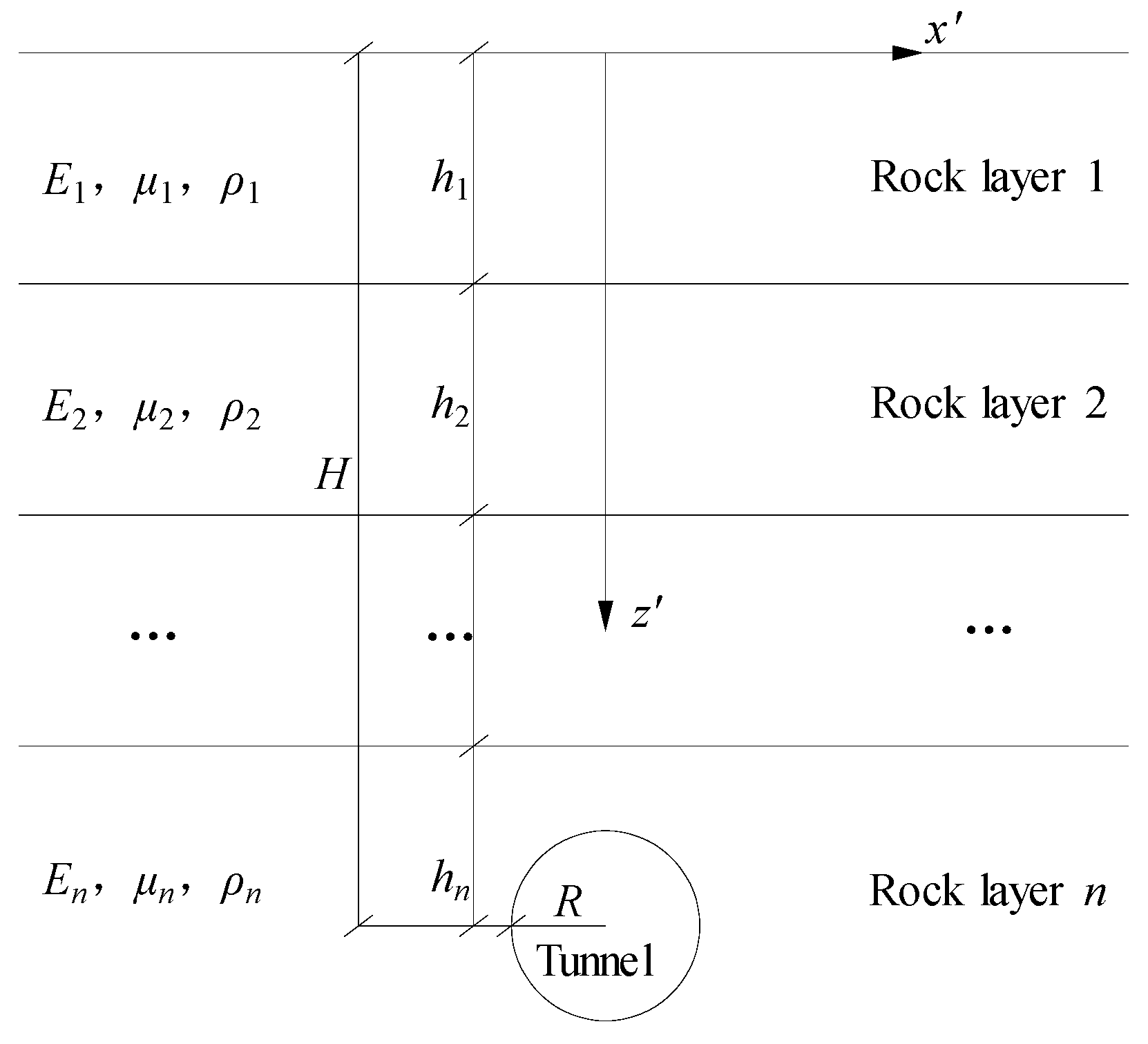
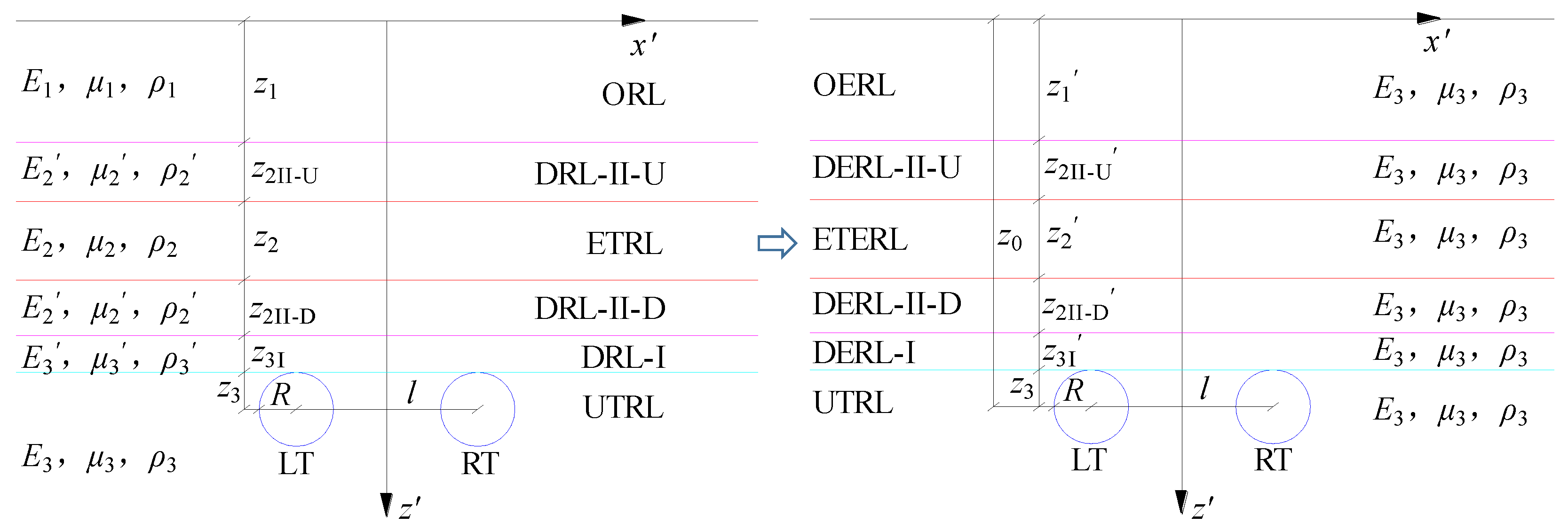
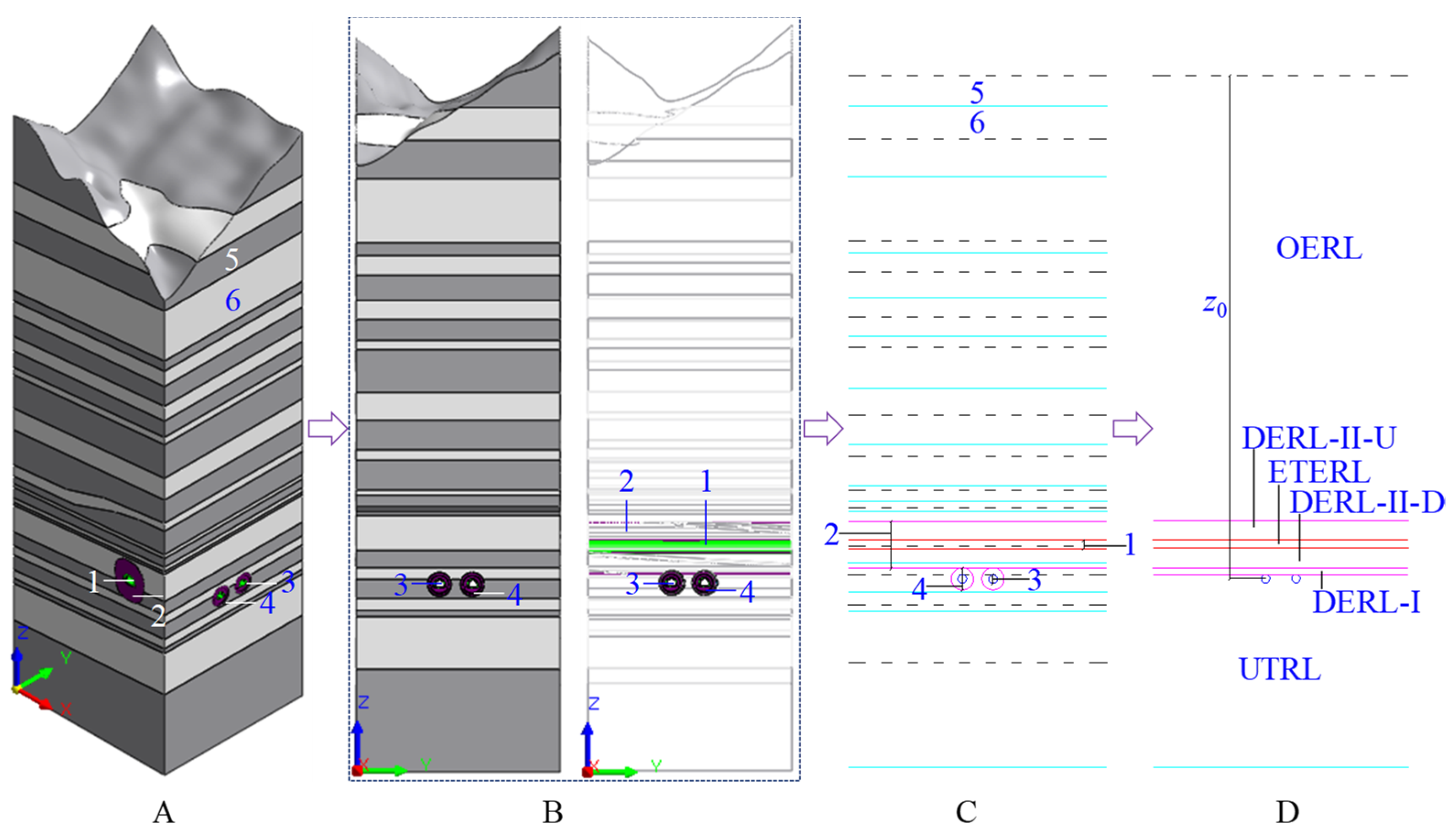
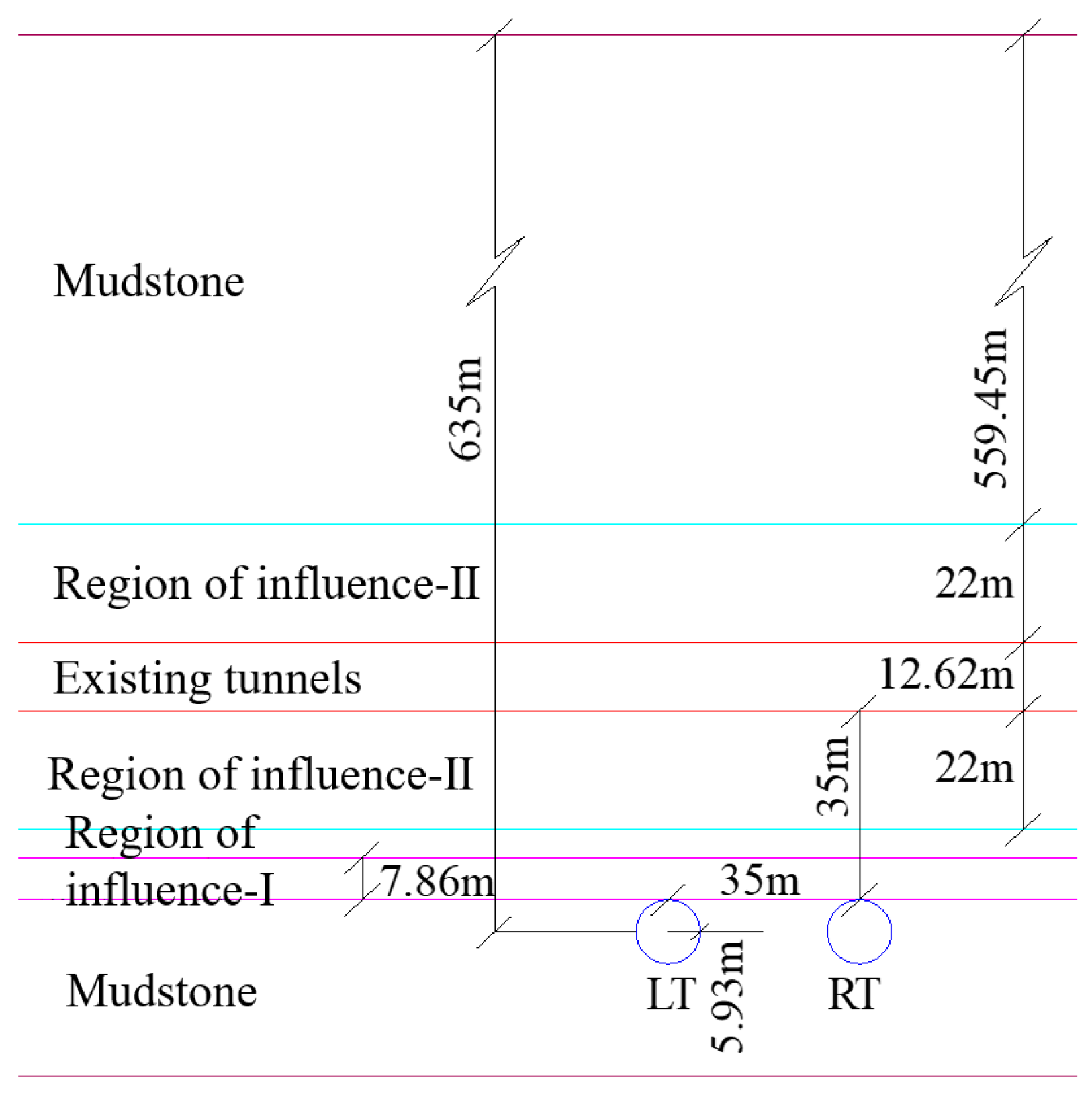
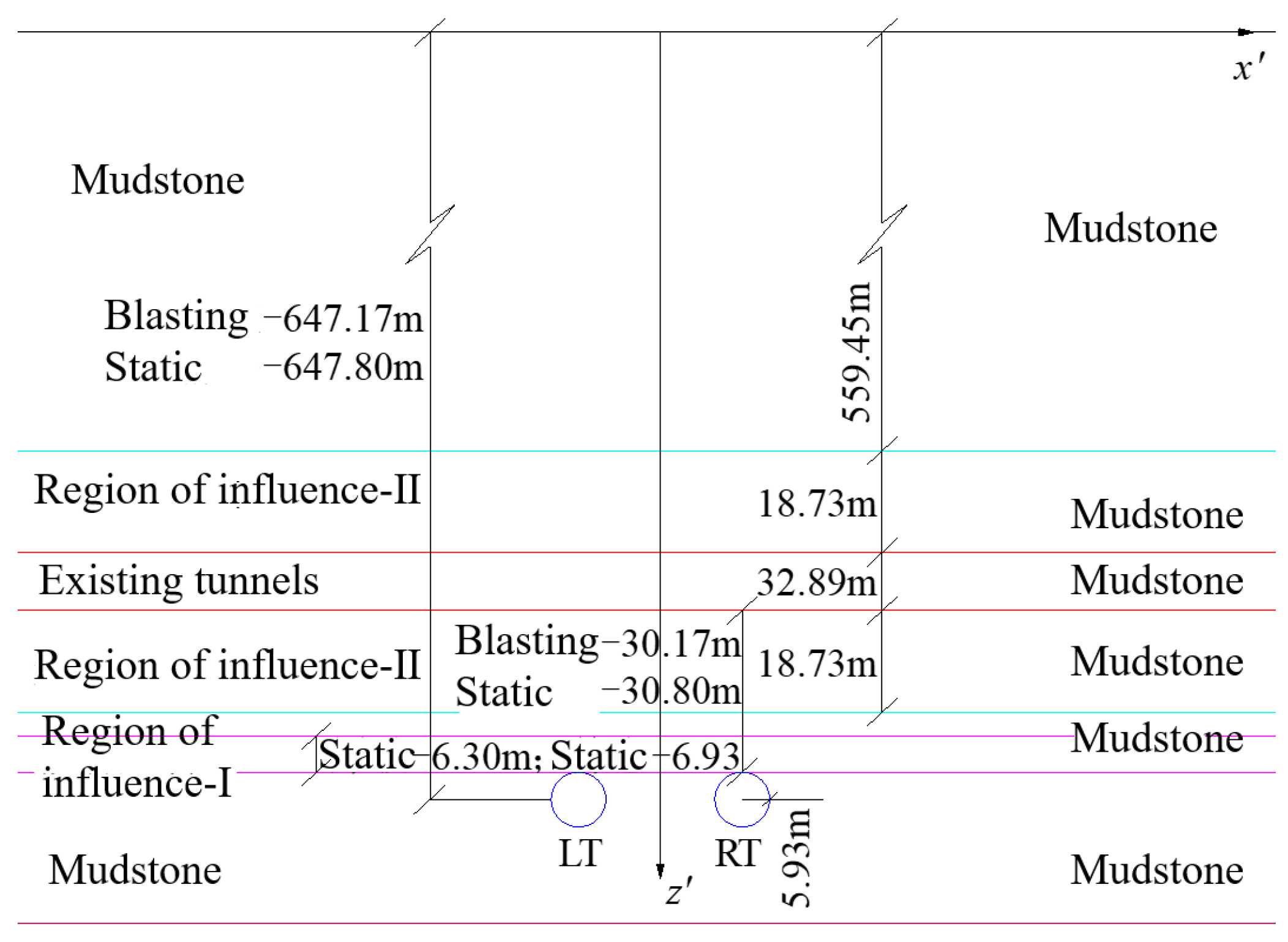

| Rock Layer (Top to Bottom) | Height (m) | Equivalent Height (m) | Remarks |
|---|---|---|---|
| Mudstone | 31.6 | 31.6 | Area equivalent |
| Malmstone | 35.5 | 47.6 | |
| Mudstone | 41.5 | 41.5 | |
| Malmstone | 68.9 | 92.3 | |
| Mudstone | 14.0 | 14.0 | |
| Malmstone | 21.2 | 28.4 | |
| Mudstone | 27.3 | 27.3 | |
| Malmstone | 20.4 | 27.3 | |
| Mudstone | 22.4 | 22.4 | |
| Malmstone | 10.0 | 13.4 | |
| Mudstone | 46.3 | 46.3 | |
| Malmstone | 30.0 | 40.2 | |
| Mudstone | 32.0 | 32.0 | |
| Malmstone | 11.0 | 14.7 | |
| Mudstone | 32.3 | 32.3 | |
| Malmstone | 5.6 | 7.5 | |
| Mudstone | 10.6 | 10.6 | |
| Malmstone | 7.4 | 9.9 | |
| Mudstone | 3.9 | 3.9 | |
| Malmstone | 37.5 | 50.3 | Existing tunnel formations |
| Mudstone | 18.3 | 18.9 | |
| Malmstone | 12.1 | 16.6 | |
| Mudstone | 20.6 | 20.6 | Rock formation of the lower tunnel |
| Rock Stratum | Modulus of Elasticity (GPa) | Density (kN·m−3) |
|---|---|---|
| Mudstone | 2.15 | 23.89 |
| Existing Tunnels | 8.51 | 5.19 |
| Impact Area-I (Blasting) | 1.10 | 23.89 |
| Area of Influence-I (Static) | 1.47 | 23.89 |
| Area of Influence-II (Blasting) | 1.32 | 23.89 |
| Area of Influence-II (Static) | 1.32 | 23.89 |
| Working Condition | z0/m | z/m | l/m | R/m | n | λα | λg | V/% | ηd | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| UPBM | 641.17 | 617.00 | 35.00 | 5.93 | 0.99 | 2.06 | 0.20 | 0.230 | 1.06 | 1.06 | 1.05 |
| UPSM | 641.80 | 617.00 | 35.00 | 5.93 | 0.99 | 2.06 | 0.20 | 0.193 | 1.06 | 1.05 | 1.06 |
| CDBM | 641.17 | 617.00 | 35.00 | 5.93 | 0.99 | 2.06 | 0.20 | 0.173 | 1.06 | 1.05 | 1.06 |
| CDSM | 641.80 | 617.00 | 35.00 | 5.93 | 0.99 | 2.06 | 0.20 | 0.148 | 1.06 | 1.06 | 1.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Huang, C.; Lu, H.; Mou, C. Deformation Prediction Model of Existing Tunnel Structures with Equivalent Layered Method–Peck Coupled under Multiple Factors. Mathematics 2024, 12, 1479. https://doi.org/10.3390/math12101479
Li Y, Huang C, Lu H, Mou C. Deformation Prediction Model of Existing Tunnel Structures with Equivalent Layered Method–Peck Coupled under Multiple Factors. Mathematics. 2024; 12(10):1479. https://doi.org/10.3390/math12101479
Chicago/Turabian StyleLi, Yifan, Changfu Huang, Hongjian Lu, and Chao Mou. 2024. "Deformation Prediction Model of Existing Tunnel Structures with Equivalent Layered Method–Peck Coupled under Multiple Factors" Mathematics 12, no. 10: 1479. https://doi.org/10.3390/math12101479
APA StyleLi, Y., Huang, C., Lu, H., & Mou, C. (2024). Deformation Prediction Model of Existing Tunnel Structures with Equivalent Layered Method–Peck Coupled under Multiple Factors. Mathematics, 12(10), 1479. https://doi.org/10.3390/math12101479




