Election Optimizer Algorithm: A New Meta-Heuristic Optimization Algorithm for Solving Industrial Engineering Design Problems
Abstract
:1. Introduction
- EOA imitates the complete process of the presidential election during the optimization process.
- EOA focuses on the explicit behaviors of candidates during the election process, such as strategy reference, innovative suggestions from the staff team, televised debates, and campaign speeches.
- EOA shows the superior effectiveness on each test and outperforms the existing HBs.
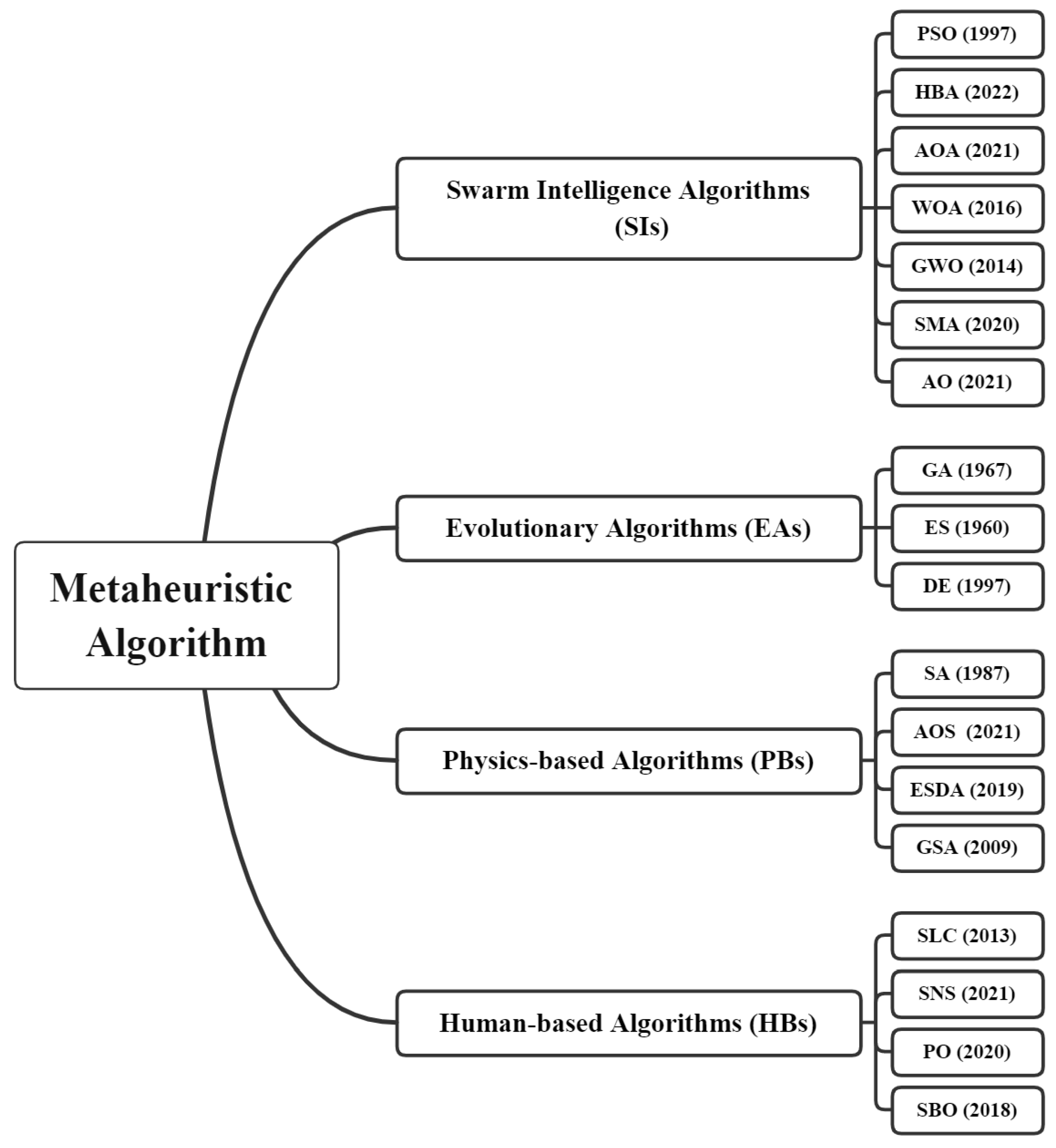
2. Related Work
3. Election Optimizer Algorithm
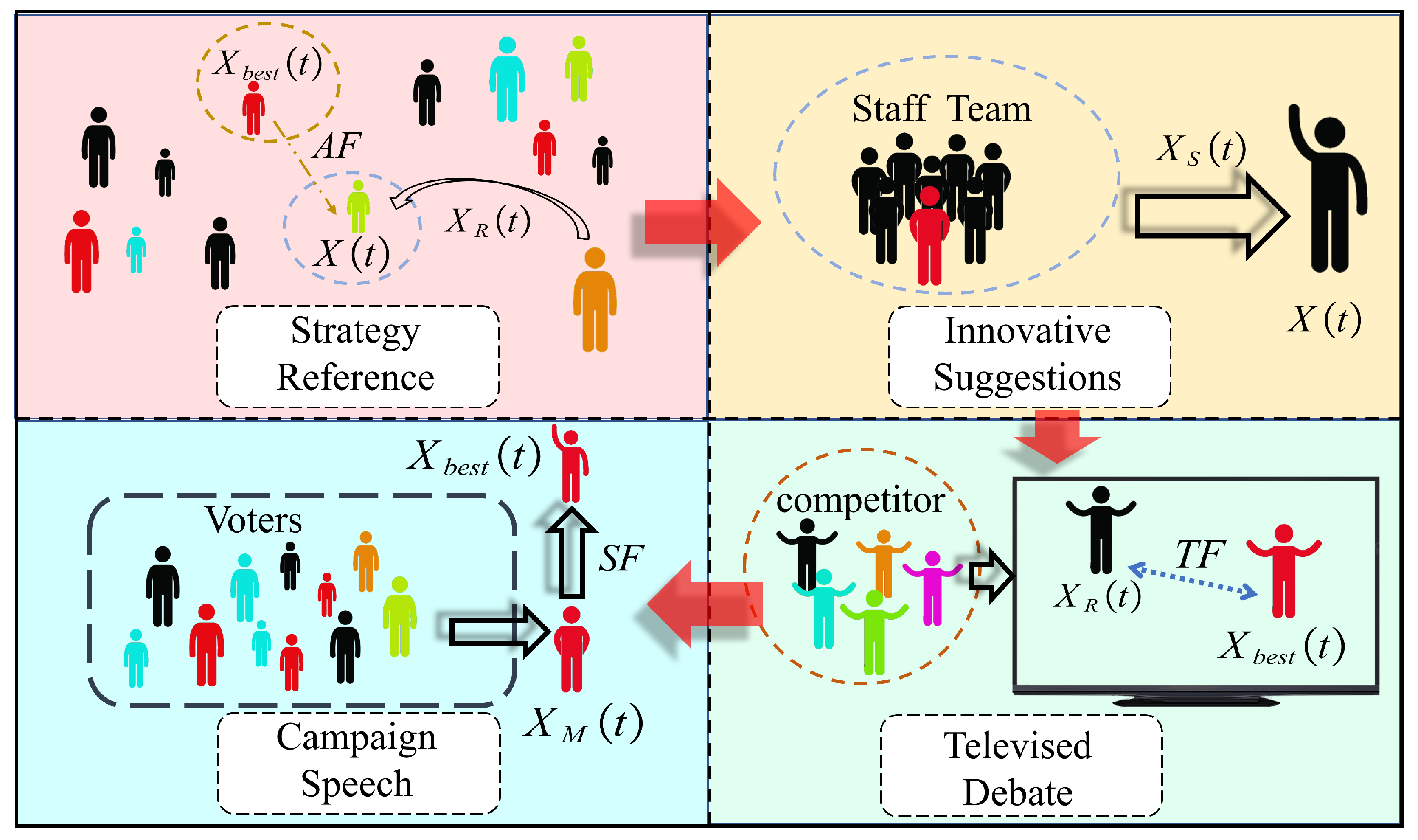
3.1. Inspiration
- The process of EOA is divided into two phases: party nomination and presidential election. The party nomination reflects the exploration phase, while the later one reflects the exploitation phase.
- In the party nomination phase, candidates win the nomination through two behaviors: strategy reference and innovative suggestions of the staff team.
- In the presidential election phase, candidates increase their poll approval rate via two approaches: televised debate and campaign speech.
3.2. Initialization Model
3.3. Party Nomination
3.3.1. Strategy Reference
3.3.2. Innovative Suggestions of the Staff Team
3.4. Presidential Election
3.4.1. Televised Debate
3.4.2. Campaign Speech
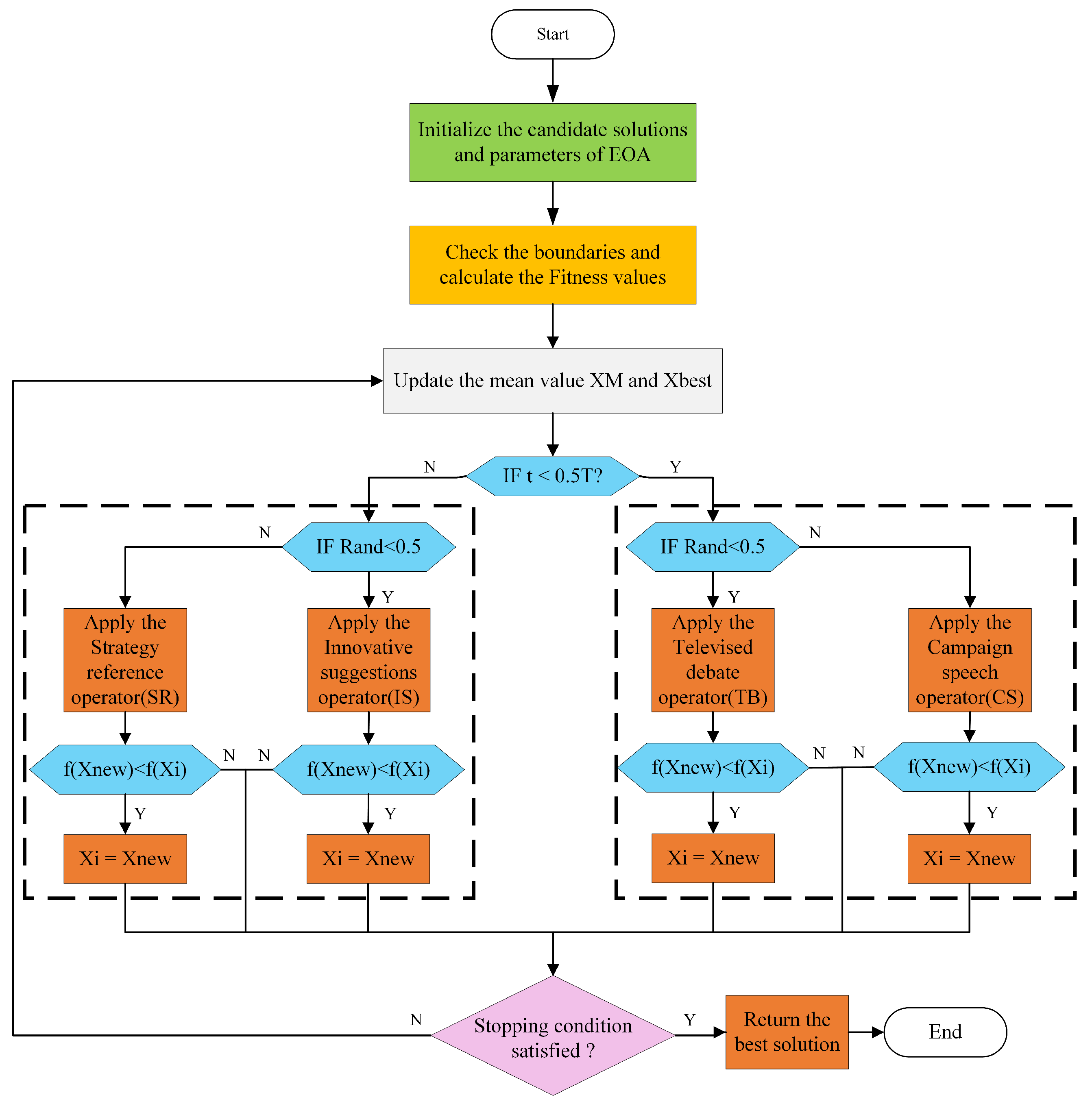
3.5. Pseudo-Code of the EOA
| Algorithm 1: Election Optimizer Algorithm |
| Input: N, T, , , |
| Output: |
| Initialize the population X and the parameters of EOA |
 |
| return the best solution |
3.6. Computational Complexity of EOA
4. Experimental Results and Discussions
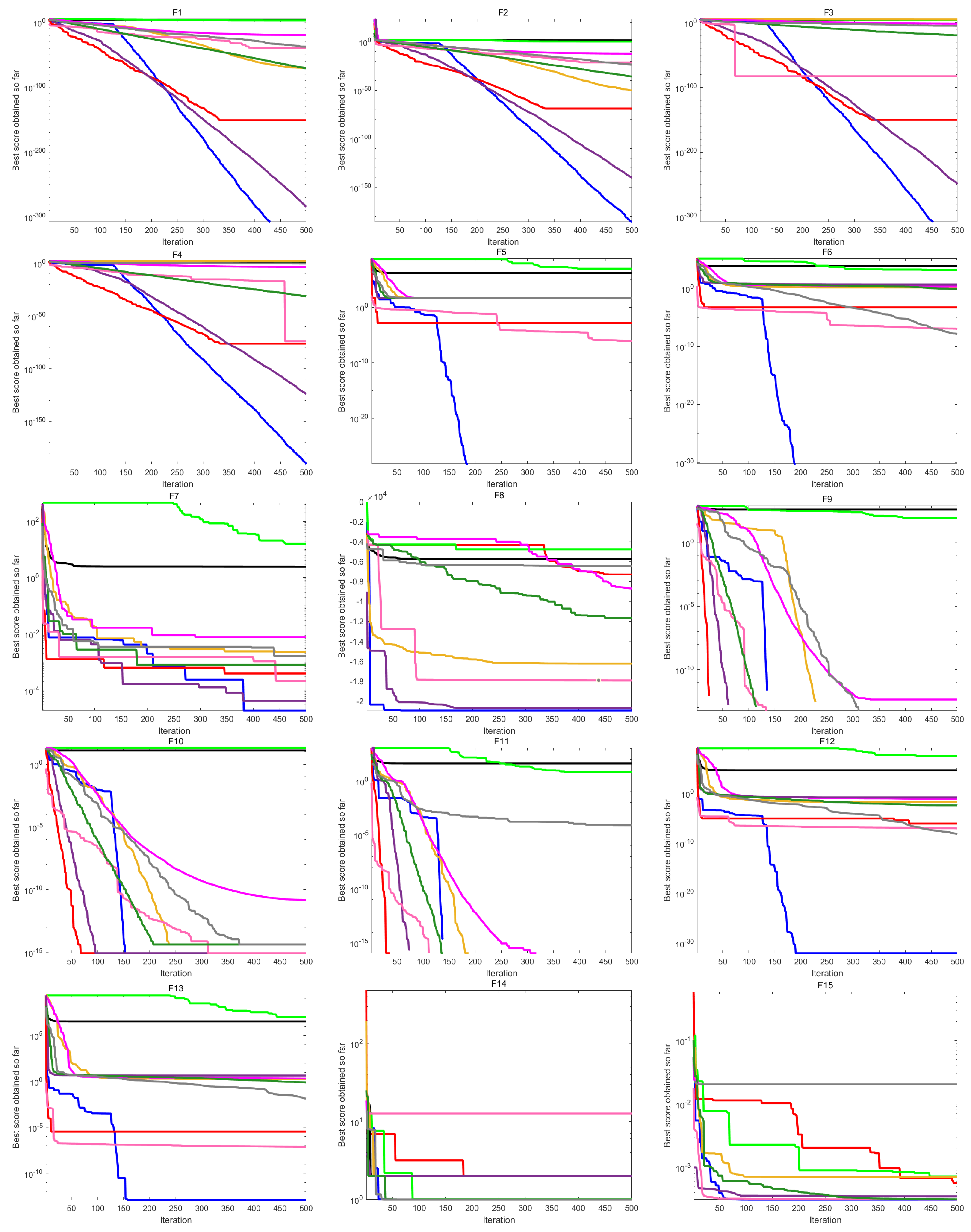
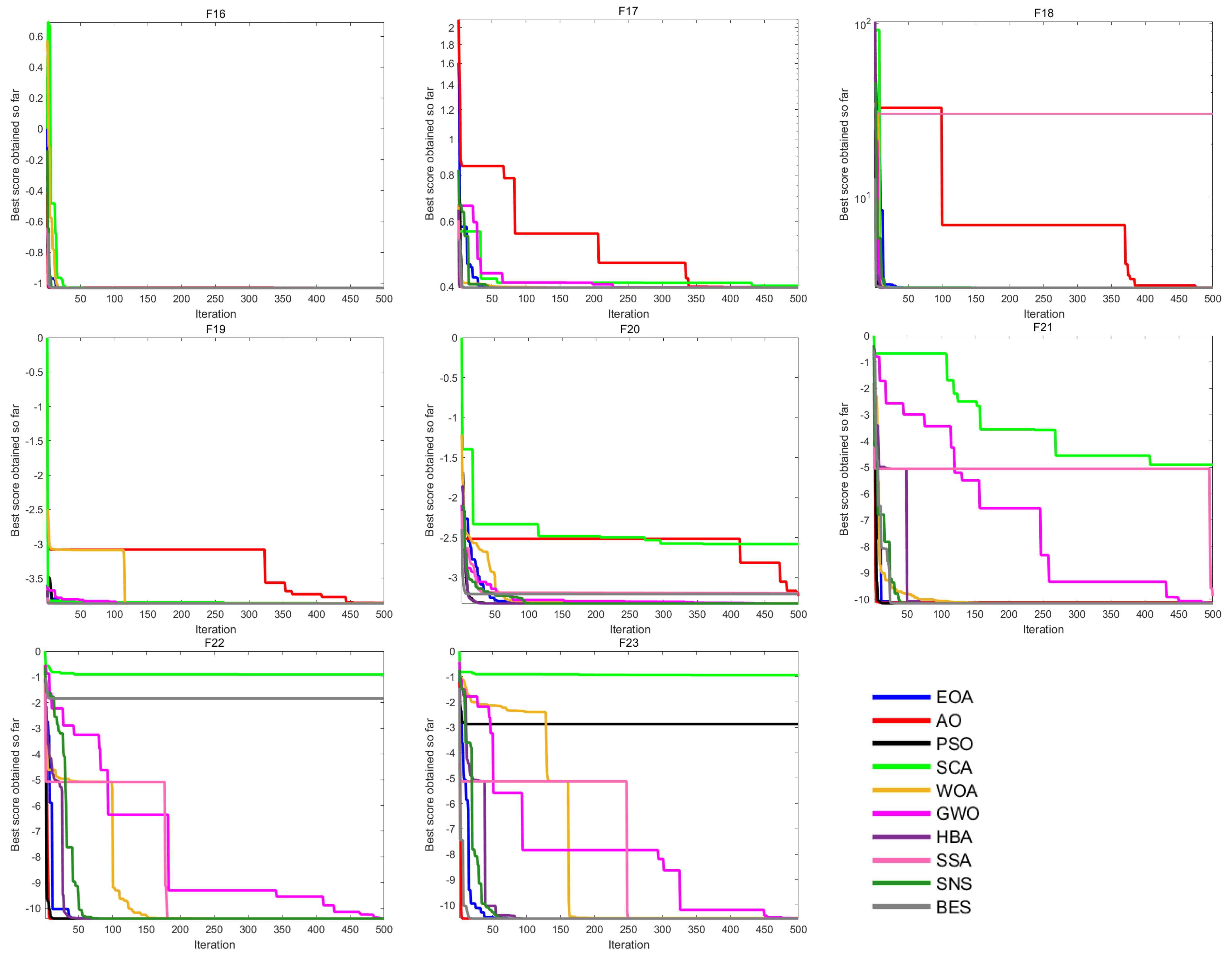
4.1. Experiment 1: Twenty-Three Benchmark Test Functions
- Aquila Optimizer (AO) [16];
- Particle Swarm Optimization (PSO) [10];
- Sine Cosine Algorithm (SCA) [33];
- Whale Optimization Algorithm (WOA) [13];
- Grey Wolf Optimizer (GWO) [14];
- Honey Badger Algorithm (HBA) [11];
- Sparrow Search Algorithm (SSA) [34];
- Social Network Search (SNS) [25];
- Bald Eagle Search (BES) [35].
4.1.1. The Parameter Sensitivity Analysis of EOA
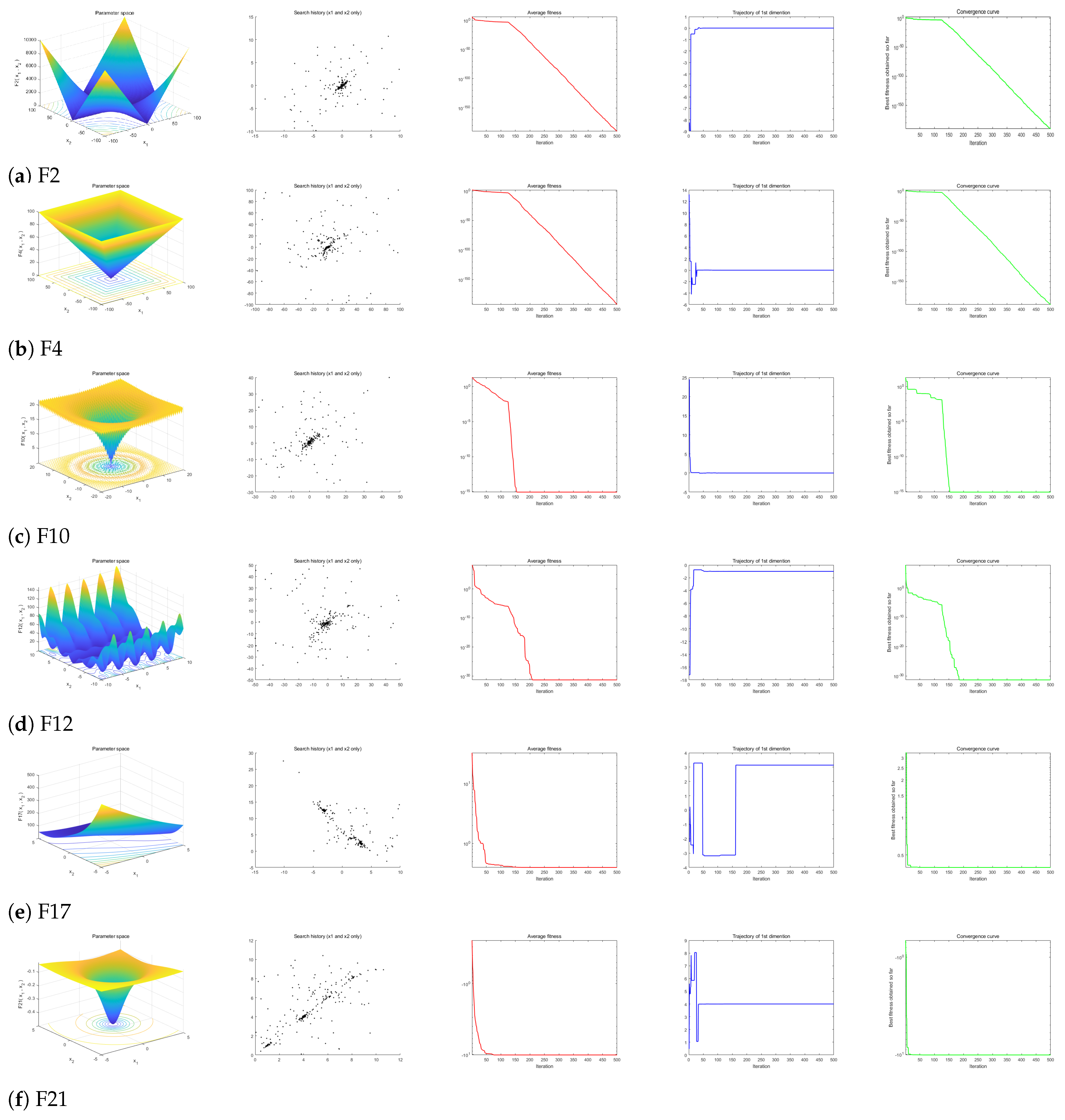
4.1.2. Qualitative Analysis for Convergence of EOA
4.1.3. Exploration and Exploitation Evaluation of EOA
4.1.4. Wilcoxon Rank-Sum Test Analysis of EOA
4.1.5. Time Consuming Test of EOA
4.2. Experiment 2: IEEE CEC2019 Test Suite
5. EOA for Solving Industrial Engineering Design Problems
5.1. Speed Reducer Design Problem
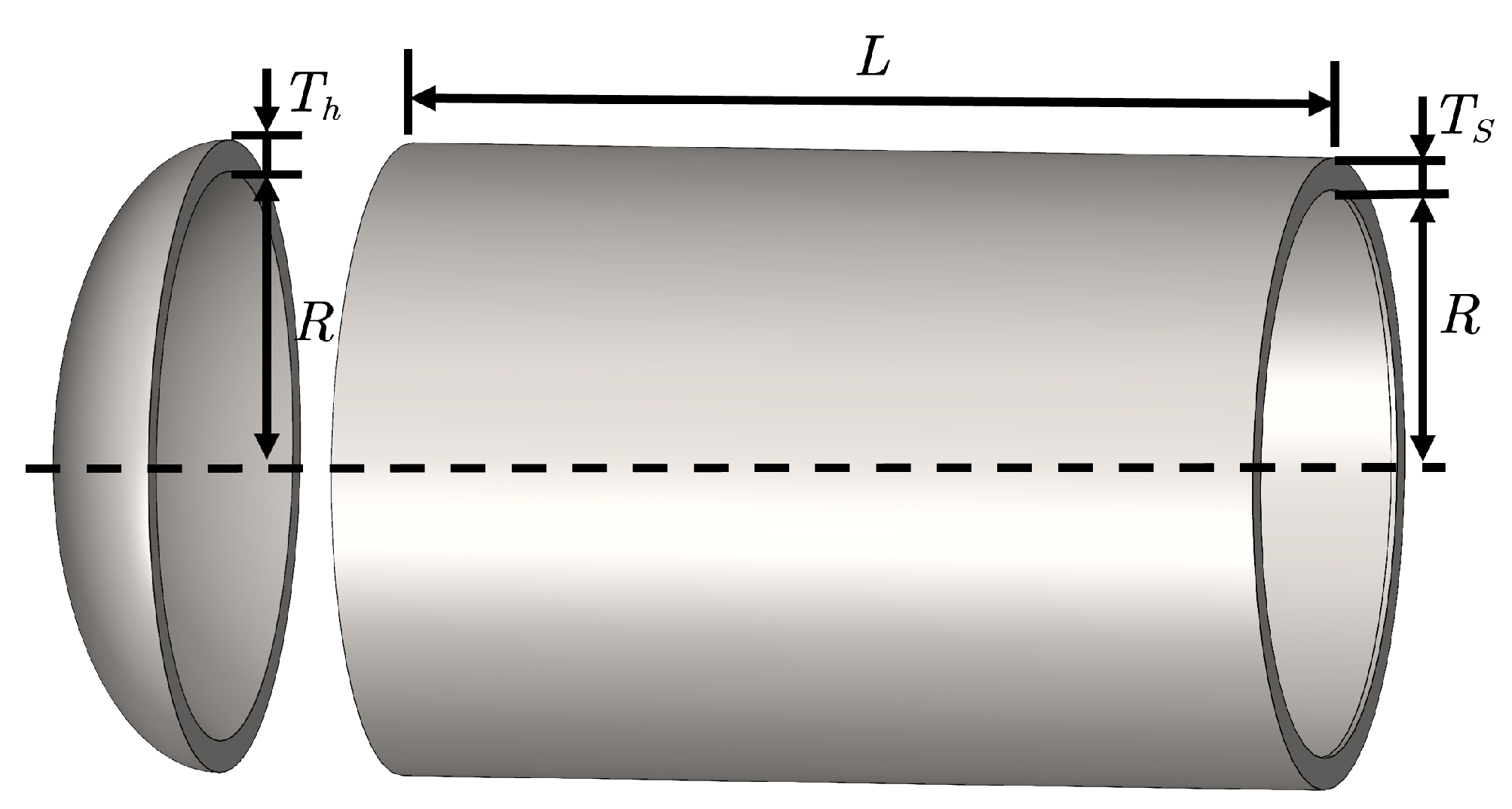
5.2. Pressure Vessel Design Problem
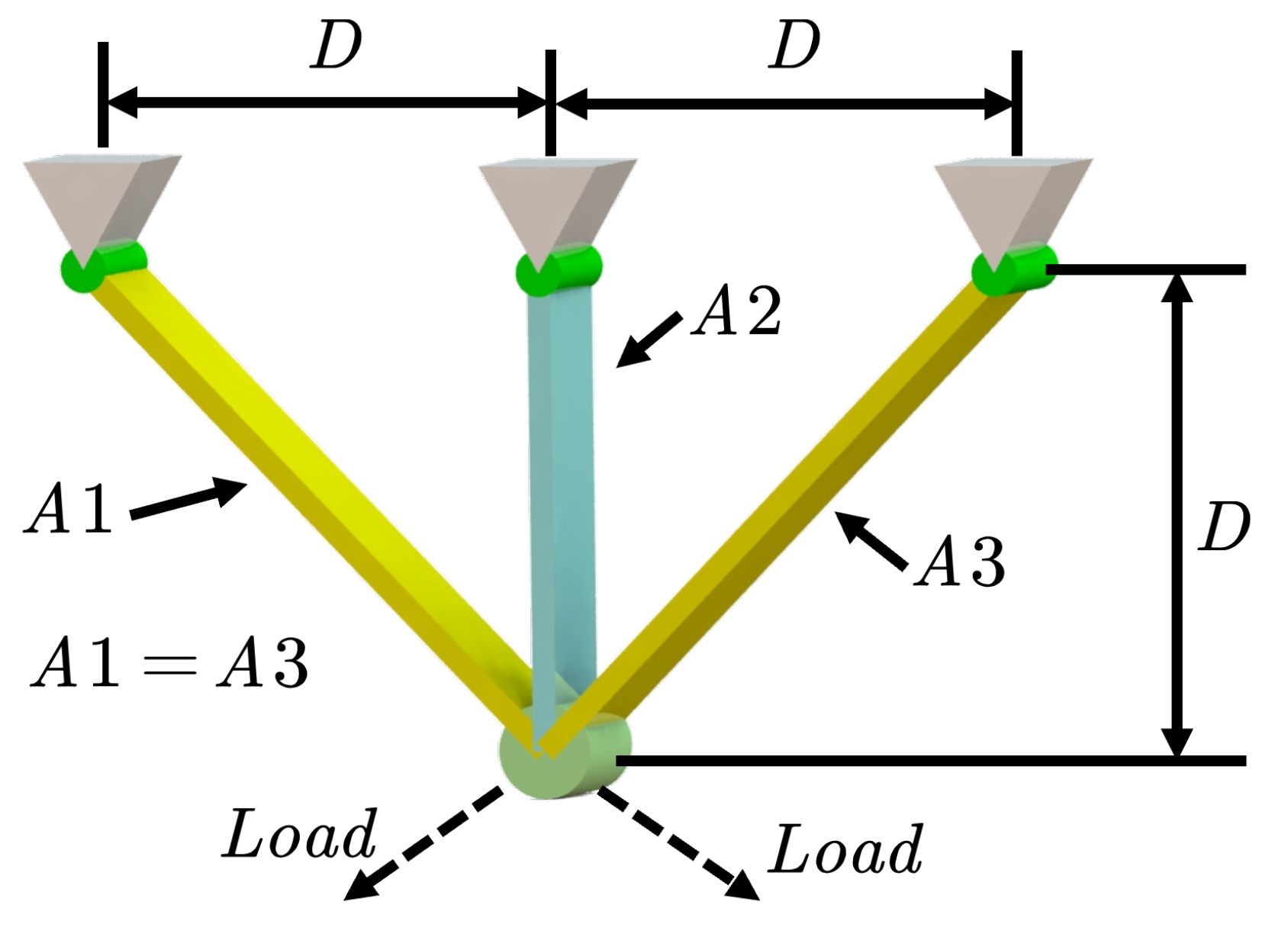
5.3. Three-Bar Truss Design Problem
5.4. Welded Beam Design Problem
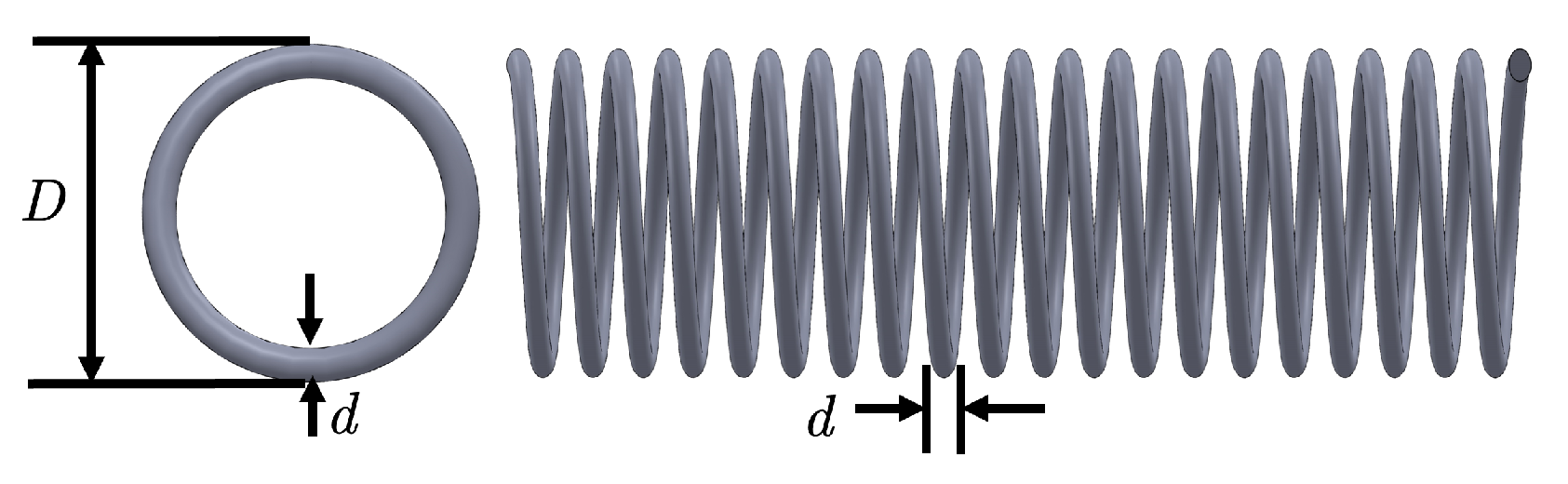
5.5. Tension/Compression Spring Design Problem
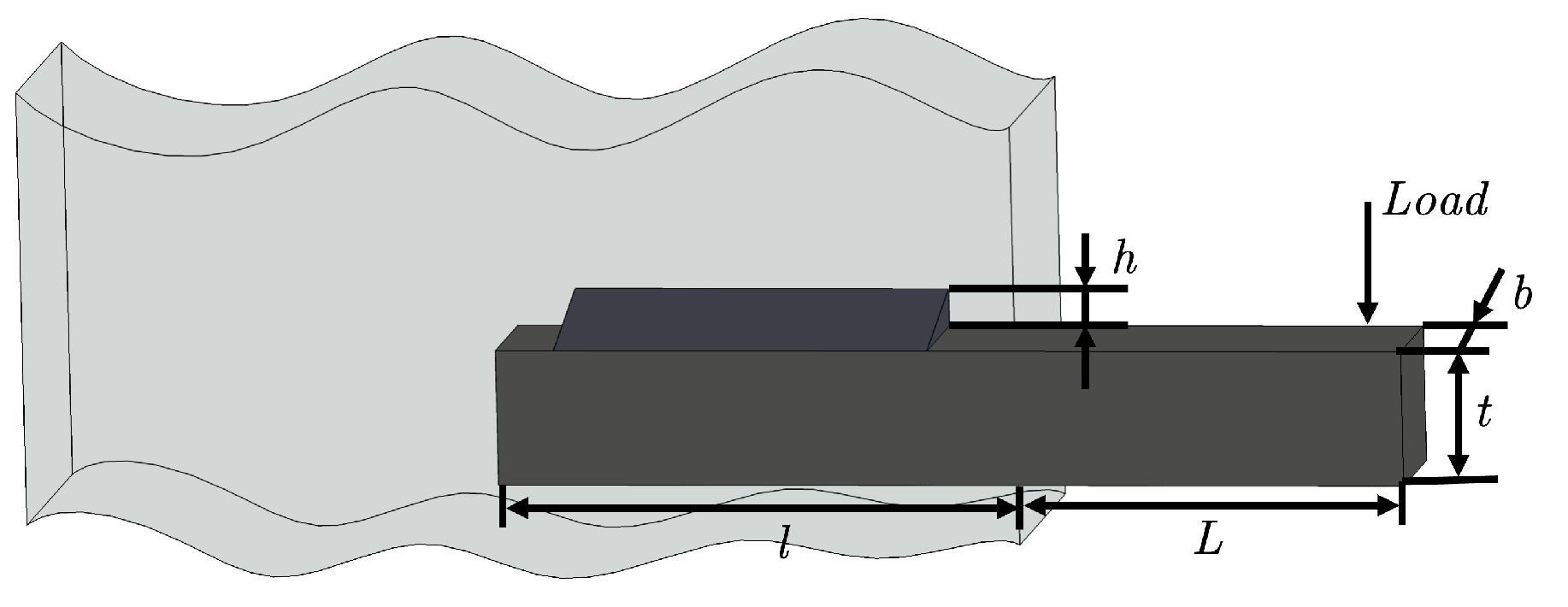
5.6. Cantilever Beam Design Problem
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, J.; Sha, Y.; Chen, Y.; Zhao, X. A Novel ensemble of arithmetic optimization algorithm and Harris hawks optimization for solving industrial engineering optimization problems. Machines 2022, 10, 602. [Google Scholar] [CrossRef]
- Alnowibet, K.A.; Mahdi, S.; El-Alem, M.; Abdelawwad, M.; Mohamed, A.W. Guided hybrid modified simulated annealing algorithm for solving constrained global optimization problems. Mathematics 2022, 10, 1312. [Google Scholar] [CrossRef]
- Yang, X.; Wang, R.; Zhao, D.; Yu, F.; Huang, C.; Heidari, A.A.; Cai, Z.; Bourouis, S.; Algarni, A.D.; Chen, H. An adaptive quadratic interpolation and rounding mechanism sine cosine algorithm with application to constrained engineering optimization problems. Expert Syst. Appl. 2023, 213, 119041. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Dhiman, G.; Malik, O.; Morales-Menendez, R.; Ramirez-Mendoza, R.A.; Dehghani, A.; Guerrero, J.M.; Parra-Arroyo, L. A spring search algorithm applied to engineering optimization problems. Appl. Sci. 2020, 10, 6173. [Google Scholar] [CrossRef]
- Tian, A.Q.; Liu, F.F.; Lv, H.X. Snow Geese Algorithm: A novel migration-inspired meta-heuristic algorithm for constrained engineering optimization problems. Appl. Math. Model. 2024, 126, 327–347. [Google Scholar] [CrossRef]
- Kalpana, C.; Booba, B. Bio-Inspired Firefly Algorithm A Methodical Survey–Swarm Intelligence Algorithm. In Proceedings of the 2021 International Conference on Computational Intelligence and Computing Applications (ICCICA), Maharashtra, India, 18–19 June 2021; IEEE: Piscataway Township, NJ, USA, 2021; pp. 1–7. [Google Scholar]
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 261–265. [Google Scholar]
- Su, H.; Zhao, D.; Heidari, A.A.; Liu, L.; Zhang, X.; Mafarja, M.; Chen, H. RIME: A physics-based optimization. Neurocomputing 2023, 532, 183–214. [Google Scholar] [CrossRef]
- Naik, A.; Satapathy, S.C. Past present future: A new human-based algorithm for stochastic optimization. Soft Comput. 2021, 25, 12915–12976. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Z.M.; Sun, W. The improved slime mould algorithm with Levy flight. J. Phys. Conf. Ser. 2020, 1617, 012033. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Coello, C.A.C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 2000, 41, 113–127. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Coello, C.A.C. An empirical study about the usefulness of evolution strategies to solve constrained optimization problems. Int. J. Gen. Syst. 2008, 37, 443–473. [Google Scholar] [CrossRef]
- Li, S.; Gu, Q.; Gong, W.; Ning, B. An enhanced adaptive differential evolution algorithm for parameter extraction of photovoltaic models. Energy Convers. Manag. 2020, 205, 112443. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S.; Mirjalili, S. A review of the application of the simulated annealing algorithm in structural health monitoring (1995–2021). Frat. Integrità Strutt. 2023, 17, 51–76. [Google Scholar] [CrossRef]
- Ali, F.; Sarwar, A.; Bakhsh, F.I.; Ahmad, S.; Shah, A.A.; Ahmed, H. Parameter extraction of photovoltaic models using atomic orbital search algorithm on a decent basis for novel accurate RMSE calculation. Energy Convers. Manag. 2023, 277, 116613. [Google Scholar] [CrossRef]
- Fallah, A.M.; Ghafourian, E.; Shahzamani Sichani, L.; Ghafourian, H.; Arandian, B.; Nehdi, M.L. Novel Neural Network Optimized by Electrostatic Discharge Algorithm for Modification of Buildings Energy Performance. Sustainability 2023, 15, 2884. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Moosavian, N.; Roodsari, B.K. Soccer league competition algorithm: A novel meta-heuristic algorithm for optimal design of water distribution networks. Swarm Evol. Comput. 2014, 17, 14–24. [Google Scholar] [CrossRef]
- Talatahari, S.; Bayzidi, H.; Saraee, M. Social Network Search for Global Optimization. IEEE Access 2021, 9, 92815–92863. [Google Scholar] [CrossRef]
- Askari, Q.; Younas, I.; Saeed, M. Political Optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowl.-Based Syst. 2020, 195, 105709. [Google Scholar] [CrossRef]
- Altunbey, F.; Alatas, B. Overlapping community detection in social networks using parliamentary optimization algorithm. Int. J. Comput. Netw. Appl. 2015, 2, 12–19. [Google Scholar]
- Farshchin, M.; Maniat, M.; Camp, C.V.; Pezeshk, S. School based optimization algorithm for design of steel frames. Eng. Struct. 2018, 171, 326–335. [Google Scholar] [CrossRef]
- Wang, L.Y.; Cao, Q.J.; Zhang, Z.X.; Mirjalili, S.; Zhao, W.G. Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 2022, 114, 105082. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Liu, J.; Zhou, H. Multi-strategy Equilibrium Optimizer: An improved meta-heuristic tested on numerical optimization and engineering problems. PLoS ONE 2022, 17, e0276210. [Google Scholar] [CrossRef]
- Xian, S.; Feng, X. Meerkat optimization algorithm: A new meta-heuristic optimization algorithm for solving constrained engineering problems. Expert Syst. Appl. 2023, 231, 120482. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Zamani, H.; Mirjalili, S.; Elaziz, M.A. MMKE: Multi-trial vector-based monkey king evolution algorithm and its applications for engineering optimization problems. PLoS ONE 2023, 18, e0280006. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Alsattar, H.A.; Zaidan, A.; Zaidan, B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Liu, J.; Li, D.; Wu, Y.; Liu, D. Lion swarm optimization algorithm for comparative study with application to optimal dispatch of cascade hydropower stations. Appl. Soft Comput. 2020, 87, 105974. [Google Scholar] [CrossRef]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Lu, S.; Kim, H.M. A regularized inexact penalty decomposition algorithm for multidisciplinary design optimization problems with complementarity constraints. J. Mech. Des. Apr. 2010, 13, 041005. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Ozsoydan, F.B. Adaptive firefly algorithm with chaos for mechanical design optimization problems. Appl. Soft Comput. 2015, 36, 152–164. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Czerniak, J.M.; Zarzycki, H.; Ewald, D. AAO as a new strategy in modeling and simulation of constructional problems optimization. Simul. Model. Pract. Theory 2017, 76, 22–33. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization. Appl. Math. Comput. 2007, 186, 1407–1422. [Google Scholar] [CrossRef]
- Ray, T.; Saini, P. Engineering design optimization using a swarm with an intelligent information sharing among individuals. Eng. Optim. 2001, 33, 735–748. [Google Scholar] [CrossRef]
- Sadollah, A.; Bahreininejad, A.; Eskandar, H.; Hamdi, M. Mine blast algorithm: A new population based algorithm for solving constrained engineering optimization problems. Appl. Soft Comput. 2013, 13, 2592–2612. [Google Scholar] [CrossRef]
- Liu, H.; Cai, Z.; Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- He, Q.; Wang, L. An effective co-evolutionary particle swarm optimization for constrained engineering design problems. Eng. Appl. Artif. Intell. 2007, 20, 89–99. [Google Scholar] [CrossRef]
- Ragsdell, K.; Phillips, D. Optimal design of a class of welded structures using geometric programming. J. Eng. Ind. Aug. 1976, 98, 1021–1025. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Oliva, D.; Xiong, S. An improved opposition-based sine cosine algorithm for global optimization. Expert Syst. Appl. 2017, 90, 484–500. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray optimization. Comput. Struct. 2012, 112, 283–294. [Google Scholar] [CrossRef]
- Arora, J. Introduction to Optimum Design; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Chickermane, H.; Gea, H.C. Structural optimization using a new local approximation method. Int. J. Numer. Methods Eng. 1996, 39, 829–846. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Prayogo, D. Symbiotic organisms search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]


| Fun | Dimensions | Range | Fmin |
|---|---|---|---|
| 10, 50, 100, 500 | [−100, 100] | 0 | |
| 10, 50, 100, 500 | [−10, 10] | 0 | |
| 10, 50, 100, 500 | [−100, 100] | 0 | |
| 10, 50, 100, 500 | [−100, 100] | 0 | |
| 10, 50, 100, 500 | [−30, 30] | 0 | |
| 10, 50, 100, 500 | [−100, 100] | 0 | |
| 10, 50, 100, 500 | [−128, 128] | 0 |
| Fun | Dimensions | Range | Fmin |
|---|---|---|---|
| 10, 50, 100, 500 | −418.9829n | ||
| 10, 50, 100, 500 | 0 | ||
| 10, 50, 100, 500 | 0 | ||
| 10, 50, 100, 500 | 0 | ||
| 10, 50, 100, 500 | 0 | ||
| 10, 50, 100, 500 | 0 |
| Fun | Dimensions | Range | Fmin |
|---|---|---|---|
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.0003 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [−1, 2] | −3.86 | |
| 6 | [0, 1] | −0.32 | |
| 4 | [0, 1] | −10.1532 | |
| 4 | [0, 1] | −10.4028 | |
| 4 | [0, 1] | −10.5363 |
| - | |
| - | |
| - | |
| - |
| Fun | Measure | = 0.1 | = 2 | = 5 | = 10 | = 15 | = 20 |
|---|---|---|---|---|---|---|---|
| F14 | Average | ||||||
| STD | |||||||
| Rank | 6 | 2 | 3 | 5 | 1 | 4 | |
| F15 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 5 | 2 | 3 | 4 | |
| F16 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 2 | 3 | 4 | 5 | |
| F17 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 3 | 2 | 4 | 5 | |
| F18 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 2 | 5 | 3 | 4 | |
| F19 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 2 | 3 | 4 | 5 | |
| F20 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 2 | 3 | 4 | 5 | |
| F21 | Average | ||||||
| STD | |||||||
| Rank | 6 | 5 | 2 | 4 | 1 | 3 | |
| F22 | Average | ||||||
| STD | |||||||
| Rank | 6 | 2 | 5 | 4 | 3 | 1 | |
| F23 | Average | ||||||
| STD | |||||||
| Rank | 6 | 1 | 5 | 3 | 4 | 2 | |
| Mean | Rank | 6 | 1.6 | 3.1 | 3.4 | 3.1 | 3.8 |
| Final | Rank | 5 | 1 | 2 | 3 | 2 | 4 |
| Fun No. Measure | Comparative Algorithms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOA | AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | |
| F1 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F2 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F3 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F4 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F5 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F6 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F7 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F8 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F9 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F10 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F11 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F12 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F13 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| W|L|T | 10|0|3 | 13|0|0 | 13|0|0 | 13|0|0 | 13|0|0 | 10|0|3 | 10|1|2 | 12|0|1 | 12|0|1 | |
| Mean Rank | ||||||||||
| Final Rank | 1 | 2 | 10 | 9 | 8 | 7 | 3 | 5 | 4 | 6 |
| Fun No. Measure | Comparative Algorithms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOA | AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | |
| F14 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F15 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F16 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F17 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F18 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F19 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F20 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F21 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F22 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F23 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| W|L|T | 9|0|1 | 8|0|2 | 9|0|1 | 9|0|1 | 7|0|3 | 8|0|2 | 8|0|2 | 5|1|4 | 6|0|4 | |
| Mean Rank | ||||||||||
| Final Rank | 1 | 6 | 9 | 10 | 8 | 3 | 7 | 5 | 2 | 4 |
| Fun No. Measure | Comparative Algorithms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOA | AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | |
| F1 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F2 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F3 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F4 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F5 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F6 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F7 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F8 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F9 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F10 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F11 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F12 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F13 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| W|L|T | 9|1|3 | 13|0|0 | 13|0|0 | 12|0|1 | 13|0|0 | 11|0|2 | 11|0|2 | 11|0|2 | 13|0|0 | |
| Mean Rank | ||||||||||
| Final Rank | 1 | 2 | 9 | 10 | 6 | 8 | 4 | 3 | 5 | 7 |
| Fun No. Measure | Comparative Algorithms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOA | AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | |
| F1 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F2 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F3 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F4 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F5 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F6 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F7 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F8 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F9 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F10 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F11 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F12 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F13 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| W|L|T | 10|0|3 | 13|0|0 | 13|0|0 | 12|0|1 | 13|0|0 | 10|0|3 | 11|0|2 | 11|0|2 | 12|0|1 | |
| Mean Rank | ||||||||||
| Final Rank | 1 | 2 | 9 | 10 | 6 | 8 | 4 | 3 | 5 | 7 |
| Fun No. Measure | Comparative Algorithms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOA | AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | |
| F1 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F2 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F3 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F4 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F5 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F6 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F7 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F8 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F9 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F10 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F11 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F12 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| F13 | ||||||||||
| Average | ||||||||||
| STD | ||||||||||
| W|L|T | 9|1|3 | 13|0|0 | 13|0|0 | 11|0|2 | 13|0|0 | 10|0|3 | 10|0|3 | 11|0|2 | 11|0|2 | |
| Mean Rank | ||||||||||
| Final Rank | 1 | 2 | 9 | 10 | 6 | 8 | 4 | 3 | 5 | 7 |
| Fun | Dimensions | Comparative Algorithms | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | ||
| p-Value | p-Value | p-Value | p-Value | p-Value | p-Value | p-Value | p-Value | p-Value | ||
| F1 | 10 | |||||||||
| F2 | 10 | |||||||||
| F3 | 10 | |||||||||
| F4 | 10 | |||||||||
| F5 | 10 | |||||||||
| F6 | 10 | |||||||||
| F7 | 10 | |||||||||
| F8 | 10 | |||||||||
| F9 | 10 | |||||||||
| F10 | 10 | |||||||||
| F11 | 10 | |||||||||
| F12 | 10 | |||||||||
| F13 | 10 | |||||||||
| F14 | 2 | |||||||||
| F15 | 4 | |||||||||
| F16 | 2 | |||||||||
| F17 | 2 | |||||||||
| F18 | 2 | |||||||||
| F19 | 3 | |||||||||
| F20 | 6 | |||||||||
| F21 | 4 | |||||||||
| F22 | 4 | |||||||||
| F23 | 4 | |||||||||
| W|L|T | 19|2|2 | 18|5|0 | 23|0|0 | 21|2|0 | 20|3|0 | 18|2|3 | 18|3|2 | 20|1|2 | 19|4|0 | |
| Fun | Comparative Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EOA | AO | PSO | SCA | WOA | GWO | HBA | SSA | SNS | BES | |
| F1 | ||||||||||
| F2 | ||||||||||
| F3 | ||||||||||
| F4 | ||||||||||
| F5 | ||||||||||
| F6 | ||||||||||
| F7 | ||||||||||
| F8 | ||||||||||
| F9 | ||||||||||
| F10 | ||||||||||
| F11 | ||||||||||
| F12 | ||||||||||
| F13 | ||||||||||
| F14 | ||||||||||
| F15 | ||||||||||
| F16 | ||||||||||
| F17 | ||||||||||
| F18 | ||||||||||
| F19 | ||||||||||
| F20 | ||||||||||
| F21 | ||||||||||
| F22 | ||||||||||
| F23 | ||||||||||
| No. | Functions | Fmin | D | Search Range |
|---|---|---|---|---|
| 1 | Storn’s Chebyshev Polynomial Fitting Problem | 1 | 9 | [−8192, 8192] |
| 2 | Inverse Hilbert Matrix Problem | 1 | 16 | [−16,384, 16,384] |
| 3 | Lennard-Jones Minimum Energy Cluster | 1 | 18 | [−4, 4] |
| 4 | Rastrigin’s Function | 1 | 10 | [−100, 100] |
| 5 | Griewangk’s Function | 1 | 10 | [−100, 100] |
| 6 | Weierstrass Function | 1 | 10 | [−100, 100] |
| 7 | Modified Schwefel’s Function | 1 | 10 | [−100, 100] |
| 8 | Expanded Schaffer’s F6 Function | 1 | 10 | [−100, 100] |
| 9 | Happy Cat Function | 1 | 10 | [−100, 100] |
| 10 | Ackley Function | 1 | 10 | [−100, 100] |
| Fun No. Measure | Comparative Methods | |||||||
|---|---|---|---|---|---|---|---|---|
| EOA | SCA | AOA | LSO | PSO | RSA | WOA | SSA | |
| F1 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F2 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F3 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F4 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F5 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F6 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F7 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F8 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F9 | ||||||||
| Average | ||||||||
| STD | ||||||||
| F10 | ||||||||
| Average | ||||||||
| STD | ||||||||
| W|L|T | 8|2|0 | 7|2|1 | 9|0|1 | 7|3|0 | 9|1|0 | 7|3|0 | 7|2|1 | |
| Mean Rank | ||||||||
| Final Rank | ||||||||
| Algorithm | Optimal Values for Variables | Optimum | Ranking | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EOA | 3.5 | 0.7 | 17 | 7.317 | 7.80572 | 3.350572 | 5.286685 | 2996.691188 | 1 |
| AOA [12] | 3.50384 | 0.7 | 17 | 7.3 | 7.72933 | 3.35649 | 5.2867 | 2997.9157 | 4 |
| AO [16] | 3.5021 | 0.7 | 17 | 7.3099 | 7.7476 | 3.3641 | 5.2994 | 3007.7328 | 6 |
| GWO [14] | 3.501 | 0.7 | 17 | 7.3 | 7.811013 | 3.350704 | 5.287411 | 2997.81965 | 3 |
| PSO [10] | 3.5001 | 0.7 | 17.0002 | 7.5177 | 7.7832 | 3.3508 | 5.2867 | 3145.922 | 12 |
| SCA [33] | 3.508755 | 0.7 | 17 | 7.3 | 7.8 | 3.46102 | 5.289213 | 3030.563 | 9 |
| GA [17] | 3.510253 | 0.7 | 17 | 8.35 | 7.8 | 3.362201 | 5.287723 | 3067.561 | 11 |
| MDA [38] | 3.5 | 0.7 | 17 | 7.3 | 7.670396 | 3.542421 | 5.245814 | 3019.583365 | 8 |
| MFO [39] | 3.49745 | 0.7 | 17 | 7.82775 | 7.71245 | 3.35178 | 5.28635 | 2998.9408 | 5 |
| FA [40] | 3.507495 | 0.7001 | 17 | 7.71967 | 8.08085 | 3.35151 | 5.28705 | 3010.137492 | 7 |
| HS [41] | 3.520124 | 0.7 | 17 | 8.37 | 7.8 | 3.36697 | 5.288719 | 3029.002 | 10 |
| AAO [42] | 3.499 | 0.6999 | 17 | 7.3 | 7.8 | 3.3502 | 5.2872 | 2996.783 | 2 |
| Algorithm | Optimal Values for Variables | Optimum | Ranking | |||
|---|---|---|---|---|---|---|
| EOA | 0.7787543 | 0.3858478 | 40.32629 | 199.9165 | 5892.3459 | 1 |
| AOA [12] | 0.8303737 | 0.4162057 | 42.75127 | 169.3454 | 6048.7844 | 4 |
| AO [16] | 1.054 | 0.182806 | 59.6219 | 38.805 | 5949.2258 | 2 |
| WOA [13] | 0.8125 | 0.4375 | 42.0982699 | 176.638998 | 6059.741 | 6 |
| SMA [15] | 0.7931 | 0.3932 | 40.6711 | 196.2178 | 5994.1857 | 3 |
| GWO [14] | 0.8125 | 0.4345 | 42.0892 | 176.7587 | 6051.5639 | 5 |
| PSO-SCA [33] | 0.8125 | 0.4375 | 42.098446 | 176.6366 | 6059.71433 | 8 |
| MVO [43] | 0.8125 | 0.4375 | 42.090738 | 176.73869 | 6060.8066 | 11 |
| GA [17] | 0.8125 | 0.4375 | 42.097398 | 176.65405 | 6059.94634 | 10 |
| HPSO [44] | 0.8125 | 0.4375 | 42.0984 | 176.6366 | 6059.7143 | 7 |
| ES [18] | 0.8125 | 0.4375 | 42.098087 | 176.640518 | 6059.7456 | 9 |
| Algorithm | Optimal Values for Variables | Optimum | Ranking | |
|---|---|---|---|---|
| EOA | 0.788576562 | 0.408197 | 263.8628605 | 1 |
| AOA [12] | 0.79369 | 0.39426 | 263.9154 | 8 |
| Ray and Sain [45] | 0.795 | 0.395 | 264.3 | 10 |
| AO [16] | 0.7926 | 0.3966 | 263.8684 | 2 |
| SSA [34] | 0.78866541 | 0.408275784 | 263.89584 | 3 |
| MBA [46] | 0.788565 | 0.4085597 | 263.89585 | 5 |
| PSO-DE [47] | 0.7886751 | 0.4082482 | 263.89584 | 3 |
| CS [48] | 0.78867 | 0.40902 | 263.9716 | 9 |
| GOA [49] | 0.788897556 | 0.40761957 | 263.8958815 | 6 |
| MFO [39] | 0.788244771 | 0.409466906 | 263.8959797 | 7 |
| Algorithm | Optimal Values for Variables | Optimum | Ranking | |||
|---|---|---|---|---|---|---|
| EOA | 0.20572584 | 3.4706 | 9.036535 | 0.2057338 | 1.724879 | 1 |
| GA [17] | 0.2489 | 6.173 | 8.1789 | 0.2533 | 2.43 | 8 |
| CPSO [50] | 0.202369 | 3.544214 | 9.04821 | 0.205723 | 1.72802 | 3 |
| WOA [13] | 0.205396 | 3.484293 | 9.037426 | 0.206276 | 1.730499 | 4 |
| MVO [43] | 0.205463 | 3.473193 | 9.044502 | 0.205695 | 1.72645 | 2 |
| DAVID [51] | 0.2434 | 6.2552 | 8.2915 | 0.2444 | 2.3841 | 7 |
| APPROX [51] | 0.2444 | 6.2189 | 8.2915 | 0.2444 | 2.3815 | 6 |
| HS [52] | 0.2442 | 6.2231 | 8.2915 | 0.24 | 2.3807 | 5 |
| SIMPLEX [51] | 0.2792 | 5.6256 | 7.7512 | 0.2796 | 2.5307 | 9 |
| Algorithm | Optimal Values for Variables | Optimum | Ranking | ||
|---|---|---|---|---|---|
| EOA | 0.051073 | 0.3420839 | 11.4717 | 0.012021 | 1 |
| AOA [12] | 0.05 | 0.349809 | 11.8637 | 0.012124 | 2 |
| PSO [10] | 0.051728 | 0.357644 | 11.244543 | 0.0126747 | 5 |
| PO [26] | 0.052482 | 0.375940 | 10.245091 | 0.0126720 | 3 |
| OBSCA [53] | 0.0523 | 0.31728 | 12.54854 | 0.012625 | 4 |
| ES [18] | 0.051643 | 0.35536 | 11.397926 | 0.012698 | 8 |
| WOA [13] | 0.051207 | 0.345215 | 12.004032 | 0.0126763 | 6 |
| RO [54] | 0.05137 | 0.349096 | 11.76279 | 0.0126788 | 7 |
| MVO [43] | 0.05251 | 0.37602 | 10.33513 | 0.01279 | 10 |
| GSA [23] | 0.050276 | 0.32368 | 13.52541 | 0.0127022 | 9 |
| CPSO [50] | 0.051728 | 0.357644 | 11.244543 | 0.0126747 | 5 |
| CC [55] | 70.05 | 0.3159 | 14.25 | 0.0128334 | 11 |
| Algorithm | Optimal Values for Variables | Optimum Weight | Ranking | ||||
|---|---|---|---|---|---|---|---|
| EOA | 6.023716 | 5.303997 | 4.4954247 | 3.49728 | 2.15328 | 1.33994 | 1 |
| SMA [15] | 6.017757 | 5.310892 | 4.493758 | 3.501106 | 2.150159 | 1.33996 | 3 |
| MFO [39] | 5.983 | 5.3167 | 4.4973 | 3.5136 | 2.1616 | 1.33998 | 6 |
| ALO [56] | 6.01812 | 5.31142 | 4.48836 | 3.49751 | 2.158329 | 1.33995 | 2 |
| MMA [57] | 6.01 | 5.3 | 4.49 | 3.49 | 2.15 | 1.34 | 5 |
| SOS [58] | 6.01878 | 5.30344 | 4.49587 | 3.49896 | 2.15564 | 1.33996 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Shi, Y.; Wang, D.; Xu, X.; Xu, M.; Deng, Y. Election Optimizer Algorithm: A New Meta-Heuristic Optimization Algorithm for Solving Industrial Engineering Design Problems. Mathematics 2024, 12, 1513. https://doi.org/10.3390/math12101513
Zhou S, Shi Y, Wang D, Xu X, Xu M, Deng Y. Election Optimizer Algorithm: A New Meta-Heuristic Optimization Algorithm for Solving Industrial Engineering Design Problems. Mathematics. 2024; 12(10):1513. https://doi.org/10.3390/math12101513
Chicago/Turabian StyleZhou, Shun, Yuan Shi, Dijing Wang, Xianze Xu, Manman Xu, and Yan Deng. 2024. "Election Optimizer Algorithm: A New Meta-Heuristic Optimization Algorithm for Solving Industrial Engineering Design Problems" Mathematics 12, no. 10: 1513. https://doi.org/10.3390/math12101513
APA StyleZhou, S., Shi, Y., Wang, D., Xu, X., Xu, M., & Deng, Y. (2024). Election Optimizer Algorithm: A New Meta-Heuristic Optimization Algorithm for Solving Industrial Engineering Design Problems. Mathematics, 12(10), 1513. https://doi.org/10.3390/math12101513






