Quadratic Tracking Control of Linear Stochastic Systems with Unknown Dynamics Using Average Off-Policy Q-Learning Method

Abstract

This article investigates the optimal tracking control problem for data-based stochastic discrete-time linear systems. An average off-policy Q-learning algorithm is proposed to solve the optimal control problem with random disturbances. Compared with the existing off-policy reinforcement learning (RL) algorithm, the proposed average off-policy Q-learning algorithm avoids the assumption of an initial stability control. First, a pole placement strategy is used to design an initial stable control for systems with unknown dynamics. Second, the initial stable control is used to design a data-based average off-policy Q-learning algorithm. Then, this algorithm is used to solve the stochastic linear quadratic tracking (LQT) problem, and a convergence proof of the algorithm is provided. Finally, numerical examples show that this algorithm outperforms other algorithms in a simulation.

1. Introduction

The optimal control problem (OCP) requires that a model of the system is known, and the solution of the problem is offline, which can not adapt to an unknown dynamic system. Therefore, data-driven reinforcement learning methods have emerged and are widely used to solve the OCP for discrete-time [1,2,3] and continuous-time uncertain systems [4,5,6,7,8].

Reinforcement learning (RL) has been applied for solving optimal control problems in uncertain environments. Reinforcement learning (RL) methods are categorized into two classes: on-policy and off-policy. On-policy methods evaluate or improve the same policy that is used to make decisions. Off-policy methods, on the other hand, evaluate one policy, while following another policy. In other words, in off-policy methods, the policy that is used to generate data, called the behavior policy, may in fact be unrelated to the policy that is being evaluated and improved, called the estimation policy or target policy [9].

Regarding an on-policy algorithm, the iterated control gain will be returned to the system for real-time data generation along the system trajectory [8]. Regarding the collection of off-policy algorithm data, in the early stages, the data are collected over a period of time and reused for an iterative solution of the control gain. That is, the control gain obtained from each subsequent iteration is no longer returned to the system to generate new data [10]. Comparing on-policy and off-policy learning strategies, it can be seen that the former spreads the computational burden over different iteration time points, at the price of a longer learning process. The latter can achieve faster learning by making full use of online measurements, at the expense of a heavier computational effort at a single iteration time point. Comparing the on-policy and the off-policy learning strategies, it can be seen that the former spreads the computational burden over different iteration time points, at the price of a longer learning process. The latter can achieve faster learning by making full use of online measurements, at the expense of heavier computational effort at a single iteration time point [11].

When a linear system contains external stochastic disturbances, the OCP is solved for linear systems with additive noise and state-dependent noise when the system model are known [12]. But for situations where there are partial unknowns in the system model, reference [13] solved the optimal control problem with control-dependent noise. Furthermore, for cases where the system dynamics are completely unknown, reference [14] discussed the OCP of linear systems with an external stochastic disturbance. However, reference [14] required that random disturbances were measurable, which is not very practical in reality. In [15], the OCP was studied when the system was unknown, and the problem of an un-measurable stochastic disturbance mentioned above was solved. In the literature above, when solving external stochastic disturbances, the performance index for selecting the optimal control problem is the average performance index function [16]. By utilizing an average cost function, Reference [17] tackled the output regulation problem for linear systems with unknown dynamics. Data-driven average Q-learning algorithms can also handle linear quadratic control problems, especially when there are un-measurable stochastic disturbances [18,19].

The field of modern control has focused much of its research efforts on the stochastic optimization problem [20,21]. It is commonly known that the solvability of the stochastic algebra equation (SAE) is equal to the feasibility of the stochastic linear quadratic (SLQ) optimal control problem [22]. The nonlinear features of the SAE make it difficult to obtain an analytical solution. For example, optimal control is obtained by solving the SAE using linear matrix inequality [23]. Liu [24] adopted the Lagrange multiplier theorem to obtain the condition of well-posedness and a state feedback solution for the SLQ problem.

However, the aforementioned literature did not take into account the tracking problem for unknown linear systems. The LQT problem of linear discrete time systems was solved when the system is unknown in [25]. However, that paper [25] did not consider external noises in the system. In reference [18], the authors considered the case of external noises to address the optimal control problem (OCP), but the tracking control problem was not taken into account. In reference [26], the Q-learning method was employed to address the LQT problem in the presence of partially unknown system dynamics. However, the specific case of the LQT problem with stochastic disturbances in the system was not considered in [26]. In [27], an off-policy algorithm was proposed to solve the LQT problem of linear systems with stochastic disturbance, but the algorithm still required the assumption of initial admissible control, which is difficult to choose with unknown dynamics.

In comparison to the aforementioned existing references, we introduce a novel approach called the average off-policy Q-learning (AOPQ) algorithm to tackle the LQT problem in unknown linear systems subjected to external stochastic disturbances. Our first contribution is that we introduce an average off-policy Q-learning algorithm to solve the LQT problem with stochastic disturbance. The second contribution is that we propose a method for solving an initial stable control when the system is unknown, thus avoiding the assumption of an initial stable control. The contributions of this paper are mainly reflected in the following aspects:

• In reference [25,28], they studied the LQT problem of linear systems, but did not consider the problems of stochastic disturbance. Due to stochastic disturbances that may occur error in state and output information, the standard Q-learning algorithm cannot be used directly.
  We proposed the AOPQ algorithm to overcome this problem.
• In reference [29], the authors investigated the set-point tracking problem in linear systems with disturbance when system models are unknown. However, this tracking signal is limited and can only track constant values and the proposed algorithm requires the assumption of an initial stable control. The tracking signal studied in this paper does not have this limitation and provides a data-driven method for providing an initial stable control.
• In contrast to reference [30], this paper applies off- policy Q-learning to solve the LQR problem of unknown discrete systems. It provides a data-based method for designing an initial stable control, which can obtain an initial stable controller using a pole placement strategy, with the system coefficient matrix constructed from data. However, this does not take into account the situation when the system output is tracking an external reference. For LQT problems with external stochastic disturbances, this paper solves the LQT problem of a linear discrete system using an average off-policy Q-learning algorithm.

This paper’s organizational structure is as follows: The LQT control problem for a stochastic linear discrete system is described in the next section. In Section 3, a model-free AOPQ algorithm is proposed for the stochastic LQT problem. In Section 4, simulation experiments were conducted to verify the effectiveness of the AOPQ algorithm. The conclusions are presented in Section 5.

Notations: $P>0(P\ge 0)\in {\mathbb{R}}^{n\times n}$ is (semi) positive definite. $Trace\left(P\right)$ is the trace of $P\in {\mathbb{R}}^{n\times n}$. Let $vec\left(C\right)={[c_1^T,c_2^T,\cdots ,c_q^T]}^T$ denote the vectorization of matrix $A=[c_1,\cdots ,c_q],c_i\in {\mathbb{R}}^n,i=1,\cdots ,q$. Let $vecs\left(P\right)={[p_{11},\cdots ,p_{1n},p_{22},\cdots ,p_{2n},\cdots ,p_{nn}]}^T$ denote the vectorization of the upper-triangular part of a symmetric matrix $P\in {\mathbb{R}}^{n\times n}$. Let $vecv\left(x\right)={[x_1^2,2x_1{x}_2,\cdots ,2x_1{x}_n,x_2^2,\cdots ,2x_2{x}_n,\cdots ,x_n^2]}^T$ be the quadratic vector of the vector $x\in {\mathbb{R}}^n$. $x^{T}Px=vecs{\left(P\right)}^{T}vecv\left(x\right)$. ⊗ stands for the Kronecker product.

2. LQT Problem with Stochastic Disturbance

Problem Description

Consider a linear stochastic dynamical system

$$\begin{array}{cc}\hfill x_{k+1}& =A{x}_k+B{u}_k+D{\omega }_k\hfill \\ \hfill y_k& =C{x}_k\hfill \end{array}$$

(1)

where $x_k\in {\mathbb{R}}^n$ is the state vector, $u_k\in {\mathbb{R}}^m$ is the control input, ${\omega }_k\in {\mathbb{R}}^p$ is the stochastic process disturbance from a Gaussian distribution $N(0,W_{\omega })$, and $y_k\in {\mathbb{R}}^q$ is the system output. The system dynamics are $A\in {\mathbb{R}}^{n\times n},B\in {\mathbb{R}}^{n\times m}$ are unknown, and $C\in {\mathbb{R}}^{q\times n}$, $D\in {\mathbb{R}}^{n\times p}$ are unknown.

Remark 1.

In practical application scenarios, discrete linear stochastic systems find extensive practical utilization, such as in population models and climate models [31]. In [32], ecological balance was studied, mainly in a mathematical model of population ecology, where the population size is not large, or births or deaths occur in discrete time.In economic models [33], the monetary multiplier in macroeconomic models can be regarded as a stochastic variable. In [34], when the system matrix was unknown, data-based methods were used to study certain problems. With the development of reinforcement learning technology, these methods have been widely used in practice, mainly in self-driving vehicles, distributed sensor networks, and agile robotics.

Remark 2.

We consider random disturbances ${\omega }_k$ that follow a Gaussian distribution $N(0,W_{\omega })$, where the mean is $E\left({\omega }_k\right)=0$ and the variance is $D\left({\omega }_k\right))=W_{\omega }$ of ${\omega }_k$. $E\left(X_0{\omega }_k\right)=0$, the initial state $X_0$ is independent of the stochastic disturbance input sequence ${\omega }_k$. In practical application scenarios, discrete linear stochastic systems find extensive practical utilization, such as in population models and climate models [31]. In practice, this type of random interference will appear in the design of autonomous vehicles, distributed sensor networks, and agile robots [34].

Assume 1.

The pair $(A,B)$ is stabilizable, and the pair $(A,C)$ is observable.

Assume 2.

Assume that the reference trajectory $r_k$ is generated by the following system:

$$r_{k+1}=F{r}_k$$

(2)

where $F\in {\mathbb{R}}^{q\times q}$ is a constant matrix.

Remark 3.

In order to design an initial stable control based on the data in average off-policy Q-learning algorithom when the system is unknown, it is assumed that the command generation system in (2) provides a constrained trajectory for tracking, by assuming that the constant matrix F is stable.

Remark 4.

In this article, we consider random disturbances ${\omega }_k$ that follow a Gaussian distribution $N(0,W_{\omega })$, where the mean is $E\left({\omega }_k\right)=0$ and the variance is $D\left({\omega }_k\right))=W_{\omega }$ of ${\omega }_k$. $E\left(X_0{\omega }_k\right)=0$, the initial state $X_0$ is independent of the stochastic disturbance input sequence ${\omega }_k$.

For simplicity, we define the augment system

$$\begin{array}{cc}\hfill X_{k+1}& =\overline{A}{X}_k+\overline{B}{u}_k+\overline{D}{\omega }_k\hfill \\ \hfill y_k& =C{x}_k\hfill \end{array}$$

(3)

where

$$X_{k+1}=\left[\begin{array}{c}{x}_{k+1}\\ r_{k+1}\end{array}\right],\overline{A}=\left[\begin{array}{cc}A& 0\\ 0& F\end{array}\right],\overline{B}=\left[\begin{array}{c}B\\ 0\end{array}\right],\overline{D}=\left[\begin{array}{c}D\\ 0\end{array}\right]$$

Problem 1.

Consider the augmented dynamical system in (3). The so-called stochastic linear quadratic tracking problem refers to designing a control policy

$$u_k=L_1{x}_k+L_2{r}_k\equiv L{X}_k$$

such that the system output $y_k$ can track the external reference signal $r_k$ and makes the following average performance index function achieve a minimum value (4).

The average performance index function [35] is defined by

$$J\left(x_k,r_k\right)=\mathbf{E}\left[\sum _{t=k}^{+\infty }\left(O_t)-\beta \left(L\right)\right)\mid x_k\right]$$

(4)

where $\beta \left(L\right)$ associated with the control policy $u_k=L{X}_k$ is defined as

$$\begin{array}{c}\hfill \beta \left(L\right)=\underset{\tau \to \infty }{lim}\frac{1}{\tau }\mathbf{E}\left[\sum _{t=1}^{\tau }{O}_t\right]\end{array}$$

(5)

$$\begin{array}{cc}\hfill O_t& ={(y_t-r_t)}^T{R}_1(y_t-r_t)+u_t^T{R}_2{u}_t\hfill \end{array}$$

(6)

where $R_1\in {\mathbb{R}}^{q\times q}>0,R_2\in {\mathbb{R}}^{m\times m}>0$ are symmetric positive matrices.

Remark 5.

In solving the LQT problem, the setting of the performance indicator function can choose either an average performance indicator [35] or a discounted performance indicator [28]. In the case of discounting, it is necessary to choose a discount factor to prevent stability loss, but the discount factor cannot affect unmeasurable disturbance data, so the cost function of discounts has certain limitations, such as $H_{\infty }$ tracking. Because the system state is affected by an external stochastic disturbance, the influence of the external stochastic disturbance on the value function is reduced by subtracting the average cost in the defined value function.

According to the augment system (3), the average performance index function (5) associated with the control policy $u_k=L{X}_k$ can be expressed as

$$\begin{array}{c}\hfill \beta \left(L\right)=\underset{\tau \to \infty }{lim}\frac{1}{\tau }\mathbf{E}\left[\sum _{t=1}^{\tau }{O}_t\right]\end{array}$$

(7)

$$\begin{array}{cc}\hfill O_t& =X_t^T{\overline{R}}_1{X}_t+u_t^T{R}_2{u}_t\hfill \end{array}$$

(8)

where ${\overline{R}}_1={[C^T-I]}^T{R}_1[C-I]\in {\mathbb{R}}^{(n+q)\times (n+q)}$. Thus, the average performance index function (4) can be expressed as

$$J\left(x_k,r_k\right)\equiv V\left(X_k\right)=\mathbf{E}\left[\sum _{t=k}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]$$

(9)

Due to the influence of noise on the system state, we eliminate the impact of estimated costs by subtracting the average cost. Thus, the remaining cost in (9) is only due to control issues. Equation (9) can be described as

$$\begin{array}{cc}\hfill V\left(X_k\right)=& \mathbf{E}\left[\sum _{t=k}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\hfill \\ \hfill =& \mathbf{E}\left[((O_t-\beta \left(L\right))+\sum _{t=k+1}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\hfill \\ \hfill =& \mathbf{E}\left[((O_t-\beta \left(L\right))\mid X_k\right]+\mathbf{E}\left[\sum _{t=k+1}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\hfill \end{array}$$

(10)

Because the first term on the right side of Equation (10) does not contain a random variable, thus $\mathbf{E}\left[(O_t-\beta \left(L\right))\mid X_k\right]=(O_t-\beta \left(L\right))$. According to the property of conditional expectation, i.e., the double expectation formula, second term on the right side of Equation (10) can be represented by the following equation:

$$\begin{array}{cc}\hfill \mathbf{E}\left[\sum _{t=k+1}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]=& \mathbf{E}\left[\mathbf{E}\left[\sum _{t=k+1}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\mid X_{k+1}\right]\hfill \\ \hfill =& \mathbf{E}\left[\mathbf{E}\left[\sum _{t=k+1}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_{k+1}\right]\mid X_k\right]\hfill \\ \hfill =& \mathbf{E}\left[V\left(X_{k+1}\right)\mid X_k\right]\hfill \end{array}$$

(11)

Based on the descriptions of (11) , we can obtain the form of the Bellman equation for Equation (9)

$$\begin{array}{cc}\hfill V\left(X_k\right)=& \mathbf{E}\left[\sum _{t=k}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\hfill \\ \hfill =& (O_k-\beta \left(L\right))+\mathbf{E}\left[V\left(X_{k+1}\right)\mid X_k\right]\hfill \end{array}$$

(12)

Based on the augmented system (3), the LQT problem can be converted into an optimal regulation problem. This problem can be rephrased as designing a controller $u_k^{*}=L^{*}{X}_k$ to minimize the following average performance index functions.

$$\begin{array}{cc}\hfill V^{*}\left(X_k\right)& =mi{n}_L\mathbf{E}\left[\sum _{t=k}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\hfill \end{array}$$

(13)

where

$$O_t=X_t^T{\overline{R}}_1{X}_t+u_t^T{R}_2{u}_t$$

$$\beta \left(L\right)=\underset{\tau \to \infty }{lim}\frac{1}{\tau }\mathbf{E}\left[\sum _{t=1}^{\tau }{O}_t\right]$$

In the following lemma, the Bellman Equation (12) can be proven to be quadratic under the control policy $u_k=L{X}_k$.

Lemma 1

(See [19]). Consider system (3). Assume that the policy gain L is stabilizing. P is the solution to the following stochastic ARE equation:

$$\begin{array}{c}\hfill {(\overline{A}+\overline{B}L)}^{T}P(\overline{A}+\overline{B}L)-P+{\overline{R}}_1+L^T{R}_{2}L=0\end{array}$$

(14)

and the average cost is $\beta \left(L\right)=Tr\left({\overline{D}}^{T}P\overline{D}{W}_{\omega }\right)$, where $W_{\omega }$ is the covariance of the stochastic noise ${\omega }_k$. Then, $V\left(X_k\right)=X_k^{T}P{X}_k$.

Lemma 2

(See [18]). Consider problem 1 and system (3). The optimal control gain $L^{*}$ is

$$L^{*}=-{\left(R_2+{\overline{B}}^T{P}^{*}\overline{B}\right)}^{-1}{\overline{B}}^T{P}^{*}\overline{A}$$

(15)

where $P^{*}>0$ is the solution to the stochastic ARE

$$\begin{array}{cc}\hfill {\overline{A}}^T{P}^{*}\overline{A}& -P^{*}-{\overline{A}}^T{P}^{*}\overline{B}{\left(B^T{P}^{*}\overline{B}+R_2\right)}^{-1}{\overline{B}}^T{P}^{*}\overline{A}+{\overline{R}}_1=\mathbf{0}.\hfill \end{array}$$

(16)

the average cost associated with $K^{*}$ is given by

$$\begin{array}{cc}\hfill \beta \left(L^{*}\right)=& Tr\left({\overline{D}}^T{P}^{*}\overline{D}{W}_{\omega }\right)\hfill \end{array}$$

(17)

Based on Lemma 2, the  optimal solution to Problem 1 can be found from the stochastic ARE in (16) . Even in the case of known system dynamics, the ARE is a nonlinear equation that is challenging to solve directly. To address this, Algorithm 1 can be employed to iteratively solve the ARE equation. Consequently, Algorithm 1 can be used to iteratively solve the control gain L.

Algorithm 1 PI Algorithm with System Model [2]

1: Initialization: Set $i=1$, select a stabilizing gain $L^1$ 2: Policy evaluation: Solution $P^i$ based on the following equation $${(\overline{A}+\overline{B}{L}^i)}^T{P}^i(\overline{A}+\overline{B}{L}^i)-P^i+{\overline{R}}_1+L^{iT}{R}_2{L}^i=0$$ (18) 3: Policy improvement: $$\begin{array}{cc}\hfill L^{i+1}& =-{(R_2+{\overline{B}}^T{P}^i\overline{B})}^{-1}\overline{B}{P}^i\overline{A}\hfill \end{array}$$ (19) 4: Stop if: $$\begin{array}{c}\hfill \mid L^{i+1}-L^i\mid \le \epsilon \end{array}$$ (20) for a small positive $\epsilon >0$, otherwise set $j=j+1$ and go to step 2.

Algorithm 1 provides an iterative solution to the optimal control gain when the model is known. Below we demonstrate that, under the optimal control $u_k^{*}=L^{*}{X}_k$, the tracking error can converge to the neighborhood of origin.

Corollary 1.

Consider system (3). Assume $P^{*}$ is the solution of ARE (16), then, under $u_k^{*}=L^{*}{X}_k$, the error $e_k=y_k-r_k$ converges to a neighborhood of the origin, i.e., the $e_k$ is uniformly ultimately bounded (UUB) with bound $\parallel e_k\parallel \le \sqrt{\beta \left(L\right)/\parallel R_1\parallel }$. Moreover, $u_k^{*}=L^{*}{X}_k$ minimizes the average performance index function (9).

Proof. 

According to (1) and (2),

$$\begin{array}{c}\hfill e_k=y_k-r_k=[C-I]\left[\begin{array}{c}{x}_k\\ u_k\end{array}\right]\end{array}$$

(21)

$$\begin{array}{cc}\hfill X_{k+1}& =\overline{A}{X}_k+\overline{B}{u}_k+\overline{D}{\omega }_k\hfill \\ \hfill & =(\overline{A}+\overline{B}L)X_k+\overline{D}{\omega }_k\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill V\left(X_k\right)& =\mathbf{E}\left[\sum _{t=k}^{+\infty }\left(O_t-\beta \left(L\right)\right)\mid X_k\right]\hfill \\ & =(X_k^T{\overline{R}}_1{X}_k+X_k^T{L}^T{R}_{2}L{X}_k-\beta \left(L\right))+\mathbf{E}\left[V\left(X_{k+1}\right)\mid X_k\right]\hfill \end{array}$$

(23)

Based on (23), we can derive the following equation:

$$\begin{array}{cc}\hfill V\left(X_k\right)-V\left(X_{k+1}\right)& =\mathbf{E}\left[X_k^{T}P{X}_k-X_{k+1}^{T}P{X}_{k+1}\mid X_k\right]\hfill \\ & =X_k^T{\overline{R}}_1{X}_k+u_k^T{R}_2{u}_k-\beta \left(L\right)\hfill \\ & =e_k^T{R}_1{e}_k+u_k^T{R}_2{u}_k-\beta \left(L\right)\hfill \end{array}$$

(24)

so

$$\begin{array}{c}\hfill V\left(X_{k+1}\right)-V\left(X_k\right)=-(e_k^T{R}_1{e}_k+u_k^T{R}_2{u}_k-\beta \left(L\right))\end{array}$$

(25)

if we want $V\left(X_{k+1}\right)-V\left(X_k\right)<0$, then the condition $e_k^T{R}_1{e}_k-\beta \left(K\right)>0$, i.e., $\parallel e_k\parallel >\sqrt{{\displaystyle \frac{\beta \left(L\right)}{\parallel R_1\parallel }}}$ must be met. Thus, $e_k$ is UUB [17] and $\parallel e_k\parallel >\sqrt{{\displaystyle \frac{\beta \left(L\right)}{\parallel R_1\parallel }}}$ .    □

Remark 6.

Referring to reference [17], under the designed control law $u_k^{*}=L^{*}{X}_k$ , we determined that the tracking error of the system can converge to neighborhood of the origin, and the size of this neighborhood can be adjusted by adjusting the parameter matrix $\overline{R}$.

In the analysis presented in the Section 2, Algorithm 1 was utilized to solve the stochastic LQT problem when the model is known. However, in practical applications, it is often unrealistic to have complete knowledge of the system model. In the next section, we propose Algorithm 2 to address the problem of a stochastic LQT when the system model is unknown.

3. Solving Stochastic LQT Problems with Unknown System

In this section, it is useful to define the Quality (Q) function in parallel to the value function (9). AOPQ algorithms have been proposed to solve stochastic LQT problems with an unknown system.

3.1. Model Free Average Off-Policy Q-Learning Algorithm

Within this subsection, we establish the Q function and present the Bellman equation, which is rooted in the Q function, as a means to address the stochastic LQT problem.

Define the Q function under the control policy $u_k=L{X}_k$

$$Q\left(X_k,u_k\right)=O_k-\beta \left(L\right)+\mathbf{E}\left[V\left(X_{k+1}\right)\mid Z_k\right]$$

(26)

where $Z_k={\left[\begin{array}{c}{X}_k^T{u}_k^T\end{array}\right]}^T$. The value function $V\left(X_k\right)$ can be derived by choosing $u_k=L{X}_k$ from the $Q\left(X_k,u_k\right)$ function [18]

$$V\left(X_k\right)=Q\left(X_k,L{X}_k\right)=Q\left(Z_k\right)$$

(27)

Remark 7.

In this article, we mainly apply the mean and variance of random disturbances, as well as the properties of conditional expectations, which are described as follows: $\mathbf{E}\left[a\right|Y]=a$; $\mathbf{E}[aX+bZ|Y]=a\mathbf{E}[X\left|Y\right]+b\mathbf{E}\left[Z\right|Y]$; $\mathbf{E}\left[X\right|Y]=\mathbf{E}[X]$, if X and Y are independent; $\mathbf{E}\left[\mathbf{E}\right[X\left|Y\right]]=\mathbf{E}[X]$; $\mathbf{E}\left[\mathbf{E}\right[X|Y,Z]\left|Y\right]=\mathbf{E}\left[X\right|Y]$, where $X,Y,Z$ are random variables , $a,b\in \mathbb{R}$ [36]. Applying the above properties, Equations (10)–(12) in the article derive the Bellman equation for optimal control problems with random disturbances. Furthermore, the extended average Q-learning method can be used to solve stochastic optimal control problems.

Lemma 3.

Consider the system in (3) and (26). Suppose that the control policy gain L is stabilizing. $G\ge 0$ is a solution to the equation

$$\left[\begin{array}{c}{\overline{A}}^T\\ {\overline{B}}^T\end{array}\right]\left[\begin{array}{cc}I\hfill & L^T\hfill \end{array}\right]G\left[\begin{array}{c}I\\ L\end{array}\right]\left[\begin{array}{cc}\overline{A}& \overline{B}\end{array}\right]-G+\left[\begin{array}{cc}{\overline{R}}_1& 0\\ 0& R_2\end{array}\right]=0$$

(28)

and the average cost is represented by $\beta \left(L\right)=Tr\left({\overline{D}}^T\left[\begin{array}{c}I{L}^T\hfill \end{array}\right]G\left[\begin{array}{c}I\\ L\end{array}\right]\overline{D}{W}_{\omega }\right)$. Then, we can obtain $Q\left(Z_k\right)=Z_k^{T}G{Z}_k$.

Proof. 

Based on the definition of $Z_k=\left[\begin{array}{c}{X}_k\\ u_k\end{array}\right]$ and control input $u_k=L{X}_k$, the  $Z_{k+1}=\left[\begin{array}{c}{X}_{k+1}\\ L{X}_{k+1}\end{array}\right]$ can be obtained. Next, set

$$P=\left[I{L}^T\right]G\left[\begin{array}{c}I\\ L\end{array}\right]$$

the $\beta \left(L\right)$ can be rewritten as $tr\left(\overline{P}{W}_{\omega }\right)$. Using $u_k=L{X}_k+{\sigma }_k$, the system (3) can be restated as

$$\begin{array}{cc}\hfill X_{k+1}& =\overline{A}{X}_k+\overline{B}{u}_k+\overline{D}{\omega }_k\hfill \\ \hfill & =(\overline{A}+\overline{B}L)X_k+\overline{D}{\omega }_k+\overline{B}{\sigma }_k\hfill \\ \hfill & =L{X}_k+\overline{D}{\omega }_k+\overline{B}{\sigma }_k\hfill \end{array}$$

(29)

where ${\sigma }_k$ is the detection noise. Based on (27), this gives the following

$$\begin{array}{c}\hfill \mathbf{E}\left[V\left(X_{k+1}\right)\mid Z_k\right]=\mathbf{E}\left[Q\left(X_{k+1}\right)\mid Z_k\right]\end{array}$$

(30)

thereby,

$$\begin{array}{cc}\hfill & \mathbf{E}\left[Q\left(X_{k+1}\right)\mid Z_k\right]\hfill \\ & =\mathbf{E}\left[Z_{k+1}^{T}G{Z}_{k+1}\mid Z_k\right]\hfill \\ & =\mathbf{E}\left[\left[X_{k+1}^T{\left(L{X}_{k+1}\right)}^T\right]G{\left[X_{k+1}^T{\left(L{X}_{k+1}\right)}^T\right]}^T\mid Z_k\right]\hfill \\ & =\mathbf{E}\left[X_{k+1}^{T}P{X}_{k+1}\mid Z_k\right]\hfill \end{array}$$

(31)

By plugging (29) into (31), this gives the following equation:

$$\begin{array}{cc}\hfill & \mathbf{E}\left[X_{k+1}^{T}P{X}_{k+1}\mid Z_k\right]\hfill \\ \hfill =& \mathbf{E}\left[{(L{X}_k+\overline{D}{\omega }_k+\overline{B}{\sigma }_k)}^{T}P(L{X}_k+\overline{D}{\omega }_k+\overline{B}{\sigma }_k)\mid Z_k\right]\hfill \\ \hfill =& \mathbf{E}\left[X_k^T{L}^{T}PL{X}_k\mid Z_k\right]+2\mathbf{E}\left[X_k^T{L}^{T}P\overline{B}{\sigma }_k\mid Z_k\right]\hfill \\ \hfill & +\mathbf{E}\left[{\sigma }_k^T{\overline{B}}^{T}P\overline{B}{\sigma }_k\mid Z_k\right]+\mathbf{E}\left[{\omega }_k^T\overline{D}M\overline{D}{\omega }_k\mid Z_k\right]\hfill \end{array}$$

(32)

thus, we have the following

$$\begin{array}{cc}\hfill & \mathbf{E}\left[X_{k+1}^{T}P{X}_{k+1}\mid Z_k\right]\hfill \\ \hfill =& X_k^T{L}^{T}PL{X}_k+2X_k^T{L}^{T}P\overline{B}{\sigma }_k+{\sigma }_k^T{\overline{B}}^{T}P\overline{B}{\sigma }_k+tr\left(\overline{P}{W}_{\omega }\right)\hfill \\ \hfill =& (X_k^T{(\overline{A}+\overline{B}K)}^{T}P(\overline{A}+\overline{B}K)X_k+2X_k^T(\overline{A}+\overline{B}K)P\overline{B}{\sigma }_k\hfill \\ & +{\sigma }_k^T{\overline{B}}^{T}P\overline{B}{\sigma }_k+tr\left(\overline{P}{W}_{\omega }\right)\hfill \end{array}$$

(33)

where $\overline{P}={\overline{D}}^{T}P\overline{D}$. Because of $u_k=K{X}_k+{\sigma }_k$, the above equation can be written as

$$\begin{array}{cc}\hfill & \mathbf{E}\left[X_{k+1}^{T}P{X}_{k+1}\mid Z_k\right]\hfill \\ \hfill =& \left[X_k^T{u}_k^T\right]\left[\begin{array}{cc}{\overline{A}}^{T}P\overline{A}\hfill & {\overline{A}}^{T}P\overline{B}\hfill \\ {\overline{B}}^{T}P\overline{A}\hfill & {\overline{B}}^{T}P\overline{B}\hfill \end{array}\right]\left[\begin{array}{c}{X}_k\\ u_k\end{array}\right]+tr\left(\overline{P}{W}_{\omega }\right)\hfill \\ \hfill =& Z_k^T\left[\begin{array}{cc}{\overline{A}}^{T}P\overline{A}\hfill & {\overline{A}}^{T}P\overline{B}\hfill \\ {\overline{B}}^{T}P\overline{A}\hfill & {\overline{B}}^{T}P\overline{B}\hfill \end{array}\right]Z_k+tr\left(\overline{P}{W}_{\omega }\right)\hfill \end{array}$$

(34)

By plugging (34) into (26), we obtain the following equation

$$\begin{array}{cc}\hfill Q\left(Z_k\right)=& O_k-\beta \left(L\right)+\mathbf{E}\left[V\left(X_{k+1},L\right)\mid Z_k\right]\hfill \\ \hfill =& X_k^T{\overline{R}}_1{X}_k+u_k^T{R}_2{u}_k-\beta \left(L\right)+Z_k^T\left[\begin{array}{cc}{\overline{A}}^{T}P\overline{A}\hfill & {\overline{A}}^{T}P\overline{B}\hfill \\ {\overline{B}}^{T}P\overline{A}\hfill & {\overline{B}}^{T}P\overline{B}\hfill \end{array}\right]Z_k\hfill \\ & +tr\left(\overline{P}{W}_{\omega }\right)\hfill \\ \hfill =& Z_k^T\left[\begin{array}{cc}{\overline{R}}_1\hfill & 0\hfill \\ 0\hfill & R_2\hfill \end{array}\right]Z_k-\beta \left(L\right)\hfill \\ & +Z_k^T\left[\begin{array}{cc}{\overline{A}}^{T}P\overline{A}\hfill & {\overline{A}}^{T}P\overline{B}\hfill \\ {\overline{B}}^{T}P\overline{A}\hfill & {\overline{B}}^{T}P\overline{B}\hfill \end{array}\right]Z_k+tr\left(\overline{P}{W}_{\omega }\right)\hfill \\ \hfill =& Z_k^{T}G{Z}_k\hfill \end{array}$$

(35)

thus, (28) is satisfied.    □

Remark 8.

In the proof of Lemma 3, we added detection noise after the applied control input, to ensure that the sampled data of the system meet the persistent excitation condition [37]. However, this also leads to the G being biased compared to not adding detection noise.

According to Lemma 3, equation of Q function defined (26) can be rewritten as

$$\begin{array}{c}\hfill Z_k^{T}G{Z}_k=X_k^{\mathrm{T}}{\overline{R}}_1{X}_k+u_k^{\mathrm{T}}{R}_2{u}_k-\beta \left(L\right)+\mathbf{E}\left[V\left(X_{k+1}\right)\mid Z_k\right]\end{array}$$

(36)

where

$$G=\left[\begin{array}{cc}Q+{\overline{A}}^{\top }P\overline{A}& {\overline{A}}^{\top }P\overline{B}\\ {\overline{B}}^{\top }P\overline{A}& R+{\overline{B}}^{\top }P\overline{B}\end{array}\right].$$

Due to the definition of the Q function (26), the minimization problem has been solved

$$\begin{array}{c}\hfill \mu \left(X_k\right):=arg\underset{u}{min}Q(X_k,u_k)=arg\underset{u}{min}{Z}_k^{\top }G{Z}_k\end{array}$$

(37)

By solving (37), we obtain an expression for $\mu$ as follows:

$${\mu }_k=\mu \left(X_k\right)=-G_{uu}^{-1}{G}_{ux}{X}_k$$

(38)

where $G_{uu}\in {\mathbb{R}}^{m\times m}$ and $G_{ux}\in {\mathbb{R}}^{m\times n}$ are the sub-matrices of G defined by

$$G:=\left[\begin{array}{cc}{G}_{xx}& G_{ux}^{\top }\\ G_{ux}& G_{uu}\end{array}\right]$$

However, the $\beta \left(L\right)$ and $\mathbf{E}\left[V\left(X_{k+1}\right)\mid Z_k\right]$ in (36) are hard to obtain for unknown system dynamics. Therefore, we propose to estimate this using historical data over a period of time. Based on (7),  $\widehat{\beta }\left(L\right)$ is an estimate of $\beta \left(L\right)$

$$\begin{array}{c}\hfill \widehat{\beta }\left(L\right)={\displaystyle \frac{1}{N}}\sum _{k=1}^N{O}_k={\displaystyle \frac{1}{N}}\sum _{k=1}^N{X}_k^T{\overline{R}}_1{X}_k+u_k^T{R}_2{u}_k\end{array}$$

(39)

Using the above definition,  (36) can be written in the following form:

$$\begin{array}{cc}\hfill & Z_k^{T}G{Z}_k-Z_{k+1}^{T}G{Z}_{k+1}+Z_{k+1}^{T}G{Z}_{k+1}-\mathbf{E}\left[Z_{k+1}^{T}G{Z}_{k+1}\mid Z_k\right]\hfill \\ \hfill & =Z_k^{T}Q{Z}_k-\widehat{\beta }\left(L\right).\hfill \end{array}$$

(40)

Based on the Kronecker product, we have

$$(Z_k^T\otimes Z_k^T-Z_{k+1}^T\otimes Z_{k+1}^T)vec\left(G\right)+{\epsilon }_1=Z_k^{T}Q{Z}_k-\widehat{\beta }\left(L\right).$$

(41)

where ${\epsilon }_1=Z_{k+1}^{T}G{Z}_{k+1}-\mathbf{E}\left[Z_{k+1}^{T}G{Z}_{k+1}\mid Z_k\right]$. Define ${\Phi }_k=Z_k^T\otimes Z_k-Z_{k+1}^T\otimes Z_{k+1}$, the (41) can be written as

$${\Phi }_{k}vec\left(G\right)+{\epsilon }_1=Z_k^{T}Q{Z}_k-\widehat{\beta }\left(L\right)$$

(42)

Because of the presence of ${\epsilon }_1$ and the difference between $\widehat{\beta }\left(L\right)$ and $\beta \left(L\right)$, we obtain $\widehat{G}$ as the estimate of G. Thus, this yields

$$vec\left(\widehat{G}\right)={\left({\left({\Phi }_k\right)}^T{\Phi }_k\right)}^{-1}{\left({\Phi }_k\right)}^T(Z_k^{T}Q{Z}_k-\widehat{\beta }\left(L\right)).$$

(43)

Based on $\widehat{G}$, this gives the following:

$$L={\left({\widehat{G}}_{uu}\right)}^{-1}{\widehat{G}}_{ux}.$$

(44)

Based on Equations (40) and (44), an average off-policy Q-learning algorithm can be constructed to solve the LQT problem of stochastic linear systems. However, many iterative algorithms require the assumption of an initial stable control [28], which is somewhat complicated when the system model is unknown. Therefore, in the following sections, we first obtain an initial stable control based on the pole assignment method, and based on this design, we provide a data-driven average off-policy Q-learning algorithm.

3.2. Data-Driven Average Off-Policy Q-Learning Algorithm

In this subsection, the purpose of the data-driven control is to construct controllers directly from data, without the need for (explicit) identification of system models. The coefficient matrix of the system is constructed based on persistent excitation (PE) data, and pole placement strategy is used to let the constructed system matrix obtain the initial stable control [30].

Based on the overview of Willems’ lemma [38], the Hankel matrix of sequence ${\left\{X_k\right\}}_{k=0}^{N-1}$ is defined as

$$H_S\left(X_{[0,N-1]}\right)=\left[\begin{array}{cccc}{X}_0\hfill & X_1\hfill & \cdots \hfill & X_{N-S}\hfill \\ X_1\hfill & X_2\hfill & \cdots \hfill & X_{N-S+1}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ X_{S-1}\hfill & X_S\hfill & \cdots \hfill & X_{N-1}\hfill \end{array}\right]\in {\mathbb{R}}^{L(n+p)\times (N-S+1)}$$

Definition 1.

Let $N\ge (m+1)S-1$. An input sequence ${\left\{u_k\right\}}_{k=0}^{N-1}$ is PE of the order S if the Hankel matrix $H_S\left(u[0,N-1]\right)$ has full row rank $mS$.

Remark 9.

Based on the definition of Hankel matrix, we can obtain a matrix $H_S\left(u[0,N-1]\right)\in {\mathbb{R}}^{mS\times (N-S+1)}$ containing the input sequence ${\left\{u_k\right\}}_{k=0}^{N-1}$.

Apply the control input by adding detection noise to the system (3), collect data on PE related to system dynamics, and thus derive the following lemma.

Lemma 4

([30]). Apply the PE input ${\left\{u_k\right\}}_{k=0}^{N-1}$ to the controllable system (3) and collect data ${\left\{X_k\right\}}_{k=0}^{N-1}$ from the controllable system (3), building matrix

$$H_1\left(X[0,N-L]\right)=\left[\begin{array}{cccc}{X}_0\hfill & X_1\hfill & \cdots \hfill & X_{N-S}\hfill \end{array}\right]\in {\mathbb{R}}^{(n+p)\times (N-S+1)}$$

$$H_S\left(u_{[0,N-1]}\right)=\left[\begin{array}{cccc}{u}_0\hfill & u_1\hfill & \cdots \hfill & u_{N-S}\hfill \\ u_1\hfill & u_2\hfill & \cdots \hfill & u_{N-S+1}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ u_{S-1}\hfill & u_S\hfill & \cdots \hfill & X_{N-1}\hfill \end{array}\right]\in {\mathbb{R}}^{mS\times (N-S+1)}$$

Then, the rank condition holds

$$rank\left(\left[\begin{array}{c}{H}_1\left(X[0,N-L]\right)\hfill \\ H_S\left(u[0,N-1]\right)\hfill \end{array}\right]\right)=(n+p)+mS.$$

(45)

Using the above data representation, we present a pole placement strategy to design an initial stable control.

Step 1: Define the data to construct the coefficient matrices $\widehat{A}$ and $\widehat{B}$ of the system;

Collect $N\ge (m+1)(n+p+1)-1$ samples of data ${\left\{X_k,u_k\right\}}_{k=0}^{N-1}$ by applying a PE input to the system. Define the matrices

$$g_0\left(x\right)=\left[\begin{array}{cccc}{X}_0\hfill & X_1\hfill & \cdots \hfill & X_{N-2}\hfill \end{array}\right]\in {\mathbb{R}}^{(n+p)\times (N-1)}$$

$$g_1\left(x\right)=\left[\begin{array}{cccc}{X}_1\hfill & X_2\hfill & \cdots \hfill & X_{N-1}\hfill \end{array}\right]\in {\mathbb{R}}^{(n+p)\times (N-1)}$$

$$g_0\left(u\right)=\left[\begin{array}{cccc}{u}_0\hfill & u_1\hfill & \cdots \hfill & u_{N-2}\hfill \end{array}\right]\in {\mathbb{R}}^{m\times (N-1)}.$$

Let H and T be the Moore–Penrose pseudoinverse of $g_0\left(x\right)$ and a basis for the nullspace of $g_0\left(x\right)$, respectively. Define the matrices $\widehat{A}=g_1\left(x\right)H$ and $\widehat{B}=g_1\left(x\right)T$.

Remark 10.

According to Willems’ lemma [38] allow a data-based representation of a controllable linear system. Nonetheless, the primary challenge encountered when applying this procedure is the matrix $\widehat{B}$ lacking a full column rank. To overcome this issue, one can resolve it by excluding the linearly dependent columns of $\widehat{B}$ and constructing a matrix ${\widehat{B}}_H$ that possesses full column rank using the remaining columns. Thus, $rank\left({\widehat{B}}_H\right)=rank\left(\widehat{B}\right)$. The full-rank matrix ${\widehat{B}}_H$ can be used to solve the pole-placement problem for linear systems [30].

Step 2: Calculate the transformation matrix $P_1$ to convert to the controllable standard form [39]. The linear transformation matrix $P_1$ can transform the system $(\widehat{A},{\widehat{B}}_H)$ into a controllable standard form $({\widehat{A}}_C,{\widehat{B}}_C)$, and calculate the controllable standard form state feedback gain matrix ${\widehat{L}}_C$;

Step 3: All the eigenvalues of $({\widehat{A}}_C-{\widehat{B}}_C){\widehat{L}}_C$ are equal to zero [30]. Using the transformation matrix $P_1$, compute the matrix ${\widehat{L}}_H={\widehat{L}}_C{P}_1$.

Step 4: Construct the matrix $\overline{L}$ by adding zero rows to ${\widehat{L}}_H$, in the same row positions as the position of the columns of $\widehat{B}$ that were removed to form ${\widehat{B}}_H$, such that $\widehat{B}\overline{L}={\widehat{B}}_H{\widehat{L}}_H$

Remark 11.

For the matrix $(\widehat{A},\widehat{B})$ constructed using PE data, the control gain matrix $\overline{L}$ needs to be designed. When we have determined a feedback matrix ${\widehat{L}}_H$ for the system $(\widehat{A},{\widehat{B}}_H)$, we only need to add zero-rows to ${\widehat{L}}_H$ in the appropriate positions to make $\widehat{B}\overline{L}={\widehat{B}}_H{\widehat{L}}_H$ hold.

Step 5: Calculate the equivalent state feedback gain matrix of the original system $L^1=-g_0\left(u\right)(H-T\overline{L})$;

Remark 12.

Based on the aforementioned steps, we can obtain an initial stable control in the case of an unknown system, due to the fact that the control designed using the pole assignment strategy can be regarded as a deadbeat control and is stable [30].

In the next section, Algorithm 2 which is a data-based algorithm, starts with an initial stability control and proceeds to iteratively solve for the optimal control gain L that minimizes the average performance index function (4).

In order to better explain Algorithm 2, we can divide it into the following three steps: First of all, prove that ${\widehat{G}}^i$ can be uniquely determined in each iteration. Lemma 5 explains that the solutions obtained from the Bellman Equation (26) based on the average off-policy Q-learning method are equivalent to those obtained from the model-based Bellman Equation (18). Equation (46) of Algorithm 2 is derived from the transformation of Equation (26), and we show that the procedure in Algorithm 2 guarantees the existence of the solution ${\widehat{G}}^i$. Second, $L^i$ generates a stabilizing control policy at every iteration. Lemma 6 proves that as long as the estimation error bound is small enough, the  iterative control gain solved by Algorithm 2 will be a stable feedback gain. Finally, Algorithm 2 converges on the limit to the solution of the LQT problem. In Theorem 1 of the article, this conclusion is guaranteed. By combining the three steps above, it can be ensured that Algorithm 2 generates stabilizing policy gains.

In order to have a more intuitive understanding of the Algorithm 2, we have provided a flowchart of the Algorithm 2, as shown in Figure 1 below.

Algorithm 2 aims to optimize the control strategy based on the available data, rather than relying solely on a known system model. By iteratively updating the control gain, Algorithm 2 seeks to improve the system’s performance and achieve the desired tracking objectives in the presence of stochastic disturbances. Based on the analysis of Algorithm 2 above, the control gain L was designed. The following subsection analyzes the convergence of Algorithm 2.

Algorithm 2 Average Off-policy Q-learning Algorithm

1: Choose of initial stability control $L^i,i=1$: From the following subsection. 2: Data collection: we execute $L^i{X}_k$ and collect $N\ge (n+1)m+n$ samples of the data ${\left\{X_k,u_k\right\}}_{k=0}^{N-1}$. We use the average cost from N samples $$\begin{array}{c}\hfill \widehat{\beta }\left(L^i\right)={\displaystyle \frac{1}{N}}\sum _{k=1}^N{O}_k={\displaystyle \frac{1}{N}}\sum _{k=1}^N{X}_k^T{\overline{R}}_1{X}_k+u_k^T{R}_2{u}_k\end{array}$$ (46) 3: Policy evaluation: Based on Equations (40), the average-cost estimator of $G^i$ has follows $$vec\left({\widehat{G}}^i\right)={\left({\left({\Phi }_k\right)}^T{\Phi }_k\right)}^{-1}{\left({\Phi }_k\right)}^T(Z_k^{T}Q{Z}_k-\widehat{\beta }\left(L^i\right)).$$ (47) where ${\Phi }_k=Z_k^T\otimes Z_k-Z_{k+1}^T\otimes Z_{k+1}$ 4: Policy improvement: Update the feedback policy matrix as $$L^{i+1}={\left({\widehat{G}}_{uu}^i\right)}^{-1}{\widehat{G}}_{ux}^i.$$ (48) 5: Stop if: $$\begin{array}{c}\hfill \mid L^{i+1}-L^i\mid \le \epsilon \end{array}$$ (49) for a small positive $\epsilon >0$, otherwise set $i=i+1$ and go to step 2.

3.3. Convergence Analysis of Algorithm 2

In this subsection, we demonstrate that the control gain obtained through the iterative solution of Algorithm 2 can converge to the optimal solution.

Lemma 5

([19]). Consider system (3). Assume that the policy gain L is stabilizing. Then, (26) is equivalent to the model-based Bellman Equation (18).

Remark 13.

Lemma 5 explains that the solutions obtained from the Bellman Equation (26) based on the average off-policy Q-learning method are equivalent to those obtained from the model-based Bellman Equation (18)

Lemma 6

([19]). Assume that the estimation errors $\parallel {\widehat{G}}^{i+1}-G^{i+1}\parallel \le \varrho$, ϱ are small positive constant. Then, Algorithm 2 produces stabilizing policy gains $L^{i+1},i=2,\dots ,\mathbf{N}$, i.e., $\rho (\overline{A}+\overline{B}{L}^{i+1})<1$.

Remark 14.

Lemma 6 proves that as long as the estimation error bound is small enough, the iterative control gain solved by Algorithm 2 will be a stable feedback gain.

Theorem 1.

Assume that the estimation errors in $\parallel {\widehat{G}}^{i+1}-G^{i+1}\parallel \le \varrho$, ϱ are small positive constant. Then, the sequence of $G^i,i=1,\dots ,\mathbf{N}$ associated with the controller gain $L^i,i=1,\dots ,\mathbf{N}$ generated in Algorithm 2 is converging $G^{*}\le G^{i+1}\le G^i$.

Proof. 

Based on Lemma 5, the solutions obtained from the Bellman Equation (26) based on the average non policy Q-learning method are equivalent to those obtained from the model-based Bellman Equation (18). Therefore, the following only needs to prove the convergence of $P^i$.

Let $P^i>0$, and the iterative form of the Bellman Equation (18) is as follows:

$$P^i={\left(\overline{A}+\overline{B}{L}^i\right)}^T{P}^i\left(\overline{A}+\overline{B}{L}^i\right)+L^{iT}{R}_2{L}^i+{\overline{R}}_1.$$

(50)

Since $\overline{A}+\overline{B}{L}^i$ is stable, the unique positive definite solution of (50) may be written as [2]

$$P^i=\sum _{k=0}^{+\infty }{\left({\left(\overline{A}+\overline{B}{L}^i\right)}^T\right)}^k\left(L^{iT}{R}_2{L}^i+{\overline{R}}_1\right){\left(\overline{A}+\overline{B}{L}^i\right)}^k.$$

(51)

Define two iteration indices i and j. Using (50), we have the following:

$$\begin{array}{cc}\hfill P^i-P^j=& {\left(\overline{A}+\overline{B}{L}^i\right)}^T{P}^i\left(\overline{A}+\overline{B}{L}^i\right)+L^{iT}{R}_2{L}^i\hfill \\ \hfill & -{\left(\overline{A}+\overline{B}{L}^j\right)}^T{P}^j\left(\overline{A}+\overline{B}{L}^j\right)-L^{jT}{R}_2{L}^j\hfill \\ \hfill =& {\left(\overline{A}+\overline{B}{L}^j\right)}^T{P}^i\left(\overline{A}+\overline{B}{L}^j\right)+L^{iT}{R}_2{L}^i\hfill \\ \hfill & -L^{jT}{\overline{B}}^T{P}^i\left(\overline{A}+\overline{B}{L}^j\right)-{\overline{A}}^T{P}^i{L}^j\hfill \\ \hfill & +L^{iT}{\overline{B}}^T{P}^i\left(\overline{A}+\overline{B}{L}^i\right)+{\overline{A}}^T{P}^i{L}^i\hfill \\ \hfill & -{\left(\overline{A}+\overline{B}{L}^j\right)}^T{P}^j\left(\overline{A}+\overline{B}{L}^j\right)-L^{jT}{R}_2{L}^j\hfill \\ \hfill =& {\left(\overline{A}+\overline{B}{L}^j\right)}^T\left(P^i-P^j\right)\left(\overline{A}+\overline{B}{L}^j\right)\hfill \\ \hfill & +{\left(L^i-L^j\right)}^T\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)\left(L^i-L^j\right)\hfill \\ \hfill & +{\left(L^i-L^j\right)}^T\left[\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)L^j+{\overline{B}}^T{P}^i\overline{A}\right]\hfill \\ \hfill & +\left[L^{jT}\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)+{\overline{A}}^T{P}^{i}B\right]\left(L^i-L^j\right)\hfill \\ \hfill =& \sum _{k=0}^{+\infty }{\left({\left(\overline{A}+\overline{B}{L}^j\right)}^T\right)}^k\hfill \\ \hfill & \left({\left(L^i-L^j\right)}^T\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)\left(L^i-L^j\right)\right.\hfill \\ \hfill & +{\left(L^i-L^j\right)}^T\left[\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)L^j+{\overline{B}}^T{P}^i\overline{A}\right]\hfill \\ \hfill & +\left.\left[L^{jT}\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)+{\overline{A}}^T{P}^i\overline{B}\right]\left(L^i-L^j\right)\right){\left(\overline{A}+\overline{B}{L}^j\right)}^k\hfill \\ \hfill \end{array}$$

(52)

Based on (19), this gives the following:

$$L^{i+1}=-{(R_2+{\overline{B}}^T{P}^i\overline{B})}^{-1}\overline{B}{P}^i\overline{A}$$

(53)

By setting $j=i+1$ in (52) and using (53), we can obtain the following: $P^i-P^{i+1}$

$$\begin{array}{c}\hfill \left[\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)L^j+{\overline{B}}^T{P}^i\overline{A}\right]=\left[L^{jT}\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)+{\overline{A}}^T{P}^i\overline{B}\right]=0\end{array}$$

(54)

so, we can obtain $P^i-P^{i+1}$

$$\begin{array}{cc}\hfill P^i-P^{i+1}=& \sum _{k=0}^{+\infty }{\left({\left(\overline{A}+\overline{B}{K}^j\right)}^T\right)}^k{\left(L^i-L^j\right)}^T\left(R_2+{\overline{B}}^T{P}^i\overline{B}\right)\left(L^i-L^j\right){\left(\overline{A}+\overline{B}{L}^j\right)}^k\ge \mathbf{0}\hfill \end{array}$$

(55)

Thus, we have $P^{i+1}\le P^i$ . By repeating this procedure for $i=1,\dots$, we can see that $P^{*}\le$$P^{i+1}\le P^i\le P^1$. Thus, according to $P^{i+1}\le P^i$ and Lemma 5, we can obtain $G^{*}\le G^{i+1}\le G^i$. □

4. Simulation Experiment

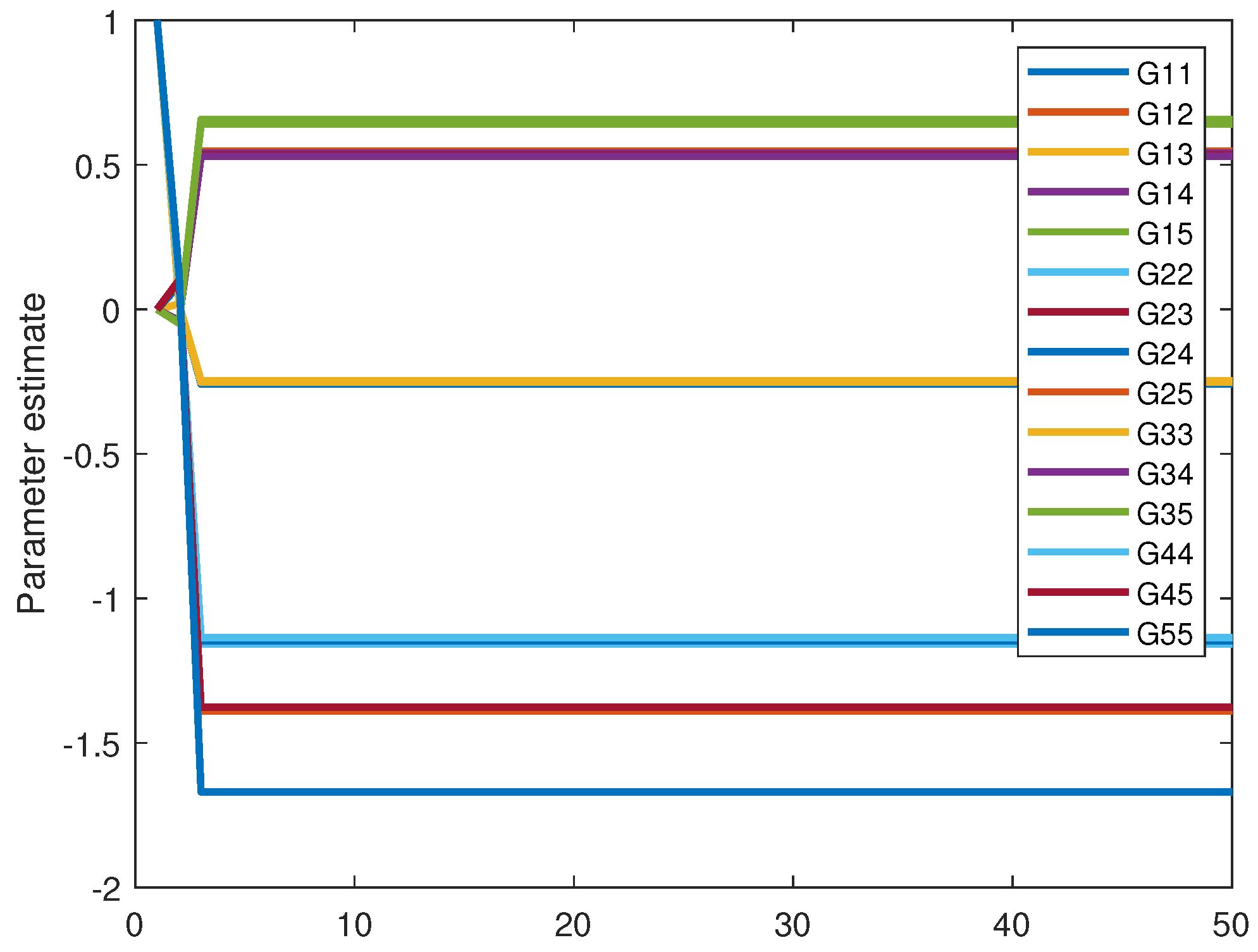
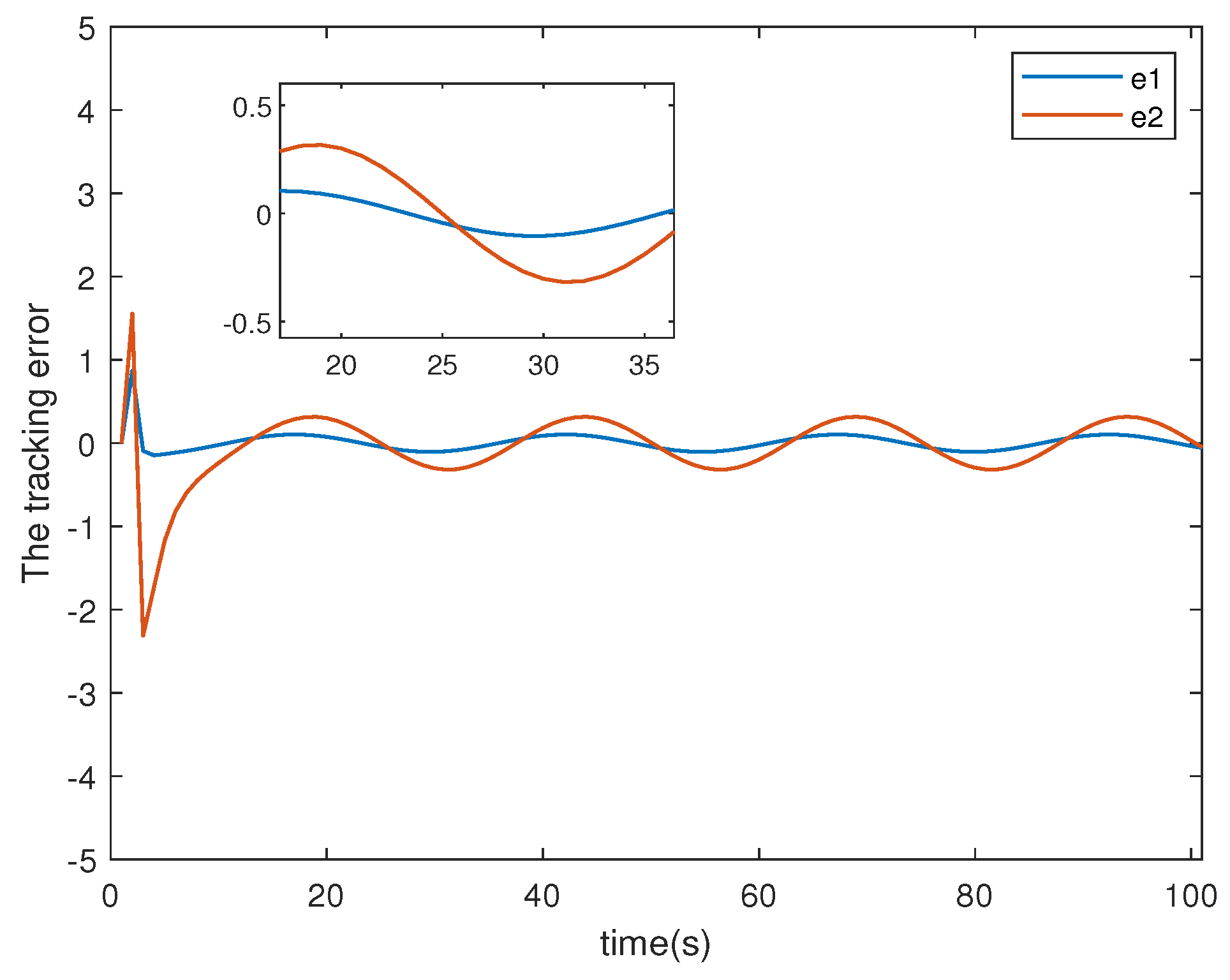
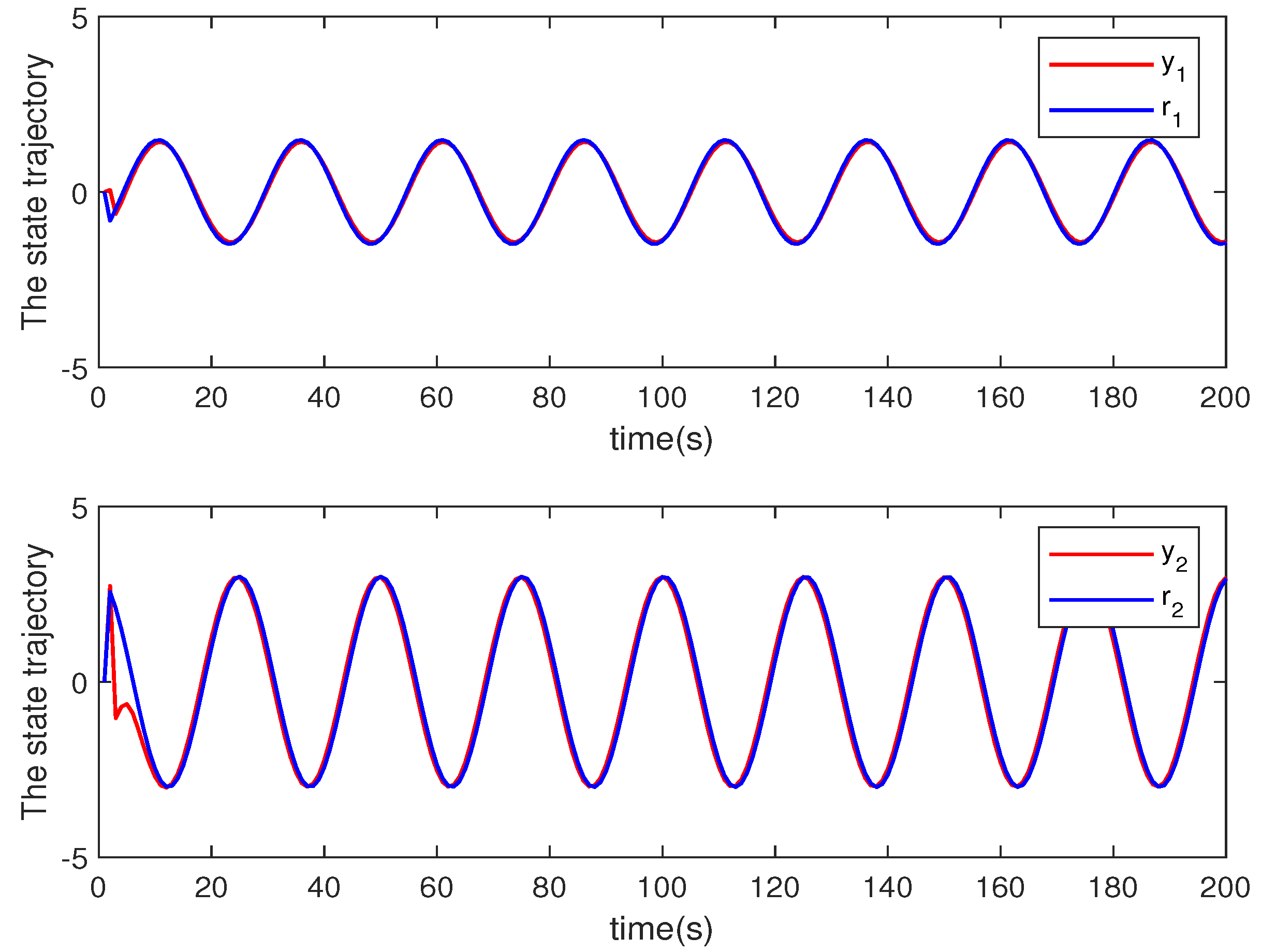
4.1. Example 1

In this section, we considered the simulation from reference [25] and considered adding external stochastic disturbances on this basis, to demonstrate the effectiveness of the designed AOPQ algorithm through simulation of the following system. Consider the following system [34]:

$$\begin{array}{cc}\hfill x_{k+1}& =A{x}_k+B{u}_k+D{\omega }_k\hfill \end{array}$$

(56)

$$\begin{array}{cc}\hfill y_k& =C{x}_k\hfill \end{array}$$

(57)

where

$$A=\left[\begin{array}{cc}2.17& 1.7\\ 0.42& 2.8\end{array}\right],B=\left[\begin{array}{c}-1\\ -1\end{array}\right]$$

$$C=\left[\begin{array}{cc}1& 0.01\\ 0.01& 1\end{array}\right],D=\left[\begin{array}{cc}-1& -2\end{array}\right]$$

The reference system is

$$\begin{array}{c}\hfill r_{k+1}=F{r}_k\end{array}$$

(58)

where

$$F=\left[\begin{array}{cc}1& -1.1\\ -0.88& 2.87\end{array}\right]$$

Set $N=200$, $R=3$, $R_d=1$, and $Q=5\times I_{2\times 2}$. The initial gains

$$\begin{array}{c}\hfill L_0=\left[\begin{array}{cccc}1.1& 2.5& -2.4& -1.99\end{array}\right]\end{array}$$

(59)

First, using model-based Algorithm 1, we have

$$\begin{array}{c}\hfill L^{*}=\left[\begin{array}{cccc}0.0946& -0.2009& 0.0928& -0.1863\end{array}\right]\end{array}$$

(60)

Next, using the data-based Algorithm 2, we can obtain the iterative control strategy converging to the optimal strategy. The following figures show the simulation results better.

Figure 2 shows the convergence of the parameter estimates G under the AOPQ algorithm. Figure 3 shows the tracking errors of the system output. According to the conclusion of Collary 1 in this paper, the tracking error converges to a neighborhood of origin, so that the error will be restrained by the boundaries given by $\parallel e_k\parallel \le \sqrt{\beta \left(L\right)/\parallel R_1\parallel }$, where we denote the upper bound of $\parallel {\omega }_k\parallel$. From Figure 4, we can be conclude that the output of the system can track the reference trajectory well, and the designed controller can converge to the optimum.

4.2. Example 2

Consider a class of DT systems with random disturbance

$$\begin{array}{cc}\hfill x_{k+1}& =A{x}_k+B{u}_k+D{\omega }_k\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill y_k& =C{x}_k\hfill \end{array}$$

(62)

where

$$A=\left[\begin{array}{ccc}1& 0.08& -9\\ 0.07& 0.9& -0.1& \\ 0& 0& 0.9\end{array}\right],B=\left[\begin{array}{c}-1.7\\ 0\\ 0.5\end{array}\right],$$

$$C=\left[\begin{array}{ccc}1& 0& 0\end{array}\right],D=\left[\begin{array}{ccc}0.1& 0& 0\end{array}\right]$$

The reference system is

$$\begin{array}{c}\hfill r_{k+1}=F{r}_k\end{array}$$

(63)

where

$$F=\left[\begin{array}{c}1\end{array}\right]$$

The initial states are set as $x_0={\left[000\right]}^T$. The initial gains $L_0=\left[\begin{array}{cccc}-5& 0& 0& 5\end{array}\right]$.

Through Figure 5, it can be concluded that the output of the system can track the different reference trajectory well, and the designed controller cannot converge to the optimal.

We compared the convergence of the parameter matrix estimation value $\widehat{G}$ by adding different detection signals in the simulation experiments.

Case 1:

$$\begin{array}{c}\hfill {\epsilon }_k=sin\left(2k\right)+sin\left(5k\right)+sin\left(9k\right)+sin\left(11k\right)\end{array}$$

(64)

Figure 6 shows the learning results of Case 1, including the convergence process of the control gain $\widehat{G}$.

Case 2:

$$\begin{array}{c}\hfill {\epsilon }_k=2sin\left(2k\right)+2sin\left(5k\right)+2sin\left(9k\right)+2sin\left(11k\right)\end{array}$$

(65)

Figure 7 shows the learning results of Case 2, including the convergence process of the control gain $\widehat{G}$. In case 1 and case 2, different magnitudes of probing noise were considered with fixed frequencies.

Case 3:

$$\begin{array}{c}\hfill {\epsilon }_k=10\times (rand\left(\right)-0.5)\end{array}$$

(66)

where $rand(·)$ is a MATLAB function that returns a single uniformly distributed random number in the interval (0, 1).

Figure 8 shows the convergence process. The convergence trend is very similar to Case 1 and Case 2.

By observing the convergence of the estimated value $\widehat{G}$ in the simulation experiment parameter matrix in Figure 6, Figure 7 and Figure 8, we can see that the detection signal has an impact on the results, but ultimately it does not change the convergence result of the parameters.

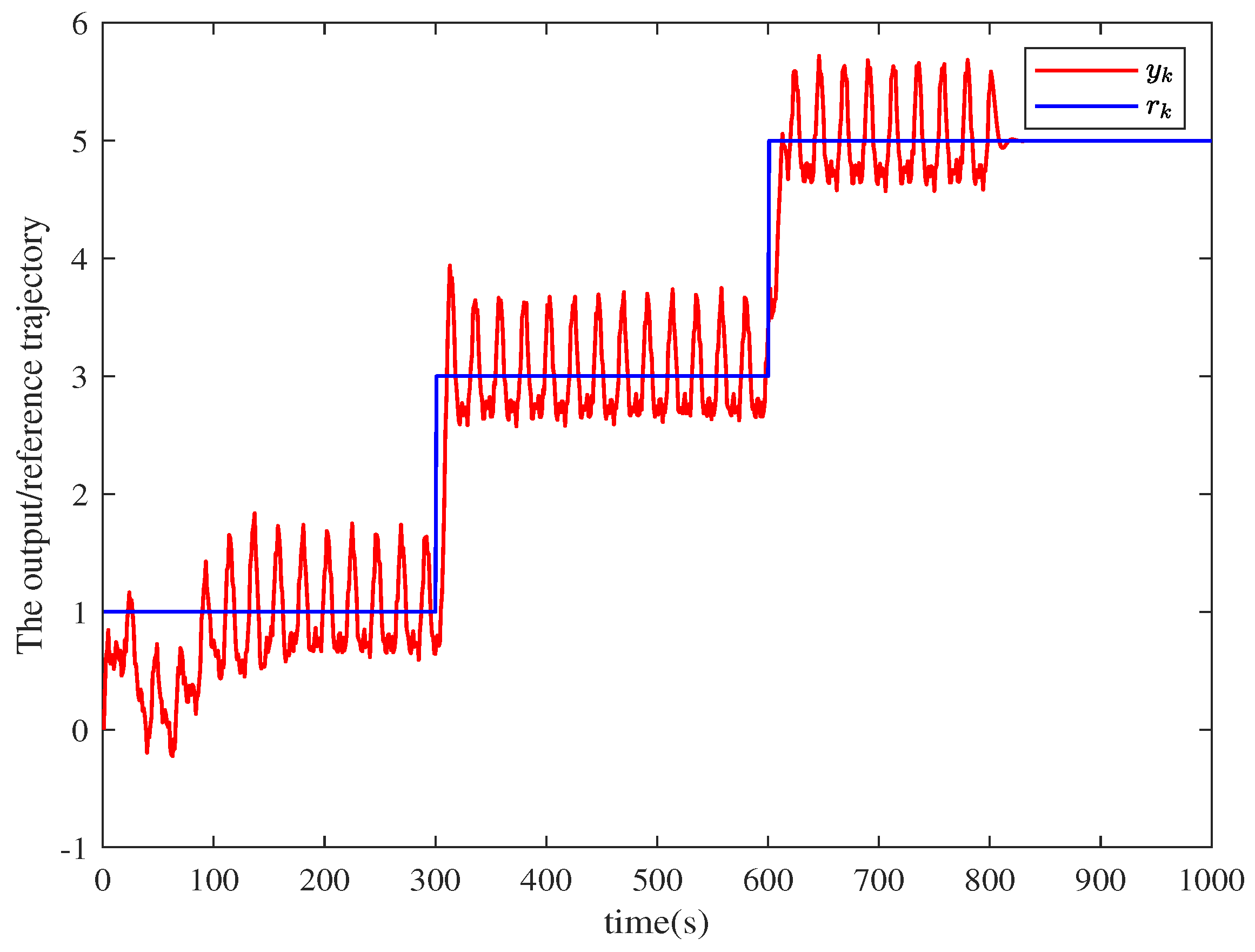
4.3. Comparison Simulation Experiment

In this section, we compare Algorithm 2 in reference [27] , which requires an initial stable control. We refer to reference [40] and give evaluation indexes of the integral absolute error (IAE), the mean square error (MSE), and iteration time.

$$IA{E}_y=\frac{1}{N}\sum _{k=1}^N|r_k-y_k|$$

(67)

$$MS{E}_y=\sqrt{\frac{1}{N}\sum _{k=1}^N{|r_k-y_k|}^2}$$

(68)

The evaluation indicators are shown in

Table 1. Comparison of errors between in Algorithm 2 and the Algorithm 2 in [27].

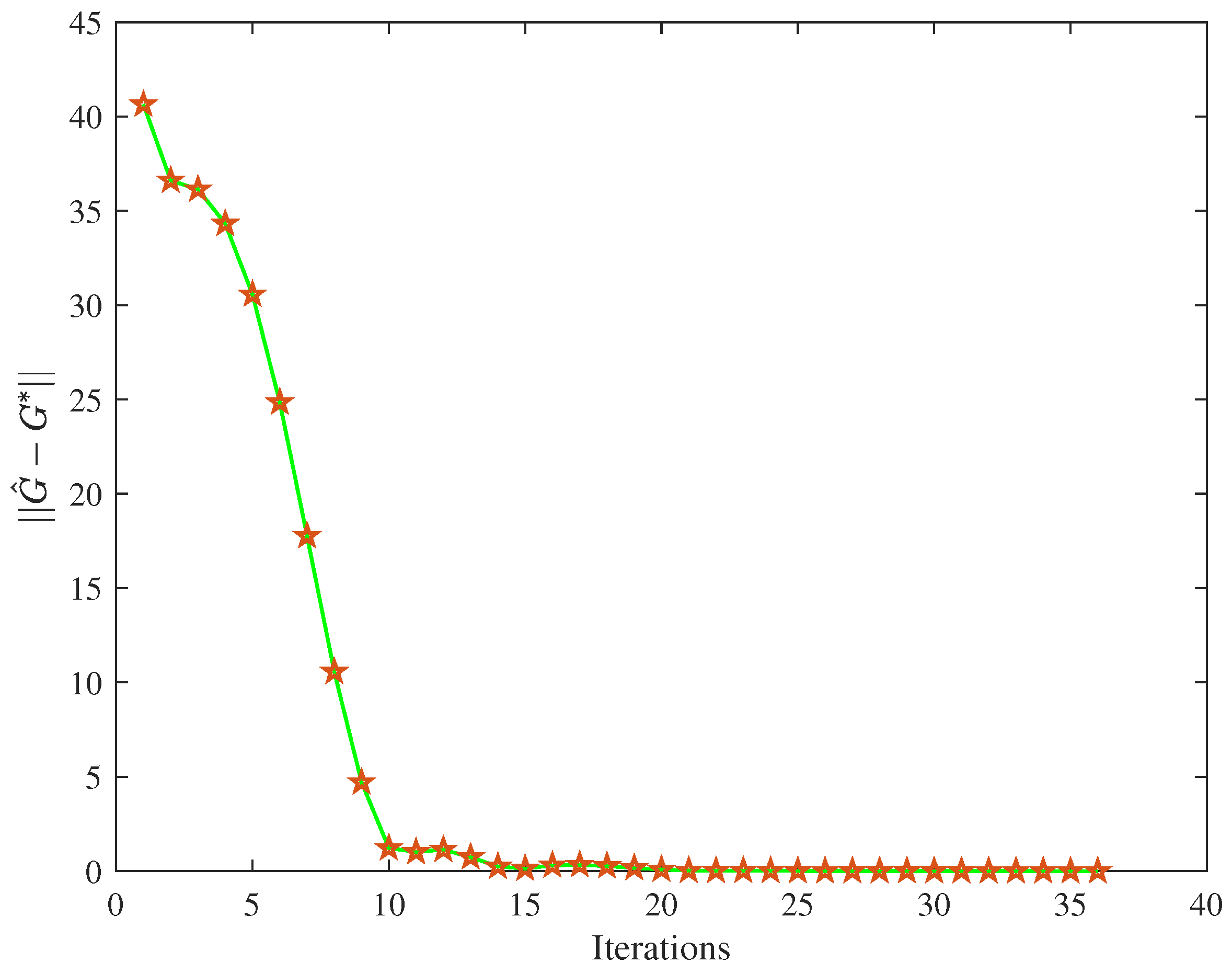
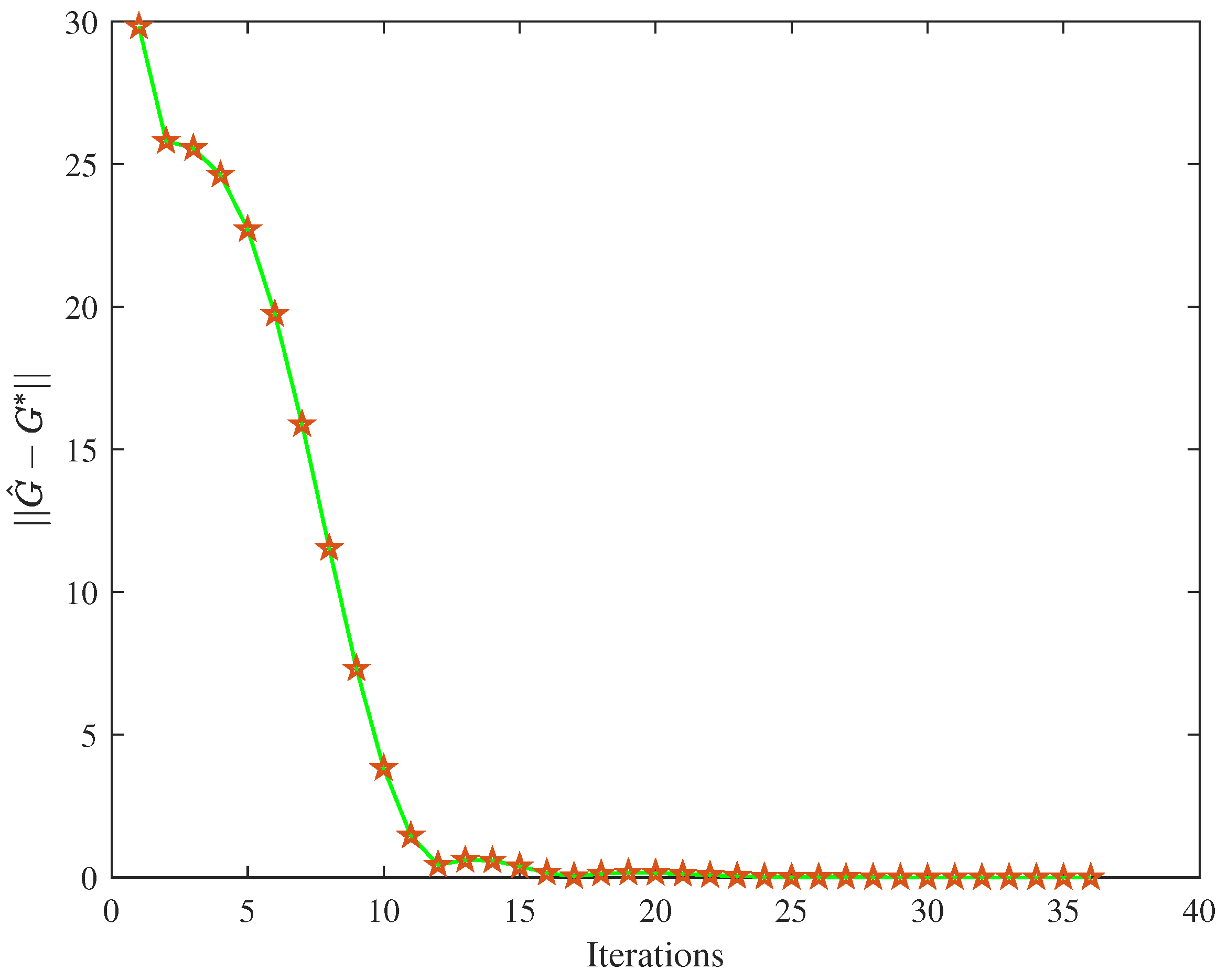
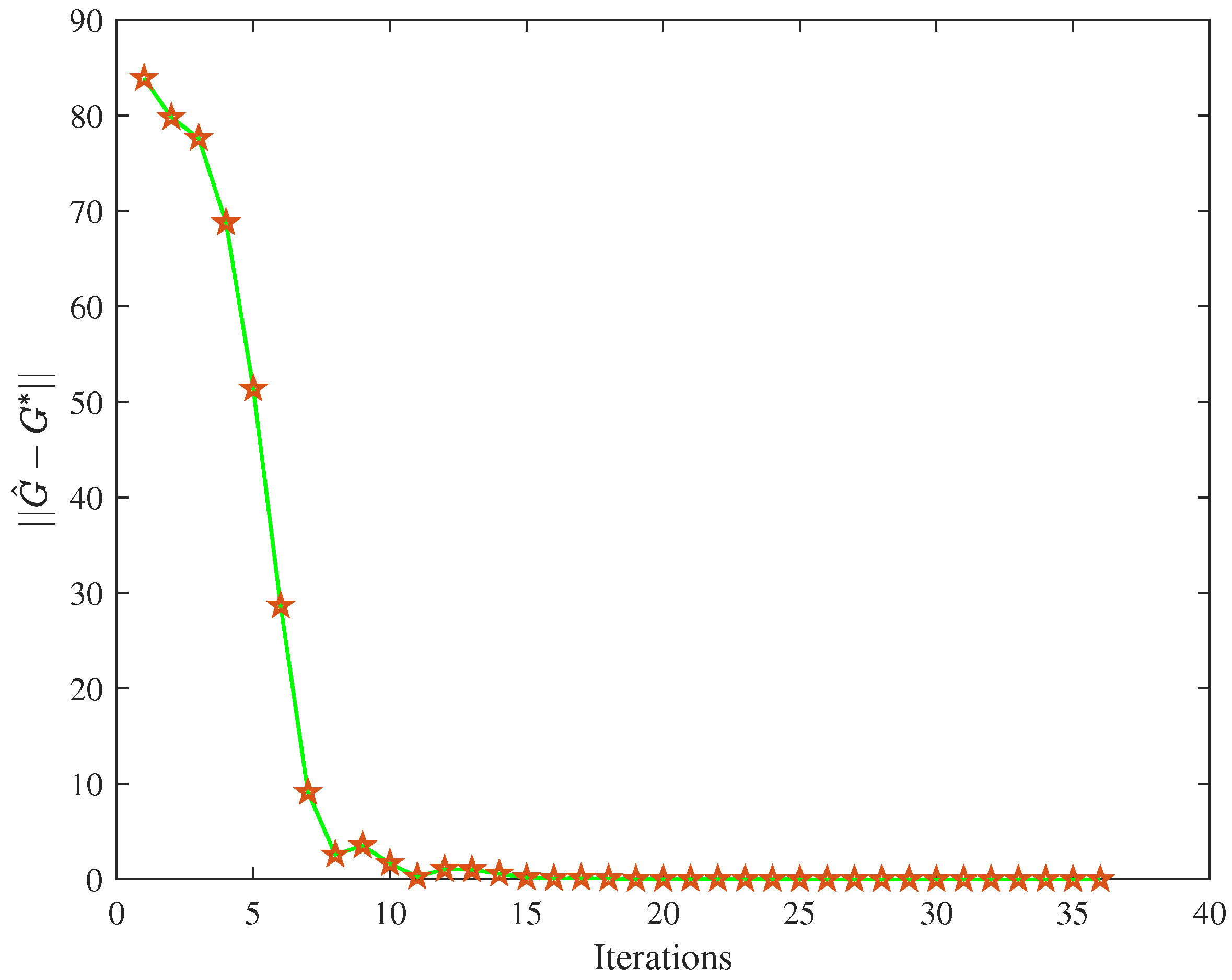
50 ≤ k ≤ 200	IAE	MSE	Iteration Time
Algorithm 2	0.63	0.74	30
Compared approach	0.81	0.78	20

. From Table 1, we can observe that the ISE and MSE performance of the proposed Algorithm 2 was superior to the comparison method, with longer iteration times than the comparison algorithm. However, due to the fact that Algorithm 2 has to search for an initial stable control based on data, our algorithm had a longer iteration time compared to the compared algorithms [27].

Considering d as the number of parameters to be estimated and N as the number of samples, the complexity of (47) for N≫d is $\mathbf{O}($dN) [41]. In the revised paper, we added a comparison of algorithm computational complexity, as reflected in

Table 2. Comparison of Algorithm Computing Complexity.

	The Number of Parameters	Complexity
Algorithm 2	$d=(n+m+q)(n+m+q+1)/2+n(n+1)/2$	$\mathbf{O}\left(dN\right)$
Compared approach	$d=(n+m+q)(n+m+q+1)/2$	$\mathbf{O}\left(dN\right)$

d: the number of parameters to be estimated. $n,m,q$: the dimensions of the state, the input and reference state. N: the rollout length.

.

Because the algorithm contains a large number of estimated parameters, it has a greater computational complexity compared to other algorithms.

5. Conclusions

In this article, we considered the LQT control problem with external stochastic noise. A data-driven AOPQ algorithm was developed to solve the stochastic LQT problem with unknown system dynamics. This algorithm utilizes a data-based initial stable control to avoid the assumption of an initial stable control. We demonstrated the stability of the designed controller and the convergence of the algorithm. Finally, the simulation results indicated that the algorithm has sufficient tracking performance.