Extreme Treatment Effect: Extrapolating Dose-Response Function into Extreme Treatment Domain
Abstract
:1. Introduction
2. Problem Statement, Notation and Preliminaries
2.1. Classical Assumptions
- Unconfoundedness: Given the observed covariates, the distribution of treatment is independent of the potential outcome. Formally, we have , where denotes the independence of random variables.
- Positivity: for all , where represents the conditional density function of the treatment given the covariates.
2.2. Extreme Value Theory
3. Our Tail Framework
3.1. Assumptions
3.2. Adjusting Only for
3.3. Model for the Conditional Expectation of Y Given a T
4. Inference and Estimation
- Estimate :
- Choose .
- Estimate the covariant-dependent threshold using a quantile regression, that is, estimate q-quantile of .
- From now on, restrict our inference on the observations from .
- Estimate in the tail model, that is, estimate from the data points in S in the model, where
- Estimate or using :
- Estimate in model (5) from the data points in S (that is, we only consider ).
- Return or .
5. Illustration and Experiments
5.1. Simple Example
5.2. Simulations
- Investigating how our method scales with respect to the dimension of the confounders .
- Comparing our method with classical methods from the literature.
- Expanding upon the simple example introduced in Section 5.1, wherein we evaluated performance across various dependence structures (employing different copulas), sample sizes, and a spectrum of causal effects.
- Examining the presence of a hidden confounder affecting both T and Y.
- Focusing on variations in the function .
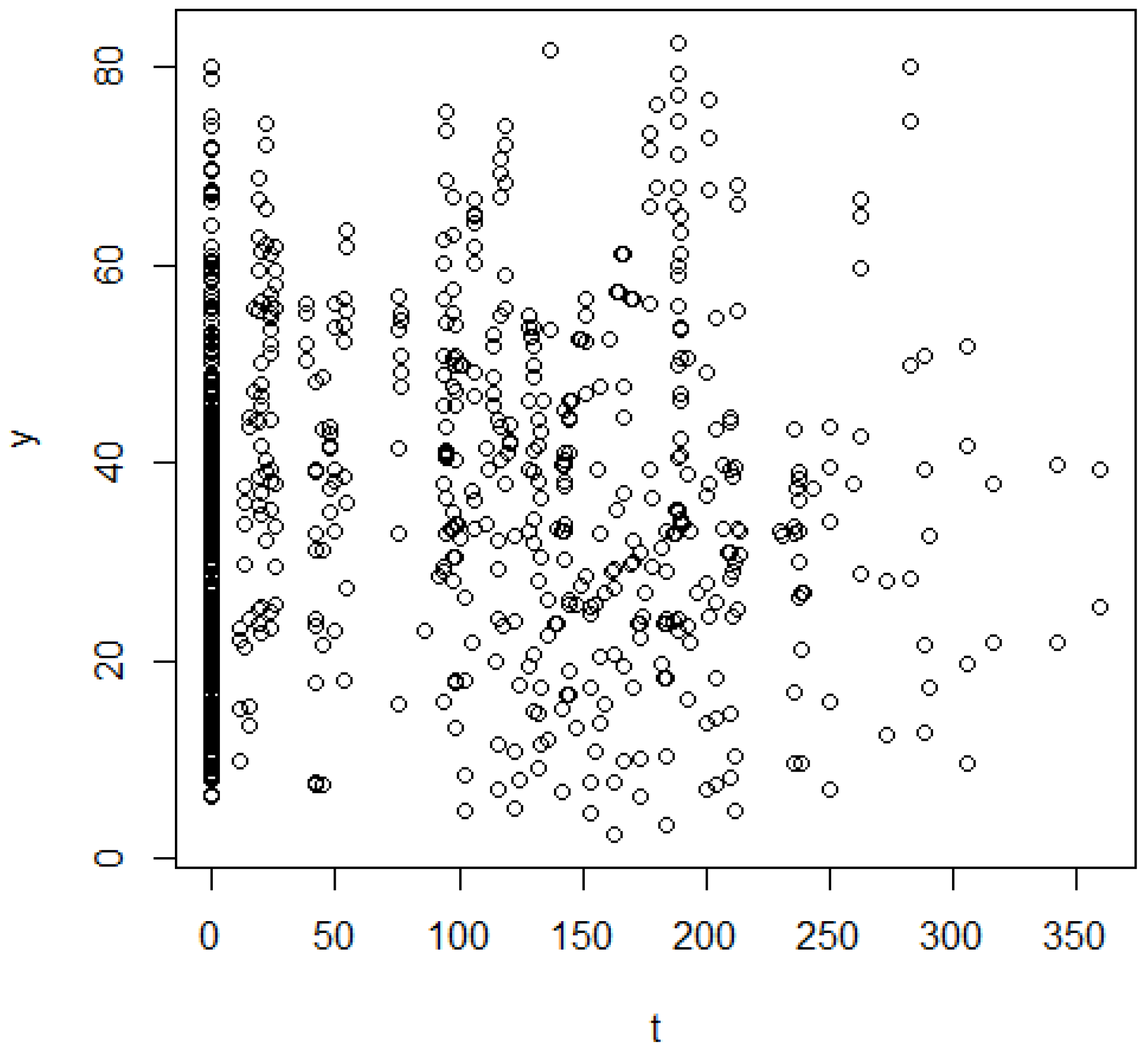
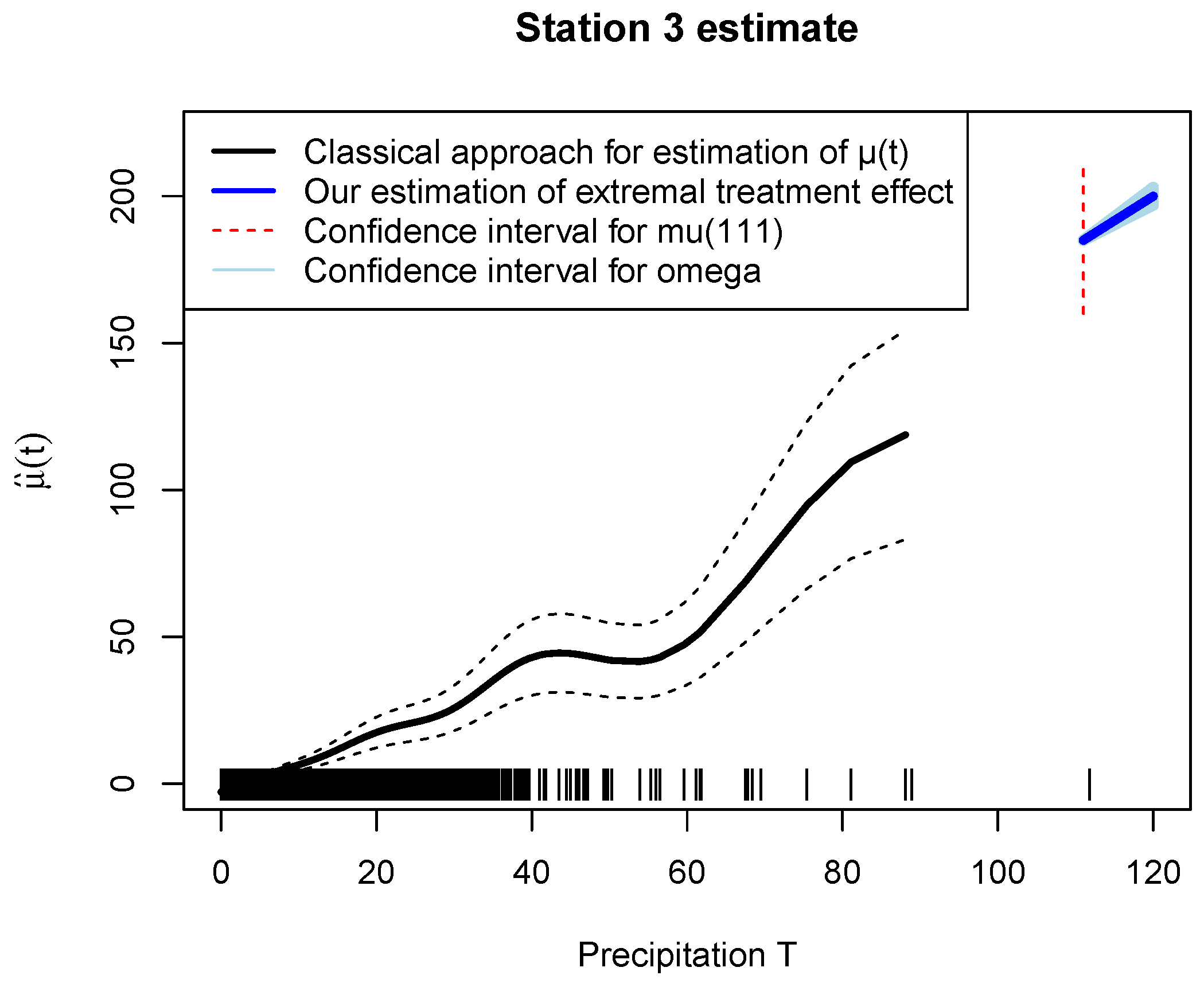
6. Application: River Discharge Dataset
6.1. Known Ground Truth
6.2. Effect of Precipitation on River Discharge
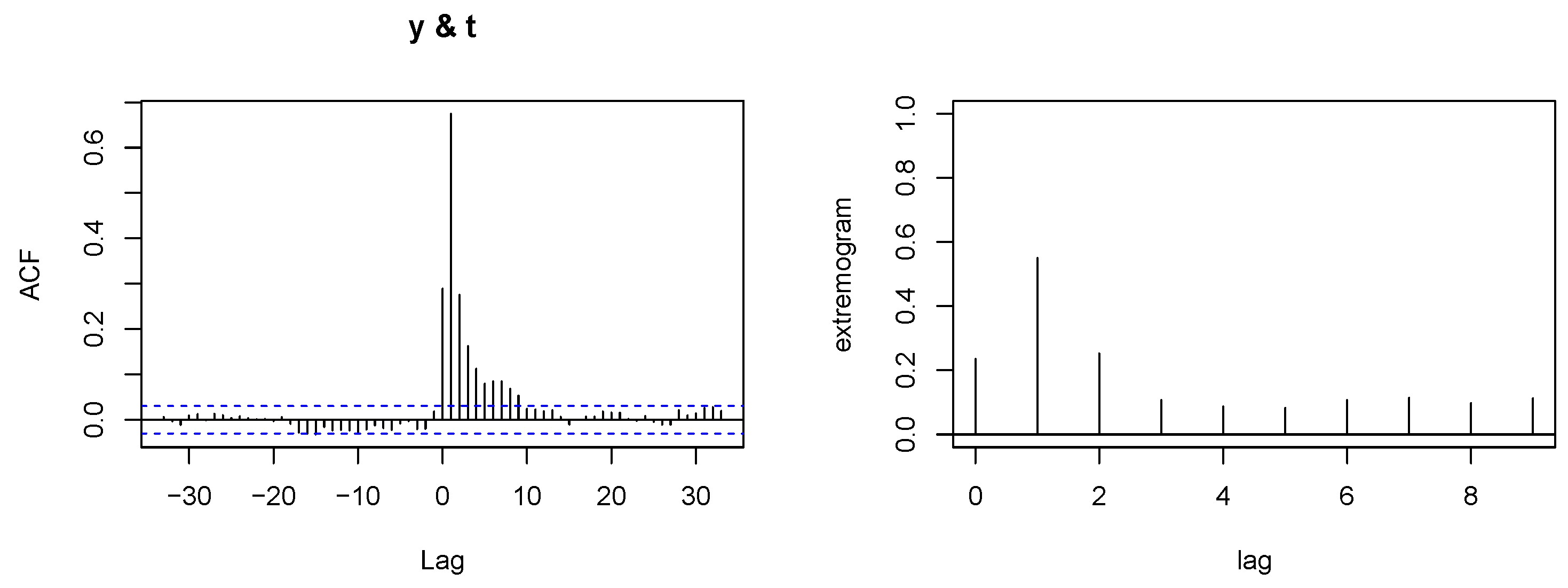
- Time issue: but also since it takes time for the rain water to reach the river and rain tends to be more frequent around midnight. In fact, correlation (and extreme correlation coefficient as well, see Figure A11) is much higher for a pair () than for (). The extreme storm on 6 June 2002 corresponded to extremely high river discharge on 7 June 2002 (where Y was about five times larger than on 6 June 2002). Hence, our interest lies in the effect (that is, we consider as precipitation on day i while is the discharge on day ). Additionally, the presence of time introduces an auto-correlation issue. This can be handled by taking for example weekly maxima or discarding consecutive observations within a certain time frame to reduce the auto-correlation effect. Alternatively, applying techniques like time series decomposition, differencing, or using autoregressive models can also mitigate the issue of auto-correlation in the data analysis process. We leave the data unchanged since the temporal dependence is primarily local, spanning only a few days, and does not introduce a substantial bias.
- Variable selection issue: choosing appropriate confounders that act as confounders of Y and T. It is not clear which variables can be safely considered as confounders: if a variable X lie on a path , adjusting for X would lead to so-called path-canceling causal effect [65]. Here, we are interested in the so-called total causal effect, so we need to be cautious of which covariates to adjust for. However, not adjusting for a common cause leads to a bias. Moreover, there is often a feedback loop: for for example humidity or temperature. However, some of the variables can be safely considered as common causes: for example, the temperature on Sunday (the day before measuring precipitation). There is a huge amount of literature for such a variable selection, and we do not aim to comment on this research area—we only provide a full list of chosen confounders in Appendix C.
7. Conclusions and Future Work
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Application 2—Concrete Compressive Strength
Appendix A.1. Main Analysis
- Given a concrete mixed with and for some specific value of , if we intervene and change T to , what effect on concrete compressive strength can we expect? Using the potential outcome notation, the quantity of interest is . Note that (we do not observe the blast furnace slag larger than 359, and there is no observation in the interval ), and hence, we have zero data in such an extreme region. We aim to answer this question for a choice where (the observation corresponding to ).
- How would an extreme increase in T change Y for an ‘average’ concrete (on a population level, i.e., integrating over the covariates)? Using the potential outcome notation, the quantity of interest is .
Appendix A.2. Detailed Computations of the Estimates
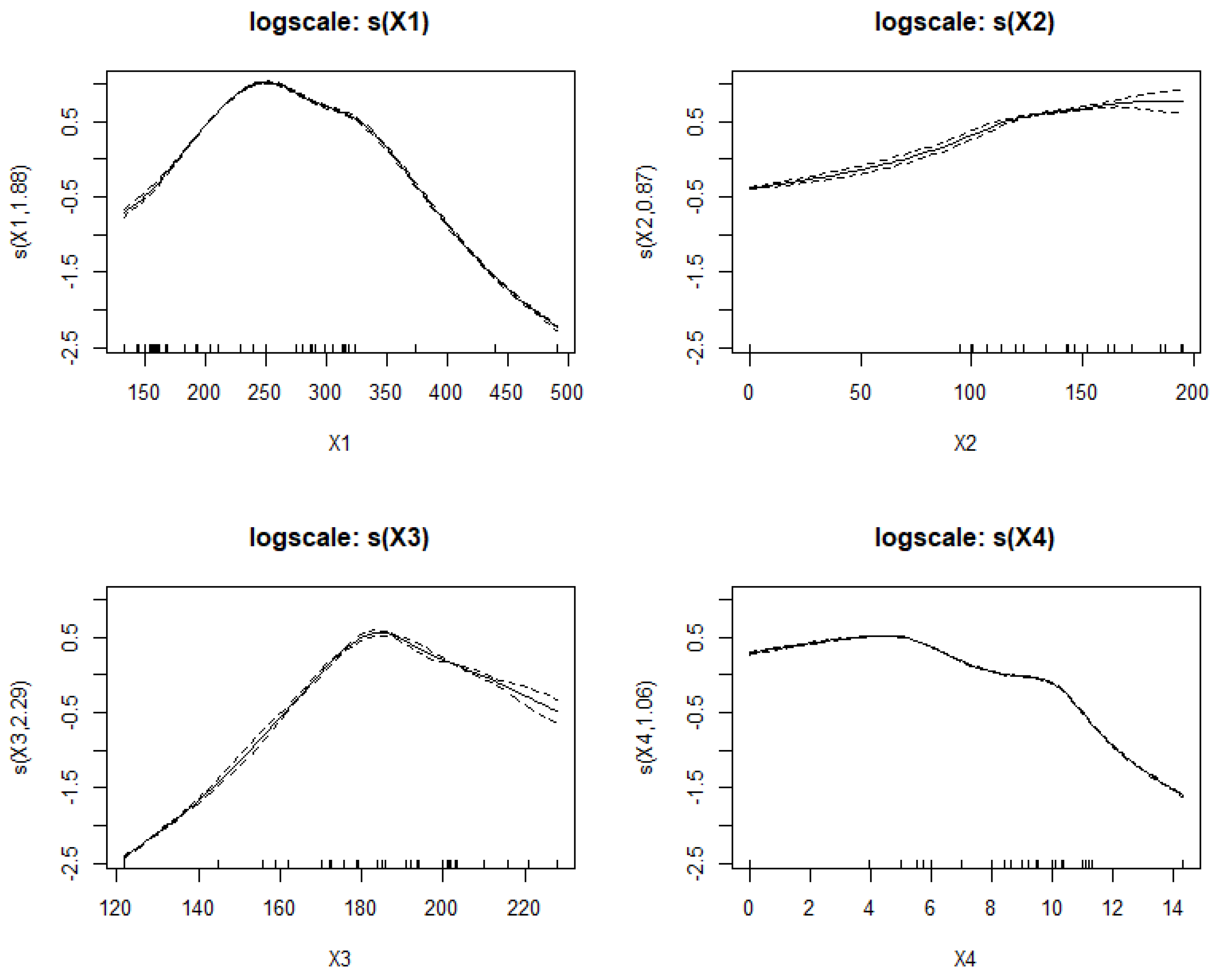
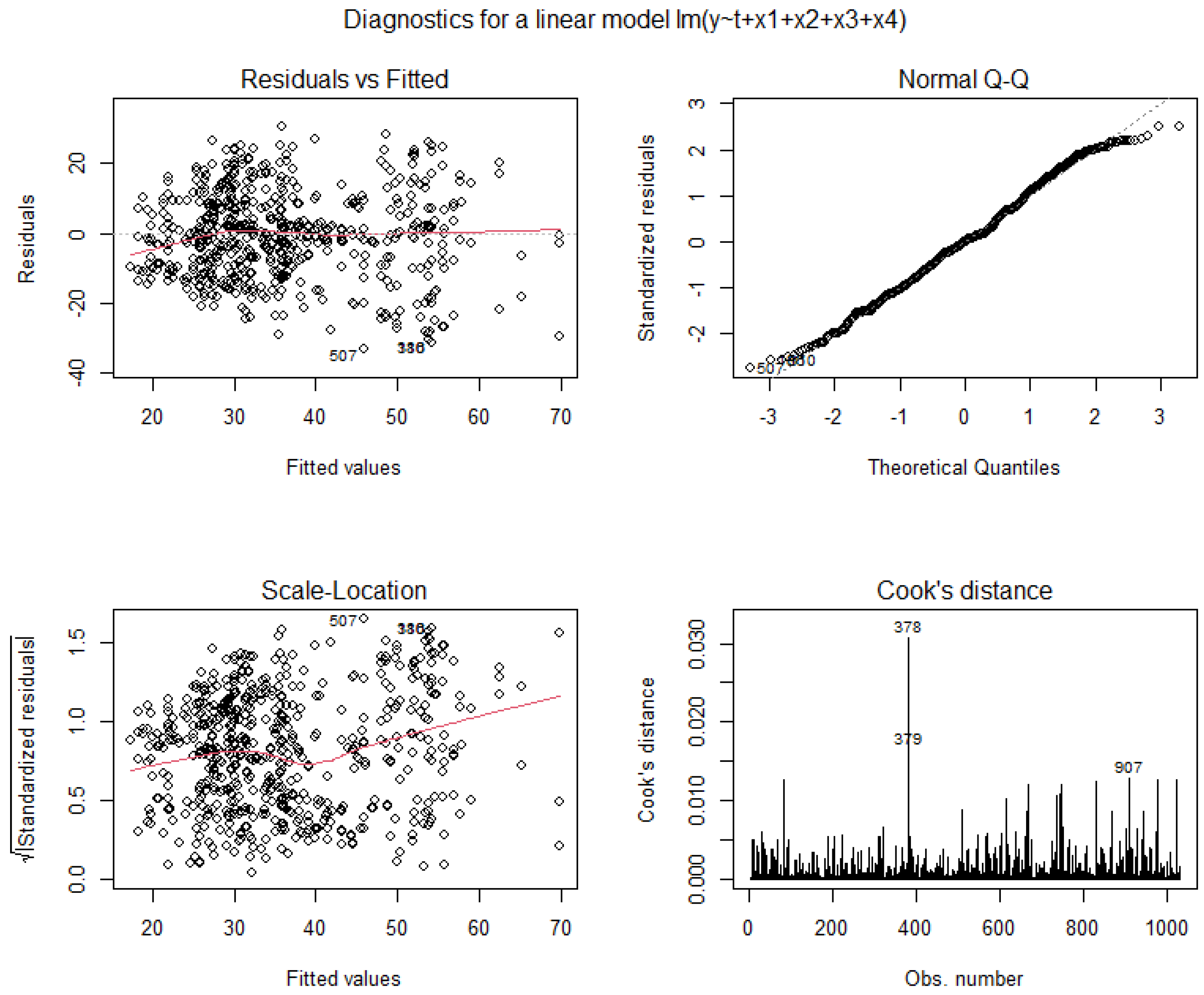
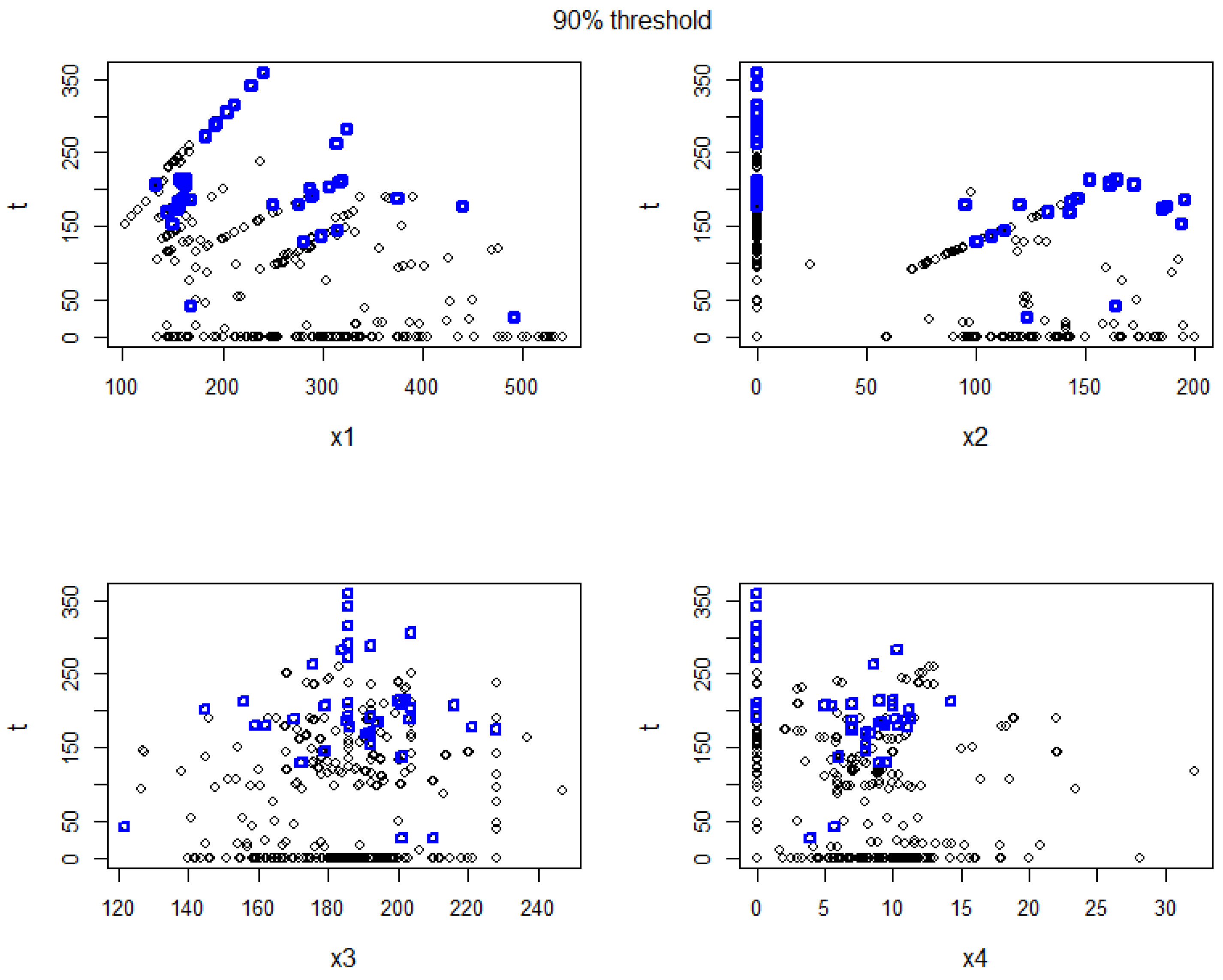
Appendix A.3. Discussion about the Results Regarding Different Threshold q
Appendix A.4. Discussion about the Assumptions
- Assumptions 1 and 3 are considered minor. As mentioned in Section 2, Assumption 1 is satisfied for most common distributions, and similar model assumptions are imposed in almost all applications utilizing extreme value theory. Assumption 3 appears to be satisfied, as there is no specific range of values in the support of T that has zero probability of occurring.
- Assumption 2 is a common and challenging aspect of every causal inference methodology. While our assumption is weaker than the classical unconfoundness assumption (requiring no hidden confounder in the tail), complete rejection of the possibility of its violation is unattainable. A potential hidden confounder could be the ‘quality of ingredients’. If the quality is low, engineers might tend to use excessive amounts of T in the mixture, potentially leading to spurious dependence between large T and low Y. However, in this case, it seems plausible that this hidden dependence due to low ingredient quality does not introduce a substantial bias. Expert knowledge is required to ensure the validity of this assumption.
- Assumption 4 is a strong assumption that allows us to extrapolate observed values into the extremal region. However, this assumption (or at least some similar model assumptions) is necessary; estimating from observed values is not feasible otherwise. In essence, Assumption 4 asserts that the relationship between T and Y (given other confounders) is linear in the unobserved region below . Since there is no other reason to believe that this relationship has any particular form, a linear assumption seems to be the most suitable choice. Although this assumption is strong, it is hypothetically possible to test by measuring values with .
Appendix B. Simulations
- Appendix B.1 provides insight into how our method scales with the dimension of the confounders .
- Appendix B.2 compares our method with classical methods from the literature.
- Appendix B.3 extends the simple example presented in Section 5.1, evaluating performance across different dependence structures (various copulas), sample sizes, and a range of causal effects.
- Appendix B.5 focuses on variations in the function and assesses the extent to which our method can extrapolate into the ‘extreme’ region.

Appendix B.1. Simulations with a High Dimensional X
- Let and be fixed numbers at the beginning of the simulations.
- Consider being centered Gaussian vector with for all and .
- Let , where is distributed according to either , , or .
- Let , where is defined in (A1) with hyper-parameters and where .
Appendix B.2. Comparison with Classical Methods
Appendix B.3. Dependence, Sample Size and the Causal Effect
- T is generated in such a way that the marginal distribution of T follows an exponential distribution with a scale parameter of 1, and the dependence structure between and T follows a Gumbel copula with parameter .
- The response variable Y is generated as follows:where f is a randomly generated smooth function (to randomly generate a d-dimensional function, we use the concept of the Perlin noise generator [71]; for more details, refer to the supplementary package, and readers can conceptualize this as a function ranging from quadratic to linear), , and is a hyper-parameter that we vary in our simulations. Figure A7 shows one realization of such a dataset.
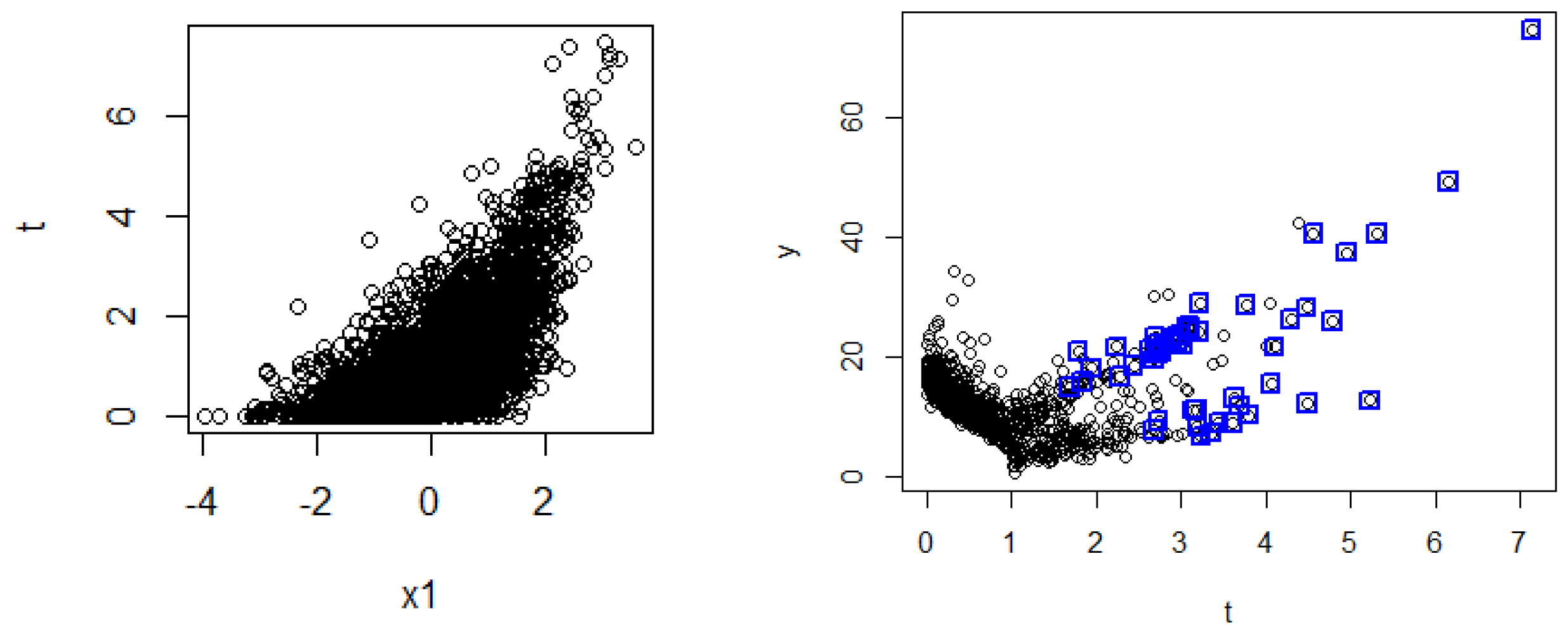
Appendix B.4. Simulations with a Hidden Confounder
Appendix B.5. Simulations with Varying Extremal Region
| True . | ||||
|---|---|---|---|---|
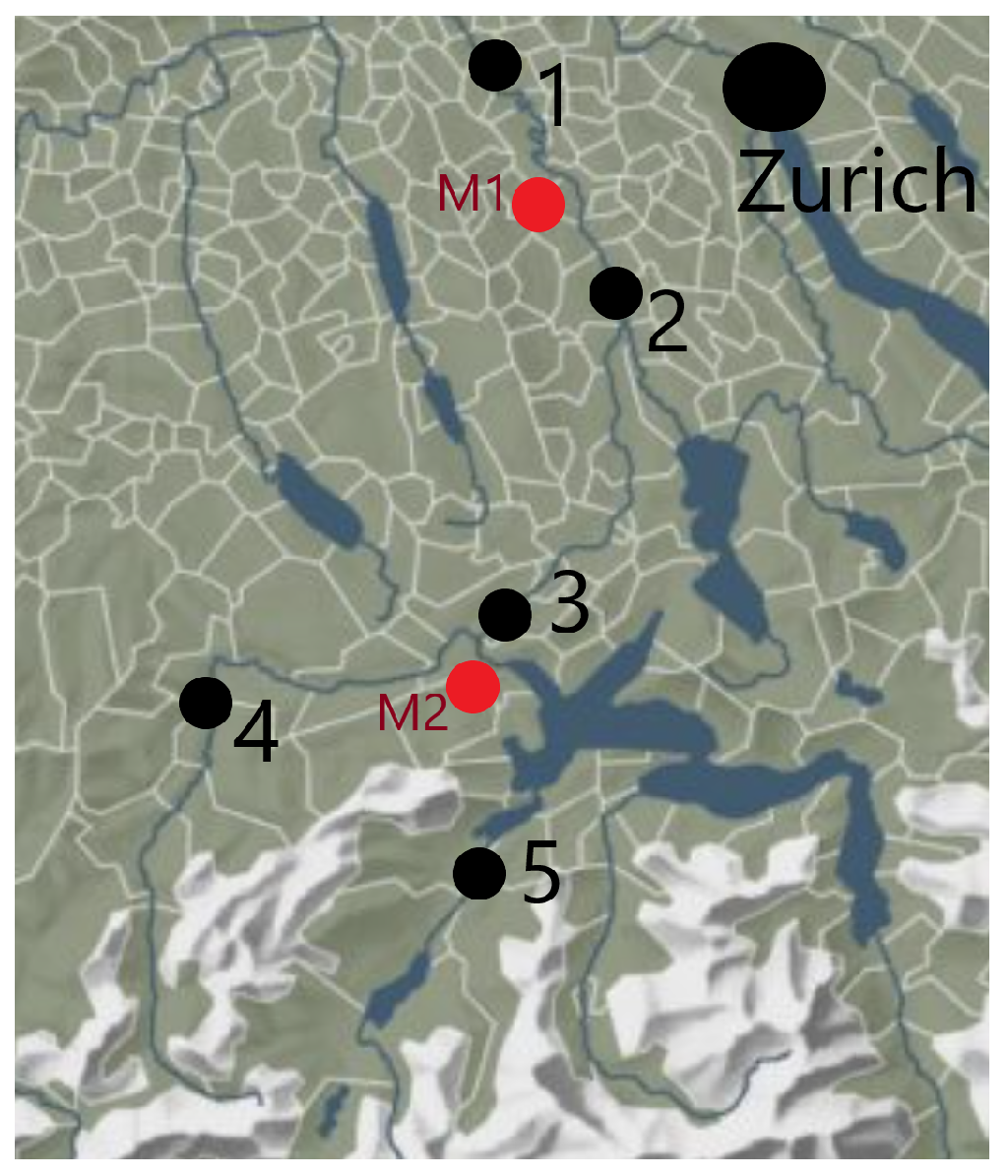
Appendix C. River Data Application
Appendix C.1. Simple Illustration with Known Ground Truth
- Total precipitation (daily);
- Total precipitation during the previous 7 days;
- Daily maximum of air temperature 2 m above ground;
- Daily maximum of relative air humidity 2 m above ground;
- Daily mean of vapor pressure 2 m above ground;
- Daily maximum of pressure reduced to sea level;
- Daily total of reference evaporation from FAO.
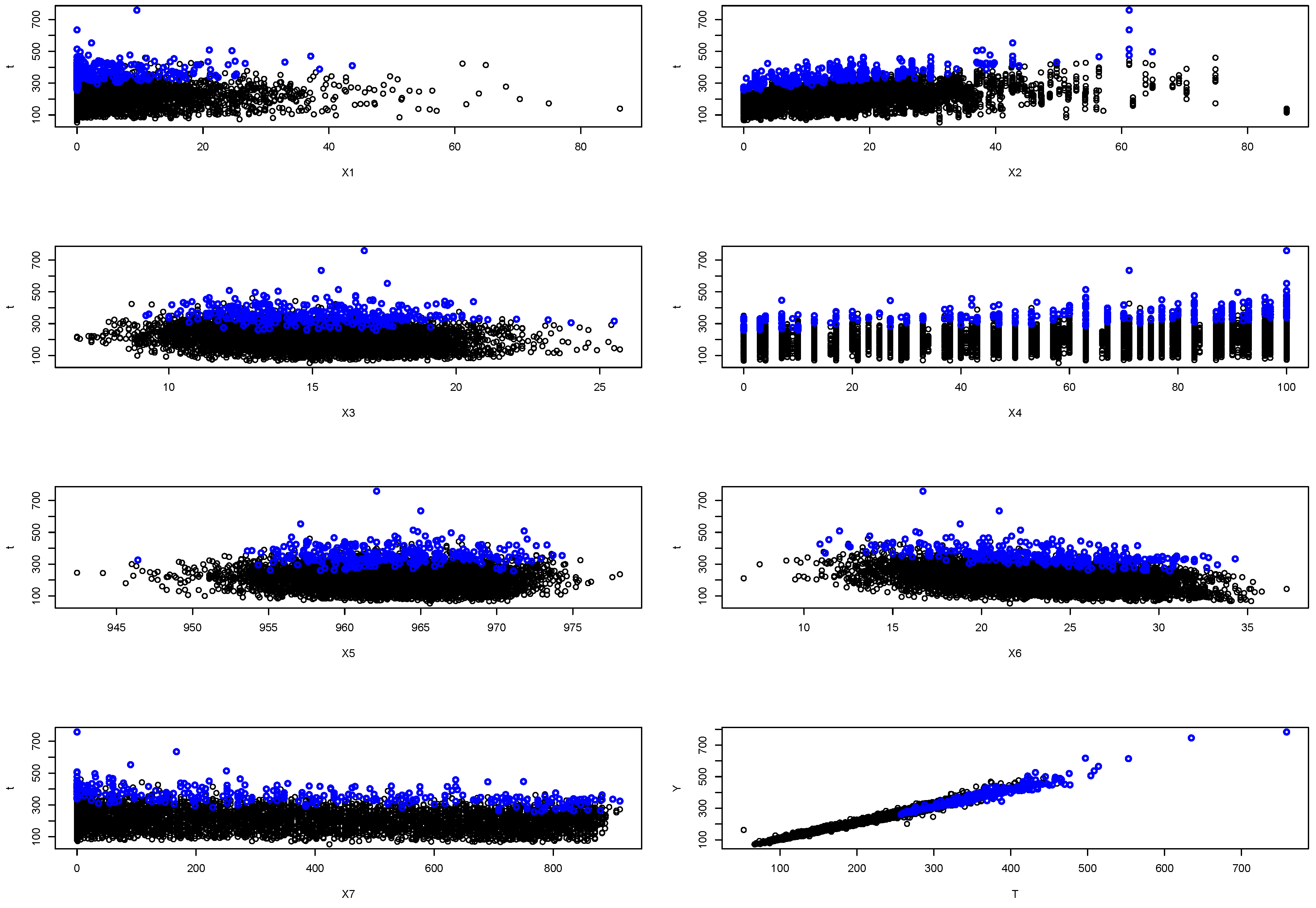

Appendix C.2. Effect of Precipitation on River Discharge
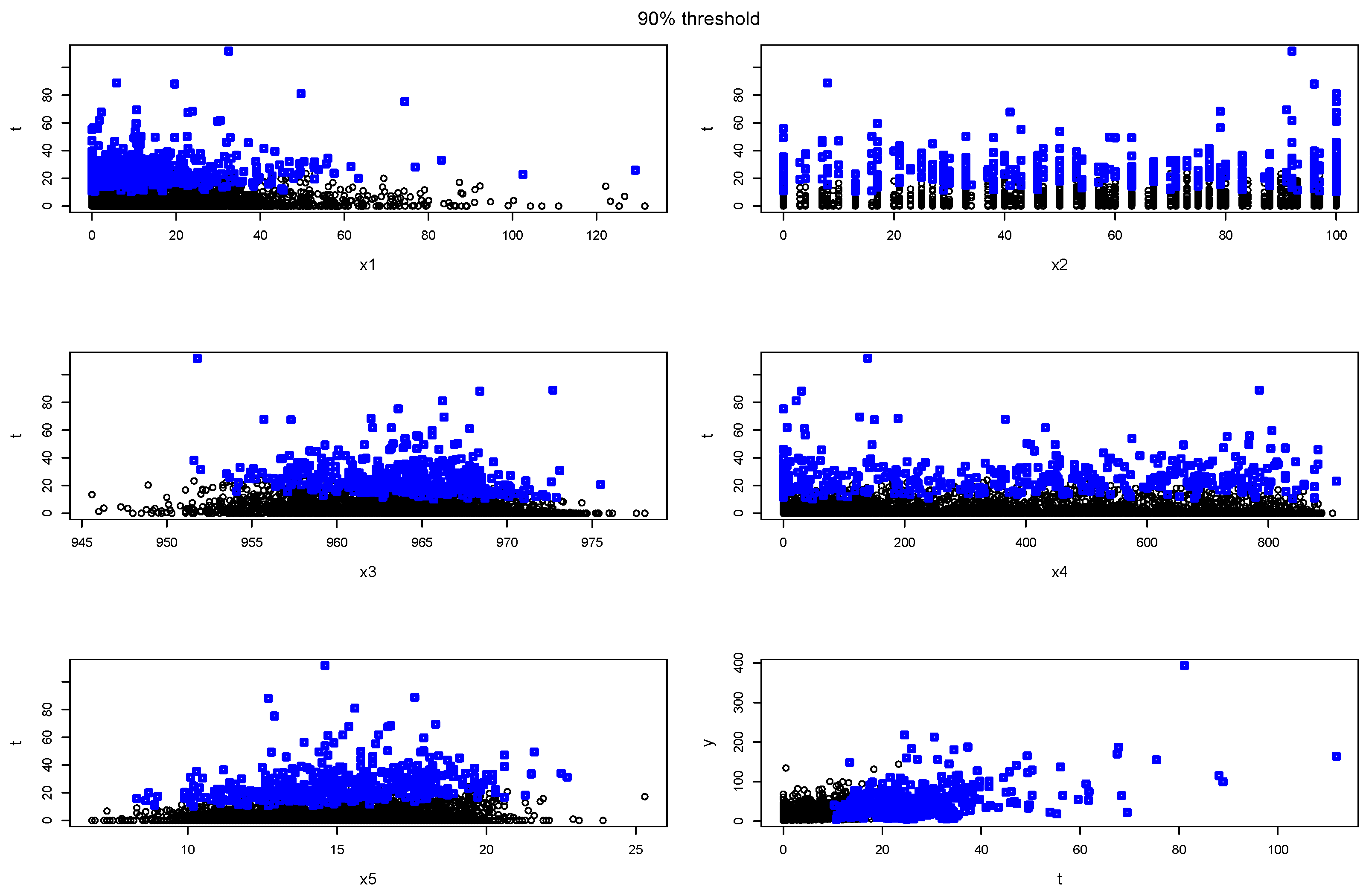
Appendix C.2.1. Choice of Variables
- River discharge on day ;
- Precipitation in the corresponding meteo-station on day ;
- Total (sum) precipitation during the previous 7 days (days );
- Daily maximum of Air temperature 2 m above ground on day i;
- Daily maximum of Relative air humidity 2 m above ground on day i;
- Daily maximum of Pressure reduced to sea level on day i;
- Daily total of Reference evaporation from FAO on day i.
Appendix C.2.2. Computation of
- Using a very straightforward approach where we model the data generating process of Y using a linear structural equation model and return the least square estimate of .
Appendix D. Consistency, Bootstrap and Its Asymptotics
Appendix D.1. Bootstrap
Appendix D.2. Simplifying Assumptions
- (A)
- (Causality justification) Consider Assumptions 1, 2 and 4 to be valid.
- (B)
- (Step 2 convergence) , and satisfy Grenander conditions (this is a minor assumption assuring that the matrix of observations have a full rank with probability tending to one. See Table 4.2 in [73]).
- (C)
- (Step 1 convergence) We assume that conditions R1, R2, and R3 from [74] are satisfied. That is, is positive semi-definite, has a compact support with existing and finite quantile densities , where , .
- (D)
- (Linearity) Assume that functions , are linear, functions are constant and that we employ linear regression for the estimation of the parameters.
- Choose ,
- (Step 1) Estimate by minimizing where .
- (Step 2) We estimate using least squares in a modelfrom the data-points in S (that is, we only consider ). Using language we run the following code: fit = lm(Y ∼ s +s:, data = data.frame(s, )), where , and .
- We output (see (A4)).
Appendix D.3. Consistency
- Assume that θ, α, and β are continuous functions, and suppose we employ consistent estimators for θ, α, and β. For instance, the Generalized Additive Model (GAM) estimator [51] has been shown to be consistent under specific smoothness conditions.
- Let be chosen such that the distribution of follows for all , where is assumed to be compact.
- (In other words, is large enough such that the -quantile of is larger than t.);
- It holds thatwhere is the -quantile of ;
- It holds that
- ;
- ;
- The first bullet-point is a trivial consequence of the assumption .
- The second bullet-point is a trivial consequence of Lemma 2 together with Assumption D.
- The third bullet-point is a trivial consequence of Assumptions 4 and D;
- The fourth bullet-point follows from a well-known consistency of . It is well known that for a fixed quantile q, the maximum likelihood estimator is consistent and even asymptotically normal (see, e.g., Theorem 4.1 in [68], noting that we assume continuous T and finite second moments of ). However, quantile q is not fixed and is increasing with the sample size with the speed and . This is a well-known generalization of quantile regression known as ‘intermediate order regression quantiles’ or ‘moderately extreme quantiles’ [75] and is as consistent and asymptotically normal under Assumption C (see Theorem 5.1 in [74]).
- The fifth bullet-point: For a moment, fix . It is an elementary knowledge that the estimation of using least squares in a model (A6), where is fixed, consistent, and even asymptotically normal under conditions , , ) satisfying Grenander conditions and the sample-size (see, e.g., Lemma A2). Observe that least squares estimate is linear in , that is, if we express explicitly, we obtain , where is a coefficient in a linear model corresponding to (A9) (where T is assumed to be larger than implicitly). Finally, using this observation, we can replace the fixed value of by a random , and we still obtain . Since by increasing n we can make arbitrarily accurate with arbitrarily large probability, the same holds for . In the following paragraph, we present an an illustration of the linearity of in for . An explicit expression of as a function of and our data is the following:where , WLOG let . Note thatwhere is the data matrix corresponding to a model (A9).
Appendix D.4. Bootstraps Correctness
- E.
- Assume that is consistent (which holds for example under assumptions A,B,C,D).
- F.
- We compute from the first data points, and we compute from the remaining data points.
- G.
- In the computation of the set S, we assume that is known and non-random; that is, instead of .
- H.
- Assumption of Theorem 3 in [76] are satisfied; that is, is non-singular matrix, the conditional density of given , denoted as f, satisfies whenever for some positive numbers , . Finally, there exists some function G such that for all and
Appendix E. Proofs of Lemmas 1 and 2
References
- Rosenbaum, P.R.; Rubin, D.B. The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika 1983, 70, 41–55. [Google Scholar] [CrossRef]
- Holland, P.W. Statistics and Causal Inference. J. Am. Stat. Assoc. 1986, 81, 945–960. [Google Scholar] [CrossRef]
- Robins, J.M.; Hernández-Díaz, S.; Brumback, B. Marginal Structural Models and Causal Inference in Epidemiology. Epidemiology 2000, 11, 550–560. [Google Scholar] [CrossRef] [PubMed]
- Imai, K.; King, G.; Stuart, E.A. Misunderstandings Between Experimentalists and Observationalists about Causal Inference. J. R. Stat. Soc. Ser. A Stat. Soc. 2008, 171, 481–502. [Google Scholar] [CrossRef]
- Imai, K.; van Dyk, D.A. Causal Inference With General Treatment Regimes. J. Am. Stat. Assoc. 2004, 99, 854–866. [Google Scholar] [CrossRef]
- Heckman, J.J.; Humphries, J.E.; Veramendi, G. Returns to Education: The Causal Effects of Education on Earnings, Health, and Smoking. J. Political Econ. 2018, 126, 197–246. [Google Scholar] [CrossRef] [PubMed]
- Hannart, A.; Naveau, P. Probabilities of Causation of Climate Changes. J. Clim. 2018, 31, 5507–5524. [Google Scholar] [CrossRef]
- Low, H.; Meghir, C. The Use of Structural Models in Econometrics. J. Econ. Perspect. 2017, 31, 33–58. [Google Scholar] [CrossRef]
- Rubin, D.B. Causal Inference Using Potential Outcomes: Design, Modeling, Decisions. J. Am. Stat. Assoc. 2005, 100, 322–331. [Google Scholar] [CrossRef]
- Imbens, G.W.; Rubin, D.B. Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Kennedy, E.H.; Ma, Z.; McHugh, M.D.; Small, D.S. Non-parametric Methods for Doubly Robust Estimation of Continuous Treatment Effects. J. R. Stat. Soc. Ser. B Stat. Methodol. 2017, 79, 1229–1245. [Google Scholar] [CrossRef]
- Westling, T.; Gilbert, P.; Carone, M. Causal Isotonic Regression. JRSSb 2020, 82, 719–747. [Google Scholar] [CrossRef]
- Galagate, D. Causal Inference with a Continuous Treatment and Outcome: Alternative Estimators for Parametric Dose-Response Functions with Applications. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2016. [Google Scholar] [CrossRef]
- Rubin, D.; van der Laan, M.J. Extending Marginal Structural Models through Local, Penalized, and Additive Learning; Working Paper 212; Division of Biostatistics, UC Berkeley: Berkeley, CA, USA, 2006. [Google Scholar]
- Neugebauer, R.; van der Laan, M.J. Nonparametric causal effects based on marginal structural models. J. Stat. Plan. Inference 2007, 137, 419–434. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Zhang, H.; Lipton, C.Z.; Li, L.E.; Xing, E. Exploring Transformer Backbones for Heterogeneous Treatment Effect Estimation. NeurIPS ML Safety Workshop 2023. [Google Scholar] [CrossRef]
- Bica, I.; Jordon, J.v.d.; Schaar, M. Estimating the Effects of Continuous-valued Interventions using Generative Adversarial Networks. In Proceedings of the Advances in Neural Information Processing Systems, virtual, 6–12 December 2020; Volume 33, pp. 16434–16445. [Google Scholar] [CrossRef]
- Zhang, Y. Extremal Quantile Treatment Effects. Ann. Stat. 2018, 46, 3707–3740. [Google Scholar] [CrossRef]
- Deuber, D.; Li, J.; Engelke, S.; Maathuis, M. Estimation and Inference of Extremal Quantile Treatment Effects for Heavy-Tailed Distributions. JASA 2023, 1–11. [Google Scholar] [CrossRef]
- Huang, W.; Li, S.; Peng, L. Extreme Continuous Treatment Effects: Measures, Estimation and Inference. arXiv 2022, arXiv:2209.00246. [Google Scholar]
- Bodik, J.; Paluš, M.; Pawlas, Z. Causality in extremes of time series. Extremes 2024, 27, 67–121. [Google Scholar] [CrossRef]
- Gnecco, N.; Meinshausen, N.; Peters, J.; Engelke, S. Causal discovery in heavy-tailed models. Ann. Stat. 2020, 49, 1755–1778. [Google Scholar] [CrossRef]
- Pasche, O.C.; Chavez-Demoulin, V.; Davison, A. Causal Modelling of Heavy-Tailed Variables and Confounders with Application to River Flow. Extremes 2023, 26, 573–594. [Google Scholar] [CrossRef]
- Krali, M.; Davison, A.C.; Klüppelberg, C. Heavy-tailed max-linear structural equation models in networks with hidden nodes. arXiv 2023, arXiv:2306.15356. [Google Scholar]
- Bodik, J.; Chavez-Demoulin, V. Structural restrictions in local causal discovery: Identifying direct causes of a target variable. arXiv 2023, arXiv:2307.16048. [Google Scholar]
- Engelke, S.; Hitz, A. Graphical models for extremes. J. R. Stat. Soc. Ser. B 2020, 82, 871–932. [Google Scholar] [CrossRef]
- Naveau, P.; Hannart, A.; Ribes, A. Statistical Methods for Extreme Event Attribution in Climate Science. Annu. Rev. Stat. Its Appl. 2020, 7, 89–110. [Google Scholar] [CrossRef]
- Courgeau, V.; Veraart, A.E.D. Extreme event propagation using counterfactual theory and vine copulas. arXiv 2021, arXiv:2106.13564. [Google Scholar]
- Kiriliouk, A.; Naveau, P. Climate extreme event attribution using multivariate peaks-over-thresholds modeling and counterfactual theory. Ann. Appl. Stat. 2020, 14, 1342–1358. [Google Scholar] [CrossRef]
- Dong, K.; Ma, T. First steps toward understanding the extrapolation of nonlinear models to unseen domains. In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Christiansen, R.; Pfister, N.; Jakobsen, M.E.; Gnecco, N.; Peters, J. A Causal Framework for Distribution Generalization. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 6614–6630. [Google Scholar] [CrossRef]
- Saengkyongam, S.; Rosenfeld, E.; Ravikumar, P.K.; Pfister, N.; Peters, J. Identifying Representations for Intervention Extrapolation. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Chen, Y.; Bühlmann, P. Domain Adaptation under Structural Causal Models. J. Mach. Learn. Res. 2021, 22, 1–80. [Google Scholar]
- Shen, X.; Meinshausen, N. Engression: Extrapolation for Nonlinear Regression? arXiv 2024, arXiv:2307.00835. [Google Scholar]
- Pfister, N.; Bühlmann, P. Extrapolation-Aware Nonparametric Statistical Inference. arXiv 2024, arXiv:2402.09758. [Google Scholar]
- Hirano, K.; Imbens, G.W. The Propensity Score with Continuous Treatments. In Applied Bayesian Modeling and Causal Inference from Incomplete-Data Perspectives; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2004; Chapter 7; pp. 73–84. [Google Scholar] [CrossRef]
- Gill, R.D.; Robins, J.M. Causal inference for complex longitudinal data: The continuous case. Ann. Stat. 2001, 29, 1785–1811. [Google Scholar] [CrossRef]
- King, G.; Zeng, L. The Dangers of Extreme Counterfactuals. Political Anal. 2006, 14, 131–159. [Google Scholar] [CrossRef]
- Crump, R.K.; Hotz, V.J.; Imbens, G.W.; Mitnik, O.A. Dealing with Limited Overlap in Estimation of Average Treatment Effects. Biometrika 2009, 96, 187–199. [Google Scholar] [CrossRef]
- Ai, C.; Linton, O.; Zhang, Z. Estimation and Inference for the Counterfactual Distribution and Quantile Functions in Continuous Treatment Models. J. Econom. 2021, 228, 39–61. [Google Scholar] [CrossRef]
- Bahadori, M.T.; Tchetgen, E.; Heckerman, D. End-to-End Balancing for Causal Continuous Treatment-Effect Estimation. In Proceedings of the 39th International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; Volume 162, pp. 1313–1326. [Google Scholar]
- Li, Y.; Kuang, K.; Li, B.; Cui, P.; Tao, J.; Yang, H.; Wu, F. Continuous Treatment Effect Estimation via Generative Adversarial De-confounding. In Proceedings of the 2020 KDD Workshop on Causal Discovery, PMLR, San Diego, CA, USA, 24 August 2020; Volume 127, pp. 4–22. [Google Scholar]
- Kreif, N.; Grieve, R.; Díaz, I.; Harrison, D. Evaluation of the Effect of a Continuous Treatment: A Machine Learning Approach with an Application to Treatment for Traumatic Brain Injury. Health Econ. 2015, 24, 1213–1228. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; van Dyk, D.A.; Imai, K. Propensity Score-based Methods for Causal Inference in Observational Studies with Non-binary Treatments. Stat. Methods Med. Res. 2020, 29, 709–727. [Google Scholar] [CrossRef] [PubMed]
- Resnick, S.I. Extreme Values, Regular Variation and Point Processes; Springer: New York, NY, USA, 2008. [Google Scholar]
- Pickands, J. Statistical Inference Using Extreme Order Statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: London, UK, 2001. [Google Scholar]
- Fisher, R.; Tippett, L. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Pearl, J. Causality: Models, Reasoning and Inference; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Soklakov, A. Occam’s razor as a formal basis for a physical theory. Found. Phys. Lett. 2002, 15, 107–135. [Google Scholar] [CrossRef]
- Wood, S. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Smith, R. Extreme Value Theory. Handb. Appl. Math. 1990, 1, 437–447. [Google Scholar]
- Davison, A.; Huser, R. Statistics of Extremes. Annu. Rev. Stat. Its Appl. 2015, 2, 203–235. [Google Scholar] [CrossRef]
- Schneider, L.F.; Krajina, A.; Krivobokova, T. Threshold selection in univariate extreme value analysis. Extremes 2021, 24, 881–913. [Google Scholar] [CrossRef]
- Caeiro, F.; Gomes, M. Threshold selection in extreme value analysis. In Extreme Value Modeling and Risk Analysis: Methods and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015; pp. 69–82. ISBN 9780429161193. [Google Scholar]
- Davison, A.; Smith, R.L. Models for exceedances over high thresholds. J. R. Stat. Soc. Ser. B (Methodol.) 1990, 52, 393–425. [Google Scholar] [CrossRef]
- van der Vaart, A.W. Bootstrap; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 1998; pp. 326–340. [Google Scholar]
- Kennedy, E.H. Nonparametric causal effects based on incremental propensity score interventions. JASA 2019, 114, 645–656. [Google Scholar] [CrossRef]
- Bia, M.; Mattei, A.; Nicolò, G. A Stata package for the application of semiparametric estimators of dose response functions. Stata J. 2014, 14, 580–604. [Google Scholar] [CrossRef]
- Galagate, D.; Schafer, J. Estimating Causal Dose Response Functions, R package version 0.4.2; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- van der Wal, W.; Geskus, R. IPW: An R package for inverse probability weighting. J. Stat. Softw. 2011, 43, 1–23. [Google Scholar]
- Davis, R.A. The rate of convergence in distribution of the maxima. Stat. Neerl. 1982, 36, 31–35. [Google Scholar] [CrossRef]
- Engelke, S.; Ivanovs, J. Sparse structures for multivariate extremes. Annu. Rev. Stat. Its Appl. 2021, 8, 241–270. [Google Scholar] [CrossRef]
- Pearl, J. Direct and indirect effects. In Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence, Seattle, WA, USA, 2–5 August 2001; UAI’01. pp. 411–420. [Google Scholar]
- Yeh, I. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Neville, A. Properties of Concrete; Pearson Education Limited: London, UK, 2011. [Google Scholar]
- Koenker, R. Quantile Regression; Econometric Society Monographs; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Youngman, B.D. Evgam: An R Package for Generalized Additive Extreme Value Models. J. Stat. Softw. 2022, 103, 1–26. [Google Scholar] [CrossRef]
- Kolesárová, A.; Mesiar, R.; Saminger-Platz, S. Generalized Farlie-Gumbel-Morgenstern Copulas. In Information Processing and Management of Uncertainty in Knowledge-Based Systems. Theory and Foundations; Springer International Publishing: Cham, Switzerland, 2018; Communications in Computer and Information Science; Volume 853, pp. 244–252. [Google Scholar] [CrossRef]
- Perlin, K. An Image Synthesizer. SIGGRAPH Comput. Graph. 1985, 19, 287–296. [Google Scholar] [CrossRef]
- Davis, R.A.; Mikosch, T. The extremogram: A correlogram for extreme events. Bernoulli 2009, 15, 977–1009. [Google Scholar] [CrossRef]
- Greene, W.H. Econometric Analysis; Pearson Education: London, UK, 2008. [Google Scholar]
- Chernozhukov, V. Extremal quantile regression. Ann. Stat. 2005, 33, 806–839. [Google Scholar] [CrossRef]
- Chernozhukov, V.; Fernández-Val, I.; Kaji, T. Extremal Quantile Regression: An Overview; Chapman and Hall: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hahn, J. Bootstrapping Quantile Regression Estimators. Econom. Theory 1995, 11, 105–121. [Google Scholar] [CrossRef]
- Freedman, D.A. Bootstrapping Regression Models. Ann. Stat. 1981, 9, 1218–1228. [Google Scholar] [CrossRef]
- Eck, D.J. Bootstrapping for multivariate linear regression models. Stat. Probab. Lett. 2018, 134, 141–149. [Google Scholar] [CrossRef]

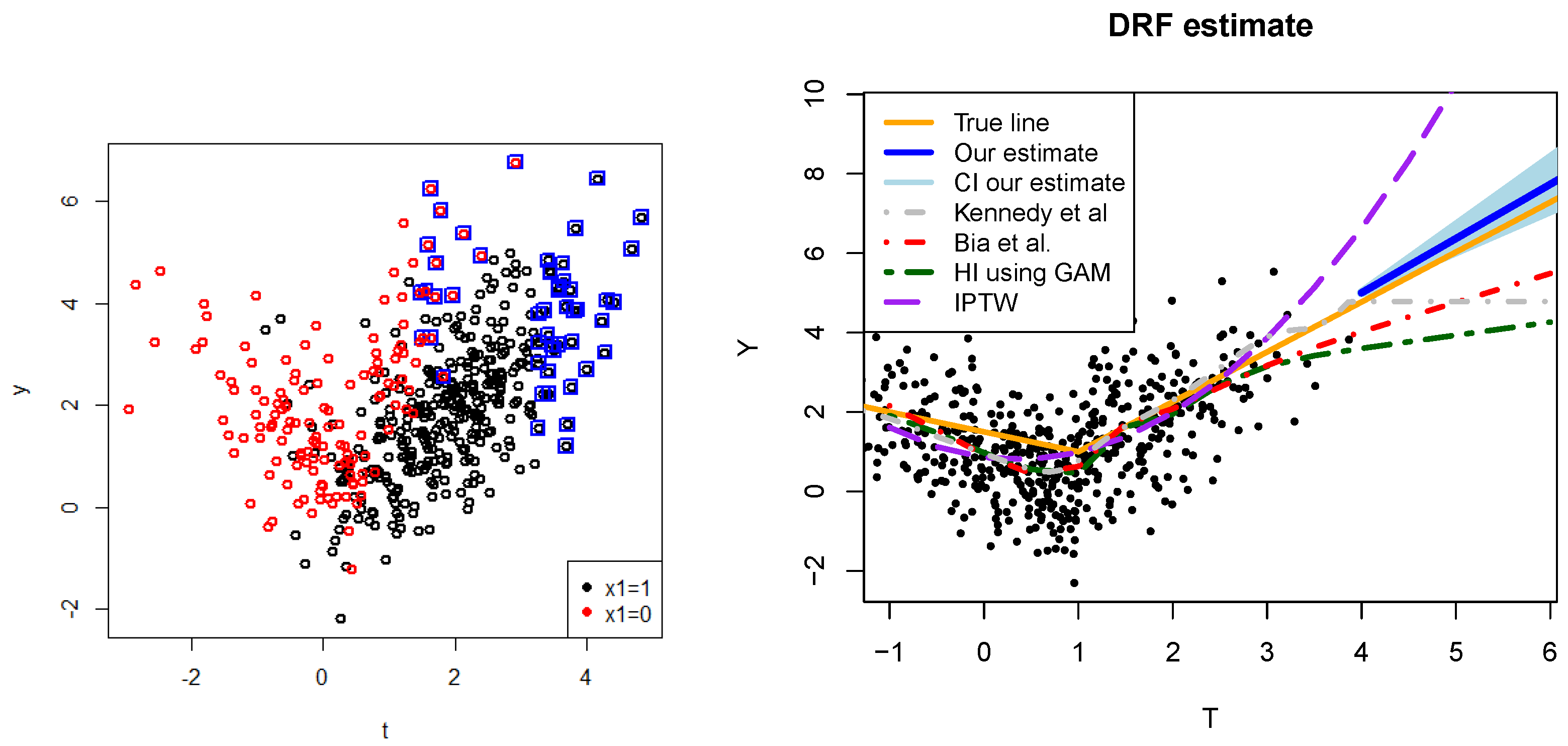
| True | Gaussian | Exponential | Pareto |
|---|---|---|---|
| Our Method | Bia et al. [60] | Kennedy et al. [11] | HI with GAM [36] | IPTW [62] | |
|---|---|---|---|---|---|
| 0.18 | 0.68 | 0.64 | 0.42 | 3.89 | |
| 0.48 | 0.81 | 0.65 | 0.67 | 5.69 | |
| 0.79 | 0.92 | could not handle | 0.92 | 4.70 |
| Truth: | Stations | Stations | Stations | Stations |
|---|---|---|---|---|
| Truth Unknown | Station 1 | Station 2 | Station 3 | Station 4 | Station 5 |
|---|---|---|---|---|---|
| * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodik, J. Extreme Treatment Effect: Extrapolating Dose-Response Function into Extreme Treatment Domain. Mathematics 2024, 12, 1556. https://doi.org/10.3390/math12101556
Bodik J. Extreme Treatment Effect: Extrapolating Dose-Response Function into Extreme Treatment Domain. Mathematics. 2024; 12(10):1556. https://doi.org/10.3390/math12101556
Chicago/Turabian StyleBodik, Juraj. 2024. "Extreme Treatment Effect: Extrapolating Dose-Response Function into Extreme Treatment Domain" Mathematics 12, no. 10: 1556. https://doi.org/10.3390/math12101556
APA StyleBodik, J. (2024). Extreme Treatment Effect: Extrapolating Dose-Response Function into Extreme Treatment Domain. Mathematics, 12(10), 1556. https://doi.org/10.3390/math12101556







