Utilizing Artificial Neural Networks for Geometric Bone Model Reconstruction in Mandibular Prognathism Patients

Abstract

Patient-specific 3D models of the human mandible are finding increasing utility in medical fields such as oral and maxillofacial surgery, orthodontics, dentistry, and forensic sciences. The efficient creation of personalized 3D bone models poses a key challenge in these applications. Existing solutions often rely on 3D statistical models of human bone, offering advantages in rapid bone geometry adaptation and flexibility by capturing a range of anatomical variations, but also a disadvantage in terms of reduced precision in representing specific shapes. Considering this, the proposed parametric model allows for precise manipulation using morphometric parameters acquired from medical images. This paper highlights the significance of employing the parametric model in the creation of a personalized bone model, exemplified through a case study targeting mandibular prognathism reconstruction. A personalized model is described as 3D point cloud determined through the utilization of series of parametric functions, determined by the application of geometrical morphometrics, morphology properties, and artificial neural networks in the input dataset of human mandible samples. With 95.05% of the personalized model’s surface area displaying deviations within −1.00–1.00 mm relative to the input polygonal model, and a maximum deviation of 2.52 mm, this research accentuates the benefits of the parametric approach, particularly in the preoperative planning of mandibular deformity surgeries.

1. Introduction

The mandible, as a crucial component of the craniofacial complex, plays a pivotal role in functions such as mastication, speech, and facial aesthetics. Trauma, congenital anomalies, or pathological conditions often necessitate mandibular reconstruction to restore form and function. The presence of these pathological conditions presents a challenge in acquiring complete data about the scanned bone, rendering the task of reconstructing a complete 3D model of the bone or specific segments of the bone problematic. In instances where volumetric scanning is not possible, reliance on two-dimensional imaging techniques, such as X-rays, becomes necessary for the reconstruction process. However, this approach introduces limitations in terms of accuracy, reproducibility, and the ability to analyze complex maxillofacial structures, often resulting in unsatisfactory outcomes. The integration of three-dimensional (3D) predictive models is a transformative approach, providing a more comprehensive understanding of mandibular anatomy and pathology. The pivotal role of 3D predictive models in the reconstruction of complex anatomical structures of the maxillofacial region is reflected in their potential to improve surgical precision and health outcomes, and ultimately contribute to better quality of life for patients [1,2,3,4].

The foundation of a 3D predictive models lies in advanced imaging modalities such as Computed Tomography (CT), Cone-Beam Computed Tomography (CBCT), and Magnetic Resonance Imaging (MRI) [5,6]. These radiological methods enable the acquisition of high-resolution, volumetric data essential for the formation of accurate 3D predictive models. Generally, methods that utilize a standard (template) model often involve statistical and parametric approaches, allowing for the prediction of the geometric characteristics of a human bone. Input data from medical imaging methods form the basis for creating both types of models (e.g., CT or MRI), applying two distinct approaches used in the modeling of human bones, each with its own set of characteristics and applications.

Statistical Shape Models (SSMs) provide a valuable mathematical framework for capturing the variability within a specific population. They not only define an average shape but also encapsulate its variations [7]. The construction of an SSM involves identifying landmarks across elements of the initial sample set and establishing a correspondence among them. Subsequently, statistical analyses are employed to model shape variations [8,9]. These models describe the natural variation present within a population, making them valuable tools in research focused on virtual surgical planning, understanding the range of anatomical variations, creating statistical atlases, and population-based studies [10,11,12,13]. Statistical models exhibit constraints in the creation of geometric models of human bones stemming from various factors. Primarily, these models rely on population data averages, potentially failing to precisely represent individual variations in bone morphology. Moreover, the comparability of shape models with other datasets and research is constrained due to the uniqueness of each Statistical Shape Model (SSM), which is tailored to a specific set of images. This limitation could be overcome by applying a collection of predefined shape models [14]. Additionally, they confront difficulties in accurately predicting intricate anatomical details and complex geometric features. This could result in oversimplified representations of bone geometry, overlooking the subtle nuances in real anatomical structures.

In contrast, the parametric model represents a mathematical framework wherein geometry is defined by parametric functions, whose parameters are determined by values found in patient data obtained through medical imaging modalities. By changing input parameters (dimensions, angles, and other geometric features that characterize the bone’s morphology) acquired from specific patients’ medical images, the parametric model has the ability to be converted into the point cloud model [15]. Parametric models are commonly used when there is a need for precise and standardized representations of bones. They are suitable for applications such as designing patient-specific implants [15,16,17] or creating anatomical models for educational purposes. In summary, the choice between statistical and parametric models depends on the specific goals of the modeling task, the level of precision required, and the nature of the anatomical variations within the population of interest. Statistical models offer more flexibility by capturing a range of variations, while parametric models prioritize precision in representing specific shapes.

The parametric model was initially developed for the Human Mandible Coronoid Process employing multiple linear regression [18]. Encouragingly, the predictive effect yielded satisfactory results. Moreover, the model encompassing the entire mandible was established through multi-regression analysis, and achieved significantly lower prediction accuracy compared to the relevant value (the error should not exceed two mm per measurement point) suggested by the maxillofacial surgeon who participated in this study. Notably, the observation data revealed indications of non-linear relationships between variables. Finally, the main idea and motivation behind the application of ANNs to the problem considered in this study relates to their inherent ability to effectively mimic non-linear associations between variables. The utilization of artificial neural networks (ANNs) in this study is supported by their advantageous features for predictive tasks. These include their ability to approximate universal functions, resilience to data noise, accommodation of non-linear variable relationships, robust generalization capabilities, and inherent upgradeability. The algorithm used to create the parametric model of the human mandible through the application of artificial intelligence was presented in the study by Mitić et al. 2022 [17]. The authors demonstrated several benefits of employing the Levenberg–Marquardt (LM) [19] algorithm in training artificial neural networks (ANNs) for predicting the coordinates of anatomical points (X, Y, and Z). Nine morphometric parameters that are essential for fully defining mandible geometry were utilized as inputs for the artificial neural network (ANN). The determination of the number of layers and the number of neurons in the hidden layer was achieved through a trial-and-error approach, according to the literature recommendations [20,21]. Nine ANN models were developed and trained. Utilizing a dataset comprising 22 mandible samples devoid of pathological or traumatic damage, partitioned into 16 samples for training and 6 samples for testing, the study revealed that the 9-50-3 ANN model yielded the most accurate predictions. The conclusion was derived from a comprehensive performance analysis conducted on the designed ANN models with different structural parameters. The results obtained were more than promising.

Within this study, the procedure for reconstruction of the geometric model of the mandible of a patient with mandibular prognathism using a parametric model will be presented. Mandibular prognathism is a congenital malocclusion, classified as anterior occlusion. Manifesting as an intensified development of the mandible in the anterior direction, this condition precipitates the formation of anomalous anatomical structures within the occlusion, culminating in the superimposition of the lower dentition upon the upper dentition [22]. Orthodontic assessment and cephalometric analysis are instrumental in diagnosing and characterizing the skeletal discrepancy, guiding treatment planning, and assessing the need for surgical intervention. Treatment modalities for mandibular prognathism are contingent upon the severity of the malocclusion, patient age, skeletal maturity, and treatment objectives. In most cases, patients with mandibular prognathism require surgery, involving the surgical repositioning of the maxilla and mandible, in order to achieve optimal facial aesthetics, occlusal function, and stability [23].

The ultimate objective of the methodology outlined in this study was to create a parametric model of the human mandible tailored to the unique anatomical features of patients diagnosed with mandibular prognathism. The development of a personalized model necessitated the creation of a mathematical framework tailored to the morphometric parameters obtained from medical imaging. The preliminary results are presented within this work, demonstrating that the resulting model may be particularly useful during the preoperative planning of surgical procedures of mandibular deformities.

2. Materials and Methods

The methodology detailed in this research constitutes a fundamental component of the Method of Anatomical Features (MAF), which introduces an approach to elucidate the geometric properties of human bones. All principles within the method of anatomical features maintain significant validity when applied to bone reconstruction processes [15]. This method facilitates the creation of two model types—3D geometrical models and predictive (parametric) models—both derived from data obtained through medical imaging modalities such as CT or MRI. This process entails a series of steps:

• Generation of the polygonal model: This process involves a sequence of procedures to create a polygonal model that represents a specific human bone;
• Anatomical analysis: This establishes correlations between geometric components within the polygonal bone model and predetermined anatomical and morphological terms documented in the medical literature.
• Definition and/or selection of Referential Geometrical Entities (RGEs): These are essential geometric components (points, lines, planes, axes, etc.) formed on the polygonal model of human bones. They form the foundation for the construction of all additional geometric elements, including surfaces.
• Creation of Constitutive Geometrical Entities (CGEs): Derived from RGEs, CGEs are integral components utilized in the creation surface and solid models for human bones, in accordance with bone morphology.
• Creation of geometric models of human bones: This encompasses the process of generating surface and solid models of human bones.
• Creation of the parametric model: This entails supplementary procedures within MAF aimed at generating a bone-specific parametric model, incorporating the following:
  • Definition of Parameters—involves defining morphometric parameters (individually specified for each human bone), which are discernible and measurable features in medical images.
  • Definition of Anatomical Points—established on CGEs or other notable anatomical points (biologically meaningful points defined by experts to ensure their consistency within the same species), mathematical points (points situated on an object as a representation of a mathematical or geometric property), or pseudo-landmarks (points situated between anatomical or mathematical landmarks) on the polygonal model. This collection of anatomical points must be defined for each bone within a given dataset.
  • Definition of the parametric model—entails the measurement of points and morphometric parameters for a polygonal model created within a set. These measured values are subsequently utilized in statistical analysis to formulate parametric functions, with morphometric parameters serving as arguments. These functions establish values for coordinates of anatomical points relative to morphometric parameters.

2.1. Creation of Parametric Model of the Human Mandible

The parametric model of the human mandible, employing the Method of Anatomical Features, is characterized by a set of parametric functions derived from the application of a mathematical model. In the context of the established model, the identification of input–output data becomes imperative. The input data utilized by the ANN model comprise morphometric parameters, which are defined on the mandible’s polygonal model with respect to the anatomical and morphological features present on the bone. These parameters are used to characterize the shape of the mandible. In our previously published study, a parametric model of the human mandible was developed, with a strictly defined number of morphometric parameters [17]. For the purposes of this study, a new ANN model was created with morphometric parameters that were lower than a precisely specified number due to the impossibility of reading their values from the medical images.

The coordinate values of the points were selected as ANN outputs, which were explicitly identified as anatomical points, appropriate geometric elements, or well-defined anatomical landmarks on the bone itself. The anatomical points in this collection were individually defined for bone samples. The foundational step in this involves establishing a coordinate system on each bone specimen to facilitate the accurate measurement of point coordinates. For instance, in the case of the mandible, an absolute coordinate system (World Coordinate System (WCS)) is established precisely at the midpoint of two anatomical landmarks—the Mental Foramen, located bilaterally on the anterior surface of the mandibular body. The coordinate system planes are the Medio-Sagittal plane (MS), Horizontal (Mandibular) plane and Coronal plane. The Medio-Sagittal plane is normal to the distance between two characteristic points, the Mental Foramen, and contains the most inferior midline point on the mandible (Gnathion). The horizontal plane is normal to the MS plane, and it contains a point along the rounded poster–inferior corner of the mandible between the ramus and the body (Gonion). The coronal plane perpendicular to the mandibular plane and divides the mandible into front (anterior) and back (posterior) sections.

2.2. Develop an Artificial Neural Network Model

The development of an Artificial Neural Network (ANN) model involved utilizing data derived from measurements taken on a series of human mandible samples acquired using the Toshiba MSCT scanner Aquillion 64 (Toshiba, Tokyo, Japan), with the following scan parameters: tube voltage 120 kV, tube current 150 mA and slice thickness 1 mm. The in-plane resolution is 0.781 × 0.781 mm (pixel size), with an acquisition matrix of 512 × 512 and field of view (FOV) measuring 400 × 400 mm. An ANN is a mathematical representation of the human brain which comprises many interconnected simple functional units known as neurons, functioning as parallel information processors that approximately correlate to inputs and outputs [24]. The ANN consists of eight input neurons, which correspond to eight morphometric parameters obtained from twenty-two mandibular samples of men without pathological conditions and deformities, aged from 24 to 82 years. MATLAB software version 2015a was used for the mathematical modeling of the ANN model.

In the implementation of the new ANN model, 22 mandible samples were used; 75% of the randomly selected bone samples were used for training, while the remaining 25% were used for testing. The input layer of the ANN model contains the same number of neurons as input variables; namely, the number of neurons in the input layer is equal to the number of morphometric parameters used in this study:

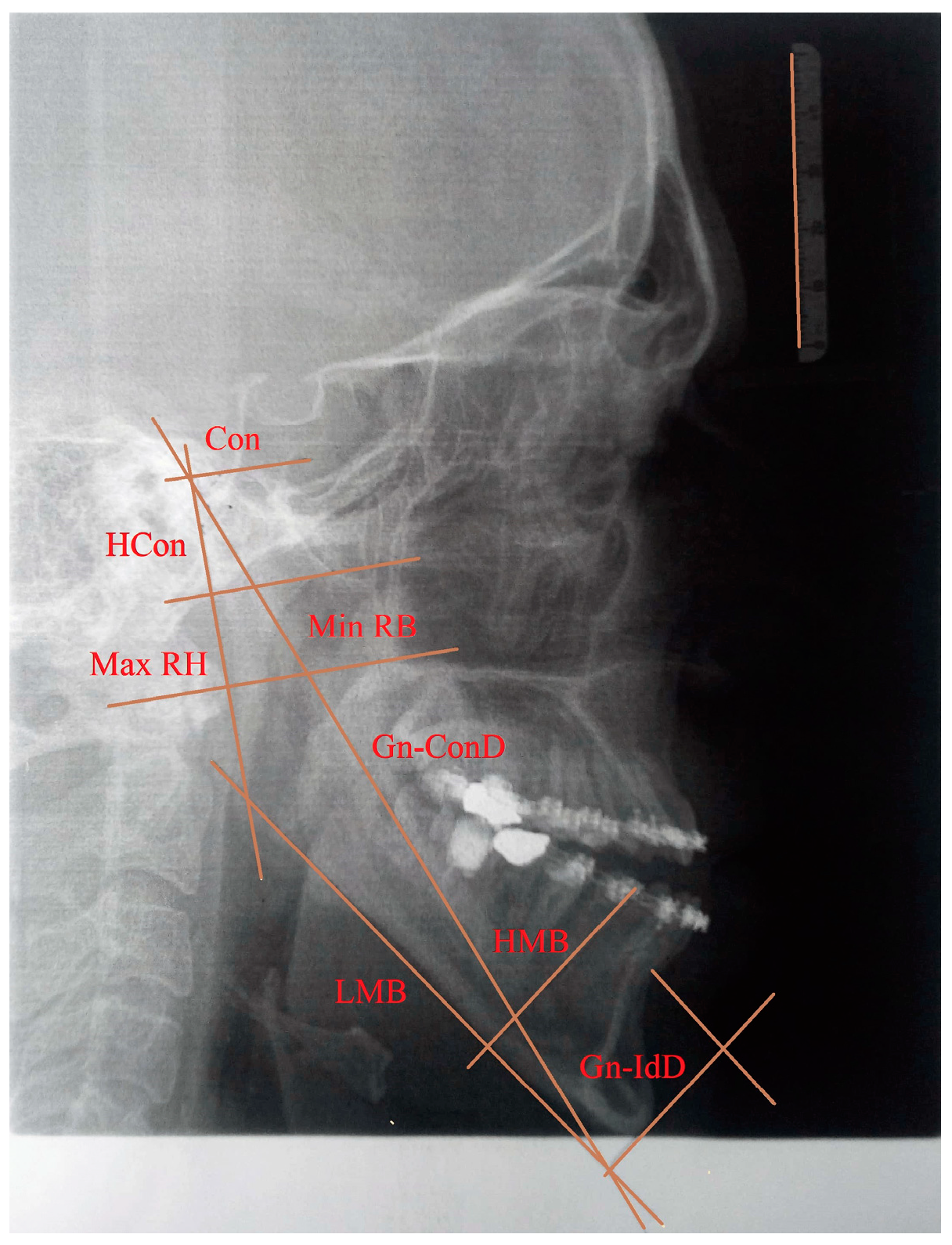
• Gnathion-interdental distance (Gn-IdD)—distance from the Gnathion to the alveolar septum between two incisors;
• Bigonial width (Go-GoD)—direct distance between right and left Gonion;
• Length of the mandibular body (LMB)—distance between Gonion and Gnathion;
• Gnathion-condylar distance (Gn-ConD)—distance between the Gnation and condylion (most prominent point on the mandibular condyle) anatomical points;
• Height of the mandibular body (HMB)—distance from the alveolar border to the mandibular base at the level of the Mental Foramen;
• Minimum ramus breadth (Min RB)—minimum breadth of the mandibular ramus measured perpendicular to the plane of the maximal height of the ramus;
• Maximum ramus height (Max RH)—distance between the highest point on the mandibular condyle and Gonion;
• Height of the condyle (Hcon)—distance between the condylion and the axis of the most inferior point of mandibular notch perpendicular to Max RH.

The definition and position of the morphometric parameters are presented in detail in the study by Arsić et al. (2010) [25]. The output layer consists of three neurons, each corresponding to the read values of anatomical point coordinates X, Y, and Z. Prior to the training phase, the normalization of input-output data was aligned with the activation function utilized by the ANN model. To develop an ANN model with a good generalization ability and robustness, in this study, the ANN architecture (i.e., the number of input data, the selection of appropriate input data, the number of hidden layers, and the number of neurons in the network layers) and ANN training parameters (i.e., momentum, number of epochs, learning rate, and the termination conditions) was determined by the trial-and-error method, guided by the existing literature [21,26], as well as the authors’ previous experience. Namely, determining the network topology (i.e., the number of hidden layers and the number of neurons in the network layers) is of great importance for the model’s prediction performance because random selection might cause model overfitting or underfitting problems [27]. The selection of training parameters has a significant effect on the ANN training results, particularly regarding the network’s convergence rate and its ability to avoid falling into a local minimum. Therefore, it is necessary to determine the optimal values of the ANN parameters. Among the model parameters, the learning rate represents one of the most impactful training parameters since it affects the training speed of the ANN model. Namely, selecting a higher learning rate can expedite model convergence but might introduce the risk of overlooking the global minimum; in contrast, selecting a lower value can impede the learning process. Further, the momentum denotes a pivotal training parameter aimed at accelerating and stabilizing the ANN training process. Setting a higher momentum value can prevent the model from falling into a local minimum; however, a lower momentum value can elevate the risk of bypassing the optimal solution. The number of epochs used during training denotes the frequency of data representations for the ANN. In addition, using the backpropagation algorithm during the model training ensures a desirable training error rate is achieved within the chosen number of training epochs; for example, the use of many epochs might lead to model overfitting. The selection of a neural network’s parameters when the backpropagation algorithm is used in the training process requires careful consideration and typically involves the trial-and-error method to achieve a balance between exploration and exploitation during the model training process.

In this study, several neural networks with different structures regarding the number of layers, the number of neurons in the layers, and the activation functions of the layers were designed and compared. The neural networks with different structures are presented in

Table 1. Topologies of neural networks.

Model	Method	Number of Hidden Neurons	Number of Hidden Layer	Trans. Fun. in Hidden Layer	Trans. Fun. in Output Layer
1	Levenberg–Marquardt	50	1	logsig	logsig
2	Levenberg–Marquardt	70	1	logsig	logsig
3	Levenberg–Marquardt	50	1	logsig	purelin
4	Levenberg–Marquardt	20/30	2	logsig	logsig
5	Levenberg–Marquardt	20/30	2	logsig	purelin
6	Levenberg–Marquardt	50	1	tansig	tansig
7	Levenberg–Marquardt	50	1	tansig	purelin
8	Gradient descent	50	1	logsig	logsig
9	Gradient descent	70	1	logsig	logsig
10	Gradient descent	20/30	2	logsig	logsig
11	Gradient descent	20/30	2	logsig	purelin
12	Gradient descent	50	1	tansig	tansig
13	Gradient descent	20/30	2	tansig	tansig

.

The performance of the ANN is evaluated using Mean Squared Error (MSE) for training and testing data through the following equation:

$$MSE=\frac{1}{N}{\sum }_{i=1}^N(F_i-y_i{)}^2$$

(1)

where N is the number of data samples, F_i represents measured values, and y_i represents predicted values.

To assess the prediction accuracy of ANN models, an additional statistical metric, absolute error, was applied, which quantifies the variance between the predicted and measured values for the X, Y, and Z coordinates of anatomical points. The absolute error holds significant importance, with orthodontists and anatomists recommending that it remain under 2 mm in the specified X, Y, and Z directions. The model’s performance is detailed in

Table 2. ANN performance.

ANN	Number of Training Epochs	Mean Squared Error		Mean Value of Absolute Error (mm)
		Training Data Set	Test Data Set	X	Y	Z
Model 1	1502	0.045	0.002	0.239	0.771	0.224
Model 2	749	0.053	0.059	0.360	0.931	0.341
Model 3	594	0.254	0.307	1.461	3.184	1.915
Model 4	980	0.070	2.212	1.161	1.066	0.490
Model 5	437	0.655	3.305	3.306	11.096	8.532
Model 6	1049	0.062	0.214	1.613	2.149	1.458
Model 7	795	0.062	0.177	1.566	2.178	1.446
Model 8	7035	0.054	0.098	0.555	0.726	0.555
Model 9	46,892	0.048	0.077	0.329	0.586	0.492
Model 10	50,000	0.554	0.077	1.258	4.907	1.867
Model 11	37,730	0.570	0.077	2.856	4.565	2.561
Model 12	3034	0.062	0.077	1.583	2.158	1.465
Modlel 13	2786	0.062	0.077	1.628	2.139	1.497

.

The ANN model with the best performance is presented in Table 2 as Model 1, trained using the Levenberg–Marquardt algorithm. The analyses of the results indicated that the transfer functions in the hidden and output layers denote one of the most influential factors in terms of the ANN models’ prediction performance. This analysis indicated the performance of the ANN models in handling nonlinear relationships between the input and output data. According to the analysis, the sigmoid transfer functions yielded the best performance for the problem considered in this study. Also, the analyses showed that the optimal ANN model, regarding the desired error, had 50 hidden neurons in the hidden layer, and adding more neurons to the hidden layer had a negative effect on the ANN model’s prediction performances. The results presented in Table 2 reveal that Models 4, 5, 10, 11, and 13, which all had two hidden layers, exhibited a worse performance compared to the top-performing model, that is, Model 1. Notably, the MSE values on the test dataset were substantially elevated, which was particularly obvious for Model 5, whose MSE value was 3.305, thereby directly impinging upon the predictive accuracy of the model. Optimal prediction performance was achieved for the learning coefficient and momentum values of 0.045 and 0.625, respectively. Through an iterative application of the trial-and-error method, the number of training epochs required for obtaining an ANN model with good robustness and generalization ability was determined.

3. Reconstruction of a Geometric Bone Model of a Patient with Mandibular Prognathism Using a Parametric Model

For the specific case under consideration, it was imperative to form a human mandible parametric model adapted to the individual anatomy of the patient with mandibular prognathism. The development of a personalized model necessitated the creation of a mathematical framework tailored to the morphometric parameters obtained from medical imaging.

3.1. Input Data

The patient with mandibular prognathism, an 18-year-old male, underwent scanning using both an X-ray scanner and the Sirona SL Orthophos 3D device (Dentsply Sirona, Charlotte, NC, USA). To ensure the accurate scaling of measured values, X-ray scanning was carried out using a reference standard in the form of an etalon. The combined use of X-ray and Sirona SL Orthophos 3D device was necessary due to the Sirona SL’s Field of View size being insufficient for generating a whole 3D model of the mandible. The scanning FOV for Sirona SL was 11 × 10 cm, resulting in the absence of both condylar processes in the 3D medical image of the patient.

The input data for this analysis consisted of the measured values of morphometric parameters obtained from the 2D X-ray image and the 3D model of the patient. Due to the lack of both condylar processes, eight morphometric parameters (bigonial width, maximum ramus height, height of the condyle, length of the mandibular body, minimum ramus breadth, Gnathion–condylar distance, height of the mandibular body, and Gnathion–interdental distance) are used and presented in Figure 1. The measured morphometric parameters from the 2D image (length of the mandibular body, height of the mandibular body, height of the condyle, minimum ramus breadth, maximum ramus height, Gnathion–condylar distance, and Gnathion–interdental distance) were scaled according to the etalon size. The morphometric parameter bigonial width was measured from a 3D model of the patient using CATIA V5 R21, 3D CAD software. The measurements of the eight morphometric parameters are presented in

Table 3. Measured values of morphometric parameters.

Sample	Gn-IdD	Go-GoD	LMB	Min RB	HCon	Gn-ConD	Max RH	HMB
1	27.00	97.40	93.90	27.00	20.50	143.00	66.00	13.10

. As a consequence of the excessive development of the mandible in the anterior direction, abnormal anatomical structures occur within the occlusion and the values of the morphometric parameters regarding the length of the mandibular body and Gnathion–condylar distance are high.

3.2. The Reconstruction of Surface Model

To determine the values of X, Y, and Z anatomical points’ coordinates on the sample that was not included in the initial training dataset, it is necessary to form mathematical equations on based on the selected network type, the activation function, the number of hidden layers in the network, and the number of neurons in the hidden layers. The network type determines how the output is generated from a given input. By applying Feedforward Neural Networks, the input signal flows through the network with eth appropriate parameters and the final output is generated on the last (output) layer. The activation function, integral to the formulation of the mathematical equation, dictates the specific function applied to input signal X, considering relevant weights and biases. The number of hidden layers influences the elements in the ultimate mesh equation, whereas the number of neurons in the hidden layers directly influences the dimensions of the matrices representing the input, complete with pertinent weight factors and biases. Derived from the architecture of the best-performance ANN Model 1, the input–output relationship can be defined as follows:

$$Y=[\frac{1}{1+e^{-(\mathit{X}·W_{ji}+b_j)}}]·W_{kj}+b_{ok}$$

(2)

where X represents the input vector, W_ji,b_j represents the coefficient in the hidden layer, W_kj, b_ok represents the coefficient in the output, and Y represents the output vector.

By applying a mathematical relation to input values not included in the initial training set, the output value was derived by incorporating the relevant weights and biases into the mathematical relations (3).

Y = b₂ + W₂ · logsig(b₁ + W₁ · X)

(3)

where X represents the input vector, Y represents the output vector, W₁ represents the weight factor in the hidden layer, W₂ represents the weight factor in the output layer, b₁ represents the biases in the hidden layer, and b₂ represents the biases in the output layer.

Using mathematical equations, a point cloud adapted to a specific patient based on the values of parameters measured from the 2D X-ray image and 3D model was created. The surface was formed using the 3D CAD software CATIA.

A crucial point to emphasize in this research is that it was not necessary to create a complete surface model of a patient with congenital malocclusion. For this reason, in collaboration with the maxillofacial surgeon engaged in this research, an appropriate anatomical section was defined, which can be utilized to generate a personalized surface model of a patient. The colored area of the anatomical section includes most of the anatomical region of the body of the mandible up to the last teeth (Figure 2). The tooth region was excluded from the analysis due to the differences in topology and number of teeth from patient to patient.

4. Results

To create a parametric model of the specific human bone, an input set of bone samples was analyzed, the parameters and point cloud model were defined, and Artificial Neural Networks were applied. The trial–error method was employed to determine the optimal values of ANN training and architectural parameters. Through the realization and testing of several neural networks of different structures, the optimal values of the ANN parameters were determined. Specified values were set for the learning coefficient (0.1), momentum (0.2), and the maximum number of epochs during training (1502), which yielded the best prediction performance for the backpropagation algorithm. Optimal values of the architecture parameters were obtained, including one hidden layer, fifty neurons in the hidden layer, and sigmoid transfer functions in both the hidden and output layers. The output of the applied process consists of a set of mathematical functions that define the correlation between the bone morphometric parameters and coordinates of anatomical points. Based on the structure of the ANN Model 1, the input–output relationship is defined. By applying a mathematical relation to the input values not included in the initial training set (measured values of eight morphometric parameters presented in Table 3), the value of the output signals (values of the points’ coordinates) was obtained by entering the appropriate weights and biases in the mathematical relations. Utilizing the obtained predictive values of the points’ coordinates, a cloud of points is formed, thus creating a surface model of the mandible in the 3D CAD software CATIA.

The results were verified by analyzing the deviation in the coordinates of the anatomical points. The results of the maximum absolute error for the X, Y, and Z coordinates (maximum deviation between measured and predicted values) are presented in

Table 4. Maximum absolute error between measured and predicted values.

Maximum Absolute Error Values (mm)
Model	X	Y	Z
1	2.25	1.58	2.48

.

The results from Table 3 indicate an increase in the absolute error values for all three coordinates. The obtained values are expected because, in the implementation of the new ANN model, eight input parameters were used, obtained from medical images of patients without mandible bone illness, fracture, or some other trauma. The optimal reference for the input data set is provided by data obtained from samples of human mandible patients without congenital and acquired anomalies.

The model analysis involved comparing the initial polygonal model of the mandible (acquired from the Sirona SL Orthophos 3D device, Dentsply Sirona, Charlotte, NC, USA) with the resultant surface model and measuring the deviation. The deviation values, referenced in relation to the input sample’s polygonal model, indicate that the created surface model possesses satisfactory overall accuracy. The overall accuracy of the model is around −0.608–0.841 mm. The maximal negative deviation was −1.82 mm and the maximal positive deviation was 2.52 mm (Figure 3), expressed in the area around the mandibular chin. The majority (95.05%) of the model surface displayed deviations within the range of −1.00 to 1.00 mm. It is noteworthy that the initial surface model of the human mandible, utilizing an artificial neural network with a strictly defined set of morphometric parameters in predictive functions, displayed maximum deviations of 0.53 mm [17]. The elevated deviation value of 2.53 mm can be attributed to the high values of the morphometric parameters integrated into the ANN model. To reduce deviations, it is essential to add additional points based on relevant medical literature information regarding inadequate areas in terms of bone shape. In further research, it will be necessary to optimize and correct the created surface model.

The maxillofacial surgeon involved in this study affirmed that these deviations are deemed acceptable. According to the requirements outlined by the surgeon, the Region of Interest (ROI) is positioned in front of the seventh tooth on both the left and the right side of the mandibular body, which serves as the contact surface between the bone and fixation plate. In the designated region for plate placement, the maximum negative deviation measured −1.84 mm, while the maximum positive deviation reached 1.1 mm (Figure 4). Additionally, 57.42% of the model surface exhibited deviations ranging from −1.00 to 1.00 mm. To improve plate geometry and position based on the surgeon’s recommendation, it is crucial to add additional points to the existing spline curves in the areas of interest (e.g., the mandibular body area).

ROIs play a pivotal role in the preoperative planning of surgical procedures and manufacturing customized plate implants and fixators for patients. Defining a Region of Interest allows practitioners to concentrate their efforts on specific areas of interest rather than analyzing the entire surface. In this case, ROI is defined as the contact surface between the bone and fixation plate. This defined surface serves the purpose of the pre-surgical bending of reconstructive plates, allowing for their shape to be adapted to the contours of the bone in the affected area. This approach enhances the provision of personalized healthcare to the patient [15].

In this example, the ANN model was tested on a specific case. The behavior of the ANN model was assessed based on the results of the analysis. As expected, the prediction accuracy of the model was lower, due to the inclusion of high values of morphometric parameters (Gn-ConD and LMB parameters) in the ANN model. In order to ensure more precise results are obtained in terms of the quality of the created model, the values of the morphometric parameters must be within certain limits to ensure an adequate anatomical section in patients with specific deformities.

5. Conclusions

A comprehensive tool was developed to predict 3D models of the human mandible, aiming to advance patient-specific bone modeling. This advancement was made possible by leveraging the correlation between the coordinates of anatomical points (defined using constitutive geometrical entities or other important anatomical landmarks in the polygonal model in relation to individual human bone) and specific morphometric parameters of the human mandible used as the input to the ANN model. The advantages of this parametric approach are manifold: it allows for the generation of a 3D geometrical model of a specific patient, without relying on costly and sometimes unavailable 3D imaging techniques (such as Computed Tomography or Magnetic Resonance Imaging); it can facilitate the forecasting of bone morphology and shape for an individual patient with morphometric parameters that are lower than a predetermined number involved in predictive functions; it is capable of predicting mandible geometry by estimating the missing components [17].

Our study centered on utilizing a 3D parametric model of the human mandible to reconstruct the geometric model of a particular patient with mandibular prognathism. The results obtained here were promising: the resulting surface model has an overall accuracy of around −0.608 to 0.841 mm, where the maximal negative deviation was −1.82 mm and the maximal positive deviation was 2.52 mm in relation to the input sample. The initial assertion regarding the geometric accuracy and anatomical correctness of the surface model can be deemed reasonably satisfactory for the prototype model. The outcome yields a 3D model of somewhat diminished accuracy, but remains a personalized representation of the human mandible. Moreover, this model holds great potential for pre-operative planning, treating skeletal disorders, and conducting clinical research focused on tailoring treatments to each patient’s specific needs, the production of personalized plate implants, or educational purposes.