The Lomax-Exponentiated Odds Ratio–G Distribution and Its Applications
Abstract
:1. Introduction
2. Lomax-Exponentiated Odds Ratio–G Family of Distributions
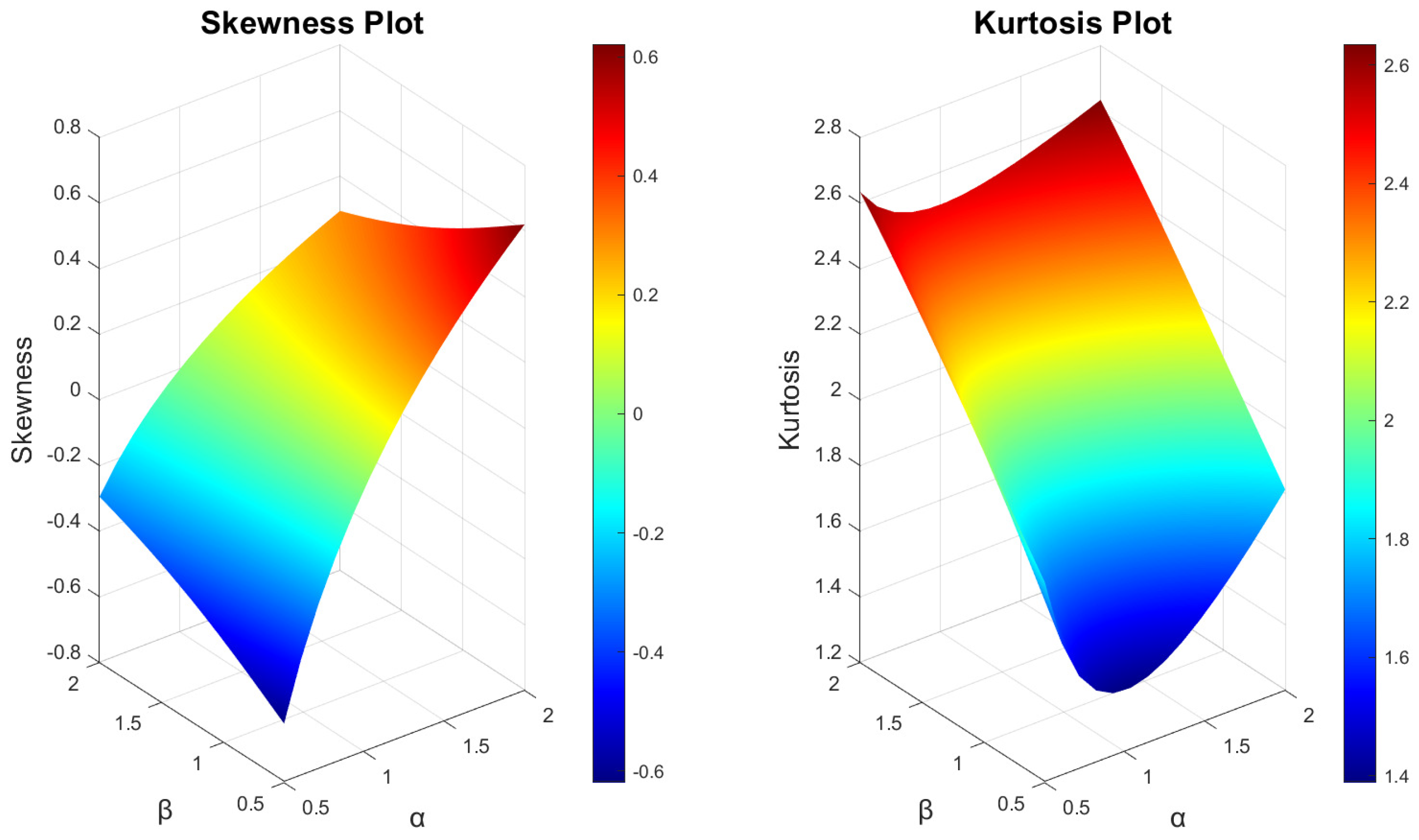
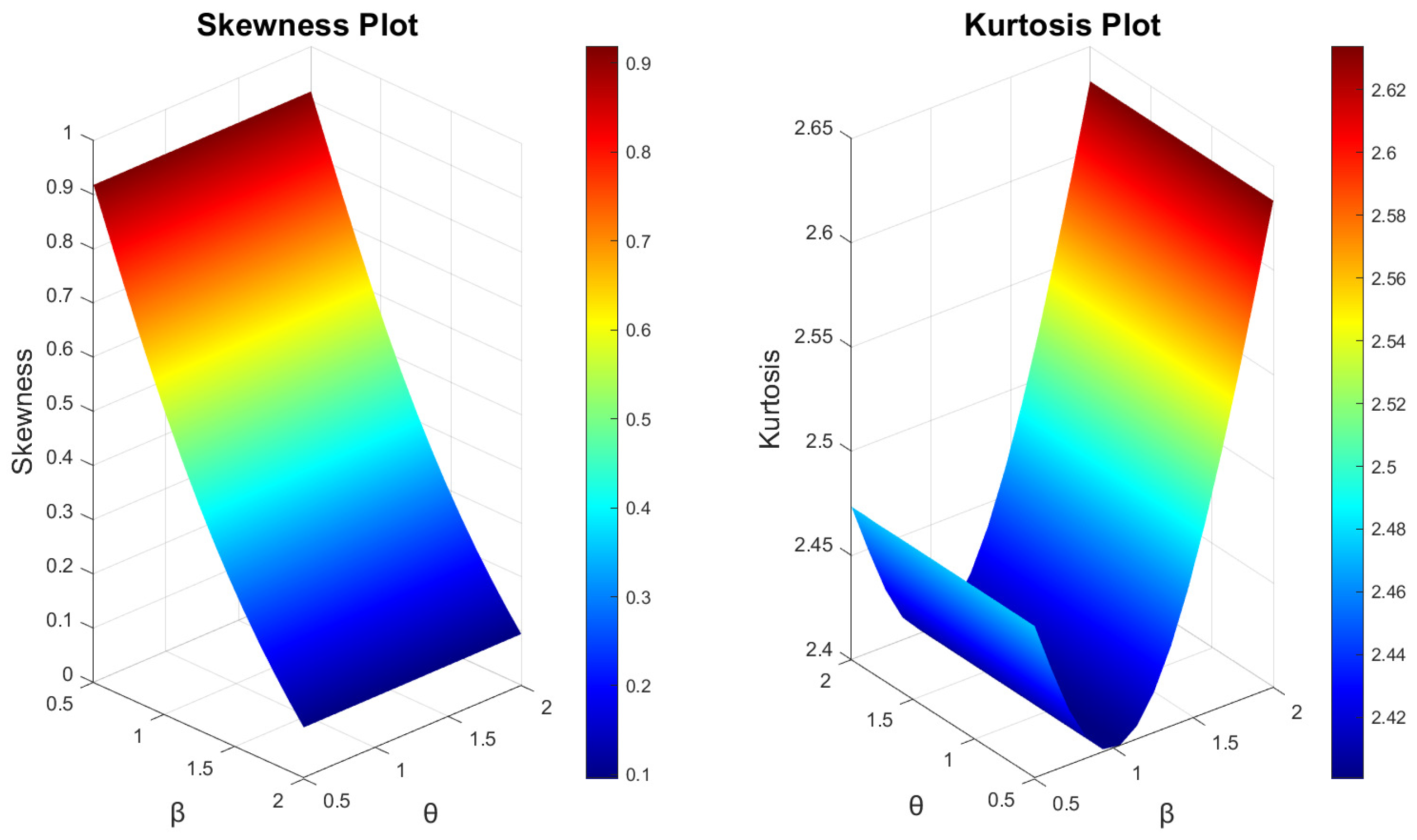
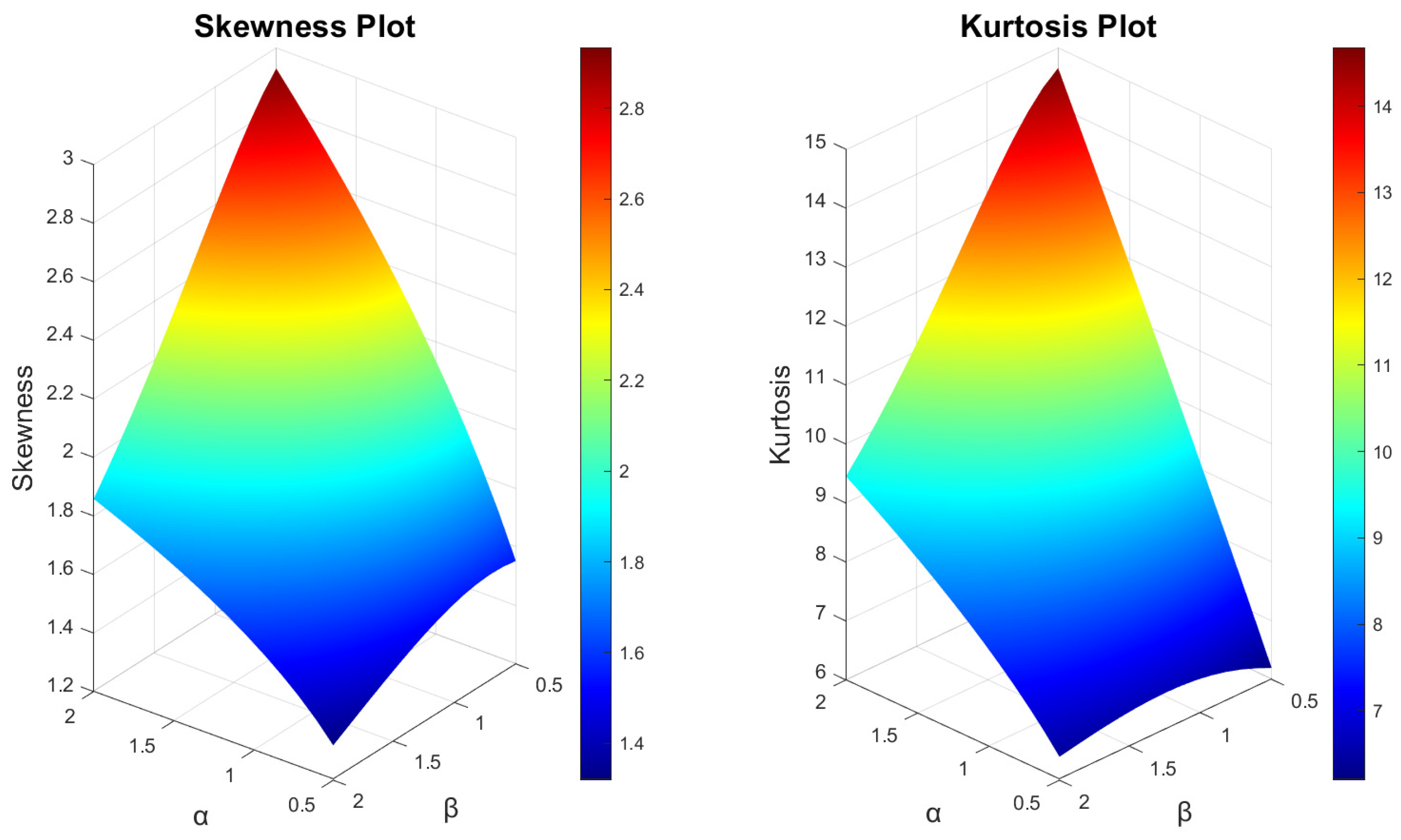
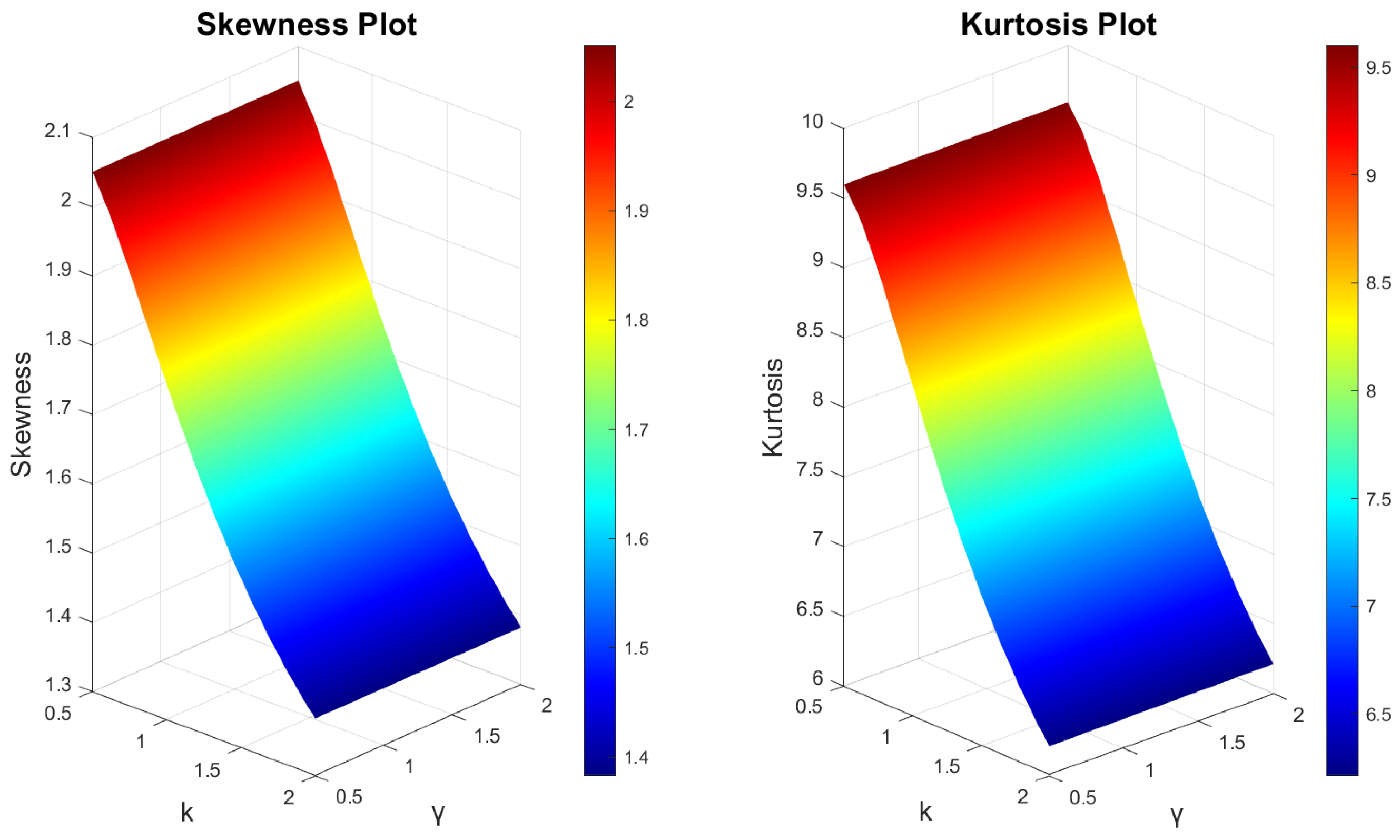
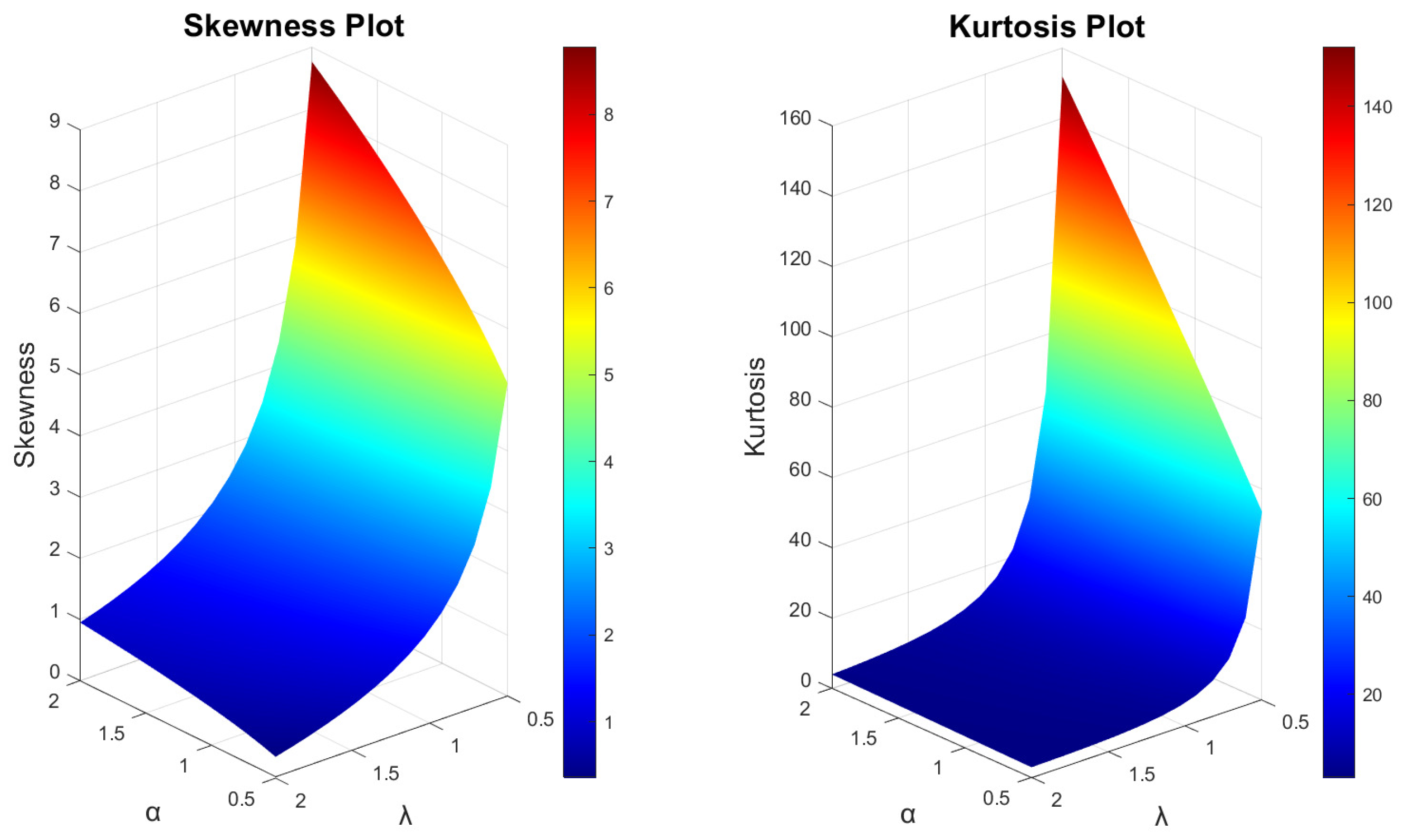
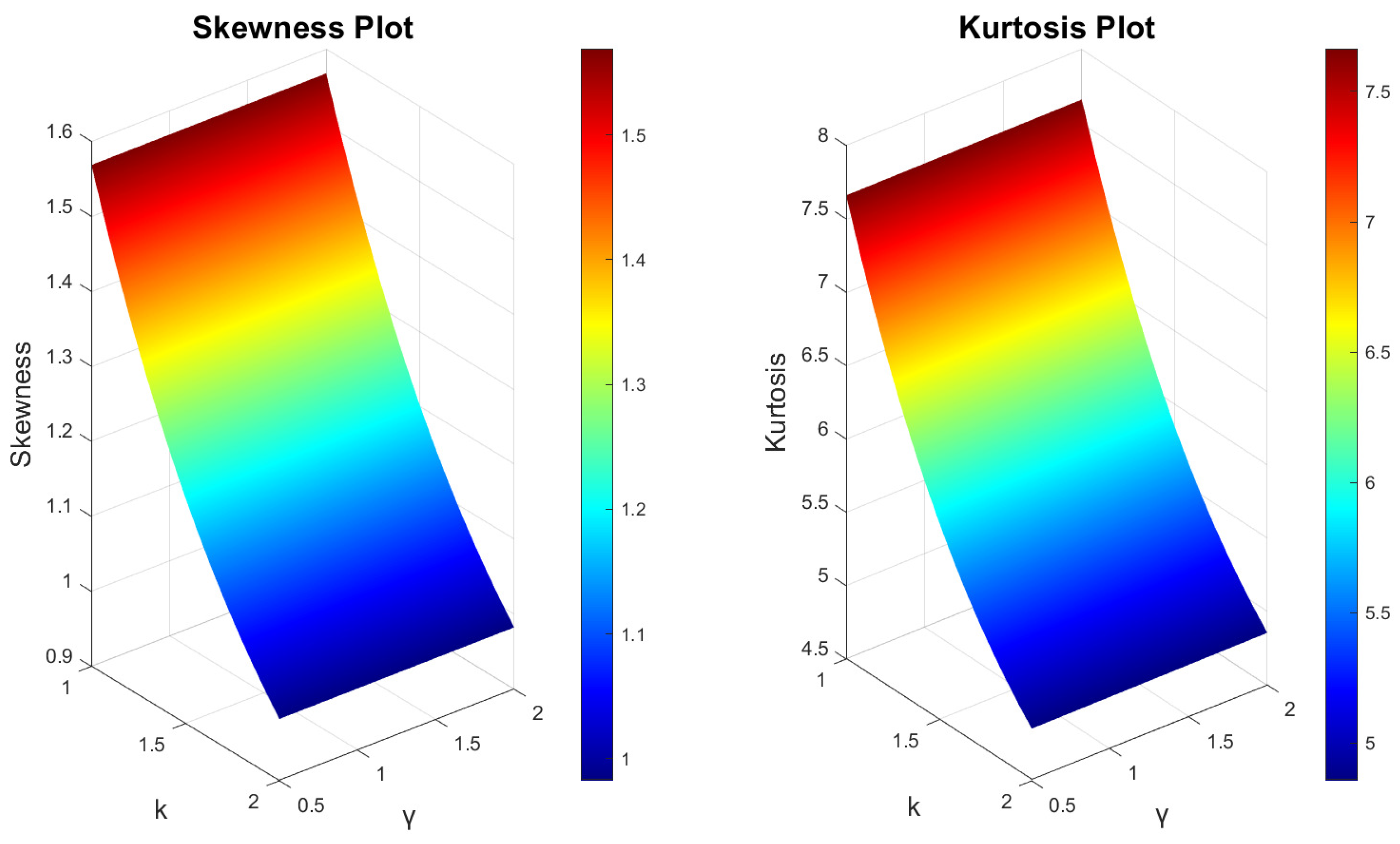
3. Mathematical and Statistical Properties
3.1. Expansion of the Probability Density Function
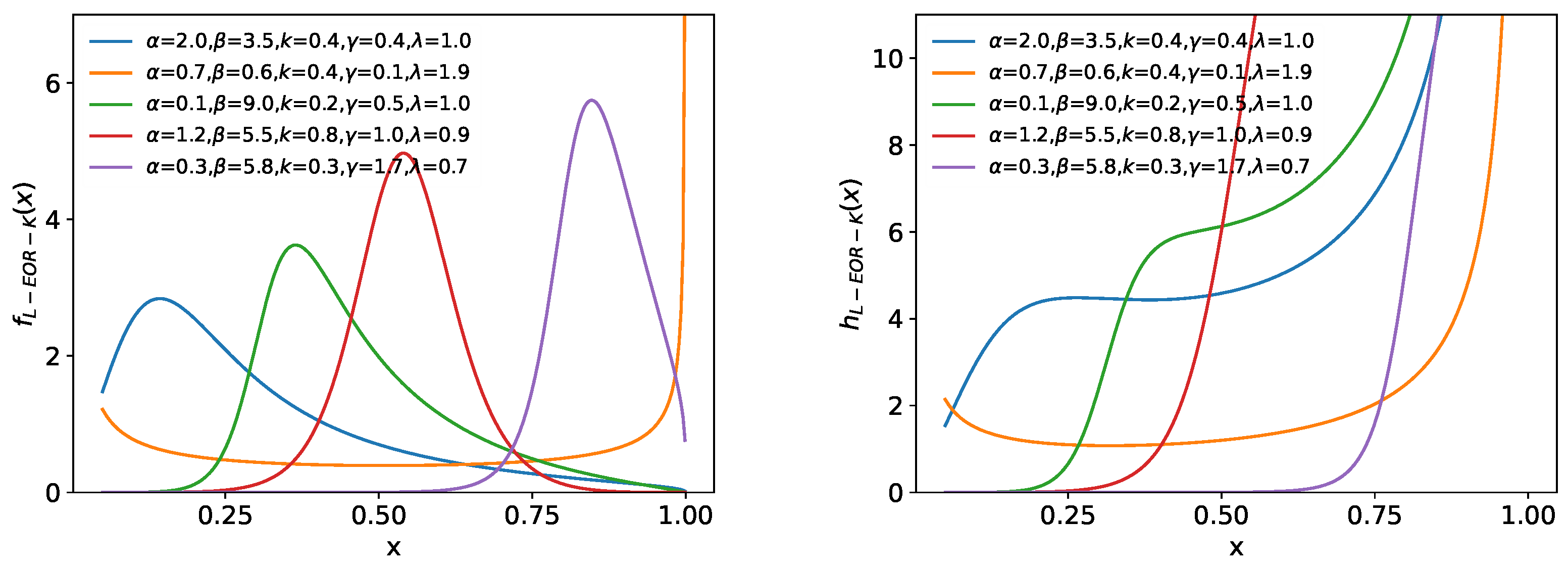
3.2. Hazard Rate
3.3. Quantile Function
3.4. Moments, Incomplete Moments and Generating Functions
3.4.1. Raw Moments
3.4.2. Central Moments
3.4.3. Incomplete Moments
3.4.4. Moment-Generating Functions
3.5. Rényi Entropy and Order Statistics
3.6. Probability-Weighted Moments
4. Special Cases of the L-EOR–G Distribution
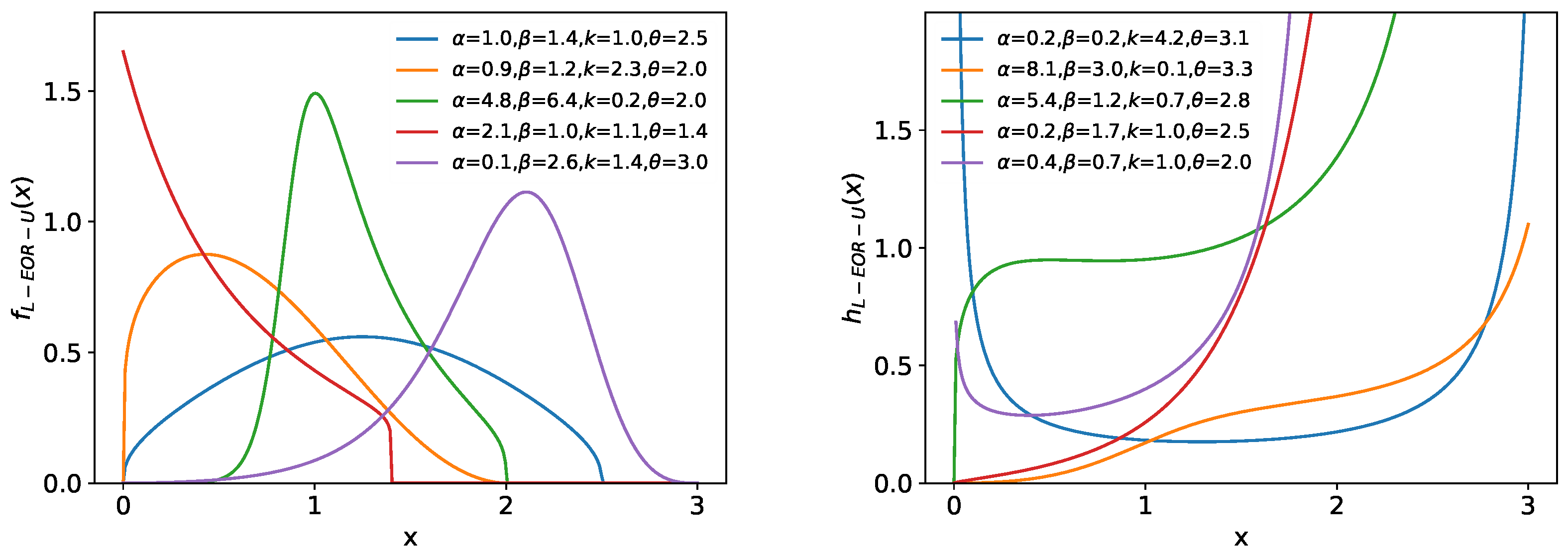
4.1. Lomax-Exponentiated Odds Ratio–Uniform Distribution
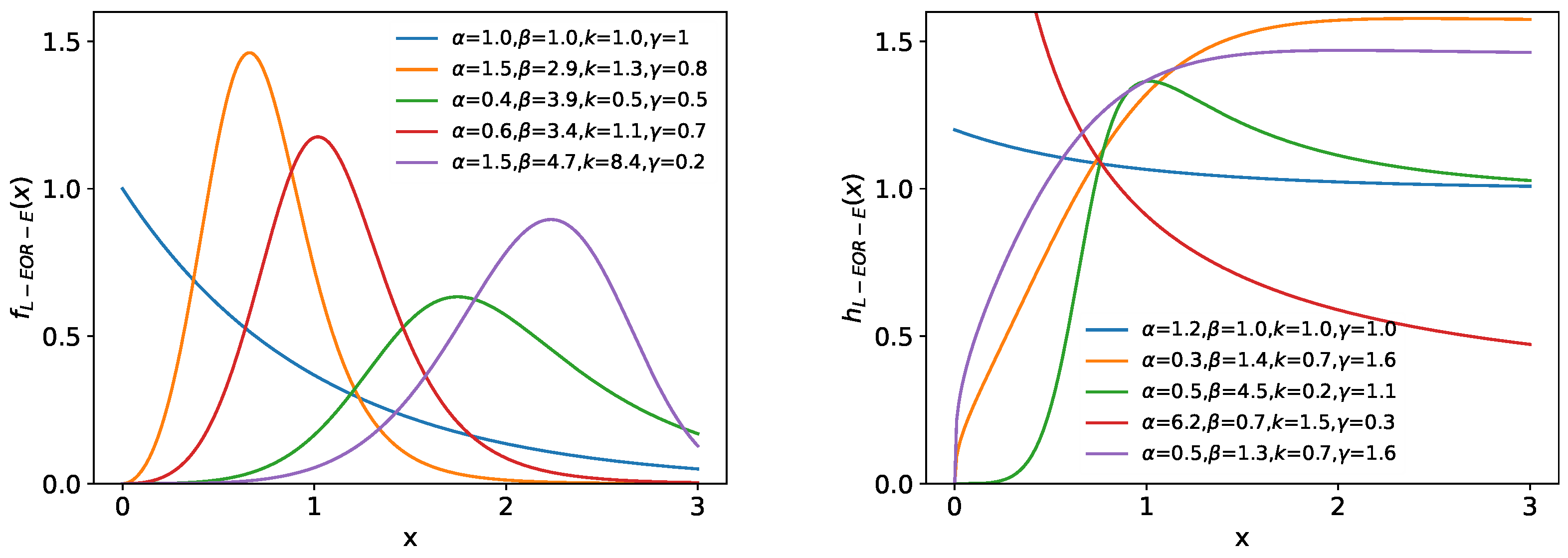
4.2. Lomax-Exponentiated Odds Ratio–Exponential Distribution
4.3. Lomax-Exponentiated Odds Ratio–Weibull Distribution
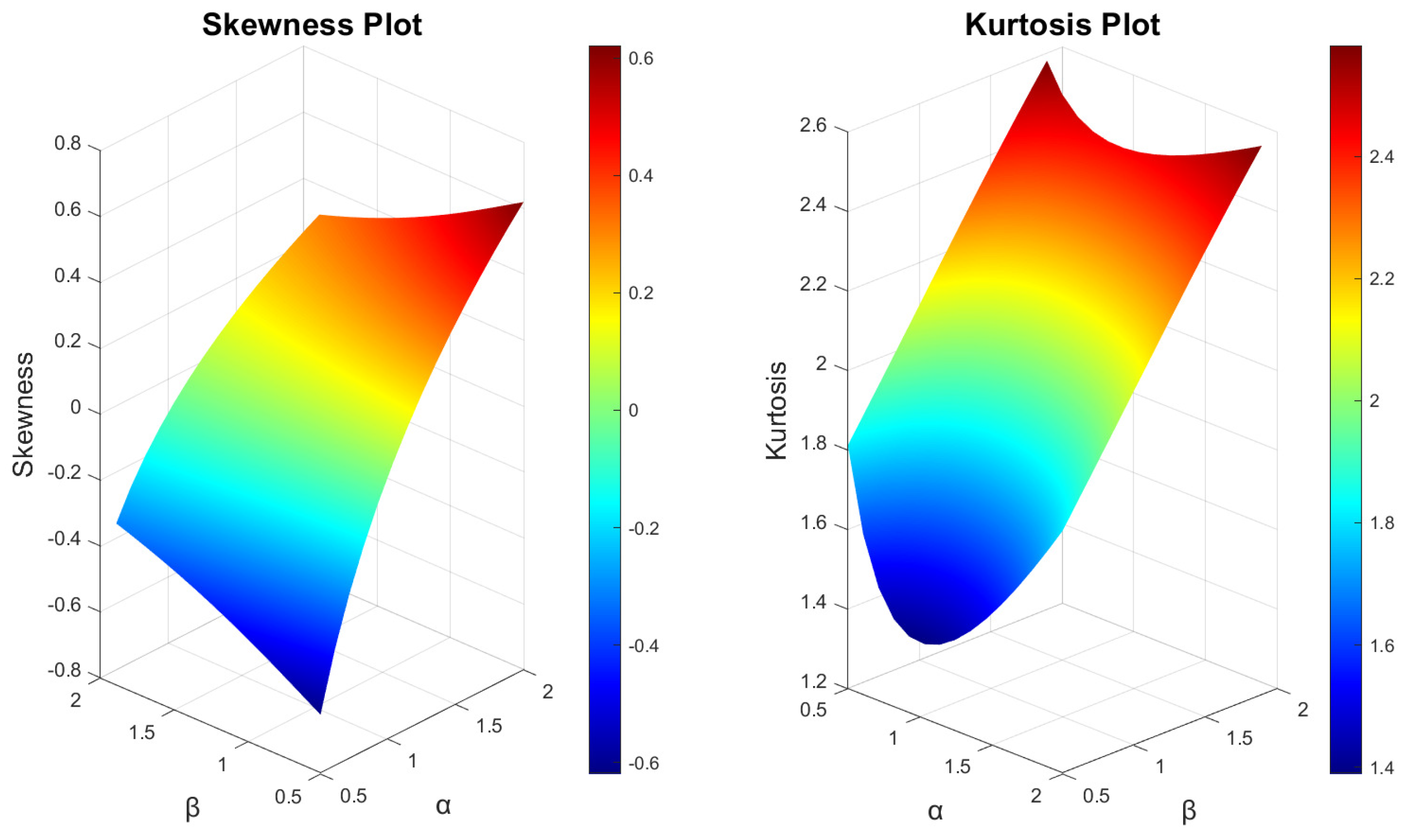
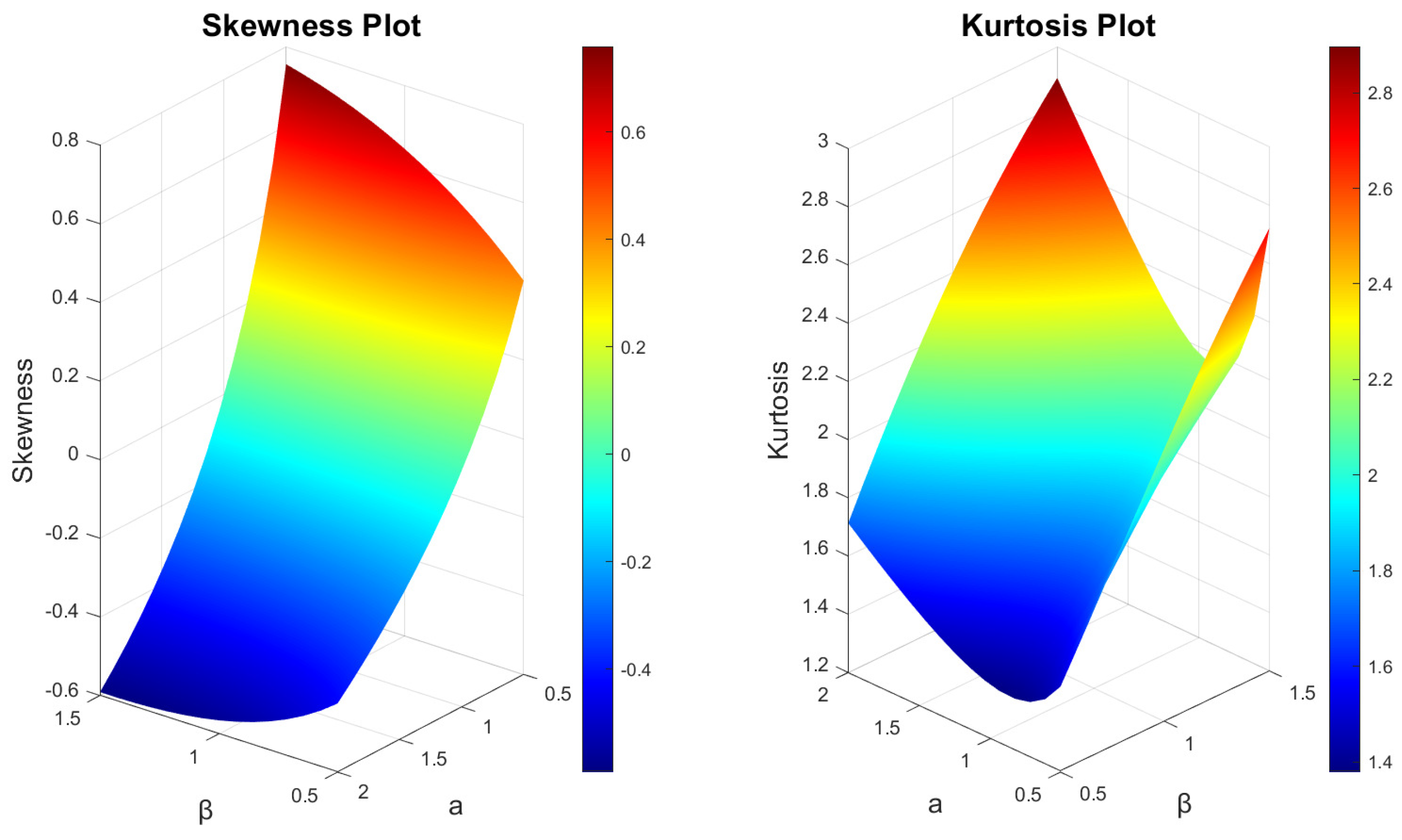
4.4. Lomax-Exponentiated Odds Ratio–Kumaraswamy Distribution
5. Methods of Estimation
5.1. Maximum Likelihood Estimation
5.2. Least Squares and Weighted Least Squares Estimation
5.3. Maximum Product Spacing Approach of Estimation
5.4. Cramér–von Mises Approach of Estimation
5.5. Anderson–Darling Approach of Estimation
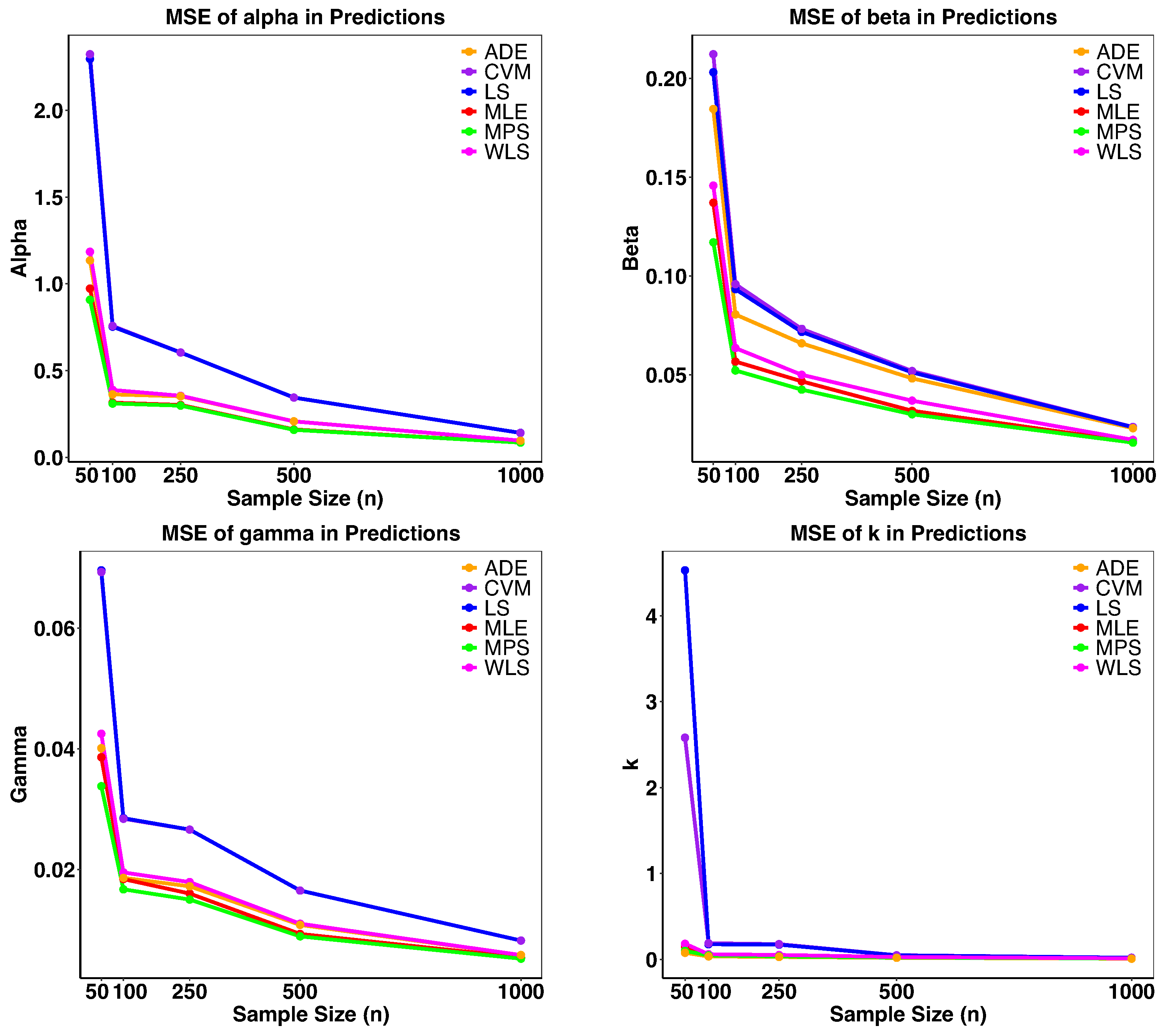
5.6. Simulation Study
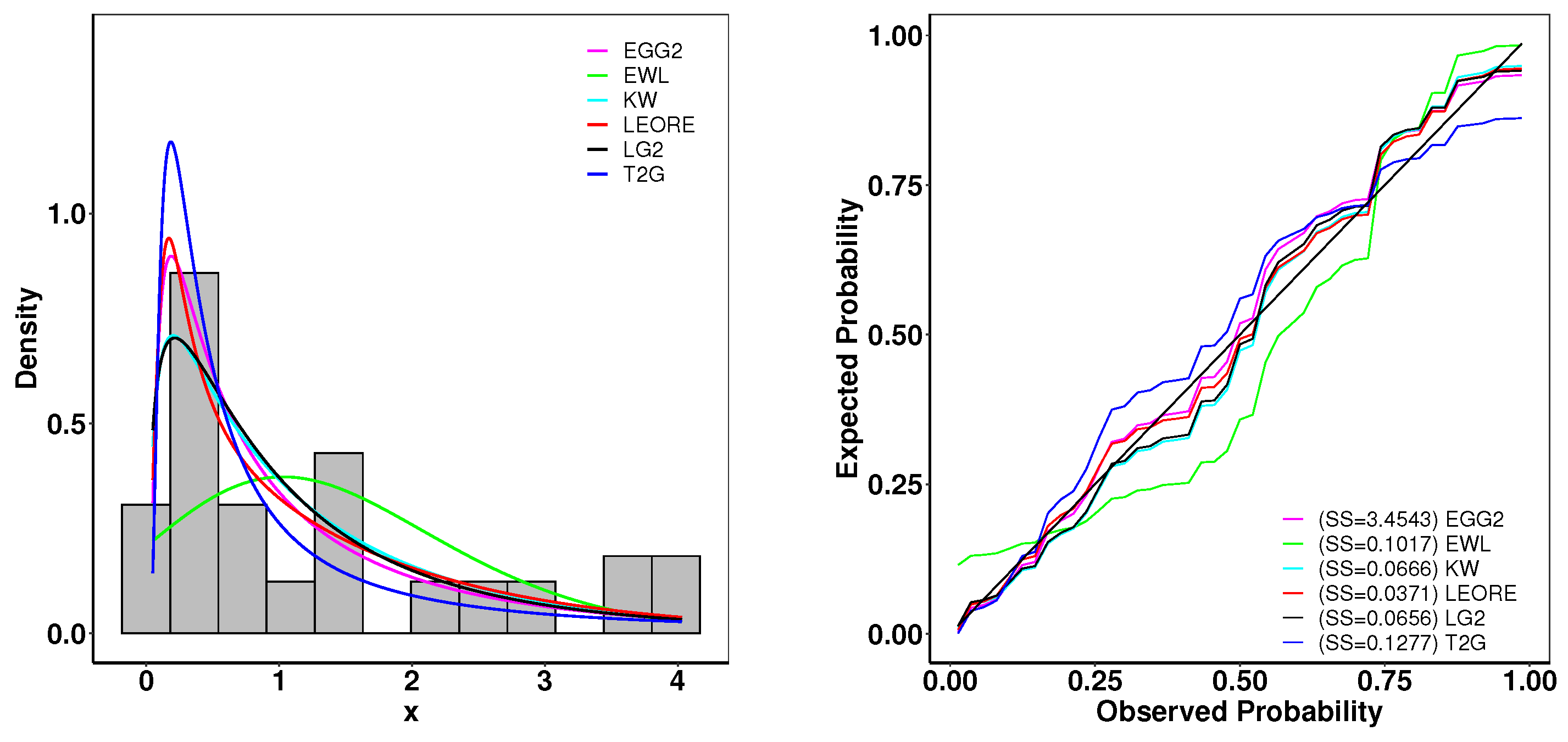
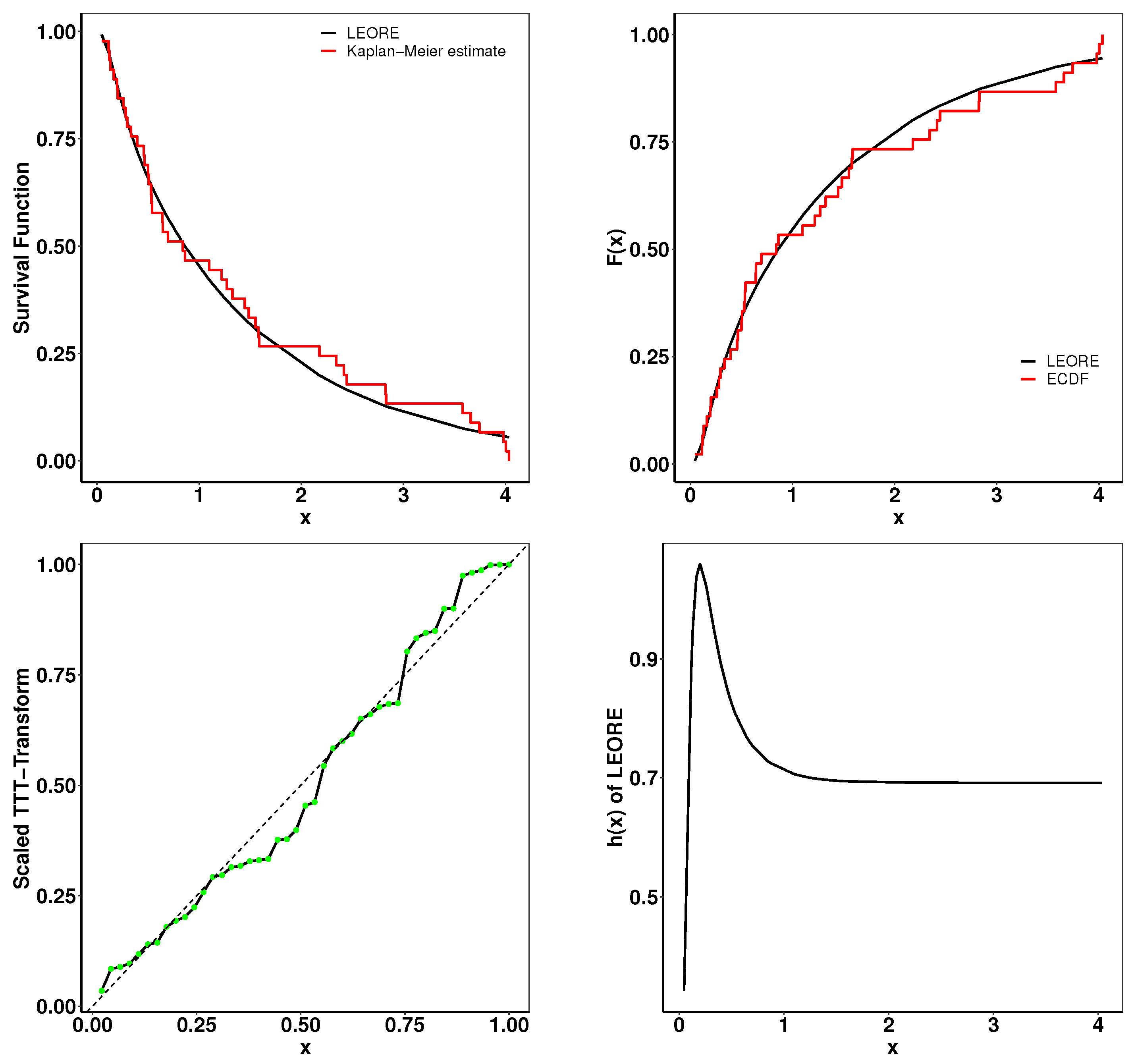
6. Applications
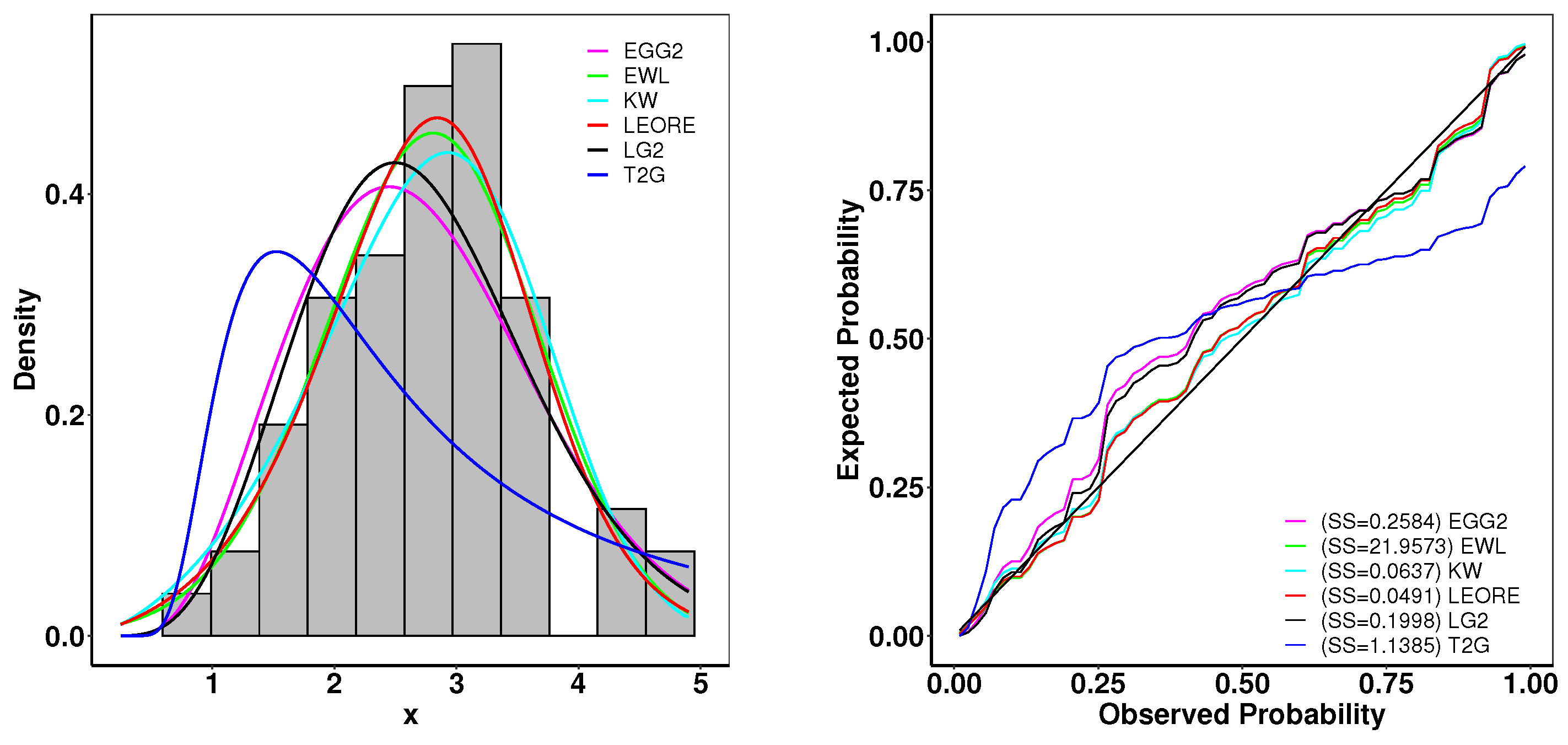
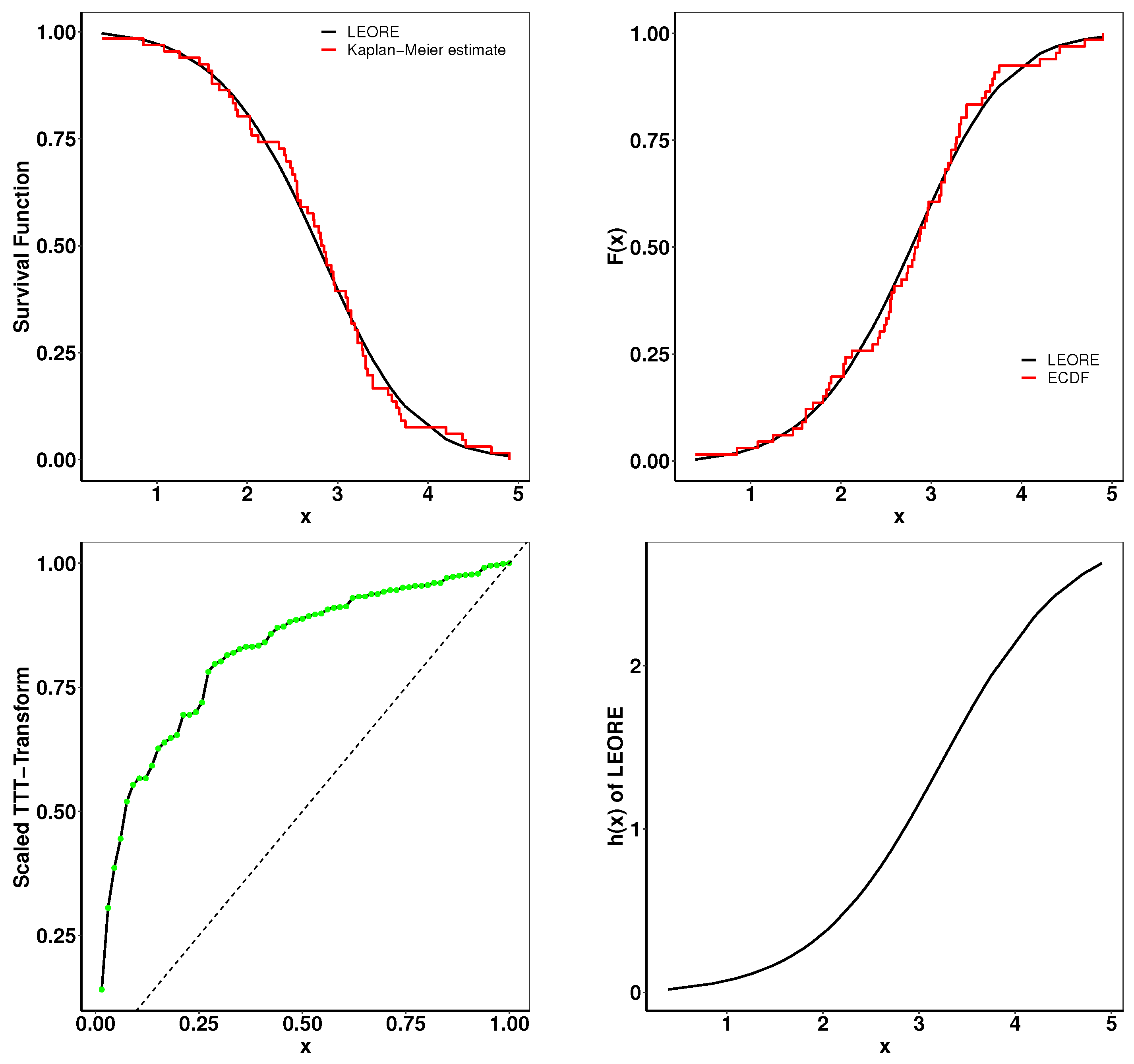
6.1. Analysis of Carbon Fiber Strength Data
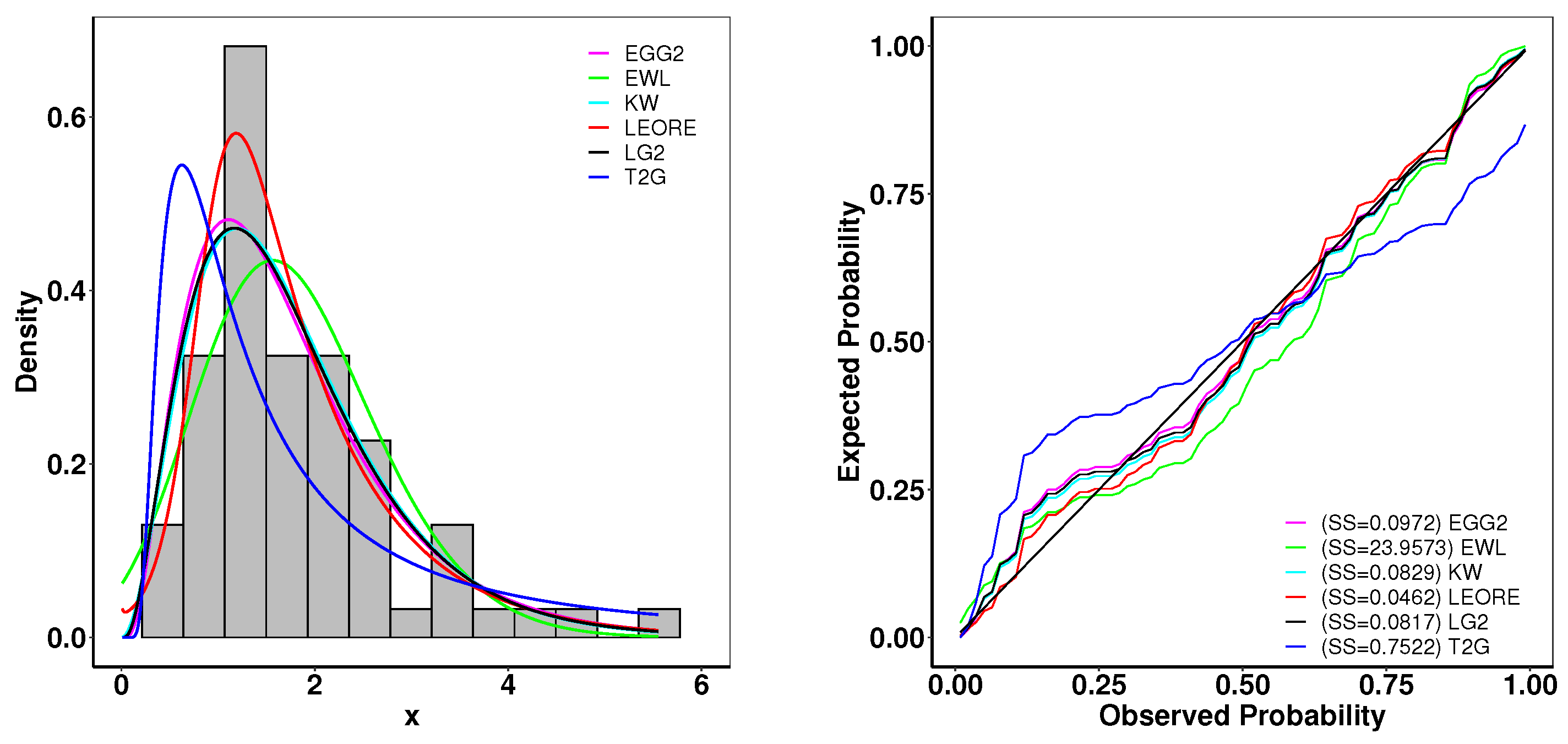
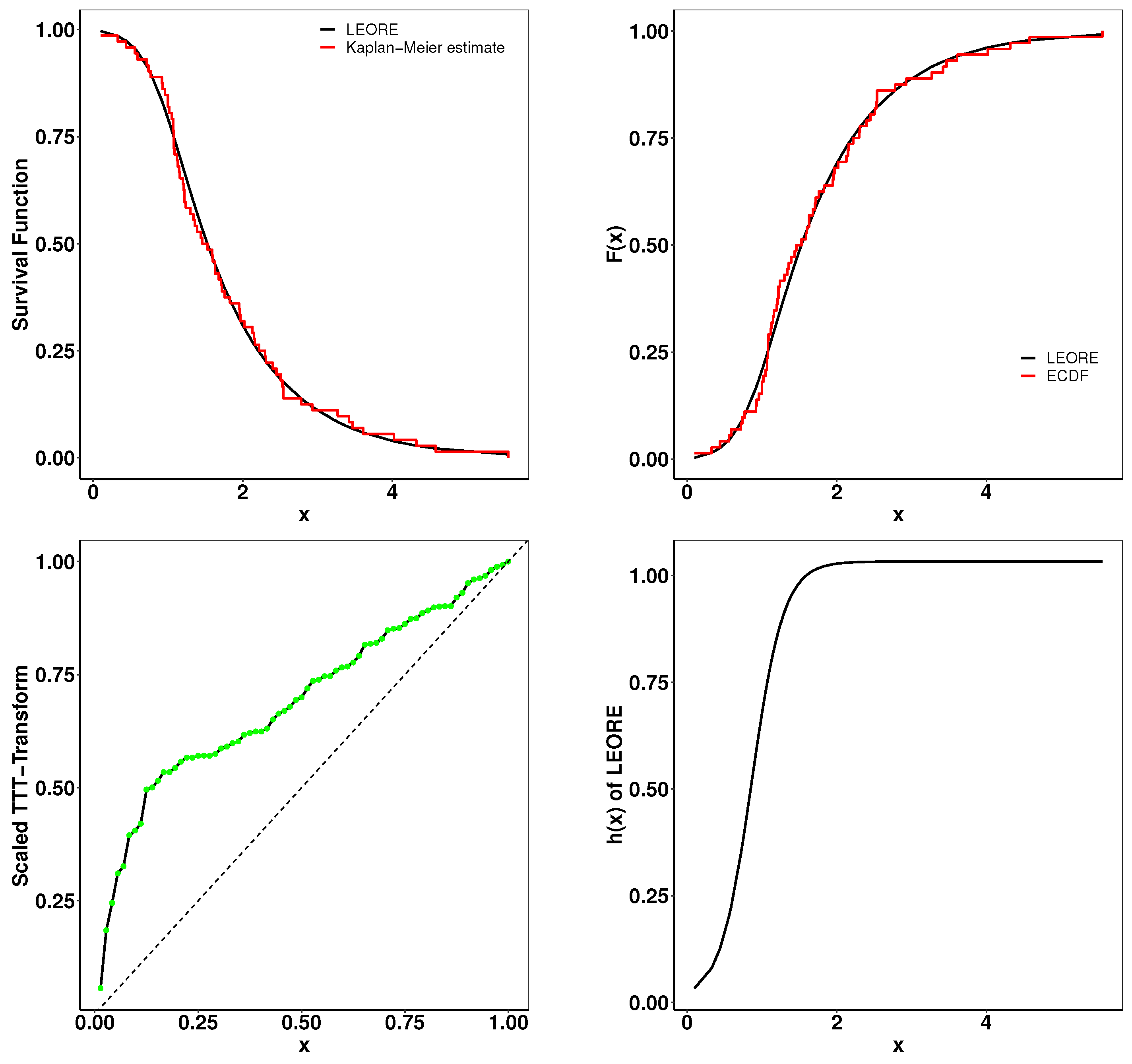
6.2. Survival Analysis of Guinea Pigs
6.3. Analysis of Chemotherapy Treatment Data
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| L-EOR–G | Lomax-exponentiated odds ratio–G |
| cdf | cumulative distribution function |
| probability density function | |
| hrf | hazard rate function |
| MLE | maximum likelihood estimate |
| MPS | maximum product spacing estimate |
| LS | least square estimates |
| WLS | weighted least square estimate |
| CVM | Cramér–von Mises estimate |
| AD | Anderson–Darling estimate |
| MSE | mean squared error |
| L-EOR–U | Lomax-exponentiated odds ratio–uniform |
| L-EOR–W | Lomax-exponentiated odds ratio–Weibull |
| L-EOR–E | Lomax-exponentiated odds ratio–exponential |
| L-EOR–K | Lomax-exponentiated odds ratio–Kumaraswamy |
| T2G | type-2 Gumbel |
| CAIC | consistent Akaike information criterion |
| BIC | Bayesian information criterion |
| HQIC | Hannan–Quinn Criterion |
| Cramér–von Mises statistic | |
| Anderson–Darling statistic | |
| K-S | Kolmogorov–Smirnov statistic |
| TCDF | theoretical cumulative distribution function |
| ECDF | empirical cumulative distribution function |
| TTT | total time on test |
| K-M | Kaplan–Meier |
References
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar] [CrossRef]
- Pu, S.; Oluyede, B.O.; Qiu, Y.; Linder, D. A Generalized Class of Exponentiated Modified Weibull Distribution with Applications. J. Data Sci. 2016, 14, 585–613. [Google Scholar] [CrossRef]
- Oluyede, B.; Pu, S.; Makubate, B.; Qiu, Y. The gamma-Weibull-G Family of distributions with applications. Austrian J. Stat. 2018, 47, 45–76. [Google Scholar] [CrossRef]
- Ishaq, A.I.; Suleiman, A.A.; Usman, A.; Daud, H.; Sokkalingam, R. Transformed Log-Burr III Distribution: Structural Features and Application to Milk Production. Eng. Proc. 2023, 56, 322. [Google Scholar] [CrossRef]
- Pu, S.; Moakofi, T.; Oluyede, B. The Ristić–Balakrishnan–Topp–Leone–Gompertz-G Family of Distributions with Applications. J. Stat. Theory Appl. 2023, 22, 116–150. [Google Scholar] [CrossRef]
- Reyes, J.; Iriarte, Y.A. A New Family of Modified Slash Distributions with Applications. Mathematics 2023, 11, 3018. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, X.; Zhou, H. The flexible gumbel distribution: A new model for inference about the mode. Stats 2024, 7, 317–332. [Google Scholar] [CrossRef]
- David, I.; Mathew, S.; Falgore, J. New Sine Inverted Exponential Distribution: Properties, Simulation and Application. Eur. J. Stat. 2024, 4, 5. [Google Scholar] [CrossRef]
- EL-Damrawy, H. The Beta-Truncated Lomax Distribution with Communications Data. Delta J. Sci. 2024, 48, 135–144. [Google Scholar] [CrossRef]
- Sarhan, A.M.; Apaloo, J.; Kundu, D. A new bivariate lifetime distribution: Properties, estimations and its extension. Commun. Stat.-Simul. Comput. 2024, 53, 879–896. [Google Scholar] [CrossRef]
- Muhi, E.F. A New Family of Power Function-Lindley Distribution. Adv. Nonlinear Var. Inequal. 2024, 27, 325–337. [Google Scholar]
- Lone, M.A.; Dar, I.H.; Jan, T. A New Family of Generalized Distributions with an Application to Weibull Distribution. Thail. Stat. 2024, 22, 1–16. [Google Scholar]
- Lomax, K.S. Business failures: Another example of the analysis of failure data. J. Am. Stat. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. The odds ratio. BMJ 2000, 320, 1468. [Google Scholar] [CrossRef] [PubMed]
- VanderWeele, T.J.; Vansteelandt, S. Odds ratios for mediation analysis for a dichotomous outcome. Am. J. Epidemiol. 2010, 172, 1339–1348. [Google Scholar] [CrossRef] [PubMed]
- Gosho, M.; Ohigashi, T.; Nagashima, K.; Ito, Y.; Maruo, K. Bias in odds ratios from logistic regression methods with sparse data sets. J. Epidemiol. 2023, 33, 265–275. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xie, Y.; Cohen, A.; Pu, S. Advancing Continuous Distribution Generation: An Exponentiated Odds Ratio Generator Approach. arXiv 2024, arXiv:2402.17294. [Google Scholar]
- Alizadeh, M.; Altun, E.; Afify, A.Z.; Gamze, O. The extended odd Weibull-G family: Properties and applications. Commun. Fac. Sci. Univ. Ank. Ser. A1 Math. Stat. 2018, 68, 161–186. [Google Scholar] [CrossRef]
- Cheng, R.C.H.; Amin, N.A.K. Estimating Parameters in Continuous Univariate Distributions with a Shifted Origin. J. R. Stat. Soc. Ser. B (Methodol.) 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Ogunde, A.; Fayose, S.; Ajayi, B.; Omosigho, D. Extended gumbel type-2 distribution: Properties and applications. J. Appl. Math. 2020, 2020, 2798327. [Google Scholar] [CrossRef]
- MURAT, U.; Gamze, Ö. Exponentiated Weibull-logistic distribution. Bilge Int. J. Sci. Technol. Res. 2020, 4, 55–62. [Google Scholar]
- Adeyemi, A.O.; Adeleke, I.A.; Akarawak, E.E. Lomax gumbel type two distributions with applications to lifetime data. Int. J. Stat. Appl. Math. 2022, 7, 36–45. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Kim, H.c. A Comparison of Reliability Factors of Software Reliability Model Following Lindley and Type-2 Gumbel Lifetime Distribution. Int. Inf. Inst. (Tokyo) Inf. 2018, 21, 1077–1084. [Google Scholar]
- Nichols, M.D.; Padgett, W. A bootstrap control chart for Weibull percentiles. Qual. Reliab. Eng. Int. 2006, 22, 141–151. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D. An extension of the generalized exponential distribution. Stat. Methodol. 2011, 8, 485–496. [Google Scholar] [CrossRef]
- Bekker, A.; Roux, J.J.J.; Mosteit, P.J. A generalization of the compound rayleigh distribution: Using a bayesian method on cancer survival times. Commun. Stat.-Theory Methods 2000, 29, 1419–1433. [Google Scholar] [CrossRef]

| MLE | LS | WLS | MPS | CVM | AD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | Bias | MSE | |
| 50 | 0.2091 | 0.9735 | 0.3720 | 2.2962 | 0.2598 | 1.1849 | 0.2434 | 0.9079 | 0.3662 | 2.3236 | 0.2490 | 1.1354 | |
| 0.0441 | 0.1371 | 0.0350 | 0.2031 | 0.0282 | 0.1458 | −0.0237 | 0.1171 | 0.0628 | 0.2122 | 0.0334 | 0.1845 | ||
| −0.0095 | 0.0386 | −0.0241 | 0.0696 | −0.0076 | 0.0425 | 0.0029 | 0.0338 | −0.0267 | 0.0693 | −0.0071 | 0.0401 | ||
| k | 0.0903 | 0.1508 | 0.3308 | 4.5287 | 0.0954 | 0.1825 | 0.0514 | 0.0982 | 0.3091 | 2.5795 | 0.0520 | 0.0767 | |
| 100 | 0.0467 | 0.3151 | 0.1472 | 0.7532 | 0.0774 | 0.3883 | 0.0741 | 0.3101 | 0.1439 | 0.7573 | 0.0721 | 0.3628 | |
| 0.0213 | 0.0568 | 0.0295 | 0.0934 | 0.0181 | 0.0636 | −0.0142 | 0.0523 | 0.0434 | 0.0959 | 0.0174 | 0.0806 | ||
| −0.0149 | 0.0184 | −0.0130 | 0.0285 | −0.0116 | 0.0195 | −0.0083 | 0.0167 | −0.0141 | 0.0284 | −0.0115 | 0.0186 | ||
| k | 0.0536 | 0.0563 | 0.0796 | 0.1760 | 0.0503 | 0.0601 | 0.0374 | 0.0465 | 0.0831 | 0.1887 | 0.0324 | 0.0346 | |
| 250 | 0.0955 | 0.3022 | 0.1288 | 0.6041 | 0.1002 | 0.3550 | 0.1197 | 0.2980 | 0.1253 | 0.6043 | 0.1041 | 0.3519 | |
| 0.0321 | 0.0468 | 0.0197 | 0.0718 | 0.0202 | 0.0501 | 0.0006 | 0.0426 | 0.0314 | 0.0733 | 0.0247 | 0.0660 | ||
| 0.0008 | 0.0160 | −0.0104 | 0.0266 | −0.0021 | 0.0179 | 0.0063 | 0.0150 | −0.0114 | 0.0266 | −0.0007 | 0.0172 | ||
| k | 0.0258 | 0.0396 | 0.0766 | 0.1720 | 0.0355 | 0.0520 | 0.0132 | 0.0341 | 0.0793 | 0.1776 | 0.0195 | 0.0285 | |
| 500 | 0.0396 | 0.1609 | 0.0987 | 0.3446 | 0.0595 | 0.2073 | 0.0572 | 0.1585 | 0.0964 | 0.3442 | 0.0628 | 0.2077 | |
| 0.0141 | 0.0319 | 0.0199 | 0.0513 | 0.0131 | 0.0370 | −0.0072 | 0.0301 | 0.0273 | 0.0520 | 0.0158 | 0.0483 | ||
| −0.0041 | 0.0093 | −0.0028 | 0.0165 | −0.0026 | 0.0110 | −0.0003 | 0.0089 | −0.0034 | 0.0165 | −0.0017 | 0.0108 | ||
| k | 0.0216 | 0.0234 | 0.0339 | 0.0479 | 0.0224 | 0.0281 | 0.0137 | 0.0212 | 0.0352 | 0.0487 | 0.0133 | 0.0177 | |
| 1000 | 0.0231 | 0.0853 | 0.0417 | 0.1410 | 0.0292 | 0.0965 | 0.0345 | 0.0850 | 0.0405 | 0.1409 | 0.0274 | 0.0961 | |
| 0.0041 | 0.0162 | 0.0023 | 0.0236 | 0.0018 | 0.0172 | −0.0078 | 0.0158 | 0.0061 | 0.0237 | 0.0015 | 0.0231 | ||
| −0.0020 | 0.0054 | −0.0026 | 0.0082 | −0.0015 | 0.0058 | −0.0002 | 0.0052 | −0.0029 | 0.0082 | −0.0020 | 0.0058 | ||
| k | 0.0106 | 0.0118 | 0.0167 | 0.0198 | 0.0105 | 0.0126 | 0.0063 | 0.0111 | 0.0173 | 0.0199 | 0.0073 | 0.0085 | |
| Model | Estimates (SE) | Statistics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K-S | p-Value | ||||||||||||
| LEORE | k | 170.0125 | 178.0125 | 178.6683 | 186.7711 | 181.4735 | 0.0542 | 0.3236 | 0.0667 | 0.9305 | |||
| 0.0096 | 1.7716 | 0.8069 | 1.9784 | ||||||||||
| (0.0080) | (0.6433) | (0.4434) | (1.3153) | ||||||||||
| EGG2 | a | b | 181.4496 | 189.4496 | 190.1054 | 198.2082 | 192.9106 | 0.2132 | 1.1734 | 0.1403 | 0.1487 | ||
| 12.3804 | 184.3605 | 0.5694 | 0.7059 | ||||||||||
| (2.4007) | (22.9474) | (0.2141) | (0.1196) | ||||||||||
| EWL | 170.8907 | 178.8907 | 179.5464 | 187.6493 | 182.3516 | 0.0630 | 0.3780 | 0.0737 | 0.866 | ||||
| 0.6300 | 1.2131 | 0.4114 | 8.2735 | ||||||||||
| (0.5545) | (25.6944) | (8.7128) | (8.2943) | ||||||||||
| LGT | k | 183.1803 | 187.1549 | 187.8107 | 195.9135 | 190.6159 | 0.1936 | 1.0469 | 0.1225 | 0.2753 | |||
| 20.0873 | 0.0079 | 12.1283 | 0.4017 | ||||||||||
| (16.4838) | (0.0039) | (1.0021) | (0.0586) | ||||||||||
| KW | a | b | c | 171.1142 | 179.1142 | 179.77 | 187.8729 | 182.5752 | 21.0186 | 131.3839 | 0.9969 | <2.2 | |
| 0.5018 | 0.6201 | 0.1625 | 3.9198 | ||||||||||
| (0.0065) | (0.0795) | (0.0216) | (0.0083) | ||||||||||
| T2G | - | - | 242.3898 | 246.3898 | 246.5803 | 250.7691 | 248.1203 | 0.0917 | 0.6079 | 0.1120 | 0.5864 | ||
| 3.2262 | 1.6480 | ||||||||||||
| (0.4193) | (0.1226) | ||||||||||||
| Model | Estimates (SE) | Statistics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K-S | p-Value | ||||||||||||
| LEORE | k | 183.4629 | 191.4629 | 192.0599 | 200.5695 | 195.0883 | 0.0452 | 0.2668 | 0.0728 | 0.8396 | |||
| 0.0172 | 0.7963 | 5.8969 | 0.2199 | ||||||||||
| (0.0151) | (0.7221) | (5.8743) | (0.0753) | ||||||||||
| EGG2 | a | b | 190.2207 | 198.2207 | 198.8177 | 207.3274 | 201.8461 | 0.0882 | 0.5873 | 0.1009 | 0.4562 | ||
| 6.0290 | 122.1410 | 1.0156 | 0.3620 | ||||||||||
| (1.3408) | (130.8008) | (0.6569) | (0.1289) | ||||||||||
| EWL | 196.7943 | 204.7943 | 205.3913 | 213.9009 | 208.4197 | 0.2387 | 1.4030 | 0.1139 | 0.3077 | ||||
| 3.8502 | 0.4699 | 0.4699 | 188.2497 | ||||||||||
| (0.7350) | (8.9080) | (8.9083) | (147.1816) | ||||||||||
| LGT | k | 189.0739 | 197.0739 | 197.6709 | 206.1806 | 200.6993 | 0.0899 | 0.5729 | 0.0956 | 0.5254 | |||
| 18.0769 | 0.0133 | 8.4828 | 0.2597 | ||||||||||
| (37.9855) | (0.0114) | (2.0439) | (0.0892) | ||||||||||
| KW | a | b | c | 188.1312 | 196.1312 | 196.7283 | 205.2379 | 199.7566 | 23.0962 | 143.1579 | 0.9994 | <2.2 | |
| 0.7667 | 3.1078 | 1.7284 | 0.9920 | ||||||||||
| (0.7008) | (3.8532) | (5.4959) | (1.0412) | ||||||||||
| T2G | - | - | 236.332 | 240.332 | 240.5059 | 244.8854 | 242.1447 | 0.5267 | 3.3523 | 0.1966 | 0.0076 | ||
| 1.0687 | 1.1731 | ||||||||||||
| (0.1324) | (0.0843) | ||||||||||||
| Model | Estimates (SE) | Statistics | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K-S | p-Value | ||||||||||||
| LEORE | k | 113.6159 | 121.6159 | 122.6159 | 128.8425 | 124.3099 | 0.0368 | 0.2895 | 0.0675 | 0.9777 | |||
| 3.2596 | 2.1545 | 3.5389 | 0.0907 | ||||||||||
| (5.4519) | (1.2061) | (3.4657) | (0.1109) | ||||||||||
| EGG2 | a | b | 116.0689 | 124.0689 | 125.0689 | 131.2956 | 126.7629 | 0.0487 | 0.3764 | 0.0874 | 0.852 | ||
| 5.2436 | 11.9916 | 0.1971 | 0.5806 | ||||||||||
| (0.0546) | (0.1520) | (0.0344) | (0.0521) | ||||||||||
| EWL | 138.8585 | 146.8585 | 147.8585 | 154.0851 | 149.5525 | 0.3160 | 1.9875 | 0.1831 | 0.0859 | ||||
| 5.5941 | 0.3379 | 0.4619 | 604.6459 | ||||||||||
| (1.2435) | (12.2857) | (16.7974) | (761.9120) | ||||||||||
| LGT | k | 116.3564 | 124.3564 | 125.3564 | 131.5831 | 127.0504 | 0.0610 | 0.4270 | 0.0892 | 0.835 | |||
| 17.9903 | 0.0196 | 7.0332 | 0.1503 | ||||||||||
| (24.8990) | (0.0298) | (1.9777) | (0.0459) | ||||||||||
| KW | a | b | c | 114.8207 | 122.8207 | 123.8207 | 130.0474 | 125.5148 | 15.8038 | 90.4623 | 0.9889 | <2.2 | |
| 9.5499 | 2.4518 | 0.1118 | 0.9081 | ||||||||||
| (0.1925) | (1.1598) | (0.0499) | (0.1267) | ||||||||||
| T2G | - | - | 127.6381 | 131.6381 | 131.9238 | 135.2515 | 132.9851 | 0.1430 | 0.9790 | 0.1382 | 0.3253 | ||
| 0.4987 | 0.8672 | ||||||||||||
| (0.0979) | (0.0928) | ||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, S.S.; Knehr, H.; McGurk, D.; Chen, X.; Cohen, A.; Pu, S. The Lomax-Exponentiated Odds Ratio–G Distribution and Its Applications. Mathematics 2024, 12, 1578. https://doi.org/10.3390/math12101578
Roy SS, Knehr H, McGurk D, Chen X, Cohen A, Pu S. The Lomax-Exponentiated Odds Ratio–G Distribution and Its Applications. Mathematics. 2024; 12(10):1578. https://doi.org/10.3390/math12101578
Chicago/Turabian StyleRoy, Sudakshina Singha, Hannah Knehr, Declan McGurk, Xinyu Chen, Achraf Cohen, and Shusen Pu. 2024. "The Lomax-Exponentiated Odds Ratio–G Distribution and Its Applications" Mathematics 12, no. 10: 1578. https://doi.org/10.3390/math12101578
APA StyleRoy, S. S., Knehr, H., McGurk, D., Chen, X., Cohen, A., & Pu, S. (2024). The Lomax-Exponentiated Odds Ratio–G Distribution and Its Applications. Mathematics, 12(10), 1578. https://doi.org/10.3390/math12101578







