A Mathematical Analysis of Competitive Dynamics and Aggressive Treatment in the Evolution of Drug Resistance in Malaria Parasites
Abstract
:1. Introduction
2. Methods
2.1. Model
2.2. Parameter Estimation
2.3. Equilibrium Analysis
- or
2.4. Uncertainty Analysis and Sensitivity Analysis Methods
2.4.1. Uncertainty Analysis
2.4.2. Local Sensitivity Analysis (LSA)
2.4.3. Global Sensitivity Analysis (GSA)
3. Results
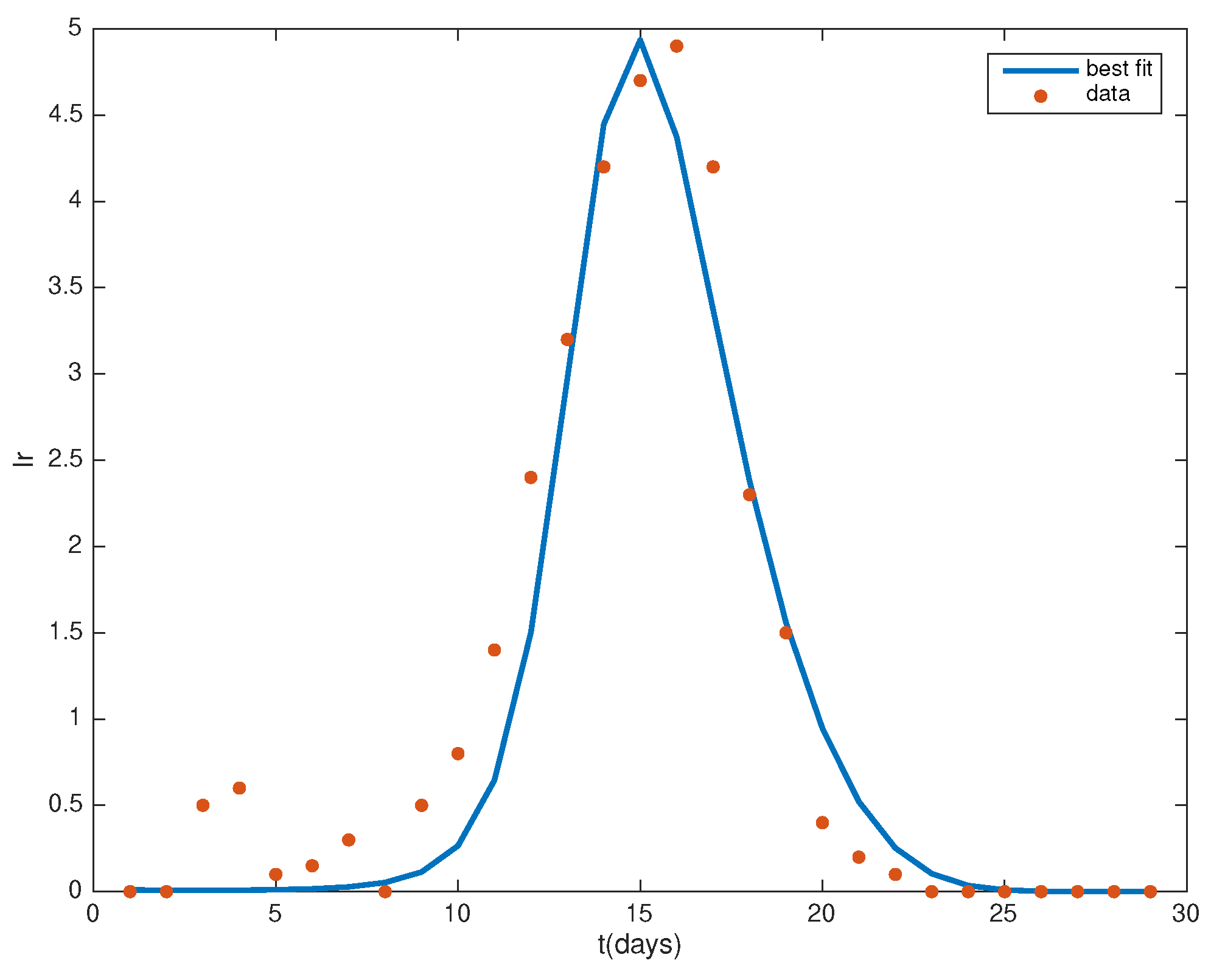
3.1. Parameter Estimates
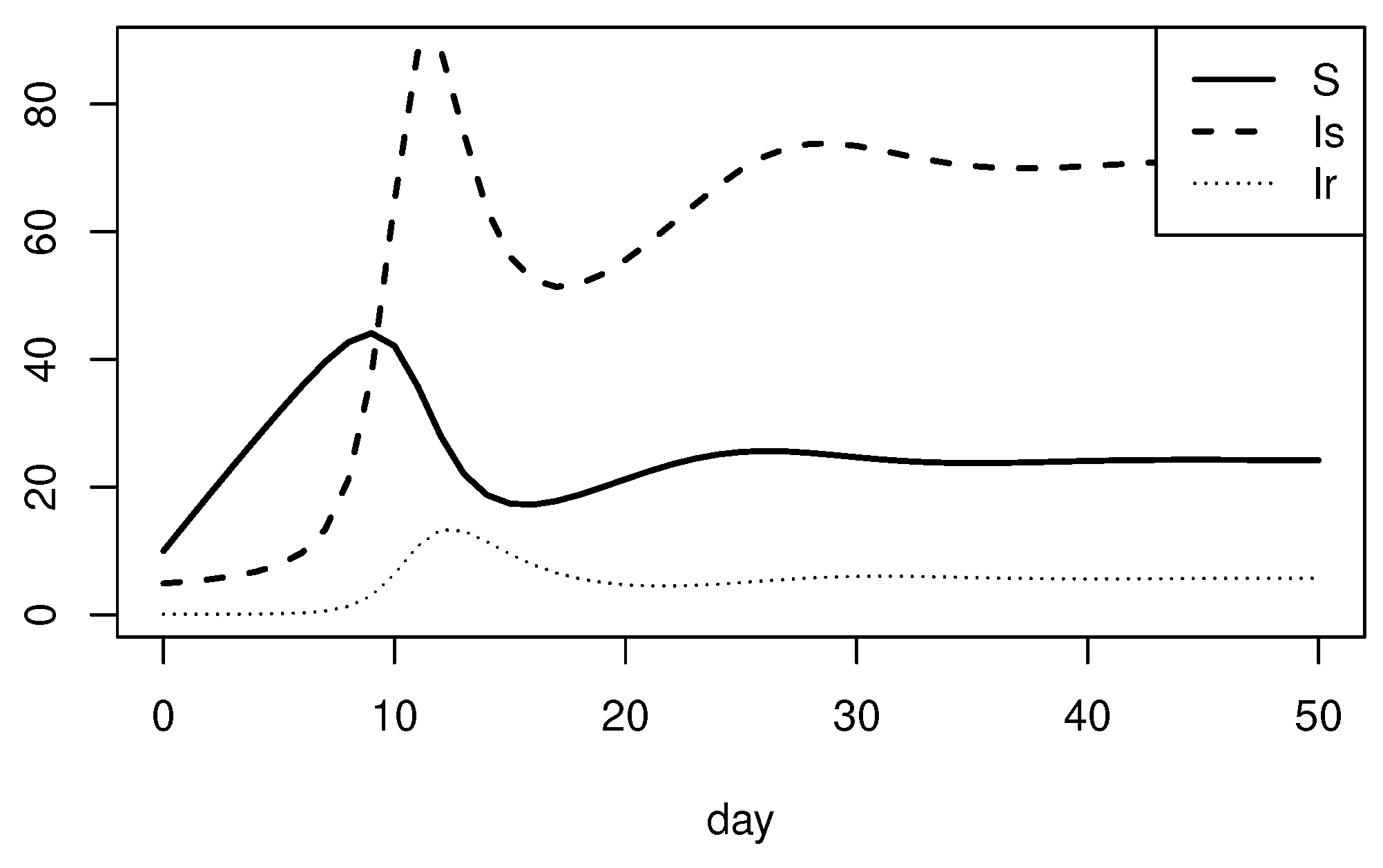
3.2. Equilibrium Analysis
3.3. Uncertainty Analysis Results
3.4. Sensitivity Analysis Results
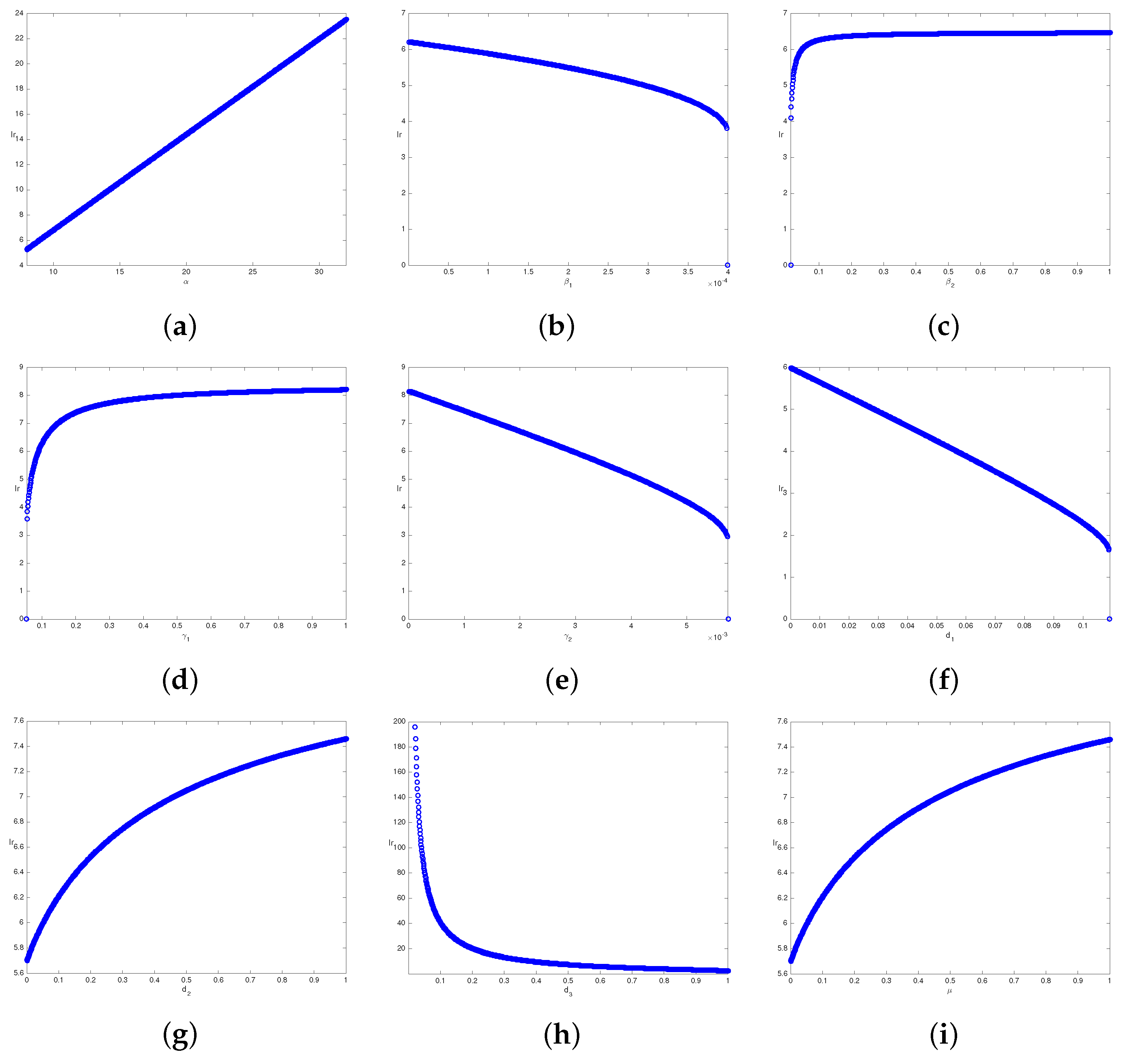
3.4.1. Local Sensitivity Analysis
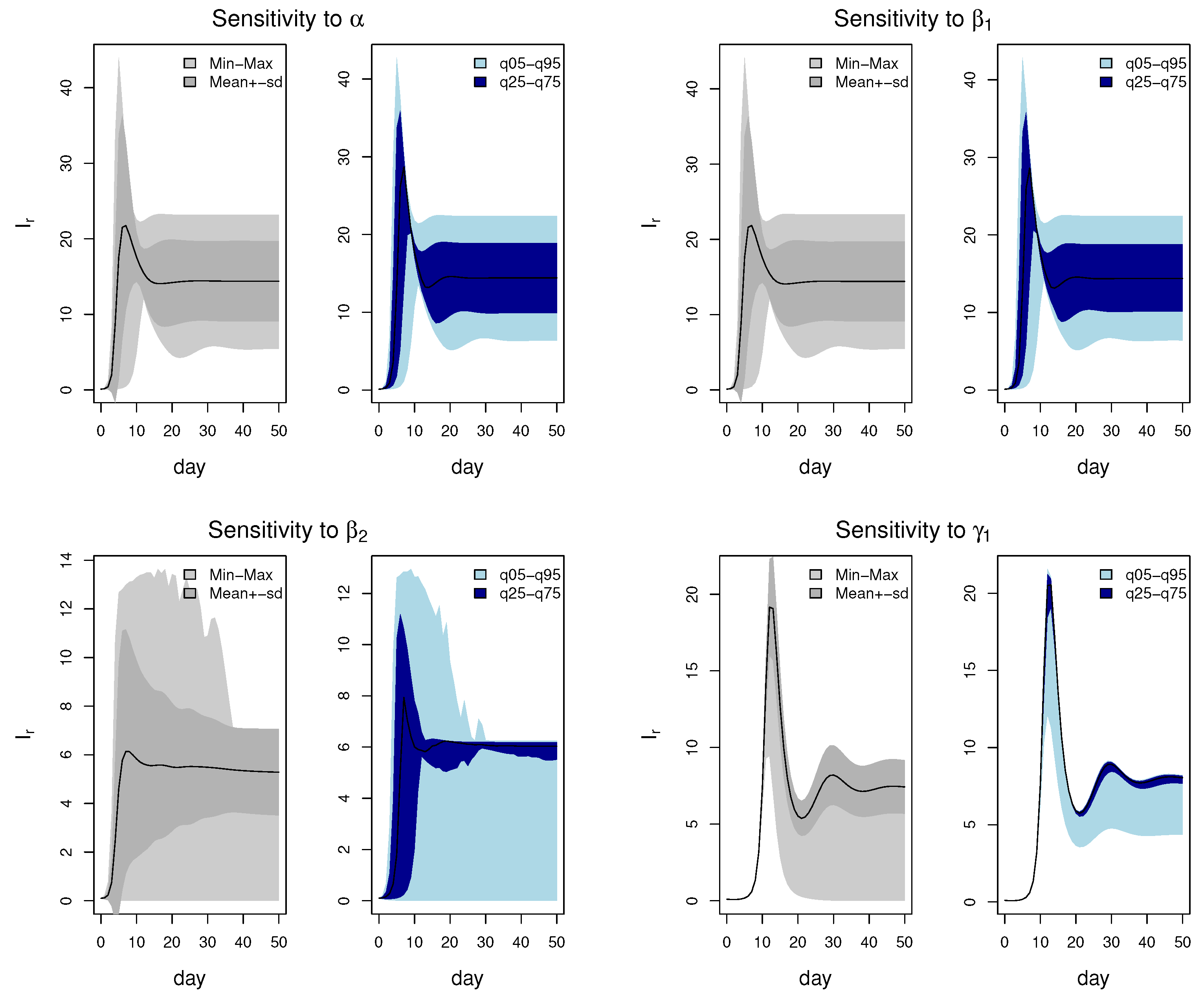
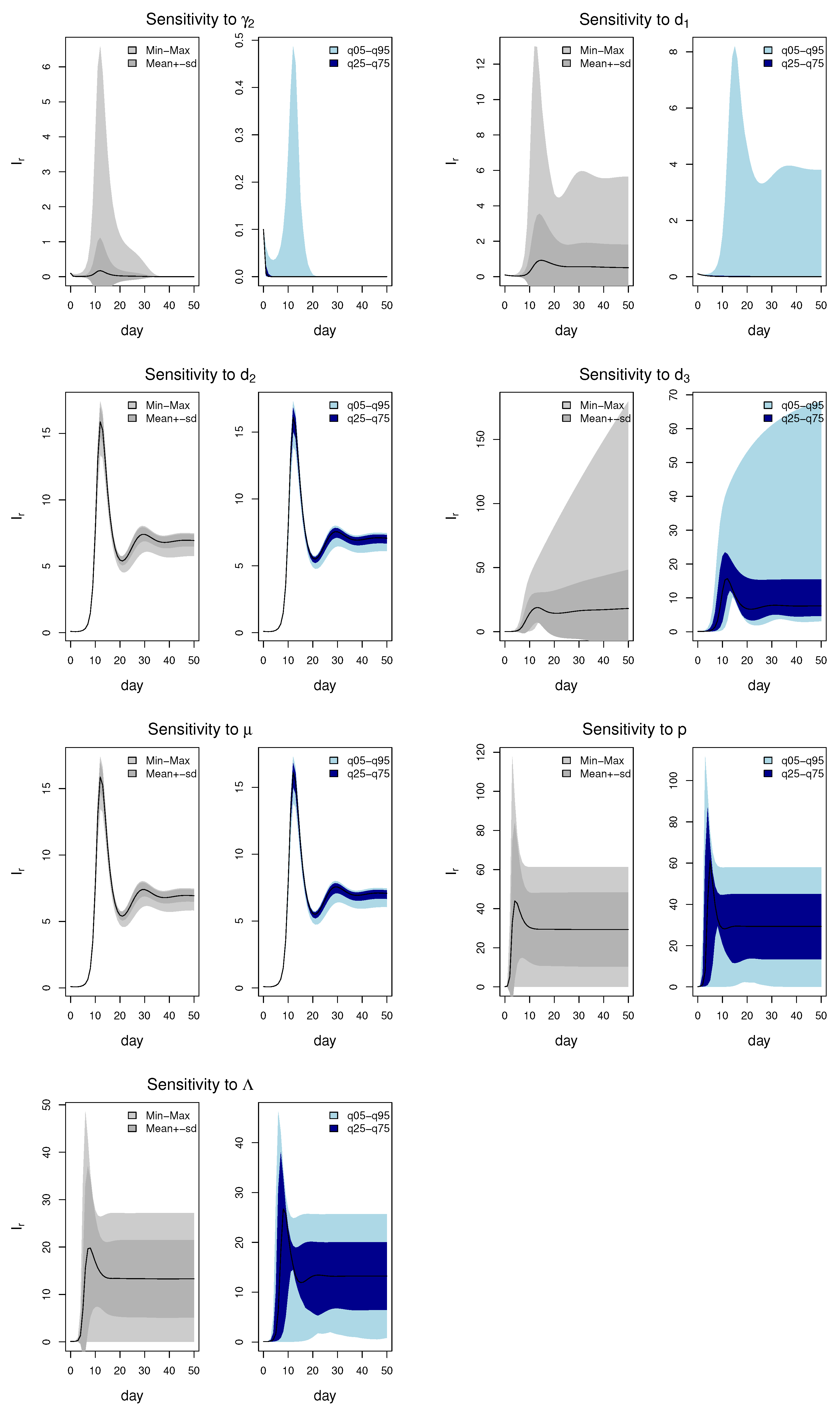
3.4.2. Global Sensitivity Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WHO. World Malaria Report 2020; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Nguyen, T.D.; Gao, B.; Amaratunga, C.; Dhorda, M.; Tran, T.N.A.; White, N.J.; Dondorp, A.M.; Boni, M.F.; Aguas, R. Preventing antimalarial drug resistance with triple artemisinin-based combination therapies. Nat. Commun. 2023, 14, 4568. [Google Scholar] [CrossRef] [PubMed]
- D’Alessandro, U.; Buttiëns, H. History and importance of antimalarial drug resistance. Trop. Med. Int. Health 2010, 6, 845–848. [Google Scholar] [CrossRef] [PubMed]
- WHO. Report on Antimalarial Drug Efficacy, Resistance and Response: 10 Years of Surveillance (2010–2019); WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Dondorp, A.M.; Nosten, F.; Yi, P.; Das, D.; Phyo, A.P.; Tarning, J.; Lwin, K.M.; Ariey, F.; Hanpithakpong, W.; Lee, S.J.; et al. Artemisinin resistance in Plasmodium falciparum malaria. New Engl. J. Med. 2009, 361, 455–467. [Google Scholar] [CrossRef] [PubMed]
- Mathieu, L.C.; Cox, H.; Early, A.M.; Mok, S.; Lazrek, Y.; Paquet, J.C.; Ade, M.P.; Lucchi, N.W.; Grant, Q.; Udhayakumar, V.; et al. Local emergence in Amazonia of Plasmodium falciparum k13 C580Y mutants associated with in vitro artemisinin resistance. Elife 2020, 9, e51015. [Google Scholar] [CrossRef] [PubMed]
- Miotto, O.; Sekihara, M.; Tachibana, S.I.; Yamauchi, M.; Pearson, R.D.; Amato, R.; Gonçalves, S.; Mehra, S.; Noviyanti, R.; Marfurt, J.; et al. Emergence of artemisinin-resistant Plasmodium falciparum with kelch13 C580Y mutations on the island of New Guinea. PLoS Pathog. 2020, 16, e1009133. [Google Scholar] [CrossRef]
- Balikagala, B.; Fukuda, N.; Ikeda, M.; Katuro, O.T.; Tachibana, S.I.; Yamauchi, M.; Opio, W.; Emoto, S.; Anywar, D.A.; Kimura, E.; et al. Evidence of artemisinin-resistant malaria in Africa. New Engl. J. Med. 2021, 385, 1163–1171. [Google Scholar] [CrossRef] [PubMed]
- Acosta, M.M.; Bram, J.T.; Sim, D.; Read, A.F. Effect of drug dose and timing of treatment on the emergence of drug resistance in vivo in a malaria model. Evol. Med. Public Health 2020, 2020, 196–210. [Google Scholar] [CrossRef] [PubMed]
- Hastings, I. A model for the origins and spread of drug-resistant malaria. Parasitology 1997, 115, 133–141. [Google Scholar] [CrossRef]
- Mackinnon, M.J.; Hastings, I.M. The evolution of multiple drug resistance in malaria parasites. Trans. R. Soc. Trop. Med. Hyg. 1998, 92, 188–195. [Google Scholar] [CrossRef]
- Hastings, I.M.; D’Alessandro, U. Modelling a predictable disaster: The rise and spread of drug-resistant malaria. Parasitol. Today 2000, 16, 340–347. [Google Scholar] [CrossRef]
- Huijben, S.; Nelson, W.A.; Wargo, A.R.; Sim, D.G.; Drew, D.R.; Read, A.F. Chemotherapy, within-host ecology and the fitness of drug-resistant malaria parasite. Evolution 2010, 64, 2952–2968. [Google Scholar] [CrossRef] [PubMed]
- Wargo, A.R.; Huijben, S.; Roode, J.C.D.; Shepherd, J.; Read, A.F. Competitive release and facilitation of drug-resistant parasites after therapeutic chemotherapy in a rodent malaria model. Proc. Natl. Acad. Sci. USA 2007, 104, 19914–19919. [Google Scholar] [CrossRef]
- Bushman, M.; Morton, L.; Duah, N.; Quashie, N.; Abuaku, B.; Koram, K.A.; Dimbu, P.R.; Plucinski, M.; Gutman, J.; Lyaruu, P.; et al. Within-host competition and drug resistance in the human malaria parasite Plasmodium falciparum. Proc. Biol. Sci. 2016, 283, 20153038. [Google Scholar] [CrossRef]
- Hansen, E.; Woods, R.J.; Read, A.F. How to use a chemotherapeutic agent when resistance to it threatens the patient. PLoS Biol. 2017, 15, e2001110. [Google Scholar] [CrossRef]
- Whitlock, A.O.; Juliano, J.J.; Mideo, N. Immune selection suppresses the emergence of drug resistance in malaria parasites but facilitates its spread. PLoS Comput. Biol. 2021, 17, e1008577. [Google Scholar] [CrossRef]
- Ayala, M.J.; Villela, D.A. Early transmission of sensitive strain slows down emergence of drug resistance in Plasmodium vivax. PLoS Comput. Biol. 2020, 16, e1007945. [Google Scholar] [CrossRef] [PubMed]
- Mackinnon, M.J. Drug resistance models for malaria. Acta Trop. 2005, 94, 207–217. [Google Scholar] [CrossRef]
- Tchuenche, J.M.; Chiyaka, C.; Chan, D.; Matthews, A.; Mayer, G. A mathematical model for antimalarial drug resistance. Math. Med. Biol. 2011, 28, 335–355. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Day, T. Coinfection and the evolution of drug resistance. J. Evol. Biol. 2015, 27, 2595–2604. [Google Scholar] [CrossRef]
- Chiyaka, C.; Garira, W.; Dube, S. Effects of treatment and drug resistance on the transmission dynamics of malaria in endemic areas. Theor. Popul. Biol. 2009, 75, 14–29. [Google Scholar] [CrossRef]
- Fatmawati.; Tasman, H. An optimal control strategy to reduce the spread of malaria resistance. Math. Biosci. 2015, 262, 73–79. [Google Scholar] [CrossRef]
- Read, A.F.; Day, T.; Huijben, S. The evolution of drug resistance and the curious orthodoxy of aggressive chemotherapy. Proc. Natl. Acad. Sci. USA 2011, 108, 10871–10877. [Google Scholar] [CrossRef]
- Jurek, A.M.; Maldonado, G.; Greenland, S.; Church, T.R. Uncertainty analysis: An example of its application to estimating a survey proportion. J. Epidemiol. Community Health 2007, 61, 650–654. [Google Scholar] [CrossRef]
- Vesselinova, N.; Alexandrov, B.S.; Wall, M.E. Dynamical Model of Drug Accumulation in Bacteria: Sensitivity Analysis and Experimentally Testable Predictions. PLoS ONE 2016, 11, e0165899. [Google Scholar] [CrossRef] [PubMed]
- Song, T.; Wang, C.; Tian, B. Modelling intra-host competition between malaria parasites strains. Comput. Appl. Math. 2020, 39, 1–17. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin/Heidelberg, Germany, 2001; pp. 267–291. [Google Scholar]
- Iman, R.L.; Helton, J.C. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal. 2010, 8, 71–90. [Google Scholar] [CrossRef]
- Blower, S.M.; Dowlatabadi, H. Sensitivity and uncertainty analysis of complex models of disease transmission: An HIV model, as an example. Int. Stat. Rev. 1994, 62, 229–243. [Google Scholar] [CrossRef]
- Borgonovo, E. Sensitivity analysis of model output with input constraints: A generalized rationale for local methods. Risk Anal. 2010, 28, 667–680. [Google Scholar] [CrossRef] [PubMed]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M.; Gupta, S. Non-linear phenomena in host-parasite interactions. Parasitology 1989, 99, S59–S79. [Google Scholar] [CrossRef]
- Hetzel, C.; Anderson, R.M. The within-host cellular dynamics of bloodstage malaria: Theoretical and experimental studies. Parasitology 1996, 113, 25–38. [Google Scholar] [CrossRef]
- Slater, H.C.; Okell, L.C.; Ghani, A.C. Mathematical modelling to guide drug development for malaria elimination. Trends Parasitol. 2017, 33, 175–184. [Google Scholar] [CrossRef]
- Samsuzzoha, M.; Singh, M.; Lucy, D. Uncertainty and sensitivity analysis of the basic reproduction number of a vaccinated epidemic model of influenza. Appl. Math. Model. 2013, 37, 903–915. [Google Scholar] [CrossRef]
- Dunn, J.M.; Davis, S.; Stacey, A.; Diuk-Wasser, M.A. A simple model for the establishment of tick-borne pathogens of Ixodes scapularis: A global sensitivity analysis of R 0. J. Theor. Biol. 2013, 335, 213–221. [Google Scholar] [CrossRef]
- Wu, J.; Dhingra, R.; Gambhir, M.; Remais, J.V. Sensitivity analysis of infectious disease models: Methods, advances and their application. J. R. Soc. Interface 2013, 10, 20121018. [Google Scholar] [CrossRef]
- Dela, A.; Shtylla, B.; de Pillis, L. Multi-method global sensitivity analysis of mathematical models. J. Theor. Biol. 2022, 546, 111159. [Google Scholar] [CrossRef]
- Qian, G.; Mahdi, A. Sensitivity analysis methods in the biomedical sciences. Math. Biosci. 2020, 323, 108306. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Fu, R.; Luo, J. Global analysis of a mathematical model on malaria with competitive strains and immune responses. Appl. Math. Comput. 2015, 259, 132–152. [Google Scholar] [CrossRef]
- Hellriegel, B. Modelling the immune response to malaria with ecological concepts: Short-term behaviour against long-term equilibrium. Proc. Biol. Sci. 1992, 250, 249–256. [Google Scholar]
- Li, Y.; Ruan, S.; Xiao, D. The within-host dynamics of malaria infection with immune response. Math. Biosci. Eng. 2013, 8, 999–1018. [Google Scholar]
- Stevenson, M.M.; Riley, E.M. Innate immunity to malaria. Nat. Rev. Immunol. 2004, 4, 169–180. [Google Scholar] [CrossRef] [PubMed]


| Parameter | Definition | Estimated Value | Range | Ref. |
|---|---|---|---|---|
| number of merozoites that an infected RBC can produce | 8.559469 | [8, 32] | ||
| infection rate of drug-sensitive malaria parasites | [0, 1] | |||
| infection rate of drug-resistant malaria parasites | 0.03018763 | [0, 1] | ||
| competitive coefficient | 0.08115581 | [0, 1] | ||
| competitive coefficient | 0.003323166 | [0, 1] | ||
| production rate of RBCs | log10 (41,500) | [34] | ||
| decay rate of RBCs | 0.00833 | [34] | ||
| decay rate of drug-sensitive malaria parasites | [0, 1] | |||
| decay rate of drug-resistant malaria parasites | 0.6355716 | [0, 1] | ||
| level of drug concentration | [0, 1] | |||
| p | proportion of drug-sensitive parasites released | 0.8605191 | [0, 1] | |
| from an infected RBC by drug-resistance parasites |
| Minimum | Maximum | Mean | Median | Variance | 5th Percentile | 5th Percentile |
|---|---|---|---|---|---|---|
| 4.610 | 200.3142 | 16.5868 | 10.7515 | 398.9929 | 1.5219 | 51.7296 |
| Para | p | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.7 | 0.46 | 5.6 | 2.7 | 2.4 | 6.7 | 0.3 | 0.00082 | 6.6 | 0.00082 | 62 | |
| 1.6 | 0.0076 | 1.5 | 0.44 | 0.4 | 1.3 | 0.0062 | 0.00013 | 1.1 | 0.00013 | 12 | |
| 6.4 | −0.46 | 1.3 | 2.7 | −2.4 | 6.2 | −0.28 | 0.00082 | −6.6 | 0.00082 | −60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, T.; Wang, Y.; Li, Y.; Fan, G. A Mathematical Analysis of Competitive Dynamics and Aggressive Treatment in the Evolution of Drug Resistance in Malaria Parasites. Mathematics 2024, 12, 1595. https://doi.org/10.3390/math12101595
Song T, Wang Y, Li Y, Fan G. A Mathematical Analysis of Competitive Dynamics and Aggressive Treatment in the Evolution of Drug Resistance in Malaria Parasites. Mathematics. 2024; 12(10):1595. https://doi.org/10.3390/math12101595
Chicago/Turabian StyleSong, Tianqi, Yishi Wang, Yang Li, and Guoliang Fan. 2024. "A Mathematical Analysis of Competitive Dynamics and Aggressive Treatment in the Evolution of Drug Resistance in Malaria Parasites" Mathematics 12, no. 10: 1595. https://doi.org/10.3390/math12101595
APA StyleSong, T., Wang, Y., Li, Y., & Fan, G. (2024). A Mathematical Analysis of Competitive Dynamics and Aggressive Treatment in the Evolution of Drug Resistance in Malaria Parasites. Mathematics, 12(10), 1595. https://doi.org/10.3390/math12101595





