A Study on Optimizing the Maximal Product in Cubic Fuzzy Graphs for Multifaceted Applications
Abstract
1. Introduction
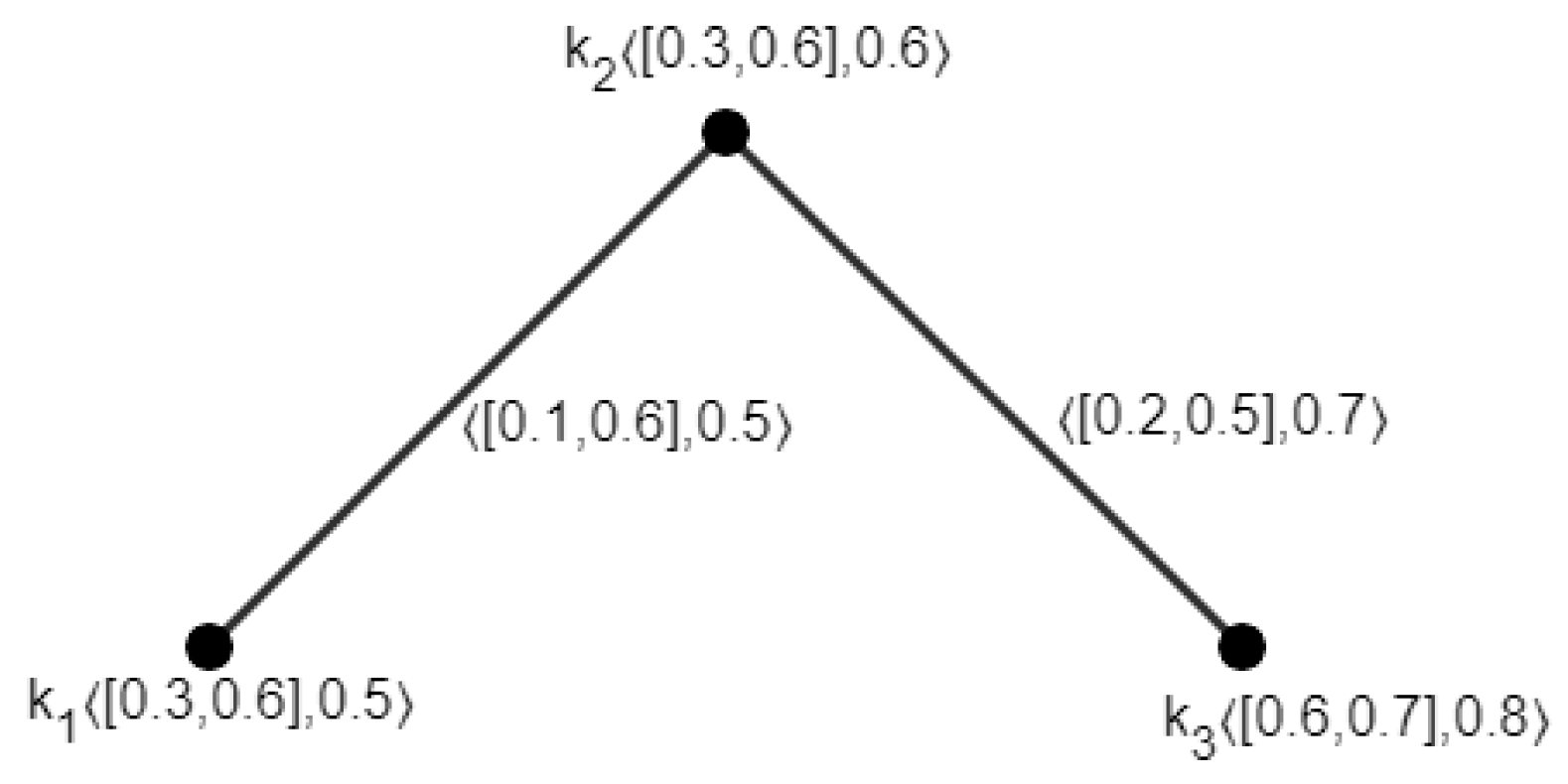
2. Preliminaries
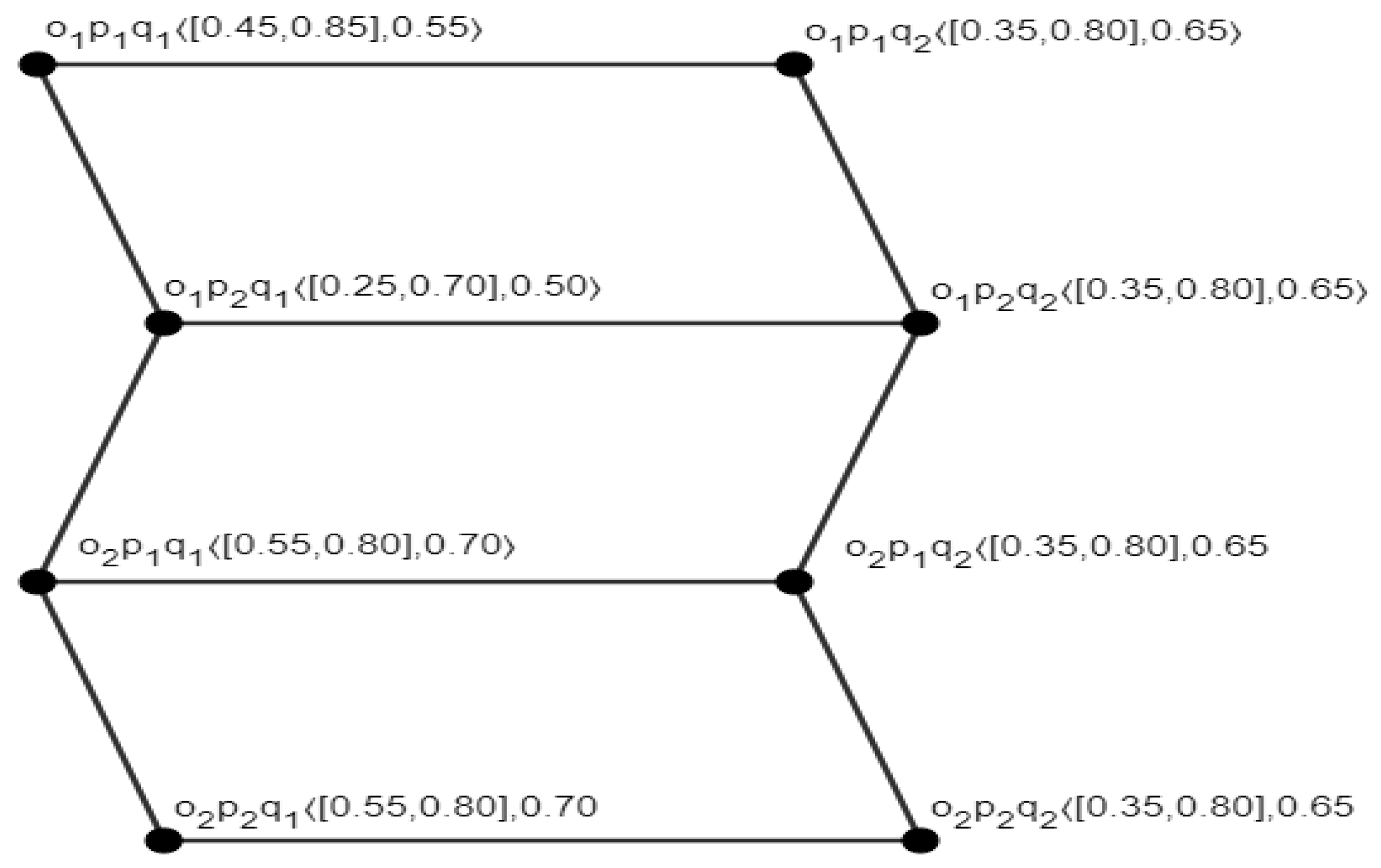
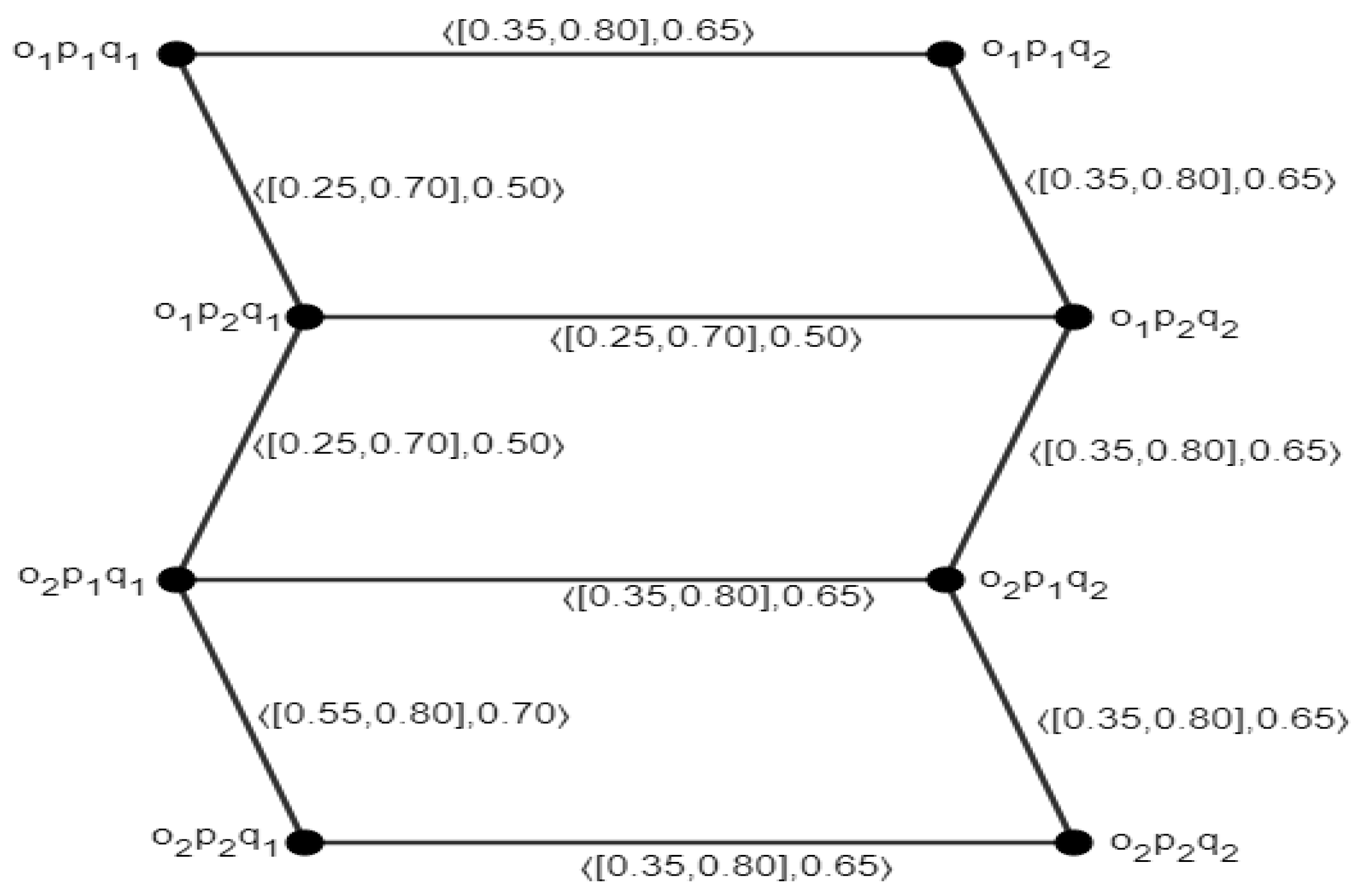
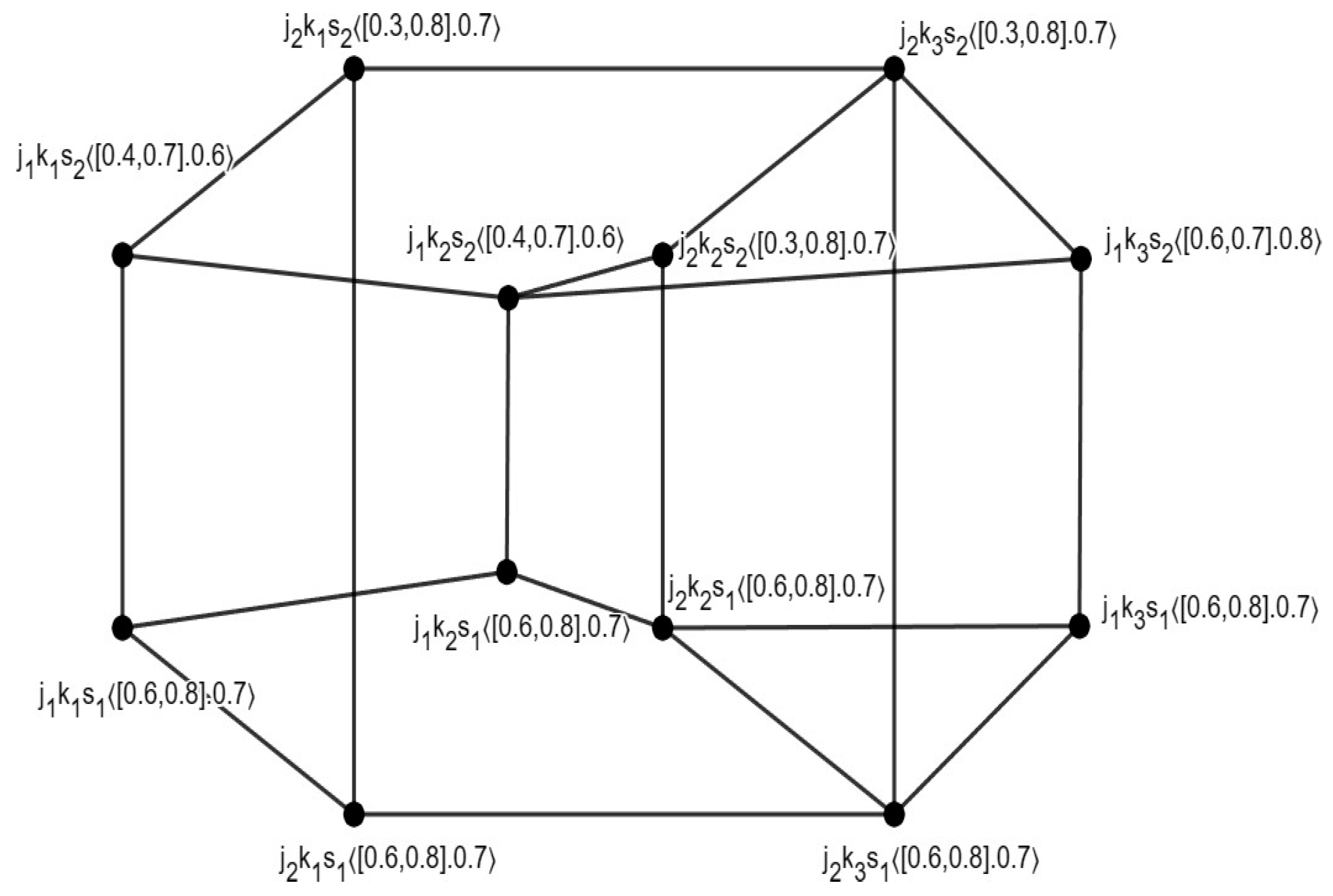
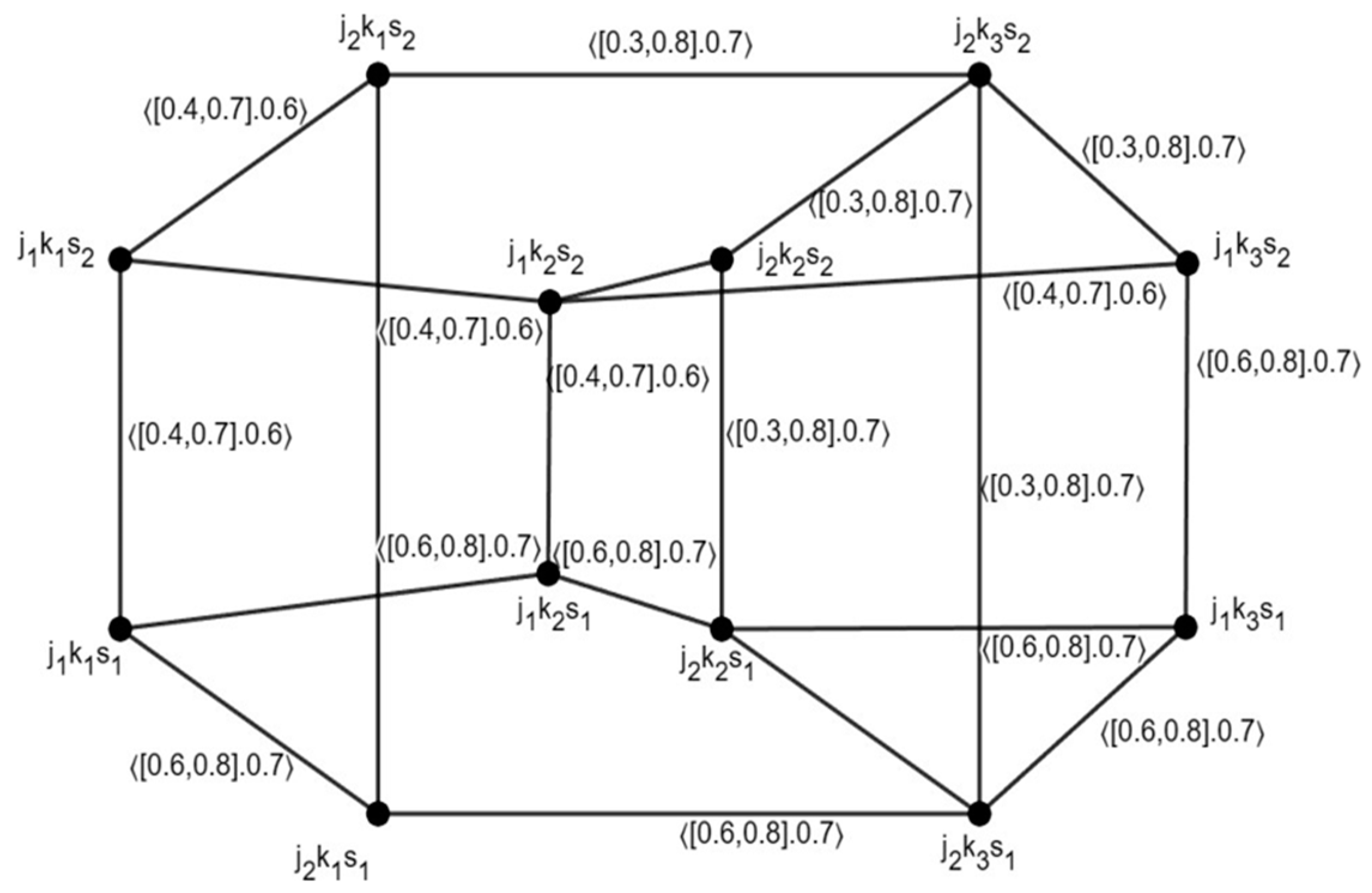
3. Maximal Product of Three Cubic Fuzzy Graphs
3.1. Definition
3.2. Definition
4. Domination on Maximal Product of Cubic Fuzzy Graph
5. Applications
5.1. Telecommunication Network
5.2. Emergency Services Coordination
5.3. Research Collaboration Network
5.4. Traffic Management
5.5. Financial Networks
5.6. Airline and Defense Systems
5.7. Network Security at Organizations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kaufmann, A. Introduction à la Théorie des Sous-Ensembles Flous à L’usage des Ingénieurs (Fuzzy Sets Theory); Masson: Paris, France, 1973; Volume 3. [Google Scholar]
- Rosenfeld, A. Fuzzy Graphs, Fuzzy Sets and Their Applications; Academic Press: New York, NY, USA, 1975; pp. 77–95. [Google Scholar]
- Talebi, A.A. Cayley fuzzy graphs on the fuzzy group. Comput. Appl. Math. 2018, 37, 4611–4632. [Google Scholar] [CrossRef]
- Borzooei, R.A.; Rashmanlou, H. New concepts of vague graphs. Int. J. Mach. Learn. Cybern. 2016, 8, 1081–1092. [Google Scholar] [CrossRef]
- Borzooei, R.A.; Rashmanlou, H.; Samanta, S.; Pal, M. Regularity of vague graphs. J. Intell. Fuzzy Syst. 2016, 30, 3681–3689. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Akram, M.; Dudek, W.A. Interval-valued fuzzy graphs. Comput. Math. Appl. 2011, 61, 289–299. [Google Scholar] [CrossRef]
- Talebi, A.A.; Rashmanlou, H.; Sadati, S.H. New concepts on m-polar interval-valued intuitionistic fuzzy graph. TWMS J. Appl. Eng. Math. 2020, 10, 808–816. [Google Scholar]
- Talebi, A.A.; Rashmanlou, H.; Sadati, S.H. Interval-valued intuitionistic fuzzy competition graph. J. Mult.-Valued Log. Soft Comput. 2020, 34, 335–364. [Google Scholar]
- Kosari, S.; Rao, Y.; Jiang, H.; Liu, X.; Wu, P.; Shao, Z. Vague graph structure with application in medical diagnosis. Symmetry 2020, 12, 1582. [Google Scholar] [CrossRef]
- Rao, Y.; Kosari, S.; Shao, Z. Certain properties of vague graphs with a novel application. Mathematics 2020, 8, 1647. [Google Scholar] [CrossRef]
- Kou, Z.; Kosari, S.; Akhoundi, M. A novel description on vague graph with application in transportation systems. J. Math. 2021, 2021, 4800499. [Google Scholar] [CrossRef]
- Rao, Y.; Kosari, S.; Shao, Z.; Cai, R.; Liu, X. A study on domination in vague incidence graph and its application in medical sciences. Symmetry 2020, 12, 1885. [Google Scholar] [CrossRef]
- Rao, Y.; Kosari, S.; Shao, Z.; Qiang, X.; Akhoundi, M.; Zhang, X. Equitable domination in vague graphs with application in medical sciences. Front. Phys. 2021, 9, 635642. [Google Scholar] [CrossRef]
- Shi, X.; Kosari, S. Certain properties of domination in product vague graphs with novel application in medicine. Front. Phys. 2021, 9, 3–85. [Google Scholar] [CrossRef]
- Shao, Z.; Kosari, S.; Rashmanlou, H.; Shoaib, M. New concepts in intuitionistic fuzzy graph with application in water supplier systems. Mathematics 2020, 8, 1241. [Google Scholar] [CrossRef]
- Sampathkumar, E. Generalized graph structures. Bull. Kerala Math. Assoc. 2006, 3, 65–123. [Google Scholar]
- Dinesh, T.; Ramakrishnan, T. On generalised fuzzy graph structures. Appl. Math. Sci. 2011, 5, 173–180. [Google Scholar]
- Akram, M. m-Polar Fuzzy Graphs, Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Akram, M.; Akmal, R. Application of bipolar fuzzy sets in graph structures. Appl. Comput. Intell. Soft Comput. 2016, 2016, 5859080. [Google Scholar] [CrossRef]
- Akram, M.; Akmal, R. Intuitionistic fuzzy graph structures. Kragujev. J. Math. 2017, 41, 219–237. [Google Scholar] [CrossRef]
- Akram, M.; Akmal, R. Operations on intuitionistic fuzzy graph structures. Fuzzy Inform. Eng. 2016, 8, 389–410. [Google Scholar] [CrossRef]
- Akram, M.; Sitara, M.; Saeid, A.B. Residue product of fuzzy graph structures. J. Mult.-Valued Log. Soft Comput. 2020, 34, 365–399. [Google Scholar]
- Kou, Z.; Akhoundi, M.; Chen, X.; Omidi, S. A study on vague graph structures with an application. Adv. Math. Phys. 2022, 2022, 3182116. [Google Scholar] [CrossRef]
- Dinesh, T. Fuzzy incidence graph structures. Adv. Fuzzy Math. (AFM) 2020, 15, 21–30. [Google Scholar]
- Akram, M.; Sitara, M. Decision-making with q-rung orthopair fuzzy graph structures. Granul. Comput. 2021, 7, 505–526. [Google Scholar] [CrossRef]
- Sitara, M.; Zafar, F. Selection of best inter-country airline service using q-rung picture fuzzy graph structures. Comput. Appl. Math. 2022, 41, 54. [Google Scholar] [CrossRef]
- Jun, Y.B.; Kim, C.S.; Yang, K.O. Cubic sets. Ann. Fuzzy Math. Inform. 2012, 4, 83–98. [Google Scholar]
- Jun, Y.B.; Smarandache, F.; Kim, C.S. Neutrosophic cubic sets. New Math. Nat. Comput. 2017, 13, 41–54. [Google Scholar] [CrossRef]
- Jun, Y.B.; Song, S.Z.; Kim, S.J. Cubic interval-valued intuitionistic fuzzy sets and their application in BCK/BCI-algebras. Axioms 2018, 7, 7. [Google Scholar] [CrossRef]
- Jun, Y.B.; Lee, K.J.; Kang, M.S. Cubic structures applied to ideals of BCI-algebras. Comput. Math. Appl. 2011, 62, 3334–3342. [Google Scholar] [CrossRef]
- Khan, M.; Jun, Y.B.; Gulistan, M.; Yaqoob, N. The generalized version of Jun’s cubic sets in semigroups. J. Intell. Fuzzy Syst. 2015, 28, 947–960. [Google Scholar] [CrossRef]
- Ali, A.; Jun, Y.B.; Khan, M.; Shi, F.G.; Anis, S. Generalized cubic soft sets and their applications to algebraic structures. Ital. J. Pure Appl. Math. 2015, 35, 393–414. [Google Scholar]
- Senapati, T.; Jun, Y.B.; Muhiuddin, G.; Shum, K.P. Cubic intuitionistic structures applied to ideals of BCI-algebras. Analele Stiintifice Univ. Ovidius Constanta-Ser. Mat. 2019, 27, 213–232. [Google Scholar] [CrossRef]
- Muhiuddin, G.; Ahn, S.S.; Kim, C.S.; Jun, Y.B. Stable cubic sets. J. Comput. Anal. Appl. 2017, 23, 802–819. [Google Scholar]
- Krishna, K.K.; Rashmanlou, H.; Talebi, A.A.; Mofidnakhaei, F. Regularity of cubic graph with application. J. Indones. Math. Soc. 2019, 25, 1–15. [Google Scholar] [CrossRef]
- Rashid, S.; Yaqoob, N.; Akram, M.; Gulistan, M. Cubic graphs with application. Int. J. Anal. Appl. 2018, 16, 733–750. [Google Scholar]
- Muhiuddin, G.; Takallo, M.M.; Jun, Y.B.; Borzooei, R.A. Cubic graphs and their application to a traffic flow problem. Int. J. Comput. Intell. Syst. 2020, 13, 1265–1280. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Muhiuddin, G.; Amanathulla, S.K.; Mofidnakhaei, F.; Pal, M. A study on cubic graphs with novel application. J. Intell. Fuzzy Syst. 2021, 40, 89–101. [Google Scholar] [CrossRef]
- Jiang, H.; Talebi, A.A.; Shao, Z.; Sadati, S.H.; Rashmanlou, H. New concepts of vertex covering in cubic graphs with its applications. Mathematics 2022, 10, 307. [Google Scholar] [CrossRef]
- Rao, Y.; Akhoundi, M.; Talebi, A.A.; Sadati, S.H. The Maximal Product in Cubic fuzzy graph structures with an application. Int. J. Comput. Intell. Syst. 2023, 16, 18. [Google Scholar] [CrossRef]
- Meenakshi, A.; Senbagamalar, J.; Kannan, A. Application of Intuitionistic fuzzy network using efficient domination. Fuzzy Log. Appl. Comput. Sci. Math. 2023, 213–232. [Google Scholar] [CrossRef]
- Meenakshi, A.; Senbagamalar, J. Equitable domination in neutrosophic graph using strong arc. Neutrosophic Sets Syst. 2023, 60, 59–73. [Google Scholar]
- Muhiuddin, G.; Talebi, A.A.; Sadati, S.H.; Rashmanlou, H. New concepts of domination in cubic graphs with application. J. Intell. Fuzzy Syst. 2022, 43, 841–857. [Google Scholar] [CrossRef]
- Meenakshi, A.; Mythreyi, O. Applications of Neutrosophic social network using max product networks. J. Intell. Fuzzy Syst. 2023, 45, 407–420. [Google Scholar] [CrossRef]
- Meenakshi, A.; Mythreyi, O.; Bramila, M.; Kannan, A.; Senbagamalar, J. Application of neutrosophic optimal network using operations. J. Intell. Fuzzy Syst. 2023, 45, 421–433. [Google Scholar] [CrossRef]




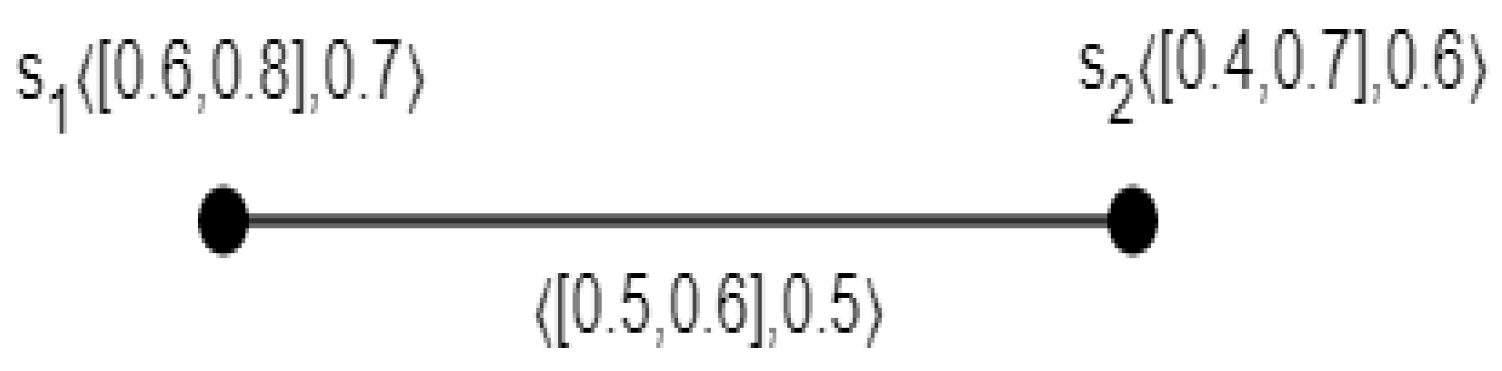
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meenakshi, A.; Mythreyi, O.; Čep, R.; Karthik, K. A Study on Optimizing the Maximal Product in Cubic Fuzzy Graphs for Multifaceted Applications. Mathematics 2024, 12, 1605. https://doi.org/10.3390/math12101605
Meenakshi A, Mythreyi O, Čep R, Karthik K. A Study on Optimizing the Maximal Product in Cubic Fuzzy Graphs for Multifaceted Applications. Mathematics. 2024; 12(10):1605. https://doi.org/10.3390/math12101605
Chicago/Turabian StyleMeenakshi, Annamalai, Obel Mythreyi, Robert Čep, and Krishnasamy Karthik. 2024. "A Study on Optimizing the Maximal Product in Cubic Fuzzy Graphs for Multifaceted Applications" Mathematics 12, no. 10: 1605. https://doi.org/10.3390/math12101605
APA StyleMeenakshi, A., Mythreyi, O., Čep, R., & Karthik, K. (2024). A Study on Optimizing the Maximal Product in Cubic Fuzzy Graphs for Multifaceted Applications. Mathematics, 12(10), 1605. https://doi.org/10.3390/math12101605






