Stochastic Patterns of Bitcoin Volatility: Evidence across Measures
Abstract
:1. Introduction
2. Literature Review
- While individual studies have focused on specific technical indicators like R/S Analysis, SMA, and RSI, there is a gap in research that integrates these tools comprehensively to analyze cryptocurrency prices and trends in combination with various volatility estimators;
- Research on the long-term memory of cryptocurrency markets using tools like the Hurst exponent and its implications for market efficiency is still nascent. More studies are needed to understand how these aspects affect trading strategies in the cryptocurrency context;
- There seems to be a lack of research tools that combine various statistical and econometric tools to develop comprehensive risk management strategies tailored to the unique characteristics of Bitcoin’s volatility dynamics.
- Integration of Multiple Technical Indicators: By employing a combination of R/S Analysis, SMA, and RSI, our paper provides a comprehensive approach to analyzing cryptocurrency dynamics and trends in function of volatility estimators. This integrated methodology offers a more holistic view of market dynamics than studies focusing on individual indicators;
- Long-Term Memory and Market Efficiency in Cryptocurrencies: By utilizing tools like the Hurst exponent, our paper delves into the long-term memory of Bitcoin markets and its implications for market efficiency. This helps in developing trading strategies that are better suited to the cryptocurrency market’s behavior;
- Comprehensive Risk Management Strategies: The combination of various statistical and econometric tools in this paper aids in the development of comprehensive risk management strategies for cryptocurrency trading, addressing the high volatility and unpredictability of these markets.
3. Methodology of Bitcoin Volatility Behavior Analysis
4. Numerical Implementation
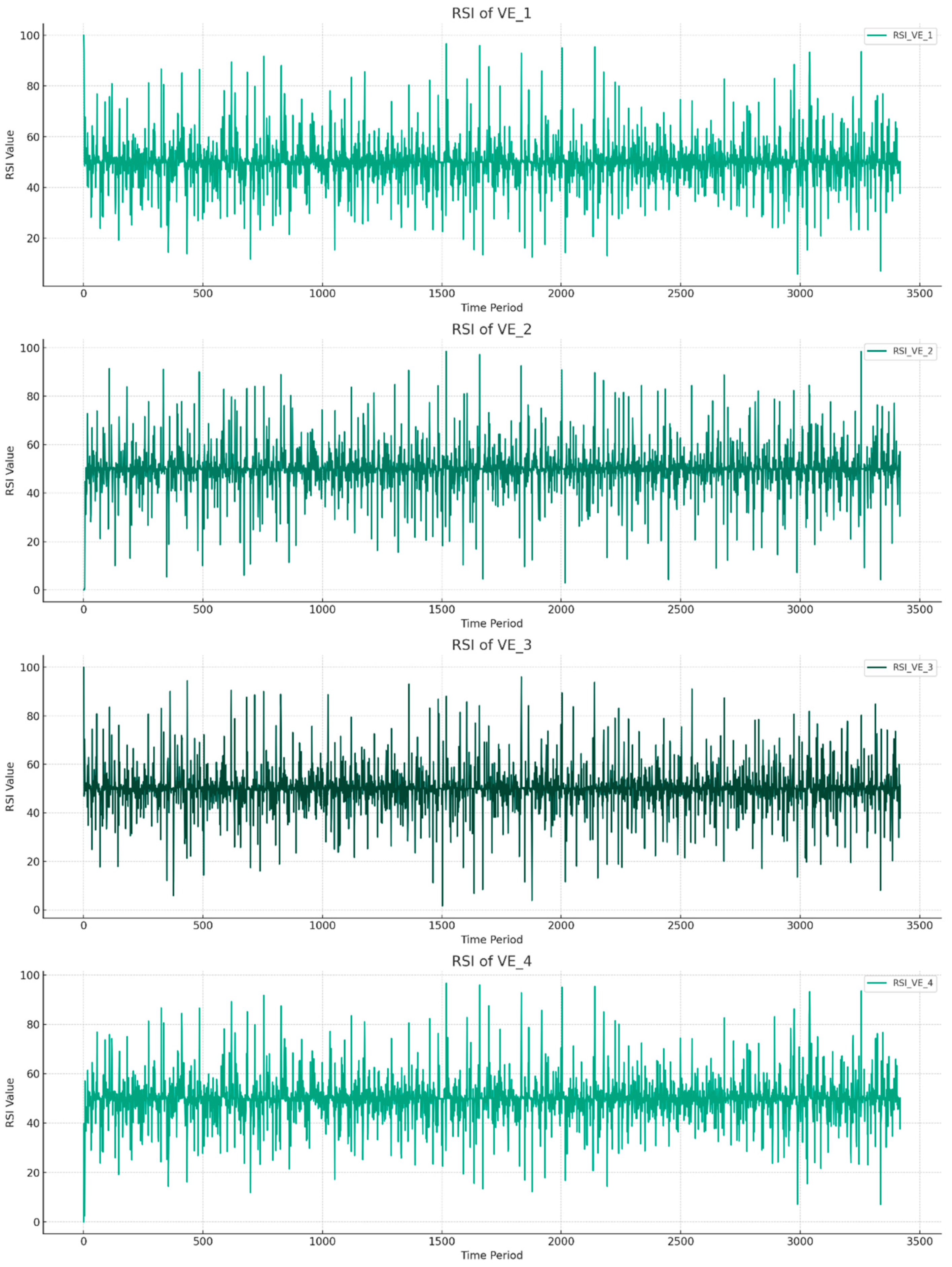
- Overbought Conditions: Volatility Estimator VE_1 exhibits the highest average overbought events, followed by VE_2, VE_3, and VE_4. This suggests that VE_1 tends to reach overbought conditions more frequently, indicating periods where the asset may be considered overvalued according to this estimator;
- Oversold Conditions: VE_4 shows a tendency for the highest average annual oversold events, suggesting it more frequently reaches conditions considered to be undervalued. This might indicate a propensity for VE_4 to experience significant valuation drops or higher volatility, leading to potential buying opportunities as per this metric;
- Momentum Fluctuations: VE_1 and VE_3 demonstrate a higher frequency of sharp increases, indicating more frequent sudden valuation changes according to these estimators. For sharp decreases, the distribution across the volatility estimators is more varied, with VE_2 and VE_4 showing slightly higher tendencies for these events. This indicates that VE_2 and VE_4 may experience more pronounced volatility in terms of sharp valuation decreases;
- Risk Management Insights: VE_1, exhibiting frequent overbought events and sharp increases, suggests this estimator might be more prone to rapid valuation changes. Consequently, risk management strategies that take into account VE_1’s characteristics might need to prepare for more frequent transitions between overvalued conditions and potentially rapidly changing market sentiments.
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andersen, T.G.; Bollerslev, T. Heterogeneous Information Arrivals and Return Volatility Dynamics: Uncovering the Long-Run in High Frequency Returns. J. Financ. 1997, 52, 975–1005. [Google Scholar] [CrossRef]
- Doumenis, Y.; Izadi, J.; Dhamdhere, P.; Katsikas, E.; Koufopoulos, D. A Critical Analysis of Volatility Surprise in Bitcoin Cryptocurrency and Other Financial Assets. Risks 2021, 9, 207. [Google Scholar] [CrossRef]
- Giot, P.; Laurent, S.; Petitjean, M. Trading activity, realized volatility and jumps. J. Empir. Financ. 2010, 17, 168–175. [Google Scholar] [CrossRef]
- Floros, C. Modelling volatility using high, low, open and closing prices: Evidence from four S&P indices. Int. Res. J. Financ. Econ. 2009, 28, 198–206. Available online: https://researchportal.port.ac.uk/en/publications/modelling-volatility-using-high-low-open-and-closing-prices-evide (accessed on 6 February 2024).
- Gkillas, K.; Floros, C.; Suleman, M.T. Quantile dependencies between discontinuities and time-varying rare disaster risks. Eur. J. Financ. 2021, 27, 932–962. [Google Scholar] [CrossRef]
- Alghalith, M. Pricing the American options: A closed-form, simple formula. Phys. A Stat. Mech. Appl. 2020, 548, 123873. [Google Scholar] [CrossRef]
- Sariannidis, N.; Giannarakis, G.; Zafeiriou, E.; Billias, I. The Effect of Crude Oil Price Moments on Socially Responsible Firms in Eurozone. Int. J. Energy Econ. Policy 2016, 6, 356–363. Available online: https://dergipark.org.tr/en/pub/ijeeep/issue/31917/351090 (accessed on 6 February 2024).
- Tsagkanos, A.; Gkillas, K.; Konstantatos, C.; Floros, C. Does Trading Volume Drive Systemic Banks’ Stock Return Volatility? Lessons from the Greek Banking System. Int. J. Financ. Stud. 2021, 9, 24. [Google Scholar] [CrossRef]
- Kanavos, P.; Fontrier, A.M.; Gill, J.; Efthymiadou, O. Does external reference pricing deliver what it promises? Evidence on its impact at national level. Eur. J. Health Econ. HEPAC Health Econ. Prev. Care 2020, 21, 129–151. [Google Scholar] [CrossRef] [PubMed]
- Zournatzidou, G.; Floros, C. Hurst Exponent Analysis: Evidence from Volatility Indices and the Volatility of Volatility Indices. J. Risk Financ. Manag. 2023, 16, 272. [Google Scholar] [CrossRef]
- Schelling, D.M. Rough Volatility and Portfolio Optimisation under Small Transaction Costs. Ph.D. Thesis, The London School of Economics and Potilical Science, London, UK, 2019. [Google Scholar]
- Zhou, J.; Liu, W. Study on the Daily Exchange Rate Movement Based on the Model of Brownian Motion. In Proceedings of the 2015 3rd International Conference on Education, Management, Arts, Economics and Social Science, Changsha, China, 28–29 December 2015; pp. 931–936. [Google Scholar] [CrossRef]
- Bianchi, N. Electrical machine analysis using finite elements. In Electrical Machine Analysis Using Finite Elements; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–275. [Google Scholar] [CrossRef]
- Beskos, A.; Roberts, G.; Thiery, A.H.; Pillai, N. Asymptotic analysis of the random walk Metropolis algorithm on ridged densities. Ann. Appl. Probab. 2018, 28, 2966–3001. [Google Scholar] [CrossRef]
- Wang, W. Asymptotic analysis for hedging errors in models with respect to geometric fractional Brownian motion. Stochastics 2019, 91, 407–432. [Google Scholar] [CrossRef]
- Çaǧlar, M.; Bahtiyar, N.; Altintaş, I. Parameter estimation of an agent-based stock price model. Appl. Stoch. Models Bus. Ind. 2014, 30, 227–239. [Google Scholar] [CrossRef]
- Qiu, J.-Y. The SME Board Stock Price Trend Analysis and Investment Strategy Under the Fractal Market Hypothesis. DEStech Trans. Soc. Sci. 2017. [Google Scholar] [CrossRef]
- Kiohos, A.; Sariannidis, N. Determinants of the asymmetric gold market. Invest. Manag. Financ. Innov. 2010, 7, 26–33. Available online: https://scholar.google.gr/citations?view_op=view_citation&hl=el&user=xU_kC08AAAAJ&citation_for_view=xU_kC08AAAAJ:M3ejUd6NZC8C (accessed on 6 February 2024).
- Sun, S.L.; Ding, Z.; Joseph, G. Expanding Inclusive Markets through Corruption Control: A Multilevel Modeling Analysis for a Grand Challenge. J. Int. Manag. 2023, 29, 101068. [Google Scholar] [CrossRef]
- Bergsli, L.Ø.; Lind, A.F.; Molnár, P.; Polasik, M. Forecasting volatility of Bitcoin. Res. Int. Bus. Financ. 2022, 59, 101540. [Google Scholar] [CrossRef]
- López-Cabarcos, M.Á.; Pérez-Pico, A.M.; Piñeiro-Chousa, J.; Šević, A. Bitcoin volatility, stock market and investor sentiment. Are they connected? Financ. Res. Lett. 2021, 38, 101399. [Google Scholar] [CrossRef]
- Bouteska, A.; Harasheh, M. Bitcoin volatility and the introduction of bitcoin futures: A portfolio construction approach. Financ. Res. Lett. 2023, 57, 104200. [Google Scholar] [CrossRef]
- Baur, D.G.; Dimpfl, T. The volatility of Bitcoin and its role as a medium of exchange and a store of value. Empir. Econ. 2021, 61, 2663–2683. [Google Scholar] [CrossRef]
- Qian, L.; Wang, J.; Ma, F.; Li, Z. Bitcoin volatility predictability–The role of jumps and regimes. Financ. Res. Lett. 2022, 47, 102687. [Google Scholar] [CrossRef]
- Raubitzek, S.; Corpaci, L.; Hofer, R.; Mallinger, K. Scaling Exponents of Time Series Data: A Machine Learning Approach. Entropy 2023, 25, 1671. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Águila, A.; Trinidad-Segovia, J.E.; Sánchez-Granero, M.A. Improvement in Hurst exponent estimation and its application to financial markets. Financ. Innov. 2022, 8, 1–21. [Google Scholar] [CrossRef]
- Kobeissi, H.Y. Multifractal Financial Markets; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Peters, E.E. Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility, 2nd ed.; Wiley: Hoboken, NJ, USA, 1996; Available online: https://www.amazon.com/Chaos-Order-Capital-Markets-Volatility/dp/0471139386 (accessed on 6 February 2024).
- Murphy, J.J. Technical analysis of the financial markets. Pa. Dent. J. 1999, 77, 33–34. Available online: http://www.ncbi.nlm.nih.gov/pubmed/20599625 (accessed on 6 February 2024).
- Pring, M.J. Technical Analysis Explained: The Successful Investor’s Guide to Spotting Investment Trends and Turning Points, 5th ed.; McGraw Hill: New York, NY, USA, 2014. [Google Scholar]
- Aronson, D.R. Evidence-Based Technical Analysis: Applying the Scientific Method and Statistical Inference to Trading Signals; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Achelis, S.B. Technical Analysis from A to Z, 2nd ed.; McGraw Hill: New York, NY, USA, 2013. [Google Scholar]
- Kirkpatrick, C.D.; Dahlquist, J.R. Technical Analysis, The Complete Resource for Market Technicians; FT Press: Upper Saddle River, NJ, USA, 2007; p. 49. Available online: https://books.google.co.th/books/about/Technical_Analysis.html?id=I5SgX5q5sQEC&redir_esc=y (accessed on 6 February 2024).
- Bollinger, J. Bollinger on Bollinger Bands; McGraw Hill: New York, NY, USA, 2002; Volume 227. [Google Scholar]
- Turiel, A.; Pérez-Vicente, C.J. Role of multifractal sources in the analysis of stock market time series. Phys. A Stat. Mech. Appl. 2005, 355, 475–496. [Google Scholar] [CrossRef]
- Barunik, J.; Kristoufek, L. On Hurst exponent estimation under heavy-tailed distributions. Phys. A Stat. Mech. Appl. 2012, 389, 3844–3855. [Google Scholar] [CrossRef]
- Gençay, R.; Selçuk, F.; Whitcher, B. Differentiating intraday seasonalities through wavelet multi-scaling. Phys. A Stat. Mech. Appl. 2001, 289, 543–556. [Google Scholar] [CrossRef]
- Kaufman, P.J. Trading Systems and Methods. 2013. Available online: https://www.wiley.com/en-us/Trading+Systems+and+Methods%2C+5th+Edition-p-9781118043561 (accessed on 6 February 2024).
- Carter, J.F. Mastering the Trade: Proven Techniques for Profiting from Intraday and Swing Trading Setups; McGraw Hill: New York, NY, USA, 2012; Volume 459. [Google Scholar]
- Szóstakowski, R. The use of the Hurst exponent to investigate the quality of forecasting methods of ultra-high-frequency data of exchange rates. Przegląd Stat. 2019, 65, 200–223. [Google Scholar] [CrossRef]
- Ceballos, R.F.; Largo, F.F. On The Estimation of the Hurst Exponent Using Adjusted Rescaled Range Analysis, Detrended Fluctuation Analysis and Variance Time Plot: A Case of Exponential Distribution. arXiv 2018, arXiv:1805.08931. Available online: https://arxiv.org/abs/1805.08931v1 (accessed on 6 February 2024).
- Zournatzidou, G.; Mallidis, I.; Farazakis, D.; Floros, C. Enhancing Bitcoin Price Volatility Estimator Predictions: A Four-Step Methodological Approach Utilizing Elastic Net Regression. Mathematics 2024, 12, 1392. [Google Scholar] [CrossRef]
- Resta, M.; Pagnottoni, P.; De Giuli, M.E. Technical Analysis on the Bitcoin Market: Trading Opportunities or Investors’ Pitfall? Risks 2020, 8, 44. [Google Scholar] [CrossRef]
- Kardile, R.; Ugale, T.; Mohanty, S.N. Stock Price Predictions using Crossover SMA. In Proceedings of the 2021 9th International Conference on Reliability 2021, Infocom Technologies and Optimization (Trends and Future Directions), ICRITO, Noida, India, 3–4 September 2021. [Google Scholar] [CrossRef]
- Okereke, A.-E.; Cornelius, O.C.; Ephraim, A.C. Comparative study on Optimized Moving Average types, Buy-and- Hold Trading Strategies. Int. J. Sci. Eng. Res. 2019, 10. Available online: http://www.ijser.org (accessed on 6 February 2024).
- Agustian, H.; Pujiastuti, A.; Varian Sayoga, M.; Studi Informatika, P.; Tinggi Teknologi Adisutjipto, S. Comparison of Simple Moving Average and Exponential Smoothing Methods To Predict Seaweed Prices. CCIT (Creat. Commun. Innov. Technol.) J. 2020, 13, 175–184. [Google Scholar] [CrossRef]
- Nau, R. Forecasting with Moving Averages; Fuqua School of Business, Duke University: Durham, NC, USA, 2014; pp. 1–3. [Google Scholar]
- Su, Y.; Cui, C.; Qu, H. Self-Attentive Moving Average for Time Series Prediction. Appl. Sci. 2022, 12, 3602. [Google Scholar] [CrossRef]
- Tilehnouei, M.H.; Shivaraj, B. A Comparative Study of Two Technical Analysis Tools: Moving Average Convergence and Divergence V/S Relative Strength Index: A Case Study of Hdfc Bank Ltd Listed In National Stock Exchange Of India (Nse). Int. J. Manag. Bus. Res. 2013, 3, 191–197. [Google Scholar]
- Uma, K.S.; Naidu, S. Prediction of intraday trend reversal in stock market index through machine learning algorithms. Adv. Intell. Syst. Comput. 2021, 1200, 331–341. [Google Scholar] [CrossRef]
- Jain, R.; Bhardwaj, P.; Soni, P. Can the Market of Cryptocurrency Be Followed with the Technical Analysis? Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 2425–2445. [Google Scholar] [CrossRef]
- Kazeminia, S.; Sajedi, H.; Arjmand, M. Real-Time Bitcoin Price Prediction Using Hybrid 2D-CNN LSTM Model. In Proceedings of the 2023 9th International Conference on Web Research (ICWR), Tehran, Iran, 3–4 May 2023; pp. 173–178. [Google Scholar] [CrossRef]
- Bolton, J.; von Boetticher, S.T. Momentum Trading on the Johannesburg Stock Exchange after the Global Financial Crisis. Procedia Econ. Financ. 2015, 24, 83–92. [Google Scholar] [CrossRef]
- Feller, W. The Asymptotic Distribution of the Range of Sums of Independent Random Variables. Ann. Math. Stat. 1951, 22, 427–432. [Google Scholar] [CrossRef]
- Garman, M.B.; Klass, M.J. On the Estimation of Security Price Volatilities from Historical Data. J. Bus. 1980, 53, 67–78. Available online: https://www.jstor.org/stable/2352358 (accessed on 6 February 2024). [CrossRef]
- Meilijson, I. The Garman-Klass volatility estimator revisited. Revstat Stat. J. 2008, 9, 199–212. Available online: https://arxiv.org/abs/0807.3492v2 (accessed on 6 February 2024).
- Malik, F.; Ewing, B.T.; Payne, J.E. Measuring volatility persistence in the presence of sudden changes in the variance of Canadian stock returns. Can. J. Econ. Rev. Can. D’économique 2005, 38, 1037–1056. [Google Scholar] [CrossRef]
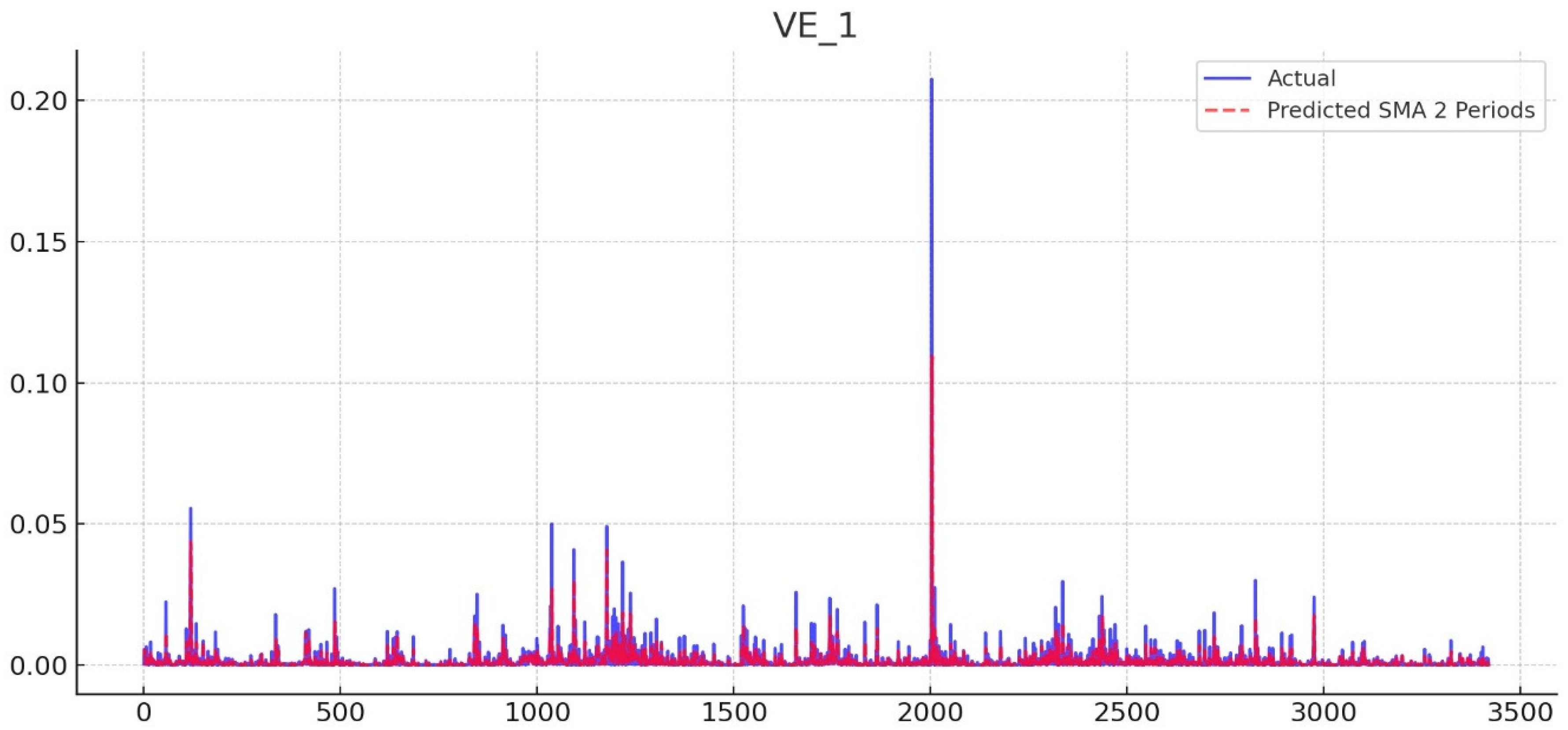

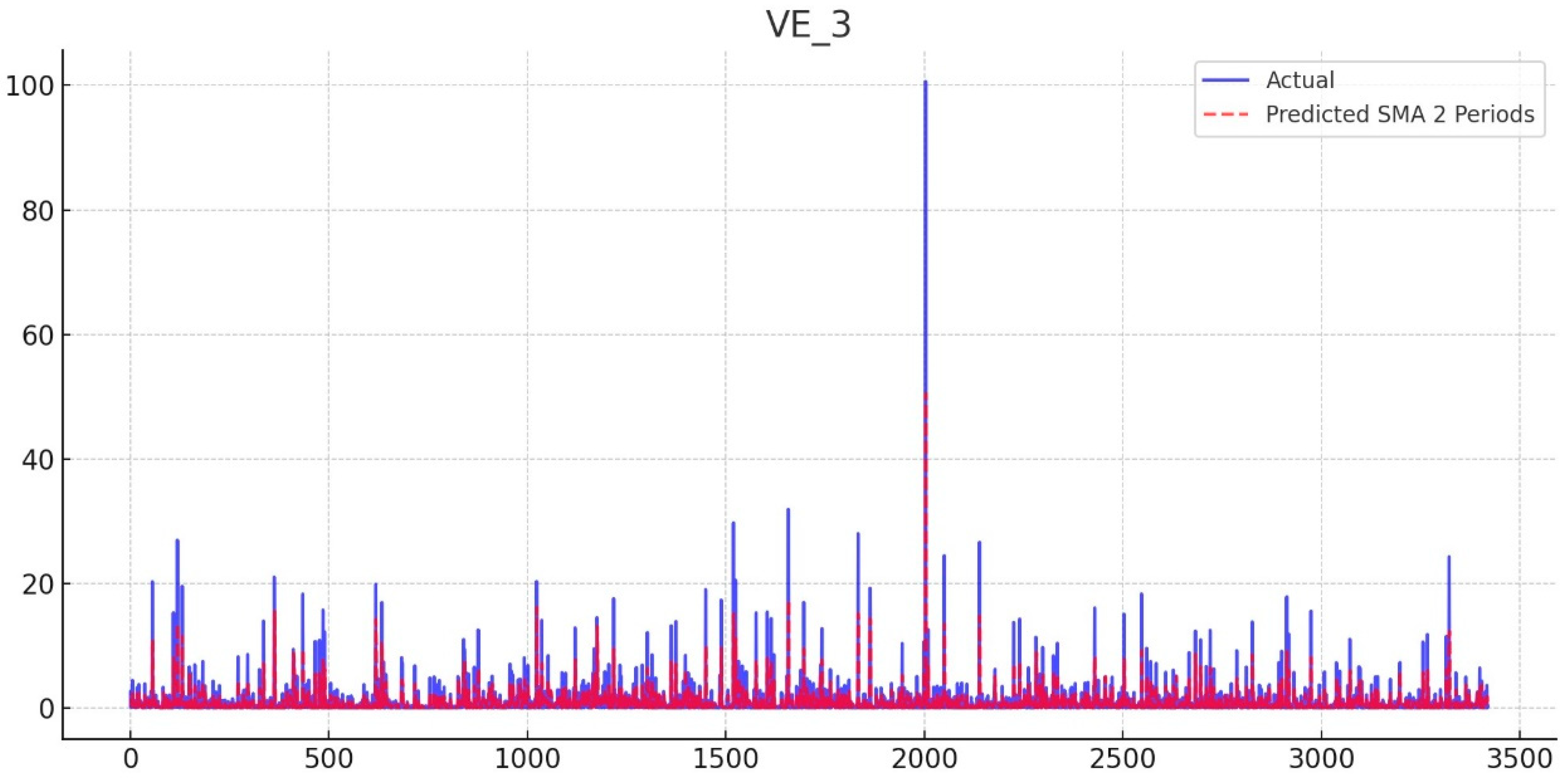
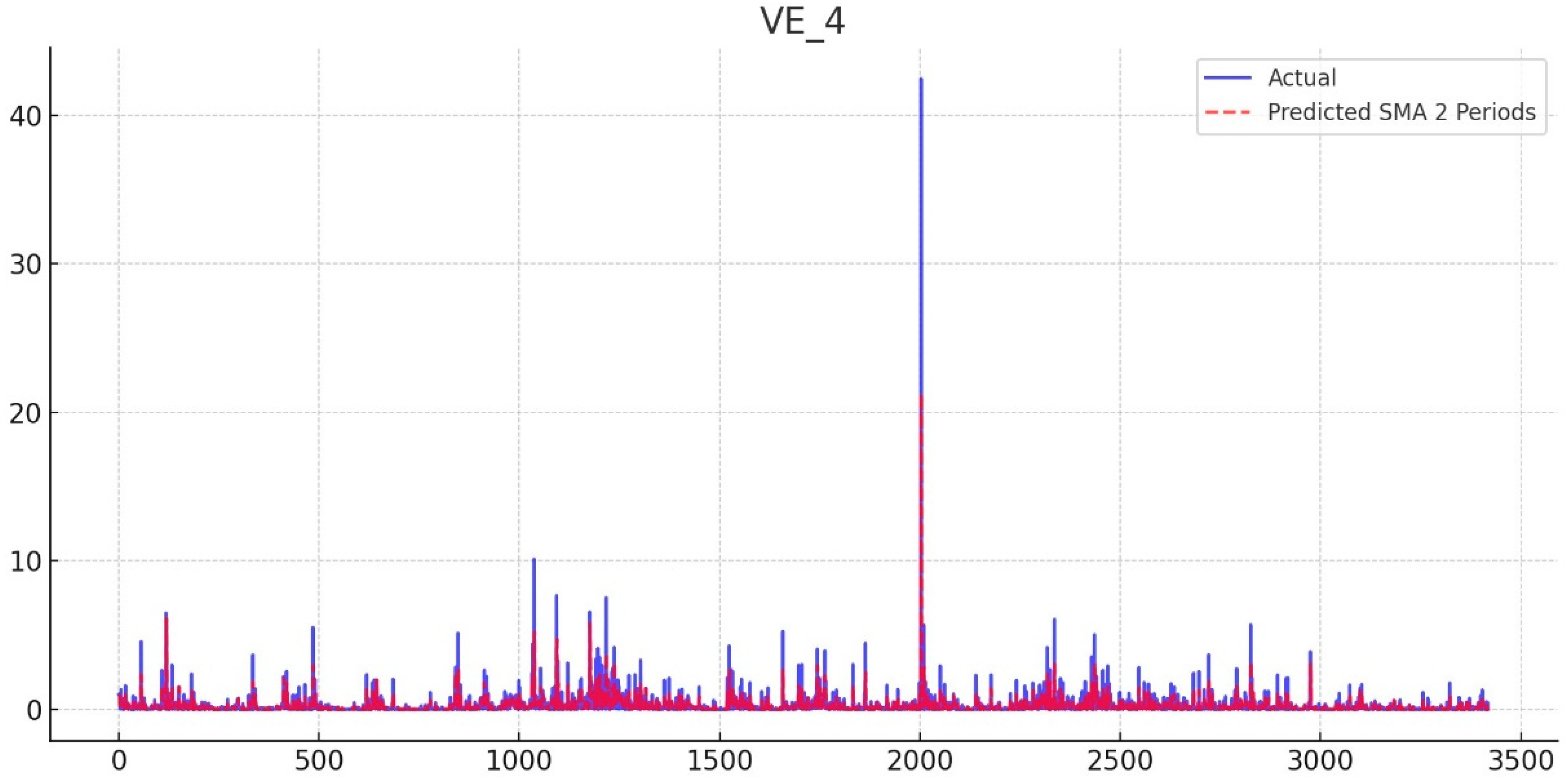
| Open | High | Low | Close | |
|---|---|---|---|---|
| count | 3421.0 | 3421.0 | 3421.0 | 3421.0 |
| mean | 14,804.1 | 15,149.2 | 14,432.4 | 14,814.9 |
| std | 16,322.8 | 16,712.6 | 15,885.8 | 16,324.6 |
| min | 176.9 | 211.7 | 171.5 | 178.1 |
| 25% | 922.2 | 940.0 | 915.8 | 922.0 |
| 50% | 8315.7 | 8509.1 | 8140.9 | 8309.3 |
| 75% | 24,640.0 | 25,190.3 | 24,225.1 | 24,664.8 |
| max | 67,549.7 | 68,789.6 | 66,382.1 | 67,566.8 |
| Hurst Exponent | 0.636 | 0.590 | 0.586 | 0.632 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zournatzidou, G.; Farazakis, D.; Mallidis, I.; Floros, C. Stochastic Patterns of Bitcoin Volatility: Evidence across Measures. Mathematics 2024, 12, 1719. https://doi.org/10.3390/math12111719
Zournatzidou G, Farazakis D, Mallidis I, Floros C. Stochastic Patterns of Bitcoin Volatility: Evidence across Measures. Mathematics. 2024; 12(11):1719. https://doi.org/10.3390/math12111719
Chicago/Turabian StyleZournatzidou, Georgia, Dimitrios Farazakis, Ioannis Mallidis, and Christos Floros. 2024. "Stochastic Patterns of Bitcoin Volatility: Evidence across Measures" Mathematics 12, no. 11: 1719. https://doi.org/10.3390/math12111719
APA StyleZournatzidou, G., Farazakis, D., Mallidis, I., & Floros, C. (2024). Stochastic Patterns of Bitcoin Volatility: Evidence across Measures. Mathematics, 12(11), 1719. https://doi.org/10.3390/math12111719






