A Bi-Starlike Class in a Leaf-like Domain Defined through Subordination via
Abstract
:1. Introduction, Definitions, and Motivation
2. Definition and Example
3. The Bounds of the Coefficients within the Class
4. The Fekete–Szegö Functional
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, S.S. Differential inequalities and Caratheodory functions. Bull. Am. Math. Soc. 1975, 81, 79–81. [Google Scholar] [CrossRef]
- Duren, P.L. Univalent Functions; Grundlehren der Mathematischen Wissenschaften, Band 259; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Tokyo, Japan, 1983. [Google Scholar]
- Ma, W.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Conference on Complex Analysis, Tianjin, China, 19–23 June 1992; pp. 157–169. [Google Scholar]
- Sokół, J.; Stankiewicz, J. Radius of convexity of some subclasses of strongly starlike functions. Zesz. Nauk. Politech. Rzesz. Mat. 1996, 19, 101–105. [Google Scholar]
- Raina, R.K.; Sokol, R.K. On Coefficient estimates for a certain class of starlike functions. Hacet. J. Math. Stat. 2015, 44, 1427–1433. [Google Scholar] [CrossRef]
- Priya, M.H.; Sharma, R.B. On a class of bounded turning functions subordinate to a leaf-like domain. J. Phys. Conf. Ser. 2018, 1000, 012056. [Google Scholar] [CrossRef]
- Rath, B.; Kumar, K.S.; Krishna, D.V.; Lecko, A. The sharp bound of the third Hankel determinant for starlike functions of order 1/2. Complex Anal. Oper. Theory 2022, 16, 1–8. [Google Scholar] [CrossRef]
- Mahmood, S.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Khan, B.; Ali, I. Upper bound of the third Hankel determinant for a subclass of q-starlike functions. Symmetry 2019, 11, 347. [Google Scholar] [CrossRef]
- Ullah, K.; Srivastava, H.M.; Rafiq, A.; Arif, M.; Arjika, S. A study of sharp coefficient bounds for a new subfamily of starlike functions. J. Inequal. Appl. 2021, 2021, 194. [Google Scholar] [CrossRef]
- Shi, L.; Shutaywi, M.; Alreshidi, N.; Arif, M.; Ghufran, S.M. The sharp bounds of the third-order Hankel determinant for certain analytic functions associated with an eight-shaped domain. Fractal Fract. 2022, 6, 223. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, 2nd ed.; Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, MA, USA, 2004; Volume 96. [Google Scholar]
- Pashaev, O.K.; Nalci, S. q-analytic functions, fractals and generalized analytic functions. J. Phys. A Math. Theor. 2014, 47, 045204. [Google Scholar] [CrossRef]
- Alsoboh, A.; Oros, G.I. A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via q-Calculus. Mathematics 2024, 12, 1594. [Google Scholar] [CrossRef]
- Ahuja, O.; Bohra, N.; Cetinkaya, A.; Kumar, S. Univalent functions associated with the symmetric points and cardioid-shaped domain involving (p,q)-calculus. Kyungpook Math. J. 2021, 61, 75–98. [Google Scholar]
- Ismail, M.E.; Merkes, E.; Styer, D. A generalization of starlike functions. Complex Var. Theory Appl. 1990, 14, 77–84. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Khan, B.; Khan, N.; Ahmad, Q.Z.; Tahir, M. A generalized conic domain and its applications to certain subclasses of analytic functions. Rocky Mt. J. Math. 2019, 49, 2325–2346. [Google Scholar] [CrossRef]
- Srivastava, H.M. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Al-Salam, W.A. Some fractional q-integrals and q-derivatives. Proc. Edinb. Math. Soc. 1966, 15, 135–140. [Google Scholar] [CrossRef]
- Agarwal, R.P. Certain fractional q-integrals and q-derivatives. Proc. Camb. Philos. 1969, 66, 365–370. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Darus, M.; Rudder, C.A. Studying the Harmonic Functions Associated with Quantum Calculus. Mathematics 2023, 11, 2220. [Google Scholar] [CrossRef]
- Uçar, H.E.Ö. Coefficient inequality for q-starlike functions. App. Math. Comput. 2016, 276, 122–126. [Google Scholar] [CrossRef]
- Amourah, A.; Frasin, B.A.; Ahmad, M.; Yousef, F. Exploiting the Pascal Distribution Series and Gegenbauer Polynomials to Construct and Study a New Subclass of Analytic Bi-Univalent Functions. Symmetry 2022, 14, 147. [Google Scholar] [CrossRef]
- Amourah, A.; Abdelkarim, H.; AL-Elaumi, A. (p, q)-Chebyshev polynomials and their applications to bi-univalent functions. J. TWMS J. Appl. Eng. Math. 2022, 12, 481–486. [Google Scholar]
- Alb Lupas, A.; Oros, G.I. Sandwich-type results regarding Riemann-Liouville fractional integral of q-hypergeometric function. Demonstr. Math. 2023, 56, 20220186. [Google Scholar] [CrossRef]
- Illafe, M.; Yousef, F.; Haji Mohd, M.; Supramaniam, S. Initial Coefficients Estimates and Fekete–Szegö Inequality Problem for a General Subclass of Bi-Univalent Functions Defined by Subordination. Axioms 2023, 12, 235. [Google Scholar] [CrossRef]
- Andrei, L.; Caus, V.A. Subordinations Results on a q-Derivative Differential Operator. Mathematics 2024, 12, 208. [Google Scholar] [CrossRef]
- Khan, M.F.; AbaOud, M. New Applications of Fractional q-Calculus Operator for a New Subclass of q-Starlike Functions Related with the Cardioid Domain. Fractal Fract. 2024, 8, 71. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Darus, M.; Rudder, C.A. Investigating New Subclasses of Bi-Univalent Functions Associated with q-Pascal Distribution Series Using the Subordination Principle. Symmetry 2023, 15, 1109. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Sakar, F.M.; Ogilat, O.; Gharib, G.M.; Zomot, N. Coefficient Estimation Utilizing the Faber Polynomial for a Subfamily of Bi-Univalent Functions. Axioms 2023, 12, 512. [Google Scholar] [CrossRef]
- Srivastava, H.M.; El-Deeb, S.M. The Faber polynomial expansion method and the Taylor-Maclaurin coefficient estimates of bi-close-to-convex functions connected with the q-convolution. AIMS Math. 2020, 5, 7087–7106. [Google Scholar] [CrossRef]
- Alkouri, A.; AbuHijleh, E.A.; Alafifi, G.; Almuhur, E.; Al-Zubi, F.M. More on complex hesitant fuzzy graphs. AIMS Mathematics 2023, 8, 30429–30444. [Google Scholar] [CrossRef]
- Alsharo, D.; Abuteen, E.; Alkouri, A.; Alkhasawneh, M.; Al-Zubi, F. Complex shadowed set theory and its application in decision-making problems. AIMS Math. 2024, 9, 16810–16825. [Google Scholar] [CrossRef]
- Fekete, M.; Szegö, G. Eine Bemerkung über ungerade schlichte Funktionen. J. Lond. Math. Soc. 1933, 1, 85–89. [Google Scholar] [CrossRef]
- Zaprawa, P. On the Fekete-Szegö problem for classes of bi-univalent functions. Bull. Belg. Math. Soc.—Simon Stevin 2014, 21, 169–178. [Google Scholar] [CrossRef]
| The Function | The Corresponding Inverse |
|---|---|
| Author/s | Year | Reference | |
|---|---|---|---|
| Sokól and Stankiewicz | 1996 | [4] | |
| Raina and Sokól | 2015 | [5] | |
| Priya and Sharma | 2018 | [6] | |
| Rath et al. | 2022 | [7] | |
| Mahmoud et al. | 2019 | [8] | |
| Ullah et al. | 2021 | [9] | |
| Shi et al. | 2022 | [10] |
| n | |
|---|---|
| ⋮ | ⋮ |
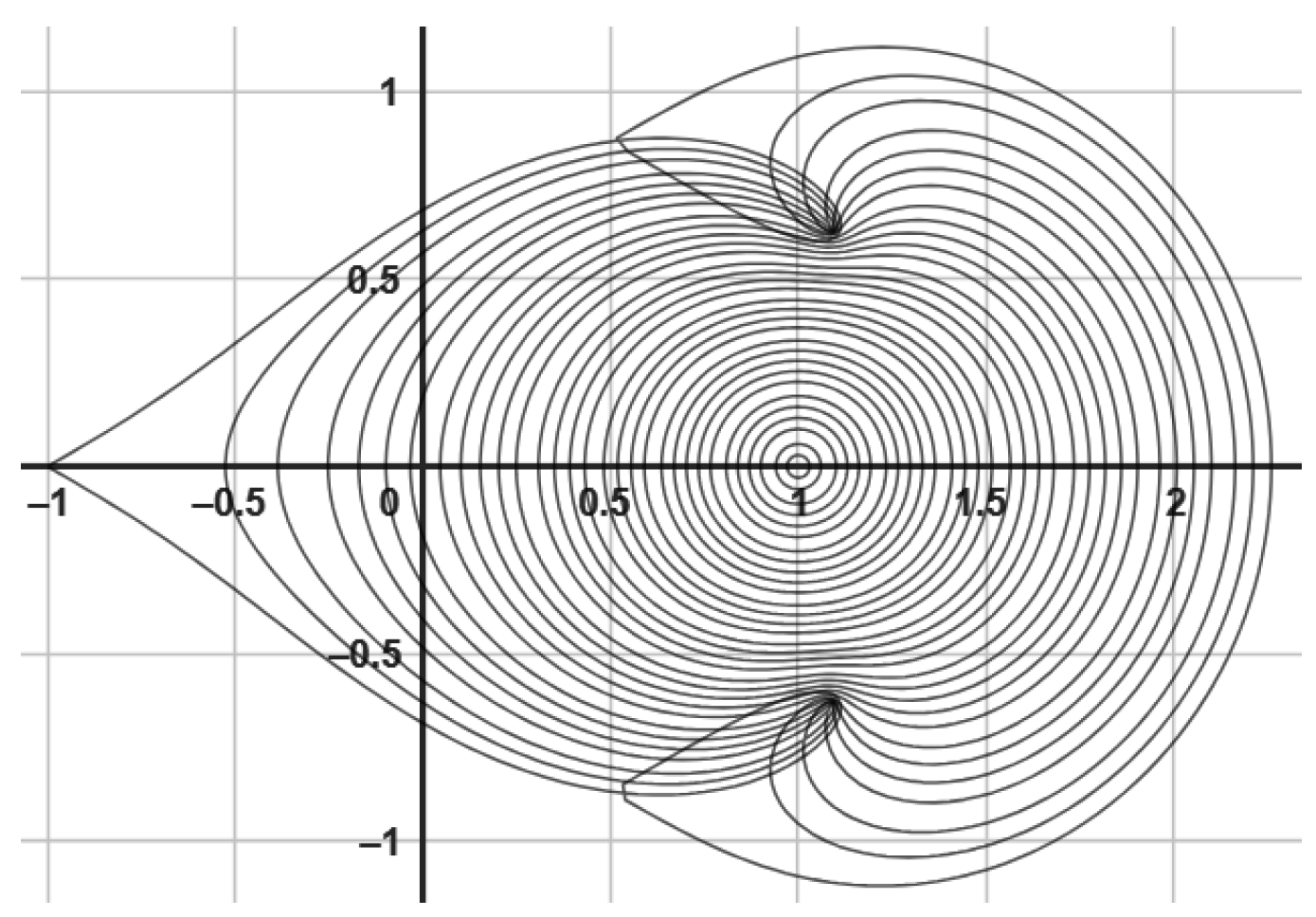
 |  |
| (a) Depicts the image of with | (b) Displays the image of with |
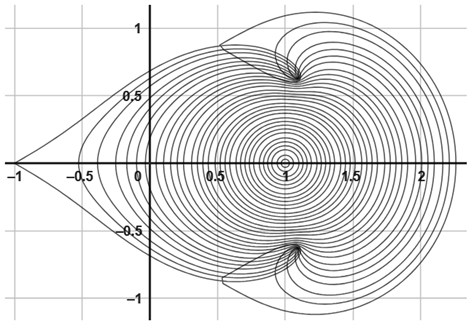
 |  |
| (c) The image of with | (d) The image of with |
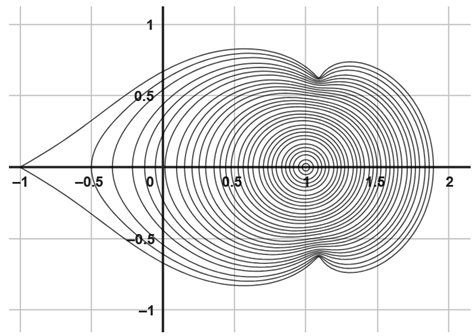
 | 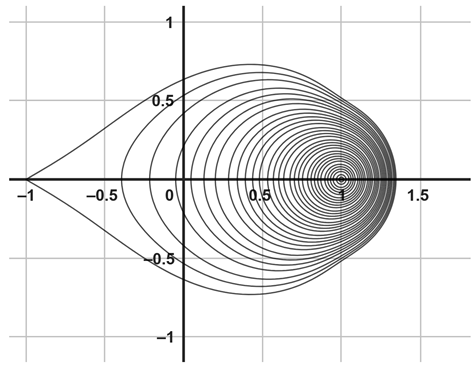 |
| (e) The image of with | (f) The image of as . |
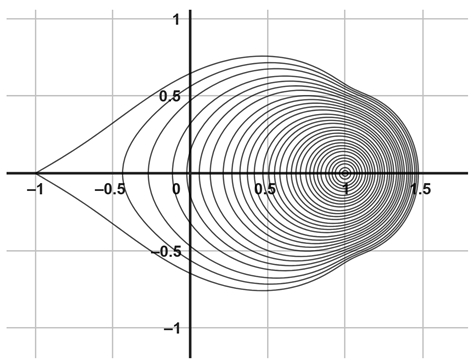
 | 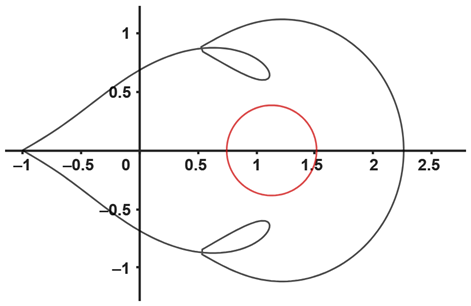 |
| (a) The image of (red color) and (black color) with , and | (b) The image of (red color) and (black color) with and |
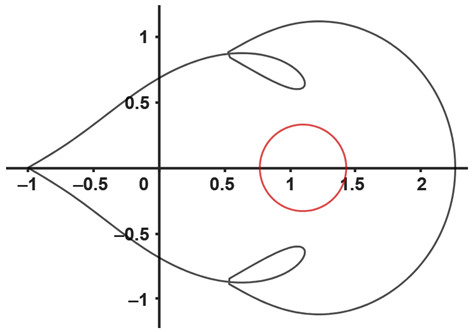 |  |
| (c) The image of (red color) and (black color) with and . | (d) The image of (red color) and (black color) with and . |
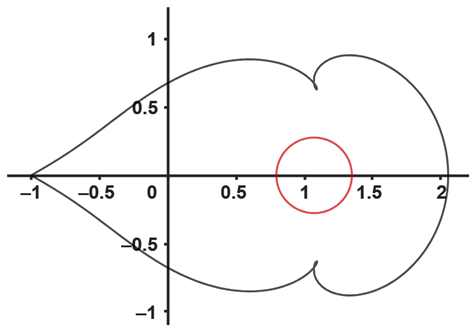 |  |
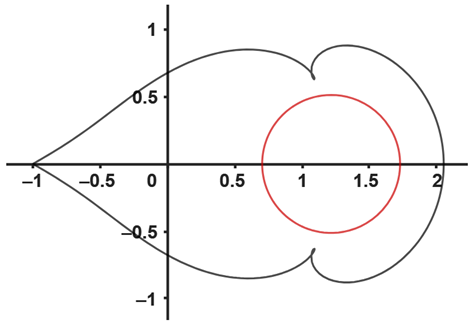
| (e) The image of (red color) and (black color) with , and | (f) The image of (red color) and (black color) with and |
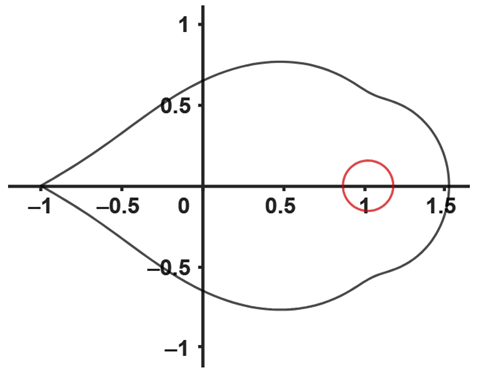 | 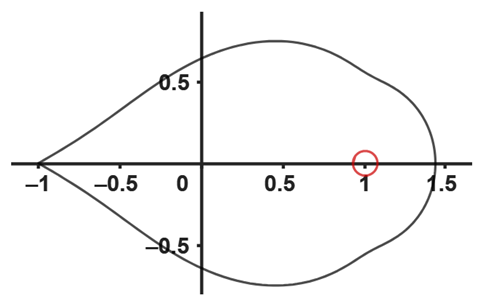 |
| (g) The image of (red color) and (black color) with , and | (h) The image of (red color) and (black color) and |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amourah, A.; Alsoboh, A.; Breaz, D.; El-Deeb, S.M.
A Bi-Starlike Class in a Leaf-like Domain Defined through Subordination via
Amourah A, Alsoboh A, Breaz D, El-Deeb SM.
A Bi-Starlike Class in a Leaf-like Domain Defined through Subordination via
Amourah, Ala, Abdullah Alsoboh, Daniel Breaz, and Sheza M. El-Deeb.
2024. "A Bi-Starlike Class in a Leaf-like Domain Defined through Subordination via





