Predicting Scientific Breakthroughs Based on Structural Dynamic of Citation Cascades
Abstract
1. Introduction
2. Background
2.1. Definition and Prediction of Breakthroughs
2.1.1. Scientific Breakthroughs
2.1.2. Predicting Breakthroughs
2.2. Citation Cascades
3. Methodology
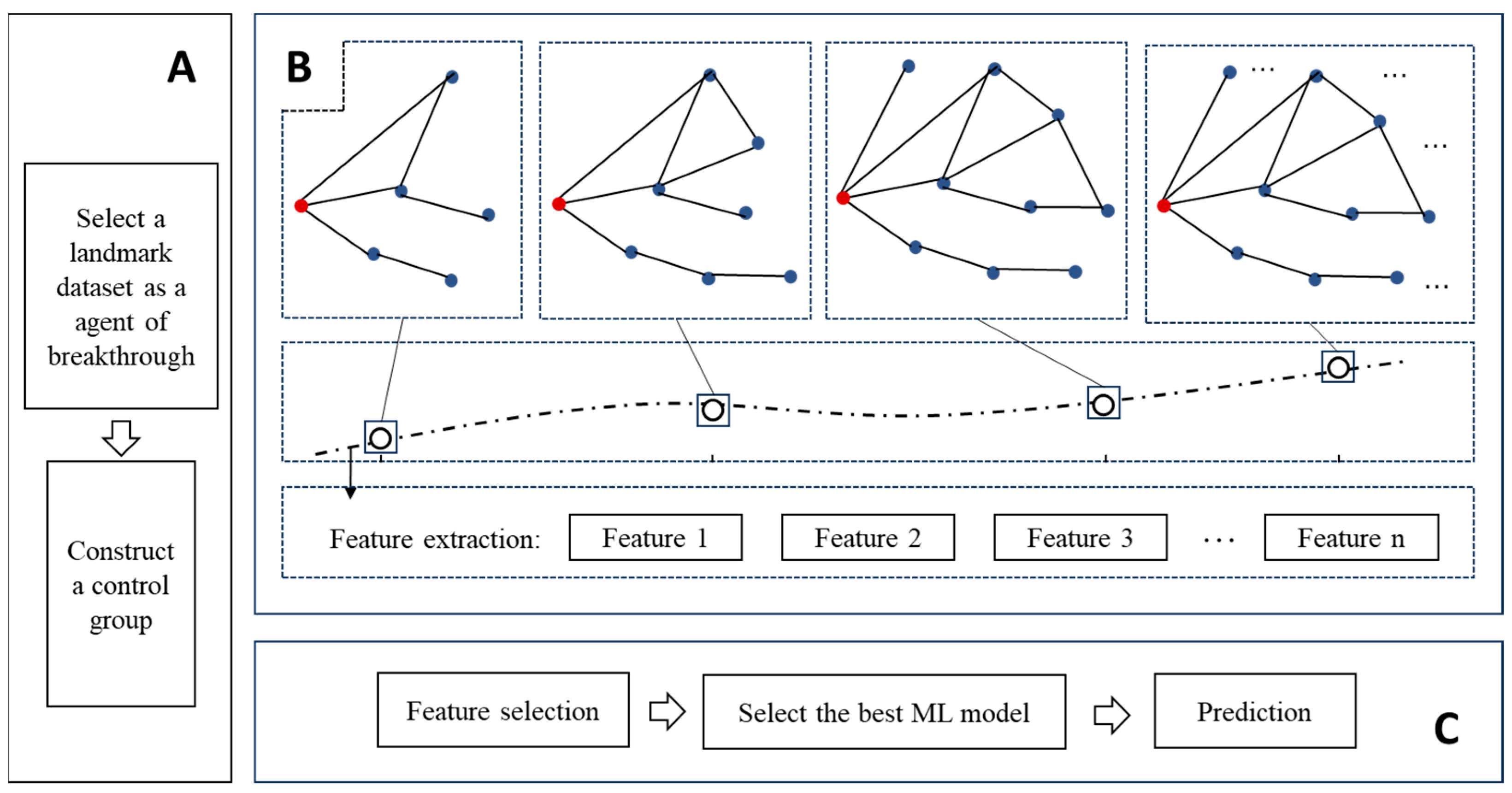
3.1. Overviews of the Research Processs
- (1)
- The dataset of Nobel Prize-winning papers is chosen as a landmark of scientific breakthroughs. (More details are shown in Section 3.2).
- (2)
- Find a control group for the breakthrough dataset, representing the non-breakthrough papers. (More details are shown in Section 3.2).
- (3)
- Construct citation cascade networks for each paper using our method. After that, a series of snapshots of the cascade networks is generated. (More details are shown in Section 3.3).
- (4)
- Calculate specific structural indicators for these series of citation cascade network snapshots. The indicators include the number of nodes, average clustering coefficient, average degree, maximum closeness centrality, number of components, PageRank value of the focus paper, mean value and variance of PageRank, and the von Neumann graph entropy. In this step, the series data for these metrics is then generated. (More details are shown in Section 3.4 and Section 3.5).
- (5)
- Feature selections: extract certain features from the series data. (More details are shown in Section 3.5).
- (6)
- Finally, the extracted features are utilized to forecast scientific breakthroughs using machine learning algorithms. (More details are shown in Section 3.5).
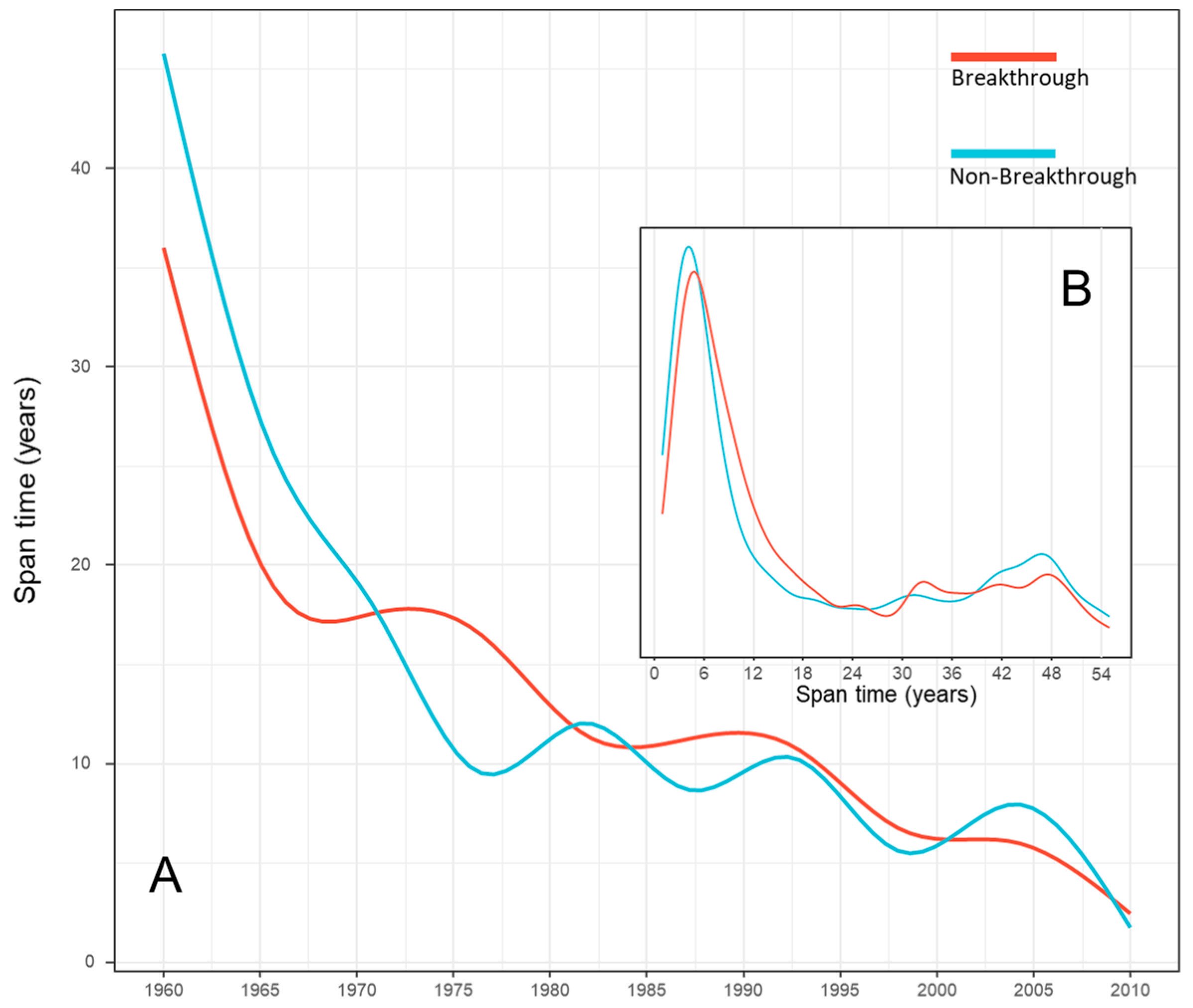
3.2. Landmark Dataset
3.3. Construction of Citation Cascades
| Algorithm 1. Create citation cascade network. |
| Input: (Focus paper). Output: Citation cascade in chronological order. |
|
3.4. Predictors
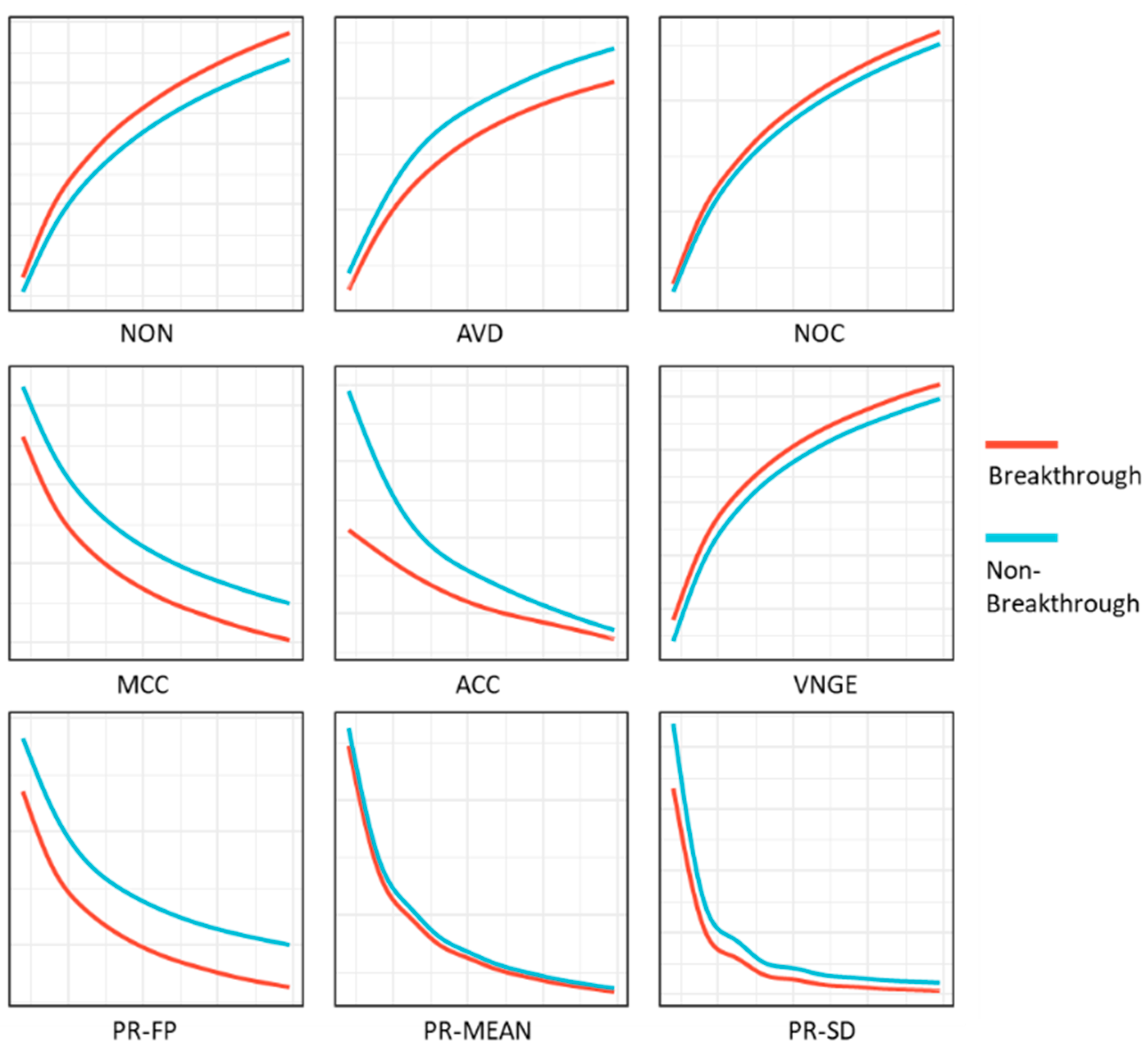
3.4.1. Topological Indicators
3.4.2. PageRank Indicator
3.4.3. Graph Entropy Indicator
| Algorithm 2. Approximate Von-Neumann Graph Entropy (VNGE). |
| Input: Adjacency matrix. Output: Approximate von Neumann graph entropy |
|
3.5. Forecasting Process
3.6. Benchmark Indicators
4. Results
4.1. Descriptive Analysis
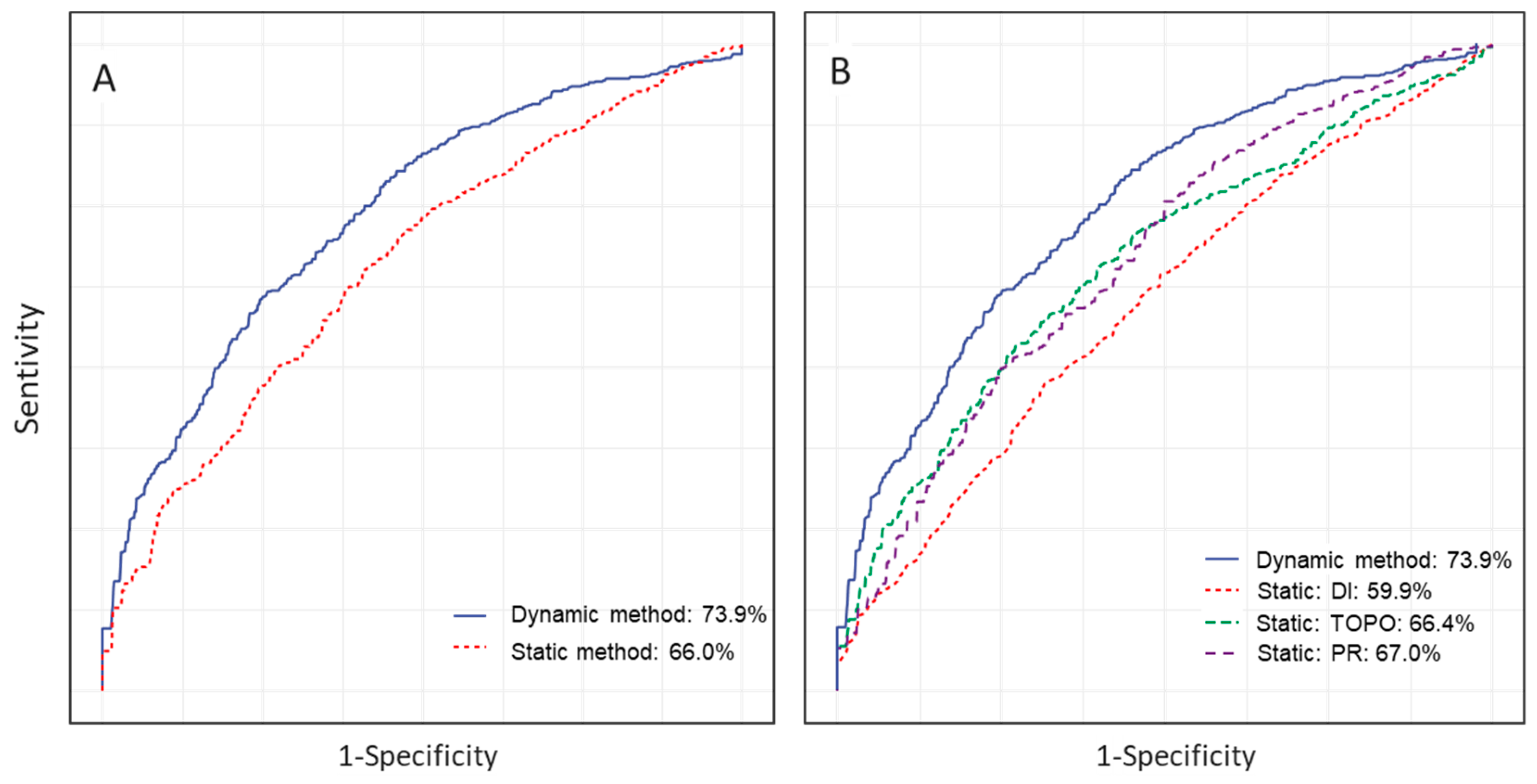
4.2. Prediction Results
4.3. Comparisons
5. Discussions and Conclusions
5.1. Main Contributions
5.2. Implications
5.3. Limitations and Future Directions
5.4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wuestman, M.; Hoekman, J.; Frenken, K. A typology of scientific breakthroughs. Quant. Sci. Stud. 2020, 1, 1203–1222. [Google Scholar] [CrossRef]
- Min, C.; Bu, Y.; Sun, J. Predicting scientific breakthroughs based on knowledge structure variations. Technol. Forecast. Soc. Chang. 2021, 164, 120502. [Google Scholar] [CrossRef]
- Ramdorai, A.; Herstatt, C.; Ramdorai, A.; Herstatt, C. Disruptive innovations theory. In Frugal Innovation in Healthcare: How Targeting Low-Income Markets Leads to Disruptive Innovation; Springer: Berlin/Heidelberg, Germany, 2015; pp. 27–38. [Google Scholar]
- Kuhn, T.S. The Structure of Scientific Revolutions; University of Chicago Press: Chicago, IL, USA, 1997; Volume 962. [Google Scholar]
- Min, C.; Sun, J.; Ding, Y. Quantifying the evolution of citation cascades. Proc. Assoc. Inf. Sci. Technol. 2017, 54, 761–763. [Google Scholar] [CrossRef]
- Min, C.; Chen, Q.; Yan, E.; Bu, Y.; Sun, J. Citation cascade and the evolution of topic relevance. J. Assoc. Inf. Sci. Technol. 2021, 72, 110–127. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Mao, J.; Bai, Y.; Liang, Z.; Li, G. Quantifying scientific breakthroughs by a novel disruption indicator based on knowledge entities. J. Assoc. Inf. Sci. Technol. 2023, 74, 150–167. [Google Scholar] [CrossRef]
- Min, C.; Bu, Y.; Wu, D.; Ding, Y.; Zhang, Y. Identifying citation patterns of scientific breakthroughs: A perspective of dynamic citation process. Inf. Process. Manag. 2021, 58, 102428. [Google Scholar] [CrossRef]
- Li, X.; Wen, Y.; Jiang, J.; Daim, T.; Huang, L. Identifying potential breakthrough research: A machine learning method using scientific papers and Twitter data. Technol. Forecast. Soc. Chang. 2022, 184, 122042. [Google Scholar] [CrossRef]
- Alberts, B. Science breakthroughs. Science 2011, 334, 1604. [Google Scholar] [CrossRef]
- Taques, F.H. Challenges in the post-covid-19 world. Socioecon. Anal. 2024, 2, 1–5. [Google Scholar] [CrossRef]
- Koshland Jr, D.E. The cha-cha-cha theory of scientific discovery. Science 2007, 317, 761–762. [Google Scholar] [CrossRef]
- Hage, J.; Mote, J. Transformational organizations and a burst of scientific breakthroughs: The Institut Pasteur and biomedicine, 1889–1919. Soc. Sci. Hist. 2010, 34, 13–46. [Google Scholar] [CrossRef]
- Grumet, G.W. Insubordination and genius: Galileo, Darwin, Pasteur, Einstein, and Pauling. Psychol. Rep. 2008, 102, 819–847. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Veugelers, R.; Stephan, P. Bias against novelty in science: A cautionary tale for users of bibliometric indicators. Res. Policy 2017, 46, 1416–1436. [Google Scholar] [CrossRef]
- Wu, L.; Wang, D.; Evans, J.A. Large teams develop and small teams disrupt science and technology. Nature 2019, 566, 378–382. [Google Scholar] [CrossRef]
- Funk, R.J.; Owen-Smith, J. A dynamic network measure of technological change. Manag. Sci. 2017, 63, 791–817. [Google Scholar] [CrossRef]
- Park, M.; Leahey, E.; Funk, R.J. Papers and patents are becoming less disruptive over time. Nature 2023, 613, 138–144. [Google Scholar] [CrossRef]
- Lin, Y.; Frey, C.B.; Wu, L. Remote collaboration fuses fewer breakthrough ideas. Nature 2023, 623, 987–991. [Google Scholar] [CrossRef] [PubMed]
- Bornmann, L.; Devarakonda, S.; Tekles, A.; Chacko, G. Are disruption index indicators convergently valid? The comparison of several indicator variants with assessments by peers. Quant. Sci. Stud. 2020, 1, 1242–1259. [Google Scholar] [CrossRef]
- Wei, C.; Zhao, Z.; Shi, D.; Li, J. Nobel-Prize-winning papers are significantly more highly-cited but not more disruptive than non-prize-winning counterparts. In iConference 2020 Proceedings; iSchools: Westford, MA, USA, 2020. [Google Scholar]
- Sizemore, A.E.; Karuza, E.A.; Giusti, C.; Bassett, D.S. Knowledge gaps in the early growth of semantic feature networks. Nat. Hum. Behav. 2018, 2, 682–692. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Berkhin, P. A survey on PageRank computing. Internet Math. 2005, 2, 73–120. [Google Scholar] [CrossRef]
- Mukherjee, S.; Romero, D.M.; Jones, B.; Uzzi, B. The nearly universal link between the age of past knowledge and tomorrow’s breakthroughs in science and technology: The hotspot. Sci. Adv. 2017, 3, e1601315. [Google Scholar] [CrossRef]
- Han, L.; Escolano, F.; Hancock, E.R.; Wilson, R.C. Graph characterizations from von Neumann entropy. Pattern Recognit. Lett. 2012, 33, 1958–1967. [Google Scholar] [CrossRef]
- Xu, H.; Luo, R.; Winnink, J.; Wang, C.; Elahi, E. A methodology for identifying breakthrough topics using structural entropy. Inf. Process. Manag. 2022, 59, 102862. [Google Scholar] [CrossRef]
- Savov, P.; Jatowt, A.; Nielek, R. Identifying breakthrough scientific papers. Inf. Process. Manag. 2020, 57, 102168. [Google Scholar] [CrossRef]
- Jia, W.; Xie, Y.; Zhao, Y.; Yao, K.; Shi, H.; Chong, D. Research on disruptive technology recognition of China’s electronic information and communication industry based on patent influence. J. Glob. Inf. Manag. (JGIM) 2021, 29, 148–165. [Google Scholar] [CrossRef]
- Kelly, B.; Papanikolaou, D.; Seru, A.; Taddy, M. Measuring technological innovation over the long run. Am. Econ. Rev. Insights 2021, 3, 303–320. [Google Scholar] [CrossRef]
- Yan, E. Disciplinary knowledge production and diffusion in science. J. Assoc. Inf. Sci. Technol. 2016, 67, 2223–2245. [Google Scholar] [CrossRef]
- Datta, A.A.; Srivastava, S. (Re) conceptualizing technological breakthrough innovation: A systematic review of the literature and proposed framework. Technol. Forecast. Soc. Chang. 2023, 194, 122740. [Google Scholar] [CrossRef]
- Sun, Y.; Latora, V. The evolution of knowledge within and across fields in modern physics. Sci. Rep. 2020, 10, 12097. [Google Scholar] [CrossRef]
- Satarova, B.; Siddiqui, T.; Raza, H.; Abbasi, N.; Kydyrkozha, S. A Systematic Review of “The Performance of Knowledge Organizations and Modelling Human Action”. Socioecon. Anal 2023, 1, 56–77. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Wu, L.; Liu, S.; Rajapakse, I. Fast incremental von neumann graph entropy computation: Theory, algorithm, and applications. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Lv, Y.; Ding, Y.; Song, M.; Duan, Z. Topology-driven trend analysis for drug discovery. J. Informetr. 2018, 12, 893–905. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Z. The effect of citation behaviour on knowledge diffusion and intellectual structure. J. Informetr. 2022, 16, 101225. [Google Scholar] [CrossRef]
- Bu, Y.; Waltman, L.; Huang, Y. A multidimensional framework for characterizing the citation impact of scientific publications. Quant. Sci. Stud. 2021, 2, 155–183. [Google Scholar] [CrossRef]
- Nepomuceno, T.C.C.; Piubello Orsini, L.; de Carvalho, V.D.H.; Poleto, T.; Leardini, C. The core of healthcare efficiency: A comprehensive bibliometric review on frontier analysis of hospitals. Healthcare 2022, 10, 1316. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Yang, X.; Zhang, Y. The effect of social media knowledge cascade: An analysis of scientific papers diffusion. Scientometrics 2023, 128, 5169–5195. [Google Scholar] [CrossRef]
- Rousseau, R. The Gozinto theorem: Using citations to determine influences on a scientific publication. Scientometrics 1987, 11, 217–229. [Google Scholar] [CrossRef]
- Van Raan, A.F. Sleeping beauties in science. Scientometrics 2004, 59, 467–472. [Google Scholar] [CrossRef]
- Yu, D.; Yan, Z. Combining machine learning and main path analysis to identify research front: From the perspective of science-technology linkage. Scientometrics 2022, 127, 4251–4274. [Google Scholar] [CrossRef]
- Nepomuceno, T.C.C.; de Carvalho, V.D.H.; Nepomuceno, K.T.C.; Costa, A.P.C. Exploring knowledge benchmarking using time-series directional distance functions and bibliometrics. Expert Syst. 2023, 40, e12967. [Google Scholar] [CrossRef]
- Van Eck, N.; Waltman, L. Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yin, Y.; Fortunato, S.; Wang, D. A dataset of publication records for Nobel laureates. Sci. Data 2019, 6, 33. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Yin, Y.; Liu, L.; Wang, D. SciSciNet: A large-scale open data lake for the science of science research. Sci. Data 2023, 10, 315. [Google Scholar] [CrossRef] [PubMed]
- Priem, J.; Piwowar, H.; Orr, R. OpenAlex: A fully-open index of scholarly works, authors, venues, institutions, and concepts. arXiv 2022, arXiv:2205.01833. [Google Scholar]
- Liu, X.; Fu, L.; Wang, X.; Zhou, C. On the similarity between von Neumann graph entropy and structural information: Interpretation, computation, and applications. IEEE Trans. Inf. Theory 2022, 68, 2182–2202. [Google Scholar] [CrossRef]
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time series feature extraction on basis of scalable hypothesis tests (tsfresh–a python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Li, X.; Ma, X.; Feng, Y. Early identification of breakthrough research from sleeping beauties using machine learning. J. Informetr. 2024, 18, 101517. [Google Scholar] [CrossRef]




| Pred-Ture | Pred-False | |
|---|---|---|
| Truth-True | 436 | 216 |
| Truth-False | 226 | 462 |
| Metrics | ROC-AUC (%) | ACCURACY (%) | F1-SCORE (%) | RECALL (%) |
|---|---|---|---|---|
| Score | 73.9 | 67.01 | 66.38 | 66.32 |
| Benchmarks | ROC-AUC | Improvement (%) |
|---|---|---|
| Dynamic method | 73.9% | \ |
| Static method | 66.0% | +7.9% |
| Static: DI (Disruption Index) | 59.9% | +14.0% |
| Static: TOPO (Topological indicator of cascades) | 66.4% | +7.5% |
| Static: PR (PageRank) | 67.0% | +6.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Liang, Y.; Xie, Y. Predicting Scientific Breakthroughs Based on Structural Dynamic of Citation Cascades. Mathematics 2024, 12, 1741. https://doi.org/10.3390/math12111741
Yu H, Liang Y, Xie Y. Predicting Scientific Breakthroughs Based on Structural Dynamic of Citation Cascades. Mathematics. 2024; 12(11):1741. https://doi.org/10.3390/math12111741
Chicago/Turabian StyleYu, Houqiang, Yian Liang, and Yinghua Xie. 2024. "Predicting Scientific Breakthroughs Based on Structural Dynamic of Citation Cascades" Mathematics 12, no. 11: 1741. https://doi.org/10.3390/math12111741
APA StyleYu, H., Liang, Y., & Xie, Y. (2024). Predicting Scientific Breakthroughs Based on Structural Dynamic of Citation Cascades. Mathematics, 12(11), 1741. https://doi.org/10.3390/math12111741






