A Rumor Propagation Model Considering Media Effect and Suspicion Mechanism under Public Emergencies
Abstract
1. Introduction
- (1)
- Propose an improved rumor propagation model, considering the suspicion mechanism. Analyze the characteristics of propagation and the evolution process of propagation at different stages to provide some theoretical support for the mathematical model for rumor governance.
- (2)
- Use the quadratic matrix method to obtain the basic reproduction number. Based on the Jacobian matrix, Lyapunov’s stability theory, and Lassalle’s invariance principle, discuss the local and global stability of the no-rumor equilibrium point.
- (3)
- Based on the above model, we establish the time-delay differential equation to study the delay in transforming the susceptible into the infectious, caused by punishment and anti-fraud awareness.
- (4)
- To study the Deffuant opinion exchange model under the influence of the media, and to simulate the evolution process of rumor propagation under the same and different views.
2. Materials and Methods
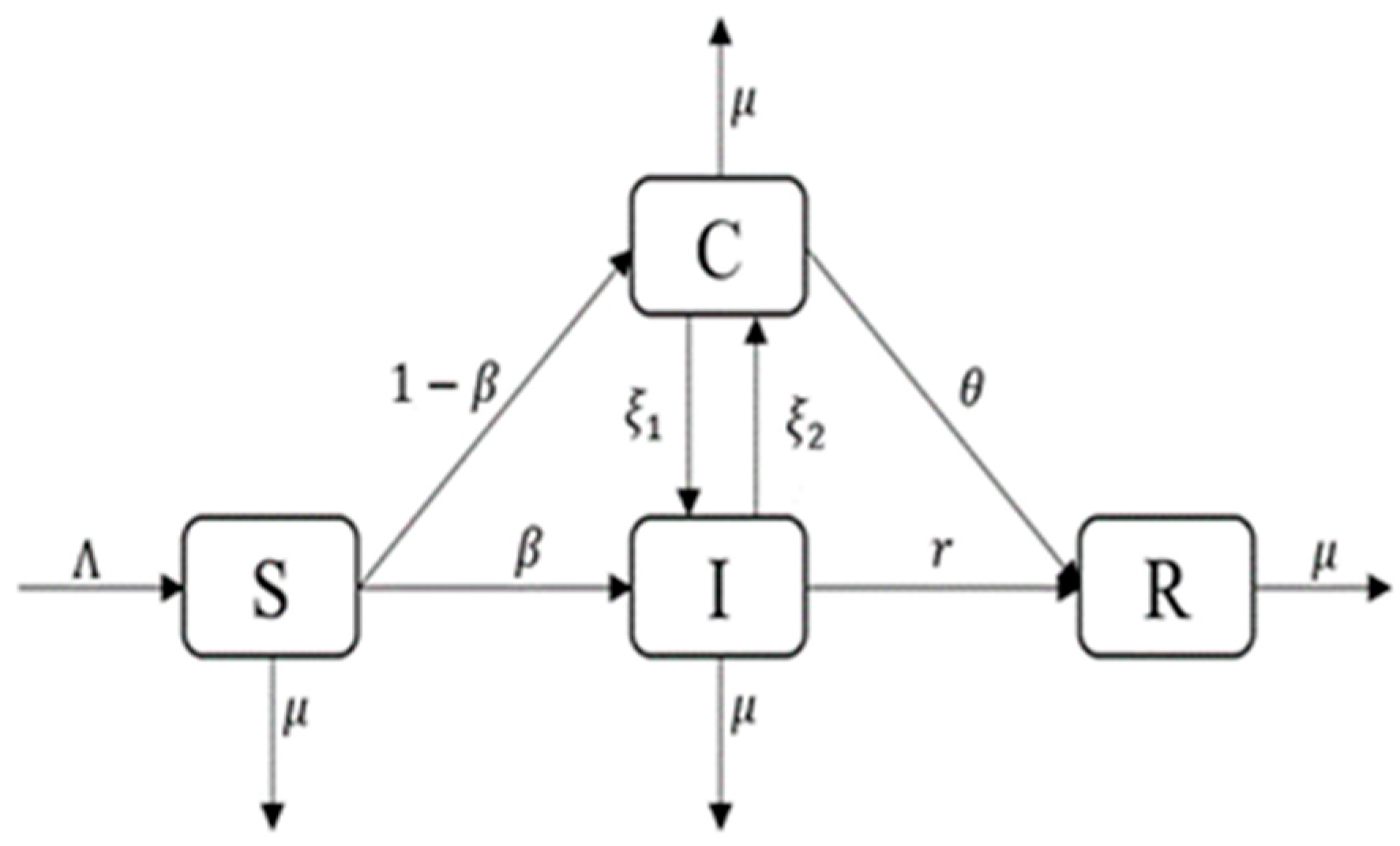
2.1. SCIR Model under Media Influence
- (1)
- When a susceptible person hears the rumor, he becomes infectious with probability β or compromised with 1 − β.
- (2)
- Infectious, due to their own reasons or the influence of the media, forgets or senses the rumor with probability γ and becomes recovered.
- (3)
- Infectious diseases become compromised with a probability of ξ2 after contact with other infectious diseases or exposure to the media.
- (4)
- The compromised recover through their own experience or the influence of the media to detect the rumor with a probability of θ, or to believe that the rumor becomes infectious with a probability of ξ1.
- (1)
- Crowd attributes: the types of crowds are evenly mixed, and the impact of regional differences on crowd density is not considered. Considering the mobility of the population, the corresponding parameters are set to reflect the incoming and outgoing of the population.
- (2)
- Mode of communication: The population is generally susceptible, and the mode of communication considers the mode of human-to-human transmission, the reasons of the people themselves, and the influence of the media.
- (3)
- Subject characteristics: the suspects in the crowd are transformed from the easily deceived and the deceived, and the deceived are contagious. In addition, once a person is confirmed to have been recovered, they are deemed to be incapable of spreading rumors.
2.2. Time-Delayed Rumor Propagation Model under Penalty Mechanism
- (1)
- When H1 holds, i.e., τ = 0, the model is locally stable.
- (2)
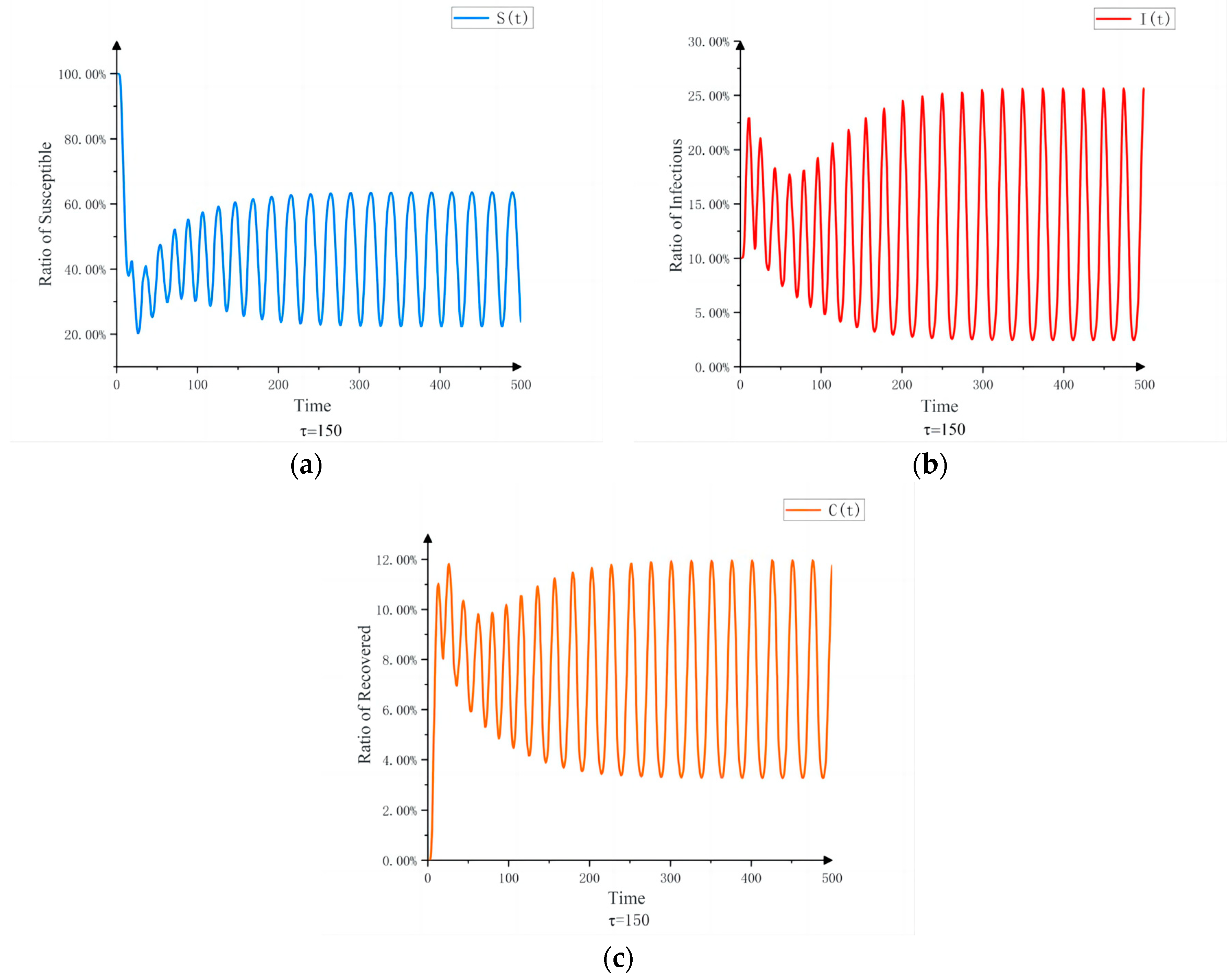
- When H2 and H3 are true, if 0 < τ < τ0, the propagation model will tend to be asymptotically stable. If τ = τ0, the propagation model starts to have a Hopf bifurcation; if τ > τ0, the propagation model will oscillate, and the model will no longer be stable.
2.3. Deffuant Model
3. Results
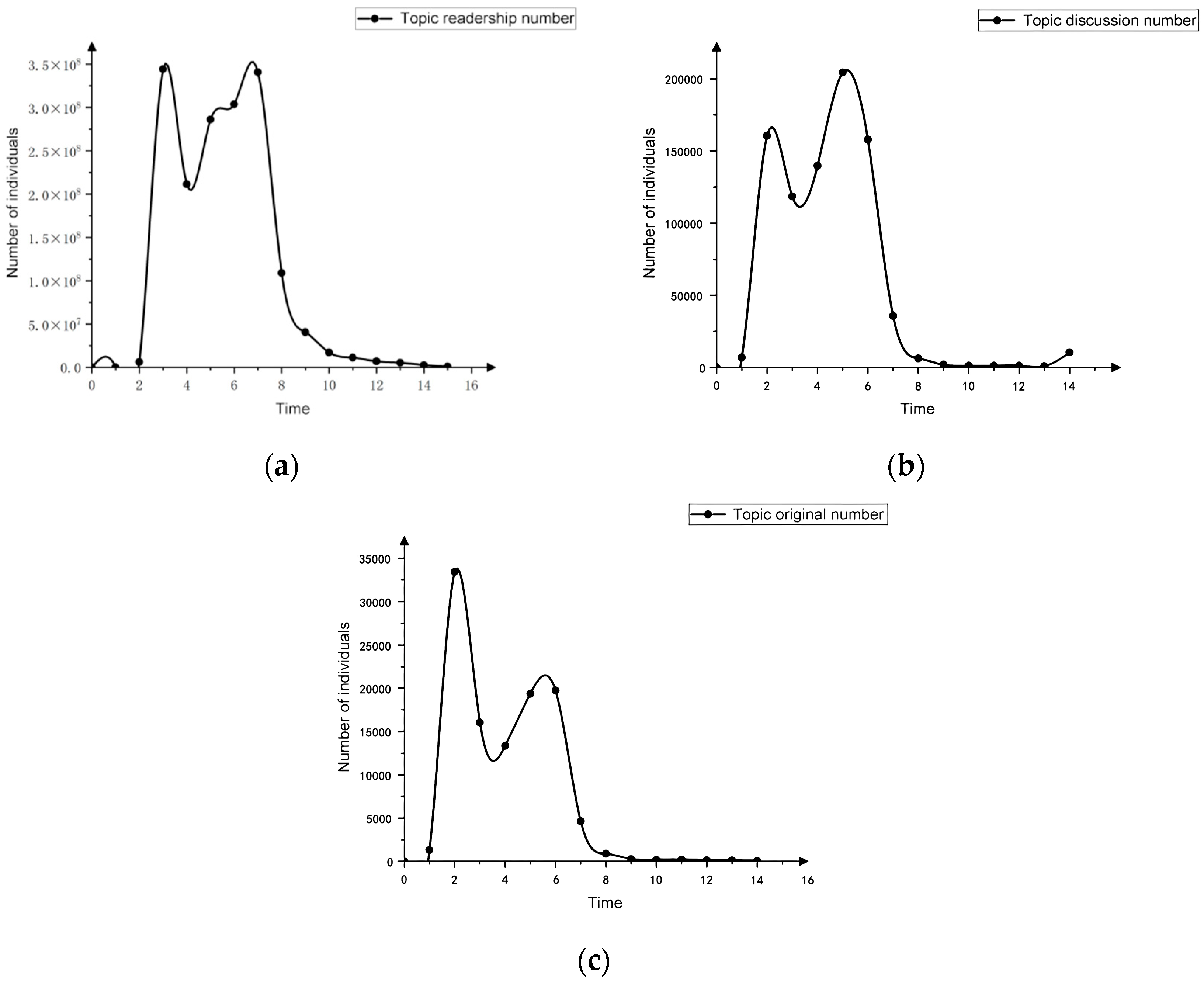
3.1. The Division of Rumor Life Cycle
3.2. SCIR Propagation Model Simulation
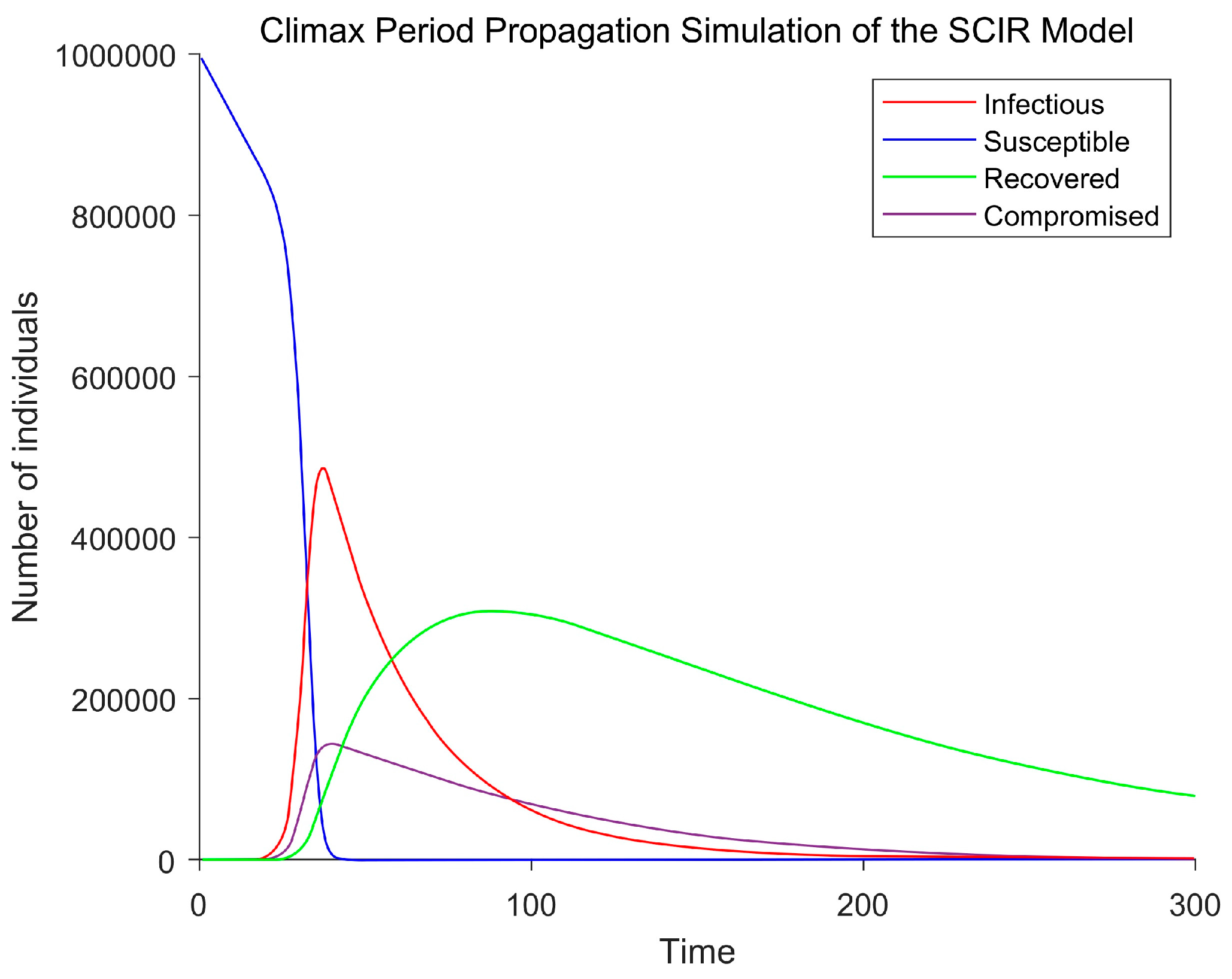
3.2.1. Simulation of SCIR Model Propagation under Media Influence
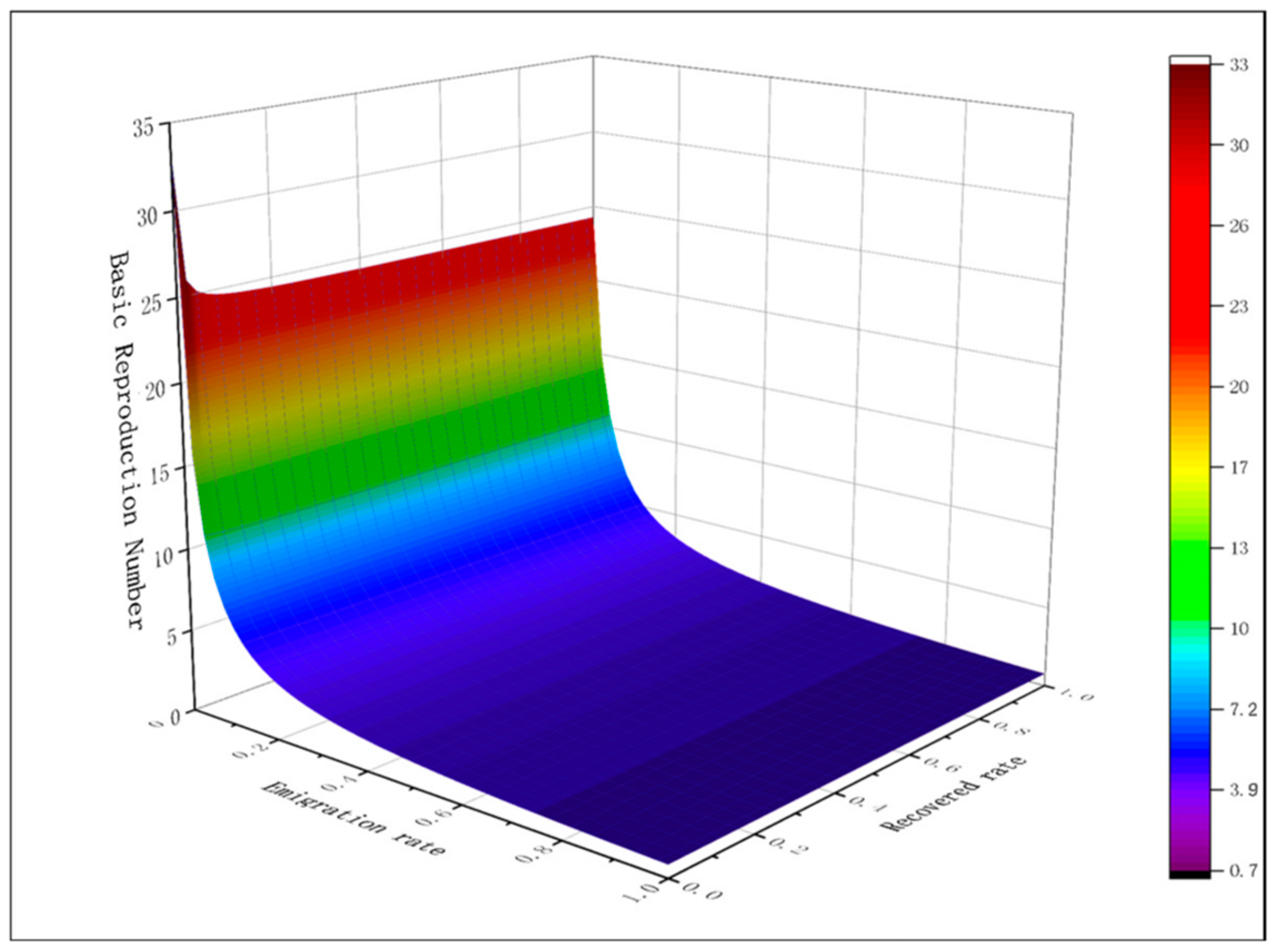
3.2.2. Analysis of Propagation Parameters of SCIR Model
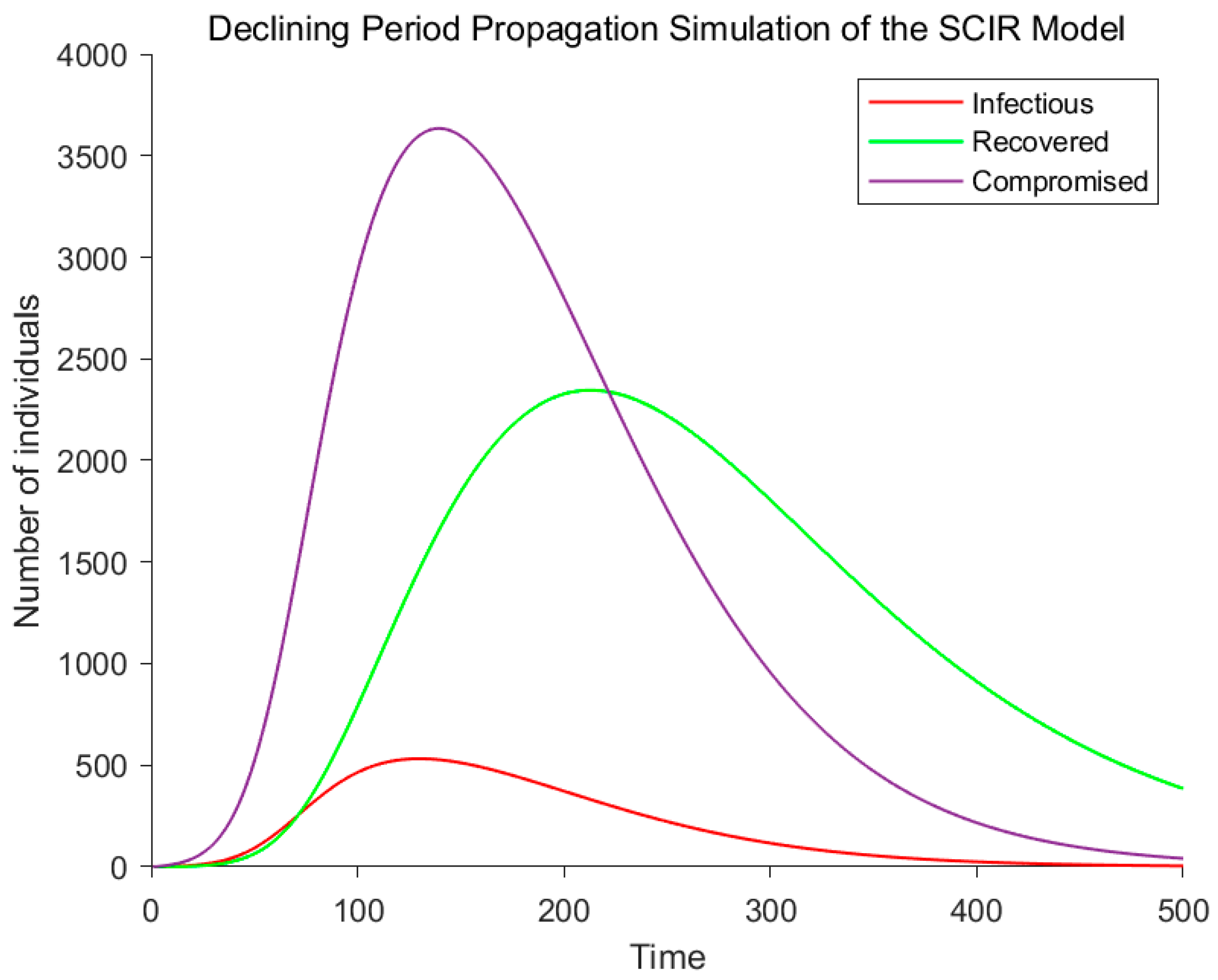
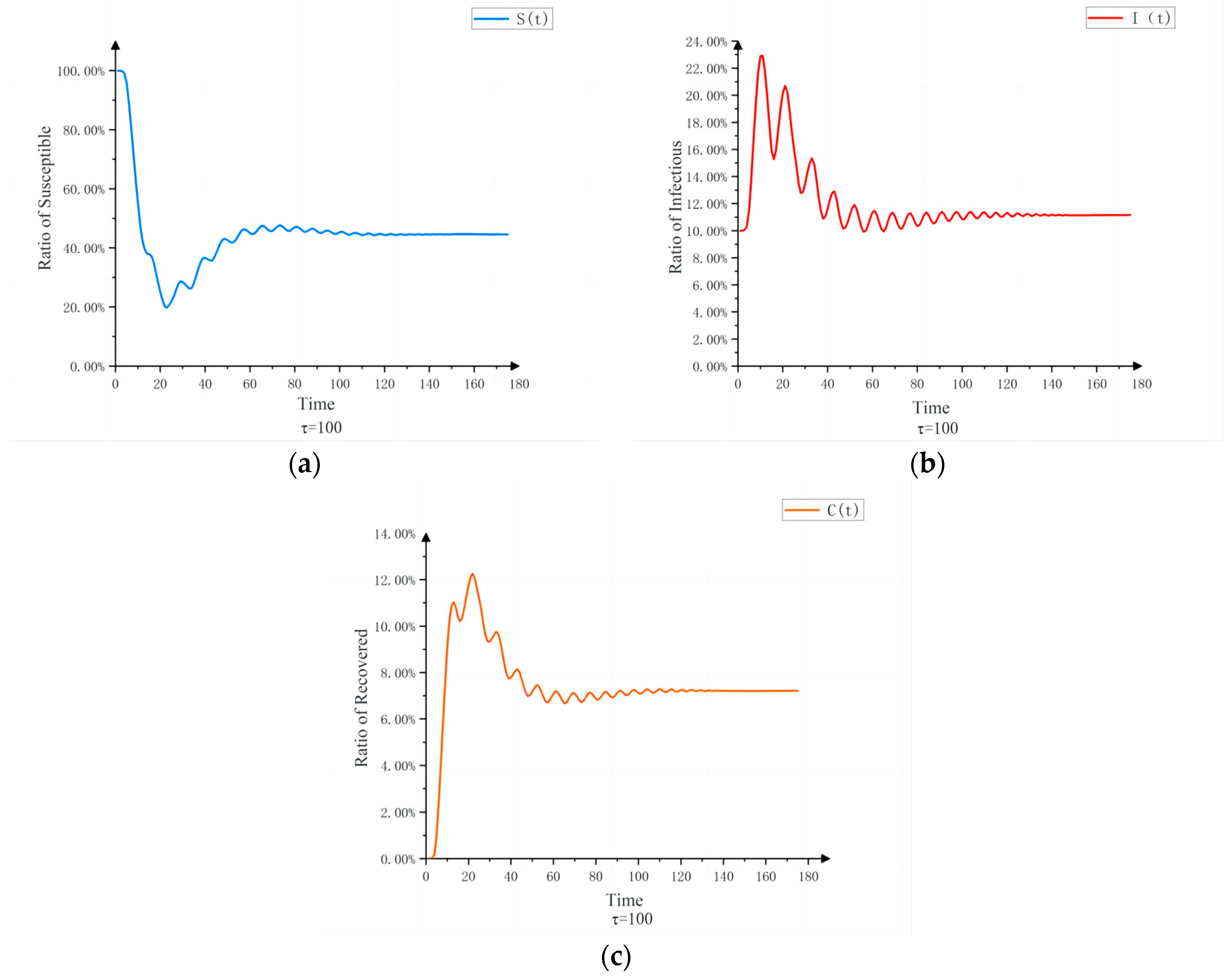
3.3. Time-Lag Propagation Model Simulation
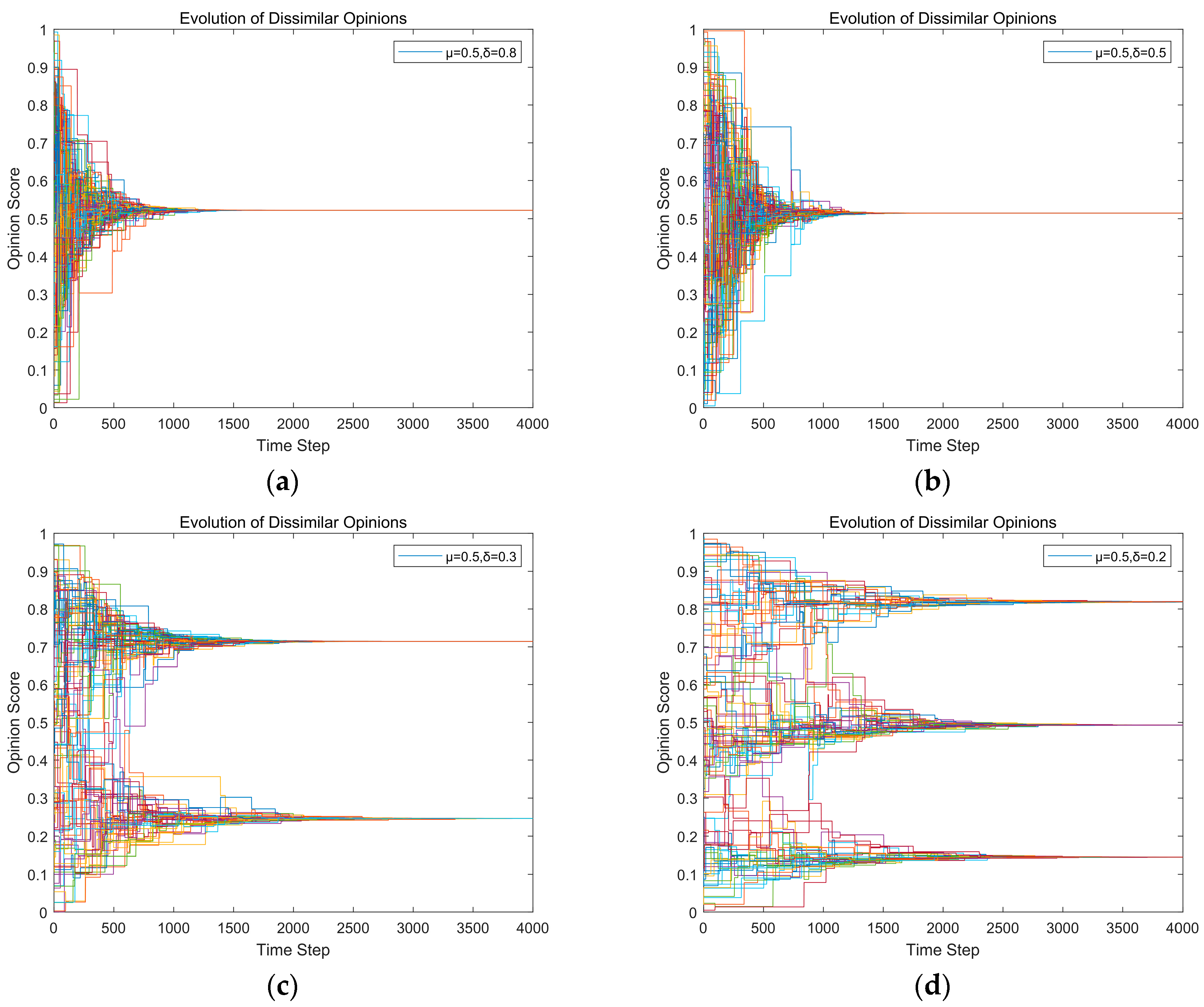
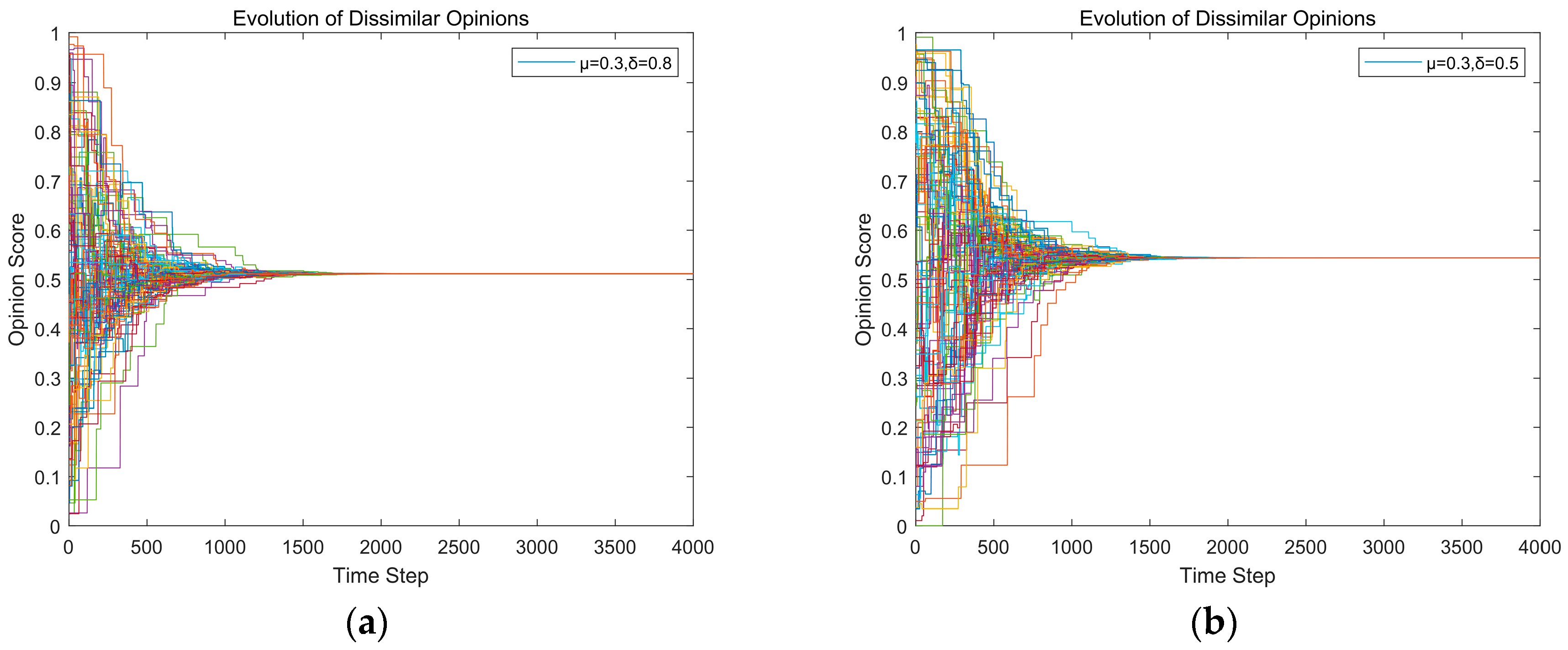
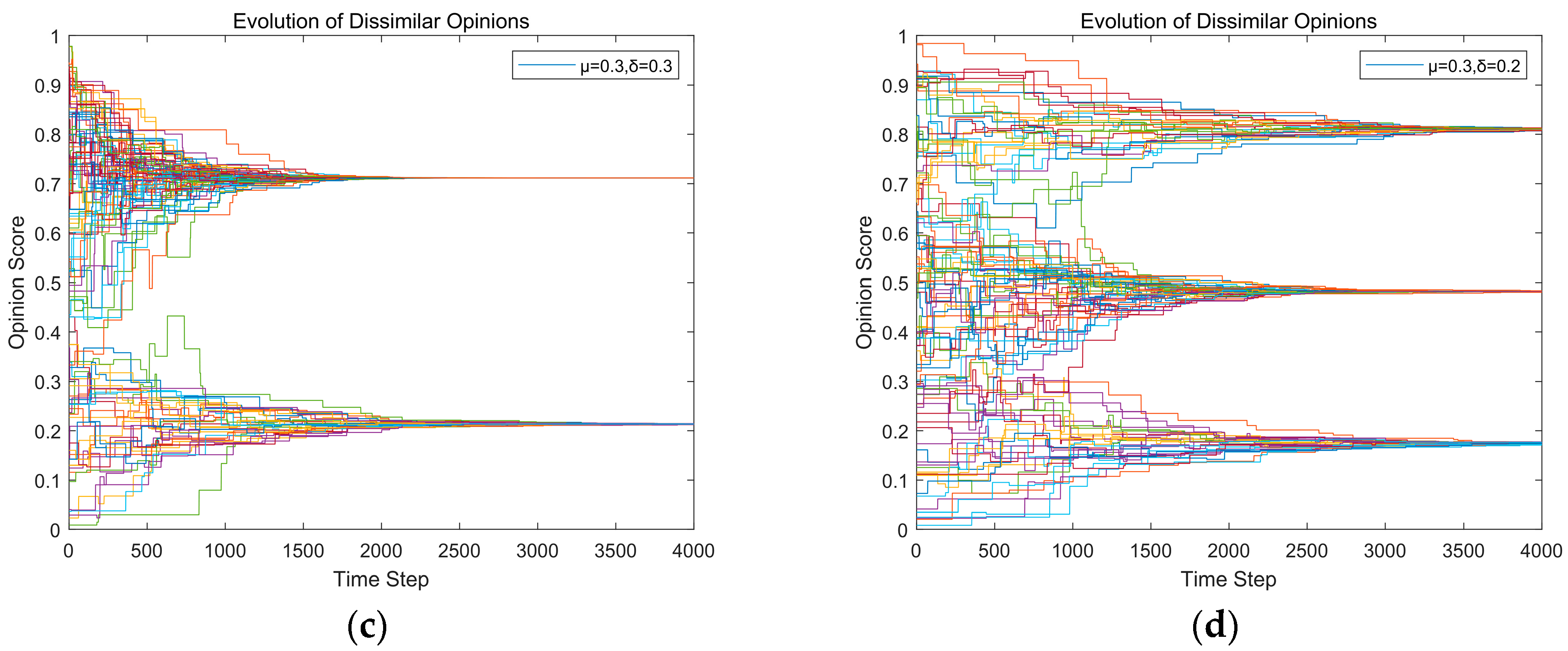
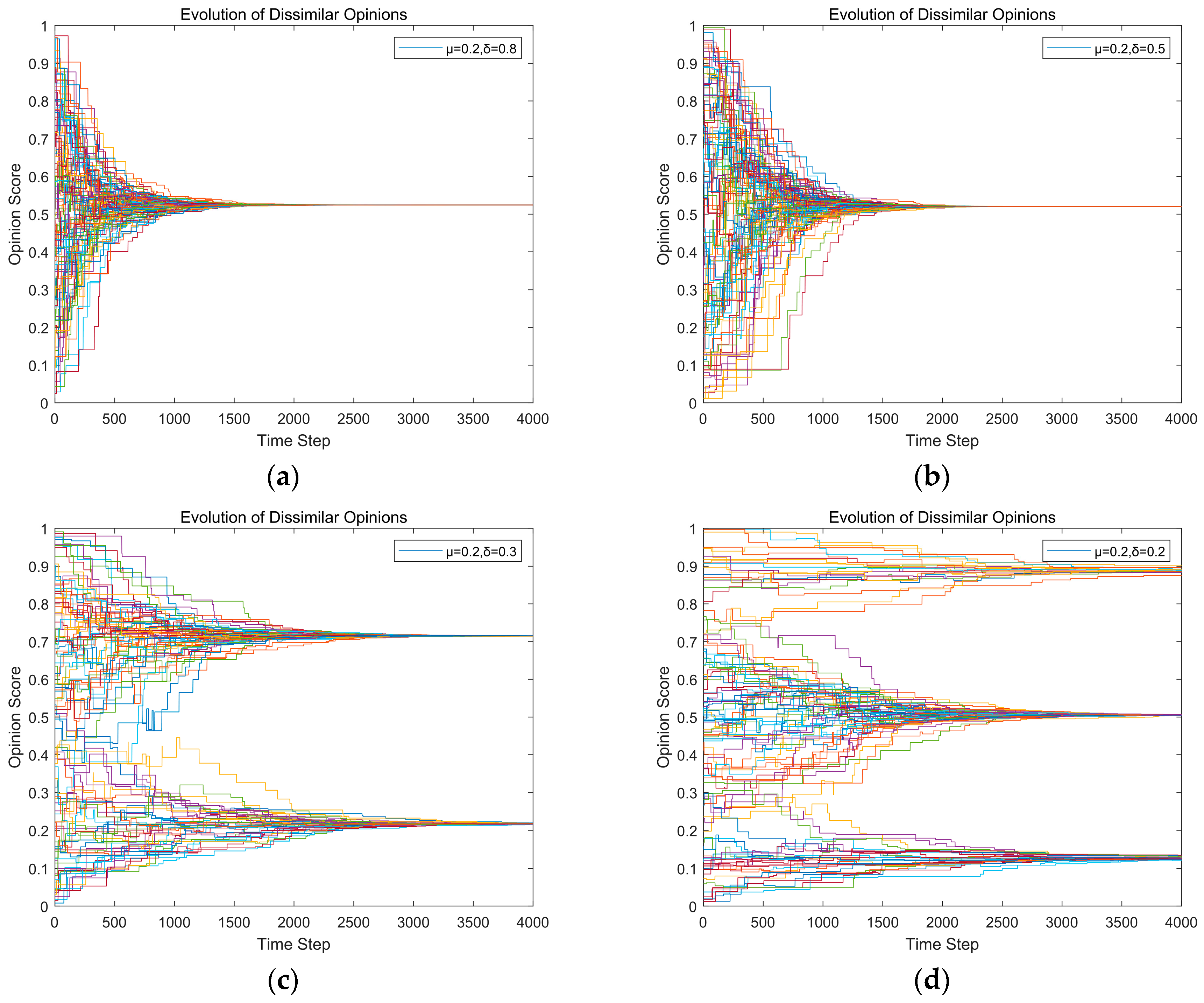
3.4. The Evolution of Views Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Bai, N.; Meng, F.; Rui, X.; Wang, Z. Rumour Detection Based on Graph Convolutional Neural Net. IEEE Access 2021, 9, 21686–21693. [Google Scholar] [CrossRef]
- Qiu, L.; Jia, W.; Niu, W. SIR-IM: SIR rumor spreading model with influence mechanism in social networks. Soft Comput. 2021, 25, 13949–13958. [Google Scholar] [CrossRef]
- Shahbazi, M.; Bunker, D. Social media trust: Fighting misinformation in the time of crisis. Int. J. Inf. Manag. 2024, 77, 102780. [Google Scholar] [CrossRef]
- Ghosh, M.; Das, P. A comparative study of deterministic and stochastic dynamics of rumor propagation model with counter-rumor spreader. Nonlinear Dyn. 2023, 111, 16875–16894. [Google Scholar] [CrossRef]
- Zhang, Z.; Mei, X.; Jiang, H.; Luo, X.; Xia, Y. Dynamical analysis of Hyper-SIR rumor spreading model. Appl. Math. Comput. 2023, 446, 127887. [Google Scholar] [CrossRef]
- Yue, X.; Huo, L. Analysis of the Stability and Optimal Control Strategy for an ISCR Rumor Propagation Model with Saturated Incidence and Time Delay on a Scale-Free Network. Mathematics 2022, 10, 3900. [Google Scholar] [CrossRef]
- Tan, J.; Zhang, M.; Liu, F. Online-Offline Higher-Order Rumor Propagation Model Based on Quantum Cellular Automata Considering Social Adaptation. Appl. Math. Comput. 2024, 461, 128320. [Google Scholar] [CrossRef]
- Zan, Y.L. DSIR double-rumors spreading model in complex networks. Chaos Solitons Fractals 2018, 110, 191–202. [Google Scholar] [CrossRef]
- Geng, L.; Yang, S.; Wang, K.; Zhou, Q.; Geng, L. Modeling public opinion dissemination in a multilayer network with SEIR model based on real social networks. Eng. Appl. Artif. Intell. 2023, 125, 106719. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, L.; Li, Q.; Liu, L. MM-SIS: Model for multiple information spreading in multiplex network. Phys. A 2019, 513, 135–146. [Google Scholar] [CrossRef]
- Masuda, N. Opinion control in complex networks. New J. Phys. 2015, 17, 33031–33041. [Google Scholar] [CrossRef]
- Tian, R.Y.; Zhang, X.F.; Liu, Y.J. SSIC model: A multi-layer model for intervention of online rumors spreading. Phys. A 2015, 427, 181–191. [Google Scholar] [CrossRef]
- Wang, H.M.; Qiu, L.Q.; Sun, C.G. ISRT rumor spreading model with different influence mechanisms in social networks. Int. J. Mod. Phys. C 2023, 34, 18. [Google Scholar] [CrossRef]
- Zhao, L.J.; Wang, J.J.; Chen, Y.C.; Wang, Q.; Cheng, J.J.; Cui, H.X. SIHR rumor spreading model in social networks. Phys. A 2012, 391, 2444–2453. [Google Scholar] [CrossRef]
- Mei, X.H.; Zhang, Z.Y.; Jiang, H.J. Dynamical Analysis of Hyper-ILSR Rumor Propagation Model with Saturation Incidence Rate. Entropy 2023, 25, 805. [Google Scholar] [CrossRef] [PubMed]
- Askarizadeh, M.; Ladani, B.T.; Manshaei, M.H. An evolutionary game model for analysis of rumor propagation and control in social networks. Physics A 2019, 523, 21–39. [Google Scholar] [CrossRef]
- Wang, Y.; Qing, F.; Wang, L. Rumor Dynamic Model considering Intentional Spreaders in Social Network. Discret. Dyn. Nat. Soc. 2022, 2022, 10. [Google Scholar] [CrossRef]
- Shu, P.P.; Liu, Q.H.; Wang, S.P.; Wang, W. Social contagions on interconnected networks of heterogeneous populations. Chaos 2018, 28, 8. [Google Scholar] [CrossRef]
- Afassinou, K. Analysis of the impact of education rate on the rumor spreading mechanism. Physics A 2014, 414, 43–52. [Google Scholar] [CrossRef]
- Daley, D.J.; Kendall, D.G. Epidemics and Rumours. Nature 1964, 204, 1118. [Google Scholar] [CrossRef]
- Zanette, D.H. Critical behavior of propagation on small-world networks. Phys. Rev. E 2001, 64, 050901. Available online: https://link.aps.org/doi/10.1103/PhysRevE.64.050901 (accessed on 21 October 2001). [CrossRef] [PubMed]
- Ye, M.L.; Li, J.R.; Han, X.; Jiang, H.J. Global analysis of a fractional-order reaction-diffusion rumor-spreading model in multi-lingual environment. Eur. Phys. J. Plus 2023, 138, 102. [Google Scholar] [CrossRef]
- Govindankutty, S.; Gopalan, S.P. From Fake Reviews to Fake News: A Novel Pandemic Model of Misinformation in Digital Networks. J. Theor. Appl. Electron. Commer. Res. 2023, 18, 1069–1085. [Google Scholar] [CrossRef]
- Hong, W.; Wang, H. Research on the evolution model of network rumor propagation based on SIRT. Mod. Intell. 2017, 37, 36–42. [Google Scholar]
- Zhang, Y.M.; Su, Y.Y.; Liu, H. Dual social reinforcement rumor propagation model and stability analysis. Syst. Sci. Math. 2017, 37, 1960–1975. [Google Scholar]
- Akshi, K.; Nipun, A.; Sanjay, K. SIRA: A model for propagation and rumor control with epidemic spreading and immunization for healthcare 5.0. Soft Comput. 2022, 27, 4307–4320. [Google Scholar] [CrossRef]
- Teng, J.; Xia, Z.J.; Luo, M.Y. Dynamic Network Public Opinion Crisis Prediction Based on Metabolic GM(1,N) Markov Model. Inf. Sci. 2020, 38, 88–94. [Google Scholar] [CrossRef]
- Tan, Z.H.; Shi, Y.C.; Shi, N.X.; Yang, G.M.; Wang, X.W. An analysis model of rumor propagation in online social network space based on gravity. Comput. Res. Dev. 2017, 54, 2586–2599. [Google Scholar]
- Degroot, M.H. Reaching a Consensus J. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion Dynamics and Bounded Confidence Models, Analysis, and Simulation. J. Artif. Soc. Simul. 2002, 5, 96–104. [Google Scholar]
- Delfuant, G.; Neau, D.; Amblard, F. Mixing Beliefs among Interacting Agents. Adv. Complex Syst. 2001, 3, 87–98. [Google Scholar] [CrossRef]
- Caridi, I.; Pinasco, J.P.; Saintier, N.; Schiaffino, P. Characterizing segregation in the Schelling–Voter model. Phys. A 2017, 487, 125–142. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Bull. Math. Biol. 1992, 8240, 80040. [Google Scholar] [CrossRef]
- Dang, Z.K.; Li, L.X.; Ni, W.; Liu, R.P.; Peng, H.P.; Yang, Y.X. How does rumor spreading affect people inside and outside an institution. Inf. Sci. 2021, 574, 377–393. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Cao, J.; Li, L. Edge-based epidemic spreading in degree-correlated complex networks. J. Theor. Biol. 2018, 454, 164–181. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Cao, J. Global dynamics of a network epidemic model for waterborne diseases spread. Appl. Math. Comput. 2014, 237, 474–488. [Google Scholar] [CrossRef]
- Driesschea, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Zhu, L.H.; Guan, G. Dynamical analysis of a rumor spreading model with self-discrimination and time delay in complex networks. Phys. A 2019, 533, 121953. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Maini, P.K. A Lyapunov function and global properties for SIR and SEIR epidemiological models with nonlinear incidence. Math. Biosci. Eng. 2004, 1, 57–60. [Google Scholar] [CrossRef]
- Guo, H.M.; Yan, X.F.; Niu, Y.B.; Zhang, J.P. Dynamic analysis of rumor propagation model with media report and time delay on social networks. J. Appl. Math. Comput. 2023, 69, 2473–2502. [Google Scholar] [CrossRef]
- Zhu, L.H.; Wang, X.W.; Zhang, Z.; Lei, C.X. Spatial dynamics and optimization method for a rumor propagation model in both homogeneous and heterogeneous environment. Nonlinear Dyn. 2021, 105, 3791–3817. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, Z.Y.; Zhu, H.M.; Hong, X.J.; Lin, P. Evolution analysis of public opinion based on improved Deffuant model. Manag. Comments 2022, 34, 147–157. [Google Scholar] [CrossRef]
- Li, M.; Li, A. A Network Public Opinion Trend Estimation Model Using a Scale-Free Network Algorithm. Mob. Inf. Syst. 2022, 2022, 10. [Google Scholar] [CrossRef]
- Aboudzadeh, N.; Shoshtari, A.H.; Hashemnia, S. Crisis management: Planning for the inevitable. Manag. Sci. Lett. 2014, 4, 6. [Google Scholar] [CrossRef]
- Li, Z.H.; He, J.L.; Wu, P.F. Period characteristics and management countermeasures of information dissemination mode of sudden public crisis. Libr. Inf. Work. 2007, 15, 88–91. [Google Scholar]
- Pan, W.H.; Han, Y.; Li, J.; Zhang, E.; He, B.K. The positive energy of netizens: Development and application of fine-grained sentiment lexicon and emotional intensity model. Curr. Psychol. 2023, 42, 27901–27918. [Google Scholar] [CrossRef] [PubMed]
- Sivasankar, E.; Krishnakumari, K.P. Balasubramanian. An enhanced sentiment dictionary for domain adaptation with multi-domain dataset in Tamil language (ESD-DA). Soft Comput. 2021, 25, 3697–3711. [Google Scholar] [CrossRef]
- Chandra, R.A. Krishna COVID-19 sentiment analysis via deep learning during the rise of novel cases. PLoS ONE 2021, 16, 0255615. [Google Scholar] [CrossRef]
- Rao, T.; Li, X.; Xu, M. Learning Multi-level Deep Representations for Image Emotion Classification. Neural Process Lett. 2020, 51, 2043–2061. [Google Scholar] [CrossRef]




| Parameter | Description | Abbreviation |
|---|---|---|
| S(t) | The number of Susceptible at t moment | Susceptible |
| C(t) | The number of Compromised at t moment | Compromised |
| I(t) | The number of Infectious at t moment | Infectious |
| R(t) | The number of Recovered at t moment | Recovered |
| ξ1 | The probability that a Compromised believe and become a Infectious after being exposed to rumor or influenced by the media | Incidence rate |
| ξ2 | The probability that Infectious becomes Compromised after contact with other Infectious or being influenced by the media | Mortality rate |
| β | The probability that a Susceptible becomes Infectious after being exposed to rumors | Transmission rate |
| Λ | The probability of people migrating into the system after exposure to rumors | Immigration rate |
| μ | The probability of moving out of the system after the population moves | Emigration rate |
| θ | The probability that the Compromised will see through the rumor and become Recovered after being affected | Recovered rate |
| γ | The probability that the Infectious becomes a Recovered after being indifferent to the rumor or after being aware of the rumor | Refresh rate |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Liu, S.; Su, K.; Chen, J. A Rumor Propagation Model Considering Media Effect and Suspicion Mechanism under Public Emergencies. Mathematics 2024, 12, 1906. https://doi.org/10.3390/math12121906
Yang S, Liu S, Su K, Chen J. A Rumor Propagation Model Considering Media Effect and Suspicion Mechanism under Public Emergencies. Mathematics. 2024; 12(12):1906. https://doi.org/10.3390/math12121906
Chicago/Turabian StyleYang, Shan, Shihan Liu, Kaijun Su, and Jianhong Chen. 2024. "A Rumor Propagation Model Considering Media Effect and Suspicion Mechanism under Public Emergencies" Mathematics 12, no. 12: 1906. https://doi.org/10.3390/math12121906
APA StyleYang, S., Liu, S., Su, K., & Chen, J. (2024). A Rumor Propagation Model Considering Media Effect and Suspicion Mechanism under Public Emergencies. Mathematics, 12(12), 1906. https://doi.org/10.3390/math12121906






