Research on Autonomous Manoeuvre Decision Making in Within-Visual-Range Aerial Two-Player Zero-Sum Games Based on Deep Reinforcement Learning
Abstract
:1. Introduction
2. A Deep Reinforcement Learning Model for Manoeuvre Decision Making in WVR Aerial Agent Zero-Sum Games
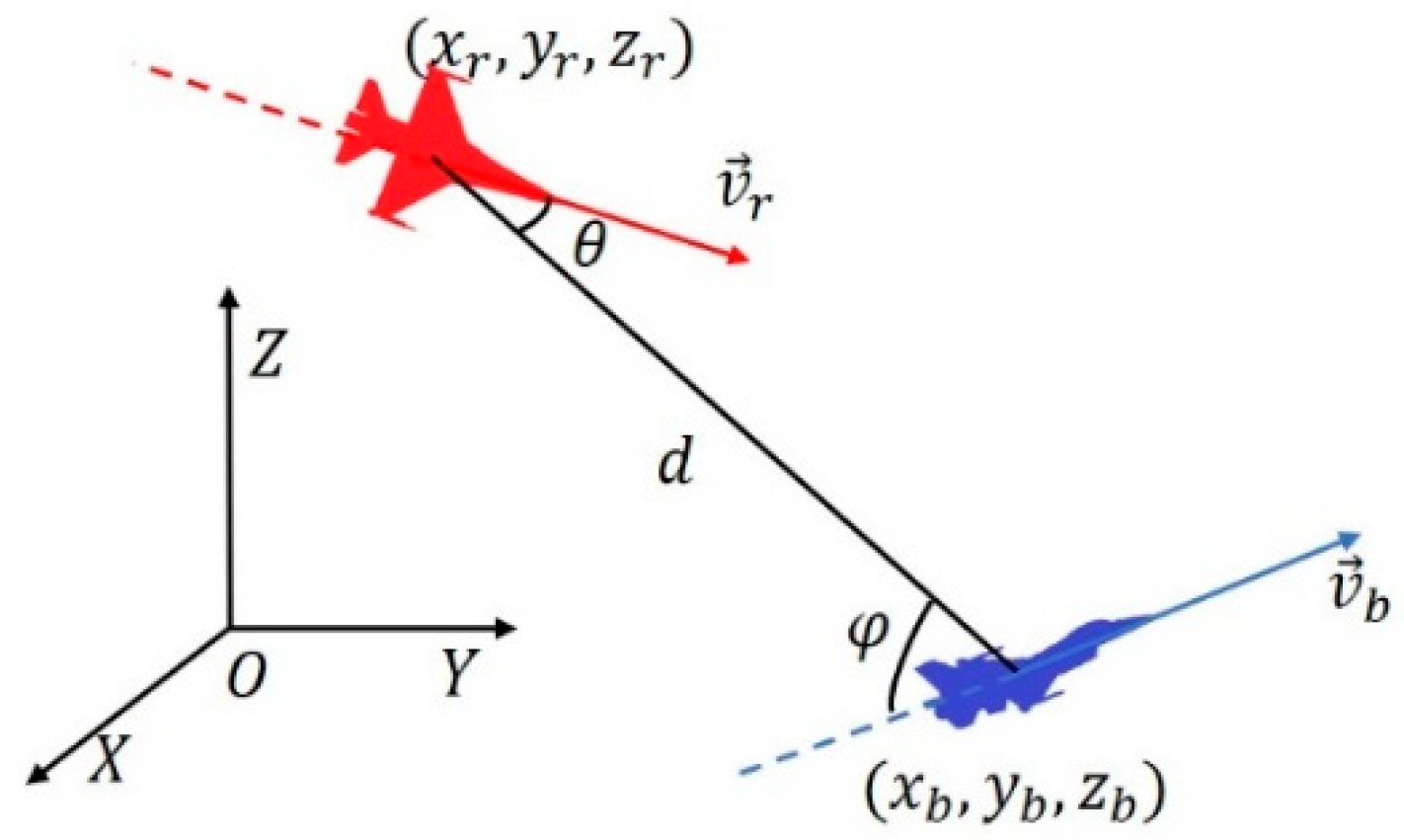
2.1. WVR Aerial Two-Player Zero-Sum Games Dynamics Modeling
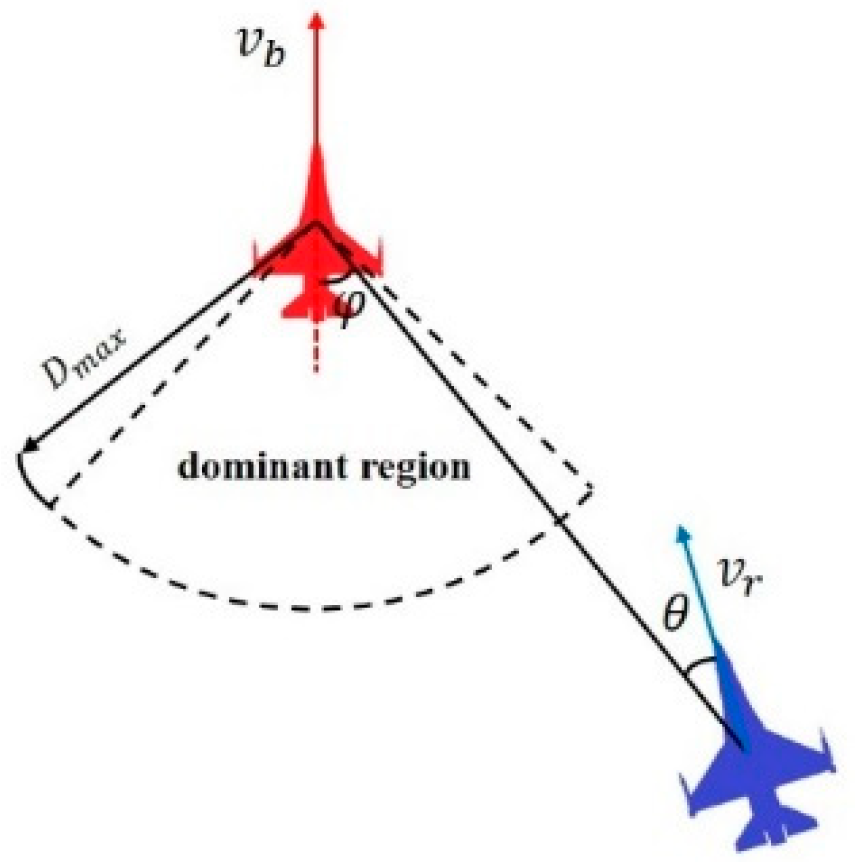
2.2. Capture Zone Modelling
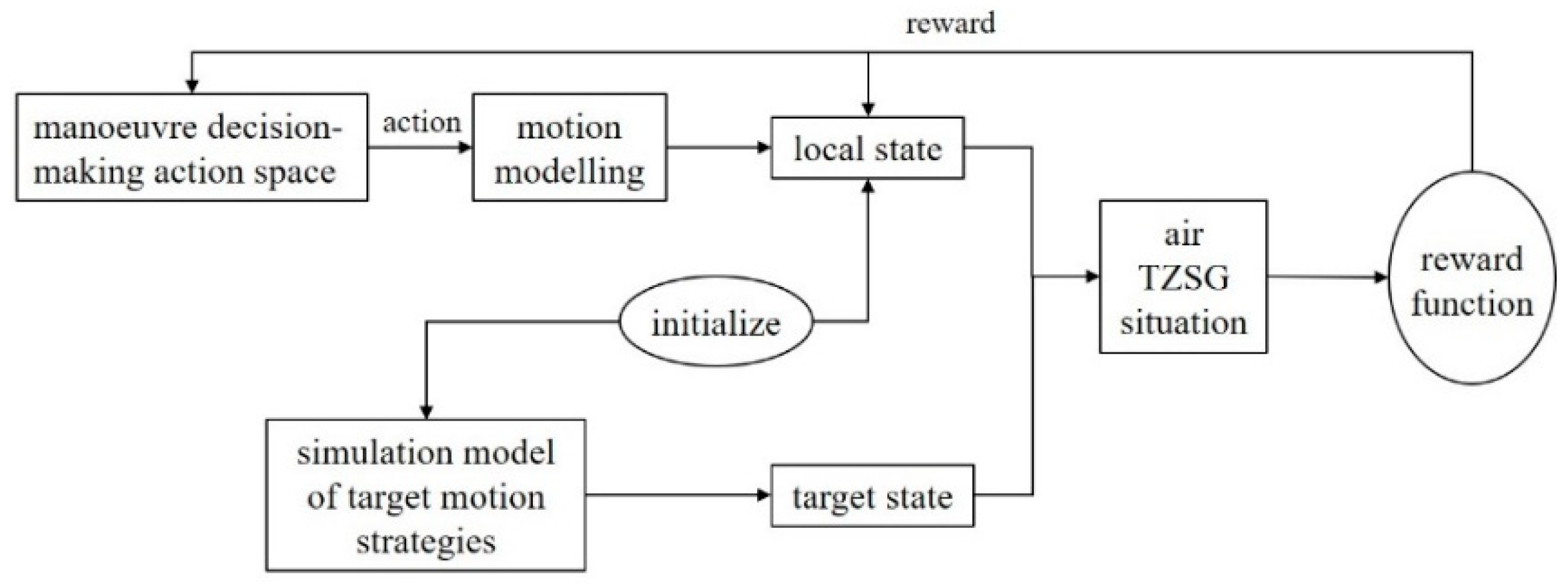
2.3. WVR Aerial TZSG MDP Modelling
2.3.1. State Space (S)
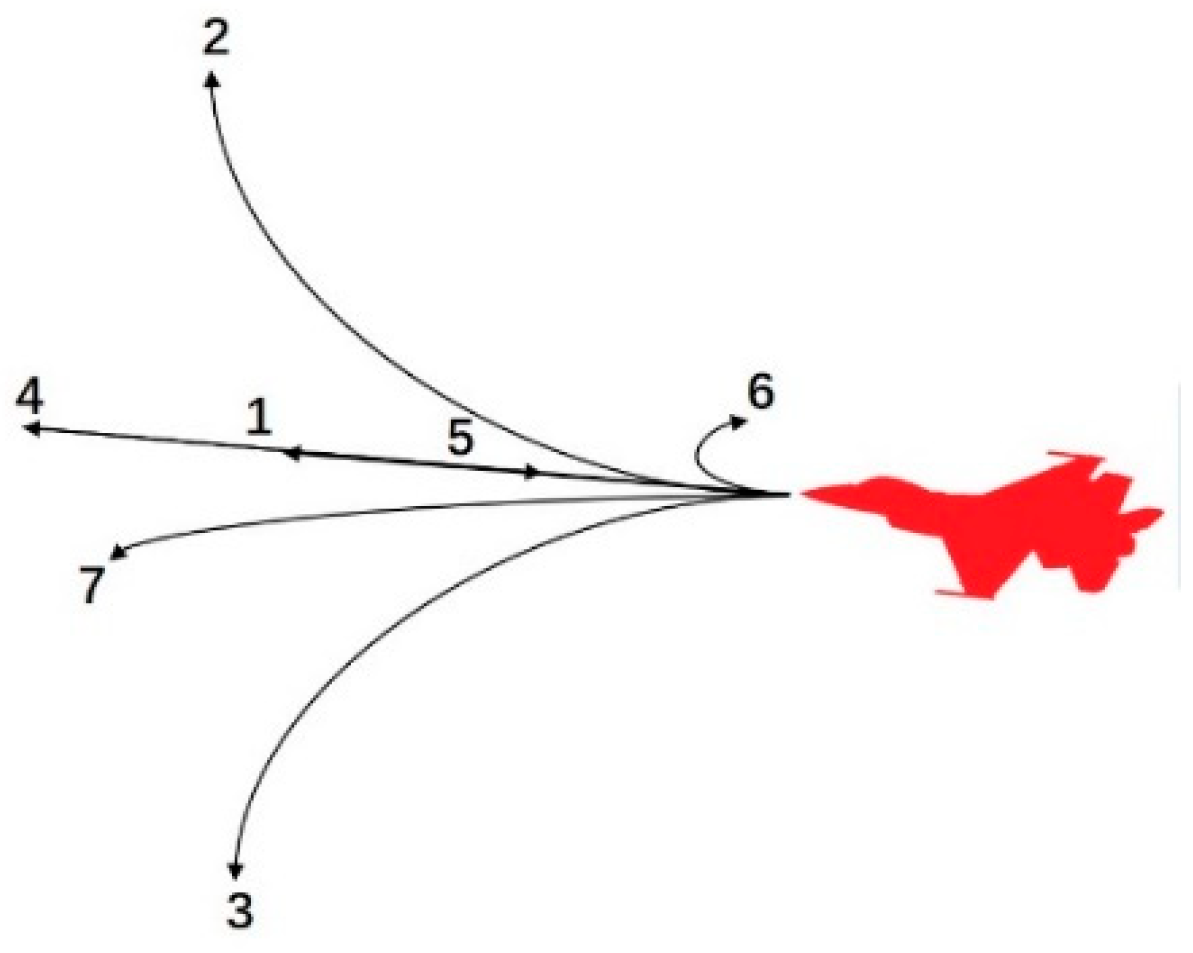
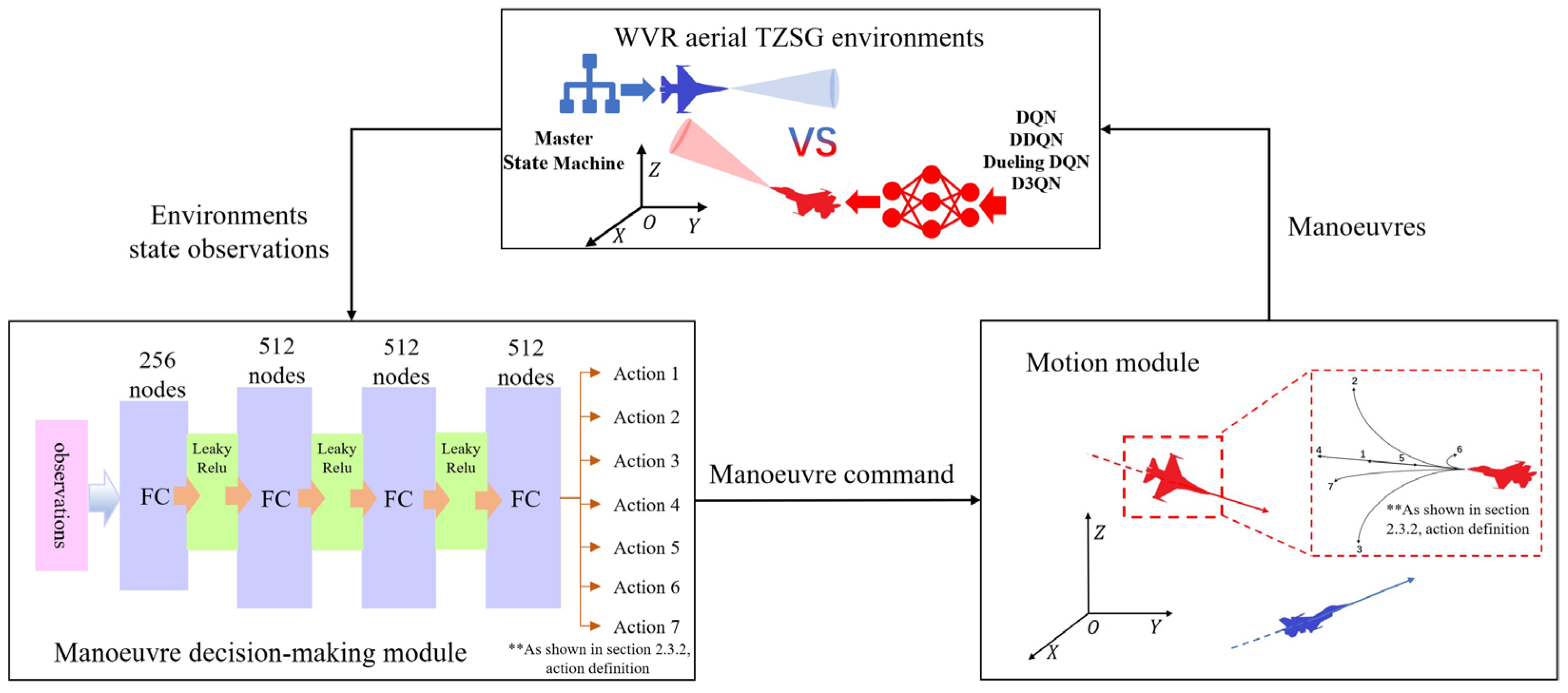
2.3.2. Action Space (A)
2.3.3. Rewards
- (1)
- Environmental reward function
- (2)
- Shaping the reward function
- where is the distance reward function, and is the direction reward function, which are defined as
- (3)
- Total reward function
3. Deep Reinforcement Learning Algorithms
3.1. Research Proposal
3.2. Principles of Reinforcement Learning
3.3. Introduction to Deep Reinforcement Learning
3.4. Several Typical Deep Reinforcement Learning Algorithms Based on Discrete Action Spaces
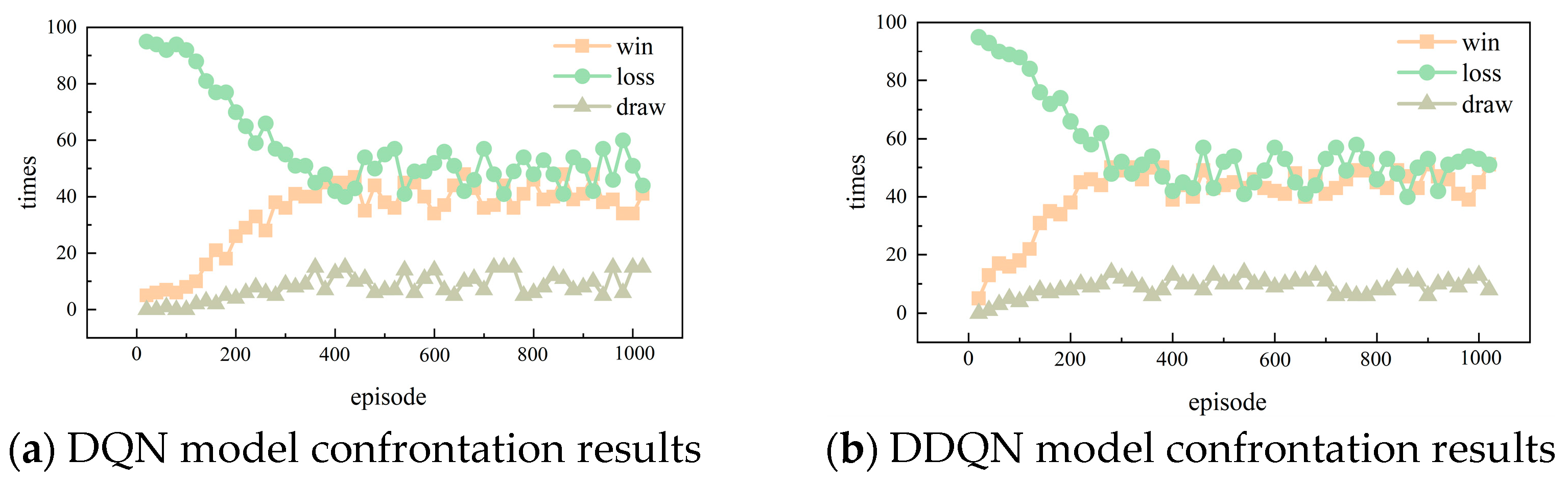
3.4.1. DQN
3.4.2. DDQN
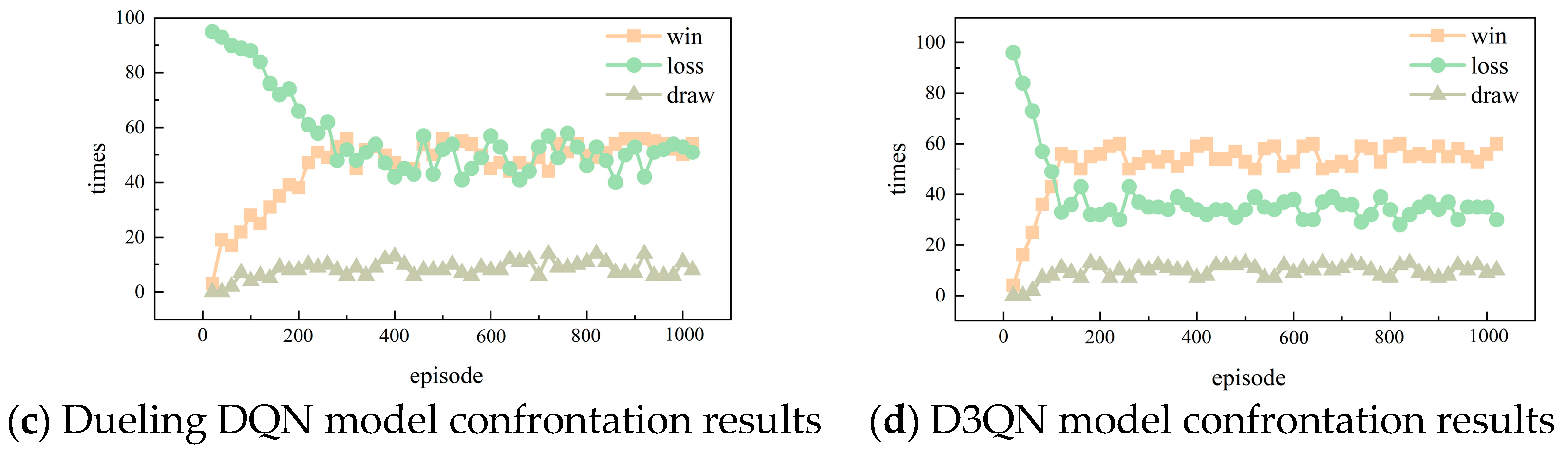
3.4.3. Dueling DQN
3.4.4. D3QN
4. Simulation Experiment
4.1. Experimental Framework
4.2. Experimental Preparation
4.2.1. Experimental Hardware Preparation
4.2.2. Experimental Software Preparation
4.2.3. Simulation Experiment Scene Setting
4.2.4. Hyperparameter Settings for Each Algorithm
4.2.5. Algorithm Convergence Criterion
- Stability of Evaluation Metrics: During training, evaluation metrics gradually stabilise and reach a certain level, indicating that the model’s performance tends to be stable. In this experiment, the primary evaluation metric of interest is the cumulative reward. By plotting the change curve of the cumulative reward over time during training, we can observe the stabilisation of the evaluation metric.
- No Significant Performance Improvement: Within a certain period, if the model’s performance no longer shows significant improvement, it suggests that further training does not yield noticeable changes in performance metrics. In this experiment, we use the adversarial win rate of the trained model as the performance metric. By setting several predefined training intervals (iterations) and observing the changes in performance metrics during these intervals, we can conclude that the model has converged if there is no significant improvement in performance.
4.3. Experimental Results and Analyses
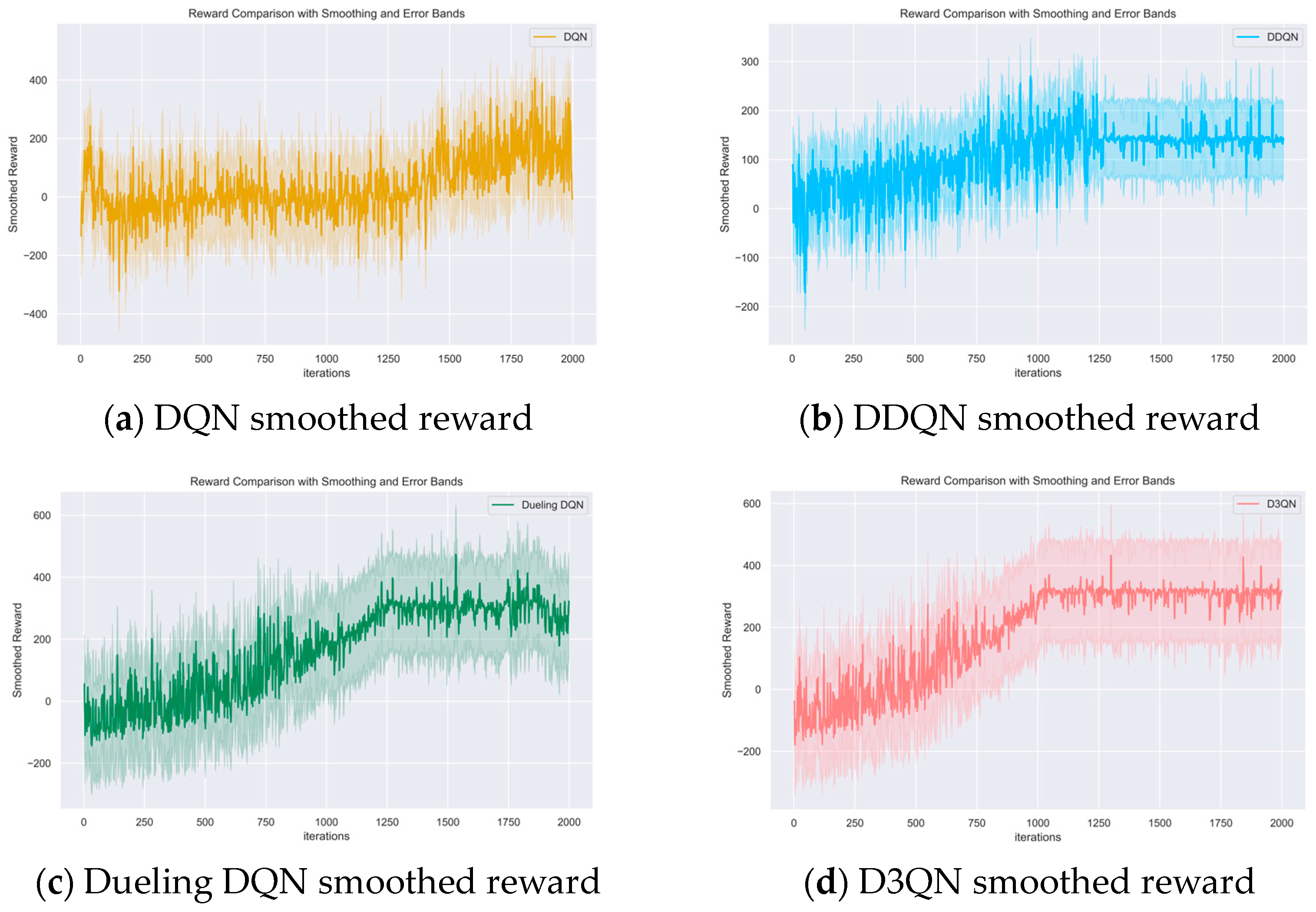

5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
- -
- Two-player zero-sum games (TZSGs): A model in game theory where the total gains and losses between two participants (players) sum to zero. In other words, one player’s gain equals the other player’s loss. This game model is frequently employed to describe decision-making problems in adversarial environments.
- -
- Witness Visual Range (WVR): A term used to describe a distance within which objects or targets can be seen with the naked eye. The typical WVR distance can vary depending on visibility conditions, but it is generally up to about 5 nautical miles (approximately 9.3 kilometres or 5.75 miles).
- -
- Unmanned Aerial Systems (UASs): A term referring to aircraft systems without a human pilot on board, which are controlled remotely or autonomously.
- -
- Capture zone: A conical spatial area in the heading direction of an aerial agent, defined by a maximum angle and distance, used to represent the agent’s effective capture range.
- -
- Dominant region: A spatial area that exerts the most influence or control in a given context due to its significant characteristics or activities.
- -
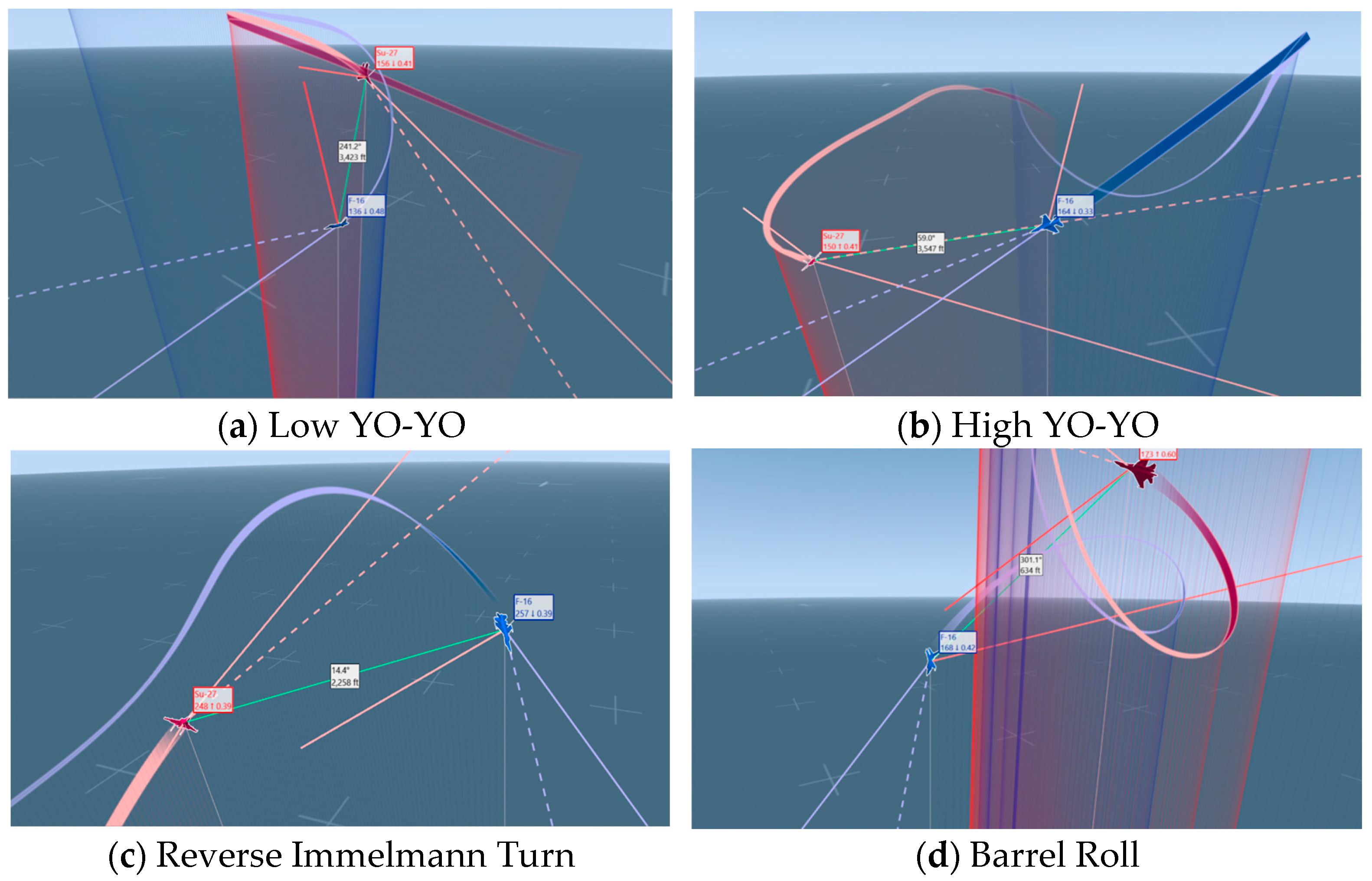
- Low YO-YO: The described aerial manoeuvre involves the aircraft pulling up to climb, rolling toward the opponent’s horizontal turn, and inverting. The pilot then pulls up again to position the aircraft towards the enemy. This manoeuvre trades speed for altitude. Thus, it is a lag pursuit manoeuvre, which increases the distance between you and the enemy aircraft.
- -
- High YO-YO: The described aerial manoeuvre involves the aircraft pushing down to descend, rolling toward the opponent’s horizontal turn, and then pulling up to position the aircraft towards the enemy. This manoeuvre trades altitude for speed. Thus, it is a lead pursuit manoeuvre, which decreases the distance between you and the enemy aircraft.
- -
- Reverse Immelmann Turn: This is the aerial combat manoeuvre described where a fighter aircraft dives to gain speed, half-rolls to invert, then pulls up into a steep climb and levels out at a higher altitude in the opposite direction. This manoeuvre aids in quickly changing direction and altitude for offensive or defensive advantage.
- -
- Barrel Roll: The described aerial manoeuvre where an aircraft rotates 360 degrees along its longitudinal axis while following a helical path. It involves pulling back on the stick to pitch up, rolling during the climb, inverting at the top, and completing the roll to return upright. This manoeuvre is used in aerobatics and combat for evasion or positioning.
References
- Han, R.; Chen, H.; Liu, Q.; Huang, J. Research on Autonomous Air Combat Maneuver Decision Making Based on Reward Shaping and D3QN. In Proceedings of the 2021 China Automation Conference, Beijing, China, 22–24 October 2021; Chinese Society of Automation: Beijing, China, 2021; pp. 687–693. [Google Scholar]
- Ernest, N.; Carroll, D.; Schumacher, C.; Clark, M.; Cohen, K.; Lee, G. Genetic fuzzy based artificial intelligence for unmanned combat aerial vehicle control in simulated air combat missions. J. Def. Manag. 2016, 6, 2167-0374. [Google Scholar] [CrossRef]
- Karimi, I.; Pourtakdoust, S.H. Optimal maneuver-based motion planning over terrain and threats using a dynamic hybrid PSO algorithm. Aerospaceence Technol. 2013, 26, 60–71. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Wu, H. Improving maneuver strategy in air combat by alternate freeze games with a deep reinforcement learning algorithm. Math. Probl. Eng. 2020, 20, 7180639. [Google Scholar] [CrossRef]
- Dong, Y.; Ai, J.; Liu, J. Guidance and control for own aircraft in the autonomous air combat: A historical review and future prospects. Proc. Inst. Mech. Eng. 2019, 233, 5943–5991. [Google Scholar] [CrossRef]
- Fu, L.; Wang, X.G. Research on close air combat modelling of differential games for unmanned combat air vehicles. Acta Armamentarii 2012, 33, 1210–1216. (In Chinese) [Google Scholar]
- Xie, J. Differential Game Theory for Multi UAV Pursuit Maneuver Technology Based on Collaborative Research. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2015. (In Chinese). [Google Scholar]
- Qian, W.Q.; Che, J.; He, K.F. Air combat decision method based on game-matrix approach. In Proceedings of the 2nd China Conference on Command and Control, Beijing, China, 4–5 August 2014; Chinese Institute of Command and Control: Beijing, China, 2014; pp. 408–412. (In Chinese). [Google Scholar]
- Xu, G.; Lu, C.; Wang, G.; Xie, Y. Research on autonomous maneuver decision-making for UCAV air combat based on double matrix countermeasures. Ship Electron. Eng. 2017, 37, 24–28+39. [Google Scholar]
- Bullock, H.E. ACE: The Airborne Combat Expert Systems: An Exposition in Two Parts: ADA170461; Defence Technical Information Center: Fort Belvoir, VA, USA, 1986. [Google Scholar]
- Chin, H.H. Knowledge-based system of supermaneuver selection for pilot aiding. J. Aircr. 1989, 26, 1111–1117. [Google Scholar] [CrossRef]
- Wei, Q.; Zhou, D.Y. Research on UCAV’s intelligent decision-making system based on expert system. Fire Control Command Control 2007, 32, 5–7. (In Chinese) [Google Scholar]
- Wang, R.P.; Gao, Z.H. Research on decision system in air combat simulation using maneuver library. Flight Dyn. 2009, 27, 72–75+79. (In Chinese) [Google Scholar]
- Virtanen, K.; Ehtamo, H.; Raivio, T.; Hamalainen, R.P. VIATO-visual interactive aircraft trajectory optimization. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 1999, 29, 409–421. [Google Scholar] [CrossRef]
- Soltanifar, M. A new interval for ranking alternatives in multi attribute decision making problems. J. Appl. Res. Ind. Eng. 2024, 11, 37–56. [Google Scholar]
- Farajpour Khanaposhtani, G. A new multi-attribute decision-making method for interval data using support vector machine. Big Data Comput. Vis. 2023, 3, 137–145. [Google Scholar]
- Smail, J.; Rodzi, Z.; Hashim, H.; Sulaiman, N.H.; Al-Sharqi, F.; Al-Quran, A.; Ahmad, A.G. Enhancing decision accuracy in dematel using bonferroni mean aggregation under pythagorean neutrosophic environment. J. Fuzzy Ext. Appl. 2023, 4, 281–298. [Google Scholar] [CrossRef]
- Hosseini Nogourani, S.; Soltani, I.; Karbasian, M. An Integrated Model for Decision-making under Uncertainty and Risk to Select Appropriate Strategy for a Company. J. Appl. Res. Ind. Eng. 2014, 1, 136–147. [Google Scholar]
- Sun, C.; Zhao, H.; Wang, Y.; Zhou, H.; Han, J. UCAV Autonomic maneuver decision- making method based on reinforcement learning. Fire Control Command Control 2019, 44, 142–149. [Google Scholar]
- He, L.; Aouf, N.; Whidborne, J.F.; Song, B. Deep reinforcement learning based local planner for UAV obstacle avoidance using demonstration data. arXiv 2020, arXiv:2008.02521. [Google Scholar]
- Ma, W. Research on Air Combat Game Decision Based on Deep Reinforcement Learning. Master’s. Thesis, Sichuan University, Chengdu, China, 2021. (In Chinese). [Google Scholar]
- Zhou, P.; Huang, J.T.; Zhang, S.; Liu, G.; Shu, B.; Tang, J. Research on UAV intelligent air combat decision and simulation based on deep reinforcement learning. Acta Aeronaut. Astronaut. Sin. 2022, 4, 1–16. Available online: http://kns.cnki.net/kcms/detail/11.1929.v.20220126.1120.014.html (accessed on 18 May 2022). (In Chinese).
- Zhang, H.P.; Huang, C.Q.; Xuan, Y.B.; Tang, S. Maneuver decision of autonomous air combat of unmanned combat aerial vehicle based on deep neural network. Acta Armamentarii 2020, 41, 1613–1622. (In Chinese) [Google Scholar]
- Pan, Y.; Zhang, K.; Yang, H. Intelligent decision-making method of dual network for autonomous combat maneuvers of warplanes. J. Harbin Inst. Technol. 2019, 51, 144–151. [Google Scholar]
- Liu, P.; Ma, Y. A deep reinforcement learning based intelligent decision method for UCAV air combat. In Modelling, Design and Simulation of Systems, Proceedings of the 17th Asia Simulation Conference, AsiaSim 2017, Melaka, Malaysia, 27–29 August 2017; Springer: Singapore, 2017; pp. 274–286. [Google Scholar]
- Zhang, Q.; Yang, R.; Yu, L.; Zhang, T.; Zuo, J. BVRair combat maneuvering decision by using Q-network reinforcement learning. J. Air Force Eng. Univ. (Nat. Sci. Ed.) 2018, 19, 8–14. (In Chinese) [Google Scholar]
- Kurniawan, B.; Vamplew, P.; Papasimeon, M.; Dazeley, R.; Foale, C. An empirical study of reward structures for actor-critic reinforcement learning in air combat maneuvering simulation. In Advances in Artificial Intelligence; Springer International Publishing: Cham, Switzerland, 2019; pp. 54–65. [Google Scholar]
- Yang, Q.; Zhu, Y.; Zhang, J.; Qiao, S.; Liu, J. UAV air combat autonomous maneuver decision based on DDPG algorithm. In Proceedings of the 2019 IEEE 15th International Conference on Control, Edinburgh, UK, 16–19 July 2019. [Google Scholar]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver decision of UAV in short-range air combat based on deep reinforcement learning. IEEE Access 2019, 8, 363–378. [Google Scholar] [CrossRef]
- Zhou, K.; Wei, R.; Zhang, Q.; Xu, Z. Learning system for air combat decision inspired by cognitive mechanisms of the brain. IEEE Access 2020, 8, 8129–8144. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, R.; Li, X. Autonomous tactical decision-making of UCAVs in air combat. Control 2012, 19, 92–96. [Google Scholar]
- Ng, A.Y.; Harada, D.; Russell, S. Policy invariance under reward transformations: Theory and application to reward shaping. In Proceedings of the 16th International Conference on Machine Learning, Bled, Slovenia, 27–30 June 1999; pp. 278–287. [Google Scholar]
- Kober, J.; Bagnell, J.A.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silva, B.P.; Ferreira, R.A.; Gomes, S.C.; Calado, F.A.; Andrade, R.M.; Porto, M.P. On-rail solution for autonomous inspections in electrical substations. Infrared Phys. Technol. 2018, 90, 53–58. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-Learning. Natl. Conf. Artif. Intell. Proc. AAAI Conf. Artif. Intell. 2016, 30, 2094–2100. [Google Scholar] [CrossRef]
- Chou, C.-H. Machine Learning; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Harrington, P. Machine Learning in Action; People’s Posts and Telecommunications Press: Beijing, China, 2013. [Google Scholar]
- Duan, Y.; Xu, X.; Xu, S. Research on multi-robot collaboration strategy based on multi-intelligent body reinforcement learning. Syst. Eng. Theory Pract. 2014, 34, 1305–1310. [Google Scholar]
- Zhang, H.C.; Zhao, K.; Li, L.M.; Liu, H. Power system restoration overvoltage prediction based on multilayer artificial neural network. Smart Power 2018, 46, 67–73+88. [Google Scholar]
- Wang, Z.Y.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; ACM: New York, NY, USA, 2016; pp. 1995–2003. [Google Scholar]



| Parameter | Agent (r) | Agent (b) |
|---|---|---|
| Spatial coordinates | ||
| Trajectory inclination | ||
| Trajectory declination | ||
| Velocity magnitude |
| Hyper Parameterisation | (Be) Worth |
|---|---|
| random seed | 1 |
| Maximum number of steps in a round | 50,000 |
| training wheels | 1000 |
| Number of hidden layer nodes | 256 |
| Update Batch | 512 |
| optimiser | Adam |
| Experience pool capacity | 1,000,000 |
| Number of hidden layer nodes | 128 |
| Frequency of target network updates | 1000 steps. |
| learning rate | 0.001 |
| probability of exploration | 0.9 |
| Incentive Discount Factor | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, B.; Ru, L.; Hu, S.; Wang, W.; Xi, H.; Zhao, X. Research on Autonomous Manoeuvre Decision Making in Within-Visual-Range Aerial Two-Player Zero-Sum Games Based on Deep Reinforcement Learning. Mathematics 2024, 12, 2160. https://doi.org/10.3390/math12142160
Lu B, Ru L, Hu S, Wang W, Xi H, Zhao X. Research on Autonomous Manoeuvre Decision Making in Within-Visual-Range Aerial Two-Player Zero-Sum Games Based on Deep Reinforcement Learning. Mathematics. 2024; 12(14):2160. https://doi.org/10.3390/math12142160
Chicago/Turabian StyleLu, Bo, Le Ru, Shiguang Hu, Wenfei Wang, Hailong Xi, and Xiaolin Zhao. 2024. "Research on Autonomous Manoeuvre Decision Making in Within-Visual-Range Aerial Two-Player Zero-Sum Games Based on Deep Reinforcement Learning" Mathematics 12, no. 14: 2160. https://doi.org/10.3390/math12142160
APA StyleLu, B., Ru, L., Hu, S., Wang, W., Xi, H., & Zhao, X. (2024). Research on Autonomous Manoeuvre Decision Making in Within-Visual-Range Aerial Two-Player Zero-Sum Games Based on Deep Reinforcement Learning. Mathematics, 12(14), 2160. https://doi.org/10.3390/math12142160






