Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations
Abstract
:1. Introduction
2. The Existence of the Optimal Control for the Semilinear Problem
3. Optimal Control Problem for the Linear Equation
4. Optimal Control Problem for the Nonlinear Equation
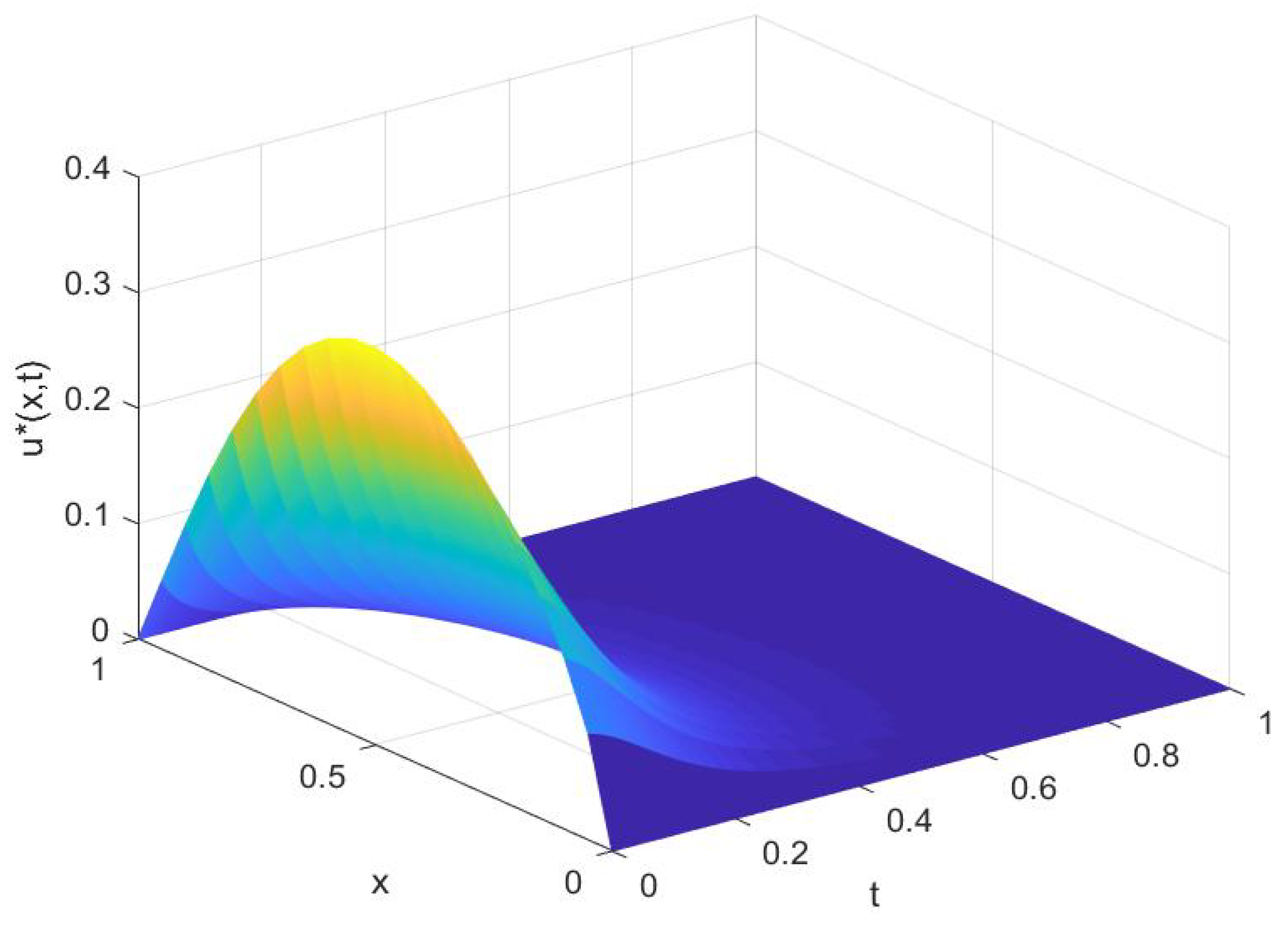
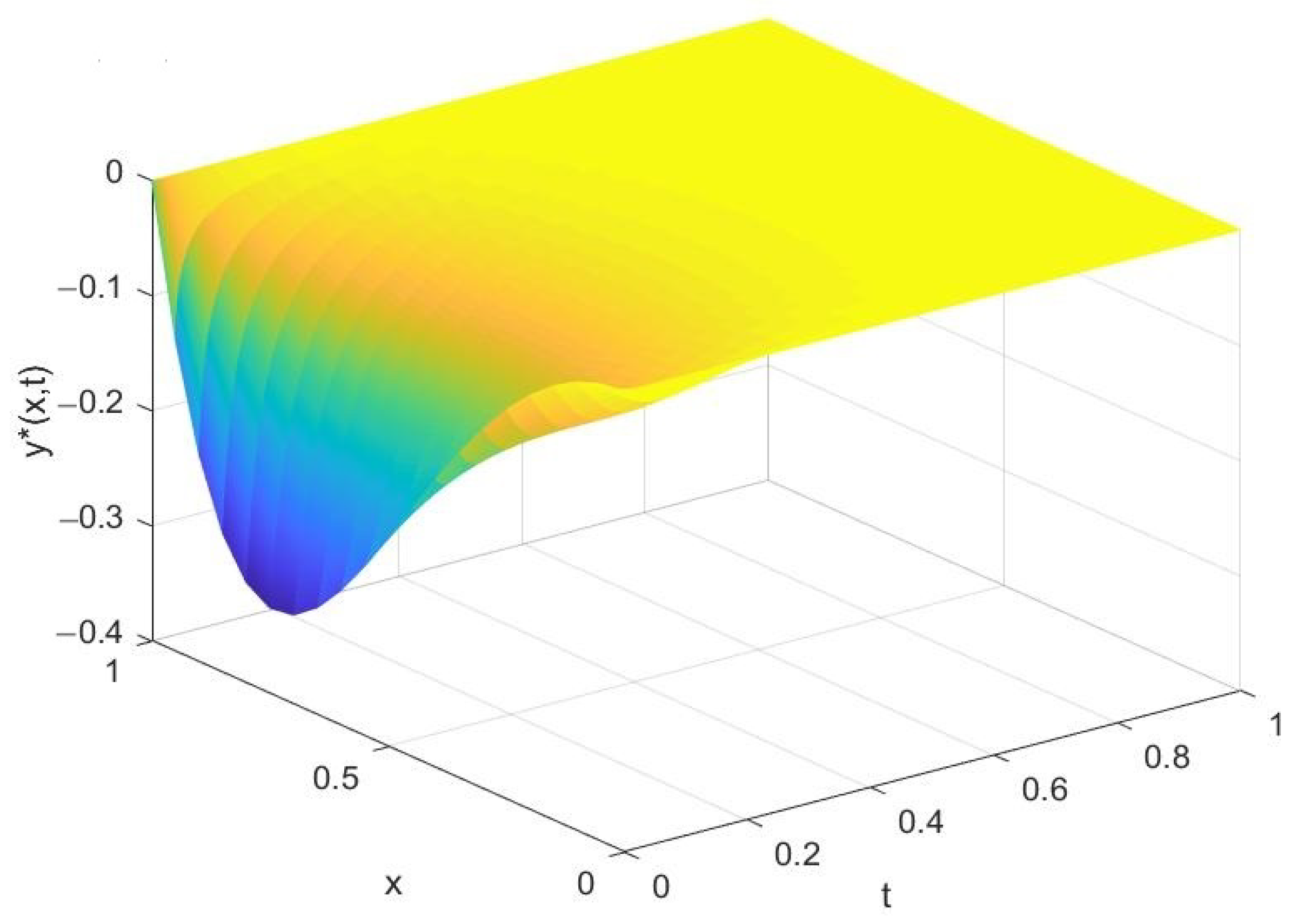
5. A Numerical Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baranovskii, E.S. Feedback optimal control problem for a network model of viscous fluid flows. Math. Notes 2022, 112, 26–39. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Optimal control for steady flows of the Jeffreys fluids with slip boundary condition. J. Appl. Ind. Math. 2014, 8, 168–176. [Google Scholar] [CrossRef]
- Hu, W.; Lai, M.J.; Lee, J. Optimal control for suppression of singularity in chemotaxis via flow advection. Appl. Math. Optim. 2024, 89, 57. [Google Scholar] [CrossRef]
- Casas, E.; Kunisch, K. Infinite horizon optimal control problems for a class of semilinear parabolic equations. SIAM J. Control Optim. 2022, 60, 2070–2094. [Google Scholar] [CrossRef]
- Casas, E.; Yong, J. Optimal control of a parabolic equation with memory. ESAIM COCV 2023, 29, 23. [Google Scholar] [CrossRef]
- Tröltzsch, F. Optimal Control of Partial Differential Equations: Theory, Methods, and Applications; American Mathematical Society: Providence, RI, USA, 2010; Volume 112. [Google Scholar]
- Lions, J.L. Optimal Control of Systems Governed by Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Cannarsa, P.; Martinez, P.; Vancostenoble, J. Null controllability of degenerate heat equations. Adv. Differ. Equ. 2005, 10, 153–190. [Google Scholar] [CrossRef]
- Jiang, L.S.; Tao, Y.S. Identifying the volatility of underlying assets from option prices. Inverse Problems 2001, 17, 137–155. [Google Scholar]
- North, G.R.; Howard, D.; Pollard, D.; Wielicki, B. Variational formulation of Budyko-Sellers climate models. J. Atmos. Sci. 1979, 36, 255–259. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L. An inverse problem of identifying the radiative coefficient in a degenerate parabolic equation. Chin. Ann. Math. Ser. B 2014, 35, 355–382. [Google Scholar] [CrossRef]
- Lenhart, S.M.; Yong, J. Optimal control for degenerate parabolic equations with logistic growth. Nonlinear Anal. 1995, 25, 681–698. [Google Scholar] [CrossRef]
- Marinoschi, G.; Mininni, R.M.; Romanelli, S. An optimal control problem in coefficients for a strongly degenerate parabolic equation with interior degeneracy. J. Optim. Theory Appl. 2017, 173, 56–77. [Google Scholar] [CrossRef]
- Cannarsa, P.; Martinez, P.; Vancostenoble, J. Carleman estimates for a class of degenerate parabolic operators. SIAM J. Control Optim. 2008, 47, 1–19. [Google Scholar] [CrossRef]
- Du, R. Null controllability for a class of degenerate parabolic equations with the gradient terms. J. Evol. Equ. 2019, 19, 585–613. [Google Scholar] [CrossRef]
- Wang, C. Approximate controllability of a class of semilinear systems with boundary degeneracy. J. Evol. Equ. 2010, 10, 163–193. [Google Scholar] [CrossRef]
- Wang, C.; Du, R. Approximate controllability of a class of semilinear degenerate systems with convection term. J. Differ. Equ. 2013, 254, 3665–3689. [Google Scholar] [CrossRef]
- Wang, C.; Du, R. Carleman estimates and null controllability for a class of degenerate parabolic equations with convection terms. SIAM J. Control Optim. 2014, 52, 1457–1480. [Google Scholar] [CrossRef]
- Yin, J.; Wang, C. Evolutionary weighted p-Laplacian with boundary degeneracy. J. Differ. Equ. 2007, 237, 421–445. [Google Scholar] [CrossRef]
- Casas, E.; Fernández, L.A. Distributed Control of Systems Governed by a General Class of Quasinlinear Elliptic Equations. J. Differ. Equ. 1993, 104, 20–47. [Google Scholar] [CrossRef]
- Stojanovic, S. Optimal damping control and nonlinear elliptic systems. SIAM J. Control Optim. 1991, 29, 594–608. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, Y.; Men, T.; Du, R.; Zhu, Y. Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations. Mathematics 2024, 12, 2181. https://doi.org/10.3390/math12142181
Na Y, Men T, Du R, Zhu Y. Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations. Mathematics. 2024; 12(14):2181. https://doi.org/10.3390/math12142181
Chicago/Turabian StyleNa, Yang, Tianjiao Men, Runmei Du, and Yingjie Zhu. 2024. "Optimal Control Problems of a Class of Nonlinear Degenerate Parabolic Equations" Mathematics 12, no. 14: 2181. https://doi.org/10.3390/math12142181



