Enhancing Stability Criteria for Linear Systems with Interval Time-Varying Delays via an Augmented Lyapunov–Krasovskii Functional

Abstract

This work investigates the stability conditions for linear systems with time-varying delays via an augmented Lyapunov–Krasovskii functional (LKF). Two types of augmented LKFs with cross terms in integrals are suggested to improve the stability conditions for interval time-varying linear systems. In this work, the compositions of the LKFs are considered to enhance the feasible region of the stability criterion for linear systems. Mathematical tools such as Wirtinger-based integral inequality (WBII), zero equalities, reciprocally convex approach, and Finsler’s lemma are utilized to solve the problem of stability criteria. Two sufficient conditions are derived to guarantee the asymptotic stability of the systems using linear matrix inequality (LMI). First, asymptotic stability criteria are induced by constructing the new augmented LKFs in Theorem 1. Then, simplified LKFs in Corollary 1 are proposed to show the effectiveness of Theorem 1. Second, asymmetric LKFs are shown to reduce the conservatism and the number of decision variables in Theorem 2. Finally, the advantages of the proposed criteria are verified by comparing maximum delay bounds in four examples. Four numerical examples show that the proposed Theorems 1 and 2 obtain less conservative results than existing outcomes. Particularly, Example 2 shows that the asymmetric LKF methods of Theorem 2 can provide larger delay bounds and fewer decision variables than Theorem 1 in some specific systems.

1. Introduction

It is well-known that time delays in system operations create unexpected dynamic situations such as quality degradation, vibration, and instability [1,2]. This is why time delays have received a lot of attention in many fields, such as aircraft, biological systems, chemical processes, networked control systems, neural networks, fuzzy systems, and so on. One of the crucial concerns in studying time-delay systems is the development of stability conditions while increasing the upper bounds of the time delay compared with others. On the other hand, the stability analysis of time-delay systems can be classified into two broad categories: delay-independent and delay-dependent. In the general case, the delay-dependent case is known to be less conservative than the delay-independent one when the size of the time delay is small [3]. Therefore, research on delay-dependent systems has been more actively conducted.

For the past decades, lots of stability criteria have been suggested based on the Lyapunov stability theorem [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Here, two methods are available for deriving enhanced stability conditions for linear systems with interval time-varying delays. One approach involves determining the Lyapunov–Krasovskii functional (LKF) to derive less conservative stability conditions for the system [8]. Another method utilizes mathematical tools to handle issues such as quadratic terms, non-LMI forms, and so on [9,10]. Indicators evaluating these methods include the maximum delay upper bound and the number of decision variables [11].

It is well recognized that finding new LKFs is also an important and significant job [12]. The conservatism of the stability results is determined by how the LKFs are constructed. A notable trend is to design them as complex integrals, including double and triple integrals and even augmented forms, within LKFs to include more information on system dynamics and delay properties. In [13,14], the integral term was integrated into the $x^T\left(t\right)Px\left(t\right)$ form in the design of LKFs, with [14] further enhancing this approach by incorporating delay terms. Moreover, refs. [15,16] expanded LKFs by proposing augmented quadratic forms for single and double integral terms, resulting in more conservative results. Refs. [3,17] improved LKFs by introducing an additional integral term for interval time-varying delays. And some researchers obtained conservative results by proposing various triple integral terms [18].

When extracting stability conditions based on LKFs, the quadratic terms within the integral term derived from the derivative of the double integral are of interest. To solve the quadratic terms within the integral, numerous integral inequalities offering the lower bound of integral terms have been proposed for decades. Many researchers have suggested various methods to reduce the conservatism of the LMI and computational burdens. The Jensen integral inequality was first used by Gu [19] to improve the stability conditions of time-delay systems. The Wirtinger-based integral inequality (WBII) [20] was introduced to obtain a tighter lower bound for the quadratic form in the integral term than that provided by Jensen’s inequality [21]. Park [22] presented the Wirtinger-based double integral inequality for the quadratic double integral form in the stability of time-delay systems. Moreover, generalized versions of the WBII were introduced using an auxiliary function in [23], while recent works in [9,24,25] have presented further generalized integral inequalities. Another mathematical technique is the reciprocally convex approach, which provides the lower bound of integral terms [26]. Since then, some improved versions have been introduced [27,28,29]. Zhang et al. [27] proposed delay-dependent matrix-based reciprocally convex inequality and estimation approaches for stability analysis with time-varying delays of linear systems. In addition to the methods mentioned so far, other techniques have been proposed to improve the stability conditions of systems. By adding a cross term to the time derivative LKF term, ref. [30] suggested several zero equations and ultimately yielded improved results. Generalized zero equality techniques that exploit the relationships among the integral terms have been introduced for linear systems with interval time-varying delays [31]. The work [32] applied the augmented zero equality method derived from Finsler Lemma and zero equalities to obtain improved results and proposed an approach to mitigate computational complexity. Numerous authors [33,34,35] adopted various functions to reduce the conservatism of stability conditions for time-delay systems. And ref. [36] proposed asymmetric LKF in which not all the involved matrix variables are required to be positive definite.

In this paper, the stability criteria for the linear systems with interval time-varying delays are studied. Two types of augmented LKFs with cross terms in integrals are suggested to improve the stability conditions for interval time-varying linear systems. To solve the problem of stability criteria, generalized integral inequality [9], zero equalities, reciprocally convex approach [26], and Finsler’s lemma [37] are utilized. In Theorem 1, stability criteria are derived by constructing augmented LKFs and employing zero equalities and WBII. In Theorem 2, asymmetric LKFs are constructed to reduce the number of decision variables. Finally, four numerical examples show that the proposed Theorems 1 and 2 obtain less conservative results than existing outcomes.

Notations. 

${\mathbb{R}}^n$, ${\mathbb{R}}^{m\times n}$, and ${\mathbb{S}}^n$ (${\mathbb{S}}_{+}^n$) denote n-vectors, $m\times n$ matrices, and $n\times n$ symmetric (positive) matrix, respectively. $I_n$ denotes an $n\times n$ identity matrix. $0_{n·m}$ denotes a $n\times m$ zero matrix. $\mathtt{Sym}\left\{X\right\}$ and $\mathtt{col}\{\cdots \}$ denote $X+X^T$ and the column vector. ∗ is used to represent symmetric terms as needed. ⊙ denotes the quadratic form of the matrix. $X_{\perp }$ denotes a basis for the null space of X. $X_{\left[\alpha \right]}$ is a matrix with respect to $\alpha$, i.e., $X_{\left[{\alpha }_0\right]}=X_{[\alpha ={\alpha }_0]}$.

2. Problem Statement

In this paper, we consider the following linear systems with time-varying delays:

$$\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =& Ax\left(t\right)+A_{d}x\left(t-\kappa \left(t\right)\right),\hfill \\ \hfill x\left(s\right)& =& \varphi \left(s\right),\forall s\in [-{\kappa }_U,0],\hfill \end{array}$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ represents the state vector, $\varphi \left(s\right)$ is the initial condition, $A,A_d\in {\mathbb{R}}^{n\times n}$ are constant matrices. $\kappa \left(t\right)$ is a time-varying delay satisfying a continuous function with $0\le {\kappa }_L\le {\kappa }_U$ and $\dot{\kappa }\left(t\right)\le {\kappa }_D$, where ${\kappa }_L$ and ${\kappa }_U$ are known positive scalars and ${\kappa }_D$ is any constant one.

The purpose of this paper is to derive the stability criteria for linear systems (1) with interval time-varying delays. The following lemmas are used to derive the main results.

Lemma 1 

([9]). For scalars $a<b$, a vector $x:[a,b]\to {\mathbb{R}}^n$, and a matrix $Q\in {\mathbb{S}}_{+}^n$, the following inequality holds:

$$\begin{array}{c}\hfill {\int }_a^b{\alpha }^T\left(s\right)Q\alpha \left(s\right)ds\ge {\displaystyle \frac{1}{b-a}}{\left({\int }_a^b{\mathbb{N}}_N(s,b-a)\otimes \alpha \left(s\right)ds\right)}^T\left({\mathbb{Q}}_N^{-1}(b-a)\otimes Q\right)\left(\odot \right),\end{array}$$

(2)

where ${\mathbb{N}}_N(s,\gamma )=\mathtt{col}\{I_n,(s-\gamma )I_n,\cdots ,{\displaystyle \frac{{(s-\gamma )}^{N-1}}{(N-1)!}}{I}_n\}$, and

$$\begin{array}{c}\hfill {\mathbb{Q}}_N^{-1}\left(h\right)={\left[\begin{array}{cccc}1& {\displaystyle \frac{h}{2}}& \cdots & {\displaystyle \frac{h^{N-1}}{N!}}\\ {\displaystyle \frac{h}{2}}& {\displaystyle \frac{h^2}{3}}& \cdots & {\displaystyle \frac{h^N}{(N+1)\times (N-1)!}}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{h^{N-1}}{N!}}& {\displaystyle \frac{h^N}{(N+1)\times (N-1)!}}& \cdots & {\displaystyle \frac{h^{2N-2}}{(2N-1)\times (N-1)!\times (N-1)!}}\end{array}\right]}^{-1}.\end{array}$$

Lemma 2 

([26]). For a scalar $\alpha \in (0,1)$, vectors $x,y\in {\mathbb{R}}^n$, matrices $M_1$, $M_2\in {\mathbb{S}}^n$, and $F\in {\mathbb{R}}^{n\times n}$, the following inequality holds: ${\displaystyle \frac{1}{\alpha }}{x}^T{M}_{1}x+{\displaystyle \frac{1}{1-\alpha }}{y}^T{M}_{2}y\ge x^T{M}_{1}x+y^T{M}_{2}y+2x^{T}Fy$, with $M_1-F{M}_2^{-1}{F}^T>0$.

Lemma 3 

([37]). Let $v\in {\mathbb{R}}^n$, $F\in {\mathbb{S}}^n$, $G\in {\mathbb{R}}^{m\times n}$. The following formulas are equivalent:

$$\begin{array}{cc}\hfill \left(i\right)& v^{T}Fv<0,\forall Gv=0,v\ne 0,\\ \hfill \left(ii\right)& \exists E\in {\mathbb{R}}^{n\times m}:F+\mathtt{Sym}\left\{EG\right\}<0,\\ \hfill \left(iii\right)& G_{\perp }^{T}F{G}_{\perp }<0.\end{array}$$

3. Main Results

This section presents the stability criteria for system (1). At first, a stability criterion is obtained by utilizing an augmented LKF and Lemmas 1–3. Following this, the stability criteria are improved through an asymmetric LKF. To simplify the expression of LMIs, an augmented vector is defined as

$$\begin{array}{ccc}\hfill \zeta \left(t\right)& =& \left\{\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-\kappa (t\left)\right)\\ x(t-{\kappa }_U)\\ \dot{x}\left(t\right)\\ \dot{x}(t-{\kappa }_L)\\ \dot{x}(t-{\kappa }_U)\end{array}\right],\left[\begin{array}{c}{\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{10}(x\left(s\right),\kappa \left(t\right),{\kappa }_L)\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,\kappa \left(t\right))\\ {\phi }_{21}(x\left(u\right),{\kappa }_L,0)\\ {\phi }_{21}(x\left(u\right),\kappa \left(t\right),{\kappa }_L)\\ {\phi }_{21}(x\left(u\right),{\kappa }_U,\kappa \left(t\right))\end{array}\right],\left[\begin{array}{c}{\phi }_{11}(x\left(s\right),\kappa \left(t\right),{\kappa }_L)\\ {\phi }_{11}(x\left(s\right),{\kappa }_U,\kappa \left(t\right))\\ {\phi }_{20}(x\left(u\right),\kappa \left(t\right),{\kappa }_L)\\ {\phi }_{20}(x\left(u\right),{\kappa }_U,\kappa \left(t\right))\end{array}\right]\right\},\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\phi }_{ij}(f(·),{\nu }_a,{\nu }_b)={\displaystyle \frac{1}{{({\nu }_a-{\nu }_b)}^j}}\underset{i-fold\mathrm{integral}}{\underbrace{{\int }_{t-{\nu }_a}^{t-{\nu }_b}{\int }_{u_1}^{t-{\nu }_b}\cdots {\int }_{u_k}^{t-{\nu }_b}}}f\left(s\right)dsd{u}_k\cdots d{u}_1.\end{array}$$

Here, ${\phi }_{21}(x\left(s\right),\kappa \left(t\right),{\kappa }_L)$ means ${\displaystyle \frac{1}{\kappa \left(t\right)-{\kappa }_L}}{\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\int }_s^{t}x\left(u\right)duds$ and ${\phi }_{10}(x\left(s\right),{\kappa }_L,0)$ means ${\int }_{t-{\kappa }_L}^{t}x\left(s\right)ds$.

And the block entry matrices ${\epsilon }_0=0_{17n·n}$, ${\epsilon }_i={[0_{n·(i-1)n},I_n,0_{n·(17-i)n}]}^T\in {\mathbb{R}}^{17n\times n}$$(i=1,2,\cdots ,17)$ are utilized, e.g., ${\epsilon }_2^T\zeta \left(t\right)=x(t-{\kappa }_L)$. Also, the following notations are defined:

$$\begin{array}{cc}\hfill {\kappa }_S& ={\kappa }_U-{\kappa }_L,\hfill \\ \hfill Q_{2i}& =Q_2+\left[\begin{array}{cc}{0}_{n·n}& S_i\\ S_i^T& 0_{n·n}\end{array}\right](i=1,2),\hfill \\ \hfill {\mathrm{\Omega }}_1& =\mathtt{diag}\{Q_{21},3Q_{21}\},{\mathrm{\Omega }}_2=\mathtt{diag}\{Q_{22},3Q_{22}\},{\mathrm{\Omega }}_3=\left[\begin{array}{cc}{\mathrm{\Omega }}_1& F_1\\ \ast & {\mathrm{\Omega }}_2\end{array}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{1,1\left[\kappa \right(t\left)\right]}& =\left[{\epsilon }_1,{\epsilon }_2,{\epsilon }_4,{\epsilon }_8,{\kappa }_L{\epsilon }_{11},{\kappa }_L({\epsilon }_8-{\epsilon }_{11}),{\epsilon }_9+{\epsilon }_{10},{\epsilon }_{16}+{\epsilon }_{17}+({\kappa }_U-\kappa \left(t\right)){\epsilon }_9\right.,\hfill \\ \hfill & \left.(\kappa \left(t\right)-{\kappa }_L){\epsilon }_9+{\kappa }_S{\epsilon }_{10}-{\epsilon }_{16}-{\epsilon }_{17}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{1,2}& =\left[{\epsilon }_5,{\epsilon }_6,{\epsilon }_7,{\epsilon }_1-{\epsilon }_2,-{\epsilon }_8+{\kappa }_L{\epsilon }_1,{\epsilon }_8-{\kappa }_L{\epsilon }_2,{\epsilon }_2-{\epsilon }_4,\right.\hfill \\ \hfill & \left.-{\epsilon }_9-{\epsilon }_{10}+{\kappa }_S{\epsilon }_2,{\epsilon }_9+{\epsilon }_{10}-{\kappa }_S{\epsilon }_4\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,1}& =\left[{\epsilon }_5,{\epsilon }_1,{\epsilon }_0,{\epsilon }_0,{\epsilon }_1-{\epsilon }_2,{\epsilon }_8\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,2}& =\left[{\epsilon }_6,{\epsilon }_2.{\epsilon }_1-{\epsilon }_2,{\epsilon }_8,{\epsilon }_0,{\epsilon }_0\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,3}& =\left[{\epsilon }_6,{\epsilon }_2,{\epsilon }_0,{\epsilon }_0,{\epsilon }_2-{\epsilon }_4,{\epsilon }_9+{\epsilon }_{10}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,4}& =\left[{\epsilon }_7,{\epsilon }_4,{\epsilon }_2-{\epsilon }_4,{\epsilon }_9+{\epsilon }_{10},{\epsilon }_0,{\epsilon }_0\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,5}& =\left[{\epsilon }_1-{\epsilon }_2,{\epsilon }_8,{\kappa }_L{\epsilon }_1-{\epsilon }_8,{\kappa }_L{\epsilon }_{11},{\epsilon }_8-{\kappa }_L{\epsilon }_2,{\kappa }_L({\epsilon }_8-{\epsilon }_{11})\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,6}& =\left[{\epsilon }_0,{\epsilon }_0,{\epsilon }_5,{\epsilon }_1,-{\epsilon }_6,-{\epsilon }_2\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,7\left[\kappa \right(t\left)\right]}& =\left[{\epsilon }_2-{\epsilon }_4,{\epsilon }_9+{\epsilon }_{10},{\kappa }_S{\epsilon }_2-{\epsilon }_9-{\epsilon }_{10},{\epsilon }_{16}+{\epsilon }_{17}+({\kappa }_U-\kappa \left(t\right)){\epsilon }_9,{\epsilon }_9+{\epsilon }_{10}-{\kappa }_S{\epsilon }_4,\right.\hfill \\ \hfill & \left.(\kappa \left(t\right)-{\kappa }_L){\epsilon }_9+{\kappa }_S{\epsilon }_{10}-{\epsilon }_{16}-{\epsilon }_{17}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{2,8}& =\left[{\epsilon }_0,{\epsilon }_0,{\epsilon }_6,{\epsilon }_2,-{\epsilon }_7,-{\epsilon }_4\right],\hfill \\ \hfill {\mathrm{\Pi }}_{3,1}& =\left[{\epsilon }_2,{\epsilon }_0,{\epsilon }_0,{\epsilon }_2-{\epsilon }_4,{\epsilon }_9+{\epsilon }_{10}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{3,2}& =\left[{\epsilon }_3,{\epsilon }_2-{\epsilon }_3,{\epsilon }_9,{\epsilon }_3-{\epsilon }_4,{\epsilon }_{10}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{3,3\left[\kappa \right(t\left)\right]}& =\left[{\epsilon }_9,(\kappa \left(t\right)-{\kappa }_L){\epsilon }_2-{\epsilon }_9,{\epsilon }_{16},{\epsilon }_9-(\kappa \left(t\right)-{\kappa }_L){\epsilon }_4,(\kappa \left(t\right)-{\kappa }_L)({\epsilon }_9+{\epsilon }_{10})-{\epsilon }_{16}\right],\hfill \\ \hfill {\mathrm{\Pi }}_{3,4}& =\left[{\epsilon }_0,{\epsilon }_6,{\epsilon }_2,-{\epsilon }_7,-{\epsilon }_4\right],\hfill \\ \hfill {\mathrm{\Lambda }}_1& =\left[{\epsilon }_2-{\epsilon }_3,{\epsilon }_9,-{\epsilon }_2-{\epsilon }_3+2{\epsilon }_{14},{\epsilon }_9-2{\epsilon }_{12}\right],\hfill \\ \hfill {\mathrm{\Lambda }}_2& =\left[{\epsilon }_3-{\epsilon }_4,{\epsilon }_{10},-{\epsilon }_3-{\epsilon }_4+2{\epsilon }_{15},{\epsilon }_{10}-2{\epsilon }_{13}\right],\hfill \\ \hfill \mathrm{\Lambda }& =[{\mathrm{\Lambda }}_1,{\mathrm{\Lambda }}_2],\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathrm{\Psi }}_{1\left[{\kappa }_t\right]}& =\mathtt{Sym}\left\{{\mathrm{\Pi }}_{1,1\left[\kappa \right(t\left)\right]}R{\mathrm{\Pi }}_{1,2}^T\right\},\hfill \\ \hfill {\mathrm{\Psi }}_{2\left[\kappa \right(t\left)\right]}& ={\mathrm{\Pi }}_{2,1}{G}_1{\mathrm{\Pi }}_{2,1}^T-{\mathrm{\Pi }}_{2,2}{G}_1{\mathrm{\Pi }}_{2,2}^T+{\mathrm{\Pi }}_{2,3}{G}_2{\mathrm{\Pi }}_{2,3}^T-{\mathrm{\Pi }}_{2,4}{G}_2{\mathrm{\Pi }}_{2,4}^T\hfill \\ \hfill & +\mathtt{Sym}\left\{{\mathrm{\Pi }}_{2,5}{G}_1{\mathrm{\Pi }}_{2,6}^T+{\mathrm{\Pi }}_{2,7\left[\kappa \right(t\left)\right]}{G}_2{\mathrm{\Pi }}_{2,8}^T\right\},\hfill \\ \hfill {\mathrm{\Psi }}_{3\left[{\kappa }_t\right]}& ={\mathrm{\Pi }}_{3,1}{G}_3{\mathrm{\Pi }}_{3,1}^T-(1-{\kappa }_D){\mathrm{\Pi }}_{3,2}{G}_3{\mathrm{\Pi }}_{3,2}^T+\mathtt{Sym}\left\{{\mathrm{\Pi }}_{3,3\left[\kappa \right(t\left)\right]}{G}_3{\mathrm{\Pi }}_{3,4}^T\right\},\hfill \\ \hfill {\mathrm{\Psi }}_{41}& ={\kappa }_L^2[{\epsilon }_5,{\epsilon }_1]Q_1{[{\epsilon }_5,{\epsilon }_1]}^T+{\kappa }_S^2[{\epsilon }_6,{\epsilon }_2]Q_2{[{\epsilon }_6,{\epsilon }_2]}^T,\hfill \\ \hfill {\mathrm{\Psi }}_{42}& ={\kappa }_S\left({\epsilon }_2{S}_1{\epsilon }_2^T-{\epsilon }_3(S_1-S_2){\epsilon }_3^T-{\epsilon }_4{S}_2{\epsilon }_4^T\right),\hfill \\ \hfill {\mathrm{\Psi }}_{43}& =[-{\epsilon }_1+{\epsilon }_2,-{\epsilon }_8]Q_1{[-{\epsilon }_1+{\epsilon }_2,-{\epsilon }_8]}^T\hfill \\ \hfill & +3[{\epsilon }_1+{\epsilon }_2-{\displaystyle \frac{2}{{\kappa }_L}}{\epsilon }_8,-{\epsilon }_8+2{\epsilon }_{11}]Q_1{[{\epsilon }_1+{\epsilon }_2-{\displaystyle \frac{2}{{\kappa }_L}}{\epsilon }_8,-{\epsilon }_8+2{\epsilon }_{11}]}^T,\hfill \\ \hfill {\mathrm{\Psi }}_{44}& ={\mathrm{\Lambda }}_1{\mathrm{\Omega }}_1{\mathrm{\Lambda }}_1^T,{\mathrm{\Psi }}_{45}={\mathrm{\Lambda }}_2{\mathrm{\Omega }}_2{\mathrm{\Lambda }}_2^T,{\mathrm{\Psi }}_{46}=-\mathrm{\Lambda }{\mathrm{\Omega }}_3{\mathrm{\Lambda }}^T,\hfill \\ \hfill {\mathrm{\Psi }}_4& ={\mathrm{\Psi }}_{41}+{\mathrm{\Psi }}_{42}+{\mathrm{\Psi }}_{43}+{\mathrm{\Psi }}_{46},\hfill \\ \hfill {\mathrm{\Psi }}_5& ={\kappa }_U({\epsilon }_{5}W{\epsilon }_5^T-{\epsilon }_{7}W{\epsilon }_7^T)-\mathtt{Sym}\left\{({\epsilon }_1-{\epsilon }_4)W{({\epsilon }_5-{\epsilon }_7)}^T\right\}\hfill \\ \hfill & -3\mathtt{Sym}\left\{\left(-{\epsilon }_1-{\epsilon }_4+{\displaystyle \frac{2}{{\kappa }_U}}({\epsilon }_8+{\epsilon }_9+{\epsilon }_{10})\right)W{\left(-{\epsilon }_5-{\epsilon }_7+{\displaystyle \frac{2}{{\kappa }_U}}({\epsilon }_1-{\epsilon }_4)\right)}^T\right\},\hfill \\ \hfill {\mathrm{\Psi }}_{\left[\kappa \right(t\left)\right]}& ={\mathrm{\Psi }}_{1\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_{2\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_{3\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_4+{\mathrm{\Psi }}_5,\hfill \\ \hfill {\mathrm{\Phi }}_{\left[\kappa \right(t\left)\right]}& =\mathtt{Sym}\left\{\mathrm{\Pi }\left((\kappa \left(t\right)-{\kappa }_L)[{\epsilon }_{14},{\epsilon }_0,{\epsilon }_{12},{\epsilon }_0]+({\kappa }_U-\kappa \left(t\right))[{\epsilon }_0,{\epsilon }_{15},{\epsilon }_0,{\epsilon }_{13}]\right.\right.\hfill \\ \hfill & \left.{\left.-[{\epsilon }_9,{\epsilon }_{10},{\epsilon }_{16},{\epsilon }_{17}]\right)}^T\right\},\hfill \end{array}$$

$$\begin{array}{c}\mathrm{\Gamma }=A{\epsilon }_1^T+A_d{\epsilon }_3^T-I_n{\epsilon }_5^T.\end{array}$$

(3)

Theorem 1. 

For given scalars ${\kappa }_L, {\kappa }_U,$ and ${\kappa }_D$ satisfying $0\le {\kappa }_L\le {\kappa }_U$ and $\dot{\kappa }\left(t\right)\le {\kappa }_D$, system (1) is asymptotically stable if there exist matrices $R\in {\mathbb{S}}_{+}^{9n},G_i\in {\mathbb{S}}_{+}^{6n},G_3\in {\mathbb{S}}_{+}^{5n},Q_i\in {\mathbb{S}}_{+}^{2n},W\in {\mathbb{S}}_{+}^n,S_i\in {\mathbb{S}}^n(i=1,2),F_1\in {\mathbb{R}}^{4n\times 4n}$ and $\mathrm{\Pi }\in {\mathbb{R}}^{4n\times 17n}$ satisfying the following LMIs:

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_{\perp }^T({\mathrm{\Psi }}_{\left[{\kappa }_L\right]}+{\mathrm{\Phi }}_{\left[{\kappa }_L\right]}){\mathrm{\Gamma }}_{\perp }<0,\end{array}$$

(4)

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_{\perp }^T({\mathrm{\Psi }}_{\left[{\kappa }_U\right]}+{\mathrm{\Phi }}_{\left[{\kappa }_U\right]}){\mathrm{\Gamma }}_{\perp }<0,\end{array}$$

(5)

$$\begin{array}{c}\hfill {\mathrm{\Omega }}_3>0.\end{array}$$

(6)

Proof of Theorem 1.

Consider the LKF candidate given by

$$\begin{array}{c}\hfill V\left(t\right)=\sum _{i=1}^5{V}_i,\end{array}$$

(7)

where

$$\begin{array}{ccc}\hfill V_1\left(t\right)& =& {\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-{\kappa }_U)\\ {\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{20}(x\left(u\right),{\kappa }_L,0)\\ {\int }_{t-{\kappa }_L}^t{\int }_{t-{\kappa }_L}^{s}x\left(u\right)duds\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)\\ {\phi }_{20}(x\left(u\right),{\kappa }_U,{\kappa }_L)\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\int }_{t-{\kappa }_U}^{s}x\left(u\right)duds\end{array}\right]}^{T}R\left(\odot \right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill V_2\left(t\right)& =& {\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\psi \left(u\right)du\\ {\int }_{t-{\kappa }_L}^s\psi \left(u\right)du\end{array}\right]}^T{G}_1\left(\odot \right)ds+{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\psi \left(u\right)du\end{array}\right]}^T{G}_2\left(\odot \right)ds,\hfill \\ \hfill V_3\left(t\right)& =& {\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\left[\begin{array}{c}x\left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\psi \left(u\right)du\end{array}\right]}^T{G}_3\left(\odot \right)ds,\hfill \\ \hfill V_4\left(t\right)& =& {\kappa }_L{\int }_{t-{\kappa }_L}^t{\int }_s^t{\psi }^T\left(u\right)Q_1\left(\odot \right)duds+{\kappa }_S{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\int }_s^{t-{\kappa }_L}{\psi }^T\left(u\right)Q_2\left(\odot \right)duds,\hfill \\ \hfill V_5\left(t\right)& =& {\kappa }_U{\int }_{t-{\kappa }_U}^t{\dot{x}}^T\left(s\right)W\dot{x}\left(s\right)ds-{\left({\int }_{t-{\kappa }_U}^t\dot{x}\left(s\right)ds\right)}^{T}W\left(\odot \right)\hfill \\ & & -3{\left({\int }_{t-{\kappa }_U}^t\dot{x}\left(s\right)ds-{\displaystyle \frac{2}{{\kappa }_U}}{\int }_{t-{\kappa }_U}^t{\int }_s^t\dot{x}\left(u\right)duds\right)}^{T}W\left(\odot \right),\hfill \end{array}$$

where $\psi \left(t\right)=\mathtt{col}\{\dot{x}\left(t\right),x\left(t\right)\}$.

The time derivative of Lyapunov–Krasovskii functionals can be represented as

$$\begin{array}{ccc}{\dot{V}}_1& =& 2{\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-{\kappa }_U)\\ {\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{20}(x\left(u\right),{\kappa }_L,0)\\ {\int }_{t-{\kappa }_L}^t{\int }_{t-{\kappa }_L}^{s}x\left(u\right)duds\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)\\ {\phi }_{20}(x\left(u\right),{\kappa }_U,{\kappa }_L)\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\int }_{t-{\kappa }_U}^{s}x\left(u\right)duds\end{array}\right]}^{T}R\left[\begin{array}{c}\dot{x}\left(t\right)\\ \dot{x}\left(t-{\kappa }_L\right)\\ \dot{x}\left(t-{\kappa }_U\right)\\ x\left(t\right)-x\left(t-{\kappa }_L\right)\\ {\kappa }_{L}x\left(t\right)-{\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{10}(x\left(s\right),{\kappa }_L,0)-{\kappa }_{L}x\left(t-{\kappa }_L\right)\\ x\left(t-{\kappa }_L\right)-x\left(t-{\kappa }_U\right)\\ {\kappa }_{S}x\left(t-{\kappa }_L\right)-{\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)-{\kappa }_{S}x\left(t-{\kappa }_U\right)\end{array}\right]\hfill \\ & =& {\zeta }^T\left(t\right){\mathrm{\Psi }}_{1\left[\kappa \right(t\left)\right]}\zeta \left(t\right)\hfill \end{array}$$

(8)

$$\begin{array}{l}{\dot{V}}_2={\left[\begin{array}{c}\psi \left(t\right)\\ 0_{2n·1}\\ x\left(t\right)-x\left(t-{\kappa }_L\right)\\ {\int }_{t-{\kappa }_L}^{t}x\left(s\right)ds\end{array}\right]}^T{G}_1\left(\odot \right)-\left[\begin{array}{c}\psi \left(t-{\kappa }_L\right)\\ x\left(t\right)-x\left(t-{\kappa }_L\right)\\ {\int }_{t-{\kappa }_L}^{t}x\left(s\right)ds\\ 0_{2n·1}\end{array}\right]G_1\left(\odot \right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+{\left[\begin{array}{c}\psi \left(t-{\kappa }_L\right)\\ 0_{2n·1}\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}\psi \left(s\right)ds\end{array}\right]}^T{G}_2\left(\odot \right)-{\left[\begin{array}{c}\psi \left(t-{\kappa }_U\right)\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}\psi \left(s\right)ds\\ 0_{2n·1}\end{array}\right]}^T{G}_2\left(\odot \right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+2{\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\psi \left(s\right)ds\\ {\int }_{t-{\kappa }_L}^s\psi \left(s\right)ds\end{array}\right]}^T{G}_1\left[\begin{array}{c}{0}_{2n·1}\\ \psi \left(t\right)\\ -\psi \left(t-{\kappa }_L\right)\end{array}\right]ds\\ \hspace{1em}\hspace{1em}\hspace{1em}+2{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(s\right)ds\\ {\int }_{t-{\kappa }_U}^s\psi \left(s\right)ds\end{array}\right]}^T{G}_2\left[\begin{array}{c}{0}_{2n·1}\\ \psi \left(t-{\kappa }_L\right)\\ -\psi \left(t-{\kappa }_U\right)\end{array}\right]ds\\ \hspace{1em}\hspace{1em}\hspace{1em}={\zeta }^T\left(t\right){\mathrm{\Psi }}_{2\left[\kappa \right(t\left)\right]}\zeta \left(t\right)\end{array}$$

(9)

$$\begin{array}{l}{\dot{V}}_3=\left[\begin{array}{c}x\left(t-{\kappa }_L\right)\\ 0_{2n·1}\\ x\left(t-{\kappa }_L\right)-x\left(t-{\kappa }_U\right)\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}x\left(s\right)ds\end{array}\right]G_3\left(\odot \right)-\left(1-\dot{\kappa }\left(t\right)\right)\left[\begin{array}{c}x\left(t-\kappa \left(t\right)\right)\\ {\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}\psi \left(s\right)ds\\ {\int }_{t-{\kappa }_U}^{t-\kappa \left(t\right)}\psi \left(s\right)ds\end{array}\right]G_3\left(\odot \right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+2{\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\left[\begin{array}{c}x\left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(s\right)ds\\ {\int }_{t-{\kappa }_U}^s\psi \left(s\right)ds\end{array}\right]}^T{G}_3\left[\begin{array}{c}{0}_{n·1}\\ \psi (t-{\kappa }_L)\\ -\psi \left(t-{\kappa }_U\right)\end{array}\right]ds\\ \hspace{1em}\hspace{1em}\le {\zeta }^T\left(t\right){\mathrm{\Psi }}_{3\left[\kappa \right(t\left)\right]}\zeta \left(t\right)\end{array}$$

(10)

$$\begin{array}{l}{\dot{V}}_4={\kappa }_L^2{\psi }^T\left(t\right)Q_1\left(\odot \right)-{\kappa }_L{\int }_{t-{\kappa }_L}^t{\psi }^T\left(s\right)Q_1\left(\odot \right)ds\\ \hspace{1em}\hspace{1em}\hspace{1em}+{\kappa }_S^2{\psi }^T(t-{\kappa }_L)Q_2\left(\odot \right)-{\kappa }_S{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\psi }^T\left(s\right)Q_2\left(\odot \right)ds\\ \hspace{1em}\hspace{1em}={\zeta }^T\left(t\right){\mathrm{\Psi }}_{4\left[\kappa \right(t\left)\right]}\zeta \left(t\right)-{\kappa }_L{\int }_{t-{\kappa }_L}^t{\psi }^T\left(s\right)Q_1\left(\odot \right)ds-{\kappa }_S{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\psi }^T\left(s\right)Q_2\left(\odot \right)ds.\end{array}$$

(11)

Let us introduce zero equalities for symmetric matrices $S_1,S_2$ inspired by the work [30].

$$\begin{array}{c}\hfill Z_1={\kappa }_S\left(x^T(t-{\kappa }_L)S_{1}x(t-{\kappa }_L)-x^T(t-\kappa \left(t\right))S_{1}x(t-\kappa \left(t\right))-2{\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\dot{x}}^T\left(s\right)S_{1}x\left(s\right)ds\right),\end{array}$$

(12)

$$\begin{array}{c}\hfill Z_2={\kappa }_S\left(x^T(t-\kappa \left(t\right))S_{2}x(t-\kappa \left(t\right))-x^T(t-{\kappa }_U)S_{2}x(t-{\kappa }_U)-2{\int }_{t-{\kappa }_U}^{t-\kappa \left(t\right)}{\dot{x}}^T\left(s\right)S_{2}x\left(s\right)ds\right).\end{array}$$

(13)

And, adding (12) and (13) to (11), the following equality can be obtained:

$$\begin{array}{ccc}\hfill {\dot{V}}_4\left(t\right)+Z_1+Z_2& =& {\zeta }^T\left(t\right){\mathrm{\Psi }}_{41}\zeta \left(t\right)+{\kappa }_S\left(x^T(t-{\kappa }_L)S_{1}x(t-{\kappa }_L)\right.\hfill \\ & & \left.-x^T(t-\kappa \left(t\right))(S_1-S_2)x(t-\kappa \left(t\right))-x^T(t-{\kappa }_U)S_{2}x(t-{\kappa }_U)\right)\hfill \\ & & -{\kappa }_L{\int }_{t-{\kappa }_L}^t{\psi }^T\left(s\right)Q_1(\odot )ds-{\kappa }_S{\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\psi }^T\left(s\right)Q_{21}(\odot )ds\hfill \\ & & -{\kappa }_S{\int }_{t-{\kappa }_U}^{t-\kappa \left(t\right)}{\psi }^T\left(s\right)Q_{22}(\odot )ds\hfill \\ & =& {\zeta }^T\left(t\right)\left({\psi }_{41}+{\psi }_{42}\right)\zeta -{\kappa }_L{\int }_{t-{\kappa }_L}^t{\psi }^T\left(s\right)Q_1(\odot )ds\hfill \\ & & -{\kappa }_S{\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\psi }^T\left(s\right)Q_{21}(\odot )ds-{\kappa }_S{\int }_{t-{\kappa }_U}^{t-\kappa \left(t\right)}{\psi }^T\left(s\right)Q_{22}(\odot )ds.\hfill \end{array}$$

(14)

Moreover, by employing Lemma 1 (N = 1), the upper bounds of integral terms in (14) can be obtained as follows:

$$\begin{array}{l}-{\kappa }_L{\int }_{t-{\kappa }_L}^t{\psi }^T\left(s\right)Q_1(\odot )ds\le -{\phi }_{10}^T(\psi \left(s\right),{\kappa }_L,0)Q_1(\odot )\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-3{\left({\phi }_{10}(\psi \left(s\right),{\kappa }_L,0)-2{\phi }_{21}(\psi \left(u\right),{\kappa }_L,0)\right)}^T{Q}_1(\odot )\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\zeta }^T\left(t\right){\psi }_{43}\zeta \left(t\right).\end{array}$$

(15)

$$\begin{array}{ccc}\hfill -{\kappa }_S{\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\psi }^T\left(s\right)Q_{21}(\odot )ds& \le & -{\displaystyle \frac{{\kappa }_S}{\kappa \left(t\right)-{\kappa }_L}}{\phi }_{10}^T(\psi \left(s\right),\kappa \left(t\right),{\kappa }_L)Q_{21}(\odot )\hfill \\ & & -3{\displaystyle \frac{{\kappa }_S}{\kappa \left(t\right)-{\kappa }_L}}{\left({\phi }_{10}^T(\psi \left(s\right),\kappa \left(t\right),{\kappa }_L)-2{\phi }_{21}^T(\psi \left(u\right),\kappa \left(t\right),{\kappa }_L)\right)}^T\hfill \\ & & \times Q_{21}(\odot )\hfill \\ & =& -{\displaystyle \frac{{\kappa }_S}{\kappa \left(t\right)-{\kappa }_L}}{\zeta }^T\left(t\right){\psi }_{44}\zeta \left(t\right).\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill -{\kappa }_S{\int }_{t-{\kappa }_U}^{t-\kappa \left(t\right)}{\psi }^T\left(s\right)Q_{22}(\odot )ds& \le & -{\displaystyle \frac{{\kappa }_S}{{\kappa }_U-\kappa \left(t\right)}}{\phi }_{10}^T(\psi \left(s\right),{\kappa }_U,\kappa \left(t\right))Q_{22}(\odot )\hfill \\ & & -3{\displaystyle \frac{{\kappa }_S}{{\kappa }_U-\kappa \left(t\right)}}{\left({\phi }_{10}(\psi \left(s\right),{\kappa }_U,\kappa \left(t\right))-2{\phi }_{21}(\psi \left(u\right),{\kappa }_U,\kappa \left(t\right))\right)}^T\hfill \\ & & \times Q_{22}(\odot )\hfill \\ & =& -{\displaystyle \frac{{\kappa }_S}{{\kappa }_U-\kappa \left(t\right)}}{\zeta }^T\left(t\right){\psi }_{45}\zeta \left(t\right).\hfill \end{array}$$

(17)

By using Lemma 2,

$$\begin{array}{c}\hfill -{\displaystyle \frac{{\kappa }_S}{\kappa \left(t\right)-{\kappa }_L}}{\zeta }^T\left(t\right){\psi }_{44}\zeta \left(t\right)-{\displaystyle \frac{{\kappa }_S}{{\kappa }_U-\kappa \left(t\right)}}{\zeta }^T\left(t\right){\psi }_{45}\zeta \left(t\right)\le {\zeta }^T\left(t\right){\psi }_{46}\zeta \left(t\right).\end{array}$$

(18)

Hence, from (11) to (18), a novel upper bound for ${\dot{V}}_4\left(t\right)$ is obtained as follows:

$$\begin{array}{c}\hfill {\dot{V}}_4\left(t\right)\le {\zeta }^T\left(t\right){\psi }_4\zeta \left(t\right),\end{array}$$

(19)

where ${\psi }_4={\psi }_{41}+{\psi }_{42}+{\psi }_{43}+{\psi }_{46}$.

Based on the relationships between the elements of the augmented vector, the following equality is derived:

$$\begin{array}{ccc}\hfill 0& =& {\zeta }^T\left(t\right)\mathtt{Sym}\left\{\mathrm{\Pi }\left((\kappa \left(t\right)-{\kappa }_L)\left[{\epsilon }_{14},{\epsilon }_0,{\epsilon }_{12},{\epsilon }_0\right]+({\kappa }_U-\kappa \left(t\right))\left[{\epsilon }_0,{\epsilon }_{15},{\epsilon }_0,{\epsilon }_{13}\right]\right.\right.\hfill \\ & & \left.\left.-\left[{\epsilon }_9,{\epsilon }_{10},{\epsilon }_{16},{\epsilon }_{17}\right]\right)\right\}\zeta \left(t\right)\hfill \\ & =& {\zeta }^T\left(t\right){\mathrm{\Phi }}_{\left[h\right(t\left)\right]}\zeta \left(t\right).\hfill \end{array}$$

(20)

Also, by Lemma 1 (N = 1), the Lyapunov functional is induced:

$$\begin{array}{ccc}\hfill V_5& =& {\kappa }_U{\int }_{t-{\kappa }_U}^t{\dot{x}}^T\left(s\right)W\dot{x}\left(s\right)ds-{\left({\int }_{t-{\kappa }_U}^t\dot{x}\left(s\right)ds\right)}^{T}W(\odot )\hfill \\ & & -3{\left({\int }_{t-{\kappa }_U}^t\dot{x}\left(s\right)ds-{\displaystyle \frac{2}{{\kappa }_U}}{\int }_{t-{\kappa }_U}^t{\int }_s^t\dot{x}\left(u\right)duds\right)}^{T}W(\odot ).\hfill \end{array}$$

(21)

Thus, ${\dot{V}}_5\left(t\right)$ is

$$\begin{array}{ccc}\hfill {\dot{V}}_5& =& {\kappa }_U{\dot{x}}^T\left(t\right)W_1\dot{x}\left(t\right)-{\kappa }_U{\dot{x}}^T\left(t-{\kappa }_U\right)W_1\dot{x}\left(t-{\kappa }_U\right)-2{\left(x\left(t\right)-x\left(t-{\kappa }_U\right)\right)}^T{W}_1(\odot )\hfill \\ & & -6{\left(-x\left(t\right)-x\left(t-{\kappa }_U\right)+2{\phi }_{11}(x\left(s\right),{\kappa }_U,0)\right)}^T{W}_1(\odot )\hfill \\ & =& {\zeta }^T\left(t\right){\mathrm{\Psi }}_5\zeta \left(t\right).\hfill \end{array}$$

(22)

From (11) to (22), $\dot{V}\left(t\right)$ can be estimated as

$$\begin{array}{c}\hfill \dot{V}\left(t\right)\le {\zeta }^T\left(t\right)\left({\mathrm{\Psi }}_{1\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_{2\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_{3\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_4+{\mathrm{\Psi }}_5+{\mathrm{\Phi }}_{\left[\kappa \right(t\left)\right]}\right)\zeta \left(t\right).\end{array}$$

(23)

Regarding system (1), a stability condition can be expressed as

$$\begin{array}{c}\hfill {\zeta }^T\left(t\right)\left({\mathrm{\Psi }}_{\kappa \left(t\right)}+{\mathrm{\Phi }}_{\left[\kappa \right(t\left)\right]}\right)\zeta \left(t\right)<0 \mathrm{subject} \mathrm{to} \mathrm{\Gamma }\zeta \left(t\right)=0.\end{array}$$

(24)

Considering parts (i) and (iii) of Lemma 3, condition (24) is equivalent to

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_{\perp }^T\left({\mathrm{\Psi }}_{\left[\kappa \right(t\left)\right]}+{\mathrm{\Phi }}_{\left[\kappa \right(t\left)\right]}\right){\mathrm{\Gamma }}_{\perp }<0.\end{array}$$

(25)

Now, if LMIs (4) and (5) are satisfied for the convexity of $\kappa \left(t\right)\in [{\kappa }_L,{\kappa }_U]$, then inequality (25) is satisfied, which means system (1) is asymptotically stable. This completes our proof. □

Remark 1. 

In ref. [3], the augmented vector for the single integral term includes only $x\left(t\right)$, $\dot{x}\left(t\right)$, and ${\int }_s^t\dot{x}\left(s\right)ds$. However, in $V_1$ of Theorem 1, double integral terms are considered such as ${\int }_{t-{\kappa }_L}^t{\int }_{t-{\kappa }_L}^{s}x\left(u\right)duds$, and in $V_2$ and $V_3$, additional single integral terms, such as ${\int }_{t-{\kappa }_L}^s\psi \left(u\right)du$, are considered. Accordingly, the augmented vector is further considered as $\zeta \left(t\right)$, and stability conditions are derived using zero equality (20). In the next section, it is shown that Theorem 1 can provide larger delay bounds than those of [3].

To show the effectiveness of LKFs (7), let us consider LKFs as $\widehat{V}\left(t\right)={\widehat{V}}_1\left(t\right)+{\widehat{V}}_2\left(t\right)+{\widehat{V}}_3\left(t\right)+{\widehat{V}}_4\left(t\right)+{\widehat{V}}_5\left(t\right)$. The LKFs are simplified by removing double integral terms in the LKFs of Theorem 1. An augmented vector for Corollary 1 is defined as follows:

$$\begin{array}{c}\hfill {\zeta }_c\left(t\right)=\left\{\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-\kappa (t\left)\right)\\ x(t-{\kappa }_U)\\ \dot{x}\left(t\right)\\ \dot{x}(t-{\kappa }_L)\\ \dot{x}(t-{\kappa }_U)\end{array}\right],\left[\begin{array}{c}{\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{10}(x\left(s\right),\kappa \left(t\right),{\kappa }_L)\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,\kappa \left(t\right))\end{array}\right],\left[\begin{array}{c}{\phi }_{11}(x\left(s\right),\kappa \left(t\right),{\kappa }_L)\\ {\phi }_{11}(x\left(s\right),{\kappa }_U,\kappa \left(t\right))\end{array}\right]\right\}.\end{array}$$

and the block entry matrices ${\widehat{\epsilon }}_i={[0_{n·(i-1)n},I_n,0_{n·(12-i)n}]}^T\in {\mathbb{R}}^{12n\times n}(i=1,2,\cdots ,12)$ are utilized. Also, the following notations are defined:

$$\begin{array}{cc}\hfill {\widehat{\mathrm{\Omega }}}_1& =\mathtt{diag}\{{\widehat{Q}}_1,3{\widehat{Q}}_1\},{\widehat{\mathrm{\Omega }}}_2=\mathtt{diag}\{{\widehat{Q}}_2,3{\widehat{Q}}_2\},\hfill \\ \hfill {\widehat{\mathrm{\Omega }}}_3& =\left[\begin{array}{cc}{\widehat{\mathrm{\Omega }}}_2& F_2\\ \ast & {\widehat{\mathrm{\Omega }}}_2\end{array}\right],\hfill \\ \hfill {\widehat{\mathrm{\Lambda }}}_1& =\left[{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2,-{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2+{\displaystyle \frac{2}{{\kappa }_L}}{\widehat{\epsilon }}_8\right],\hfill \\ \hfill {\widehat{\mathrm{\Lambda }}}_2& =\left[{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_3,-{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_3+2{\widehat{\epsilon }}_{11}\right],\hfill \\ \hfill {\widehat{\mathrm{\Lambda }}}_3& =\left[{\widehat{\epsilon }}_3-{\widehat{\epsilon }}_4,-{\widehat{\epsilon }}_3-{\widehat{\epsilon }}_4+2{\widehat{\epsilon }}_{12}\right],\hfill \\ \hfill {\widehat{\mathrm{\Psi }}}_{1\left[\kappa \right(t\left)\right]}& =\mathtt{Sym}\left\{[{\widehat{\epsilon }}_1,{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_4,{\widehat{\epsilon }}_8,{\widehat{\epsilon }}_9+{\widehat{\epsilon }}_{10}]\widehat{R}{[{\widehat{\epsilon }}_5,{\widehat{\epsilon }}_6,{\widehat{\epsilon }}_7,{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4]}^T\right\},\hfill \\ \hfill {\widehat{\mathrm{\Psi }}}_{2\left[\kappa \right(t\left)\right]}& =[{\widehat{\epsilon }}_5,{\widehat{\epsilon }}_1,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2]{\widehat{G}}_1{[{\widehat{\epsilon }}_5,{\widehat{\epsilon }}_1,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2]}^T-[{\widehat{\epsilon }}_6,{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_0]{\widehat{G}}_1{[{\widehat{\epsilon }}_6,{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_0]}^T\hfill \\ \hfill & +\mathtt{Sym}\left\{[{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_8,{\kappa }_L{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_8,{\widehat{\epsilon }}_8-{\kappa }_L{\widehat{\epsilon }}_2]{\widehat{G}}_1{[{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_5,-{\widehat{\epsilon }}_6]}^T\right\}\hfill \\ \hfill & +[{\widehat{\epsilon }}_6,{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4]{\widehat{G}}_2{[{\widehat{\epsilon }}_6,{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4]}^T-[{\widehat{\epsilon }}_7,{\widehat{\epsilon }}_4,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4,{\widehat{\epsilon }}_0]{\widehat{G}}_2{[{\widehat{\epsilon }}_7,{\widehat{\epsilon }}_4,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4,{\widehat{\epsilon }}_0]}^T\hfill \\ \hfill & +\mathtt{Sym}\left\{[{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4,{\widehat{\epsilon }}_9+{\widehat{\epsilon }}_{10},{\kappa }_S{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_9-{\widehat{\epsilon }}_{10},{\widehat{\epsilon }}_9+{\widehat{\epsilon }}_{10}-{\kappa }_S{\widehat{\epsilon }}_4]{\widehat{G}}_2{[{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_6,-{\widehat{\epsilon }}_7]}^T\right\},\hfill \\ \hfill {\widehat{\mathrm{\Psi }}}_{3\left[{\kappa }_t\right]}& =[{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4]{\widehat{G}}_3{[{\widehat{\epsilon }}_2,{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_4]}^T\hfill \\ \hfill & -(1-{\kappa }_D)[{\widehat{\epsilon }}_3,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_3,{\widehat{\epsilon }}_3-{\widehat{\epsilon }}_4]{\widehat{G}}_3{[{\widehat{\epsilon }}_3,{\widehat{\epsilon }}_2-{\widehat{\epsilon }}_3,{\widehat{\epsilon }}_3-{\widehat{\epsilon }}_4]}^T\hfill \\ \hfill & +\mathtt{Sym}\left\{[{\widehat{\epsilon }}_9,(\kappa \left(t\right)-{\kappa }_L){\widehat{\epsilon }}_2-{\widehat{\epsilon }}_9,{\widehat{\epsilon }}_9-(\kappa \left(t\right)-{\kappa }_L){\widehat{\epsilon }}_4]{\widehat{G}}_3{[{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_6,-{\widehat{\epsilon }}_7]}^T\right\},\hfill \\ \hfill {\widehat{\mathrm{\Psi }}}_4& ={\kappa }_L^2{\widehat{\epsilon }}_5{\widehat{Q}}_1{\widehat{\epsilon }}_5^T+{\kappa }_S^2{\widehat{\epsilon }}_6{\widehat{Q}}_2{\widehat{\epsilon }}_6^T-{\widehat{\mathrm{\Lambda }}}_1{\widehat{\mathrm{\Omega }}}_1{\widehat{\mathrm{\Lambda }}}_1^T-[{\mathrm{\Lambda }}_2,{\mathrm{\Lambda }}_3]{\widehat{\mathrm{\Omega }}}_3{[{\mathrm{\Lambda }}_2,{\mathrm{\Lambda }}_3]}^T,\hfill \\ \hfill {\widehat{\mathrm{\Psi }}}_5& ={\kappa }_U({\widehat{\epsilon }}_5\widehat{W}{\widehat{\epsilon }}_5^T-{\widehat{\epsilon }}_7\widehat{W}{\widehat{\epsilon }}_7^T)-\mathtt{Sym}\left\{({\widehat{\epsilon }}_1-{\widehat{\epsilon }}_4)\widehat{W}{({\widehat{\epsilon }}_5-{\widehat{\epsilon }}_7)}^T\right\}\hfill \\ \hfill & -3\mathtt{Sym}\left\{\left(-{\widehat{\epsilon }}_1-{\widehat{\epsilon }}_4+{\displaystyle \frac{2}{{\kappa }_U}}({\widehat{\epsilon }}_8+{\widehat{\epsilon }}_9+{\widehat{\epsilon }}_{10})\right)\widehat{W}{\left(-{\widehat{\epsilon }}_5-{\widehat{\epsilon }}_7+{\displaystyle \frac{2}{{\kappa }_U}}({\widehat{\epsilon }}_1-{\widehat{\epsilon }}_4)\right)}^T\right\},\hfill \\ \hfill {\widehat{\mathrm{\Psi }}}_{\left[\kappa \right(t\left)\right]}& ={\widehat{\mathrm{\Psi }}}_{1\left[\kappa \right(t\left)\right]}+{\widehat{\mathrm{\Psi }}}_{2\left[\kappa \right(t\left)\right]}+{\widehat{\mathrm{\Psi }}}_{3\left[\kappa \right(t\left)\right]}+{\widehat{\mathrm{\Psi }}}_4+{\widehat{\mathrm{\Psi }}}_5,\hfill \\ \hfill {\widehat{\mathrm{\Phi }}}_{\left[\kappa \right(t\left)\right]}& =\mathtt{Sym}\left\{\widehat{\mathrm{\Pi }}\left((\kappa \left(t\right)-{\kappa }_L)[{\widehat{\epsilon }}_{11},{\widehat{\epsilon }}_0]+({\kappa }_U-\kappa \left(t\right))[{\widehat{\epsilon }}_0,{\widehat{\epsilon }}_{12}]-[{\widehat{\epsilon }}_9,{\widehat{\epsilon }}_{10}]\right)\right\},\hfill \\ \hfill \widehat{\mathrm{\Gamma }}& =A{\widehat{\epsilon }}_1^T+A_d{\widehat{\epsilon }}_3^T-I_n{\widehat{\epsilon }}_5^T.\hfill \end{array}$$

Corollary 1. 

For given scalars ${\kappa }_L,{\kappa }_U,$ and ${\kappa }_D$ satisfying $0\le {\kappa }_L\le {\kappa }_U$ and $\dot{\kappa }\left(t\right)\le {\kappa }_D$, system (1) is asymptotically stable if there exist matrices $\widehat{R}\in {\mathbb{S}}_{+}^{5n},{\widehat{G}}_i\in {\mathbb{S}}_{+}^{4n},{\widehat{G}}_3\in {\mathbb{S}}_{+}^{3n},{\widehat{Q}}_i,\widehat{W}\in {\mathbb{S}}_{+}^n(i=1,2),F_2\in {\mathbb{R}}^{2n\times 2n}$ and $\widehat{\mathrm{\Pi }}\in {\mathbb{R}}^{2n\times 12n}$ satisfying the following LMIs:

$$\begin{array}{c}\hfill {\widehat{\mathrm{\Gamma }}}_{\perp }^T({\widehat{\mathrm{\Psi }}}_{\left[{\kappa }_L\right]}+{\widehat{\mathrm{\Phi }}}_{\left[{\kappa }_L\right]}){\widehat{\mathrm{\Gamma }}}_{\perp }<0,\end{array}$$

(26)

$$\begin{array}{c}\hfill {\widehat{\mathrm{\Gamma }}}_{\perp }^T({\widehat{\mathrm{\Psi }}}_{\left[{\kappa }_U\right]}+{\widehat{\mathrm{\Phi }}}_{\left[{\kappa }_U\right]}){\widehat{\mathrm{\Gamma }}}_{\perp }<0,\end{array}$$

(27)

$$\begin{array}{c}\hfill {\widehat{\mathrm{\Omega }}}_3>0.\end{array}$$

(28)

Proof of Corollary 1.

Consider the LKF candidate given by

$$\begin{array}{c}\hfill \widehat{V}\left(t\right)=\sum _{i=1}^5{\widehat{V}}_i,\end{array}$$

(29)

where

$$\begin{array}{ccc}\hfill {\widehat{V}}_1\left(t\right)& =& {\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-{\kappa }_U)\\ {\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)\end{array}\right]}^T\widehat{R}\left(\odot \right),\hfill \\ \hfill {\widehat{V}}_2\left(t\right)& =& {\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\dot{x}\left(u\right)du\\ {\int }_{t-{\kappa }_L}^s\dot{x}\left(u\right)du\end{array}\right]}^T{\widehat{G}}_1\left(\odot \right)ds+{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\dot{x}\left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\dot{x}\left(u\right)du\end{array}\right]}^T{\widehat{G}}_2\left(\odot \right)ds,\hfill \\ \hfill {\widehat{V}}_3\left(t\right)& =& {\int }_{t-\kappa \left(t\right)}^{t-{\kappa }_L}{\left[\begin{array}{c}x\left(s\right)\\ {\int }_s^{t-{\kappa }_L}\dot{x}\left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\dot{x}\left(u\right)du\end{array}\right]}^T{\widehat{G}}_3\left(\odot \right)ds,\hfill \\ \hfill {\widehat{V}}_4\left(t\right)& =& {\kappa }_L{\int }_{t-{\kappa }_L}^t{\int }_s^t{\dot{x}}^T\left(u\right){\widehat{Q}}_1\left(\odot \right)duds+{\kappa }_S{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\int }_s^{t-{\kappa }_L}{\dot{x}}^T\left(u\right){\widehat{Q}}_2\left(\odot \right)duds,\hfill \\ \hfill {\widehat{V}}_5\left(t\right)& =& {\kappa }_U{\int }_{t-{\kappa }_U}^t{\dot{x}}^T\left(s\right)\widehat{W}\dot{x}\left(s\right)ds-{\left({\int }_{t-{\kappa }_U}^t\dot{x}\left(s\right)ds\right)}^T\widehat{W}\left(\odot \right)\hfill \\ & & -3{\left({\int }_{t-{\kappa }_U}^t\dot{x}\left(s\right)ds-{\displaystyle \frac{2}{{\kappa }_U}}{\int }_{t-{\kappa }_U}^t{\int }_s^t\dot{x}\left(u\right)duds\right)}^T\widehat{W}\left(\odot \right).\hfill \end{array}$$

LKF (29) has some augmented components removed from (7), and the method used can be seen in the proof of Theorem 1. Thus, it is omitted.  □

In the above results, LKFs are typically expected to be symmetric. However, the LKF in Theorem 2 is asymmetric. Then, the following theorem is introduced as the result with the asymmetric functionals. The augmented vector of Theorem 2 is presented as follows:

$$\begin{array}{c}\hfill \xi \left(t\right)=\left\{\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-{\kappa }_U)\end{array}\right],\left[\begin{array}{c}{\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)\end{array}\right],\left[\begin{array}{c}{\phi }_{20}(x\left(u\right),{\kappa }_L,0)\\ {\phi }_{20}(x\left(u\right),{\kappa }_U,{\kappa }_L)\end{array}\right]\right\}\end{array}$$

And the block entry matrices ${ϵ}_i={[0_{n·(i-1)n},I_n,0_{n·(7-i)n}]}^T\in {\mathbb{R}}^{7n\times n}(i=1,2,\cdots ,7)$ are utilized. Also, the following notations are defined:

$$\begin{array}{cc}\hfill {\check{G}}_i& =\left[\begin{array}{ccc}{\check{G}}_{i,11}& {\check{G}}_{i,12}& {\check{G}}_{i,13}\\ {\check{G}}_{i,21}& {\check{G}}_{i,22}& {\check{G}}_{i,23}\end{array}\right],{\check{G}}_{augi}=\left[\begin{array}{ccc}{\check{G}}_{i,11}& {\check{G}}_{i,12}/2& ({\check{G}}_{i,13}+{\check{G}}_{i,21}^T)/2\\ \ast & Q_i& {\check{G}}_{i,22}^T/2\\ \ast & \ast & {\check{G}}_{i,23}\end{array}\right],(i=1,2),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathrm{\Xi }}_1& =[{ϵ}_1,{ϵ}_2,{ϵ}_3,{ϵ}_4,{ϵ}_6,{\kappa }_L{ϵ}_4-{ϵ}_6,{ϵ}_5,{ϵ}_7,{\kappa }_S{ϵ}_5-{ϵ}_7]\check{R}\hfill \\ \hfill & \times {[{ϵ}_1,{ϵ}_2,{ϵ}_3,{ϵ}_4,{ϵ}_6,{\kappa }_L{ϵ}_4-{ϵ}_6,{ϵ}_5,{ϵ}_7,{\kappa }_S{ϵ}_5-{ϵ}_7]}^T,\hfill \\ \hfill {\mathrm{\Xi }}_2& ={\displaystyle \frac{1}{{\kappa }_L}}[{ϵ}_1-{ϵ}_2,{ϵ}_4,{\kappa }_L{ϵ}_1-{ϵ}_4,{ϵ}_6,{ϵ}_4-{\kappa }_L{ϵ}_2,{\kappa }_L{ϵ}_4-{ϵ}_6]{\check{G}}_{aug1}\hfill \\ \hfill & \times {[{ϵ}_1-{ϵ}_2,{ϵ}_4,{\kappa }_L{ϵ}_1-{ϵ}_4,{ϵ}_6,{ϵ}_4-{\kappa }_L{ϵ}_2,{\kappa }_L{ϵ}_4-{ϵ}_6]}^T\hfill \\ \hfill & +{\displaystyle \frac{1}{{\kappa }_S}}[{ϵ}_2-{ϵ}_3,{ϵ}_5,{\kappa }_S{ϵ}_2-{ϵ}_5,{ϵ}_7,{ϵ}_5-{\kappa }_S{ϵ}_3,{\kappa }_S{ϵ}_5-{ϵ}_7]{\check{G}}_{aug2}\hfill \\ \hfill & \times {[{ϵ}_2-{ϵ}_3,{ϵ}_5,{\kappa }_S{ϵ}_2-{ϵ}_5,{ϵ}_7,{ϵ}_5-{\kappa }_S{ϵ}_3,{\kappa }_S{ϵ}_5-{ϵ}_7]}^T,\hfill \\ \hfill {\check{\mathrm{\Psi }}}_{1\left[{\kappa }_t\right]}& =\mathtt{Sym}\left\{{\mathrm{\Pi }}_{1,1\left[\kappa \right(t\left)\right]}\check{R}{\mathrm{\Pi }}_{1,2}^T\right\},\hfill \\ \hfill {\check{\mathrm{\Psi }}}_{2\left[\kappa \right(t\left)\right]}& ={\displaystyle \frac{1}{2}}\mathtt{Sym}\left\{[{\epsilon }_5,{\epsilon }_1,{\epsilon }_1-{\epsilon }_2,{\epsilon }_8]{\check{G}}_1{\mathrm{\Pi }}_{2,1}^T-[{\epsilon }_6,{\epsilon }_2,{\epsilon }_0,{\epsilon }_0]{\check{G}}_1{\mathrm{\Pi }}_{2,2}^T,\right.\hfill \\ \hfill & +[{\epsilon }_6,{\epsilon }_2,{\epsilon }_2-{\epsilon }_4,{\epsilon }_9+{\epsilon }_{10}]{\check{G}}_2{\mathrm{\Pi }}_{2,3}^T-[{\epsilon }_7,{\epsilon }_4,{\epsilon }_0,{\epsilon }_0]{\check{G}}_2{\mathrm{\Pi }}_{2,4}^T,\hfill \\ \hfill & +[{\epsilon }_0,{\epsilon }_0,-{\epsilon }_6,-{\epsilon }_2]{\check{G}}_1{\mathrm{\Pi }}_{2,5}^T+[{\epsilon }_1-{\epsilon }_2,{\epsilon }_8,{\epsilon }_8-{\kappa }_L{\epsilon }_2,{\kappa }_L({\epsilon }_8-{\epsilon }_{11})]{\check{G}}_1{\mathrm{\Pi }}_{2,6}^T,\hfill \\ \hfill & +[{\epsilon }_0,{\epsilon }_0,-{\epsilon }_7,-{\epsilon }_4]{\check{G}}_2{\mathrm{\Pi }}_{2,7\left[\kappa \right(t\left)\right]}^T\hfill \\ \hfill & +\left.\left[{\epsilon }_2-{\epsilon }_4,{\epsilon }_9+{\epsilon }_{10},{\epsilon }_9+{\epsilon }_{10}-{\kappa }_S{\epsilon }_4,{\kappa }_S{\epsilon }_{10}+(\kappa \left(t\right)-{\kappa }_L){\epsilon }_9-{\epsilon }_{16}-{\epsilon }_{17}\right]{\check{G}}_2{\mathrm{\Pi }}_{2,8}^T\right\},\hfill \\ \hfill {\check{\mathrm{\Psi }}}_{\left[\kappa \right(t\left)\right]}& ={\check{\mathrm{\Psi }}}_{1\left[\kappa \right(t\left)\right]}+{\check{\mathrm{\Psi }}}_{2\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_{3\left[\kappa \right(t\left)\right]}+{\mathrm{\Psi }}_4+{\mathrm{\Psi }}_5.\hfill \end{array}$$

Theorem 2. 

For given scalars ${\kappa }_L,{\kappa }_U,$ and ${\kappa }_D$ satisfying $0\le {\kappa }_L\le {\kappa }_U$ and $\dot{\kappa }\left(t\right)\le {\kappa }_D$, system (1) is asymptotically stable if there exist matrices $\check{R}\in {\mathbb{S}}^{9n},{\check{G}}_i\in {\mathbb{R}}^{4n\times 6n}$ with ${\check{G}}_{i,11}={\check{G}}_{i,11}^T$ and ${\check{G}}_{i,23}={\check{G}}_{i,23}^T$, $G_3\in {\mathbb{S}}_{+}^{3n},Q_i\in {\mathbb{S}}_{+}^{2n},S_i,W\in {\mathbb{S}}^n(i=1,2),F_1\in {\mathbb{R}}^{4n\times 4n}$ and $\mathrm{\Pi }\in {\mathbb{R}}^{4n\times 17n}$ satisfying the following LMIs:

$$\begin{array}{ccc}\hfill {\check{G}}_{aug1}& >& 0,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\check{G}}_{aug2}& >& 0,\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill {\mathrm{\Xi }}_1+{\mathrm{\Xi }}_2& >& 0,\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{\perp }^T({\check{\mathrm{\Psi }}}_{\left[{\kappa }_L\right]}+{\mathrm{\Phi }}_{\left[{\kappa }_L\right]}){\mathrm{\Gamma }}_{\perp }& <& 0,\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{\perp }^T({\check{\mathrm{\Psi }}}_{\left[{\kappa }_U\right]}+{\mathrm{\Phi }}_{\left[{\kappa }_U\right]}){\mathrm{\Gamma }}_{\perp }& <& 0,\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\mathrm{\Omega }}_3& >& 0.\hfill \end{array}$$

(35)

Proof of Theorem 2.

Consider the LKF candidate given by

$$\begin{array}{c}\hfill V\left(t\right)={\check{V}}_1+{\check{V}}_2+\sum _{i=3}^5{V}_i,\end{array}$$

(36)

where

$$\begin{array}{ccc}\hfill {\check{V}}_1\left(t\right)& =& {\left[\begin{array}{c}x\left(t\right)\\ x(t-{\kappa }_L)\\ x(t-{\kappa }_U)\\ {\phi }_{10}(x\left(s\right),{\kappa }_L,0)\\ {\phi }_{20}(x\left(u\right),{\kappa }_L,0)\\ {\int }_{t-{\kappa }_L}^t{\int }_{t-{\kappa }_L}^{s}x\left(u\right)duds\\ {\phi }_{10}(x\left(s\right),{\kappa }_U,{\kappa }_L)\\ {\phi }_{20}(x\left(u\right),{\kappa }_U,{\kappa }_L)\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\int }_{t-{\kappa }_U}^{s}x\left(u\right)duds\end{array}\right]}^T\check{R}\left(\odot \right)\hfill \\ & =& {\xi }^T\left(t\right){\mathrm{\Xi }}_1\xi \left(t\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\check{V}}_2\left(t\right)& =& {\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_{t-{\kappa }_L}^s\psi \left(u\right)du\end{array}\right]}^T{G}_1\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\psi \left(u\right)du\\ {\int }_{t-{\kappa }_L}^s\psi \left(u\right)du\end{array}\right]ds\hfill \\ & & +{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_{t-{\kappa }_U}^s\psi \left(u\right)du\end{array}\right]}^T{G}_2\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\psi \left(u\right)du\end{array}\right]ds.\hfill \end{array}$$

Since the sum of LKFs must be positive in an asymmetric LKF method, it must be guaranteed that ${\check{V}}_1+{\check{V}}_2+V_4$ is positive if $G_3$ of $V_3$ and W of $V_5$ are positive.

By using Lemma 1 (N = 0), $V_4$ can be bounded as

$$\begin{array}{ccc}\hfill V_4& \ge & {\int }_{t-{\kappa }_L}^t{\left({\int }_s^t\psi \left(u\right)du\right)}^T{Q}_1(\odot )ds+{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left({\int }_s^{t-{\kappa }_L}\psi \left(u\right)du\right)}^T{Q}_2(\odot )ds.\hfill \end{array}$$

(37)

By adding the lower bound of $V_4$ to $V_2$, the following can be obtained.

$$\begin{array}{ccc}\hfill {\check{V}}_2+V_4& \ge & {\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\psi \left(u\right)du\\ {\int }_{t-{\kappa }_L}^s\psi \left(u\right)du\end{array}\right]}^T{\check{G}}_{aug1}(\odot )ds\hfill \\ & & +{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\psi \left(u\right)du\end{array}\right]}^T{\check{G}}_{aug2}(\odot )ds.\hfill \end{array}$$

(38)

Then, the lower bound of (38) can be bounded as follows by using Lemma 1 (N = 0), since ${\check{G}}_{aug1}$, ${\check{G}}_{aug2}>0$:

$$\begin{array}{ccc}\hfill {\check{V}}_2+V_4& \ge & {\displaystyle \frac{1}{{\kappa }_L}}{\left({\int }_{t-{\kappa }_L}^t\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\psi \left(u\right)du\\ {\int }_{t-{\kappa }_L}^s\psi \left(u\right)du\end{array}\right]ds\right)}^T{\check{G}}_{aug1}(\odot )\hfill \\ & & +{\displaystyle \frac{1}{{\kappa }_S}}{\left({\int }_{t-{\kappa }_U}^{t-{\kappa }_L}\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(u\right)du\\ {\int }_{t-{\kappa }_U}^s\psi \left(u\right)du\end{array}\right]ds\right)}^T{\check{G}}_{aug2}(\odot )\hfill \\ & =& {\xi }^T\left(t\right){\mathrm{\Xi }}_2\xi \left(t\right).\hfill \end{array}$$

(39)

As a result, it is proven that ${\check{V}}_1+{\check{V}}_2+V_4$ is positive and (32) is obtained.

$$\begin{array}{c}\hfill {\check{V}}_1+{\check{V}}_2+V_4\ge {\xi }^T\left(t\right)\left({\mathrm{\Xi }}_1+{\mathrm{\Xi }}_2\right)\xi \left(t\right)>0.\end{array}$$

(40)

The time derivative of $V_2$ is induced as follows:

$$\begin{array}{cc}\hfill {\dot{\check{V}}}_2& ={\left[\begin{array}{c}\psi \left(t\right)\\ {\int }_{t-{\kappa }_L}^t\psi \left(s\right)ds\end{array}\right]}^T{G}_1\left[\begin{array}{c}\psi \left(t\right)\\ 0_{2n·1}\\ {\int }_{t-{\kappa }_L}^t\psi \left(s\right)ds\end{array}\right]-{\left[\begin{array}{c}\psi \left(t-{\kappa }_L\right)\\ 0_{2n·1}\end{array}\right]}^T{G}_1\left[\begin{array}{c}\psi \left(t-{\kappa }_L\right)\\ {\int }_{t-{\kappa }_L}^t\psi \left(s\right)ds\\ 0_{2n·1}\end{array}\right]\hfill \\ \hfill & +{\left[\begin{array}{c}\psi \left(t-{\kappa }_L\right)\\ 0_{2n·1}\end{array}\right]}^T{G}_2\left[\begin{array}{c}\psi \left(t-{\kappa }_L\right)\\ {\int }_{t-{\kappa }_L}^t\psi \left(s\right)ds\\ 0_{2n·1}\end{array}\right]-{\left[\begin{array}{c}\psi \left(t-{\kappa }_U\right)\\ 0_{2n·1}\end{array}\right]}^T{G}_2\left[\begin{array}{c}\psi \left(t-{\kappa }_U\right)\\ {\int }_{t-{\kappa }_U}^{t-{\kappa }_L}\psi \left(s\right)ds\\ 0_{2n·1}\end{array}\right]\hfill \\ \hfill & +{\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}{0}_{2n·1}\\ -\psi (t-{\kappa }_L)\end{array}\right]}^T{G}_1\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^t\psi \left(s\right)ds\\ {\int }_{t-{\kappa }_L}^s\psi \left(s\right)ds\end{array}\right]ds\hfill \\ \hfill & +{\int }_{t-{\kappa }_L}^t{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_{t-{\kappa }_L}^s\psi \left(u\right)du\end{array}\right]}^T{G}_1\left[\begin{array}{c}{0}_{2n·1}\\ \psi \left(t\right)\\ -\psi \left(t-{\kappa }_L\right)\end{array}\right]ds\hfill \\ \hfill & +{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}{0}_{2n·1}\\ -\psi (t-{\kappa }_U)\end{array}\right]}^T{G}_2\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_s^{t-{\kappa }_L}\psi \left(s\right)ds\\ {\int }_{t-{\kappa }_U}^s\psi \left(s\right)ds\end{array}\right]ds\hfill \\ \hfill & +{\int }_{t-{\kappa }_U}^{t-{\kappa }_L}{\left[\begin{array}{c}\psi \left(s\right)\\ {\int }_{t-{\kappa }_U}^s\psi \left(s\right)ds\end{array}\right]}^T{G}_2\left[\begin{array}{c}{0}_{2n·1}\\ \psi \left(t-{\kappa }_L\right)\\ -\psi \left(t-{\kappa }_U\right)\end{array}\right]ds\hfill \\ \hfill & ={\zeta }^T\left(t\right){\check{\mathrm{\Psi }}}_{2\left[\kappa \right(t\left)\right]}\zeta \left(t\right).\hfill \end{array}$$

(41)

Since the subsequent process is similar to Theorem 1, the proof of Theorem 2 is complete.  □

Remark 2. 

Asymmetric LKFs are proposed in [36], and asymmetric LKFs are also used in Theorems 2, but in [36], it is applied to part ${\int }_s^{t}x\left(u\right)du$, whereas in Theorem 2, it is applied to part ${\int }_s^t\psi \left(u\right)du$ because there is $V_4\left(t\right)$ to $\psi \left(u\right)$. In Section 4, Theorem 2 can provide larger delay bounds than [3,14,38] by comparing maximum delay bounds. Furthermore, Theorem 2 shows slightly larger delay bounds than Theorem 1 in Example 2, while the number of decision variables in Theorem 2 is used $20n^2+2n$ less than that of Theorem 1.

Remark 3. 

If the information of the time derivative is unavailable (${\kappa }_D$ is unknown), one can set $G_3=0$ or ${\widehat{G}}_3$ in Theorems 1 and 2 and Corollary 1 to obtain a delay-dependent stability criterion.

4. Examples

In this section, the effectiveness and superiority of the proposed stability criteria are demonstrated through four examples.

Example 1. 

Consider system (1) based on [3,14,38]:

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}-2& 0\\ 0& -0.9\end{array}\right],A_d=\left[\begin{array}{cc}-1& 0\\ -1& -1\end{array}\right].\end{array}$$

(42)

Table 1. Maximum delay bound ${\kappa }_U$ for various ${\kappa }_L$s with ${\kappa }_D=0.1$ (Example 1).

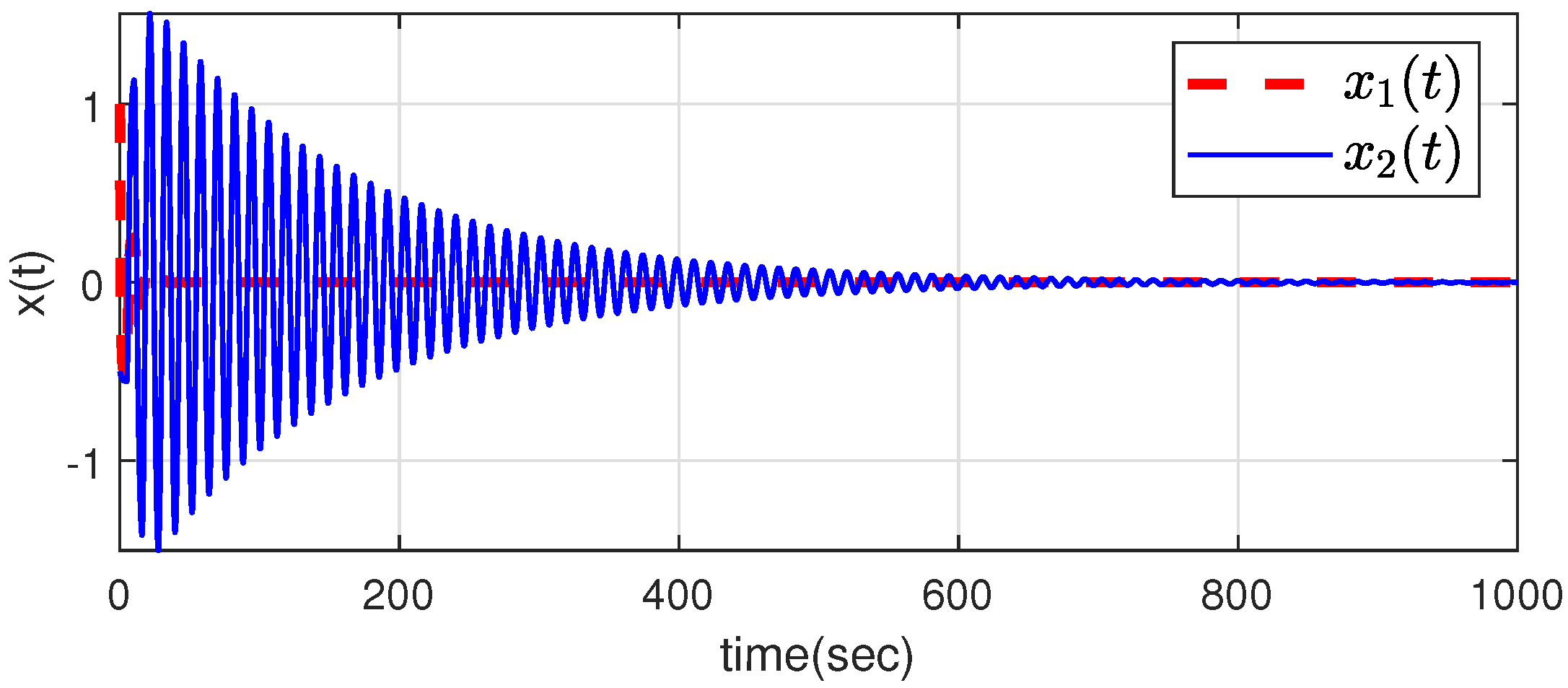
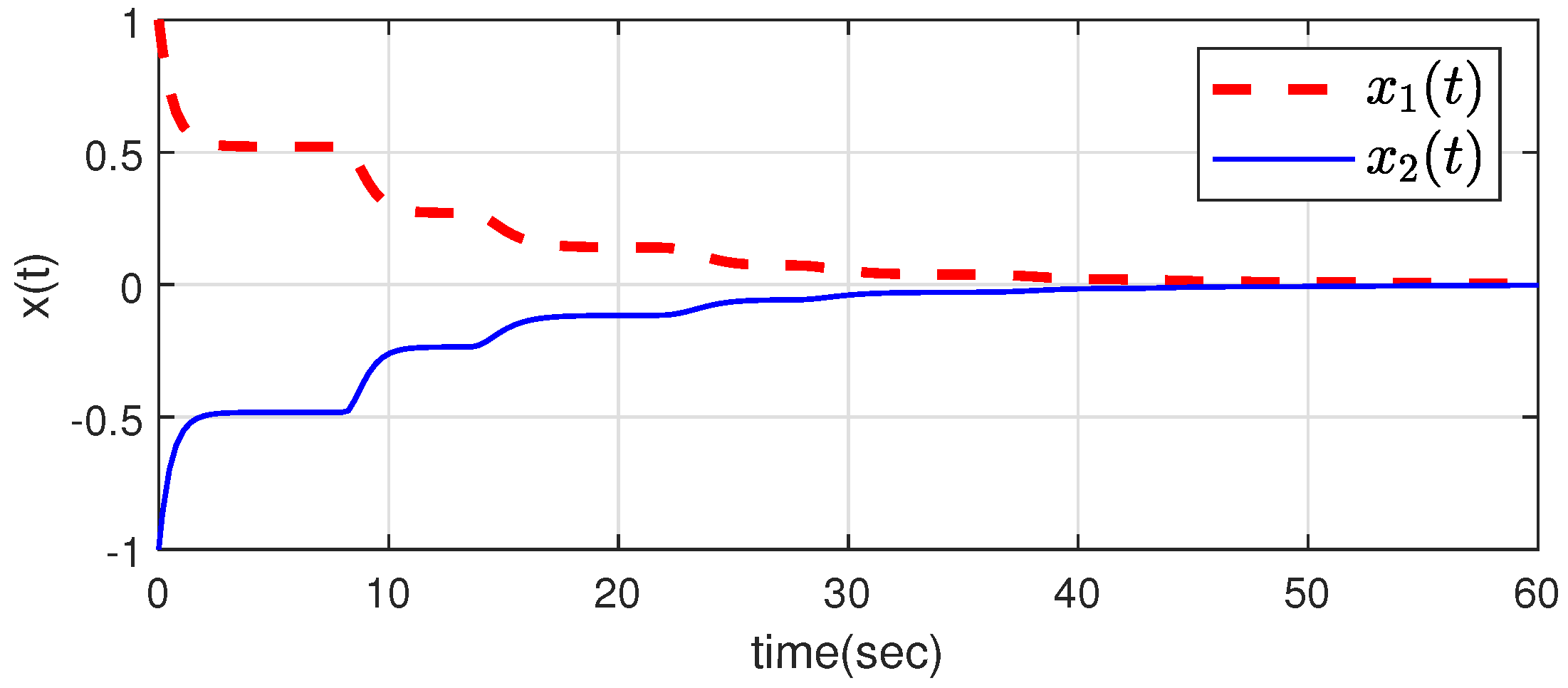
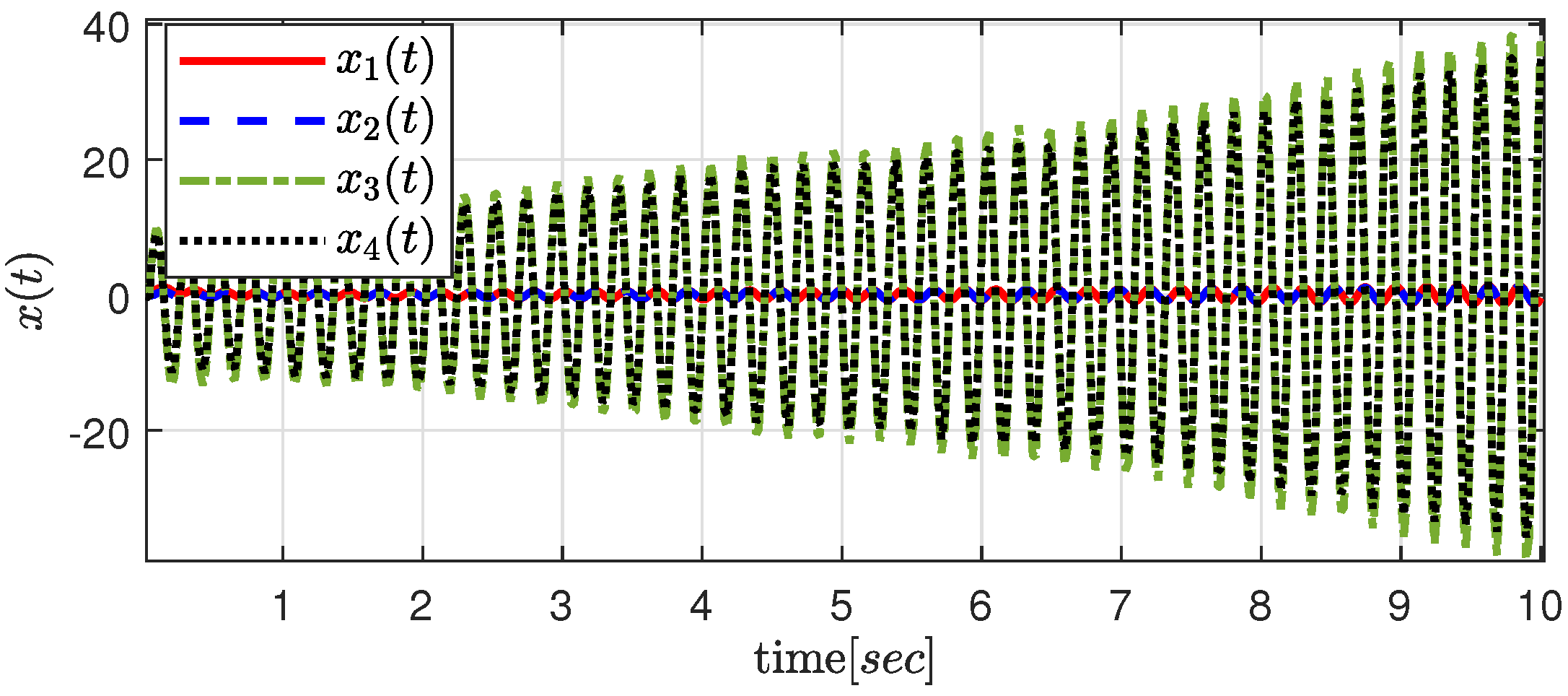
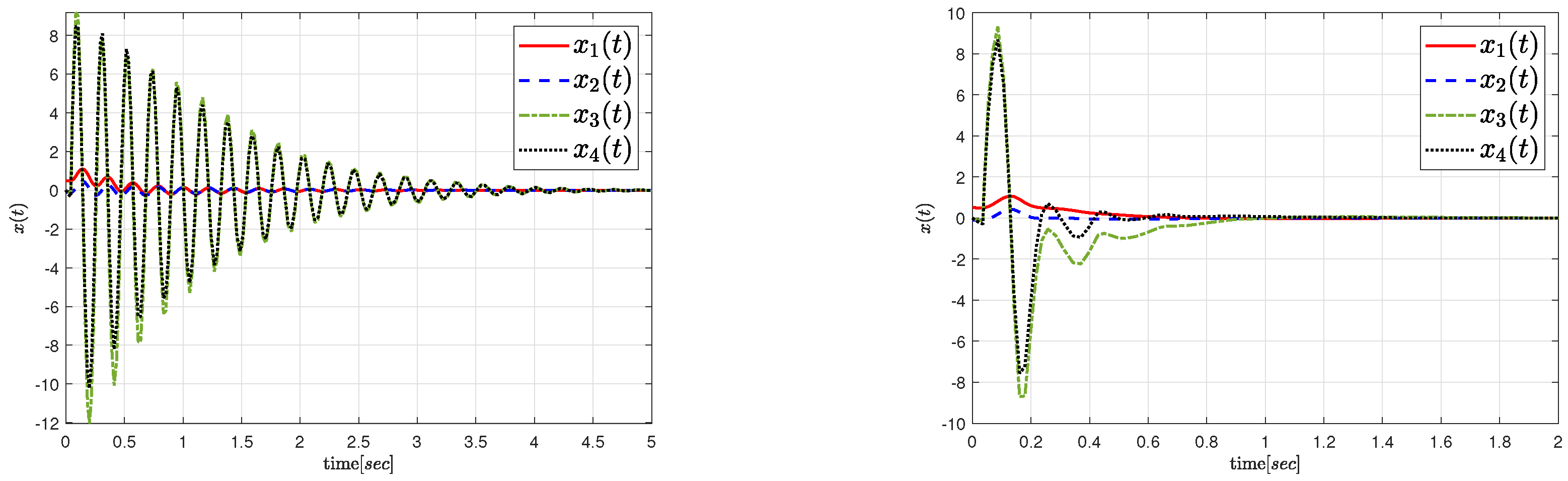
${\mathit{\kappa }}_{\mathit{L}}$	1	2	3	4	5
[14]	4.1935	4.4932	4.3979	4.1978	5.0275
[38]	4.4045	4.5729	4.5406	4.2367	5.0440
[3]	4.7561	4.7746	4.7931	4.7567	5.1372
Corollary 1	4.7577	4.7715	4.7634	4.7273	5.1373
Theorem 1	4.7952	4.8132	4.8110	4.7850	5.1511
Theorem 2	4.7951	4.8132	4.8109	4.7849	5.1500

and

Table 2. Maximum delay bound ${\kappa }_U$ for various ${\kappa }_L$s with ${\kappa }_D=0.5$ (Example 1).

${\mathit{\kappa }}_{\mathit{L}}$	1	2	3	4	5
[14]	2.3058	2.5663	3.3408	4.1690	5.0275
[38]	2.3513	2.6987	3.4186	4.2097	5.0440
[3]	2.4904	2.7994	3.4977	4.2939	5.1372
Corollary 1	2.4752	2.8111	3.4997	4.2946	5.1373
Theorem 1	2.5739	2.9247	3.5561	4.3134	5.1412
Theorem 2	2.5739	2.9247	3.5593	4.3133	5.1406

list the maximum delay bounds for various ${\kappa }_L$s as determined by Theorems 1 and 2 and Corollary 1, as well as those of [3,14,38], when ${\kappa }_D$ is 0.1 and 0.5, respectively. It is listed in Table 1 that Theorems 1 and 2 provide larger delay bounds than those of [3,14,38]. Additionally, Theorem 1 yields slightly larger delay bounds compared to Corollary 1. Table 2 also shows the superiority of Theorems 1 and 2 when ${\kappa }_D=0.5$. As a result, it can be confirmed that improved results can be obtained from the suggested Theorems 1 and 2. Figure 1 shows that the state responses of system (1) converge to zero as time goes to infinity.

Example 2. 

Consider the water pollution control problem based on [39]; the dynamical behavior is as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dz\left(t\right)}{dt}}& =-h_{1}z\left(t\right)+{\displaystyle \frac{Q_{E}m+Qz(t-\kappa )-(Q+Q_E)z\left(t\right)}{v}},\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\displaystyle \frac{dq\left(t\right)}{dt}}& =-h_{3}z\left(t\right)+h_2(q^s-q\left(t\right))+{\displaystyle \frac{Qq(t-\kappa )-(Q+Q_E)q\left(t\right)}{v}},\hfill \end{array}$$

(44)

where $z\left(t\right)$ and $q\left(t\right)$ denote states, which represent the concentrations of biochemical oxygen demand (BOD) and dissolved oxygen (DO) in the reach at time t, respectively. The definitions of parameters in (43) and (44) are shown in [39]. In the absence of disturbances and uncertainties, (43) and (44) can be described as the system (1), and the matrices of the system are as follows:

$$\begin{array}{cc}\hfill \overline{A}& =\left[\begin{array}{cc}-1.32& 0\\ -0.32& -1.2\end{array}\right],A_d=\left[\begin{array}{cc}0.9& 0\\ 0& 0.9\end{array}\right],\hfill \\ \hfill B& =\left[\begin{array}{cc}0.1& 0\\ 0& 1\end{array}\right],K=\left[\begin{array}{cc}-5& -1\\ 0.01& -1\end{array}\right],\hfill \\ \hfill A& =\overline{A}+BK.\hfill \end{array}$$

(45)

Table 3. Maximum delay bound ${\kappa }_U$ for various ${\kappa }_L$s with ${\kappa }_D=0.9$ (Example 2).

${\mathit{\kappa }}_{\mathit{L}}$	1	2	3	4	5
[3]	5.1893	6.0899	7.0461	8.0461	9.0461
Corollary 1	3.8906	4.8426	5.8413	6.8413	7.8413
Theorem 1	5.4731	6.2440	7.1456	8.0755	9.0564
Theorem 2	5.6896	6.3537	7.1932	8.0908	9.0578

lists the maximum delay bounds for various ${\kappa }_L$s at ${\kappa }_D=0.9$, comparing the results of Theorems 1 and 2, Corollary 1, and [3]. And it can also be shown that Theorem 2 provides larger delay bounds than Theorem 1.

Table 4. Number of decision variables.

Method	NoDVs
[14]	$18n^2+8n$
[38]	$22.5n^2+9.5n$
[3]	$137.5n^2+9.5n$
Corollary 1	$62.5n^2+9.5n$
Theorem 1	$178.5n^2+16.5n$
Theorem 2	$158.5n^2+14.5n$

also shows the effectiveness and superiority of Theorem 2 because the number of decision variables(NoDVs) used is smaller than that of Theorem 1. Finally, it can be seen that the state responses of system (1) in Figure 2 converge to zero.

Remark 4. 

By Example 1, Theorems 1 and 2 show the effectiveness of the proposed criteria compared with [3,14,38] based on maximum delay bound. By Example 2, the asymmetric LKFs method of Theorem 2 can provide larger delay bounds than Theorem 1 and reduce decision variables in some specific systems. This supports the fact that the considered LKFs in Theorem 2 are effective in enhancing the feasible region compared to Theorem 1.

Example 3. 

Consider the inverted pendulum problem based on [40]:

$$\begin{array}{cc}\hfill A& =\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 80.3& -45.8& -0.93\\ 0& 122.0& -44.1& -1.40\end{array}\right],\hfill \\ \hfill A_d& =\left[\begin{array}{c}0\\ 0\\ 83.4\\ 80.3\end{array}\right]\left[\begin{array}{cccc}5.26& -28.16& 2.76& -3.22\end{array}\right].\hfill \end{array}$$

(46)

In

Table 5. Maximum delay bound ${\kappa }_U$ for various ${\kappa }_L$s and ${\kappa }_D$s (Example 3).

Method	${\mathit{\kappa }}_{\mathit{D}}$	${\mathit{\kappa }}_{\mathit{L}}$ = 0.01	${\mathit{\kappa }}_{\mathit{L}}$ = 0.02	${\mathit{\kappa }}_{\mathit{L}}$ = 0.03	${\mathit{\kappa }}_{\mathit{L}}$ = 0.04
[3]	0.1	0.0422	0.0422	0.0422	0.0424
Theorem 1		0.0423	0.0423	0.0422	0.0425
Theorem 2		0.0423	0.0423	0.0423	0.0425
[3]	0.3	0.0411	0.0413	0.0415	0.0424
Theorem 1		0.0413	0.0414	0.0416	0.0424
Theorem 2		0.0413	0.0415	0.0416	0.0424

, the maximum delay bounds for various ${\kappa }_L$s and ${\kappa }_D$s are shown using Theorems 1 and 2, and these are compared with [3]. To confirm the effectiveness of the proposed results, Figure 3 and Figure 4 show the system’s state trajectories for $\kappa \left(t\right)=0.0445$, $\kappa \left(t\right)=0.0425$, and $\kappa \left(t\right)=0.011sin\left(25t\right)+0.03$ with the initial condition $x\left(0\right)={[0.5,-0.1,0,0]}^T$. Figure 3 shows that the system is unstable when $\kappa \left(t\right)=0.0445$. In contrast, Figure 4 demonstrate that the system is asymptotically stable within the maximum delay bound obtained using Theorems 1 and 2.

Example 4. 

Consider system (1) based on [41,42,43,44]:

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}0& 1\\ -10& -1\end{array}\right],A_d=\left[\begin{array}{cc}0& 0.1\\ 0.1& 0.2\end{array}\right].\end{array}$$

(47)

Table 6. Maximum delay bound ${\kappa }_U$ for various ${\kappa }_L$s with unknown ${\kappa }_D$s (Example 4).

${\mathit{\kappa }}_{\mathit{L}}$	0.3	0.7	1	2
[41]	2.76	3.15	3.41	4.04
[42]	3.13	3.48	3.53	4.16
[43]	3.91	4.02	4.25	5.20
[44]	3.81	4.19	4.53	5.08
Corollary 1	2.0110	2.4176	2.6270	3.5926
Theorem 1	12.5461	12.9353	13.2362	14.2291
Theorem 2	12.5419	12.9321	13.2313	14.2383

lists the maximum delay bounds for various ${\kappa }_L$s, as determined by Theorems 1 and 2 and Corollary 1 as well as those of [41,42,43,44] when ${\kappa }_D$ is unknown. It is listed in Table 6 that Theorems 1 and 2 provide larger delay bounds than those of [41,42,43,44]. To confirm the effectiveness of the proposed results, Figure 5 shows the system’s state trajectories for $\kappa \left(t\right)=6.119sin\left(10t\right)+8.119$ with the initial condition $x\left(0\right)={[1,-1]}^T$. Figure 5 shows that the state responses of the system (1) converge to zero as time goes to infinity.

5. Conclusions

The stability problem of linear systems with interval time-varying delays is studied in this paper. The compositions of the LKFs are considered to improve the feasible region of stability criteria for linear systems through this work. In Theorem 1, the asymptotic stability criteria of the systems are derived by constructing the augmented LKFs. Then, simplified LKFs in Corollary 1 are proposed to show the effectiveness of Theorem 1. In Theorem 2, asymmetric LKFs are presented to reduce the conservatism and the number of decision variables. Four numerical examples are given to show the effectiveness and superiority of the proposed criteria. Based on this research, the method can be applied to T-S fuzzy systems or neural network systems with interval time-varying delays.