A New Generalization of the Uniform Distribution: Properties and Applications to Lifetime Data
Abstract
:1. Introduction
- We present an approach in which we incorporate a parameter k associated with the power of the X values of the continuous random variable in the Probability Density Function. This allows us to generalize two new distributions.
- The new GPUD distribution is presented as an alternative to the Continuous Uniform Distribution for modeling data with a uniform trend.
- We present the new generalized MOE-PU distribution as an alternative for reliability analysis applications that can describe non-monotonic behaviors, such as those shown by the bathtub curve.
- The MOE-PU distribution is significantly flexible and competitive with other distributions existing in the literature that can model bathtub curve behaviors.
- We establish an attractive distribution (MOE-PU) so that engineers in the reliability area can carry out different analyses or studies, considering the benefits that modeling provides from an actuarial perspective.
2. A New Family of the Uniform Distribution Function
2.1. Reliability Measures of GPUD
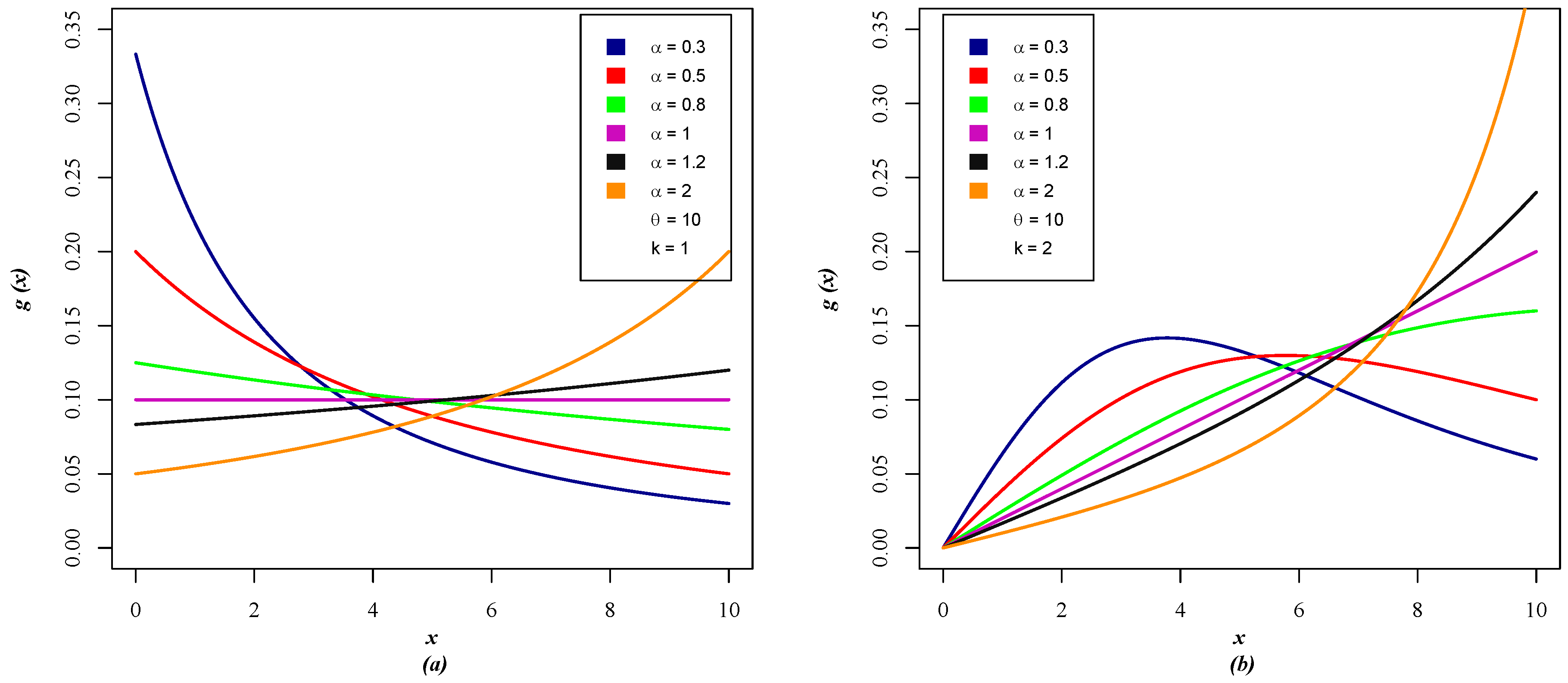
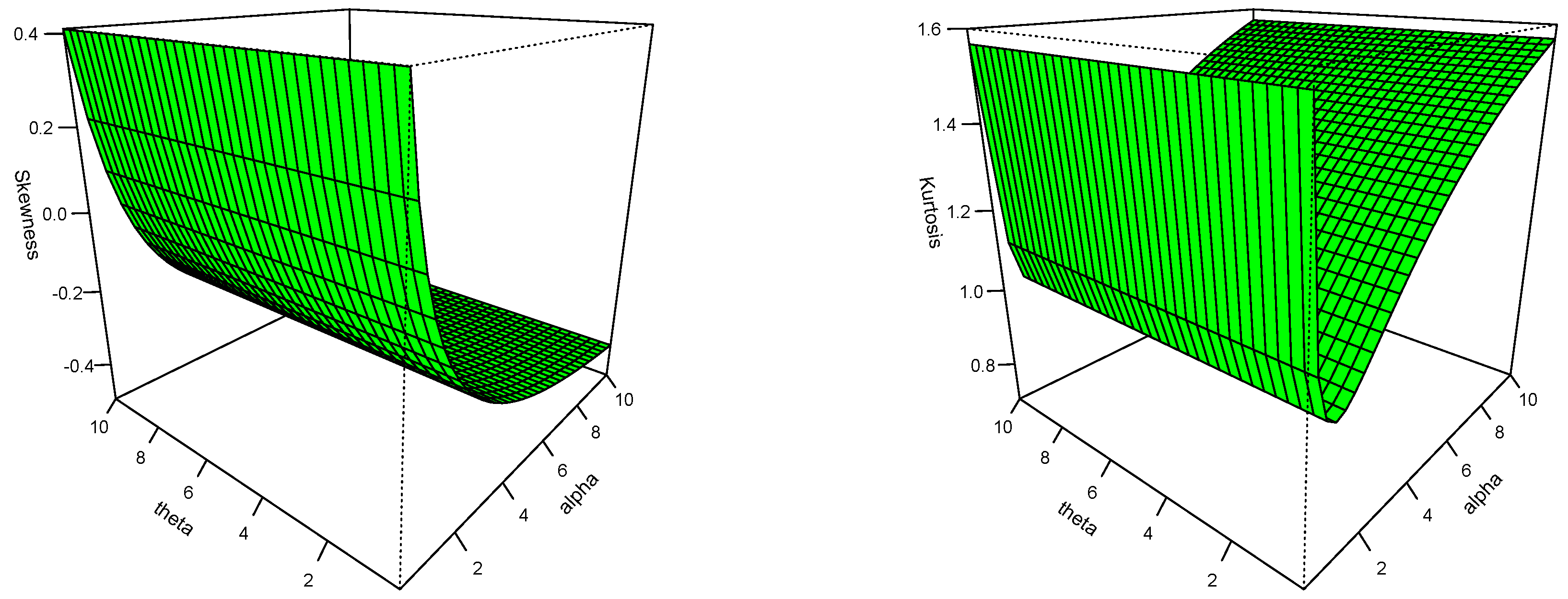
2.2. General Properties of GPUD
2.2.1. Moments
2.2.2. Quantile Function and Random Number Generation
3. Generalization of the Distribution of Jose and Krishna Using the GPUD Approach
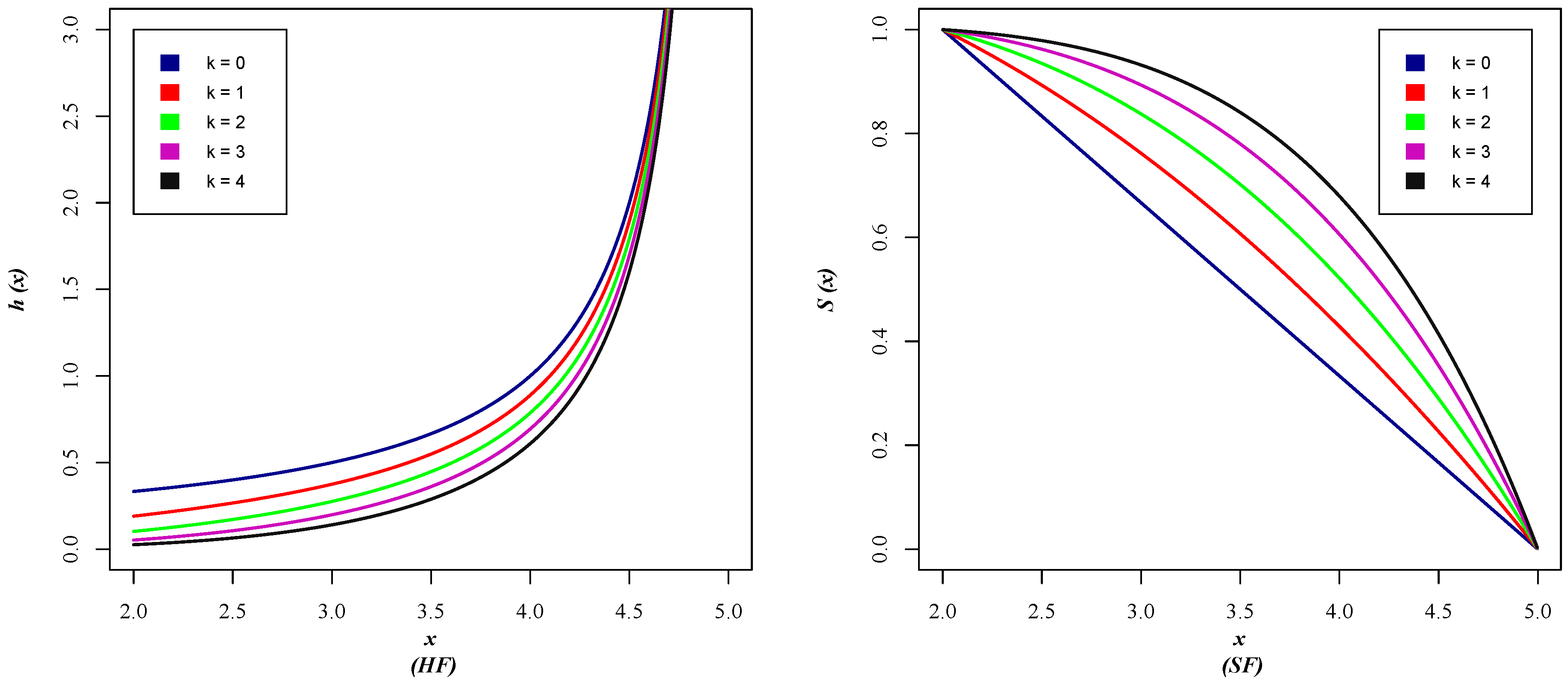
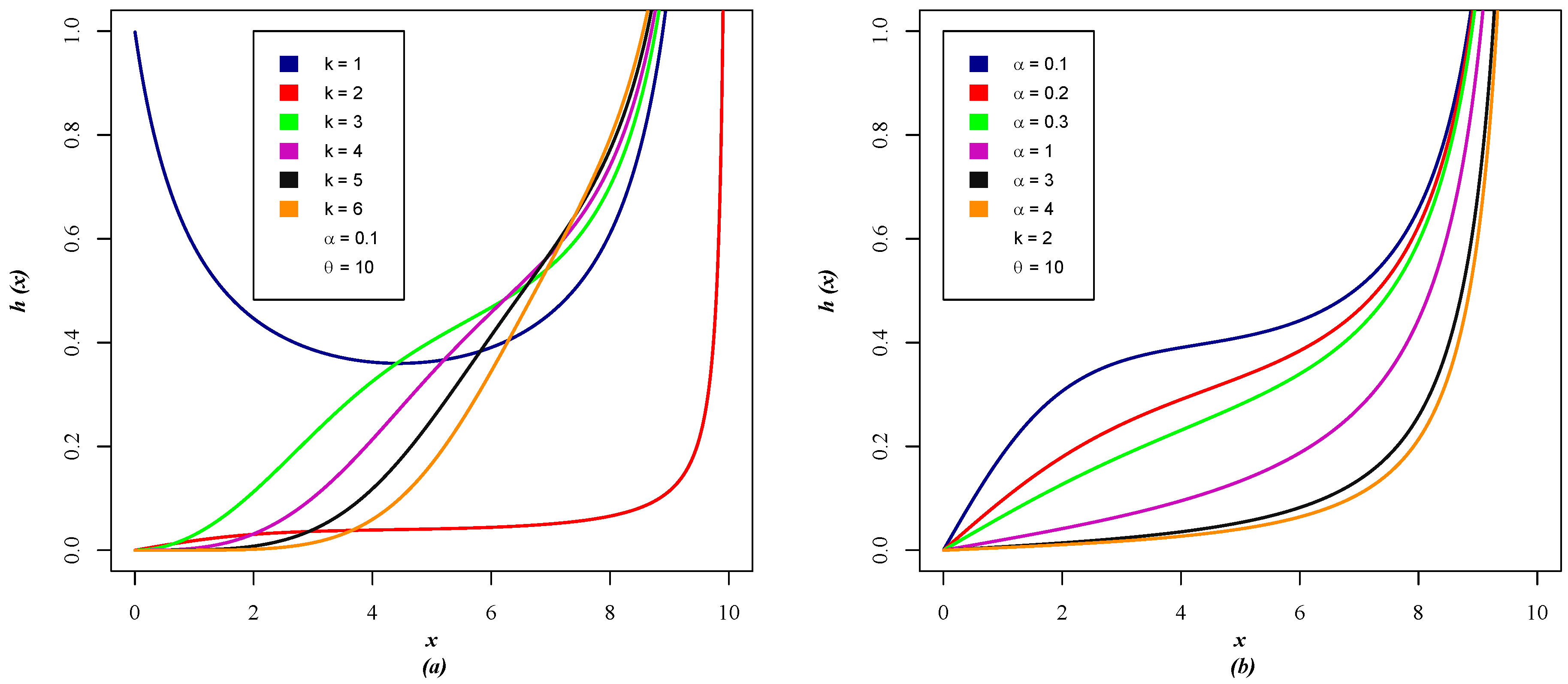
3.1. Survival Function and Hazard Function of the MOE-PU
3.2. Quantile Function of the MOE-PU
3.3. Maximum Likelihood Estimators of the MOE-PU
4. MOE-PU Monte Carlo Simulation Study
- Step 1
- First, the values of the parameters , , and k are defined for each simulation. The sample size , and 200 is also defined, as well as the number of simulations ;
- Step 2
- Generate a random sample q following the uniform distribution of size , and 200, respectively;
- Step 3
- Generate a random sample following the MOE-PU distribution from Equation (25) for , and 200, respectively;
- Step 4
- Each random sample from Step 3 is simulated N times, and the estimate of the parameters , , and k, as well as the values of the AVE, MSE, MREs, and Bias, are calculated;
- Step 5
- Step 6
| n | Parameter | AVE | MSE | MREs | Bias |
|---|---|---|---|---|---|
| 50 | 0.0092 | 5.068 × 10−6 | 0.1961 | 0.0017 | |
| 9.9883 | 3.842 × 10−8 | 1.169 × 10−6 | 1.169 × 10−6 | ||
| k | 1.9937 | 9.715 × 10−6 | 8.065 × 10−5 | 0.0001 | |
| 100 | 0.0091 | 2.623 × 10−6 | 0.1403 | 0.0012 | |
| 10.010 | 8.049 × 10−8 | 1.622 × 10−6 | 1.622 × 10−6 | ||
| k | 2.0004 | 3.614 × 10−6 | 6.689 × 10−5 | 0.0001 | |
| 150 | 0.0091 | 1.843 × 10−6 | 0.1150 | 0.0010 | |
| 10.006 | 2.128 × 10−9 | 5.215 × 10−7 | 5.215 × 10−7 | ||
| k | 2.0002 | 1.843 × 10−7 | 2.703 × 10−5 | 5.406 × 10−5 | |
| 200 | 0.0091 | 1.447 × 10−6 | 0.1025 | 0.0009 | |
| 10.002 | 1.125 × 10−7 | 4.168 × 10−7 | 4.168 × 10−6 | ||
| k | 2.0003 | 4.165 × 10−7 | 2.408 × 10−5 | 4.807 × 10−5 |
| n | Parameter | AVE | MSE | MREs | Bias |
|---|---|---|---|---|---|
| 50 | 0.0077 | 1.825 × 10−5 | 0.9597 | 0.0038 | |
| 5.8000 | 0.0399 | 0.0333 | 0.1999 | ||
| k | 2.7000 | 0.0899 | 0.0999 | 0.2999 | |
| 100 | 0.0053 | 2.801 × 10−6 | 0.3530 | 0.0014 | |
| 5.8000 | 0.0399 | 0.0333 | 0.1999 | ||
| k | 2.9000 | 0.0099 | 0.0333 | 0.0999 | |
| 150 | 0.0054 | 2.605 × 10−6 | 0.3596 | 0.0014 | |
| 5.8000 | 0.0399 | 0.0333 | 0.1999 | ||
| k | 2.9000 | 0.0099 | 0.0333 | 0.0999 | |
| 200 | 0.0041 | 2.150 × 10−7 | 0.0892 | 0.0003 | |
| 5.9999 | 1.634 × 10−8 | 1.313 × 10−6 | 7.878 × 10−6 | ||
| k | 2.9999 | 3.041 × 10−7 | 1.043 × 10−5 | 3.131 × 10−5 |
| n | Parameter | AVE | MSE | MREs | Bias |
|---|---|---|---|---|---|
| 50 | 3.3775 | 0.0191 | 0.0351 | 0.1229 | |
| 56.963 | 0.9445 | 0.0172 | 0.9686 | ||
| k | 0.9510 | 0.0351 | 0.1491 | 0.1491 | |
| 100 | 3.4142 | 0.0111 | 0.0245 | 0.0858 | |
| 56.941 | 0.9008 | 0.0168 | 0.9435 | ||
| k | 0.9207 | 0.0218 | 0.1217 | 0.1217 | |
| 150 | 3.4404 | 0.0063 | 0.0170 | 0.0598 | |
| 56.924 | 0.8730 | 0.0165 | 0.9279 | ||
| k | 0.9081 | 0.0187 | 0.1154 | 0.1154 | |
| 200 | 3.5152 | 0.0014 | 0.0066 | 0.0233 | |
| 56.002 | 0.0044 | 0.0003 | 0.0207 | ||
| k | 1.0025 | 0.0099 | 0.0784 | 0.0784 |
| n | Parameter | AVE | MSE | MREs | Bias |
|---|---|---|---|---|---|
| 50 | 0.1254 | 0.0018 | 0.3180 | 0.0318 | |
| 24.001 | 0.9977 | 0.0399 | 0.9987 | ||
| k | 3.9958 | 0.0029 | 0.0015 | 0.0061 | |
| 100 | 0.1119 | 0.0005 | 0.1845 | 0.0184 | |
| 24.499 | 0.2500 | 0.0200 | 0.5001 | ||
| k | 3.9983 | 0.0009 | 0.0006 | 0.0027 | |
| 150 | 0.1043 | 0.0002 | 0.1197 | 0.1197 | |
| 24.799 | 0.0400 | 0.0080 | 0.2000 | ||
| k | 3.9995 | 1.739 × 10−6 | 0.0002 | 0.0009 | |
| 200 | 0.1009 | 0.0001 | 0.0999 | 0.0099 | |
| 25.000 | 1.053 × 10−6 | 9.522 × 10−6 | 0.0002 | ||
| k | 3.9997 | 0.0001 | 0.0002 | 0.0011 |
5. Application to Real Data
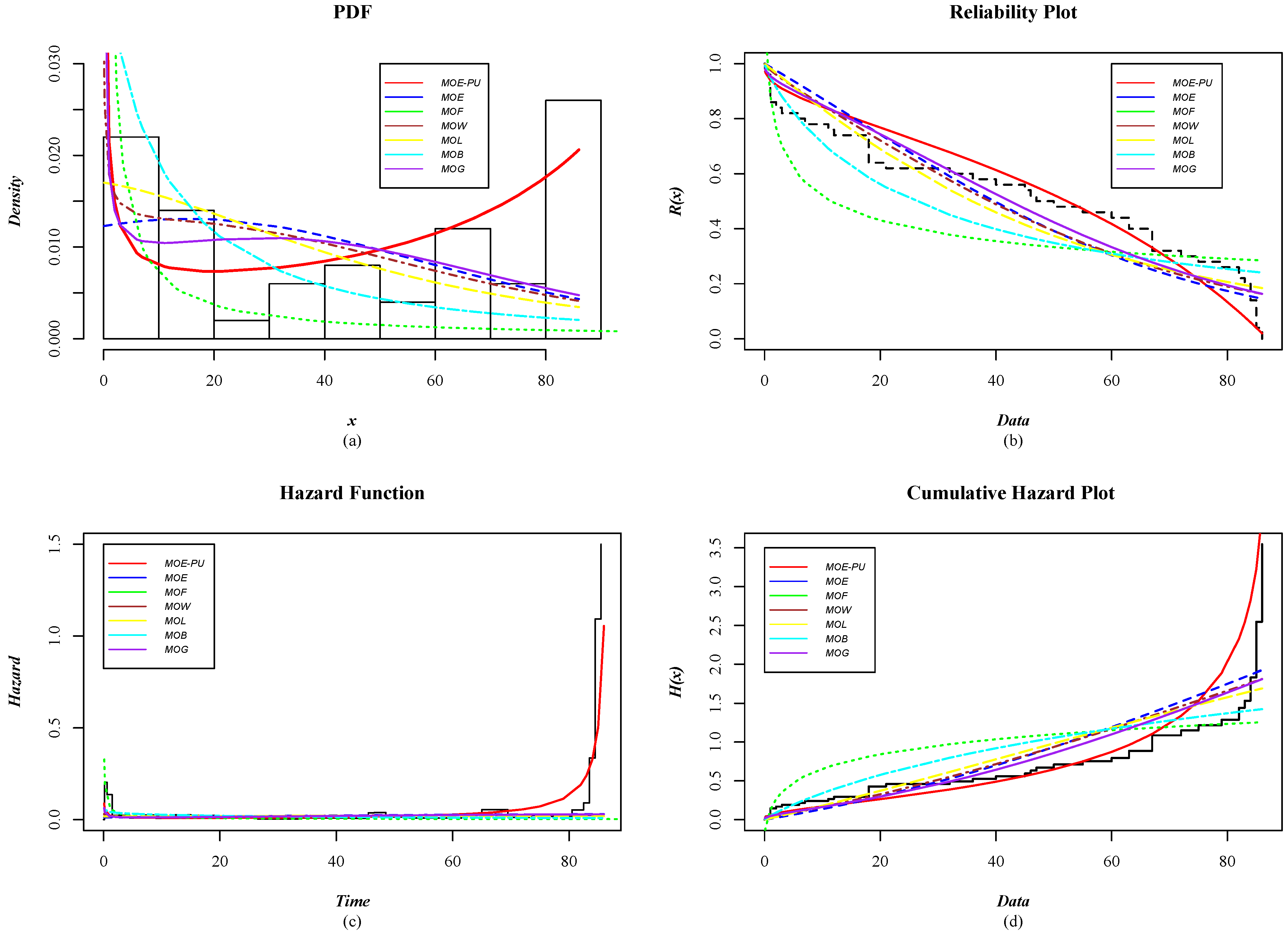
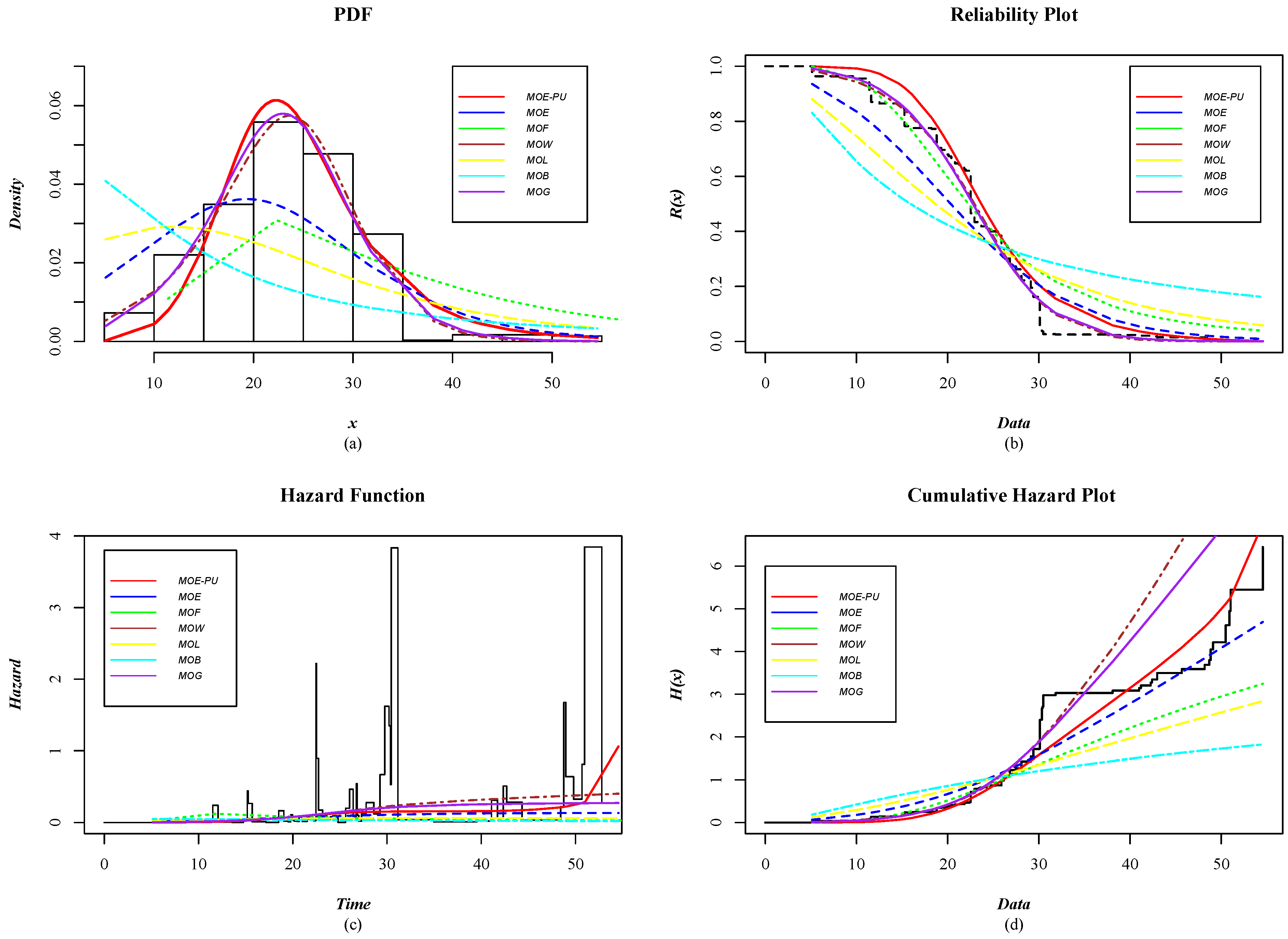
- The distributions considered were developed from the approach of Marshall and Olkin [19], as follows: Marshall–Olkin Exponential (MOE); Marshall–Olkin–Frechet (MOF); Marshall–Olkin–Weibull (MOW); Marshall–Olkin–Lomax (MOL); Marshall–Olkin–Burr XII (MOB); and Marshall–Olkin–Gamma (MOG). For more details of the distributions mentioned above, see Nadarajah and Rocha [22]. Table 7 shows the density functions of the models used to analyze and compare the performance of the MOE-PU distribution against those models.
- To estimate the parameters of the distributions used in the comparative analysis, the open-source software “R” (version R-4.4.1) was used with the MaxLik library (version 1.5-2.1). It is worth mentioning that “R” is one of the environments most used by the scientific community for statistical analysis. The code used in R to estimate the parameters of the MOE-PU distribution is attached in Appendix A.
- In the three study cases, uncensored data were considered; all the information (all measurements) of the study variable was known.
5.1. Case Study 1: Reliability Analysis for Fatigue Times for 6061-T6 Aluminum Coupons
5.2. Case Study 2: Reliability Analysis for Bladder Cancer Data
5.3. Case Study 3: Reliability Analysis for Failure-Time Data
5.4. Case Study 4: Reliability Analysis for Productivity Performance in a Textile Industry
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| library(maxLik) x<- (place the data set, that is, the failure times) n<- length(x) loglik <- function(param) { alpha <- param[1] theta <- param[2] k <- param[3] ll <- (assign Equation (30)) return(ll) } loglikGrad<- function(param) { alpha <- param[1] theta <- param[2] k <- param[3] loglikGradValues<- numeric(3) loglikGradValues[1] <- (assign Equation (31)) loglikGradValues[2] <- (assign Equation (32)) loglikGradValues[3] <- (assign Equation (33)) return(loglikGradValues) } loglikHess<- function(param) { alpha <- param[1] theta <- param[2] k <- param[3] loglikHessValues <- matrix(0, nrow=3, ncol=3) loglikHessValues[1,1]<- (assign Equation (34)) loglikHessValues[1,2]<- (assign Equation (37)) loglikHessValues[1,3]<- (assign Equation (38)) loglikHessValues[2,1]<- (assign Equation (37)) loglikHessValues[2,2]<- (assign Equation (35)) loglikHessValues[2,3]<- (assign Equation (39)) loglikHessValues[3,1]<- (assign Equation (38)) loglikHessValues[3,2]<- (assign Equation (39)) loglikHessValues[3,3]<- (assign Equation (36)) return(loglikHessValues) } est<- maxLik(loglik,loglikGrad,loglikHess,start=c(alpha=(assign an initial value), theta=(assign an initial value), k=(assign an initial value)), method=(select method), control=list(tol=-1,reltol=1e-12, gradtol=1e-12), iterlim=10000) summary(est) |
References
- Akarawak, E.E.; Adeyeye, S.J.; Khaleel, M.A.; Adedotun, A.F.; Ogunsanya, A.S.; Amalare, A.A. The inverted Gompertz-Fréchet distribution with applications. Sci. Afr. 2023, 21, e01769. [Google Scholar] [CrossRef]
- Rondero-Guerrero, C.; González-Hernández, I.; Soto-Campos, C. An extended approach for the generalized powered uniform distribution. Comput. Stat. 2022. [Google Scholar] [CrossRef]
- Maya, R.; Irshad, M.R.; Ahammed, M.; Chesneau, C. The Harris Extended Bilal Distribution with Applications in Hydrology and Quality Control. Appliedmath 2023, 3, 221–242. [Google Scholar] [CrossRef]
- González-Hernández, I.J.; Granillo-Macías, R.; Rondero-Guerrero, C.; Simón-Marmolejo, I. Marshall-Olkin distributions: A bibliometric study. Scientometrics 2021, 126, 9005–9029. [Google Scholar] [CrossRef]
- Méndez-González, L.C.; Rodríguez-Picón, L.A.; Borbón, M.I.R.; Sohn, H. The Chen–Perks Distribution: Properties and Reliability Applications. Mathematics 2023, 11, 3001. [Google Scholar] [CrossRef]
- Méndez-González, L.C.; Rodríguez-Picón, L.A.; Pérez-Olguin, I.J.C.; Garcia, V.; Quezada-Carreón, A.E. A reliability analysis for electronic devices under an extension of exponentiated perks distribution. Qual. Reliab. Eng. Int. 2023, 39, 776–795. [Google Scholar] [CrossRef]
- Sindhu, T.N.; Hussain, Z.; Shafiq, A. A new flexible extension to a lifetime distributions, properties, inference, and applications in engineering science. In Engineering Reliability and Risk Assessment; Garg, H., Ram, M., Eds.; Advances in Reliability Science; Elsevier: Amsterdam, The Netherlands, 2023; pp. 65–89. [Google Scholar]
- El-Bar, A.M.T.A.; do Carmo, S.; Lima, M. Exponentiated odd Lindley-X family with fitting to reliability and medical data sets. J. King Saud Univ.-Sci. 2023, 35, 102444. [Google Scholar] [CrossRef]
- Jha, M.K.; Dey, S.; Alotaibi, R.; Alomani, G.; Tripathi, Y.M. Multicomponent Stress-Strength Reliability estimation based on Unit Generalized Exponential Distribution. Ain Shams Eng. J. 2022, 13, 101627. [Google Scholar] [CrossRef]
- Alshanbari, H.M.; Gemeay, A.M.; El-Bagoury, A.A.A.H.; Khosa, S.K.; Hafez, E.; Muse, A.H. A novel extension of Fréchet distribution: Application on real data and simulation. Alex. Eng. J. 2022, 61, 7917–7938. [Google Scholar] [CrossRef]
- Sherwani, R.A.K.; Saima Ashraf, S.A.; Aslam, M. Marshall Olkin Exponentiated Dagum Distribution: Properties and Applications. J. Stat. Theory Appl. 2023, 22, 70–97. [Google Scholar] [CrossRef]
- Kilany, N.M.; El-Qareb, F.G. Modelling bivariate failure time data via bivariate extended Chen distribution. Stoch. Environ. Res. Risk Assess. 2023, 37, 3517–3525. [Google Scholar] [CrossRef]
- Nassar, M.; Kumar, D.; Dey, S.; Cordeiro, G.M.; Afify, A.Z. The Marshall–Olkin alpha power family of distributions with applications. J. Comput. Appl. Math. 2019, 351, 41–53. [Google Scholar] [CrossRef]
- Balogun, O.S.; Iqbal, M.Z.; Arshad, M.Z.; Afify, A.Z.; Oguntunde, P.E. A new generalization of Lehmann type-II distribution: Theory, simulation, and applications to survival and failure rate data. Sci. Afr. 2021, 12, e00790. [Google Scholar] [CrossRef]
- Sobhi, M.M.A. The extended Weibull distribution with its properties, estimation and modeling skewed data. J. King Saud Univ.-Sci. 2022, 34, 101801. [Google Scholar] [CrossRef]
- Moakofi, T.; Oluyede, B.; Chipepa, F. Type II exponentiated half-logistic Topp-Leone Marshall-Olkin-G family of distributions with applications. Heliyon 2021, 7, e08590. [Google Scholar] [CrossRef]
- Abbas, S.; Muhammad, M.; Muhammad, M.; Chesneau, C.; Chesneau, C.; Bouchane, M. A New Extension of the Kumaraswamy Generated Family of Distributions with Applications to Real Data. Computation 2023, 11, 26. [Google Scholar] [CrossRef]
- Jose, K.; Krishna, E. Marshall-Olkin Extended Uniform Distribution. Probstat Forum 2011, 4, 78–88. [Google Scholar]
- Marshall, A.W.; Olkin, I. A New Method for Adding a Parameter to a Family of Distributions with Application to the Exponential and Weibull Families. Biometrika 1997, 87, 641–652. [Google Scholar] [CrossRef]
- Rondero-Guerrero, C.; González-Hernández, I.; Soto-Campos, C. On a Generalized Uniform Distribution. Adv. Appl. Stat. 2020, 60, 93–103. [Google Scholar] [CrossRef]
- Jayakumar, K.; Sankaran, K.K. On a Generalisation of Uniform Distribution and its Properties. Statistica 2016, 76, 83–91. [Google Scholar]
- Nadarajah, S.; Rocha, R. Newdistns: An R package for new families of distributions. J. Stat. Softw. 2016, 69, 1–32. [Google Scholar] [CrossRef]
- Birnbaum, Z.; Saunders, S. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]
- Shakhatreh, M.K. A new three-parameter extension of the log-logistic distribution with applications to survival data. Commun. Stat.-Theory Methods 2018, 47, 5205–5226. [Google Scholar] [CrossRef]
- Aarset, M.V. How to Identify a Bathtub Hazard Rate. IEEE Trans. Reliab. 1987, 36, 106–108. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Productivity Prediction of Garment Employees; UCI Machine Learning Repository: Irvine, CA, USA, 2020. [Google Scholar] [CrossRef]
- Toomet, O.; Henningsen, A.; Graves, S.; Croissant, Y.; Hugh-Jones, D.; Scrucca, L. Maximum Likelihood Estimation and Related Tools, Version 1.5-2.1. 2024; pp. 1–57.



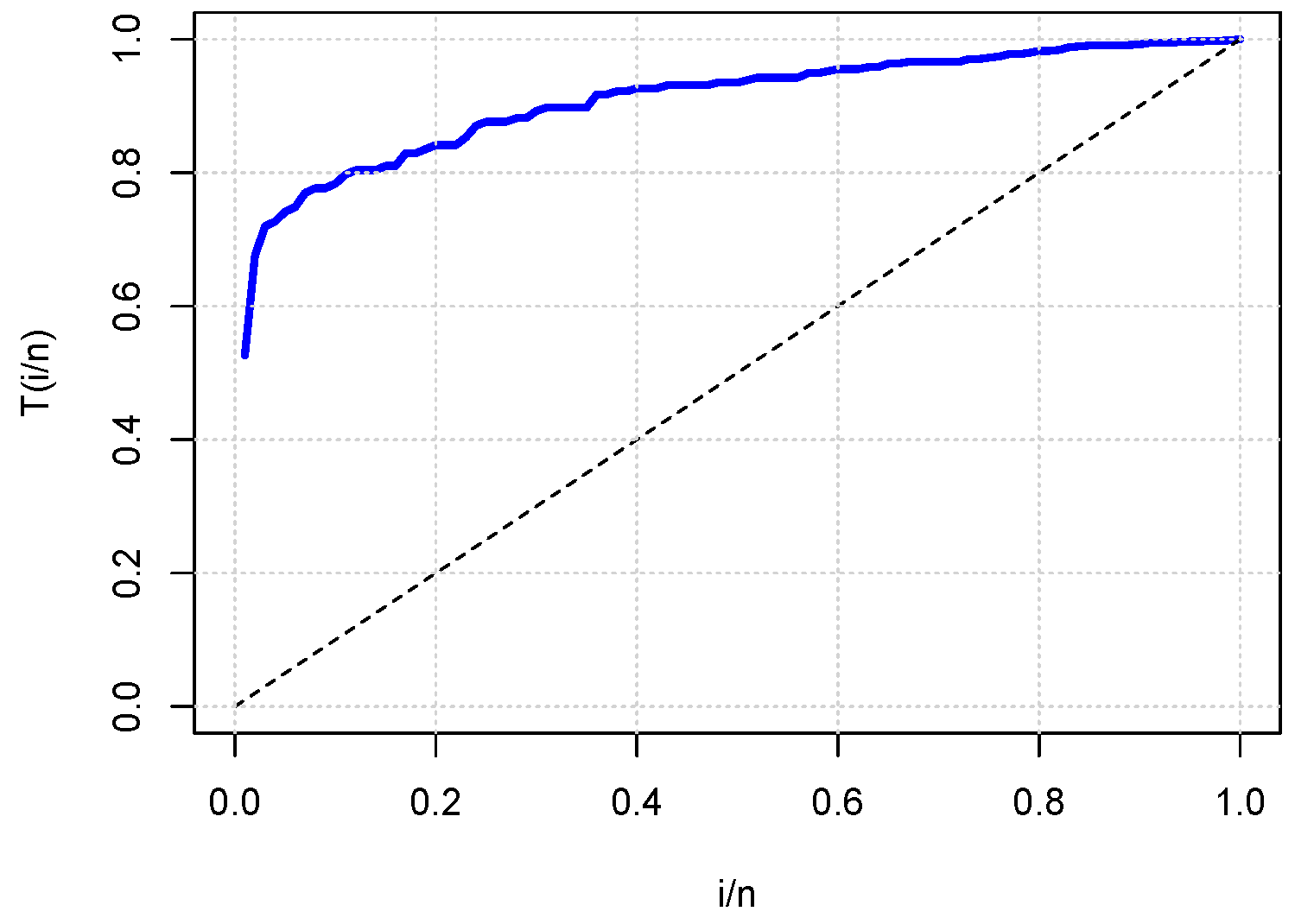



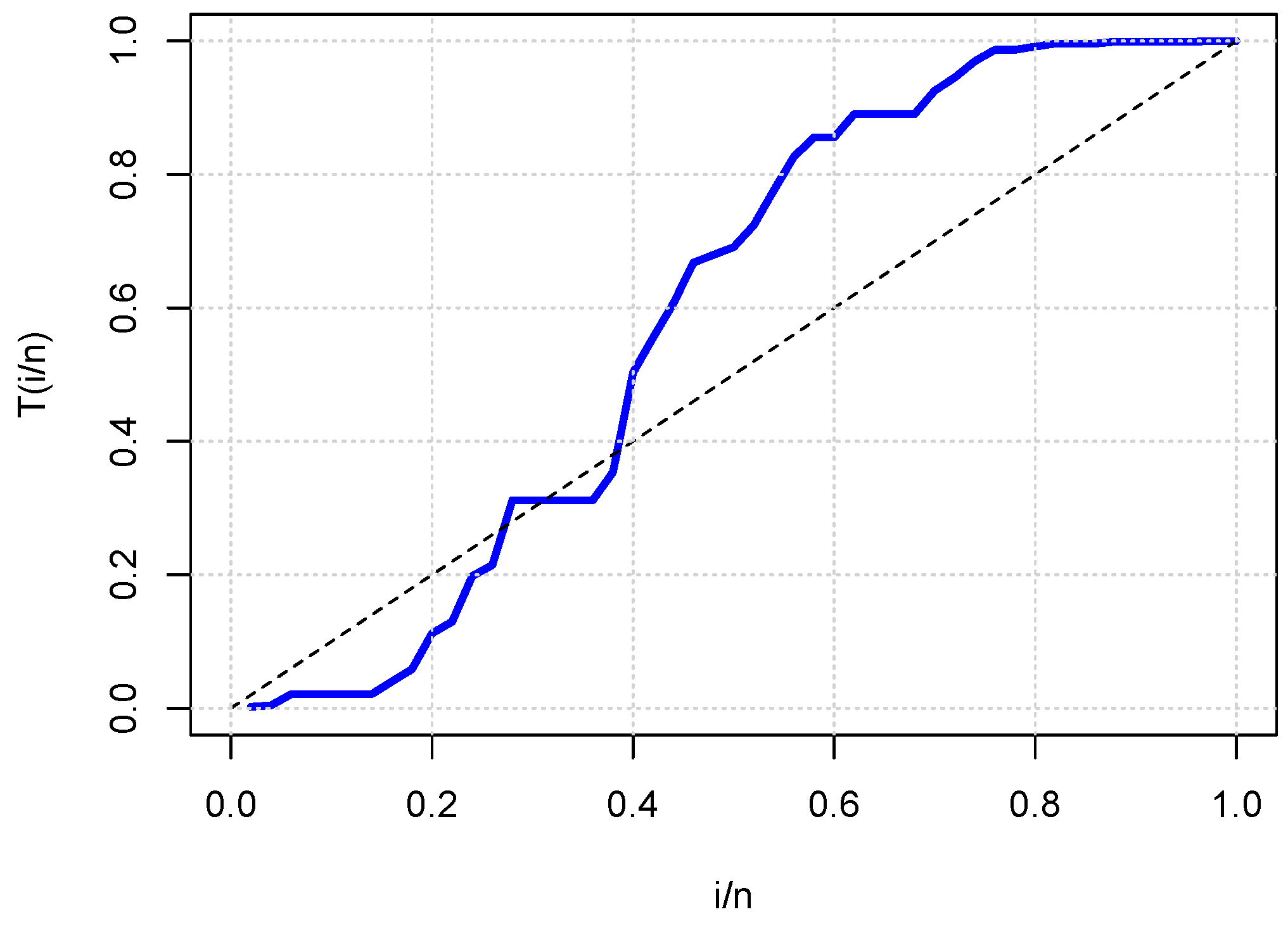
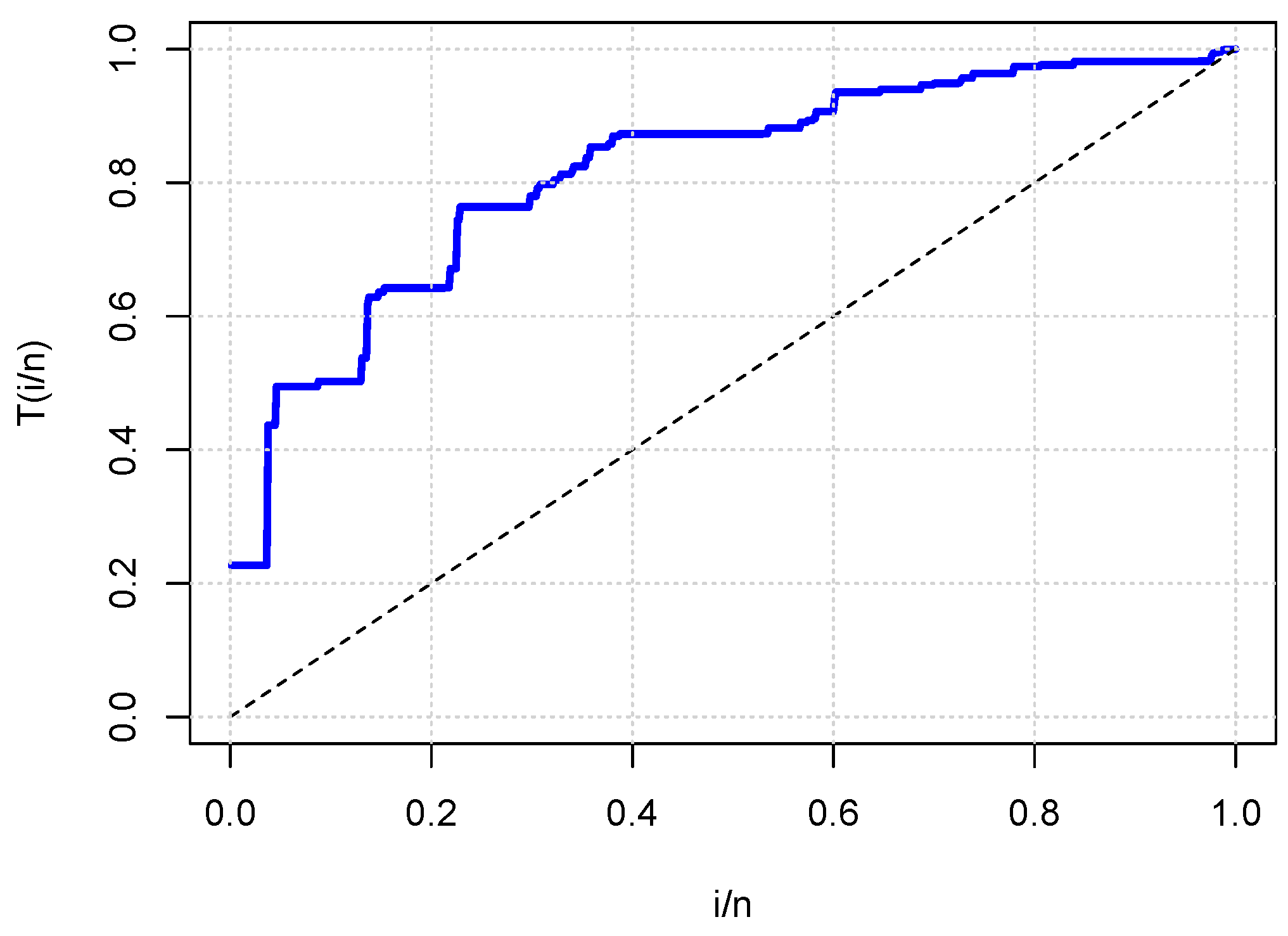
| 3.5 | 0.75 | 0 | −1.2 | |
| 3.71 | 0.70 | −0.29 | −1.05 | |
| 3.90 | 0.62 | −0.55 | −0.70 | |
| 4.06 | 0.52 | −0.79 | −0.21 | |
| 4.19 | 0.43 | −0.98 | 0.34 | |
| 4.29 | 0.35 | −1.14 | 0.92 |
| a | b | k | Median |
|---|---|---|---|
| 2 | 5 | 0 | 3.5 |
| 2 | 5 | 1 | 3.80 |
| 2 | 5 | 2 | 4.05 |
| 2 | 5 | 3 | 4.23 |
| 2 | 5 | 4 | 4.36 |
| 2 | 5 | 5 | 4.45 |
| Statistical Distribution | |
|---|---|
| MOE | |
| MOF | |
| MOW | |
| MOL | |
| MOB | |
| MOG |
| Lifetimes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 70 | 90 | 96 | 97 | 99 | 100 | 103 | 104 | 104 | 105 |
| 107 | 108 | 108 | 108 | 109 | 109 | 112 | 112 | 113 | 114 |
| 114 | 114 | 116 | 119 | 120 | 120 | 120 | 121 | 121 | 123 |
| 124 | 124 | 124 | 124 | 124 | 128 | 128 | 129 | 129 | 130 |
| 130 | 130 | 131 | 131 | 131 | 131 | 131 | 132 | 132 | 132 |
| 133 | 134 | 134 | 134 | 134 | 134 | 136 | 136 | 137 | 138 |
| 138 | 138 | 139 | 139 | 141 | 141 | 142 | 142 | 142 | 142 |
| 142 | 142 | 144 | 144 | 145 | 146 | 148 | 148 | 149 | 151 |
| 151 | 152 | 155 | 156 | 157 | 157 | 157 | 157 | 158 | 159 |
| 162 | 163 | 163 | 164 | 166 | 166 | 168 | 170 | 174 | 196 |
| Model | MLEs | logL | AIC | BIC | W* | A* | K-S | p-Value |
|---|---|---|---|---|---|---|---|---|
| MOE-PU | −446.21 | 898.42 | 906.23 | 0.0484 | 0.4135 | 0.0588 | 0.8788 | |
| MOE | −545.08 | 1094.16 | 1099.37 | 0.0513 | 0.3042 | 0.4439 | 7.77 × | |
| MOF | −459.81 | 925.62 | 933.44 | 0.1120 | 0.6530 | 0.1622 | 0.0103 | |
| MOW | −499.90 | 1005.81 | 1013.62 | 0.0449 | 0.2730 | 0.3623 | 7.88 × | |
| MOL | −582.36 | 1170.72 | 1178.53 | 0.0708 | 0.4107 | 0.4267 | 3.33 × | |
| MOB | −653.78 | 1313.57 | 1321.39 | 0.1017 | 0.5829 | 0.5264 | 0.02 × | |
| MOG | −457.11 | 920.22 | 928.04 | 0.0379 | 0.2552 | 0.1383 | 0.0435 | |
| Lifetimes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.08 | 0.20 | 0.40 | 0.50 | 0.51 | 0.81 | 0.90 | 1.05 | 1.19 | 1.26 |
| 1.35 | 1.40 | 1.46 | 1.76 | 2.02 | 2.02 | 2.07 | 2.09 | 2.23 | 2.26 |
| 2.46 | 2.54 | 2.62 | 2.64 | 2.69 | 2.69 | 2.75 | 2.83 | 2.87 | 3.02 |
| 3.25 | 3.31 | 3.36 | 3.36 | 3.48 | 3.52 | 3.57 | 3.64 | 3.70 | 3.82 |
| 3.88 | 4.18 | 4.23 | 4.26 | 4.33 | 4.34 | 4.40 | 4.50 | 4.51 | 4.87 |
| 4.98 | 5.06 | 5.09 | 5.17 | 5.32 | 5.32 | 5.34 | 5.41 | 5.41 | 5.49 |
| 5.62 | 5.71 | 5.85 | 6.25 | 6.54 | 6.76 | 6.93 | 6.94 | 6.97 | 7.09 |
| 7.26 | 7.28 | 7.32 | 7.39 | 7.59 | 7.62 | 7.63 | 7.66 | 7.87 | 7.93 |
| 8.26 | 8.37 | 8.53 | 8.65 | 8.66 | 9.02 | 9.22 | 9.47 | 9.74 | 10.06 |
| 10.34 | 10.66 | 10.75 | 11.25 | 11.64 | 11.79 | 11.98 | 12.02 | 12.03 | 12.07 |
| 12.63 | 13.11 | 13.29 | 13.80 | 14.24 | 14.76 | 14.77 | 14.83 | 15.96 | 16.62 |
| 17.12 | 17.14 | 17.36 | 18.10 | 19.13 | 20.28 | 21.73 | 22.69 | 23.63 | 25.74 |
| 25.82 | 26.31 | 32.15 | 34.26 | 36.66 | 43.01 | 46.12 | 79.05 | ||
| Model | MLEs | logL | AIC | BIC | W* | A* | K-S | p-Value |
|---|---|---|---|---|---|---|---|---|
| MOE-PU | −410.46 | 826.92 | 835.47 | 0.0310 | 0.2441 | 0.0451 | 0.9565 | |
| MOE | −414.32 | 832.65 | 838.36 | 0.1268 | 0.7591 | 0.0793 | 0.3955 | |
| MOF | −425.48 | 856.97 | 865.52 | 0.2463 | 1.6384 | 0.1168 | 0.0607 | |
| MOW | −414.24 | 834.49 | 843.04 | 0.1339 | 0.8011 | 0.0771 | 0.4309 | |
| MOL | −410.62 | 827.25 | 835.81 | 0.0577 | 0.3311 | 0.0497 | 0.9092 | |
| MOB | −410.80 | 827.79 | 836.15 | 0.0310 | 0.2260 | 0.0527 | 0.8687 | |
| MOG | −424.44 | 854.71 | 863.27 | 0.4146 | 2.4478 | 0.0855 | 0.3065 | |
| Lifetimes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 1 | 1 | 1 | 1 | 1 | 2 | 3 | 6 |
| 7 | 11 | 12 | 18 | 18 | 18 | 18 | 18 | 21 | 32 |
| 36 | 40 | 45 | 46 | 47 | 50 | 55 | 60 | 63 | 63 |
| 67 | 67 | 67 | 67 | 72 | 75 | 79 | 82 | 82 | 83 |
| 84 | 84 | 84 | 85 | 85 | 85 | 85 | 85 | 86 | 86 |
| Model | MLEs | logL | AIC | BIC | W* | A* | K-S | p-Value |
|---|---|---|---|---|---|---|---|---|
| MOE-PU | −213.56 | 433.12 | 438.85 | 0.2641 | 2.2680 | 0.1622 | 0.1437 | |
| MOE | −239.59 | 483.18 | 487.00 | 0.3945 | 2.4587 | 0.1687 | 0.1161 | |
| MOF | −255.08 | 516.16 | 521.89 | 0.8121 | 4.5126 | 0.2556 | 0.0029 | |
| MOW | −240.21 | 486.42 | 492.16 | 0.4647 | 2.8406 | 0.2038 | 0.0313 | |
| MOL | −242.21 | 490.43 | 496.17 | 0.4537 | 2.7755 | 0.1694 | 0.1131 | |
| MOB | −251.48 | 508.96 | 514.70 | 0.7053 | 4.0855 | 0.2277 | 0.0111 | |
| MOG | −235.08 | 476.16 | 481.90 | 0.3478 | 2.2178 | 0.1643 | 0.1340 | |
| Model | MLEs | logL | AIC | BIC | W* | A* | K-S | p-Value |
|---|---|---|---|---|---|---|---|---|
| MOE-PU | −2392.61 | 4791.22 | 4804.94 | 0.997 | 7.709 | 0.076 | 0.0089 | |
| MOE | −2562.83 | 5129.67 | 5138.82 | 1.999 | 12.852 | 0.2066 | 4.85 × | |
| MOF | −2573.76 | 5153.53 | 5167.26 | 5.321 | 30.961 | 0.1801 | 7.26 × | |
| MOW | −2452.942 | 4911.88 | 4925.60 | 1.1219 | 8.3981 | 0.1066 | 1.65 × | |
| MOL | −2757.98 | 5521.96 | 5535.69 | 3.149 | 18.903 | 0.3137 | 2.51 × | |
| MOB | −3058.43 | 6122.87 | 6136.60 | 5.582 | 32.086 | 0.3457 | 6.39 × | |
| MOG | −2451.04 | 4908.09 | 4921.82 | 1.4129 | 9.6821 | 0.1085 | 9.04 × | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Hernández, I.J.; Méndez-González, L.C.; Granillo-Macías, R.; Rodríguez-Muñoz, J.L.; Pacheco-Cedeño, J.S. A New Generalization of the Uniform Distribution: Properties and Applications to Lifetime Data. Mathematics 2024, 12, 2328. https://doi.org/10.3390/math12152328
González-Hernández IJ, Méndez-González LC, Granillo-Macías R, Rodríguez-Muñoz JL, Pacheco-Cedeño JS. A New Generalization of the Uniform Distribution: Properties and Applications to Lifetime Data. Mathematics. 2024; 12(15):2328. https://doi.org/10.3390/math12152328
Chicago/Turabian StyleGonzález-Hernández, Isidro Jesús, Luis Carlos Méndez-González, Rafael Granillo-Macías, José Luis Rodríguez-Muñoz, and José Sergio Pacheco-Cedeño. 2024. "A New Generalization of the Uniform Distribution: Properties and Applications to Lifetime Data" Mathematics 12, no. 15: 2328. https://doi.org/10.3390/math12152328







