New Trends in Applying LRM to Nonlinear Ill-Posed Equations
Abstract
1. Introduction
2. Main Results
3. Approximating Sequence
- (a)
- where
- (b)
- where
- (c)
4. Adaptive Choice and Stopping Rule
5. Algorithm
- Choose and
- Choose
- (i)
- Set
- (ii)
- Choose the minimum n, such that (say ).
- (iii)
- Compute using the iteration (9).
- (iv)
- If then, take and return
- (v)
- Else, put and get back to (ii).
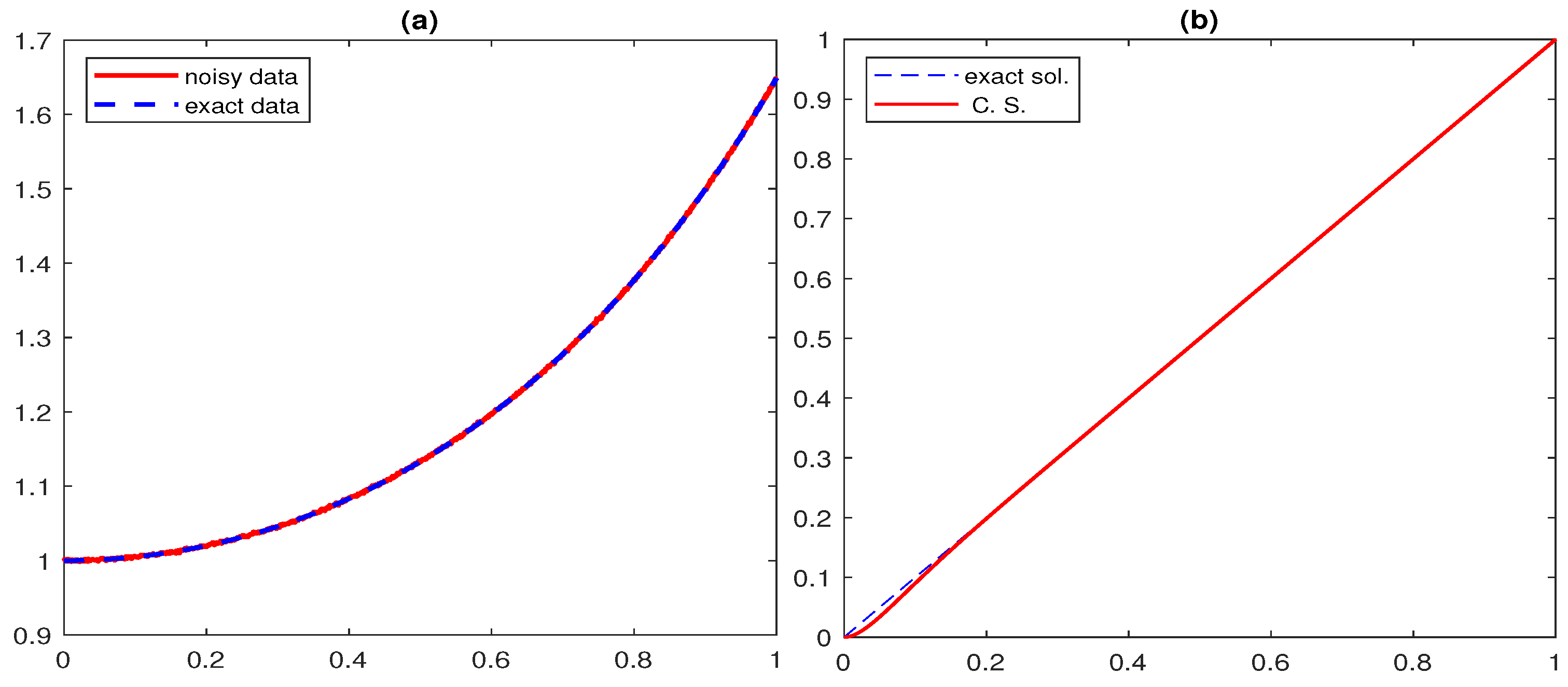
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tautenhahn, U. On the method of Lavrentiev regularization for nonlinear ill-posed problems. Inverse Probl. 2002, 18, 191–207. [Google Scholar] [CrossRef]
- Bakushinsky, A.B.; Smirnova, A. A study of frozen iteratively regularized Gauss-Newton algorithm for nonlinear ill-posed problems under generalized normal solvability condition. J. Inverse Ill-Posed Probl. 2020, 28, 275–286. [Google Scholar] [CrossRef]
- Mahale, P.; Dixit, S. Simplified iteratively regularized Gauss-Newton method in Banach spaces under a general source condition. Comput. Methods Appl. Math. 2020, 20, 321–341. [Google Scholar] [CrossRef]
- Mahale, P.; Shaikh, F. Simplified Levenberg-Marquardt meethod in Banach spaces for nonlinear ill-posed operator equations. Appl. Anal. 2021, 102, 124–148. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. Iteratively regularized Landweber iteration method: Convergence analysis via Holder stability. Appl. Math. Comput. 2021, 392, 125744. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. Convergence rates for iteratively regularized Gauss-Newton method subject to stability constraints. J. Comput. Appl. Math. 2022, 400, 113744. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. Nonstationary iterated Tikhonov regularization: Convergence analysis via Holder stability. Inverse Probl. 2022, 38, 125008. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. Convergence analysis of iteratively regularized Gauss-Newton method with frozen derivative in Banach spaces. J. Inverse Ill-Posed Probl. 2022, 30, 857–876. [Google Scholar] [CrossRef]
- Mittal, G.; Giri, A.K. Convergence analysis of an optimally accurate frozen multi-level projected steepest descent iteration for solving inverse problems. J. Complex. Artic. 2022, 75, 101711. [Google Scholar] [CrossRef]
- George, S.; Sabari, M. Numerical approximation of a Tikhonov type regularizer by a discretized frozen steepest descent method. J. Comput. Appl. Math. 2018, 330, 488–498. [Google Scholar] [CrossRef]
- Xia, Y.; Han, B.; Fu, Z. Convergence analysis of inexact Newton -Landweber iteration under Holder stability. Inverse Problems 2023, 39, 015004. [Google Scholar] [CrossRef]
- Alber, Y.; Ryazantseva, I. Nonlinear Ill-Posed Problems of Monotone Type; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Mahale, P.; Nair, M.T. Iterated Lavrentiev regularization for nonlinear ill-posed problems. ANZIAM J. 2009, 51, 191–217. [Google Scholar] [CrossRef]
- Semenova, E. Lavrentiev regularization and balancing principle for solving ill-posed problems with monotone operators. Comput. Methods Appl. Math. 2010, 10, 444–454. [Google Scholar] [CrossRef]
- Vasin, V.; George, S. An analysis of Lavrentiev regularization method and Newton type process for nonlinear ill-posed problems. Appl. Math. Comput. 2014, 230, 406–413. [Google Scholar] [CrossRef]
- Mahale, P.; Nair, M.T. Lavrentiev regularization of non-linear ill-posed equations under general source condition. J. Nonlinear Anal. Optim. 2013, 4, 193–204. [Google Scholar]
- Nair, M.T. Regularization of ill-posed operator equations: An overview. J. Anal. 2021, 29, 519–541. [Google Scholar] [CrossRef]
- George, S.; Kanagaraj, K. Derivative free regularization method for nonlinear ill-posed equations in Hilbert scales. Comput. Methods Appl. Math. 2019, 19, 765–778. [Google Scholar] [CrossRef]
- George, S.; Nair, M.T. A derivative-free iterative method for nonlinear ill-posed equations with monotone operators. J. Inverse Ill-Posed Probl. 2017, 25, 543–551. [Google Scholar] [CrossRef]
- George, S.; Nair, M.T. A modified Newton-Lavrentiev regularization for nonlinear ill-posed Hammerstein-type operator equations. J. Complex. 2008, 24, 228–240. [Google Scholar] [CrossRef]
- Hofmann, B.; Kaltenbacher, B.; Resmerita, E. Lavrentiev’s regularization method in Hilbert spaces revisited. arXiv 2015, arXiv:1506.01803. [Google Scholar] [CrossRef]
- Nair, M.T.; Ravishankar, P. Regularized versions of continuous Newton’s method and continuous modified Newton’s method under general source conditions. Numer. Funct. Anal. Optim. 2008, 29, 1140–1165. [Google Scholar] [CrossRef]
- Jidesh, P.; Shubha, V.S.; George, S. A quadratic convergence yielding iterative method for the implementation of Lavrentiev regularization method for ill-posed equations. Appl. Math. Comput. 2015, 254, 148–156. [Google Scholar] [CrossRef]
- Vasin, V.; Prutkin, I.L.; Yu Timerkhanova, L. Retrieval of a three-dimensional relief of geological boundary from gravity data. Izv. Phys. Solid Earth 1996, 11, 901–905. [Google Scholar]
- Argyros, I.K. The Theory and Applications of Iteration Methods, 2nd ed.; Engineering Series; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: Oxfordshire, UK, 2022. [Google Scholar]
- Argyros, C.I.; Regmi, S.; Argyros, I.K.; George, S. Contemporary Algorithms: Theory and Applications; NOVA Publishers: Hauppauge, NY, USA, 2023; Volume III. [Google Scholar]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis, 2nd ed.; Pergamon Press: Elmsford, NY, USA, 1982. [Google Scholar] [CrossRef]
- Plato, R.; Vainikko, G. On the regularization of projection methods for solving ill-posed problems. Numer. Math. 1990, 57, 63–79. [Google Scholar] [CrossRef]
- Pereverzyev, S.; Schock, E. On the adaptive selection of the parameter in regularization of ill-posed problems. SIAM J. Numer. Anal. 2005, 43, 2060–2076. [Google Scholar] [CrossRef]
- Lu, S.; Pereverzyev, S. Sparsity reconstruction by the standard Tikhonov method. RICAM Rep. 2008, 17, 2008. [Google Scholar]
- Vasin, V. Modified Newton-type processes generating Fejér approximations of regularized solutions to nonlinear equations. Tr. Instituta Mat. Mekhaniki UrO RAN 19 2013, 2, 85–97. [Google Scholar] [CrossRef]
- Vasin, V. Irregular nonlinear operator equations: Tikhonov’s regularization and iterative approximation. J. Inverse Ill-Posed Probl. 2013, 21, 109–123. [Google Scholar] [CrossRef][Green Version]
- Shubha, V.S.; George, S.; Jidesh, P. Finite dimensional realization of a Tikhonov gradient type-method under weak conditions. Rend. Del Circ. Mat. Palermo Ser. 2016, 65, 395–410. [Google Scholar] [CrossRef]
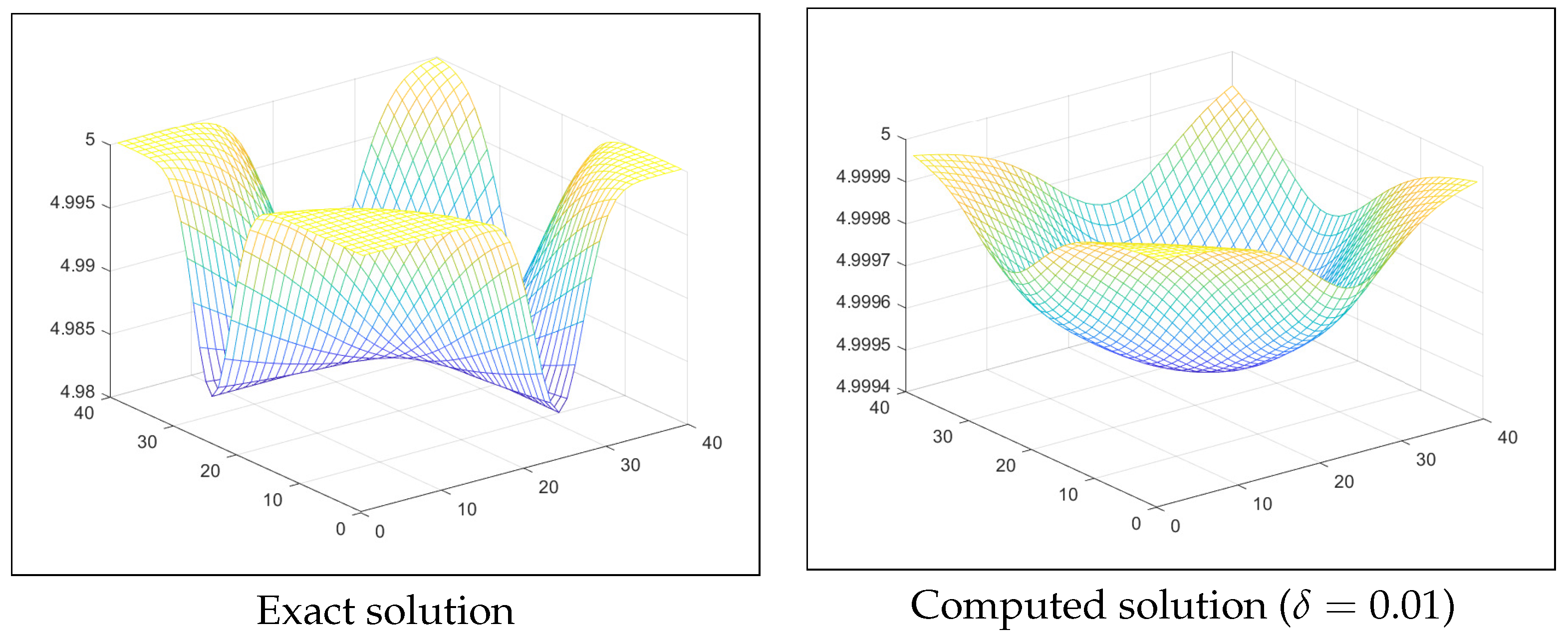
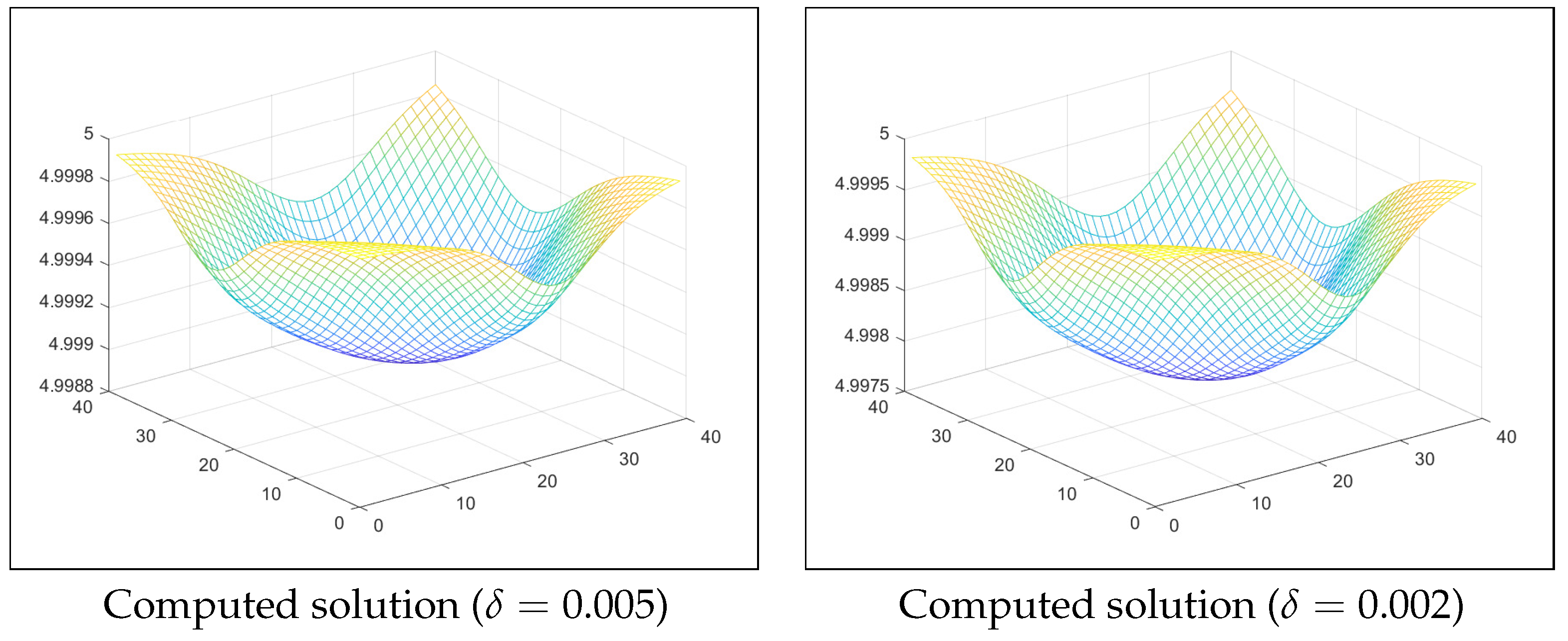
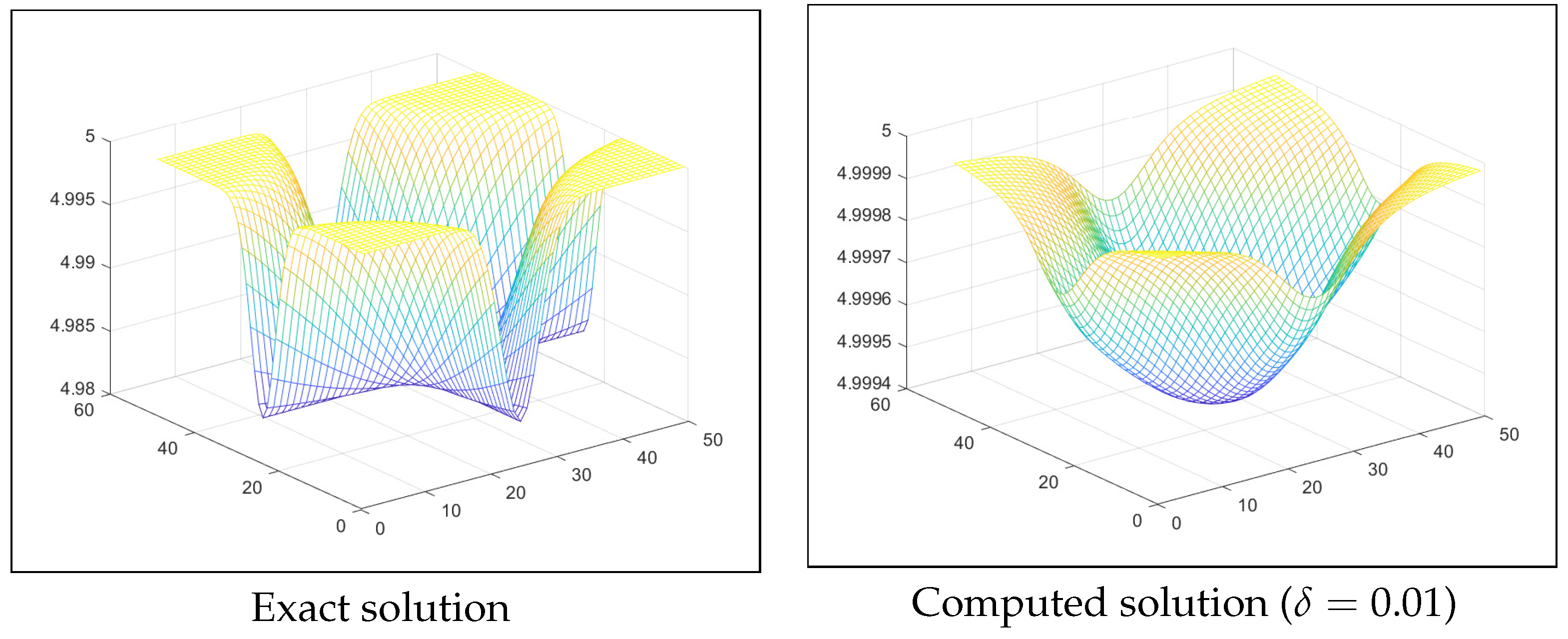

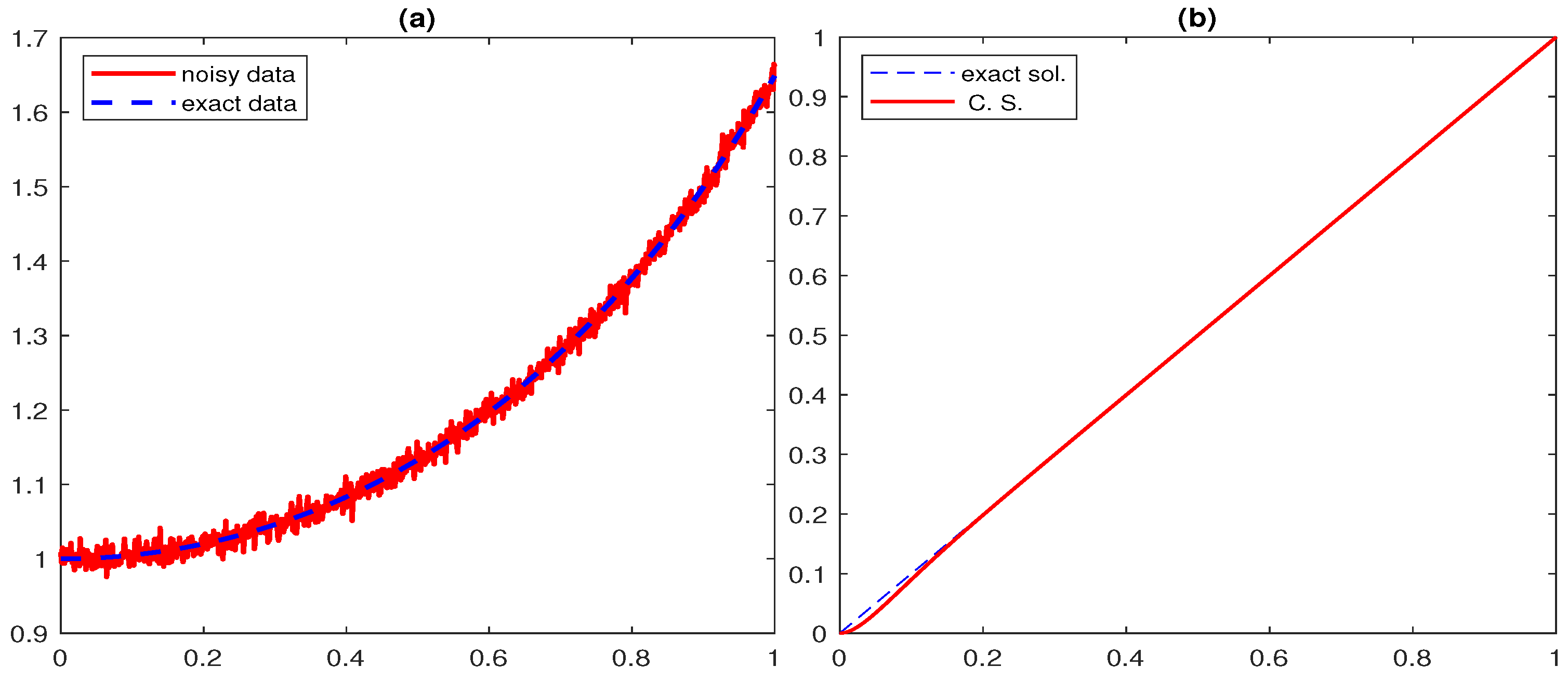




| m | CPU | [33] | [33] | CPU | ||||
|---|---|---|---|---|---|---|---|---|
| Time | Time [33] | |||||||
| 0.01 | 0.0256 | 0.002089 | 0.000420 | 4.02 | 2.3448 × | 7.0843 × | 4.31 | |
| 0.005 | 0.0128 | 40 | 0.002030 | 0.000407 | 3.84 | 2.3448 × | 7.0871 × | 4.19 |
| 0.002 | 0.0051 | 0.001875 | 0.000372 | 3.79 | 2.3448 × | 7.0888 × | 4.04 | |
| 0.01 | 0.0256 | 0.002211 | 0.000491 | 2.44 | 3.0643 × | 1.0248 × | 2.92 | |
| 0.005 | 0.0128 | 35 | 0.002151 | 0.000476 | 2.41 | 3.0643 × | 1.0252 × | 2.84 |
| 0.002 | 0.0051 | 0.001994 | 0.000438 | 2.37 | 3.064 3× | 1.0255 × | 2.65 |
| m | ||||
|---|---|---|---|---|
| 0.01 | 5.7002 | |||
| 0.001 | 1000 | 5.6951 | ||
| 0.0001 | 5.6947 | |||
| 0.01 | 5.6796 | |||
| 0.001 | 800 | 5.6931 | ||
| 0.0001 | 5.6936 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
George, S.; Sadananda, R.; Padikkal, J.; Kunnarath, A.; Argyros, I.K. New Trends in Applying LRM to Nonlinear Ill-Posed Equations. Mathematics 2024, 12, 2377. https://doi.org/10.3390/math12152377
George S, Sadananda R, Padikkal J, Kunnarath A, Argyros IK. New Trends in Applying LRM to Nonlinear Ill-Posed Equations. Mathematics. 2024; 12(15):2377. https://doi.org/10.3390/math12152377
Chicago/Turabian StyleGeorge, Santhosh, Ramya Sadananda, Jidesh Padikkal, Ajil Kunnarath, and Ioannis K. Argyros. 2024. "New Trends in Applying LRM to Nonlinear Ill-Posed Equations" Mathematics 12, no. 15: 2377. https://doi.org/10.3390/math12152377
APA StyleGeorge, S., Sadananda, R., Padikkal, J., Kunnarath, A., & Argyros, I. K. (2024). New Trends in Applying LRM to Nonlinear Ill-Posed Equations. Mathematics, 12(15), 2377. https://doi.org/10.3390/math12152377









