A Discrete Resistance Network Based on a Multiresolution Grid for 3D Ground-Return Current Forward Modeling
Abstract
:1. Introduction
2. Related Works
2.1. Background
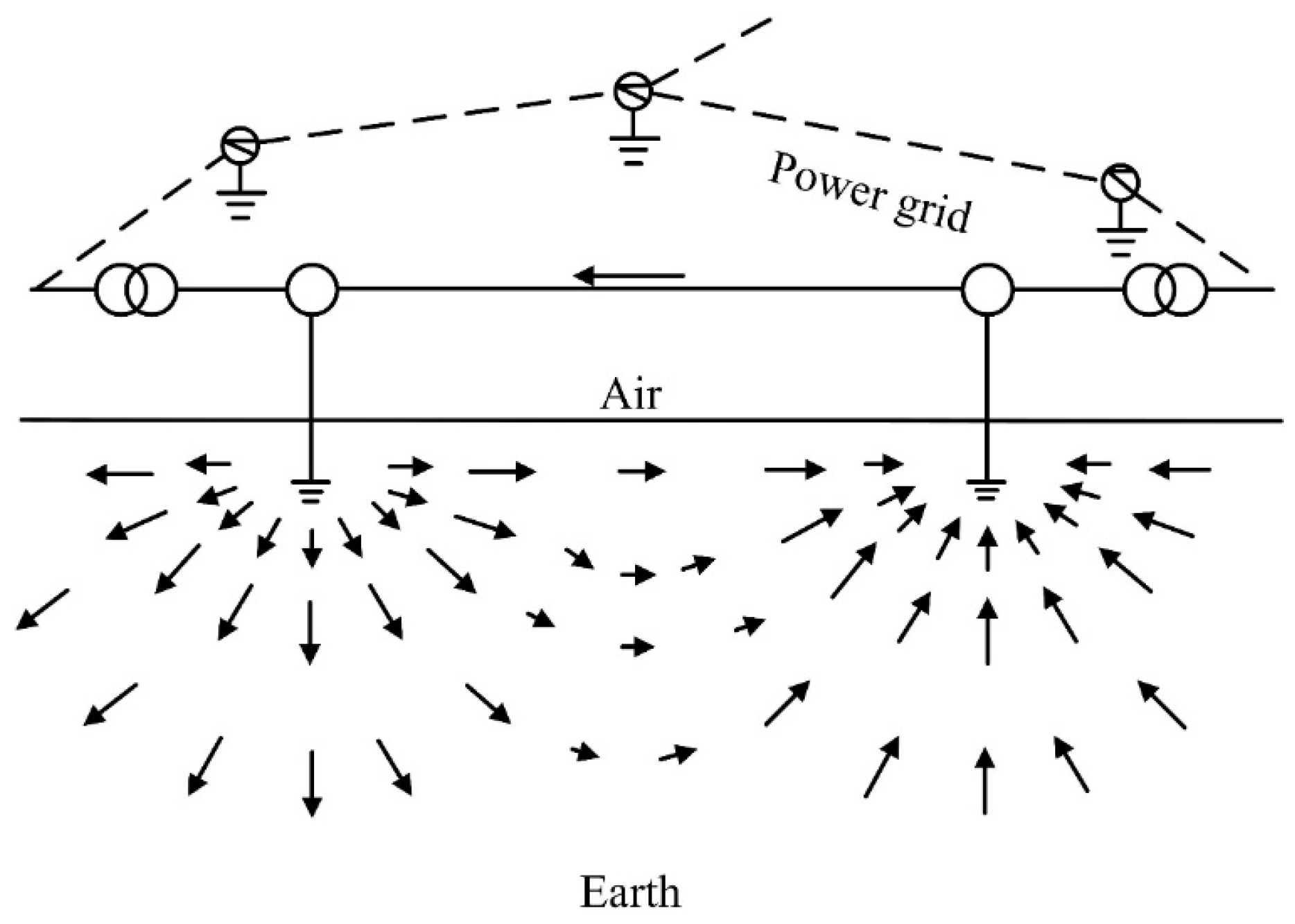
2.2. GRC Calculation
2.3. Discrete Grid
2.4. Contributions
- (1)
- The proposed resistance network system does not require the continuity of regular elements to establish an equipotential surface for circulating currents on a face, and it maintains good symmetry, resulting in higher solving efficiency.
- (2)
- The grid is refined at the source point and near the surface to enhance accuracy. This helps avoid redundant elements caused by lateral extension in regular grid refinement, reduces the degrees of freedom, and improves the solving efficiency of the resistance network system.
- (3)
- For hanging nodes in a multiresolution grid’s discretized resistance network, we compared three different interpolation methods and determined that the ghost fine interpolation resistance value method is suitable for MR resistance network discretization.
3. 3D RN Method
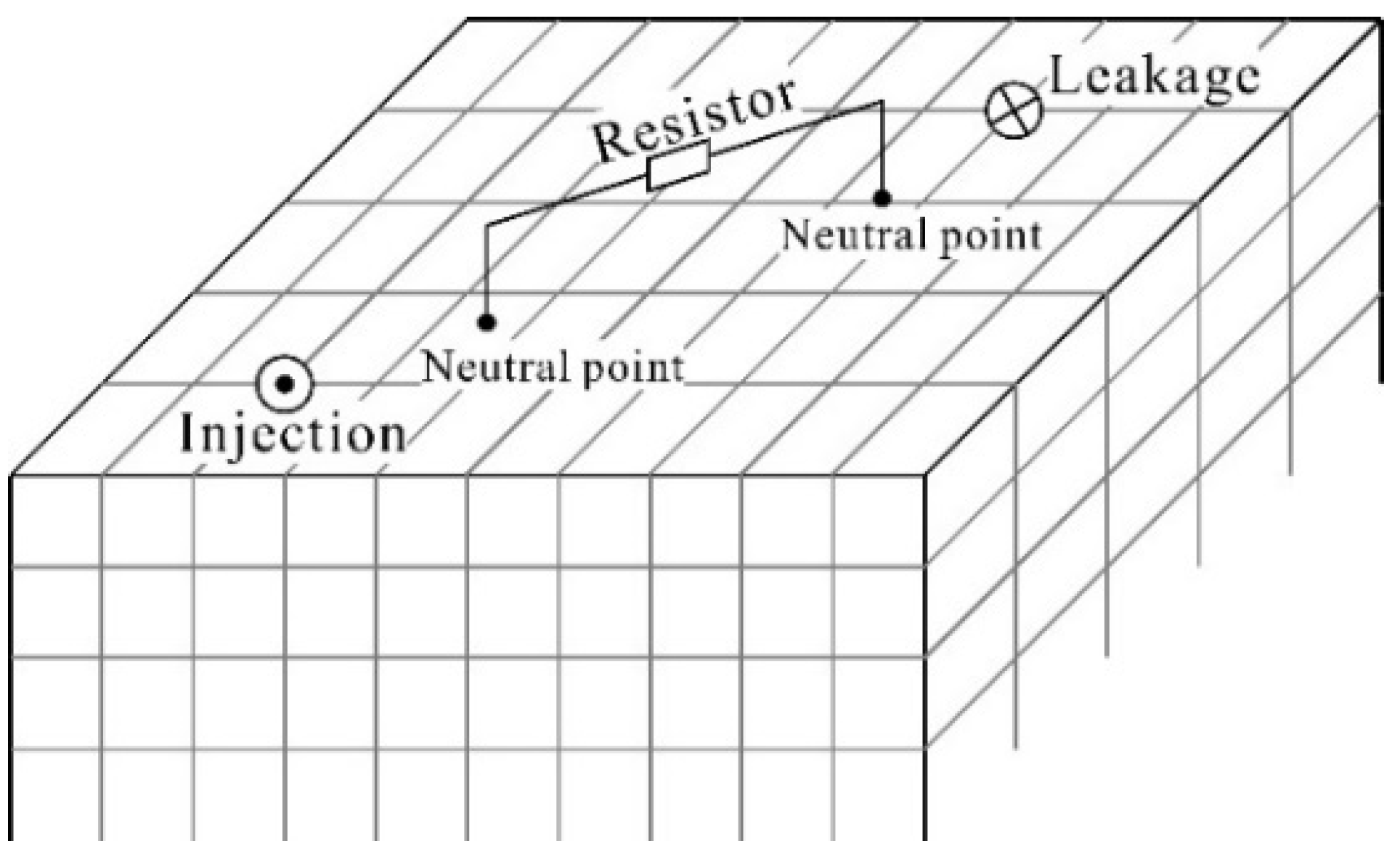
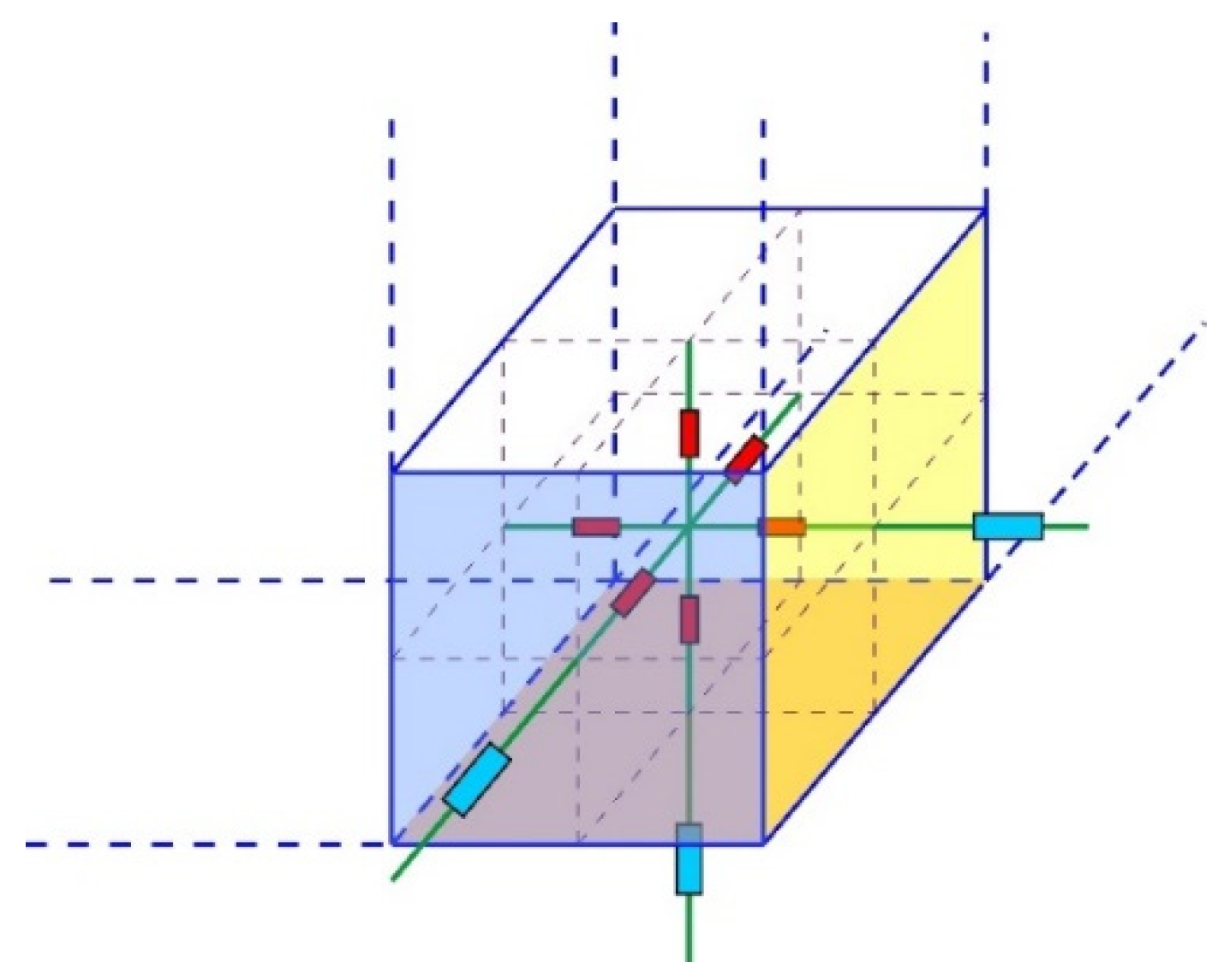
3.1. Stereo NV-RN on an SG
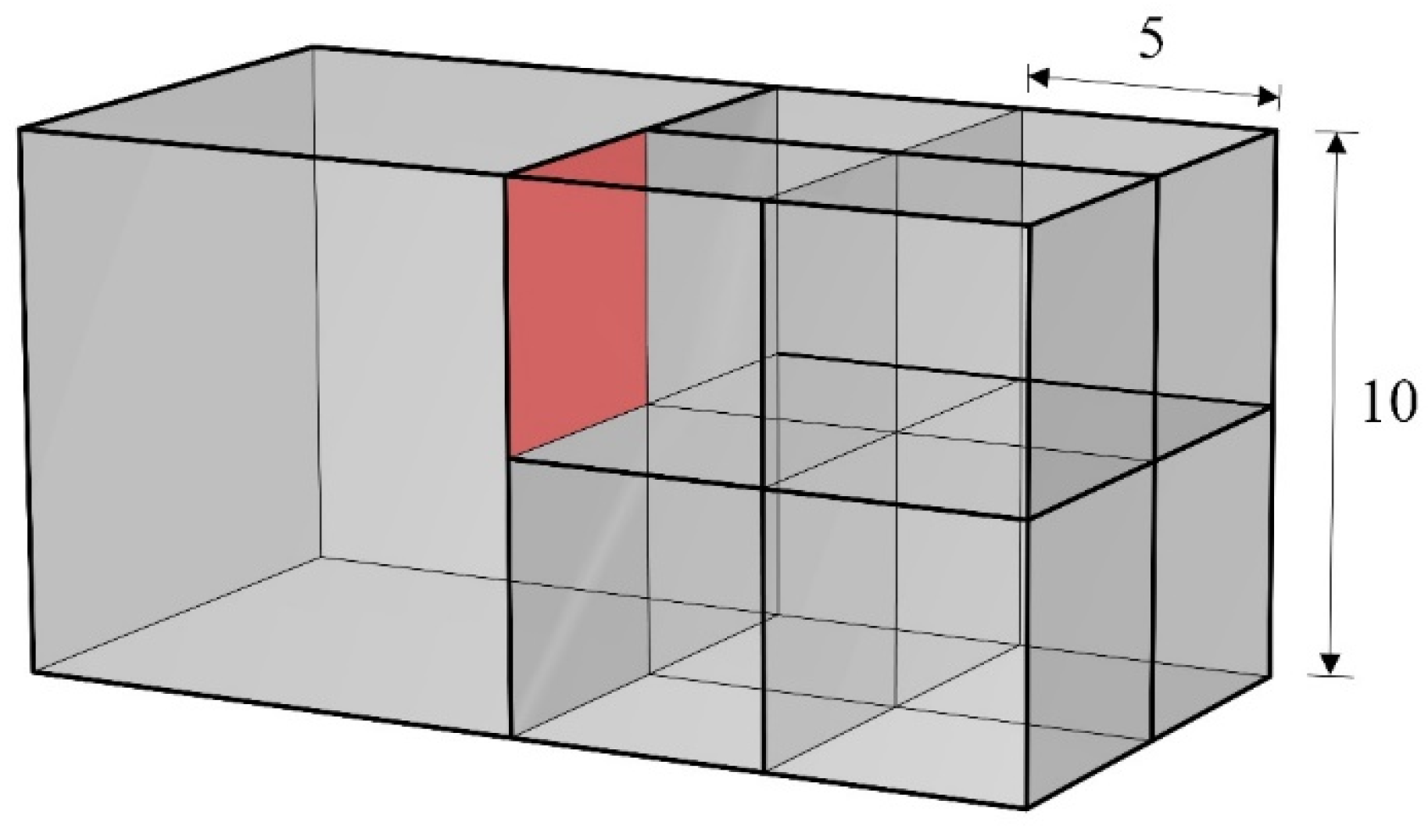
3.2. MR Grid
3.3. MR Stereo NV-RN
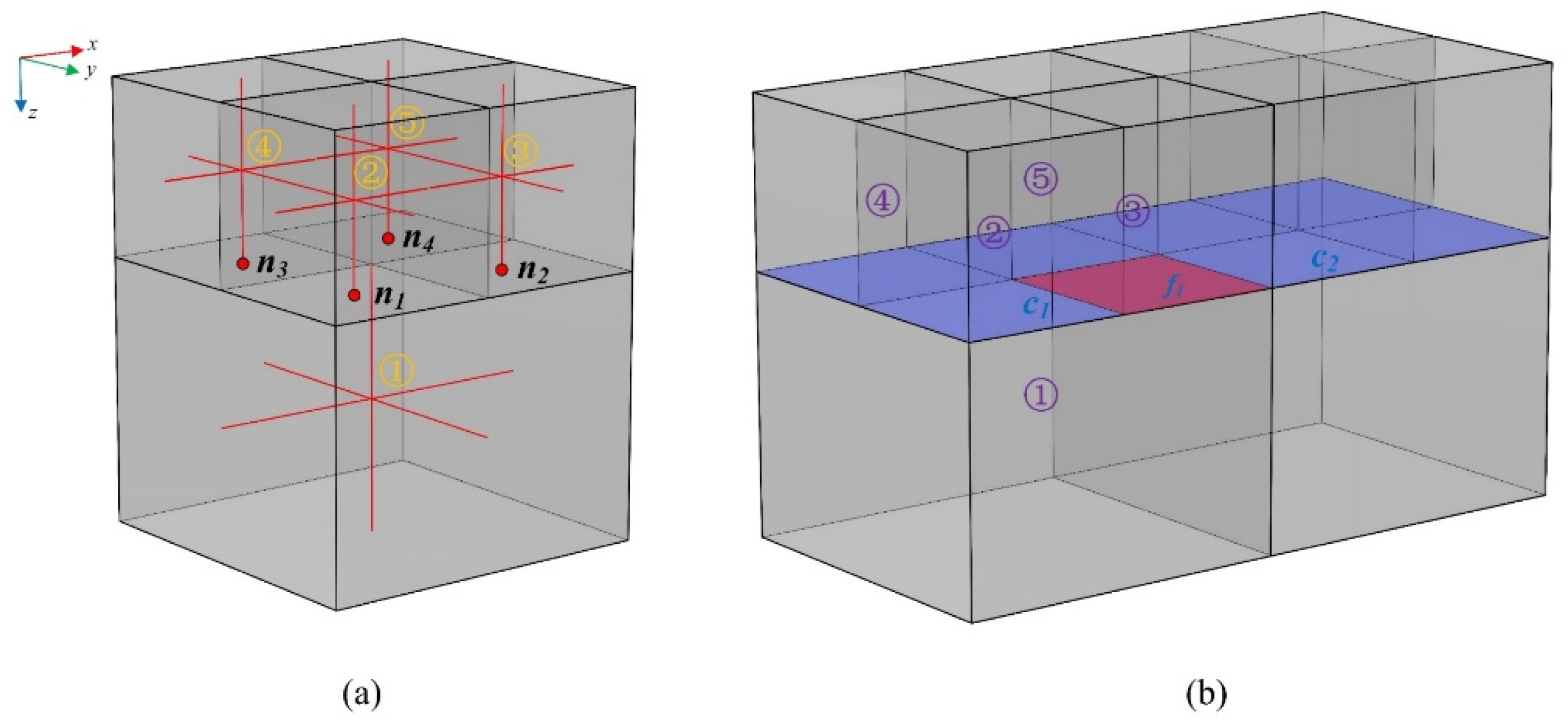
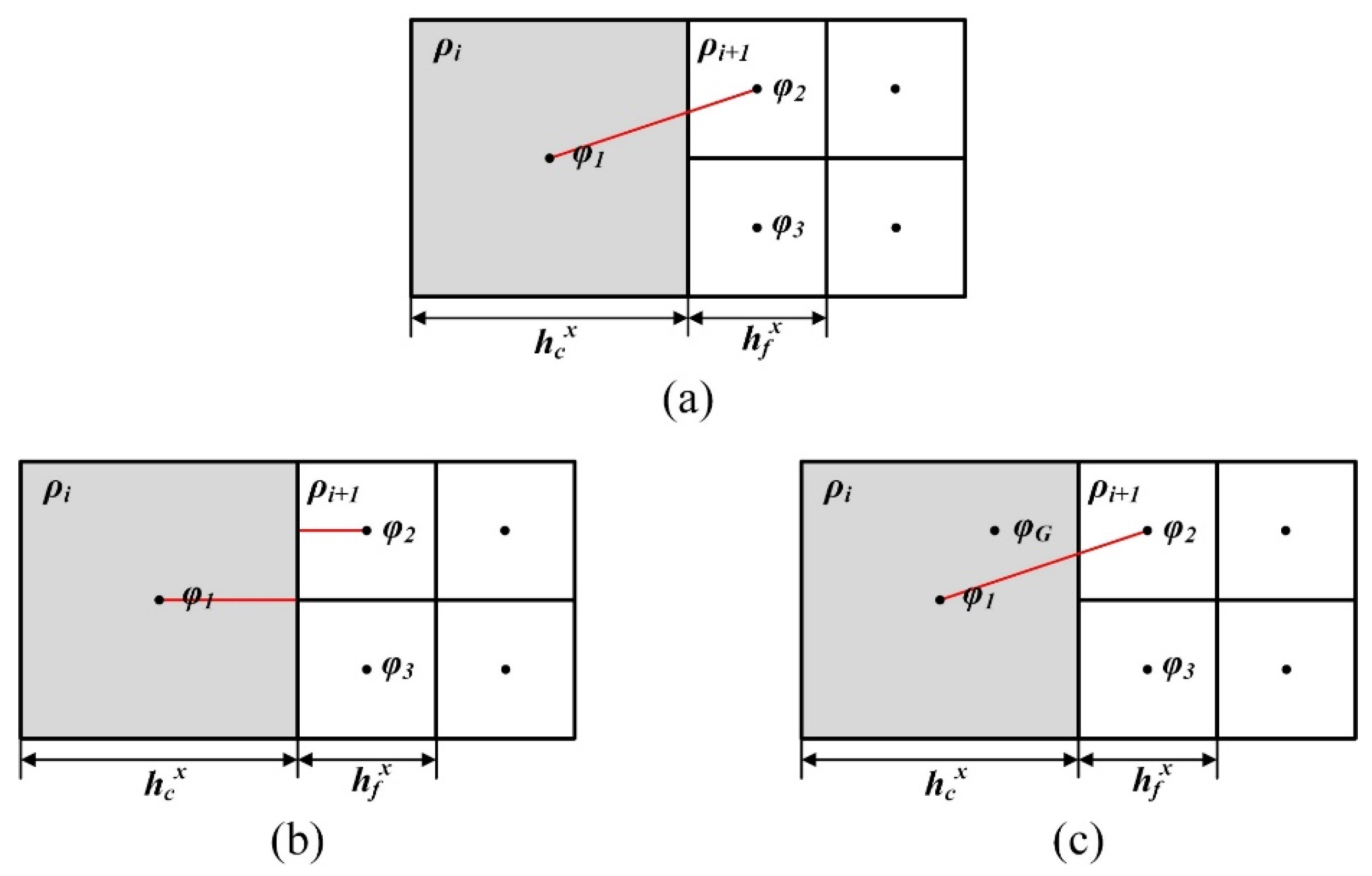
3.3.1. Hanging Nodes
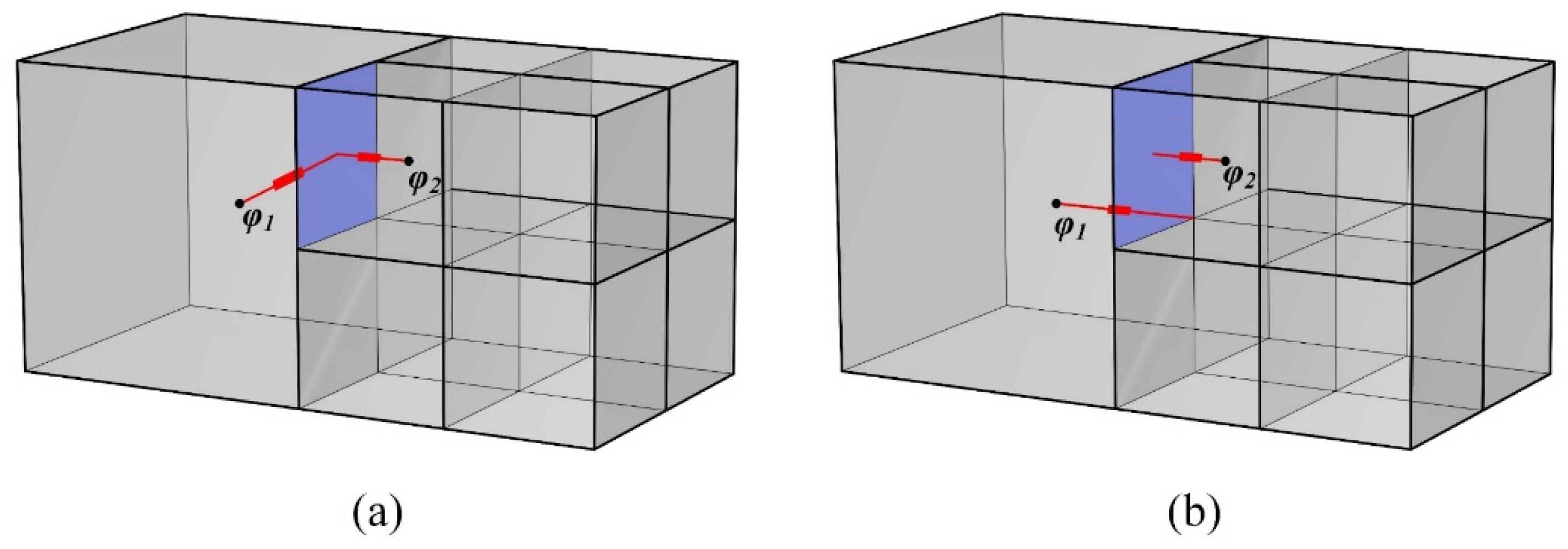
3.3.2. Hanging Node Interpolation
3.3.3. Boundary Conditions
4. Numerical Examples
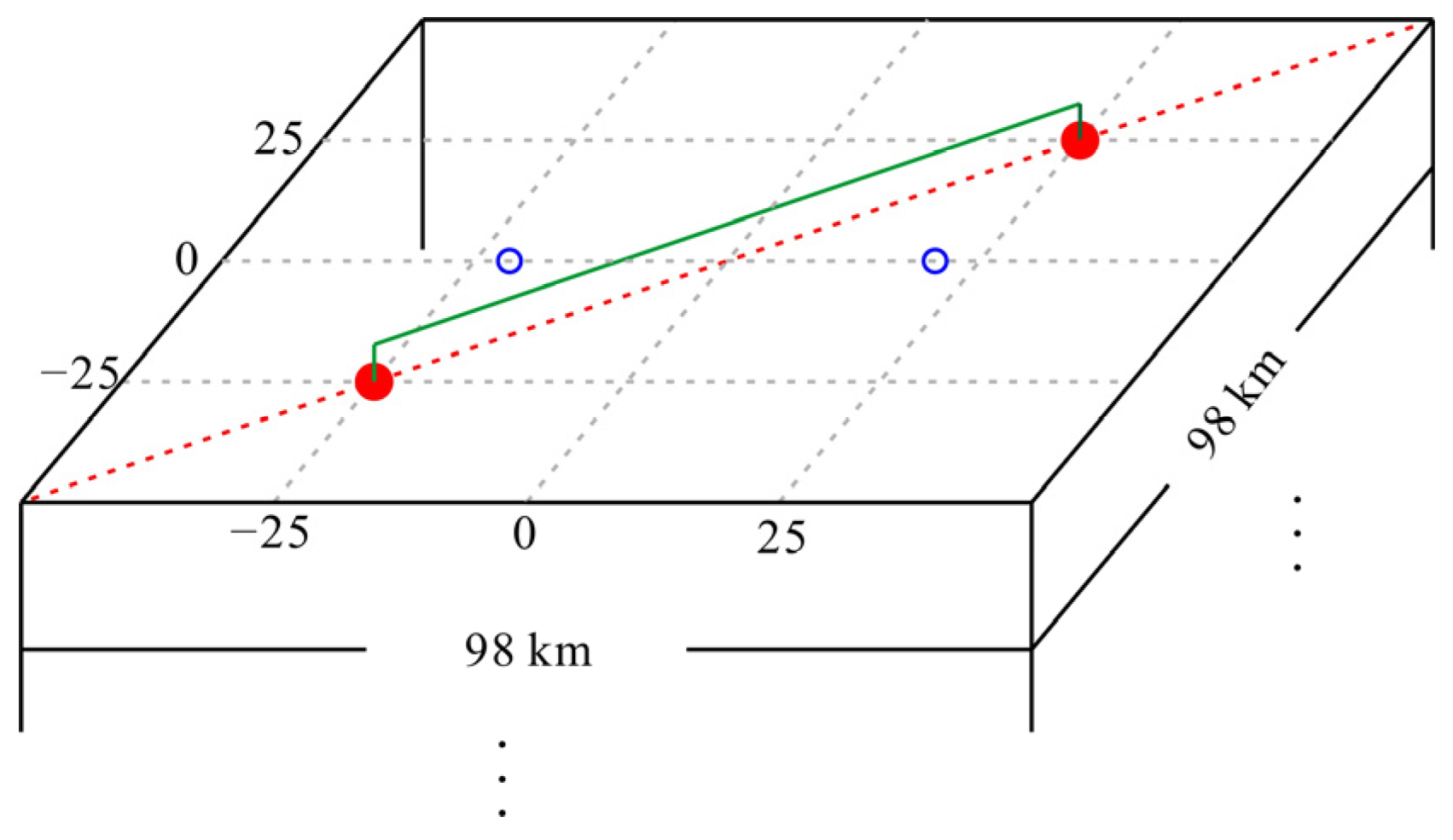
4.1. Homogenous Model
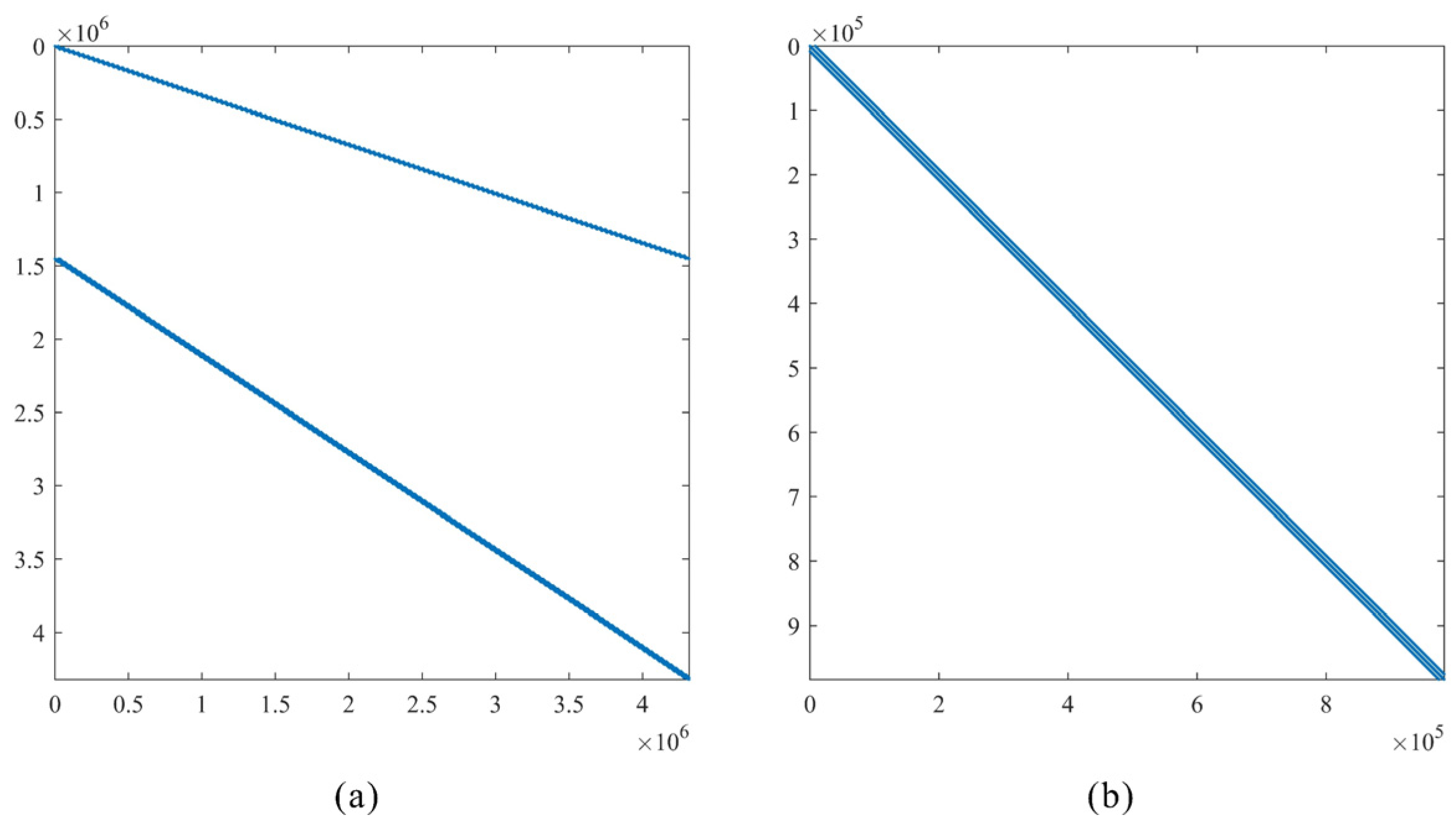
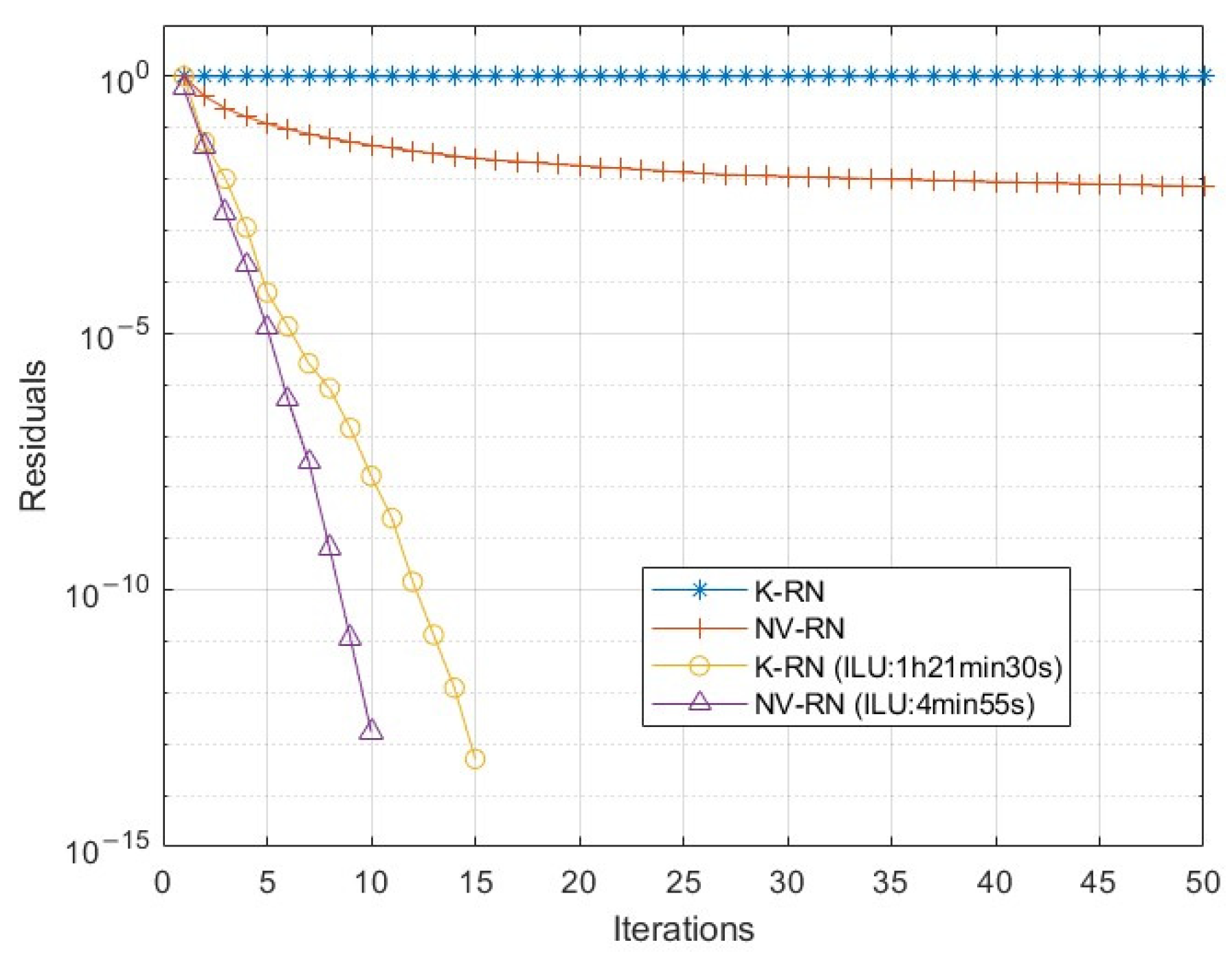
4.1.1. Comparison of Solving Efficiency
4.1.2. Mesh Discretization Efficiency
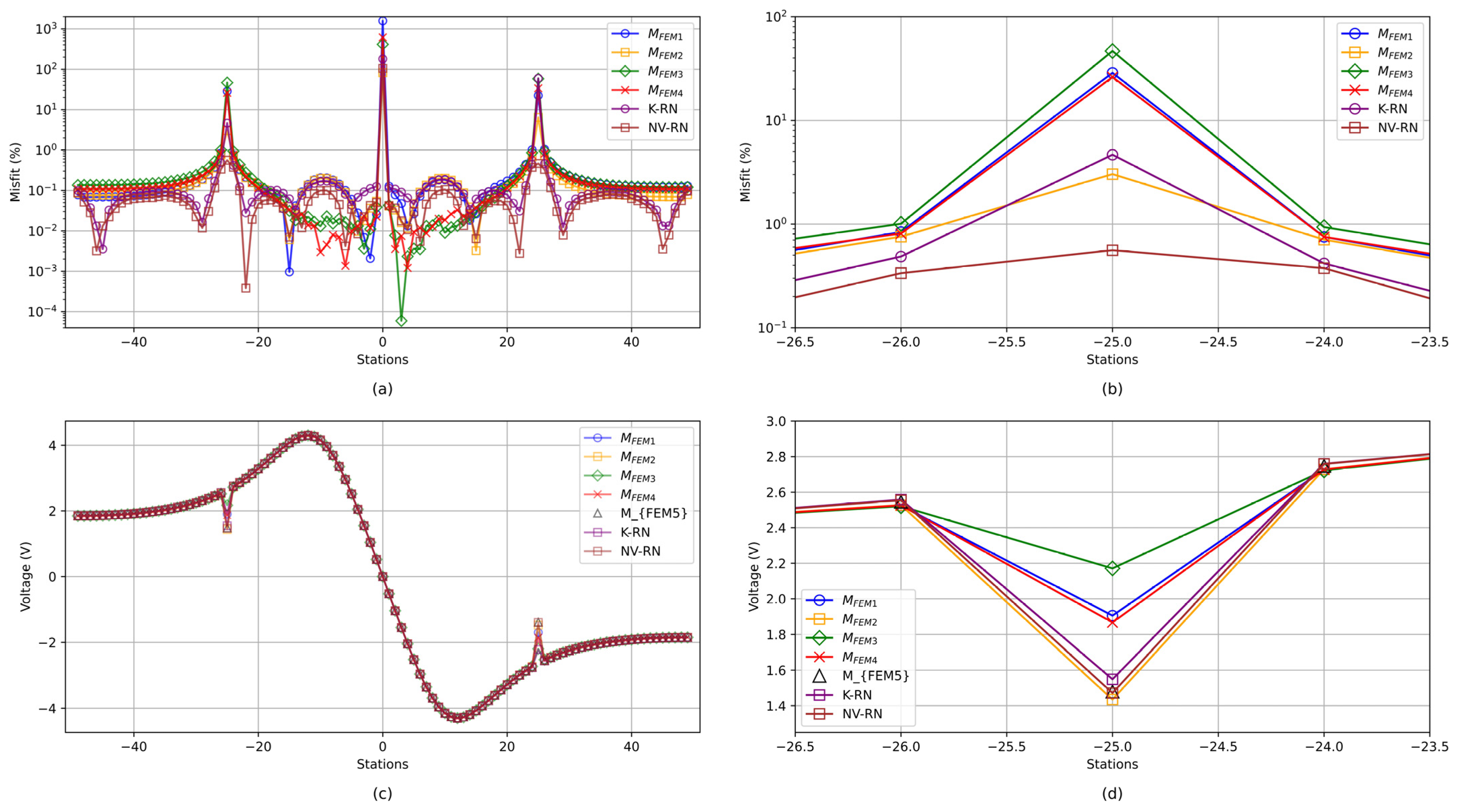
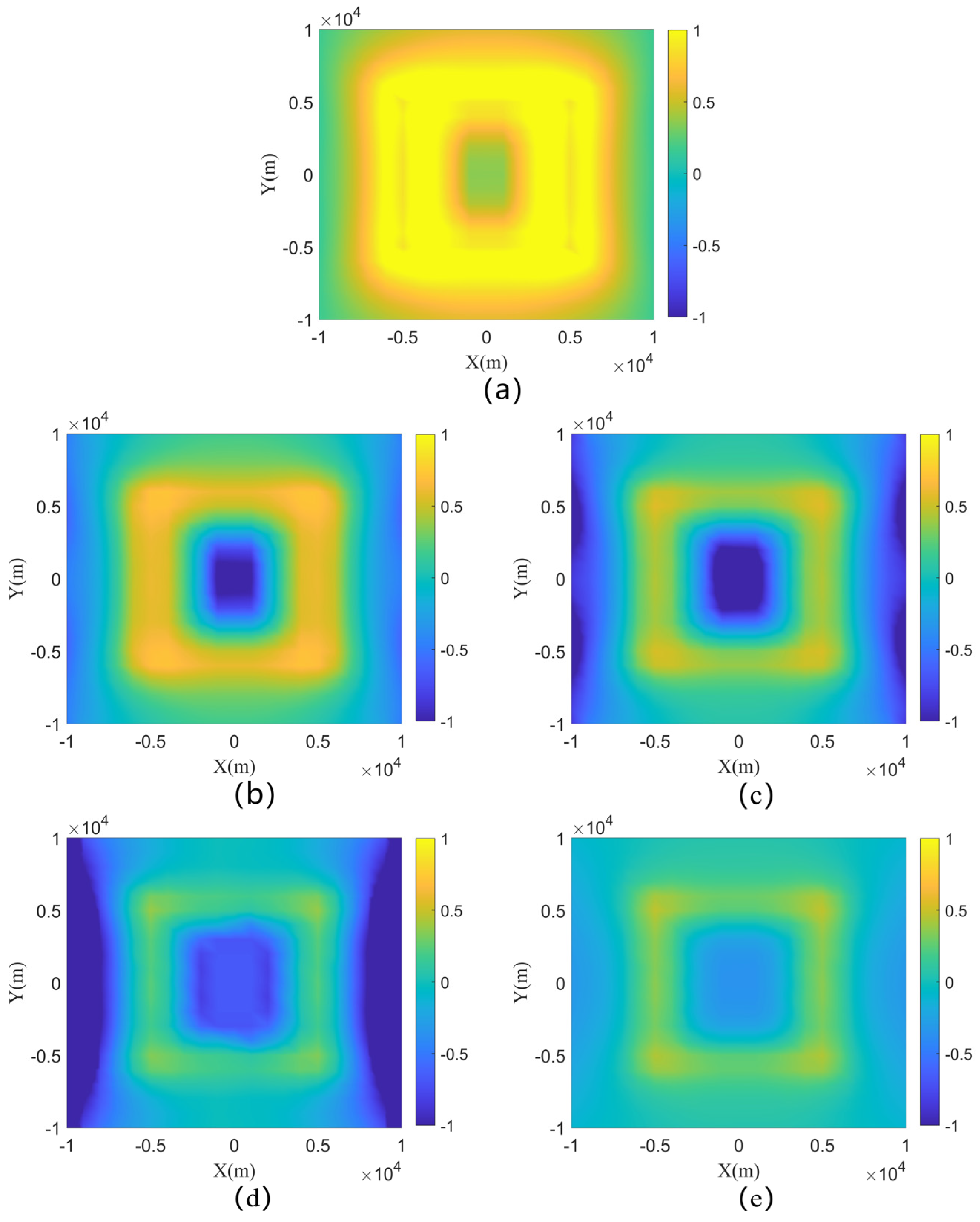
4.2. Abnormal Body Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Yu, N.; Wang, E.; Sun, Z.; Wu, X.; Wang, X.; Ma, L. Airborne Transient Electromagnetic Simulation: Detecting Geoelectric Structures for HVdc Monopole Operation. IEEE Geosci. Remote Sens. Mag. 2022, 10, 274–288. [Google Scholar] [CrossRef]
- Yu, N.; Cai, Z.; Li, R.; Zhang, Q.; Gao, L.; Sun, Z. Calculation of Earth Surface Potential and Neutral Current Caused by HVDC Considering Three-Dimensional Complex Soil Structure. IEEE Trans. Electromagn. Compat. 2021, 63, 1480–1490. [Google Scholar] [CrossRef]
- Altaf, M.W.; Arif, M.T.; Islam, S.N.; Haque, M.E. Microgrid Protection Challenges and Mitigation Approaches–A Comprehensive Review. IEEE Access 2022, 10, 38895–38922. [Google Scholar] [CrossRef]
- Khalid, M.R.; Khan, I.A.; Hameed, S.; Asghar, M.S.J.; Ro, J.-S. A Comprehensive Review on Structural Topologies, Power Levels, Energy Storage Systems, and Standards for Electric Vehicle Charging Stations and Their Impacts on Grid. IEEE Access 2021, 9, 128069–128094. [Google Scholar] [CrossRef]
- Faúndez Urbina, C.A.; Alanís, D.C.; Ramírez, E.; Seguel, O.; Fustos, I.J.; Donoso, P.D.; de Miranda, J.H.; Rakonjac, N.; Palma, S.E.; Galleguillos, M. Estimating Soil Water Content in a Thorny Forest Ecosystem by Time-Lapse Electrical Resistivity Tomography (ERT) and HYDRUS 2D/3D Simulations. Hydrol. Process. 2023, 37, e15002. [Google Scholar] [CrossRef]
- Blechschmidt, J.; Ernst, O.G. Three Ways to Solve Partial Differential Equations with Neural Networks—A Review. GAMM-Mitteilungen 2021, 44, e202100006. [Google Scholar] [CrossRef]
- Bai, N.; Zhou, J.; Hu, X.; Han, B. 3D Edge-Based and Nodal Finite Element Modeling of Magnetotelluric in General Anisotropic Media. Comput. Geosci. 2022, 158, 104975. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.; Kong, W.; Yu, N.; Li, T.; Wang, C. An Adaptive Hybrid Grids Finite-Element Approach for Plane Wave Three-Dimensional Electromagnetic Modeling. Comput. Geosci. 2023, 180, 105437. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, X.; Xiao, T.; Cai, H.; Li, J.; Peng, R.; Long, Z. Three-Dimensional Edge-Based Finite Element Modeling of Magnetotelluric Data in Anisotropic Media with a Divergence Correction. J. Appl. Geophys. 2021, 189, 104324. [Google Scholar] [CrossRef]
- Pfeifer, N.; Kizilcay, M.; Malicki, P. Analytical and Numerical Study of an Iron-Core Shunt-Compensation Reactor on a Mixed Transmission Line. Electr. Power Syst. Res. 2023, 220, 109315. [Google Scholar] [CrossRef]
- Arshia, G. 3D Electrical Resistivity Forward Modeling Using the Kirchhoff’s Method for Solving an Equivalent Resistor Network. J. Appl. Geophys. 2018, 159, 135–145. [Google Scholar] [CrossRef]
- Yang, D.; Oldenburg, D.; Heagy, L. 3D DC Resistivity Modeling of Steel Casing for Reservoir Monitoring Using Equivalent Resistor Network. In Proceedings of the Seg Technical Program Expanded, Dallas, TX, USA, 16–21 October 2016. [Google Scholar]
- Zhang, D.; Li, J.; Hui, D. Coordinated Control for Voltage Regulation of Distribution Network Voltage Regulation by Distributed Energy Storage Systems. Prot. Control. Mod. Power Syst. 2018, 3, 3. [Google Scholar] [CrossRef]
- Asim, K.M.; Schorlemmer, D.; Hainzl, S.; Iturrieta, P.; Savran, W.H.; Bayona, J.A.; Werner, M.J. Multi-Resolution Grids in Earthquake Forecasting: The Quadtree Approach. Bull. Seismol. Soc. Am. 2023, 113, 333–347. [Google Scholar] [CrossRef]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. ACM Trans. Graph. 2022, 41, 102:1–102:15. [Google Scholar] [CrossRef]
- Lowry, T.; Allen, M.; Shive, P. Singularity Removal—A Refinement of Resistivity Modeling Techniques. Geophysics 1989, 54, 766–774. [Google Scholar] [CrossRef]
- Zhang, Z.; Dan, Y.; Zou, J.; Liu, G.; Li, Y. Research on Discharging Current Distribution of Grounding Electrodes. IEEE Access 2019, 7, 59287–59298. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, H.; Yang, F.; Luo, H.; Li, W.; Han, J. FEM Analysis and Sensor-Based Measurement Scheme of Current Distribution for Grounding Electrode. Appl. Sci. 2020, 10, 8151. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, D.; Sun, Z. A Finite Difference Method for Modeling the DC Electrical Potential Field Including Surface Topography. In SEG Technical Program Expanded Abstracts 2009; SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2009; pp. 664–668. [Google Scholar]
- Pidlisecky, A.; Haber, E.; Knight, R. RESINVM3D: A 3D Resistivity Inversion Package. Geophysics 2007, 72, H1–H10. [Google Scholar] [CrossRef]
- Hetita, I.; Zalhaf, A.S.; Mansour, D.-E.A.; Han, Y.; Yang, P.; Wang, C. Modeling and Protection of Photovoltaic Systems during Lightning Strikes: A Review. Renew. Energy 2022, 184, 134–148. [Google Scholar] [CrossRef]
- Kim, Y.W.; Oh, I.H.; Choi, S.; Nam, I.; Chang, S.T. Vertical Integration of Multi-Electrodes inside a Single Sheet of Paper and the Control of the Equivalent Circuit for High-Density Flexible Supercapacitors. Chem. Eng. J. 2023, 454, 140117. [Google Scholar] [CrossRef]
- Molero, C.; Alex-Amor, A.; Mesa, F.; Palomares-Caballero, Á.; Padilla, P. Cross-Polarization Control in FSSs by Means of an Equivalent Circuit Approach. IEEE Access 2021, 9, 99513–99525. [Google Scholar] [CrossRef]
- Hussain, S.M.; Jamshed, W. A Comparative Entropy Based Analysis of Tangent Hyperbolic Hybrid Nanofluid Flow: Implementing Finite Difference Method. Int. Commun. Heat Mass Transf. 2021, 129, 105671. [Google Scholar] [CrossRef]
- Rasheed, M.; Ali, A.H.; Alabdali, O.; Shihab, S.; Rashid, A.; Rashid, T.; Hamad, S.H.A. The Effectiveness of the Finite Differences Method on Physical and Medical Images Based on a Heat Diffusion Equation. J. Phys. Conf. Ser. 2021, 1999, 012080. [Google Scholar] [CrossRef]
- Cai, H.; Liu, M.; Zhou, J.; Li, J.; Hu, X. Effective 3D-Transient Electromagnetic Inversion Using Finite-Element Method with a Parallel Direct Solver. Geophysics 2022, 87, E377–E392. [Google Scholar] [CrossRef]
- Long, Z.; Cai, H.; Hu, X.; Zhou, J.; Yang, X. Three-Dimensional Inversion of CSEM Data Using Finite Element Method in Data Space. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2001711. [Google Scholar] [CrossRef]
- Yao, H.; Ren, Z.; Tang, J.; Lin, Y.; Yin, C.; Hu, X.; Huang, Q.; Zhang, K. 3D Finite-Element Modeling of Earth Induced Electromagnetic Field and Its Potential Applications for Geomagnetic Satellites. Sci. China Earth Sci. 2021, 64, 1798–1812. [Google Scholar] [CrossRef]
- Cai, H.; Kong, R.; He, Z.; Wang, X.; Liu, S.; Huang, S.; Kass, M.A.; Hu, X. Joint Inversion of Potential Field Data with Adaptive Unstructured Tetrahedral Mesh. Geophysics 2024, 89, G45–G63. [Google Scholar] [CrossRef]
- Han, X.; Yin, C.; Su, Y.; Zhang, B.; Liu, Y.; Ren, X.; Ni, J.; Farquharson, C.G. 3D Finite-Element Forward Modeling of Airborne EM Systems in Frequency-Domain Using Octree Meshes. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5912813. [Google Scholar] [CrossRef]
- Liu, Y.; Yogeshwar, P.; Peng, R.; Hu, X.; Han, B.; Blanco-Arrué, B. Three-Dimensional Inversion of Time-Domain Electromagnetic Data Using Various Loop Source Configurations. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5910515. [Google Scholar] [CrossRef]
- Peng, R.; Han, B.; Liu, Y.; Hu, X. EM3DANI: A Julia Package for Fully Anisotropic 3D Forward Modeling of Electromagnetic Data. Geophysics 2021, 86, F49–F60. [Google Scholar] [CrossRef]
- Yang, H.; Cai, H.; Liu, M.; Xiong, Y.; Long, Z.; Li, J.; Hu, X. Three-dimensional Inversion of Semi-airborne Transient Electromagnetic Data Based on Finite Element Method. Near Surf. Geophys. 2022, 20, 661–678. [Google Scholar] [CrossRef]
- Zhou, J.; Bai, N.; Hu, X.; Xiao, T. An Efficient Hybrid Direct-Iterative Solver for Three-Dimensional Higher-Order Edge-Based Finite Element Simulation for Magnetotelluric Data in Anisotropic Media. Phys. Earth Planet. Inter. 2023, 339, 107029. [Google Scholar] [CrossRef]
- Gillis, T.; van Rees, W.M. MURPHY---A Scalable Multiresolution Framework for Scientific Computing on 3D Block-Structured Collocated Grids. SIAM J. Sci. Comput. 2022, 44, C367–C398. [Google Scholar] [CrossRef]
- Xie, J.; Cai, H.; Hu, X.; Long, Z.; Xu, S.; Fu, C.; Wang, Z.; Di, Q. 3-D Magnetotelluric Inversion and Application Using the Edge-Based Finite Element with Hexahedral Mesh. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4503011. [Google Scholar] [CrossRef]
- Tang, W.; Li, Y.; Liu, J.; Deng, J. Three-Dimensional Controlled-Source Electromagnetic Forward Modeling by Edge-Based Finite Element with a Divergence Correction. Geophysics 2021, 86, E367–E382. [Google Scholar] [CrossRef]
- Haber, E.; Heldmann, S.; Modersitzki, J. An Octree Method for Parametric Image Registration. SIAM J. Sci. Comput. 2007, 29, 2008–2023. [Google Scholar] [CrossRef]
- Horesh, L.; Haber, E. A Second Order Discretization of Maxwell’s Equations in the Quasi-Static Regime on Octree Grids. SIAM J. Sci. Comput. 2011, 33, 2805–2822. [Google Scholar] [CrossRef]
- Saad, Y.; Schultz, M.H. GMRES: A Generalized Minimal Residual Algorithm for Solving Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
- Calgaro, C.; Chehab, J.-P.; Saad, Y. Incremental Incomplete LU Factorizations with Applications. Numer. Linear Algebra Appl. 2010, 17, 811–837. [Google Scholar] [CrossRef]
- Ren, Z.; Qiu, L.; Tang, J.; Wu, X.; Xiao, X.; Zhou, Z. 3-D Direct Current Resistivity Anisotropic Modelling by Goal-Oriented Adaptive Finite Element Methods. Oxf. Acad. 2018, 212, 76–87. [Google Scholar] [CrossRef]

| NV-RN | KRN | MFEM-1 | MFEM-2 | MFEM-3 | MFEM-4 | MFEM-Bench | |
|---|---|---|---|---|---|---|---|
| Mesh Type | Hexahedron | Tetrahedron | |||||
| Ground NoE (1.0 × 106) | 0.98 | 4.3 | 0.97 | 0.97 | 0.05 | 0.06 | 2.4 |
| Line NoE | 10,598 | 62,222 | 6996 | 61,191 | 117,481 | ||
| Total NoE (1.0 × 106) | 0.98 | 4.3 | 0.98 | 1.04 | 0.06 | 0.12 | 2.52 |
| Run time (s) | 23 | 127 | 666 | 1253 | 640 | 846 | 33,744 |
| Grid Type | Range (X, km) | Depth (Z, m) | CL | Grid Spacing (km) | Grid Number | DoFs | Solving | |
|---|---|---|---|---|---|---|---|---|
| Iter | Time | |||||||
| MR1 | −20.5–20.5 | 0–7 | 1 | 0.09 | 15661877 | 15816485 | 442 | 3 min 56 s |
| −27.5–27.5 | 7–55 | 2 | 1 | 154608 | ||||
| MR2 | −20.5–20.5 | 0–7 | 1 | 0.2 | 1470875 | 1625483 | 354 | 31 s |
| −27.5–27.5 | 7–55 | 2 | 1 | 154608 | ||||
| MR3 | −20.5–20.5 | 0–7 | 1 | 0.33 | 317709 | 472317 | 261 | 14 s |
| −27.5–27.5 | 7–55 | 2 | 1 | 154608 | ||||
| SG1 | −27.5–27.5 | 0–7 | 0.09 | 221445125 | 221445125 | 1654 | 20 h 3 min 29 s | |
| SG2 | −27.5–27.5 | 7–55 | 1 | 1 | 166375 | 166375 | 184 | 3.02 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, L.; Feng, X.; Li, R.; Li, T.; Di, Y.; Hao, T. A Discrete Resistance Network Based on a Multiresolution Grid for 3D Ground-Return Current Forward Modeling. Mathematics 2024, 12, 2392. https://doi.org/10.3390/math12152392
Duan L, Feng X, Li R, Li T, Di Y, Hao T. A Discrete Resistance Network Based on a Multiresolution Grid for 3D Ground-Return Current Forward Modeling. Mathematics. 2024; 12(15):2392. https://doi.org/10.3390/math12152392
Chicago/Turabian StyleDuan, Lijun, Xiao Feng, Ruiheng Li, Tianyang Li, Yi Di, and Tian Hao. 2024. "A Discrete Resistance Network Based on a Multiresolution Grid for 3D Ground-Return Current Forward Modeling" Mathematics 12, no. 15: 2392. https://doi.org/10.3390/math12152392






