Optimizing the Capacity Allocation of the Chinese Hierarchical Healthcare System under Heavy Traffic Conditions
Abstract
:1. Introduction
2. Literature Review
3. Models
3.1. Notations and Assumptions
- Assume parameters are exogenous and .
- Assume the arrival of patients follows a queue.
- Assume parameters are exogenous.
- Assume .
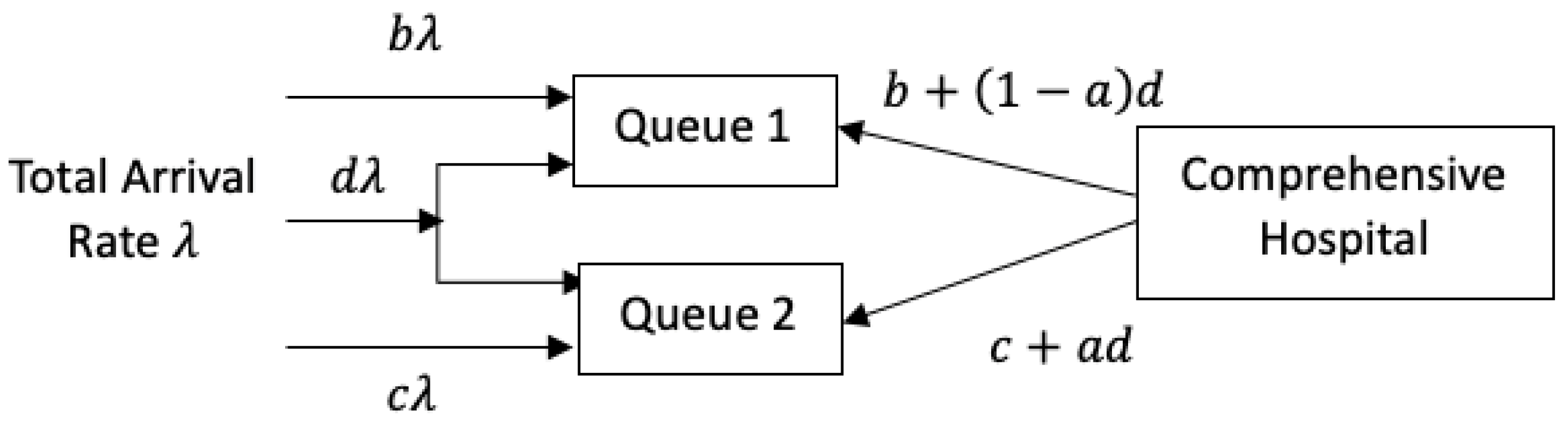
3.2. Model Introduction
3.3. System Analysis
4. Optimization of Approximation Problem
4.1. Arrival Rate Is Equal to Service Rate
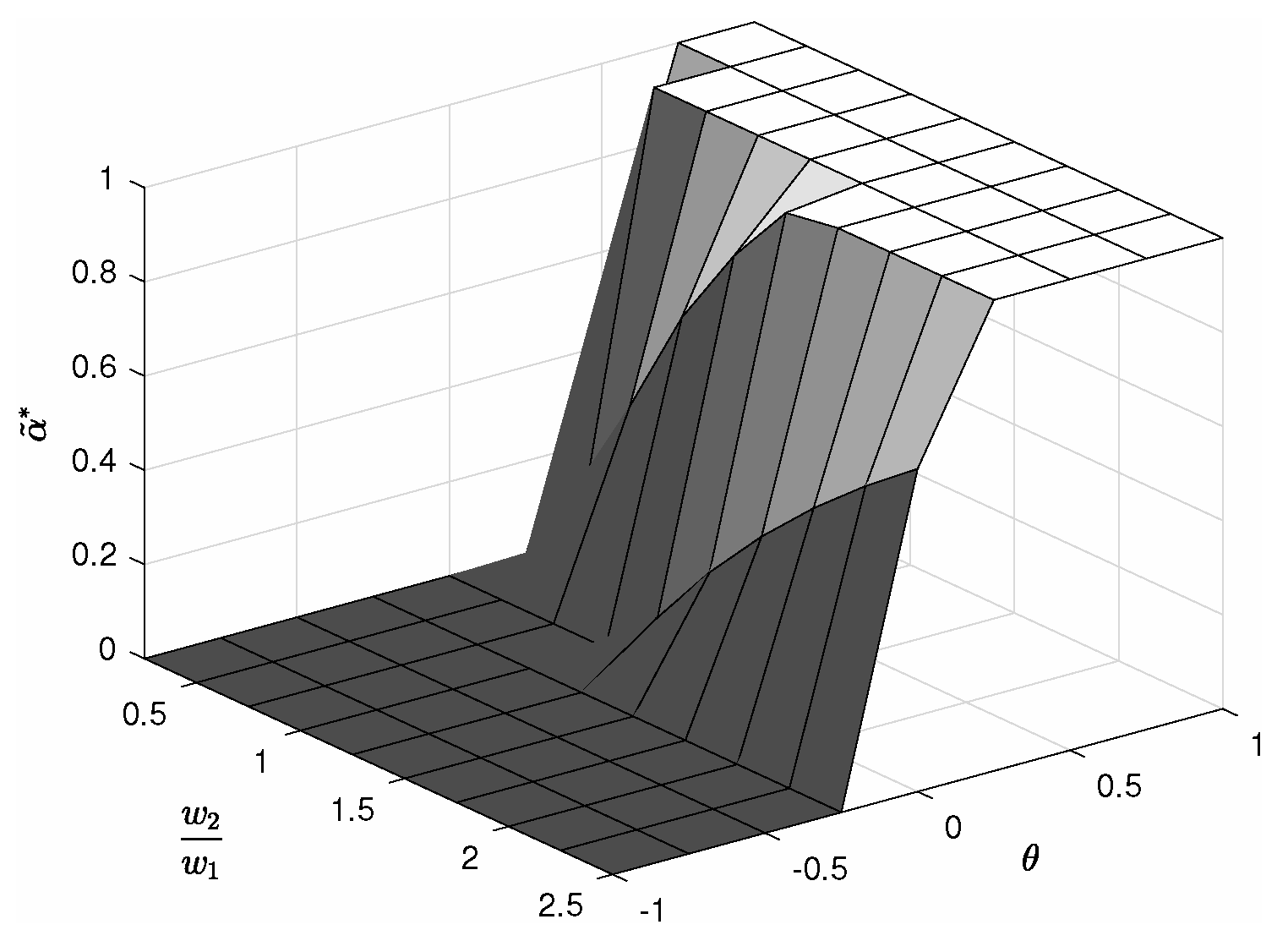
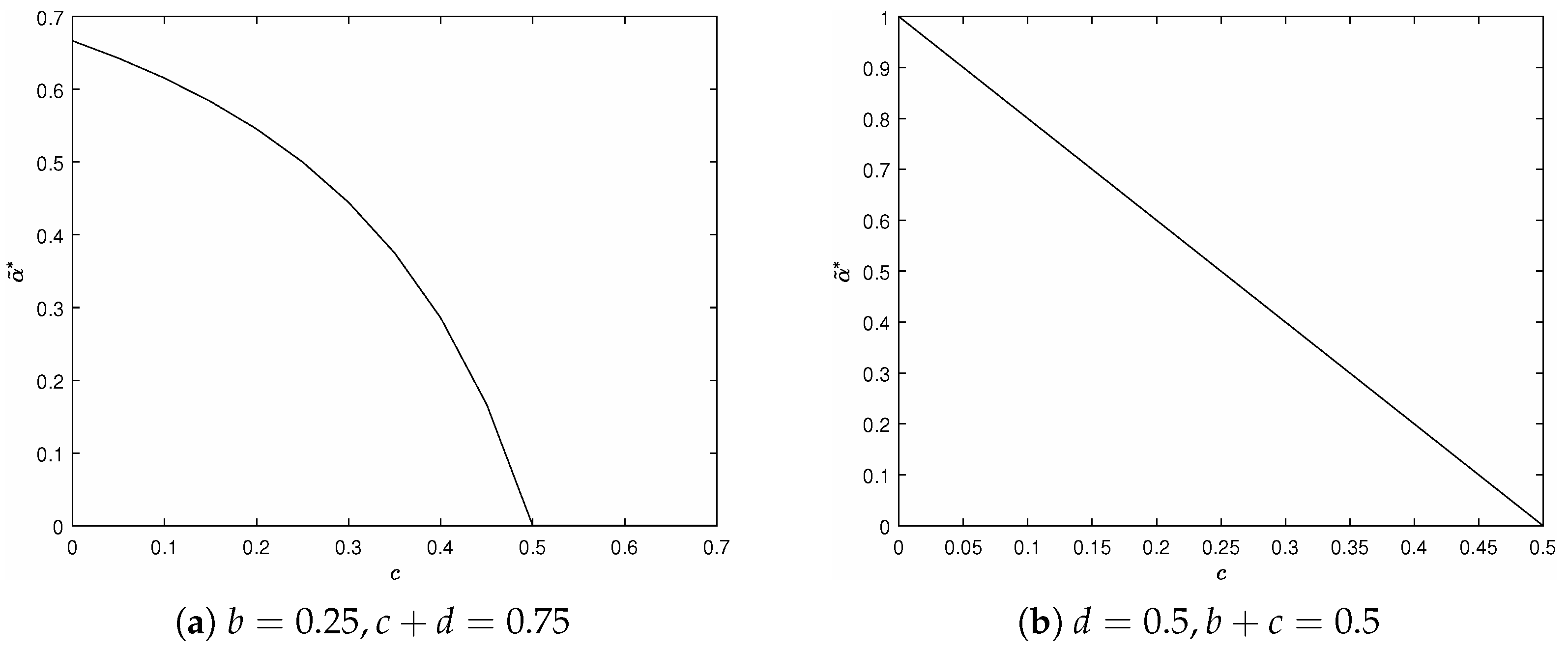
4.2. Arrival Rate Is Not Equal to Service Rate
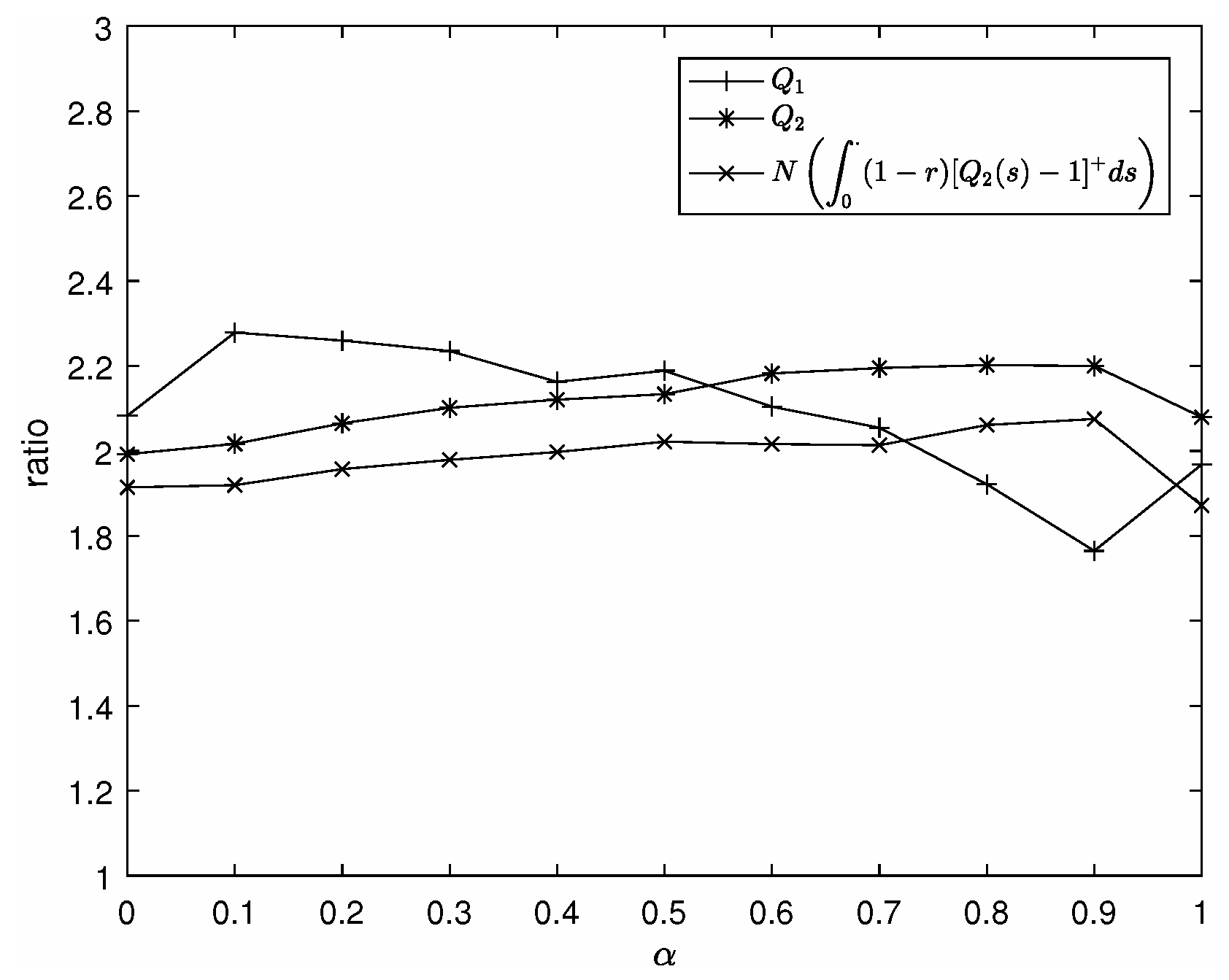
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, Y.; Yu, Y.; She, R.; Huang, W.; Zhao, X. Research on the Development History and Policy Evolution of Hierarchical Medical Care in China. China Hosp. Manag. 2017, 37, 24–27. [Google Scholar]
- Liu, X.; Chen, Y.; Bi, K. Drawing from the UK Healthcare System to Solve the Challenges of Implementing the Two-way Referral System in China. Chin. Gen. Pract. 2013, 16, 2926–2929. [Google Scholar]
- Zhang, W.; Sun, R. A Study on the Graded Diagnosis and Treatment System from the Perspective of Patient Needs. Chin. Gen. Pract. 2017, 20, 1410. [Google Scholar]
- Shumsky, R.A.; Pinker, E.J. Gatekeepers and referrals in services. Manag. Sci. 2003, 49, 839–856. [Google Scholar] [CrossRef]
- Lee, H.H.; Pinker, E.J.; Shumsky, R.A. Outsourcing a two-level service process. Manag. Sci. 2012, 58, 1569–1584. [Google Scholar] [CrossRef]
- Wang, X.; Debo, L.G.; Scheller-Wolf, A.; Smith, S.F. Design and analysis of diagnostic service centers. Manag. Sci. 2010, 56, 1873–1890. [Google Scholar] [CrossRef]
- Ahuja, V.; Staats, B.R. Continuity in gatekeepers: Quantifying the impact of care fragmentation. SMU Cox IT Oper. Manag. (Topic) 2018. [Google Scholar] [CrossRef]
- Lv, J. Improving the Graded Diagnosis and Treatment System in the Process of Deepening Healthcare Reform in China. China Hosp. Manag. 2014, 34, 1–3. [Google Scholar]
- Yang, J.; Xie, T.; Jin, J.; Feng, Z.; Zhang, L. An Analysis of Graded Diagnosis and Treatment Policies in Various Provinces of China. Chin. Health Econ. 2016, 35, 14–17. [Google Scholar]
- Reiman, M.I. Some diffusion approximations with state space collapse. In Modelling and Performance Evaluation Methodology; Springer: Berlin/Heidelberg, Germany, 1984; pp. 207–240. [Google Scholar]
- Kostami, V.; Ward, A.R. Managing service systems with an offline waiting option and customer abandonment. Manuf. Serv. Oper. Manag. 2009, 11, 644–656. [Google Scholar] [CrossRef]
- Gallay, O.; Hongler, M.O. Market sharing dynamics between two service providers. Eur. J. Oper. Res. 2008, 190, 241–254. [Google Scholar] [CrossRef]
- Anderson, R.M. Stochastic Models and Data Driven Simulations for Healthcare Operations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Bittencourt, O.; Verter, V.; Yalovsky, M. Hospital capacity management based on the queueing theory. Int. J. Product. Perform. Manag. 2018, 67, 224–238. [Google Scholar] [CrossRef]
- Saini, B.; Sharma, K.C. Application of queuing theory for improved efficiency in healthcare systems. Int. J. Eng. Sci. Math. 2022, 11, 110–121. [Google Scholar]
- Peter, P.O.; Sivasamy, R. Queueing theory techniques and its real applications to health care systems—Outpatient visits. Int. J. Healthc. Manag. 2021, 14, 114–122. [Google Scholar] [CrossRef]
- Yaduvanshi, D.; Sharma, A.; More, P. Application of queuing theory to optimize waiting-time in hospital operations. Oper. Supply Chain Manag. Int. J. 2019, 12, 165–174. [Google Scholar] [CrossRef]
- Amalia, P.; Cahyati, N. Queue analysis of public healthcare system to reduce waiting time using flexsim 6.0. Int. J. Ind. Optim. 2020, 1, 101. [Google Scholar] [CrossRef]
- Aziati, A.N.; Hamdan, N.S.B. Application of queuing theory model and simulation to patient flow at the outpatient department. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Bandung, Indonesia, 6–8 March 2018; pp. 3016–3028. [Google Scholar]
- Browne, S.; Whitt, W.; Dshalalow, J. Piecewise-linear diffusion processes. Adv. Queueing Theory Methods Open Probl. 1995, 4, 463–480. [Google Scholar]
- Zuo, M.; Gong, D.; Wang, Y.; Ye, X.; Zeng, B.; Meng, F. Process knowledge-guided autonomous evolutionary optimization for constrained multiobjective problems. IEEE Trans. Evol. Comput. 2023, 28, 193–207. [Google Scholar] [CrossRef]



| Notation | Meaning |
|---|---|
| arrival rate of all the patients | |
| service rate of comprehensive hospitals | |
| parameter such that | |
| b | proportion of service capacity allocated to Queue 1 |
| c | proportion of service capacity allocated allocated to Queue 2 |
| a | proportion of the remaining service capacity allocated to community center |
| d | proportion of remaining service |
| length of queue 1 | |
| length of queue 2 | |
| t | time |
| r | proportion of patients in Queue 2 that are referred to comprehensive hospitals |
| waiting time cost for third type of patients in Queue 1 | |
| waiting time cost for third type of patients in Queue 2 | |
| holding cost for patients waiting in Queue 1 | |
| holding cost for patients waiting in Queue 2 | |
| p | revenue generated from each patient cured by the community health center |
| waiting time estimates for Queue 1 provided by the service system | |
| waiting time estimates for Queue 2 provided by the service system | |
| C | total cost |
| Method | Advantages | Disadvantages |
|---|---|---|
| This Paper |
|
|
| Existing Methods (General Healthcare System Modeling) |
|
|
| Simulated Cost | Approx. Cost | Cost Error (%) | Simulated Queue Length Q | Approx. Queue Length | Approx. Queue Length Error | |
|---|---|---|---|---|---|---|
| 0 | ||||||
| (%) | Approximated Minimum Cost | Simulated Minimum Cost | Error (%) | ||
|---|---|---|---|---|---|
| 100 | 0 | ||||
| 101 | 1 | ||||
| 102 | 2 | ||||
| 103 | 3 | ||||
| 104 | 4 | ||||
| 105 | 5 | ||||
| 106 | 6 | ||||
| 107 | 7 | ||||
| 108 | 8 | ||||
| 109 | 9 | ||||
| 110 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Han, K.; Wu, H.; Shi, Y.; Liu, C. Optimizing the Capacity Allocation of the Chinese Hierarchical Healthcare System under Heavy Traffic Conditions. Mathematics 2024, 12, 2399. https://doi.org/10.3390/math12152399
Wu L, Han K, Wu H, Shi Y, Liu C. Optimizing the Capacity Allocation of the Chinese Hierarchical Healthcare System under Heavy Traffic Conditions. Mathematics. 2024; 12(15):2399. https://doi.org/10.3390/math12152399
Chicago/Turabian StyleWu, Linjia, Kevin Han, Han Wu, Yu Shi, and Canyao Liu. 2024. "Optimizing the Capacity Allocation of the Chinese Hierarchical Healthcare System under Heavy Traffic Conditions" Mathematics 12, no. 15: 2399. https://doi.org/10.3390/math12152399





