Abstract
In the article, we propose a combination method based on the multigrid method and constraint data to solve the inverse problem in the context of the nonlinear convection–diffusion equation in the multiphase porous media flow. The inverse problem consists of a data-fitting term involving the discretization of a direct problem, a constraint term concerning the incorporation of constraint data, and a regularization term dealing with the improvement of stability. A multigrid method, which is specialized for large-scale problems and works by keeping the consistence of objective functionals between different grids, is applied in the process of inversion. Based on the numerical results, the proposed combination method has the advantages of fast calculation, high precision, good stability, and strong anti-noise ability in computation. It obtains good performance under various noise levels, as well as outperforming any one method used alone.
Keywords:
nonlinear convection–diffusion equation; inversion; multigrid; constraint data; porous media flow MSC:
35R30; 65M32; 65M55; 60J60; 76S05
1. Introduction
Convection–diffusion equations (CDEs), as a type of partial differential equation, are ubiquitous in applications in physics and chemistry as models for flow problems [1,2,3], or heat and mass transfer [4,5], and have received considerable attention over the past decades. Espedal and Karlsen [6] provided the saturation equation in the fractional flow formulation of the multiphase porous media flow equations, which served as the origin of the inverse problem of the nonlinear CDE. The nonlinear CDE inverse problem has exhibited substantial potential in reservoir simulation [7] and plays a significant role in geologic mapping [8], and oil and gas exploration [9].
Among earlier works on inverse problems of CDE, a multitude of approaches were utilized [10,11,12,13]. While tremendous accomplishments have been made, the inversion remains to be an arduous and intricate process due to the substantial investment of time and computational resources, hence hindering its employment. Such problems can be tackled by conventional inversion techniques such as the gradient, Gauss–Newton, and full Newton methods [14,15,16]. Nevertheless, there are a few challenges associated with these methods. For instance, the computation efficiencies of these approaches are reduced as the number of parameters requiring estimation increases, leading to additional search space. Furthermore, numerous scholars have directed their efforts towards exploring the potential of artificial intelligence algorithms, including but certainly not limited to deep learning [17,18,19] and dictionary learning [20,21,22]. Consequently, due to the limitations of the aforementioned inversion techniques, a nonlinear multigrid method is developed.
The multigrid method is one of the most precise and efficient approaches that has proven to be effective in addressing direct problems as documented in references [23,24,25,26]. In addressing inverse problems, this method demonstrates an impressive capability to drastically reduce the dimensions of objective functionals and to prevent getting trapped in the local minima by way of ensuring the consistency between the objective functionals on coarse and fine grids [27,28]. Al-Mahdawi et al. [29,30] proposed the V-cycle multigrid method and parallel multigrid method for the inverse problems for the boundary value and initial value in a heat equation. Xie et al. [31] solved the non-self-adjoint Steklov eigenvalue problems in inverse scattering based on a kind of full multigrid method. Zhang et al. [32] showcased the advantages of the multigrid method in the total variation minimization problems, demonstrating its efficacy on medium- and large-scale image denoising and reconstruction problems. Furthermore, multigrid methods have attained remarkable progress in the context of tomography problems [33,34,35,36]. Likewise, this method has found considerable utility in problems related to parameter inversion [37,38,39].
When compared with the utilization of solely surface-recorded data pertaining to an examined entity, parameter inversion that incorporates constraint data, possibly provides a method to obtain reliable inversion results, resulting in less noise and a greater quality of inversion. Numerous fields, such as tectonophysics [40], geophysics [41,42], oceanography [43], and atmospheric research [44], have implemented parameter inversion with constraints. For instance, Fournier et al. [45] applied the constraints from well-log data to solve a seismoelectric inverse problem and displayed how inversion is improved when using constraints. Wisén and Christiansen [46] studied laterally and mutually constrained inversion techniques, and demonstrated that the constrained inversion methods can improve the model resolution greatly.
In this paper, we focus on the combination of multigrid method and constraint data for solving the inverse problem of the nonlinear CDE in the multiphase porous media flow. First, we use an upwind difference numerical scheme to discretize the direct problem at different grids. Second, we formulate the inverse problem as an optimization problem, which consists of three terms: a data-fitting term involving the discretization of the direct problem, a constraint term concerning the incorporation of constraint data, and a regularization term dealing with the improvement in stability. Third, a V-cycle multigrid method is proposed to solve the resulted optimization problem. Finally, the efficiency and accuracy of the proposed multigrid method are illustrated by some numerical examples.
The remaining part of the paper is organized as follows. In next section, we display the nonlinear CDE in the multiphase porous media flow and introduce the upwind difference scheme. Section 3 states the nonlinear CDE inverse problem. In Section 4, we derive the multigrid method, utilized together with constraint data. In Section 5, some numerical examples are presented to validate the superiority of the proposed strategy. Finally, the paper ends with some concluding remarks in Section 6.
2. Direct Problem
2.1. Nonlinear Convection–Diffusion Equation
In this part, we firstly introduce a set of partial differential equations, modeling the immiscible displacement of oil by water in a porous medium under no gravity condition, which can be described as [6]:
where and D are, respectively, the nonlinear S-shaped fractional flow and diffusion functions, and the specific parameter definitions are as follows:
- —porosity;
- —permeability;
- —height;
- —global pressure;
- —total Darcy velocity;
- —total mobility of the phases;
- —phase mobility of the nonwetting phase;
- —density of the wetting phase;
- —density of the nonwetting phase;
- —production well;
- —injection well.
Then, with the above set-up, we will lead to the nonlinear CDE to be considered by adding some constraints. In Equation (1), if the coefficient of time derivative term and the convection term have no varying coefficient and no permeability dependence, then Equation (1) ends up as:
which is the nonlinear CDE in the multiphase porous media flow, and subjected to the following initial-boundary conditions
where and are the nonlinear S-shaped Buckley–Leverett flux functions, and D is the nonlinear diffusion function.
2.2. Upwind Difference Scheme
The upwind difference scheme is a stable scheme which does not introduce unphysical numerical oscillations. To facilitate the presentation, the computational domain is assumed to be unit square and discretized as a difference grid with the steps in the direction x, in the direction y, and in the direction t, where , , and are respectively the number of space and time steps. The numerical approximation of the solution is denoted by
where , , and . By applying the Engquist–Osher upwind difference scheme [47] to Equation (5), we have
where the discrete expressions of the convection term and diffusion term have been described in [48].
Solving the difference Equation (8), combining with the discrete initial-boundary conditions and for , the concentration field can be numerically determined from the given permeability , which is the direct problem for the nonlinear CDE.
3. Inverse Problem Formulation
After describing the direct problem, this section presents the inverse problem for the nonlinear CDE in the multiphase porous media flow and related constraint data. The setting of the inverse problem is stated as follows: the permeability coefficient is regarded as being unknown, while everything else in Equations (5)–(7) is known. In addition, the measurement data of concentration taken at some fixed points (such as ) are considered available. The objective of the inverse problem is to predict the unknown space-dependent permeability coefficient from the knowledge of the available measurement data.
In order to develop expressions for the determination of the permeability coefficient , we firstly reformulate Equation (8) into a nonlinear operator equation
where
Let the measurement data at position and time be denoted by , then the solution of the present inverse problem is to be obtained in such a way that the following functional is minimized:
where
Let
where is the permeability from the well logs of a well located at point in x, , and used as the constraint data. Let denote an admissible set, then the inverse problem combined with constraint data can be written as
Assume
and
Obviously,
With the combination of the constraint and objective functional, we can obtain a minimization problem under no constraints:
where represents the constraint parameter, which plays a role in managing the strengths of constraint. In the inversion procedure, designing to be large enough is of great concern in making sure that the solution of Equation (12) is in the near vicinity of that of Equation (11).
Due to the ill-posedness of the inverse problem, Equation (12) is regularized by
where is the regularization term which serves to incorporate mathematical or physical information to arrive at a better inversion result, and is the regularization parameter. For solving Equation (13), we can use the iterative method similar to the regularized Gauss–Newton method
4. Inversion Method
In the context of multigrid, the problem is discretized on a sequence of grids with increasing grid sizes rather than on a single grid. From this point, we need to build a sequence of discretization grids. Starting from the finest discretization grid with the grid size , is generated from by multiplying the grid size of by . This results in a grid sequence
where the symbol ⊂ stands for the nesting of grids. Then, on grid , we discretize the direct problem and obtain the corresponding objective functional of inverse problem:
whose dimension and local minima are fewer, thus substantially improving the calculation speed and preventing being trapped in local minima.
Next, two main operators of multigrid are introduced. The first is the smoothing operator (also named ‘smoother’) which is aimed at updating the solution on a fixed grid and is defined as
where is the iterative method Equation (14), and and are respectively the initial guess and objective functional of . The second is grid transfer operators, which consist of two operators: restriction and prolongation operators. The restriction operator
can transfer information from a fine grid to a coarse grid. Inversely, the transmission from a coarse grid to a fine grid needs to use the prolongation operator
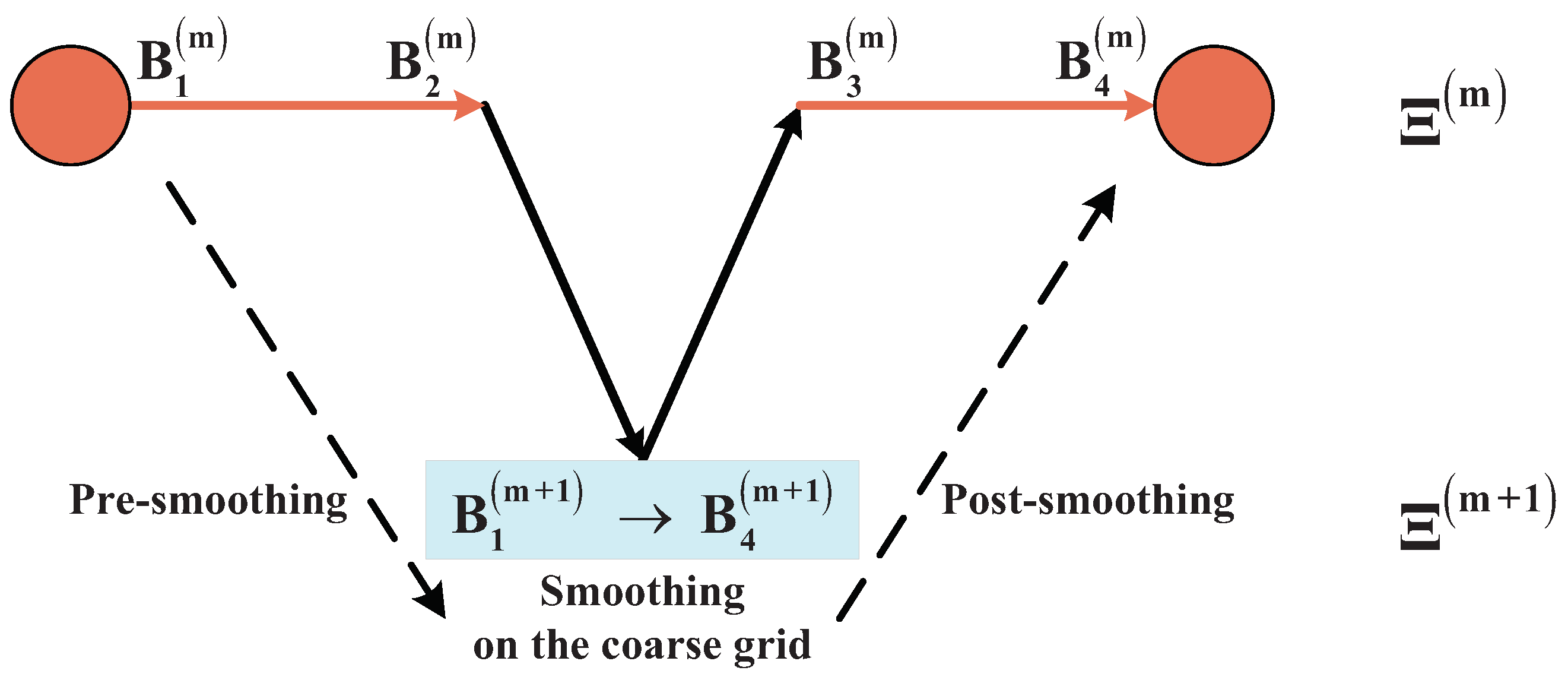
Finally, we demonstrate the three procedures of the multigrid method: the pre-smoothing, smoothing on the coarse grid, and post-smoothing. Take the simple two-grid method for example. In the pre-smoothing step, the method first applies a smoother to the initial approximation on the fine grid, and then the resulting solution is restricted to the coarse grid. In the smoothing on the coarse grid step, a smoother is applied on the coarse grid. In the post-smoothing step, the change on the coarse grid is prolongated to the fine grid, and a smoother is applied one more time. The entire process is described in Figure 1 and Algorithm 1.
| Algorithm 1: Two-grid method. |
|
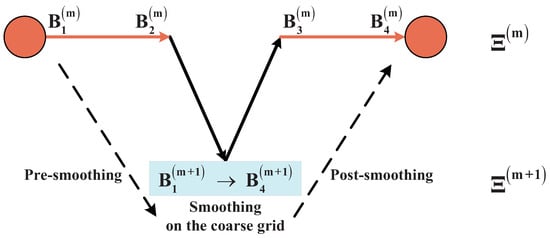
Figure 1.
Two-grid method. , are respectively the initial approximation and resulting solution in the pre-smoothing step, , are respectively the corrected approximation and resulting solution in the post-smoothing step. , are respectively the values before and after applying the smoother on the coarse grid.
In the multigrid method, it is ideal that after smoothing on a coarse grid, the solution is more exact than , but it is not always tenable because of the potential inconsistence between the objective functionals. Hence, with the aim of the monotonic convergence of the multigrid method, some supplementary conditions should necessarily be enforced.
First of all, a correction term is attached to the objective functionals to adapt the gradients:
Here, is a row vector with initial value , having .
Then, let the data-fitting terms between adjacent grids be equal:
which gives
Next, like the data-fitting term, the same operation is applied to the constraint and regularization terms:
which arrives at
Finally, let objective functional gradients between adjacent grids be equal:
which leads to
Under all of the above conditions, the monotonic convergence of the multigrid method can be assured [27].
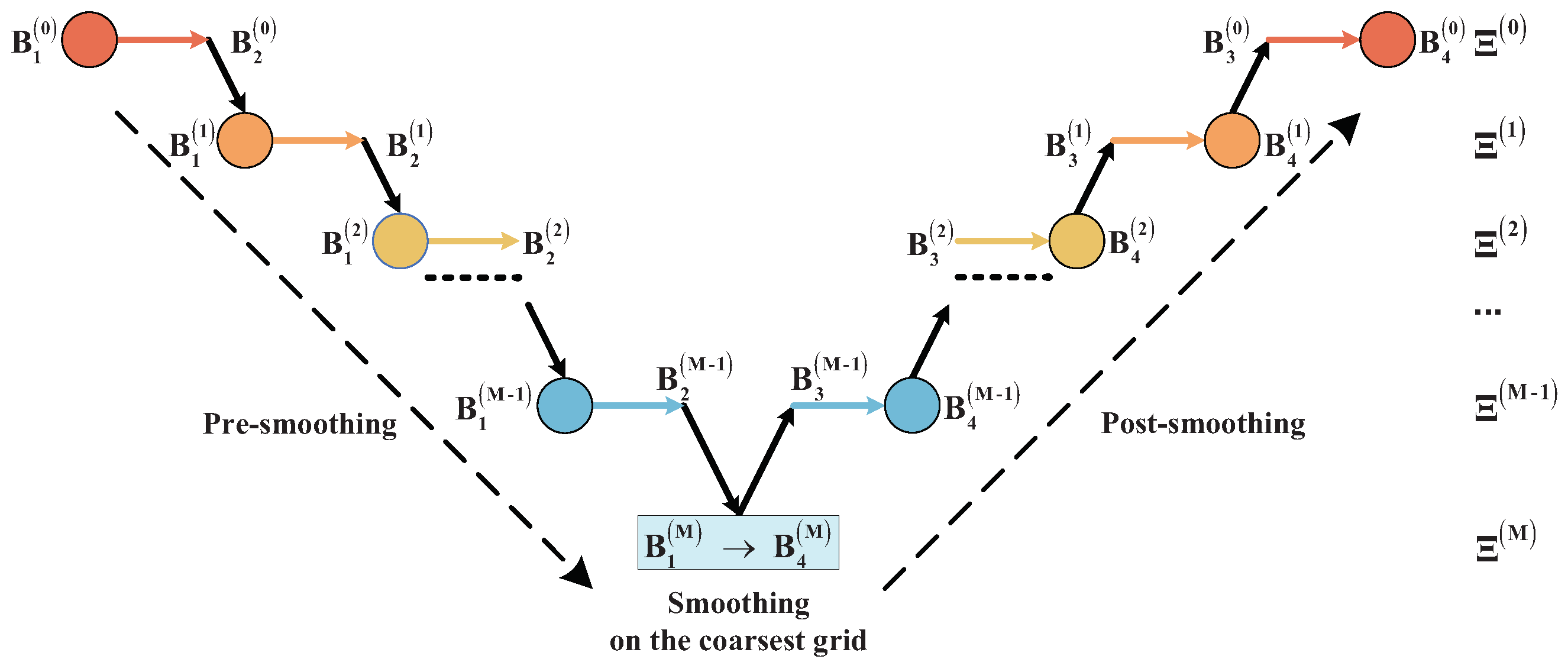
By recursively substituting another two-grid method for the smoother on the coarse grid of the two-grid method and enforcing the above conditions, we can easily obtain the fast and convergent V-cycle multigrid method (see Figure 2 and Algorithm 2).
| Algorithm 2: Multigrid method. |
|
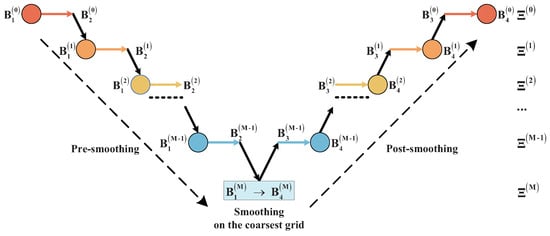
Figure 2.
Multigrid method.
5. Numerical Examples
To validate the proposed inversion method, we use two permeability models (Figure 3 and Figure 6). These two models are compared with the traditional fixed grid iterative method with constraint data and the multigrid method without constraint data, which allows us to assess the computational performance of multigrid and necessity of the introduction of constraint data. The necessary parameters in the inversion process are taken as
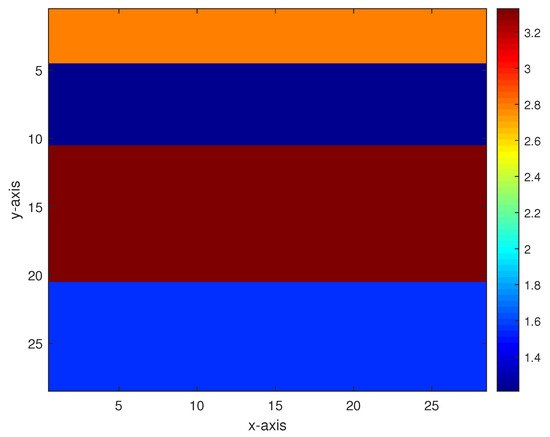
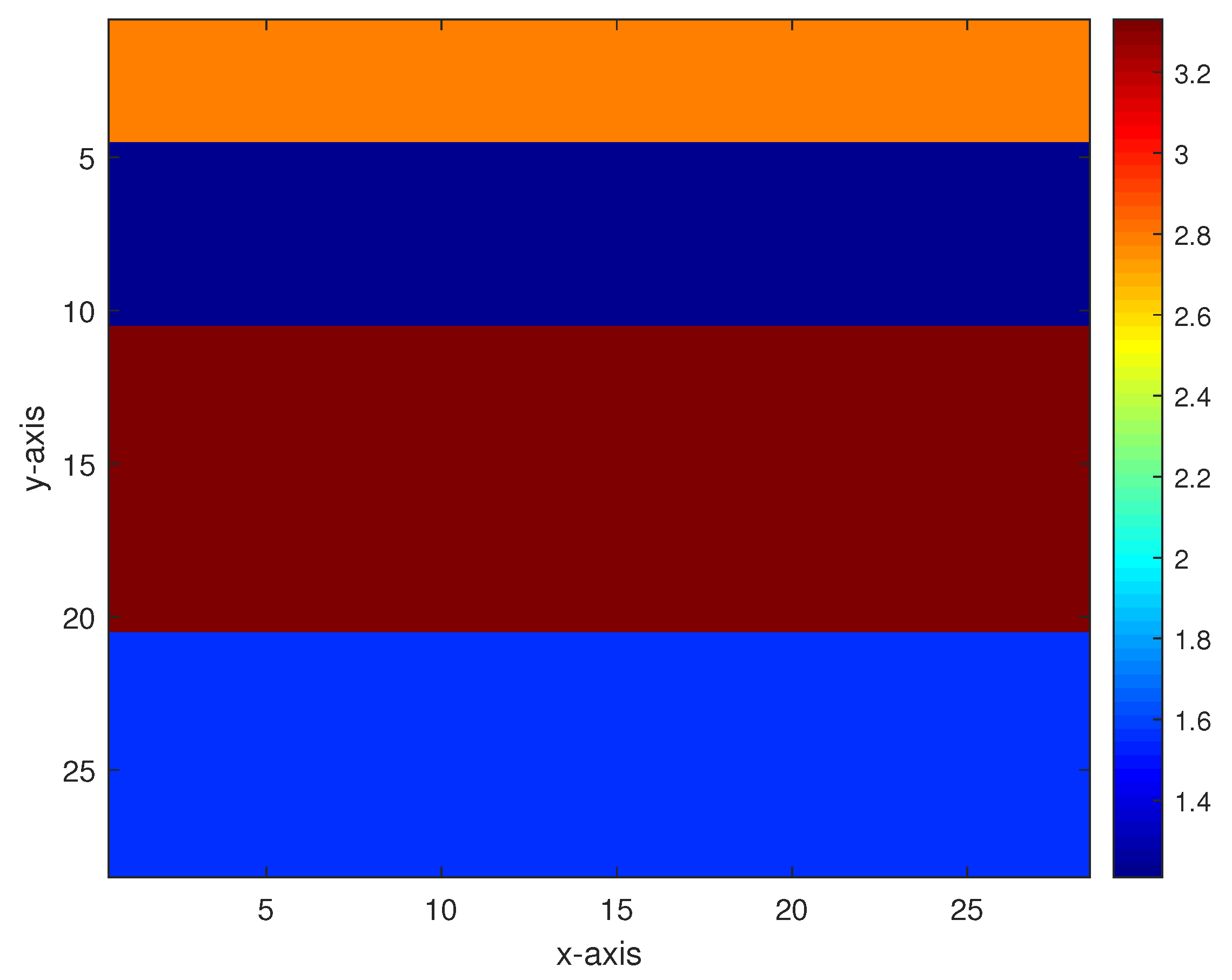
Figure 3.
A level-stratified permeability model.
Under the above parameter settings, the dimensions of the permeability and measurement data vectors and are respectively and .
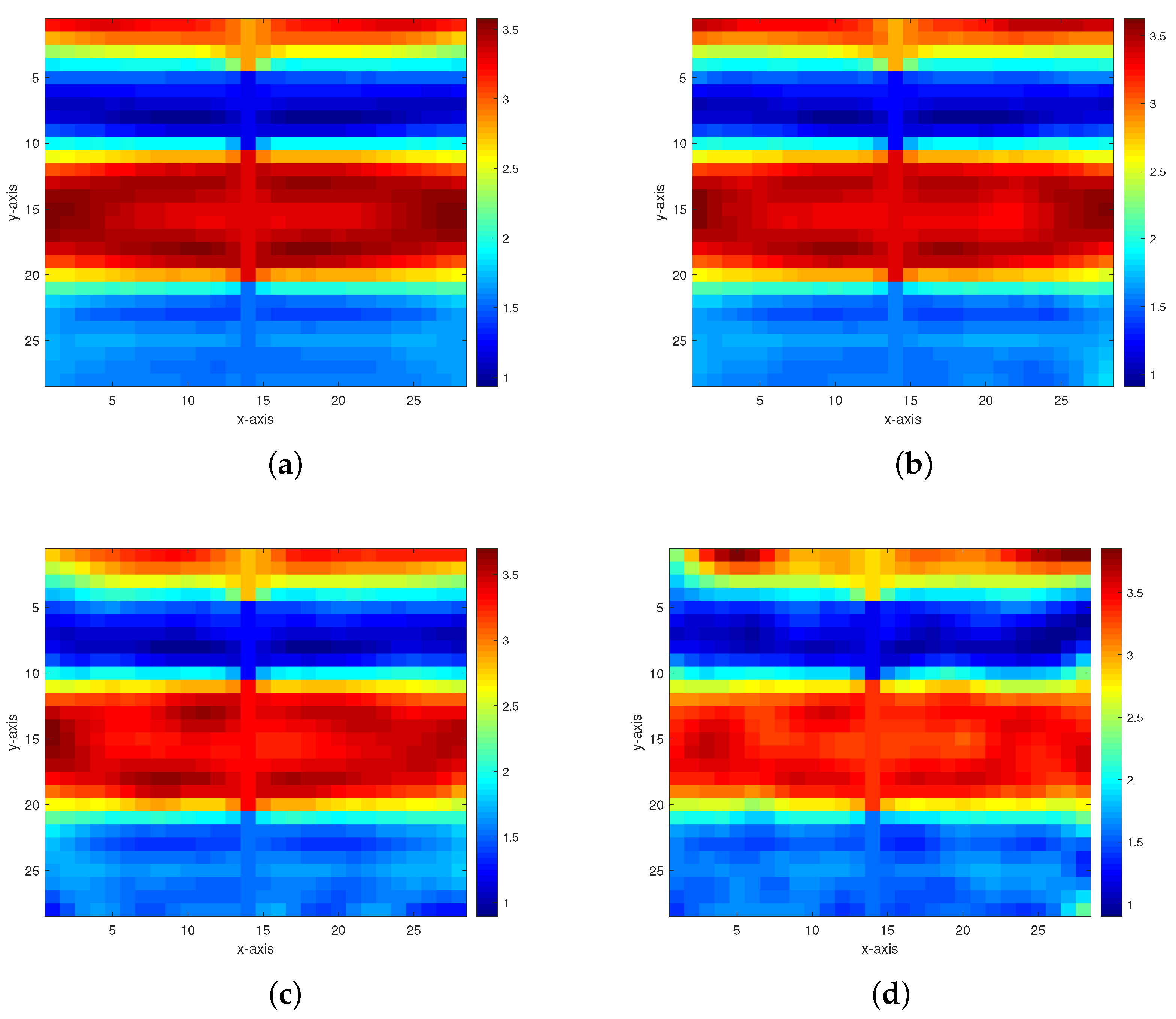
- Model 1. The first model is a level-stratified permeability model comprising three interfaces, and the permeability values from bottom to top are 1.55, 3.33, 1.21, and 2.80 as shown in Figure 3. For the addition of 40 dB, 30 dB, 20 dB, and 10 dB Gaussian noises (which are generated by the function AWGN in MATLAB) to the measurement data, the inversion results of the multigrid method with constraint data and the multigrid method without constraint data are respectively displayed in Figure 4 and Figure 5.
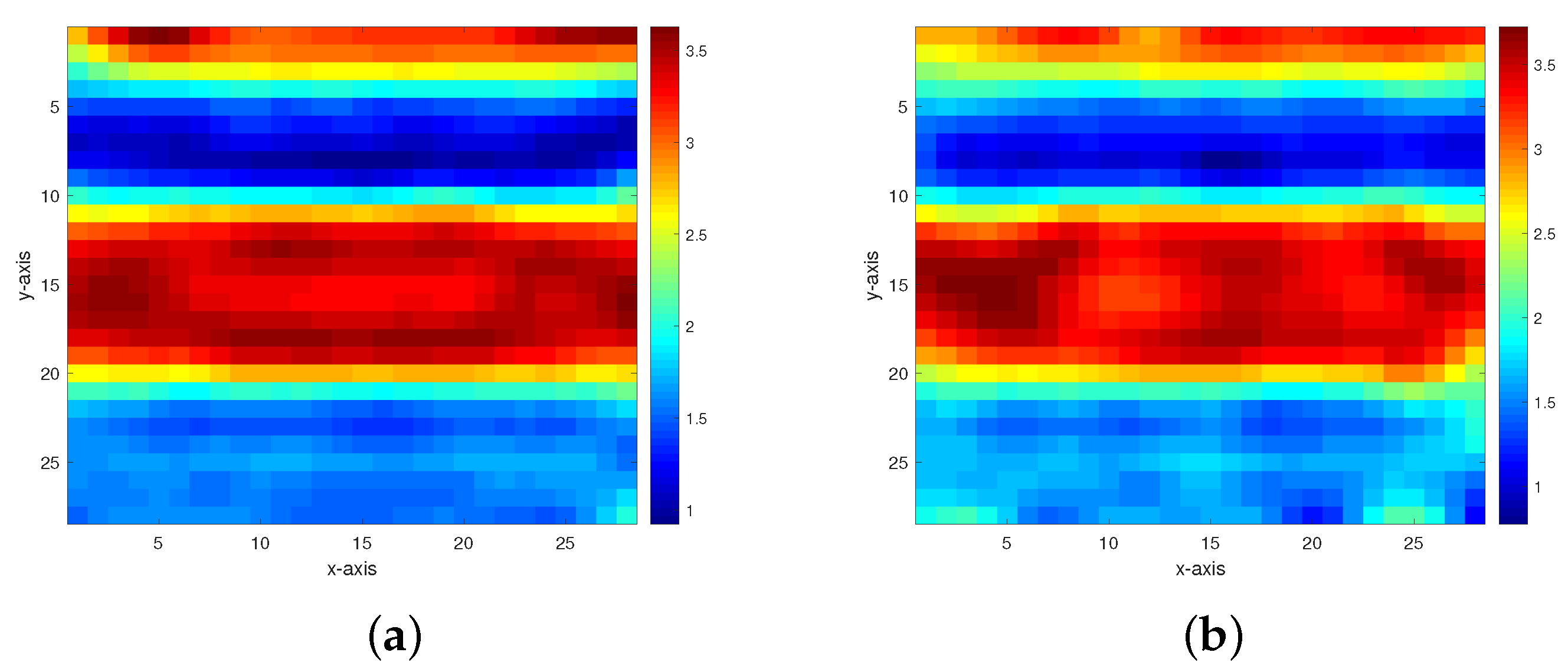
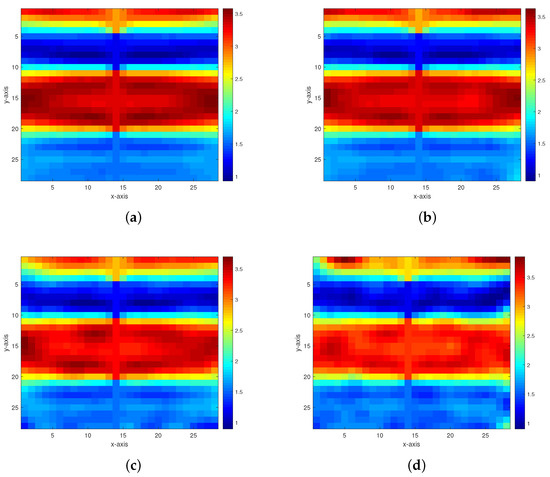 Figure 4. Inversion results of the permeability model in Figure 3 from the multigrid method with constraint data. (a–d) The respective inversion results with 40 dB, 30 dB, 20 dB, and 10 dB Gaussian noises added.
Figure 4. Inversion results of the permeability model in Figure 3 from the multigrid method with constraint data. (a–d) The respective inversion results with 40 dB, 30 dB, 20 dB, and 10 dB Gaussian noises added.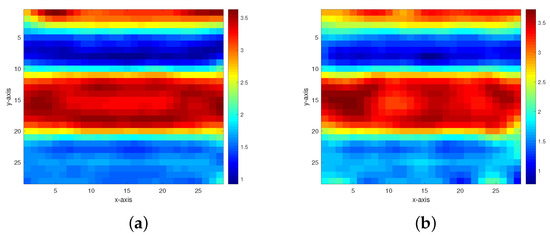 Figure 5. Inversion results of the permeability model in Figure 3 from the multigrid method without constraint data. (a,b) The respective inversion results with 40 dB and 30 dB Gaussian noises added.
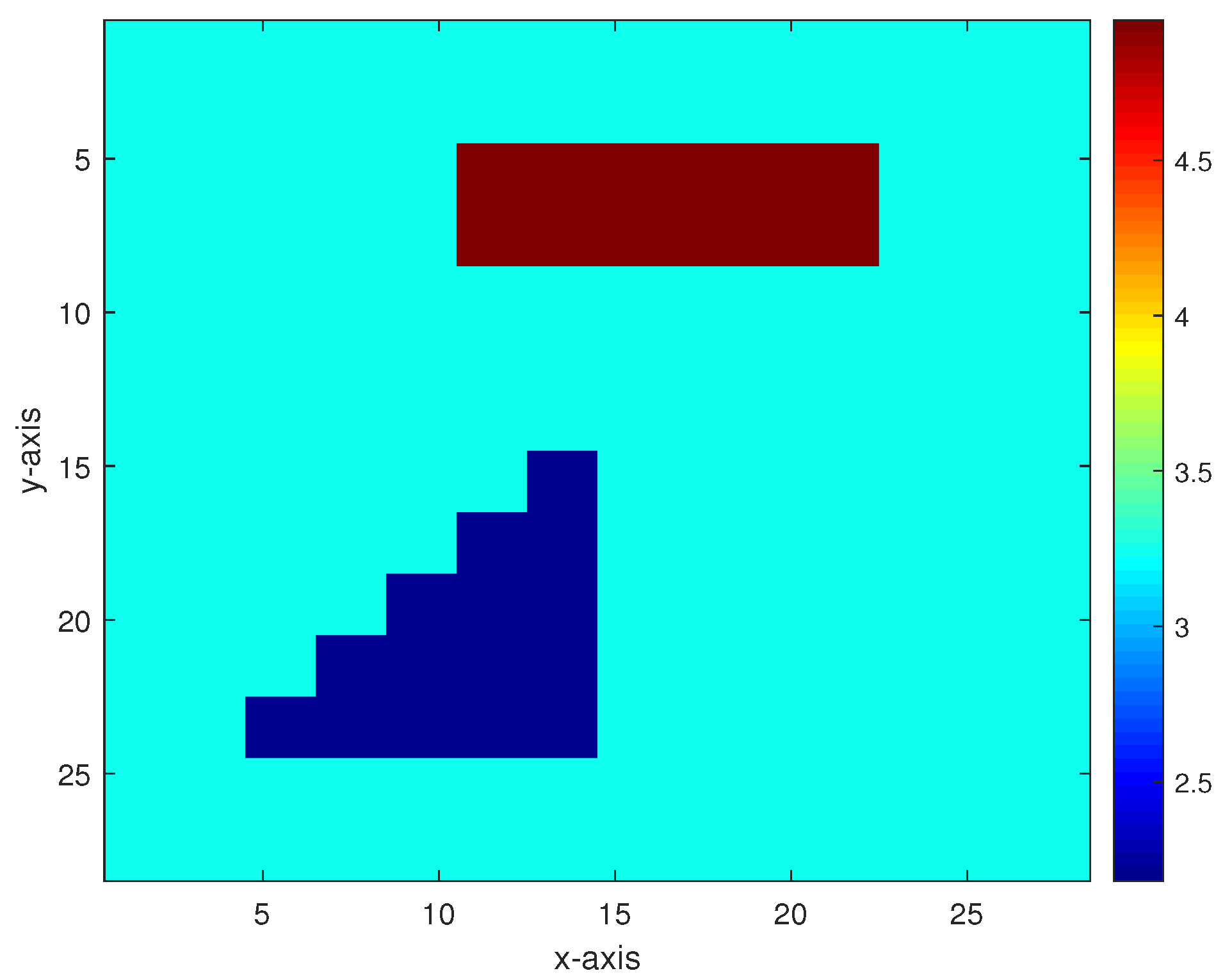
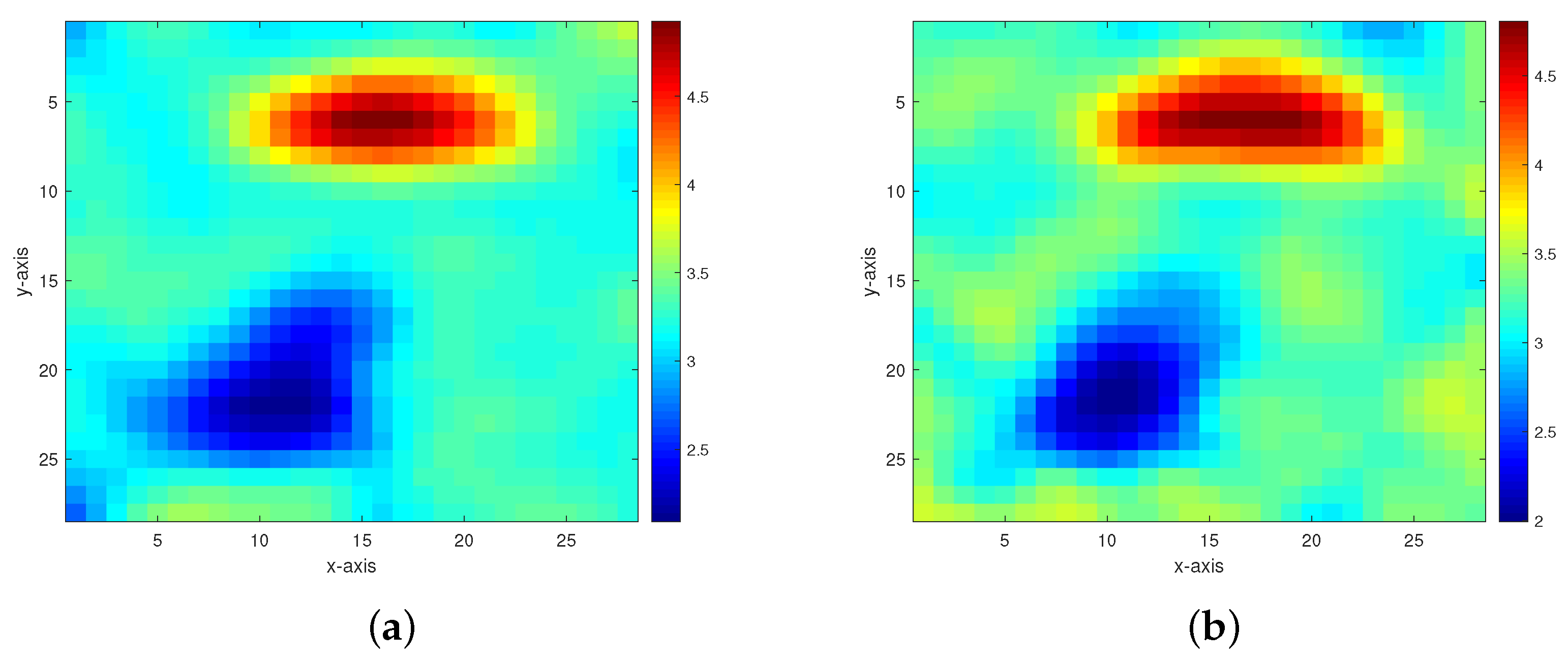
Figure 5. Inversion results of the permeability model in Figure 3 from the multigrid method without constraint data. (a,b) The respective inversion results with 40 dB and 30 dB Gaussian noises added. - Model 2. The second model as shown in Figure 6 is composed of two anomalous bodies embedded into a homogeneous background. The background permeability value is 3.25. The permeability values of the two anomalous bodies are 4.95 and 2.18. Figure 7 and Figure 8 respectively display the inversion results of the multigrid method with constraint data and the multigrid method without constraint data, with 40 dB, 30 dB, 20 dB, and 10 dB Gaussian noises added.
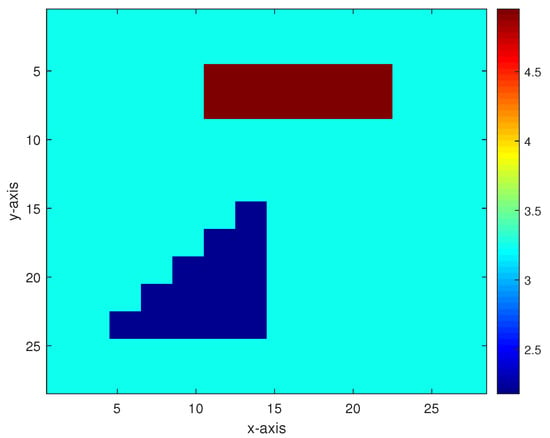 Figure 6. A permeability model containing two anomalous bodies.
Figure 6. A permeability model containing two anomalous bodies.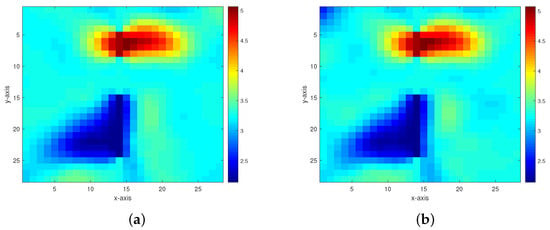
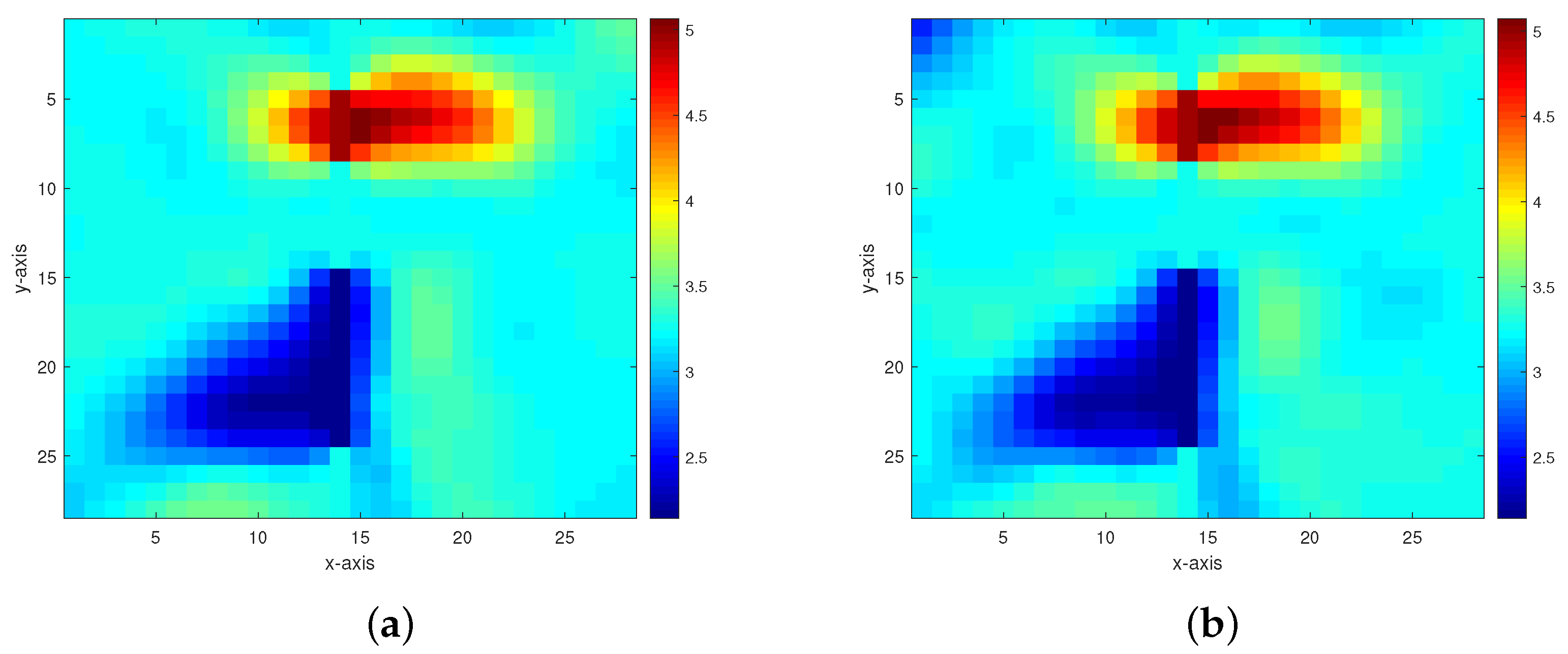
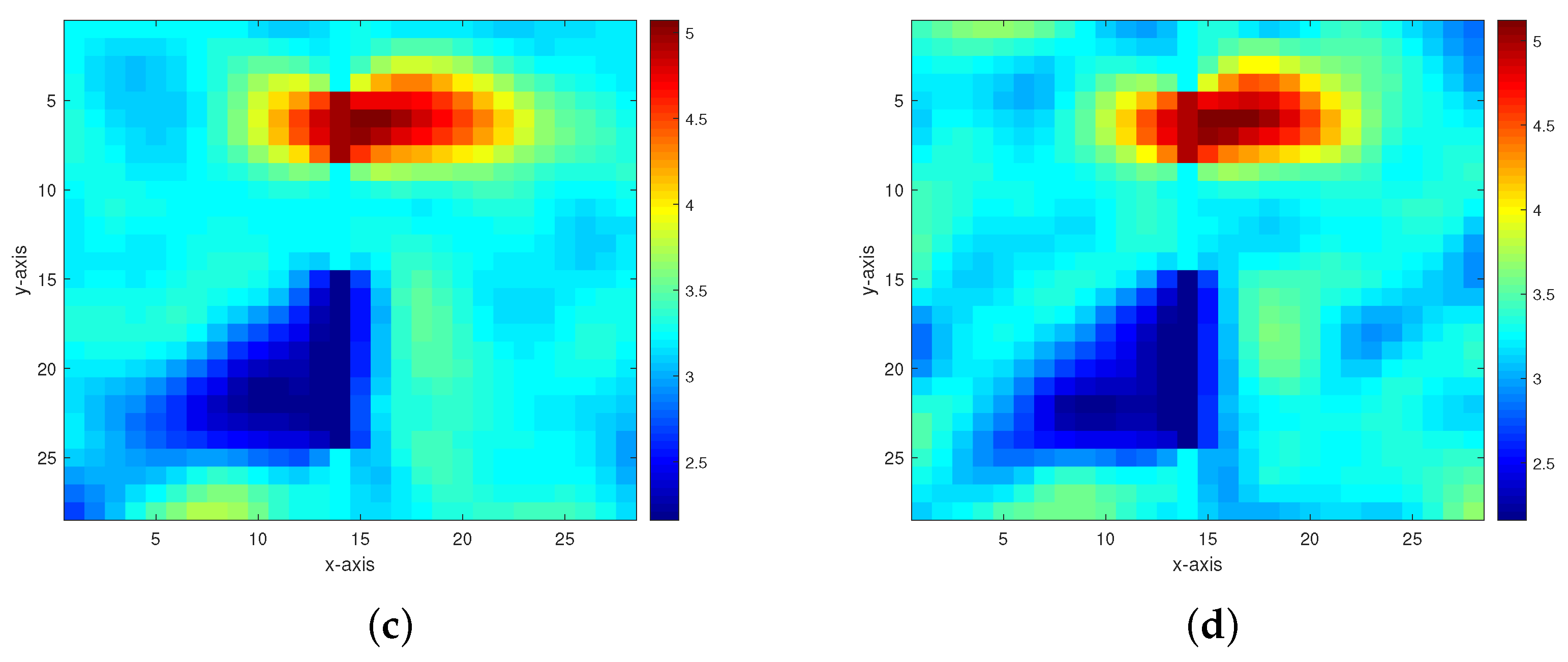
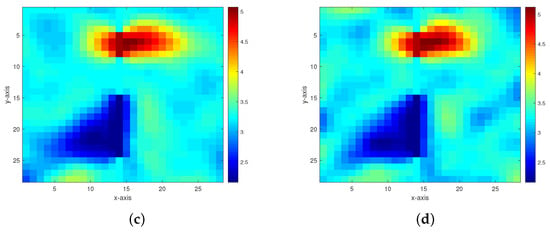 Figure 7. Inversion results of the permeability model in Figure 6 from the multigrid method with constraint data. (a–d) The respective inversion results with 40 dB, 30 dB, 20 dB, and 10 dB Gaussian noises added.
Figure 7. Inversion results of the permeability model in Figure 6 from the multigrid method with constraint data. (a–d) The respective inversion results with 40 dB, 30 dB, 20 dB, and 10 dB Gaussian noises added.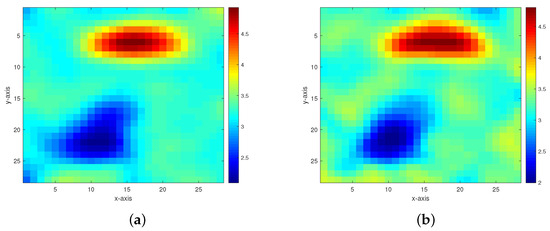 Figure 8. Inversion results of the permeability model in Figure 6 from the multigrid method without constraint data. (a,b) The respective inversion results with 40 dB and 30 dB Gaussian noises added.
Figure 8. Inversion results of the permeability model in Figure 6 from the multigrid method without constraint data. (a,b) The respective inversion results with 40 dB and 30 dB Gaussian noises added.
We give and compare the CPU times and relative errors between three different methods, the multigrid method with constraint data, the fixed grid iterative method with constraint data, and the multigrid method without constraint data as presented in Table 1 and Table 2. From Table 1, we can calculate that the average CPU times of the above three methods are respectively 330.1592 s, 628.2748 s, and 388.6597 s in Model 1, and 238.1196 s, 442.5765 s, and 287.4428 s in Model 2. The multigrid method with constraint data is evidently superior compared to the other two methods. In particular, it is noted that the CPU times of the fixed grid iterative method with constraint data are nearly twice as much as those of the other two multigrid schemes, suggesting that the use of multigrid can effectively accelerate the computational speed. The fixed grid iterative method with constraint data misses the global minimum for 10 dB Gaussian noise; the multigrid method without constraint data misses the global minimum for 20 dB and 10 dB Gaussian noises. Accordingly, it is concluded that our proposed method can effectively avoid local minima.

Table 1.
CPU times (seconds) of inversion results from three different methods.

Table 2.
Relative errors of inversion results from three different methods.
Table 2 shows that the multigrid method with constraint data performs better in terms of the relative errors of the inversion results. The addition of 20 dB Gaussian noise does not impede the satisfactory inversion results from the multigrid method with constraint data and the fixed grid iterative method with constraint data, although the multigrid method without constraint data is incapable of producing an acceptable result. With the inclusion of 10 dB Gaussian noise, only the multigrid method with constraint data is satisfying, and the other two methods are disappointing. This is because the combination of multigrid (which can allow escaping the influence of the local minima) and constraint data (which can offer the advantage of a high signal-to-noise ratio) makes the proposed method able to strongly suppress the noise.
Figure 4 and Figure 7 and Table 2 also show that, under various levels of disturbance of the measurement data, the multigrid method with constraint data can obtain stable inversion results. This indicates that the combination method based on the multigrid method and constraint data has computational stability. The truncation errors of the proposed method are the same as those of the regularized Gauss–Newton method. This is because the adopted smoothing operator is the iterative method Equation (14), which is a variant of the regularized Gauss–Newton method, and the truncation errors are caused by neglecting higher-order nonlinear terms in the Taylor-series expansion. In the regularized Gauss–Newton method, ignoring the second-order term in the derivative and approximating the first-order term allows the iteration to be written as a sequence of linear least squares problems. Some papers [49,50] have focused on reducing the truncation errors, which is also one of the future research directions.
6. Conclusions
In the article, we have proposed a combination method based on multigrid and constraint data to solve the inverse problem of the nonlinear CDE in the multiphase porous media flow. The proposed method possesses the advantages of both multigrid and constraint data, such as fast calculation speed, high calculation precise, good computational stability, and strong noise resistance. These advantages are especially obvious in the numerical simulation, which also shows that the performance of the multigrid method with constraint data is much better than that of the other two methods: the fixed grid iterative method with constraint data and the multigrid method without constraint data. Studying the multigrid method with constraint data in high-dimensional problems is expected to be the subject of future research.
Author Contributions
Conceptualization, S.W., S.L., H.C. and T.L.; methodology, S.W., S.L., H.C. and Y.Q.; software, S.L. and H.C.; validation, W.Z. and Q.M.; formal analysis, S.L. and H.C.; investigation, S.W., S.L. and H.C.; resources, Y.Q.; data curation, W.Z. and Q.M.; writing—original draft preparation, S.L. and H.C.; writing—review and editing, S.L., H.C. and T.L.; visualization, W.Z. and Q.M.; supervision, Y.Q. and T.L.; project administration, Y.Q. and T.L.; funding acquisition, Y.Q. and T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research Project on Graduate Education and Teaching Reform of Hebei Province of China (YJG2024133), the Open Fund Project of Marine Ecological Restoration and Smart Ocean Engineering Research Center of Hebei Province (HBMESO2321), the Technical Service Project of Eighth Geological Brigade of Hebei Bureau of Geology and Mineral Resources Exploration (KJ2022-021), the Technical Service Project of Hebei Baodi Construction Engineering Co., Ltd. (KJ2024-012), the Natural Science Foundation of Hebei Province of China (A2020501007), the Fundamental Research Funds for the Central Universities (N2123015).
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available because the research data are confidential.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zureigat, H.; Al-Smadi, M.; Al-Khateeb, A.; Al-Omari, S.; Alhazmi, S.E. Fourth-order numerical solutions for a fuzzy time-fractional convection-diffusion equation under Caputo generalized hukuhara derivative. Fractal Fract. 2023, 7, 47. [Google Scholar] [CrossRef]
- Thiele, J.C.; Gregor, I.; Karedla, N.; Enderlein, J. Efficient modeling of three-dimensional convection-diffusion problems in stationary flows. Phys. Fluids 2020, 32, 112015. [Google Scholar] [CrossRef]
- Al-Khateeb, A. Efficient numerical solutions for fuzzy time fractional convection diffusion equations using two explicit finite difference methods. Axioms 2024, 13, 221. [Google Scholar] [CrossRef]
- Moraga, N.O.; Jaime, J.I.; Cabrales, R.C. An approach to accelerate the convergence of SIMPLER algorithm for convection-diffusion problems of fluid flow with heat transfer and phase change. Int. Commun. Heat Mass 2021, 129, 105715. [Google Scholar] [CrossRef]
- Salmi, A.; Madkhali, H.A.; Nawaz, M.; Alharbi, S.O.; Malik, M.Y. Computational analysis for enhancement of heat and mass transfer in MHD-polymer with hybrid nano-particles using generalized laws. Case Stud. Therm. Eng. 2022, 31, 101851. [Google Scholar] [CrossRef]
- Espedal, M.S.; Karlsen, K.H. Numerical solution of reservoir flow models based on large time step operator splitting algorithm. In Filtration in Porous Media and Industrial Applications: Lecture Notes in Mathematics; Fasano, A., Ed.; Springer: Berlin, Germany, 2000; Volume 1734, pp. 9–77. [Google Scholar]
- Subbey, S.; Christie, M.; Sambridge, M. Prediction under uncertainty in reservoir modeling. J. Petrol. Sci. Eng. 2004, 44, 143–153. [Google Scholar] [CrossRef]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.; Liu, P.; Liu, S. Gas diffusion coefficient estimation of coal: A dimensionless numerical method and its experimental validation. Int. J. Heat Mass Tran. 2020, 162, 120336. [Google Scholar] [CrossRef]
- Pohjola, V. A uniqueness result for an inverse problem of the steady state convection-diffusion equation. SIAM J. Math. Anal. 2015, 47, 2084–2103. [Google Scholar] [CrossRef]
- Burman, E.; Nechita, M.; Oksanen, L. A stabilized finite element method for inverse problems subject to the convection-diffusion equation. I: Diffusion-dominated regime. Numer. Math. 2020, 144, 451–477. [Google Scholar] [CrossRef]
- Burman, E.; Nechita, M.; Oksanen, L. A stabilized finite element method for inverse problems subject to the convection-diffusion equation. II: Convection-dominated regime. Numer. Math. 2022, 150, 769–801. [Google Scholar] [CrossRef]
- Sharma, M.; Hahn, M.; Leyffer, S.; Ruthotto, L.; van Bloemen Waanders, B. Inversion of convection-diffusion equation with discrete sources. Optim. Eng. 2021, 22, 1419–1457. [Google Scholar] [CrossRef]
- Kelbert, A.; Egbert, G.D.; Schultz, A. Non-linear conjugate gradient inversion for global EM induction: Resolution studies. Geophys. J. Int. 2008, 173, 365–381. [Google Scholar] [CrossRef]
- Bauer, F.; Hohage, T.; Munk, A. Iteratively regularized Gauss–Newton method for nonlinear inverse problems with random noise. SIAM J. Numer. Anal. 2009, 47, 1827–1846. [Google Scholar] [CrossRef]
- Pan, W.; Innanen, K.A.; Margrave, G.F.; Fehler, M.C.; Fang, X.; Li, J. Estimation of elastic constants for HTI media using Gauss-Newton and full-Newton multiparameter full-waveform inversion. Geophysics 2016, 81, R275–R291. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. Regularization, Bayesian inference, and machine learning methods for inverse problems. Entropy 2021, 23, 1673. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep learning for geophysics: Current and future trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Singhal, V.; Majumdar, A. A domain adaptation approach to solve inverse problems in imaging via coupled deep dictionary learning. Pattern Recogn. 2020, 100, 107163. [Google Scholar] [CrossRef]
- Liu, L.; Ma, J.; Plonka, G. Sparse graph-regularized dictionary learning for suppressing random seismic noise. Geophysics 2018, 83, V215–V231. [Google Scholar] [CrossRef]
- Liu, L.; Ma, J. Structured graph dictionary learning and application on the seismic denoising. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1883–1893. [Google Scholar] [CrossRef]
- Ahmad, D.; Donatelli, M.; Mazza, M.; Serra-Capizzano, S.; Trotti, K. A note on the convergence of multigrid methods for the Riesz-Space equation and an application to image deblurring. Mathematics 2024, 12, 1916. [Google Scholar] [CrossRef]
- Donatelli, M.; Krause, R.; Mazza, M.; Trotti, K. Multigrid for two-sided fractional differential equations discretized by finite volume elements on graded meshes. J. Comput. Appl. Math. 2024, 444, 115787. [Google Scholar] [CrossRef]
- Teunissen, J.; Schiavello, F. Geometric multigrid method for solving Poisson’s equation on octree grids with irregular boundaries. Comput. Phys. Commun. 2023, 286, 108665. [Google Scholar] [CrossRef]
- Bolten, M.; Donatelli, M.; Ferrari, P.; Furci, I. Symbol based convergence analysis in block multigrid methods with applications for Stokes problems. Appl. Numer. Math. 2023, 193, 109–130. [Google Scholar] [CrossRef]
- Oh, S.; Milstein, A.B.; Bouman, C.A.; Webb, K.J. A general framework for nonlinear multigrid inversion. IEEE Trans. Image Process. 2004, 14, 125–140. [Google Scholar]
- Liu, T. A multigrid-homotopy method for nonlinear inverse problems. Comput. Math. Appl. 2020, 79, 1706–1717. [Google Scholar] [CrossRef]
- Al-Mahdawi, H.K.I.; Abotaleb, M.; Alkattan, H.; Tareq, A.M.Z.; Badr, A.; Kadi, A. Multigrid method for solving inverse problems for heat equation. Mathematics 2022, 10, 2802. [Google Scholar] [CrossRef]
- Al-Mahdawi, H.K.; Sidikova, A.I.; Alkattan, H.; Abotaleb, M.; Kadi, A.; El-Kenawy, E.S.M. Parallel multigrid method for solving inverse problems. MethodsX 2022, 9, 101887. [Google Scholar] [CrossRef]
- Xie, M.; Xu, F.; Yue, M. A type of full multigrid method for non-selfadjoint Steklov eigenvalue problems in inverse scattering. ESAIM Math. Model. Numer. Anal. 2021, 55, 1779–1802. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.; Duan, Y.; Yin, K.; Tai, X.C. An efficient multi-grid method for TV minimization problems. Inverse Probl. Imag. 2021, 15, 1199–1221. [Google Scholar] [CrossRef]
- Marlevi, D.; Kohr, H.; Buurlage, J.W.; Gao, B.; Batenburg, K.J.; Colarieti-Tosti, M. Multigrid reconstruction in tomographic imaging. IEEE Trans. Radiat. Plasma Med. Sci. 2019, 4, 300–310. [Google Scholar] [CrossRef]
- Edjlali, E.; Bérubé-Lauzière, Y. Lq-Lp optimization for multigrid fluorescence tomography of small animals using simplified spherical harmonics. J. Quant. Spectrosc. Ra. 2018, 205, 163–173. [Google Scholar] [CrossRef]
- Li, S.; Montcel, B.; Yuan, Z.; Liu, W.; Vray, D. Multigrid-based reconstruction algorithm for quantitative photoacoustic tomography. Biomed. Opt. Express 2015, 6, 2424–2434. [Google Scholar] [CrossRef] [PubMed]
- Sorsa, L.I.; Takala, M.; Eyraud, C.; Pursiainen, S. A time-domain multigrid solver with higher-order born approximation for full-wave radar tomography of a complex-shaped target. IEEE Trans. Comput. Imaging 2020, 6, 579–590. [Google Scholar] [CrossRef]
- Ascher, U.M.; Haber, E. A multigrid method for distributed parameter estimation problems. Electron. Trans. Numer. Anal. 2003, 15, 1–17. [Google Scholar]
- Adavani, S.S.; Biros, G. Multigrid algorithms for inverse problems with linear parabolic PDE constraints. SIAM J. Sci. Comput. 2008, 31, 369–397. [Google Scholar] [CrossRef][Green Version]
- Liu, T. Parameter estimation with the multigrid-homotopy method for a nonlinear diffusion equation. J. Comput. Appl. Math. 2022, 413, 114393. [Google Scholar] [CrossRef]
- Christiansen, R.; Morosini, A.; Enriquez, E.; Muñoz, B.; Klinger, F.L.; Martinez, M.P.; Suárez, A.O.; Kostadinoff, J. 3D litho-constrained inversion model of southern Sierra Grande de San Luis: New insights into the Famatinian tectonic setting. Tectonophysics 2019, 756, 1–24. [Google Scholar] [CrossRef]
- Dobróka, M.; Szabó, N.P.; Tóth, J.; Vass, P. Interval inversion approach for an improved interpretation of well logs. Geophysics 2016, 81, D155–D167. [Google Scholar] [CrossRef]
- Dobróka, M.; Szabó, N.P. Interval inversion of well-logging data for automatic determination of formation boundaries by using a float-encoded genetic algorithm. J. Petrol. Sci. Eng. 2012, 86, 144–152. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Moore, A.M.; Arango, H.G.; Cornuelle, B.D.; Miller, A.J.; Powell, B.; Chua, B.S.; Bennett, A.F. Weak and strong constraint data assimilation in the inverse Regional Ocean Modeling System (ROMS): Development and application for a baroclinic coastal upwelling system. Ocean Model. 2007, 16, 160–187. [Google Scholar] [CrossRef]
- Gao, L.; Sadeghi, M.; Ebtehaj, A. Microwave retrievals of soil moisture and vegetation optical depth with improved resolution using a combined constrained inversion algorithm: Application for SMAP satellite. Remote Sens. Environ. 2020, 239, 111662. [Google Scholar] [CrossRef]
- Fournier, A.; Clerget, C.H.; Bharadwaj, P.; Merciu, A.; Skar, G. A seismoelectric inverse problem with well-log data and borehole-confined acquisition. In Proceedings of the SEG International Exposition and Annual Meeting, San Antonio, TX, USA, 15–20 September 2019; p. SEG-2019-3216905. [Google Scholar]
- Wisén, R.; Christiansen, A.V. Laterally and mutually constrained inversion of surface wave seismic data and resistivity data. J. Environ. Eng. Geophys. 2005, 10, 251–262. [Google Scholar] [CrossRef][Green Version]
- Engquist, B.; Osher, S. One-sided difference approximations for nonlinear conservation laws. Math. Comput. 1981, 36, 321–351. [Google Scholar] [CrossRef]
- Nilssen, T.K.; Karlsen, K.H.; Mannseth, T.; Tai, X.C. Identification of diffusion parameters in a nonlinear convection-diffusion equation using the augmented Lagrangian method. Comput. Geosci. 2009, 13, 317–329. [Google Scholar] [CrossRef][Green Version]
- Guo, Z.; Chen, C.; Gao, G.; Vink, J. Enhancing the performance of the distributed Gauss-Newton optimization method by reducing the effect of numerical noise and truncation error with support-vector regression. SPE J. 2018, 23, 2428–2443. [Google Scholar] [CrossRef]
- Nissinen, A.; Heikkinen, L.M.; Kolehmainen, V.; Kaipio, J.P. Compensation of errors due to discretization, domain truncation and unknown contact impedances in electrical impedance tomography. Meas. Sci. Technol. 2009, 20, 105504. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).