Multidimensional Evolution Effects on Non-Cooperative Strategic Games
Abstract
1. Introduction
1.1. Background and Relationship to Previous Works
1.2. Our Contribution
- We introduce a dynamic generalized Nash equilibrium problem (DGNEP) in the terms of a path-independent curvilinear integral, which is a functional, and a dynamic quasi-variational inequality problem (DQVIP) over multiple time scales, which we call multiple parameters of evolution. First, we establish an equivalent relationship between the DGNEP and the DQVIP by using the classic tools of convex analysis. However, in this work, we exploit the form of the functionals, given in the terms of path-independent curvilinear integrals, by using the convexity of the considered functional. Furthermore, we also prove the existence of solutions to the DGNEP by exploiting its equivalence with the DQVIP, and by using the techniques of proving existence results for generalized vector quasi-variational inequality and quasi-equilibrium problems, studied in [51,52]. We note that papers [51,52] deal with functions of a finite number of independent variables, but our work deals with functions of a number of independent functions, i.e., functionals, and there is no such ‘universal’ space; indeed, problems are defined in a function space. Moreover, if all the functions are independent of the multiple parameters of evolutions t, then our introduced problems and established results can be converted into the problems and results of the static case, which were studied in [8,9,17,18,19,20,21,22,51,52,53]. In essence, our results can be seen as dynamic generalizations of the corresponding (static) derived results of the aforementioned papers. This outcome promotes a new approach aimed at relationships between mathematical programming and the classical calculus of variations. We recall that Hanson [54], who was the first to observe such kind of relationships, emphasized that some of the duality theorems of mathematical programming have analogues in the variational calculus.
- Our intention is to open a window to understanding and exploring the performance of the decision making models of non-cooperative strategic games with respect to multiple time scales, where we can investigate how the strategy of players over multiple time scales impact the decision making, resulting payoffs, and costs in this kind of games. We emphasize that neither theoretical results, nor experimental results related to generalized Nash equilibrium problems and concerning their applications to electricity market problems, have been investigated so far in the setting of multiple time scales (multiple parameters of evolution). In our recent study [55], we managed to formulate a multi-time generalized Nash equilibrium problem involving multiple integrals, and investigated its theoretical and experimental applications to solving traffic network problems, the aim of which is to minimize the traffic cost of each route, and to solving a river basin pollution problem.
- We also present a comparative numerical experiment for checking the evolution of resulting payoffs in multiple time scales in comparison to a single time scale. We find that the maximum profit value of each generator in the case of multiple time scales is higher than the corresponding value in the single time scale case.
- Our results also demonstrate how the three theories, (1) ISO-operated spot electricity markets, (2) projected dynamical system theory, and (3) multidimensional optimization problems, which have almost been developed in parallel, can be connected in the single frame of ‘Nash equilibrium problems’ in order to enhance the modeling and analysis of problems that arise in the disciplines of engineering, operations research and management, and economics. More precisely, we use the multidimensional optimization formulations, studied by the research group of Udrişte [46,47,48], to study the GNEP and its application to the ISO centralized dynamic spot electricity market, influenced by [14,23,24] and references therein, by using the techniques of projected dynamical system theory developed by Nagureny’s research group [30,31,32,33,34,35,36]. We would like to mention here that projected dynamical system theory [30,31,32,33,34,35,36] has also been used to study the electricity market from the perspective of supply chain networks.
- Today’s decisions can affect the long-run future. For example, companies like Nike, Disney, Walmart, MacDonald’s, Nestlé, Johnson & Johnson, and many more have realized that their actions in purchasing and supply chain management strongly affect their reputation and long-term success. They have suffered damage to their reputations and sales as a result of public awareness campaigns, external pressure from activists, and internal pressure from investors demanding that companies acknowledge responsibility for labor rights abuses in factories that make their products [58]. The same phenomena also occur in the setting of decision making problems in other industrial areas such as electricity markets and oligopoly markets, and we could go on. Aussel et al. [14], and Cotrina and Zúñiga [15] studied the decision making problem via the GNEP in single time settings, but the above-mentioned long-run effects are not considered by them. The mathematical framework of a decision making problem over multiple time scales makes us capable of capturing the long-term effects, and observing how the decision making, resulting payoffs, and costs evolve in a decision making game when players of such a game make their strategies over multiple time scales. These facts motivated us to study the GNEP in multiple time settings and to examine its application to solving spot electricity market network problems. Multi-period decision making problems with applications in supply chain networks are studied in [59,60] and in the references therein, but our approach and results are completely different from theirs.
2. Preliminaries and Problem Formulations
- (i)
- The abbreviation “a.e.” stands for “almost everywhere”, and represents the set of non-negative vectors in ;
- (ii)
- The non-cooperative strategic game comprises N players;
- (iii)
- in is the planning horizon of players. It is an m-dimensional hypercube with the fixed opposite diagonal points and in , which with the product order relation can be written as ;
- (iv)
- is a piecewise smooth curve joining the opposite diagonal points and in ;
- (v)
- The point is the multiple parameters of evolution, which we call time periods, where is the given time, is another given time, and so on. It follows that the evolution is m-dimensional, which leads us to say that the evolution is multidimensional;
- (vi)
- The dynamic behavior of the non-cooperative strategic game is described by the strategy vector of all the players. In fact, at a given point ;
- (vii)
- is the strategy vector of the player w, i.e., at a given point ;
- (viii)
- is the strategy vector of all the players except player w, i.e., at a given point ;
- (ix)
- ;
- (x)
- To emphasize the strategy vector of the player w, we write the strategy vector x of all the players as . This is just another way of writing the vector ;
- (xi)
- We recall that ;
- (xii)
- is a nonempty, closed, and convex subset;
- (xiii)
- is the nonempty, closed and convex feasible set of the player w for any given strategy vector of the rival players;
- (xiv)
- We say that the strategy vector x of all the players is feasible if for all and for all , we have ;
- (xv)
- We use the following notation, which we need in Section 6, to denote the value of the functional represented by p at the point q:for all , where represents the Euclidean inner product;
- (xvi)
- Each player w has an objective function, which is known as the cost/loss function and which depends on both the player’s own decision variable and on the rival players’ decision variables . We interpret the total cost/loss function that the player w incurs when the rival players have chosen the strategy , , in terms of the path-independent curvilinear integralwhere is the differential element of the multiple parameters of evolution , is a real-valued continuously differentiable function for every and the running cost/loss of the player w, and we use summation over the repeated indices , i.e.,We also assume that the condition , where and are the total derivative operators, is satisfied.
- is the line segment from to ;
- is a parabola from to .
- I
- We need to use the condition for and for numerical experiments;
- II
- We can integrate the integrals over and, using a simple calculus rule, we see that the value of the integral is
- (1)
- If the multiple parameters of evolution are reduced to the single time scale, i.e., and , then and are simply the closed real interval in (the set of non-negative real numbers). We may then write , where T denotes an arbitrary time. Now, the DGNEP reduces to the time-dependent generalized Nash equilibrium problem, which is studied by Aussel et al. in [14].
- (2)
- If all the functions are independent of the multiple parameters of evolution t, then the DGNEP reduces to the generalized Nash equilibrium problem, which is investigated, for example, in [8,9,17,18,19,20,21,22,53].For the formulation of the dynamic quasi-variational inequality problem, we first consider a nonempty, closed and convex subset K of , and define a set-valued map by
- (a)
- It is evident from the above definition that every open (respectively, closed) set is compactly open (respectively, compactly closed).
- (b)
- The union or intersection of a finite number of compactly open (respectively, compactly closed) sets is compactly open (respectively, compactly closed).
- (c)
- If and are compactly open (respectively, compactly closed) in and , respectively, then is compactly open (respectively, compactly closed) in .
- ;
- ;
- is convex;
- is compactly open;
- There exists a nonempty, closed and compact subset D of K and such that .
3. The Dynamic Generalized Nash Equilibrium Problem as a Quasi-Variational Inequality Problem
4. Existence of Equilibria
5. The Dynamic Spot Electricity Market Problem
5.1. The ISO Problem
5.2. The Generator Problem
6. The DGNEP as a Projected Dynamical System
7. Solving the DGNEP
- Step 1. Consider a partition of such thatwhich satisfies the following convention of equalities and inequalities:
- Step 3. According to Euler’s method for finding a critical point of a projected dynamical system, studied in [30,31], we have the following algorithm for finding critical points of PDS (17) at each discrete point :where is a sequence of positive scalars. Since , , and are all equal in the dynamic spot electricity market structure of Section 5, we can find a critical point of PDS (17) for any . Moreover, the solution to the ISO problem is unique for ; the reason behind this is explained in the further test case paragraph. Therefore, we take advantage of this and solve our problem for . Keeping in mind the terminologies given in (18), at each and the uniqueness the solution to the ISO problem, we obtain
8. A Comparative Study
9. Conclusions and Further Developments
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neumann, J.V.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Nash, J.F. The bargaining problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Nash, J.F. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Cournot, A.A. Recherches sur les Principes Mathématiques de la Théorie des Richesses; Hachette: Paris, France, 1838. [Google Scholar]
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.F. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Arrow, K.J.; Debreu, G. Existence of an equilibrium for a competitive economy. Econometrica 1954, 22, 265–290. [Google Scholar] [CrossRef]
- Facchinei, F.; Kanzow, C. Generalized Nash equilibrium problems. Ann. Oper. Res. 2010, 175, 177–211. [Google Scholar] [CrossRef]
- Fischer, A.; Herrich, M.; Schönefeld, K. Generalized Nash equilibrium problems-recent advances and challenges. Pesqui. Oper. 2014, 34, 521–558. [Google Scholar] [CrossRef]
- Britzelmeier, A.; Gerdts, M.; Rottmann, T. Control of interacting vehicles using model-predictive control, generalized Nash equilibrium problems, and dynamic inversion. IFAC PapersOnLine 2020, 53, 15146–15153. [Google Scholar] [CrossRef]
- Cadrea, H.L.; Jacquot, P.; Wan, C.; Alasseur, C. Peer-to-peer electricity market analysis: From variational to Generalized Nash Equilibrium. Eur. J. Oper. Res. 2020, 282, 753–771. [Google Scholar] [CrossRef]
- Nagurney, A.; Dutta, P. Supply chain network competition among blood service organizations: A Generalized Nash Equilibrium framework. Ann. Oper. Res. 2019, 275, 551–586. [Google Scholar] [CrossRef]
- Nagurney, A.; Flores, E.A.; Soylu, C. A Generalized Nash Equilibrium network model for post-disaster humanitarian relief. Transp. Res. Part E 2016, 95, 1–18. [Google Scholar] [CrossRef]
- Aussel, D.; Gupta, R.; Mehra, A. Evolutionary variational inequality formulation of the generalized Nash equilibrium problem. J. Optim. Theory Appl. 2016, 169, 74–90. [Google Scholar] [CrossRef]
- Cotrina, J.; Ziga, J. Time-Dependent Generalized Nash Equilibrium Problem. J. Optim. Theory Appl. 2018, 179, 1054–1064. [Google Scholar] [CrossRef]
- Bensoussan, A. Points de Nash dans le cas de fontionnelles quadratiques et jeux differentiels linéaires à N personnes. SIAM J. Control 1974, 12, 460–499. [Google Scholar] [CrossRef]
- Harker, P.T. Generalized Nash games and quasi-variational inequalities. Eur. J. Oper. Res. 1991, 54, 81–94. [Google Scholar] [CrossRef]
- Aussel, D.; Sultana, A.; Vetrivel, V. On the existence of projected solutions of quasi-variational inequalities and generalized Nash equilibrium problems. J. Optim. Theory Appl. 2016, 170, 818–837. [Google Scholar] [CrossRef]
- Bueno, O.; Cotrina, J. Existence of Projected Solutions for Generalized Nash Equilibrium Problems. J. Optim. Theory Appl. 2021, 191, 344–362. [Google Scholar] [CrossRef]
- Cotrina, J.; Ziga, J. Quasi-equilibrium problems with non-self constraint map. J. Glob. Optim. 2019, 75, 177–197. [Google Scholar] [CrossRef]
- Nagurney, A. Supply chain game theory network modeling under labor constraints: Applications to the COVID-19 pandemic. Eur. J. Oper. Res. 2021, 293, 880–891. [Google Scholar] [CrossRef]
- Nagurney, A.; Salarpour, M.; Dong, J.; Dutta, P. Competition for Medical Supplies Under Stochastic Demand in the Covid-19 Pandemic: A Generalized Nash Equilibrium Framework. In Nonlinear Analysis and Global Optimization; Themistocles M. Rassias, T.M., Pardalos, P.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Hu, X.; Ralph, D. Using EPECs to model bilevel games in restructured electricity markets with locational prices. Oper. Res. 2007, 55, 809–827. Available online: http://www.jstor.org/stable/25147124 (accessed on 1 July 2024). [CrossRef]
- Aussel, D.; Correa, R.; Marechal, M. Electricity spot market with transmission losses. J. Ind. Manag. Optim. 2013, 9, 275–290. [Google Scholar] [CrossRef]
- Berry, C.A.; Hobbs, B.F.; Meroney, W.A.; O’Neill, R.P.; Stewart, W.R., Jr. Understanding how market power can arise in network competition: A game theoretic approach. Util. Policy 1999, 8, 139–158. [Google Scholar] [CrossRef]
- Escobar, J.F.; Jofré, A. Monopolistic competition in electricity networks with resistance losses. Econ. Theory 2010, 44, 101–121. [Google Scholar] [CrossRef][Green Version]
- Hobbs, B.J.; Member Metzler, C.B.; Pang, J.-S. Strategic gaming analysis for electric power systems: An MPEC approach. IEEE Trans. Power Syst. 2000, 15, 638–645. [Google Scholar] [CrossRef]
- Nagurney, A.; Matsypura, D. A Supply Chain Network Perspective for Electric Power Generation, Supply, Transmission, and Consumption. In Optimisation, Econometric and Financial; Kontoghiorghes, E.J., Gatu, C., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Henry, C. An existence theorem for a class of differential equations with multivalued right-hand side. J. Math. Anal. Appl. 1973, 41, 179–186. [Google Scholar] [CrossRef]
- Nagurney, A.; Zhang, D. Projected Dynamical Systems and Variational Inequalities with Applications; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Nagurney, A.; Liu, Z.; Cojocaru, M.-G.; Daniele, P. Dynamic electric power supply chains and transportation networks: An evolutionary variational inequality formulation. Transp. Res. Part E 2007, 43, 624–646. [Google Scholar] [CrossRef]
- Cojocaru, M.G.; Daniele, P.; Nagurney, A. Projected dynamical systems and evolutionary variational inequalities via Hilbert spaces with applications. J. Optim. Theory Appl. 2005, 127, 549–563. [Google Scholar] [CrossRef]
- Cojocaru, M.G.; Daniele, P.; Nagurney, A. Double-layered dynamics: A unified theory of projected dynamical systems and evolutionary variational inequalities. Eur. J. Oper. Res. 2006, 175, 494–507. [Google Scholar] [CrossRef]
- Cojocaru, M.G.; Daniele, P.; Nagurney, A. Projected dynamical systems, evolutinary variational inequalities, applications, and a computational procedure. In Pareto Optimality, Game Theory and Equilibria; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Cojocaru, M.G.; Jonker, L.B. Existence of solutions to projected differential equations in Hilbert spaces. Proc. Am. Math. Soc. 2004, 132, 183–193. [Google Scholar] [CrossRef]
- Migot, T.; Cojocaru, M.-G. Nonsmooth dynamics of generalized Nash games. J. Nonlinear Var. Anal. 2020, 4, 27–44. [Google Scholar] [CrossRef]
- Ekeland, I.; Témam, R. Convex Analysis and Variational Problems; North-Holland: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Guseĭnov, F.V. On the question of extension of multidimensional variational problems. Math. USSR-Izv. 1987, 28, 1–19. [Google Scholar] [CrossRef]
- Fonseca, I.; Marcellini, P. Relaxation of Multiple Integrals in Subcritical Sobolev Spaces. J. Geom. Anal. 1997, 7, 57–81. [Google Scholar] [CrossRef]
- Hüsseinov, F. Relaxation of multidimensional variational problems with constraints of general form. Nonlinear Anal. 2001, 45, 651–659. [Google Scholar] [CrossRef]
- Pickenhain, S.; Wagner, M. Pontryagin principle for state-constrained control problems governed by a first-order PDE system. J. Optim. Theory Appl. 2000, 107, 297–330. [Google Scholar] [CrossRef]
- Pickenhain, S.; Wagner, M. Piecewise continuous controls in Dieudonne-Rashevsky type problems. J. Optim. Theory Appl. 2005, 127, 145–163. [Google Scholar] [CrossRef]
- Wagner, M. Pontryagin’s maximum principle for Dieudonné-Rashevsky type problems involving lipschitz functions. Optimization 1999, 46, 165–184. [Google Scholar] [CrossRef]
- Wagner, M. Pontryagin’s Maximum Principle for multidimensional control problems in image processing. J. Optim. Theory Appl. 2009, 140, 543–576. [Google Scholar] [CrossRef]
- Udrişte, C.; Ţevy, I. Multi-time Euler-Lagrange-Hamilton theory. WSEAS Trans. Math. 2007, 6, 701–709. [Google Scholar]
- Udrişte, C. Multitime controllability, observability and bang-bang principle. J. Optim. Theory Appl. 2008, 139, 141–157. [Google Scholar] [CrossRef]
- Udrişte, C.; Dogaru, O.; Ţevy, I. Null Lagrangian forms and Euler-Lagrange PDEs. J. Adv. Math. Study 2008, 1, 143–156. [Google Scholar]
- Udrişte, C.; Ferrara, M. Multitime models of optimal growth. WSEAS Trans. Math. 2008, 7, 51–55. [Google Scholar]
- Singh, S.; Pitea, A.; Qin, X. An iterative method and weak sharp solutions for multitime-type variational inequalities. Appl. Anal. 2021, 302, 265–287. [Google Scholar] [CrossRef]
- Treanţă, S.; Singh, S. Weak sharp solutions associated with a multidimensional variational-type inequality. Positivity 2021, 25, 329–351. [Google Scholar] [CrossRef]
- Ansari, Q.H.; Schaible, S.; Yao, J.C. Generalized vector quasi-variational inequality problems over product sets. J. Glob. Optim. 2005, 32, 437–449. [Google Scholar] [CrossRef]
- Ding, X.P. Existence of solutions for quasi-equilibrium problems in noncompact topological spaces. Comput. Math. Appl. 2000, 39, 13–21. [Google Scholar] [CrossRef]
- Pang, J.S.; Fukushima, M. Quasi-variational inequalities, generalized Nash equilibria, and multi-leader-follower games. Comput. Manag. Sci. 2005, 2, 21–56. [Google Scholar] [CrossRef]
- Hanson, M.A. Bounds for functionally convex optimal control problems. J. Math. Anal. Appl. 1964, 8, 84–89. [Google Scholar] [CrossRef]
- Singh, S.; Gibali, G.; Reich, S. Multi-time generalized Nash equilibria with dynamic flow applications. Mathematics 2021, 9, 1658. [Google Scholar] [CrossRef]
- Alvarado, F.L.; Demarco, C.L.; Dobson, I.; Sauer, P.W.; Greene, S.; Engdahl, H.; Zhang, J. Electric Power Transfer Capability: Concepts, Applications, Sensitivity and Uncertainty. March 2001. Available online: https://www.researchgate.net/publication/2892623 (accessed on 1 July 2024).
- Alvarado, F.L.; Meng, J.; Demarco, C.L.; Mota, W.S. Stability analysis of interconnected power systems coupled with market dynamics. IEEE Trans. Power Syst. 2001, 16, 695–701. [Google Scholar] [CrossRef]
- Svendsen, A.; Boutilier, R.G.; Abbott, R.M.; Wheeler, D. Measuring the Business Value of Stakeholder Relationships (Part One). Available online: https://partnersinchange.co.nz/wp-content/uploads/2017/10/Canadian-Measuring-the-value-of-Stakeholder-relationships.pdf (accessed on 1 July 2024).
- Cruz, J.M.; Liu, Z. Modeling and analysis of the multiperiod effects of social relationship on supply chain networks. Eur. J. Oper. Res. 2011, 214, 39–52. [Google Scholar] [CrossRef]
- Cruz, J.M.; Wakolbinger, T. Multiperiod effects of corporate social responsibility on supply chain networks, transaction costs, emissions, and risk. Int. J. Prod. Econ. 2008, 116, 61–74. [Google Scholar] [CrossRef]
- Treanţă, S. On a modified optimal control problem with first-order PDE constraints and the associated saddle-point optimality criterion. Eur. J. Control 2020, 51, 1–9. [Google Scholar] [CrossRef]
- Jayswal, A.; Singh, S.; Kurdi, A. Multitime multiobjective variational problems and vector variational-like inequalities. Eur. J. Oper. Res. 2016, 254, 739–745. [Google Scholar] [CrossRef]
- Mititelu, Ş.; Treanţă, S. Efficiency conditions in vector control problems governed by multiple integrals. J. Appl. Math. Comput. 2018, 57, 647–665. [Google Scholar] [CrossRef]
- Singh, S.; Reich, S. A multidimensional approach to traffic analysis. Pure Appl. Funct. Anal. 2021, 6, 383–397. [Google Scholar]
- Matsushita, S.-Y.; Xu, L. On finite convergence of iterative methods for variational inequalities in Hilbert spaces. J. Optim. Theory Appl. 2014, 161, 701–715. [Google Scholar] [CrossRef]
- Cegielski, A. Iterative Methods for Fixed Point Problems in Hilbert Spaces; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Rockafellar, R.T.; Wets, R.J.-B. Variational Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Saadat, H. Power System Analysis; McGraw-Hill: Boston, MA, USA, 1999. [Google Scholar]

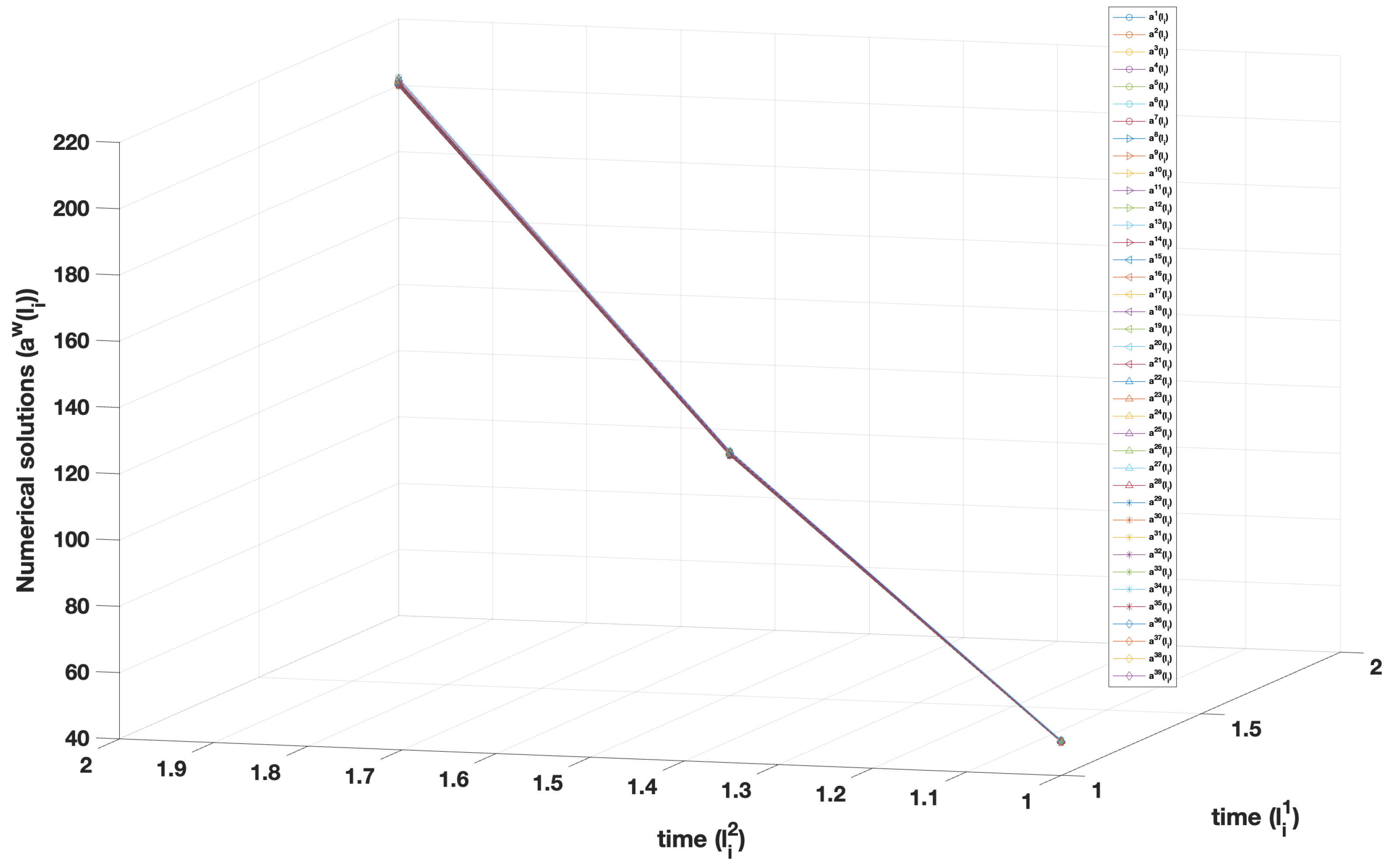
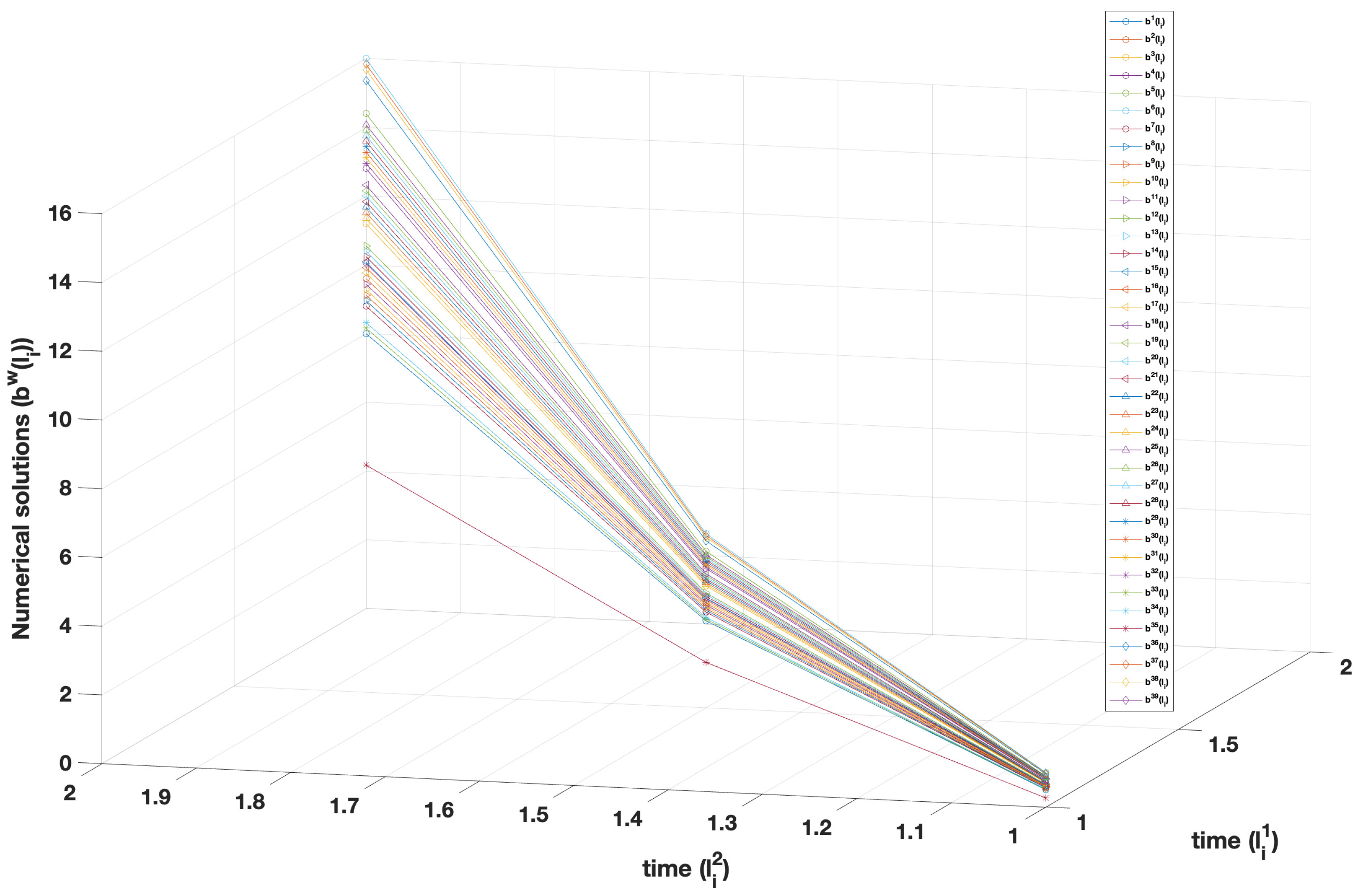
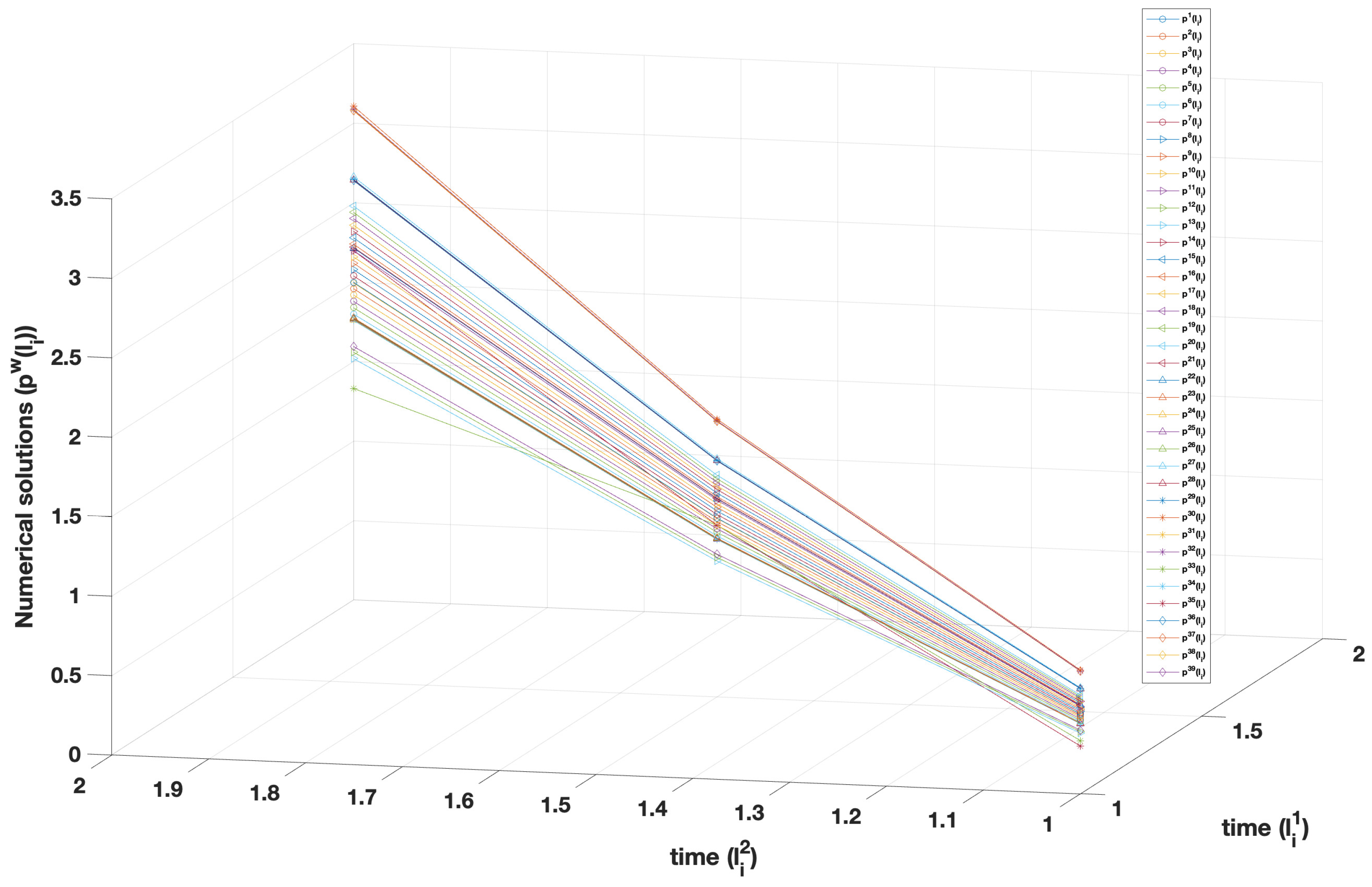
| w | No. of Iter. | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 57 | ||||||
| 2 | 86 | ||||||
| 3 | 124 | ||||||
| 4 | 174 | ||||||
| 5 | 237 | ||||||
| 6 | 318 | ||||||
| 7 | 63 | ||||||
| 8 | 59 | ||||||
| 9 | 57 | ||||||
| 10 | 55 | ||||||
| 11 | 53 | ||||||
| 12 | 248 | ||||||
| 13 | 265 | ||||||
| 14 | 51 | ||||||
| 15 | 52 | ||||||
| 16 | 54 | ||||||
| 17 | 43 | ||||||
| 18 | 63 | ||||||
| 19 | 58 | ||||||
| 20 | 53 | ||||||
| 21 | 80 | ||||||
| 22 | 78 | ||||||
| 23 | 177 | ||||||
| 24 | 177 | ||||||
| 25 | 265 | ||||||
| 26 | 257 | ||||||
| 27 | 52 | ||||||
| 28 | 54 | ||||||
| 29 | 51 | ||||||
| 30 | 28 | ||||||
| 31 | 28 | ||||||
| 32 | 28 | ||||||
| 33 | 276 | ||||||
| 34 | 98 | ||||||
| 35 | 114 | ||||||
| 36 | 67 | ||||||
| 37 | 40 | ||||||
| 38 | 204 | ||||||
| 39 | 205 |
| w | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 |
| n (Iterations) | |||
|---|---|---|---|
| 1 | (49.5500, 0.0504, 0.5000) | (111.4825, 0.2537, 1.125) | (198.2000, 0.8008, 2) |
| 2 | (49.5750, 0.0754, 0.5000) | (111.5388, 0.3802, 1.125) | (198.3000, 1.2008, 2) |
| 3 | (4.9600, 0.1004, 0.5000) | (111.5950, 0.5068, 1.125) | (198.4000, 1.6008, 2) |
| 4 | (49.6166, 0.1170, 0.5000) | (111.6325, 0.5912, 1.125) | (198.4667, 1.8674, 2) |
| 5 | (49.6333, 0.1337, 0.5000) | (111.6700, 0.6756, 1.125) | (198.5333, 2.1341, 2) |
| 6 | (49.6500, 0.1504, 0.5000) | (111.7075, 0.7599, 1.125) | (198.6000, 2.4008, 2) |
| 7 | (49.6625, 0.1629, 0.5000) | (111.7356, 0.8232, 1.125) | (198.6500, 2.6008, 2) |
| 8 | (4.9675, 0.1754, 0.5000) | (111.7638, 0.8865, 1.125) | (198.7000, 2.8008, 2) |
| 9 | (49.6875, 0.1879, 0.5000) | (111.7919, 0.9498, 1.125) | (198.7500, 3.0008, 2) |
| 10 | (49.7000, 0.2004, 0.5000) | (111.8200, 0.1013, 1.125) | (198.8000, 3.2008, 2) |
| 11 | (49.7100, 0.2104, 0.5000) | (111.8425, 0.1063, 1.125) | (198.8400, 3.3608, 2) |
| 12 | (49.7200, 0.2204, 0.5000) | (111.8650, 0.1114, 1.125) | (198.8800, 3.5208, 2) |
| 13 | (49.7300, 0.2304, 0.5000) | (111.8875, 0.1164, 1.125) | (198.9200, 3.6808, 2) |
| 14 | (49.7400, 0.2404, 0.5000) | (111.9100, 0.1215, 1.125) | (198.9600, 3.8408, 2) |
| 15 | (49.7500, 0.2504, 0.5000) | (111.9325, 0.1266, 1.125) | (199.0000, 4.0008, 2) |
| 16 | (49.7583, 0.2587, 0.5000) | (111.9512, 0.1308, 1.125) | (199.0333, 4.1341, 2) |
| 17 | (49.7666, 0.2670, 0.5000) | (111.9700, 0.1350, 1.125) | (199.0667, 4.2674, 2) |
| 18 | (49.7750, 0.2754, 0.5000) | (111.9887, 0.1392, 1.125) | (199.1000, 4.4008, 2) |
| 19 | (49.7833, 0.2837, 0.5000) | (112.0075, 0.1434, 1.125) | (199.1333, 4.5341, 2) |
| 20 | (49.7916, 0.2920, 0.5000) | (112.0262, 0.1477, 1.125) | (199.1667, 4.6674, 2) |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| 50 | (49.9750, 0.4754, 0.5000) | (112.4387, 2.4052, 1.125) | (199.9000, 7.6008, 2) |
| 51 | (49.9800, 0.4804, 0.5000) | (112.4500, 2.4306, 1.125) | (199.9200, 7.6808, 2) |
| 52 | (49.9850, 0.4854, 0.5000) | (112.4612, 2.4559, 1.125) | (199.9400, 7.7608, 2) |
| 53 | (49.9900, 0.4904, 0.5000) | (112.4725, 2.4812, 1.125) | (199.9600, 7.8408, 2) |
| 54 | (49.9950, 0.4954, 0.5000) | (112.4837, 2.5065, 1.125) | (199.9800, 7.9208, 2) |
| 55 | (50, 0.5000, 0.5000) | (112.4950, 2.5312, 1.125) | (200, 8, 2) |
| 56 | (50, 0.5000, 0.5000) | (112.5000, 2.5312, 1.125) | (200, 8, 2) |
| 57 | (50, 0.5000, 0.5000) | (112.5000, 2.5312, 1.125) | (200, 8, 2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Gibali, A.; Reich, S. Multidimensional Evolution Effects on Non-Cooperative Strategic Games. Mathematics 2024, 12, 2453. https://doi.org/10.3390/math12162453
Singh S, Gibali A, Reich S. Multidimensional Evolution Effects on Non-Cooperative Strategic Games. Mathematics. 2024; 12(16):2453. https://doi.org/10.3390/math12162453
Chicago/Turabian StyleSingh, Shipra, Aviv Gibali, and Simeon Reich. 2024. "Multidimensional Evolution Effects on Non-Cooperative Strategic Games" Mathematics 12, no. 16: 2453. https://doi.org/10.3390/math12162453
APA StyleSingh, S., Gibali, A., & Reich, S. (2024). Multidimensional Evolution Effects on Non-Cooperative Strategic Games. Mathematics, 12(16), 2453. https://doi.org/10.3390/math12162453







