Dynamics of a Dengue Transmission Model with Multiple Stages and Fluctuations
Abstract
:1. Introduction
2. Model Formulation
3. Survival Analysis of Infective Mosquitoes and Infective Human Beings
3.1. Fitness
3.2. Persistence in the Mean
3.3. Existence of a Unique Stationary Distribution
3.4. Extinction
4. Sensitivity Analysis and Numerical Simulations
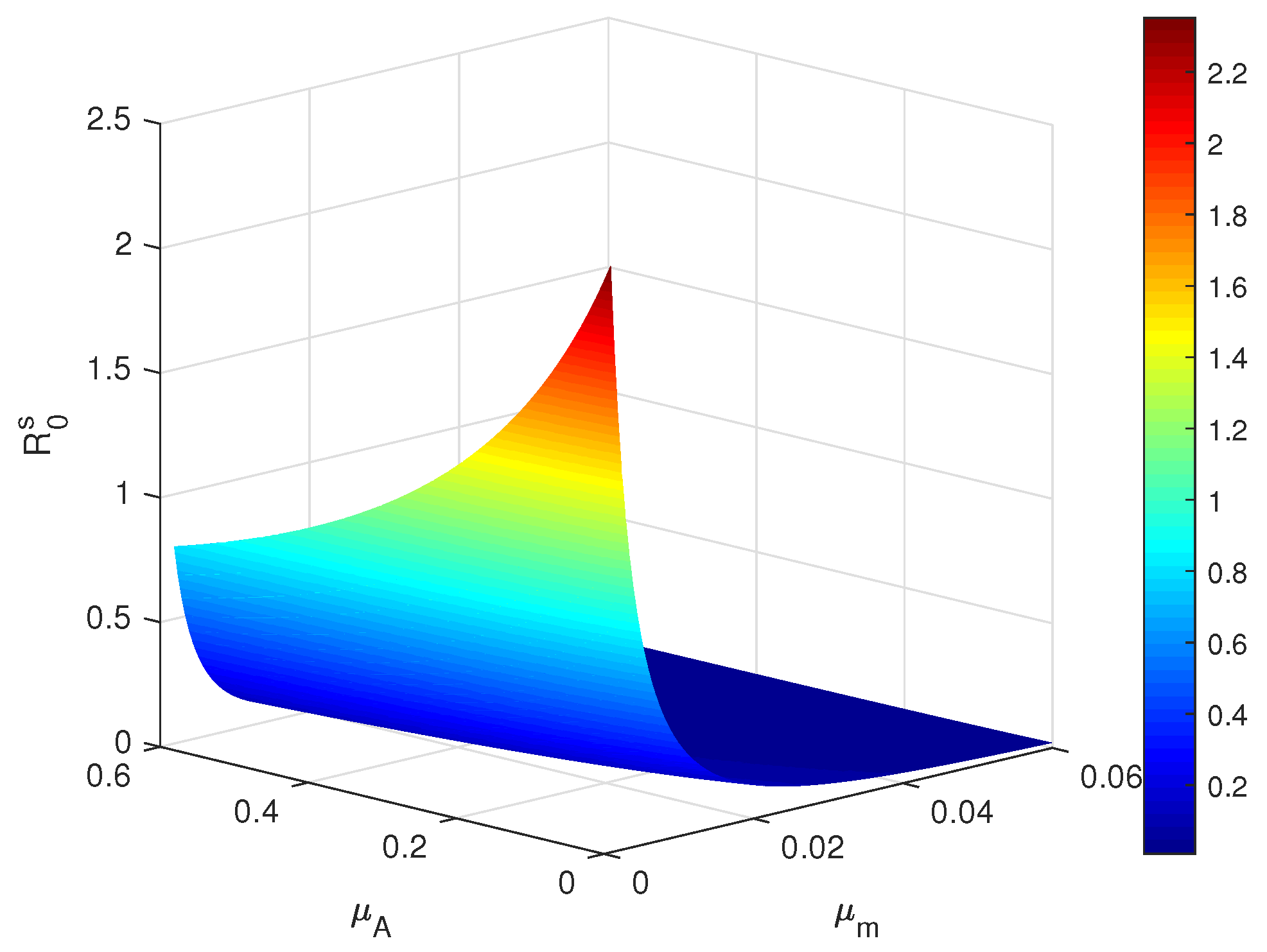
4.1. Sensitivity Analysis of Main Parameters
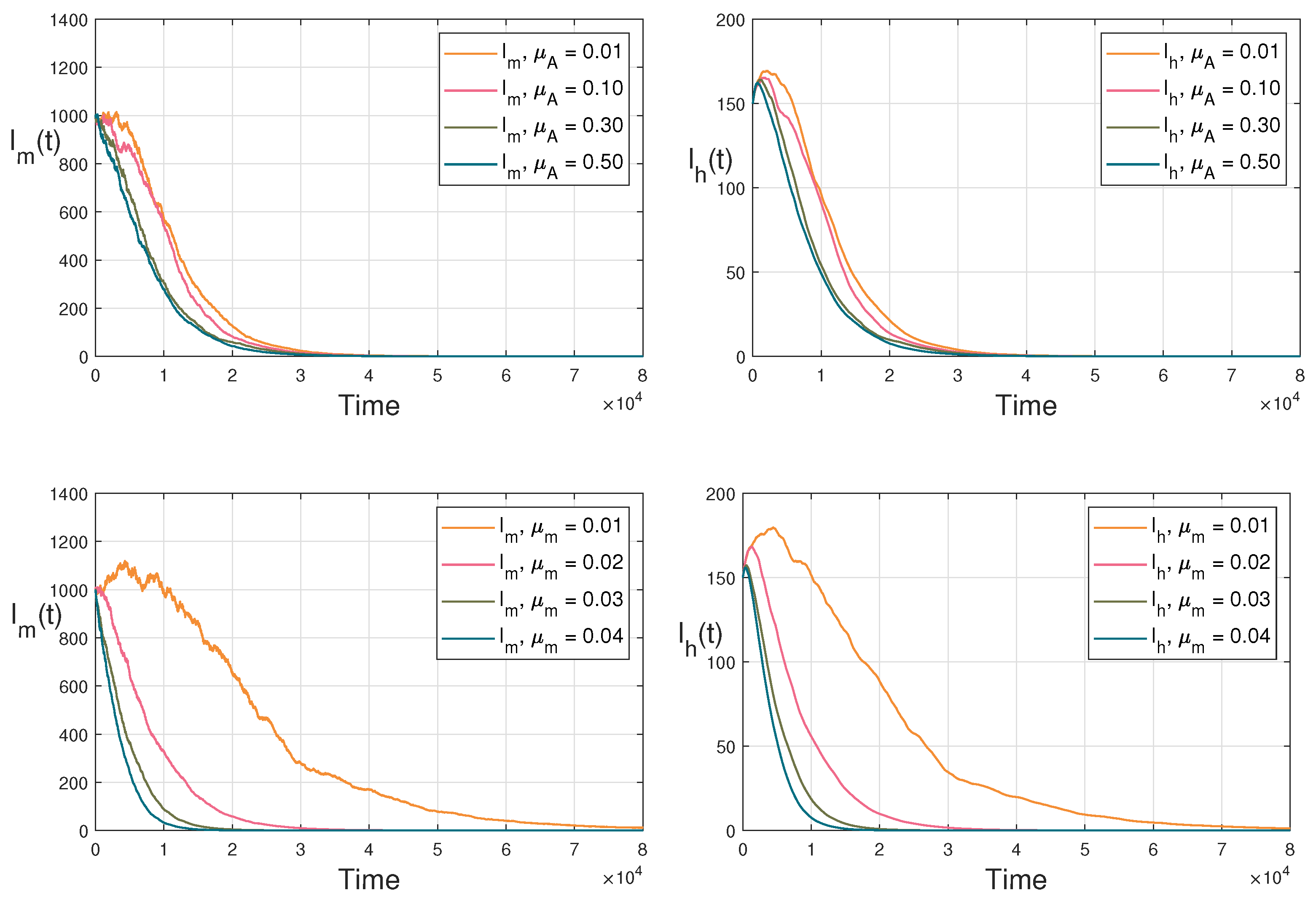
4.2. Persistence in the Mean
4.3. Extinction
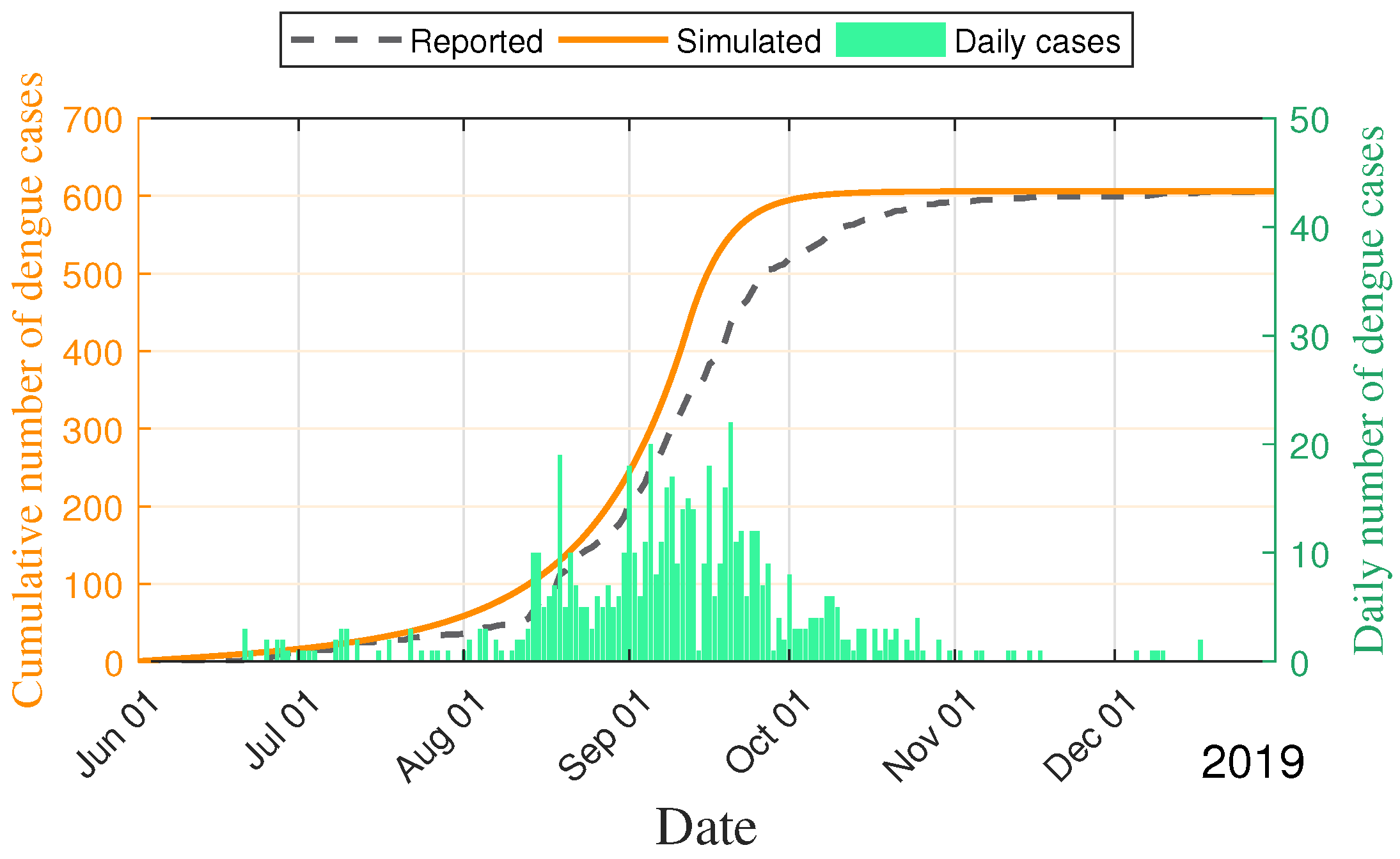
4.4. Application of Dengue in Fuzhou City
5. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Vector-Borne Disease-Key Facts. Available online: https://www.who.int/news-room/fact-sheets/detail/vector-borne-diseases (accessed on 9 May 2024).
- World Health Organization. Dengue and Severe Dengue-Key Facts. Available online: https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 9 May 2024).
- Wilder-Smith, A.; Ooi, E.E.; Horstick, O.; Wills, B. Dengue. Lancet 2019, 393, 350–363. [Google Scholar] [CrossRef]
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.G.; Reiner, R.C.; Brady, O.J.; Messina, J.P.; Gilbert, M.; Pigott, D.M.; Yi, D.; Johnson, K.; Earl, L.; Marczak, L.B.; et al. Past and future spread of the arbovirus vectors Aedes aegypti and Aedes albopictus. Nat. Microbiol. 2019, 4, 854–863. [Google Scholar] [CrossRef] [PubMed]
- Colón-González, F.J.; Sewe, M.O.; Tompkins, A.M.; Sjödin, H.; Casallas, A.; Rocklöv, J.; Caminade, C.; Lowe, R. Projecting the risk of mosquito-borne diseases in a warmer and more populated world: A multi-model, multi-scenario intercomparison modelling study. Lancet Planet. Health 2021, 5, e404–e414. [Google Scholar] [CrossRef]
- Reiter, P.; Newton, E.A.C. A model of the transmission of dengue fever with an evaluation of the impact of Ultra-Low Volume (ULV) insecticide applications on dengue epidemics. Am. J. Trop. Med. Hyg. 1992, 47, 709–720. [Google Scholar]
- Lotka, A.J. Contribution to the analysis of malaria epidemiology. II. General part (continued). Comparison of two formulae given by Sir Ronald Ross. Am. J. Epidemiol. 1923, 3, 38–45. [Google Scholar] [CrossRef]
- Jan, R.; Xiao, Y. Effect of partial immunity on transmission dynamics of dengue disease with optimal control. Math. Methods Appl. Sci. 2019, 42, 1967–1983. [Google Scholar] [CrossRef]
- Xue, L.; Jin, X.; Zhu, H. Assessing the impact of serostatus-dependent immunization on mitigating the spread of dengue virus. J. Math. Biol. 2023, 87, 5. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Yankson, E.; Okyere, E.; Sun, G.; Jin, Z.; Jan, R.; Fatmawati. Optimal control and cost-effectiveness analysis for dengue fever model with asymptomatic and partial immune individuals. Results. Phys. 2021, 31, 104919. [Google Scholar] [CrossRef]
- Xue, L.; Ren, X.; Magpantay, F.; Sun, W.; Zhu, H. Optimal control of mitigation strategies for dengue virus transmission. Bull. Math. Biol. 2021, 83, 8. [Google Scholar] [CrossRef]
- Bian, G.; Xu, Y.; Lu, P.; Xie, Y.; Xi, Z. The endosymbiotic bacterium wolbachia induces resistance to dengue v irus in Aedes aegypti. PLoS Pathog. 2010, 6, e1000833. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Tang, S.; Cheke, R.A. Models to assess how best to replace dengue virus vectors with Wolbachia-infected mosquito populations. Math. Biosci. 2015, 269, 164–177. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, L.; Huang, Q.; Yan, R.; Zheng, B. A mosquito population suppression model with a saturated Wolbachia release strategy in seasonal succession. J. Math. Biol. 2023, 86, 51. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wang, Z.; Yan, Y.; Qu, Y.; Hou, L.; Li, Y.; Chu, C.; Woodward, A.; Schikowski, T.; Saldiva, P.H.N.; et al. Association between hydrological conditions and dengue fever incidence in coastal southeastern China from 2013 to 2019. JAMA Netw. Open. 2023, 6, e2249440. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, X.; Tang, S.; Cheke, R.A. The relative importance of key meteorological factors affecting numbers of mosquito vectors of dengue fever. PLoS Neglected Trop. Dis. 2023, 17, e0011247. [Google Scholar] [CrossRef] [PubMed]
- Abdelrazec, A.; Gumel, A.B. Mathematical assessment of the role of temperature and rainfall on mosquito population dynamics. J. Math. Biol. 2017, 74, 1351–1395. [Google Scholar] [CrossRef] [PubMed]
- Adams, B.; Boots, M. How important is vertical transmission in mosquitoes for the persistence of dengue? Insights from a mathematical model. Epidemics 2010, 2, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Amaku, M.; Coutinho, F.A.B.; Raimundo, S.M.; Lopez, L.F.; Burattini, M.N.; Massad, E. A comparative yanalysis of the relative efficacy of vector-control strategies against dengue fever. Bull. Math. Biol. 2014, 76, 697–717. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Chen, J.; Feng, X.; Ruan, S. Analysis of a dengue model with vertical transmission and application to the 2014 dengue outbreak in Guangdong Province, China. Bull. Math. Biol. 2018, 80, 2633–2651. [Google Scholar] [CrossRef]
- Li, M.; Sun, G.; Yakob, L.; Zhu, H.; Jin, Z.; Zhang, W. The driving force for 2014 dengue outbreak in Guangdong, China. PLoS ONE 2016, 11, e0166211. [Google Scholar] [CrossRef]
- Defterli, O. Comparative analysis of fractional order dengue model with temperature effect via singular and non-singular operators. Chaos Solitons Fractals 2021, 144, 110654. [Google Scholar] [CrossRef]
- Hamdan, N.I.; Kilicman, A. Mathematical modelling of dengue transmission with intervention strategies using fractional derivatives. Bull. Math. Biol. 2022, 84, 138. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Li, X.; Fang, B.; Ruan, S. Global properties of vector-host disease models with time delays. J. Math. Biol. 2017, 74, 1397–1423. [Google Scholar] [CrossRef] [PubMed]
- Abdelrazec, A.; Bélair, J.; Shan, C.; Zhu, H. Modeling the spread and control of dengue with limited public health resources. Math. Biosci. 2016, 271, 136–145. [Google Scholar] [CrossRef] [PubMed]
- Hajji, M.E.; Aloufi, M.F.S.; Alharbi, M.H. Influence of seasonality on Zika virus transmission. AIMS Math. 2024, 9, 19361–19384. [Google Scholar] [CrossRef]
- Otero, M.; Solari, H.G. Stochastic eco-epidemiological model of dengue disease transmission by Aedes aegypti mosquito. Math. Biosci. 2010, 223, 32–46. [Google Scholar] [CrossRef] [PubMed]
- Jovanović, M.; Krstić, M. Stochastically perturbed vector-borne disease models with direct transmission. Appl. Math. Model. 2012, 36, 5214–5228. [Google Scholar] [CrossRef]
- Britton, T.; Traoré, A. A stochastic vector-borne epidemic model: Quasi-stationarity and extinction. Math. Biosci. 2017, 289, 89–95. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A. Stationary distribution and extinction of a stochastic dengue epidemic model. J. Frankl. Inst. 2018, 355, 8891–8914. [Google Scholar] [CrossRef]
- Sun, W.; Xue, L.; Yan, X. Stability of a dengue epidemic model with independent stochastic perturbations. J. Math. Anal. Appl. 2018, 468, 998–1017. [Google Scholar] [CrossRef]
- Liu, P.; Din, A.; Zenab. Impact of information intervention on stochastic dengue epidemic model. Alex. Eng. J. 2021, 60, 5725–5739. [Google Scholar] [CrossRef]
- Guo, M.; Hu, L.; Nie, L. Stochastic dynamics of the transmission of dengue fever virus between mosquitoes and humans. Int. J. Biomath. 2021, 14, 2150062. [Google Scholar] [CrossRef]
- Kiouach, D.; El-idrissi, S.E.A.; Sabbar, Y. A novel mathematical analysis and threshold reinforcement of a stochastic dengue epidemic model with Lévy jumps. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107092. [Google Scholar] [CrossRef]
- Valdez, L.D.; Sibona, G.J.; Diaz, L.A.; Contigiani, M.S.; Condat, C.A. Effects of rainfall on Culex mosquito population dynamics. J. Theor. Biol. 2017, 421, 28–38. [Google Scholar] [CrossRef]
- Wang, X.; Tang, S.; Wu, J.; Xiao, Y.; Cheke, R.A. A combination of climatic conditions determines major within-season dengue outbreaks in Guangdong Province, China. Parasites Vectors 2019, 12, 45. [Google Scholar] [CrossRef] [PubMed]
- Fuzhou City Bureau of Statistics. Available online: https://tjj.fuzhou.gov.cn/zz/zwgk/tjzl/tjxx/202111/t20211115_4242144.htm (accessed on 9 May 2024).
- Van Den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Lan, X.; Chen, G.; Zhou, R.; Zheng, K.; Cai, S.; Wei, F.; Jin, Z.; Mao, X. An SEIHR model with age group and social contact for analysis of Fuzhou COVID-19 large wave. Infect. Dis. Model. 2024, 9, 728–743. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Jiang, D. The threshold of a stochastic SIS epidemic model with vaccination. Appl. Math. Comput. 2014, 243, 718–727. [Google Scholar] [CrossRef]
- Mao, X.; Marion, G.; Renshaw, E. Environmental Brownian noise suppresses explosions in population dynamics. Stoch. Process Appl. 2002, 97, 95–110. [Google Scholar] [CrossRef]
- Wei, F.; Xue, R. Stability and extinction of SEIR epidemic models with generalized nonlinear incidence. Math. Comput. Simul. 2020, 170, 1–15. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Horwood Publishing Limited: Chichester, UK, 2007. [Google Scholar]
- Zhao, Y.; Jiang, D. Dynamics of stochastically perturbed SIS epidemic model with vaccination. Abstr. Appl. Anal. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Li, D.; Wei, F.; Mao, X. Stationary distribution and density function of a stochastic SVIR epidemic model. J. Frankl. Inst. 2022, 359, 9422–9449. [Google Scholar] [CrossRef]
- Li, W.; Cai, S.; Zhai, X.; Ou, J.; Zheng, K.; Wei, F.; Mao, X. Transmission dynamics of symptom-dependent HIV/AIDS models. Math. Biosci. Eng. 2024, 21, 1819–1843. [Google Scholar] [CrossRef]
- Wei, F.; Jiang, H.; Zhu, Q. Dynamical behaviors of a heroin population model with standard incidence rates between distinct patches. J. Frankl. Inst. 2021, 358, 4994–5013. [Google Scholar] [CrossRef]
- Ikeda, N.; Watanabe, S. A comparison theorem for solutions of stochastic differential equations and its applications. Osaka J. Math. 1977, 14, 619–633. [Google Scholar]
- Peng, S.; Zhu, X. Necessary and sufficient condition for comparison theorem of 1-dimensional stochastic differential equations. Stoch. Process Appl. 2006, 116, 370–380. [Google Scholar] [CrossRef]
- Wei, F.; Wang, C. Survival analysis of a single-species population model with fluctuations and migrations between patches. Appl. Math. Model. 2020, 81, 113–127. [Google Scholar] [CrossRef]
- Kutoyants, Y.A. Statistical Inference for Ergodic Diffusion Processes; Springer: London, UK, 2004. [Google Scholar]
- Berman, A.; Plemmons, R.J. Nonnegative Matrices in the Mathematical Sciences; SIAM Publisher: Philadelphia, PA, USA, 1994. [Google Scholar]
- Fuzhou City Bureau of Statistics. Available online: https://tjj.fuzhou.gov.cn/zz/zwgk/tjzl/ndbg/202105/t20210524_4105019.htm (accessed on 9 May 2024).
- Mao, X.; Wei, F.; Wiriyakraikul, T. Positivity preserving truncated Euler-Maruyama Method for stochastic Lotka-Volterra competition model. J. Comput. Appl. Math. 2021, 394, 113566. [Google Scholar] [CrossRef]
- Cai, Y.; Mao, X.; Wei, F. An advanced numerical scheme for multi-dimensional stochastic Kolmogorov equations with superlinear coefficients. J. Comput. Appl. Math. 2024, 437, 115472. [Google Scholar] [CrossRef]
- Zhai, X.; Li, W.; Wei, F.; Mao, X. Dynamics of an HIV/AIDS transmission model with protection awareness and fluctuations. Chaos Solitons Fractals 2023, 169, 113224. [Google Scholar] [CrossRef]
- Wang, L.; Teng, Z.; Ji, C.; Feng, X.; Wang, K. Dynamical behaviors of a stochastic malaria model: A case study for Yunnan, China. Phys. Stat. Mech. Appl. 2019, 521, 435–454. [Google Scholar] [CrossRef]



| Variable | Definition |
|---|---|
| A | Number of aquatic mosquitoes |
| Number of susceptible mosquitoes with no dengue infection | |
| Number of infective mosquitoes | |
| Number of susceptible human beings | |
| Number of infective human beings | |
| Number of recovered human beings |
| Parameter | Unit | Definition | Range | Source |
|---|---|---|---|---|
| dimensionless | Constant recruitment rates of aquatic mosquitoes | / | ||
| dimensionless | Constant recruitment rates of human beings | / | ||
| Death rate of aquatic mosquitoes | [21] | |||
| Maturity proportion of aquatic mosquitoes | [26] | |||
| Death rate of adult mosquitoes | [22] | |||
| Average recovery time in human population | [21] | |||
| b | Average biting rate | / | ||
| dimensionless | Probability of dengue virus transmitted from to | [22] | ||
| dimensionless | Probability of dengue virus spread from to | [22] | ||
| Death rate of human beings | [10,38] |
| Parameter | (I) | (II) | (III) | (IV) | ||||
|---|---|---|---|---|---|---|---|---|
| Value | Source | Value | Source | Value | Source | Value | Source | |
| 2000 | Fitted | 100 | Fitted | 2000 | Fitted | 1,800,000 | Fitted | |
| (0, 0.06] | Fitted | 0.05 | [22] | 0.03 | [22] | Fitted | ||
| b | Fitted | Fitted | Fitted | Fitted | ||||
| 0 | Fitted | 0 | Fitted | 0 | Fitted | [2] | ||
| (0.01, 0.6] | Fitted | 0.01 | [21] | 0.01 | [21] | 0.01 | [21] | |
| 0.1428 | [21] | 0.1428 | [21] | 0.1428 | [21] | 0.1428 | [21] | |
| 0.75 | [22] | 0.6 | [22] | 0.75 | [22] | 0.7 | [22] | |
| 0.5 | [22] | 0.5 | [22] | 0.4 | [22] | 0.5 | [22] | |
| 0.3 | [26] | 0.1 | [26] | [0.1, 0.7] | Fitted | 0.2 | [26] | |
| [10] | [10] | [10] | [38] | |||||
| 0.56 | Fitted | 100 | Fitted | 0.56 | Fitted | [38,54] | ||
| Variable | (I) | (II) | (III) | (IV) |
|---|---|---|---|---|
| 40,000 | 20,000 | 40,000 | 9,000,000 | |
| 20,000 | 20,000 | 20,000 | 10,000,000 | |
| 1,000 | 10 | 1,000 | 15 | |
| 15,000 | 15,596 | 15,000 | 8,291,266 | |
| 150 | 2 | 150 | 2 | |
| 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Cai, S.; Chen, G.; Zheng, K.; Wei, F.; Jin, Z.; Mao, X.; Xie, J. Dynamics of a Dengue Transmission Model with Multiple Stages and Fluctuations. Mathematics 2024, 12, 2491. https://doi.org/10.3390/math12162491
Wang Z, Cai S, Chen G, Zheng K, Wei F, Jin Z, Mao X, Xie J. Dynamics of a Dengue Transmission Model with Multiple Stages and Fluctuations. Mathematics. 2024; 12(16):2491. https://doi.org/10.3390/math12162491
Chicago/Turabian StyleWang, Zuwen, Shaojian Cai, Guangmin Chen, Kuicheng Zheng, Fengying Wei, Zhen Jin, Xuerong Mao, and Jianfeng Xie. 2024. "Dynamics of a Dengue Transmission Model with Multiple Stages and Fluctuations" Mathematics 12, no. 16: 2491. https://doi.org/10.3390/math12162491






