Adaptive Fixed-Time Safety Concurrent Control of Vehicular Platoons with Time-Varying Actuator Faults under Distance Constraints
Abstract
:1. Introduction
- (1)
- A new Nussbaum function with smaller amplitudes is designed, with which the unknown time-varying actuator fault directions are dealt with, without depending on the precise boundary values for the efficiency loss factor.
- (2)
- A unified BLF method based on the bias constraint function is proposed, which can transform the asymmetric constraint into a symmetric one, making the control design simpler.
- (3)
- Together with the proposed Nussbaum function and BLF method, an adaptive fixed-time sliding mode control scheme is developed for a third-order platoon system, with which the individual vehicle stability and string stability can all be guaranteed within a settling time.
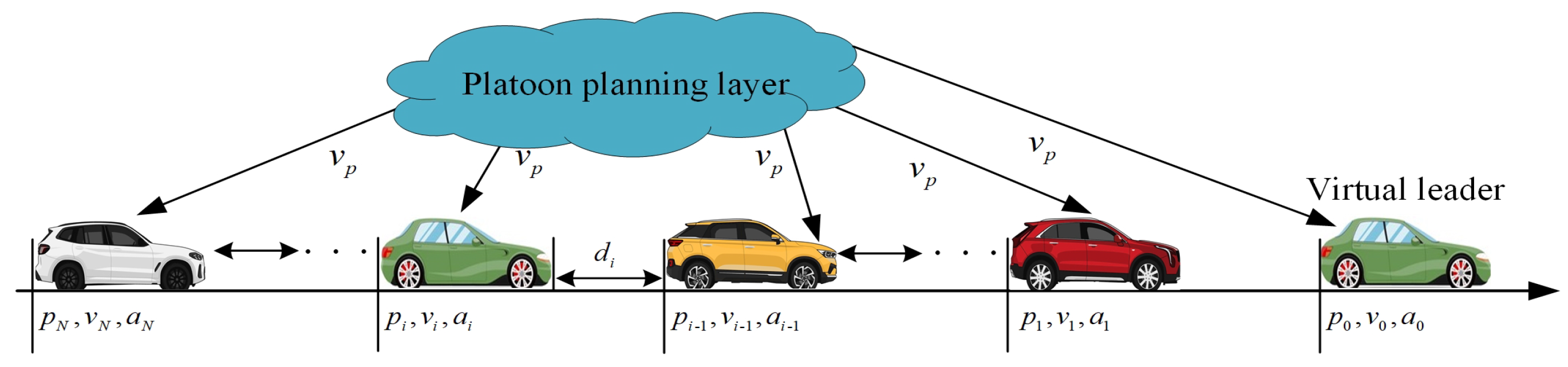
2. Preliminaries and Problem Formulation
2.1. Preliminaries
2.2. Vehicle Dynamics
2.3. Distance Constraints
- Then, the error constraints become
2.4. Control Objectives
- (1)
- Fixed-time individual vehicle stability: A desired inter-vehicle distance can be maintained in a given time (i.e., and when ).
- (2)
- Fixed-time string stability: After a given time , the inter-vehicle spacing tracking error does not increase along the platoon, that iswhere denotes the Laplace transform of and .
3. Fixed-Time Sliding Mode Surface and Nussbaum Function
3.1. Sliding Mode Surface Design
3.2. Nussbaum Function
4. Controller Design and Stability Analysis
4.1. Controller Design
4.2. Stability Analysis
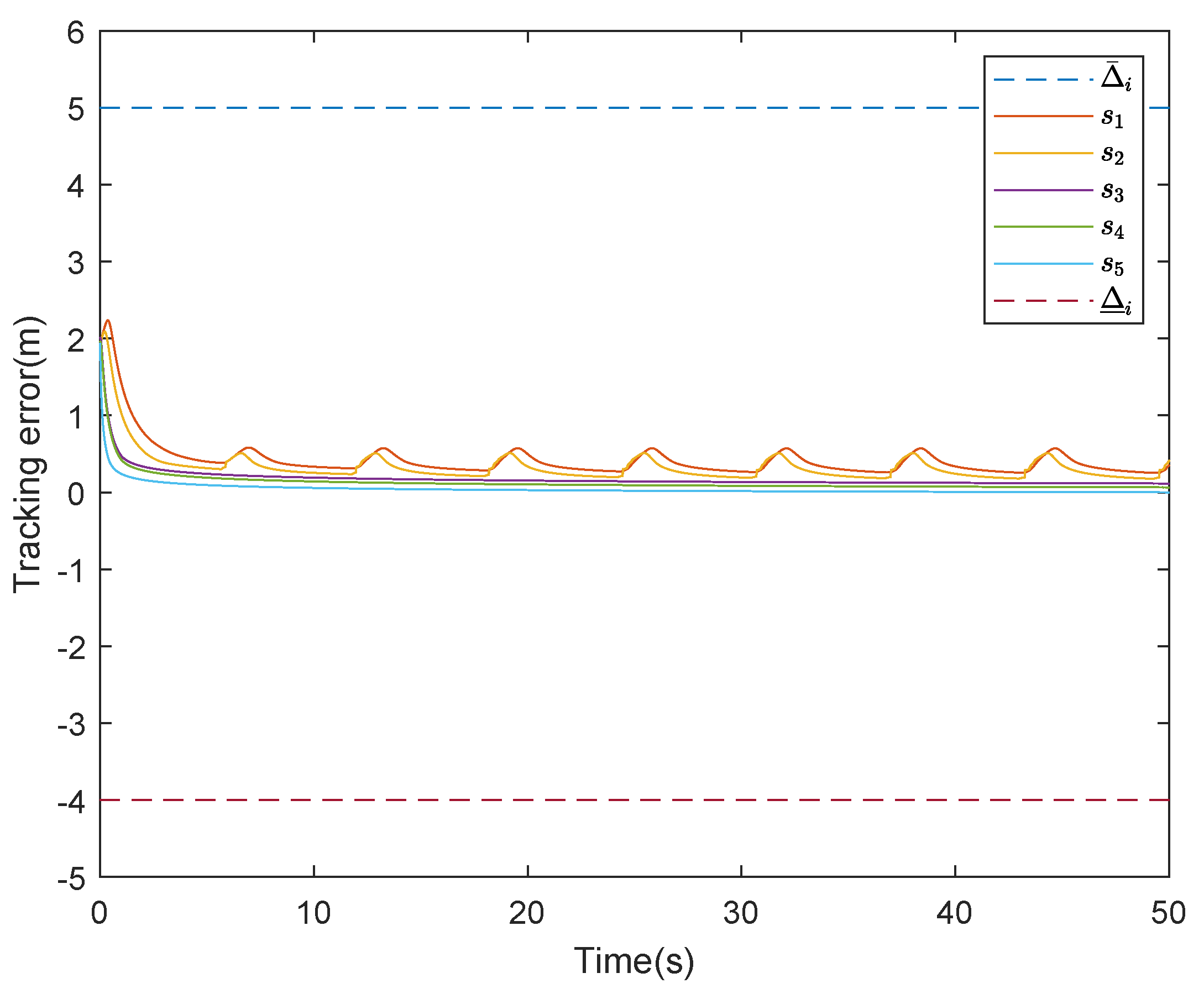
5. Simulation Studies
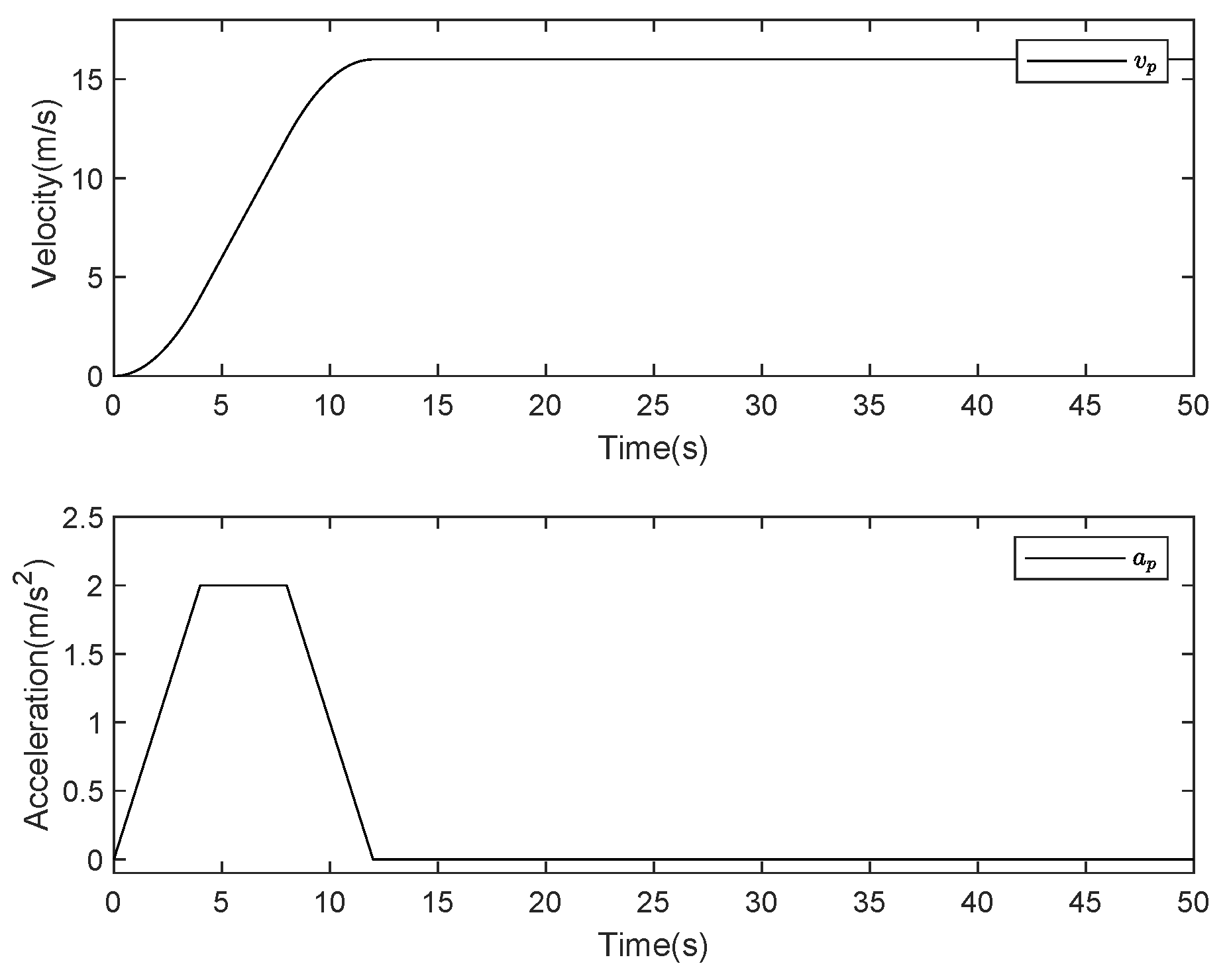
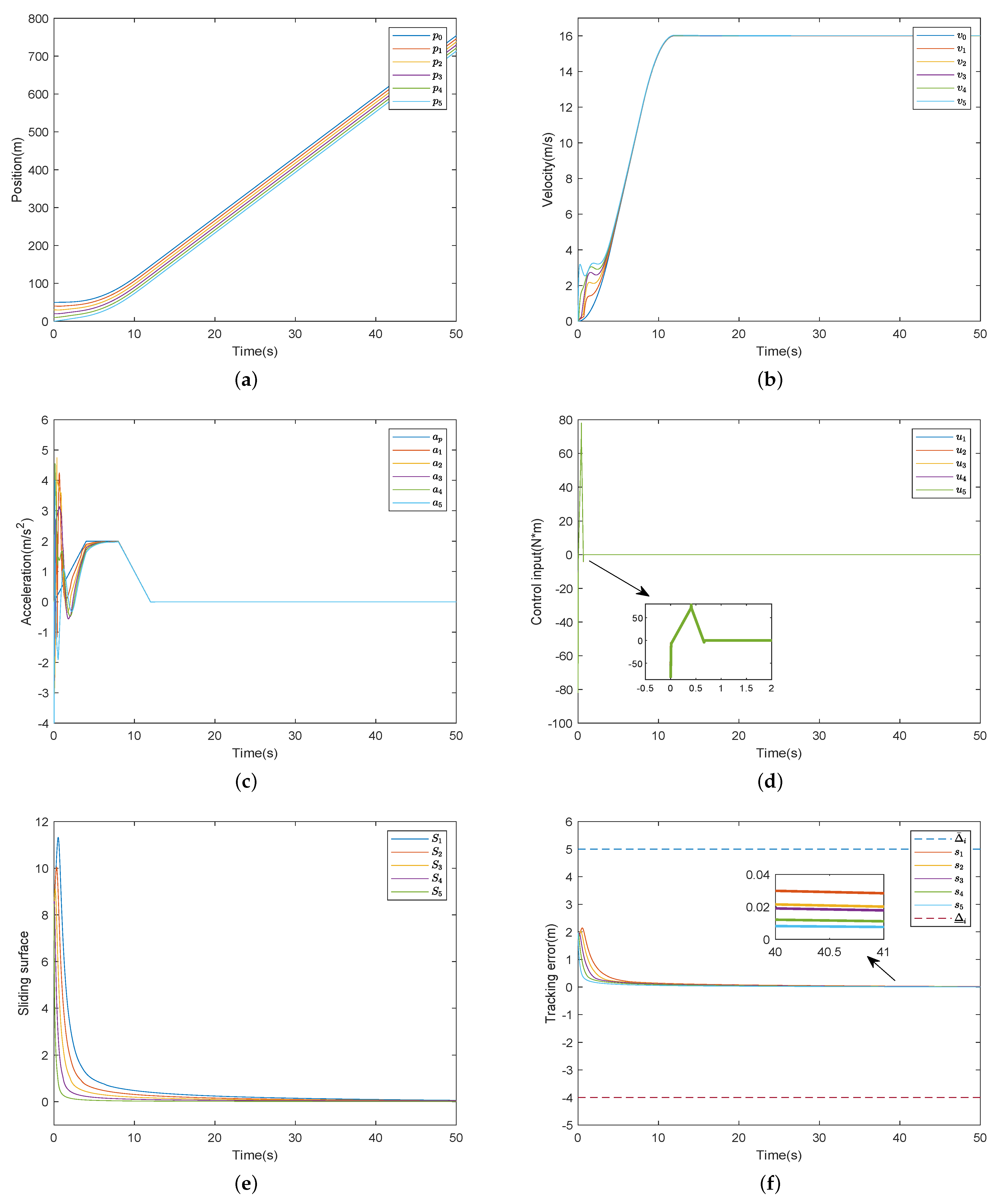
5.1. The Results of the Proposed Control Scheme without Actuator Faults
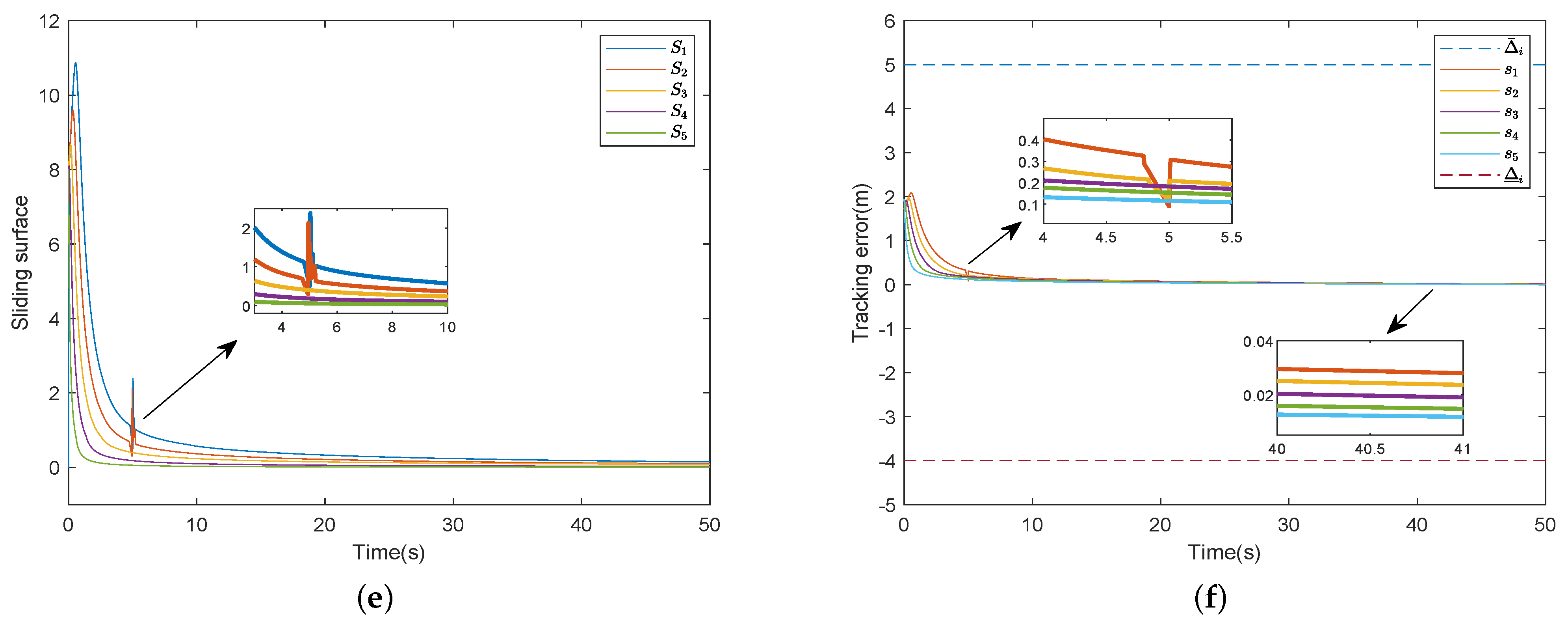
5.2. The Effect of Unknown Actuator Fault Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Li, S.E.; Li, K.; Wang, L. Stability margin improvement of vehicular platoon considering undirected topology and asymmetric control. IEEE Trans. Control Syst. Technol. 2016, 24, 1253–1265. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.-L.; Wang, J.; Zhang, X.M. A scalable adaptive approach to multi-vehicle formation control with obstacle avoidance. IEEE/CAA J. Autom. Sin. 2022, 9, 990–1004. [Google Scholar] [CrossRef]
- Rödönyi, G. An adaptive spacing policy guaranteeing string stability in multi-brand ad hoc platoons. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1902–1912. [Google Scholar] [CrossRef]
- Wang, J.; Luo, X.; Wong, C.; Guan, X. Specified-time vehicular platoon control with flexible safe distance constraint. IEEE Trans. Veh. Technol. 2019, 68, 10489–10503. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhu, F.; Xu, D.; Guo, S.; Dai, Y. Event-triggered multi-lane fusion control for 2-D vehicle platoon systems with distance constraints. IEEE Trans. Intell. Veh. 2023, 8, 1498–1511. [Google Scholar] [CrossRef]
- Guo, G.; Li, D. Adaptive sliding mode control of vehicular platoons with prescribed tracking performance. IEEE Trans. Veh. Technol. 2019, 68, 7511–7520. [Google Scholar] [CrossRef]
- Guo, X.; Wang, J.; Liao, F.; Teo, R.S.H. Distributed adaptive integrated-sliding-mode controller synthesis for string stability of vehicle platoons. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2419–2429. [Google Scholar] [CrossRef]
- Guo, X.G.; Xu, W.D.; Wang, J.L.; Park, J.H.; Yan, H. BLF-based neuroadaptive fault-tolerant control for nonlinear vehicular platoon with time-varying fault directions and distance restrictions. IEEE Trans. Intell. Transp. Syst. 2022, 23, 12388–12398. [Google Scholar] [CrossRef]
- Aaron, D.; Xu, X.; Grizzle, W.; Tabuada, P. Control barrier function based quadratic programs for safety critical systems. IEEE Trans. Autom. Control 2017, 62, 3861–3876. [Google Scholar]
- Wu, Z.; Albalawi, F.; Zhang, Z.; Zhang, J.; Durand, H.; Panagiotis, D. Control Lyapunov-barrier function-based model predictive control of nonlinear systems. Automatica 2019, 109, 108508. [Google Scholar] [CrossRef]
- Wei, H.; Liu, J.; Chen, H.; Liu, L. Fuzzy adaptive control for vehicular platoons with constraints and unknown dead-zone input. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4403–4412. [Google Scholar] [CrossRef]
- Lei, Y.; Li, X.; Tong, C. Distributed adaptive asymptotic tracking of 2-D vehicular platoon systems with actuator faults and spacing constraints. IEEE/CAA J. Autom. Sin. 2023, 10, 1352–1354. [Google Scholar] [CrossRef]
- Guo, X.G.; Xu, W.D.; Wang, J.L.; Park, J.H. Distributed neuroadaptive fault-tolerant sliding-mode control for 2-D plane vehicular platoon systems with spacing constraints and unknown direction faults. Automatica 2021, 129, 109–675. [Google Scholar] [CrossRef]
- Li, L.; Luo, H.; Ding, X.; Yang, Y.; Peng, X. Performance-based fault detection and fault-tolerant control for automatic control systems. Automatica 2019, 99, 308–316. [Google Scholar] [CrossRef]
- Xiao, Y.; Dong, X. Distributed fault-tolerant containment control for nonlinear multi-agent systems under directed network topology via hierarchical approach. IEEE/CAA J. Autom. Sin. 2021, 8, 806–816. [Google Scholar] [CrossRef]
- Pan, C.; Chen, Y.; Liu, Y.; Ali, I. Adaptive resilient control for interconnected vehicular platoon with fault and saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10210–10222. [Google Scholar] [CrossRef]
- Guo, G.; Li, P.; Hao, L.Y. A new quadratic spacing policy and adaptive fault-tolerant platooning with actuator saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1200–1212. [Google Scholar] [CrossRef]
- Gao, Z.Y.; Zhang, Y.; Guo, G. Finite-time fault-tolerant prescribed performance control of connected vehicles with actuator saturation. IEEE Trans. Veh. Technol. 2023, 72, 1438–1448. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, F.; Liu, Z.; Zhang, Y.; Chen, C.L.P. Fixed-time fuzzy control for a class of nonlinear systems. IEEE Trans. Cybern. 2022, 52, 3880–3887. [Google Scholar] [CrossRef]
- Yang, H.; Ye, D. Adaptive fixed-time bipartite tracking consensus control for unknown nonlinear multi-agent systems: An information classification mechanism. Inf. Sci. 2018, 459, 238–254. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Ren, B.; Ge, S.S.; Tee, K.P.; Lee, T.H. Adaptive neural control for output feedback nonlinear systems using a barrier Lyapunov function. IEEE Trans. Neural Netw. 2010, 21, 1339–1345. [Google Scholar] [PubMed]
- Shahvali, M.; Shojaei, K. Distributed adaptive neural control of nonlinear multi-agent systems with unknown control directions. Nonlinear Dyn. 2016, 83, 2213–2228. [Google Scholar] [CrossRef]
- Li, D.; Guo, G. Prescribed performance concurrent control of connected vehicles with nonlinear third-order dynamics. IEEE Trans. Veh. Technol. 2020, 69, 14793–14802. [Google Scholar] [CrossRef]
- Kwon, J.W.; Chwa, D. Adaptive bidirectional platoon control using a coupled sliding mode control method. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2040–2048. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Y.; Guo, G. Adaptive fixed-time prescribed performance control of vehicular platoons with unknown dead-zone and actuator saturation. Int. J. Robust Nonlinear Control 2023, 33, 1231–1253. [Google Scholar] [CrossRef]

| The vehicle’s mass | The external disturbances | ||
| The air density | The drag coefficient | ||
| The frontal cross-area | The control input | ||
| The engine time constant | The engine/brake input |
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| (kg) | 1550 | 1450 | 1520 | 1510 | 1390 |
| (s) | 0.15 | 0.25 | 0.32 | 0.41 | 0.35 |
| (kg/m3) | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 |
| (m2) | 2.2 | 2.2 | 2.2 | 2.2 | 2.2 |
| 0.414 | 0.414 | 0.414 | 0.414 | 0.414 | |
| (N) | 236.2 | 236.2 | 236.2 | 236.2 | 236.2 |
| (m) | 4 | 4 | 4 | 4 | 4 |
| 0.1 | 0.1 | 0.1 | 800 | 5000 | 0.9 | 3/7 | 5/3 | 0.2 |
| 5 | 0.001 | 2 | 0.01 | 10 | 1 | 10 | 0.0001 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Wei, Z.; Liu, Y.; Gao, Z. Adaptive Fixed-Time Safety Concurrent Control of Vehicular Platoons with Time-Varying Actuator Faults under Distance Constraints. Mathematics 2024, 12, 2560. https://doi.org/10.3390/math12162560
Liu W, Wei Z, Liu Y, Gao Z. Adaptive Fixed-Time Safety Concurrent Control of Vehicular Platoons with Time-Varying Actuator Faults under Distance Constraints. Mathematics. 2024; 12(16):2560. https://doi.org/10.3390/math12162560
Chicago/Turabian StyleLiu, Wei, Zhongyang Wei, Yuchen Liu, and Zhenyu Gao. 2024. "Adaptive Fixed-Time Safety Concurrent Control of Vehicular Platoons with Time-Varying Actuator Faults under Distance Constraints" Mathematics 12, no. 16: 2560. https://doi.org/10.3390/math12162560





