Polynomial Iterative Learning Control (ILC) Tracking Control Design for Uncertain Repetitive Continuous-Time Linear Systems Applied to an Active Suspension of a Car Seat †
Abstract
1. Introduction
2. Problem Statement and Preliminaries
Stability along the Pass for 2D Repetitive Systems
- (i)
- A is stable and
- (ii)
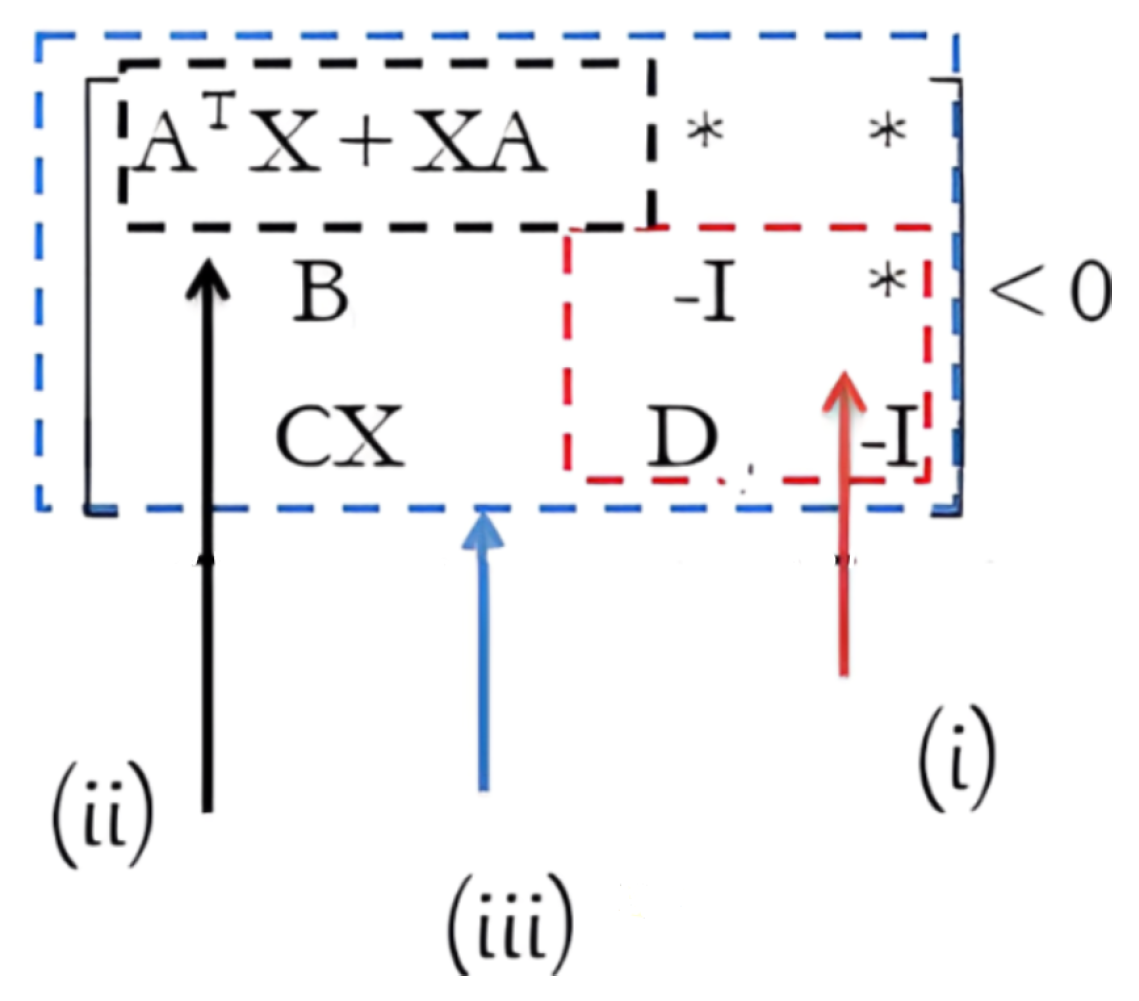
- There exists a positive symmetric matrix X such that the following LMI is feasible:
3. Main Results
3.1. Control Objective
- (A1) The desired output is given a prior over the same time duration; it is assumed that the initial resetting condition is satisfied, i.e., .
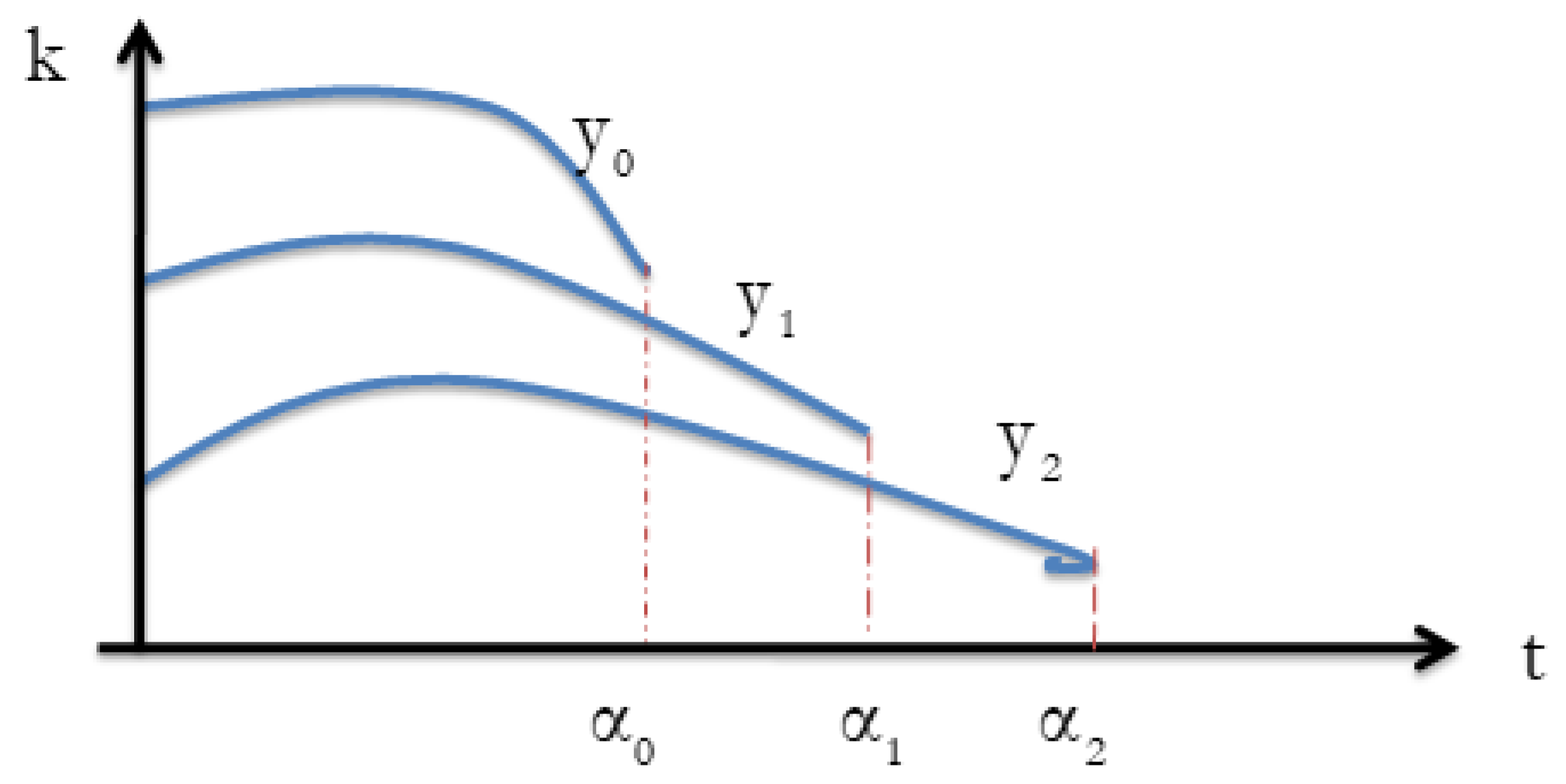
- (A2) The initial state remains the same at each iteration, i.e., . For any given assumption A1 and A2, one desirable objective in ILC is that converges monotonically to when k tends to infinity for all t within the time interval since it can guarantee reasonable transients during the learning process [3]. In the sense of the, norm, this objective can be transformed by considering the index [8].where is a prescribed scalar and is the tracking error at the kth iteration, expressed asObviously, the norm error can be guaranteed to converge monotonically along the iteration axis k if holds for any .
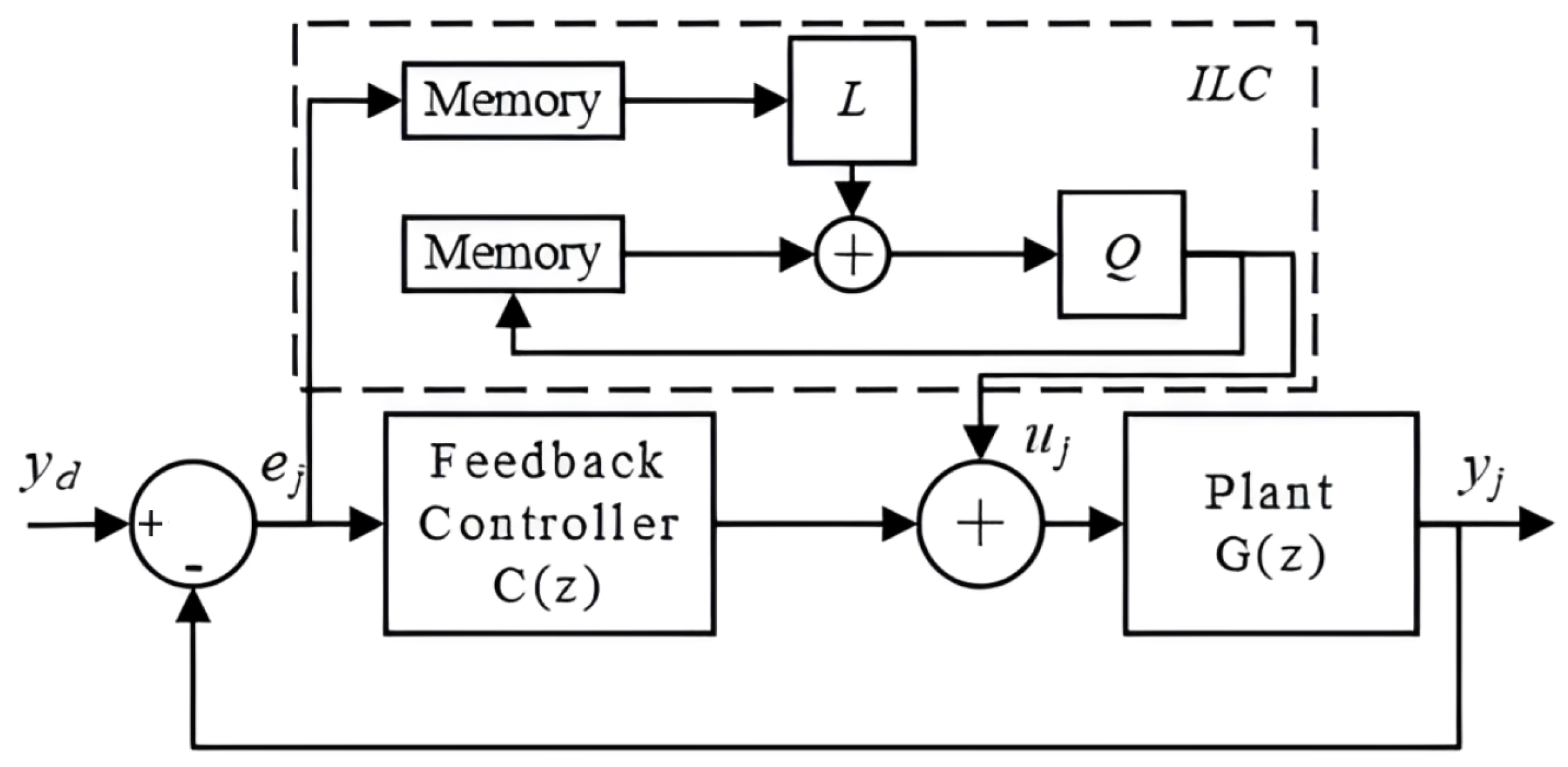
3.2. ILC Tracking Control
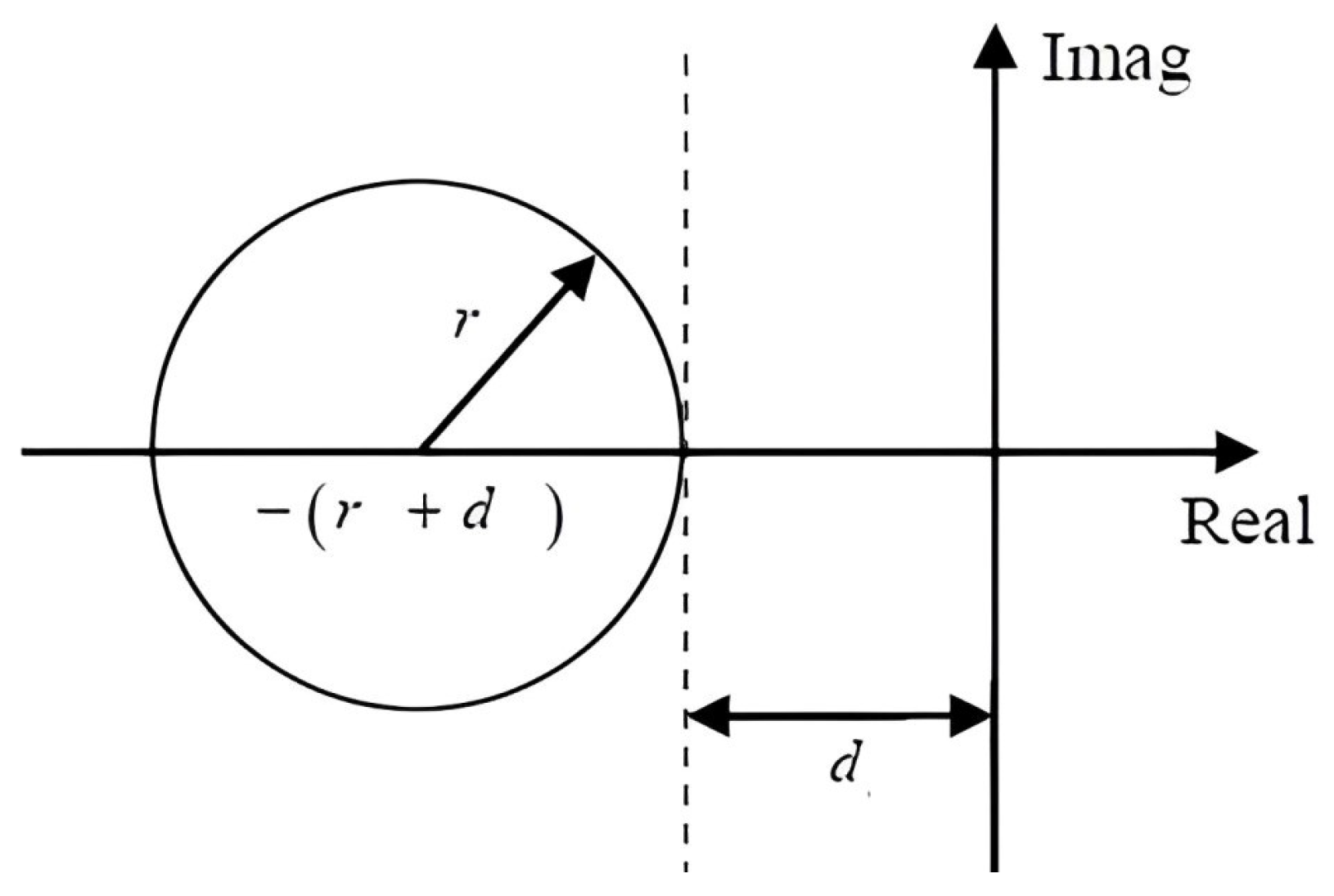
3.3. ILC Tracking Control Using D-Stability along the Pass
3.4. D-Stability along the Pass for Continuous Linear Repetitive Process
3.5. Polynomial ILC Control
- Introducing a novel polynomial-based approach to iterative learning control, which offers a flexible and intuitive framework for defining desired trajectories.
- Advancing existing techniques by providing a systematic methodology for designing and optimizing polynomial-based control laws for repetitive systems.
- Demonstrating improved tracking performance and robustness compared to traditional ILC methods, particularly in applications with complex and time-varying dynamics. Overall, Poly-ILC represents a significant advancement in the field of iterative learning control, offering a powerful and versatile approach for achieving accurate and reliable tracking in repetitive systems.
4. Uncertain LRP Systems
4.1. Problem Formulation
4.2. Poly-Quadratic Stability
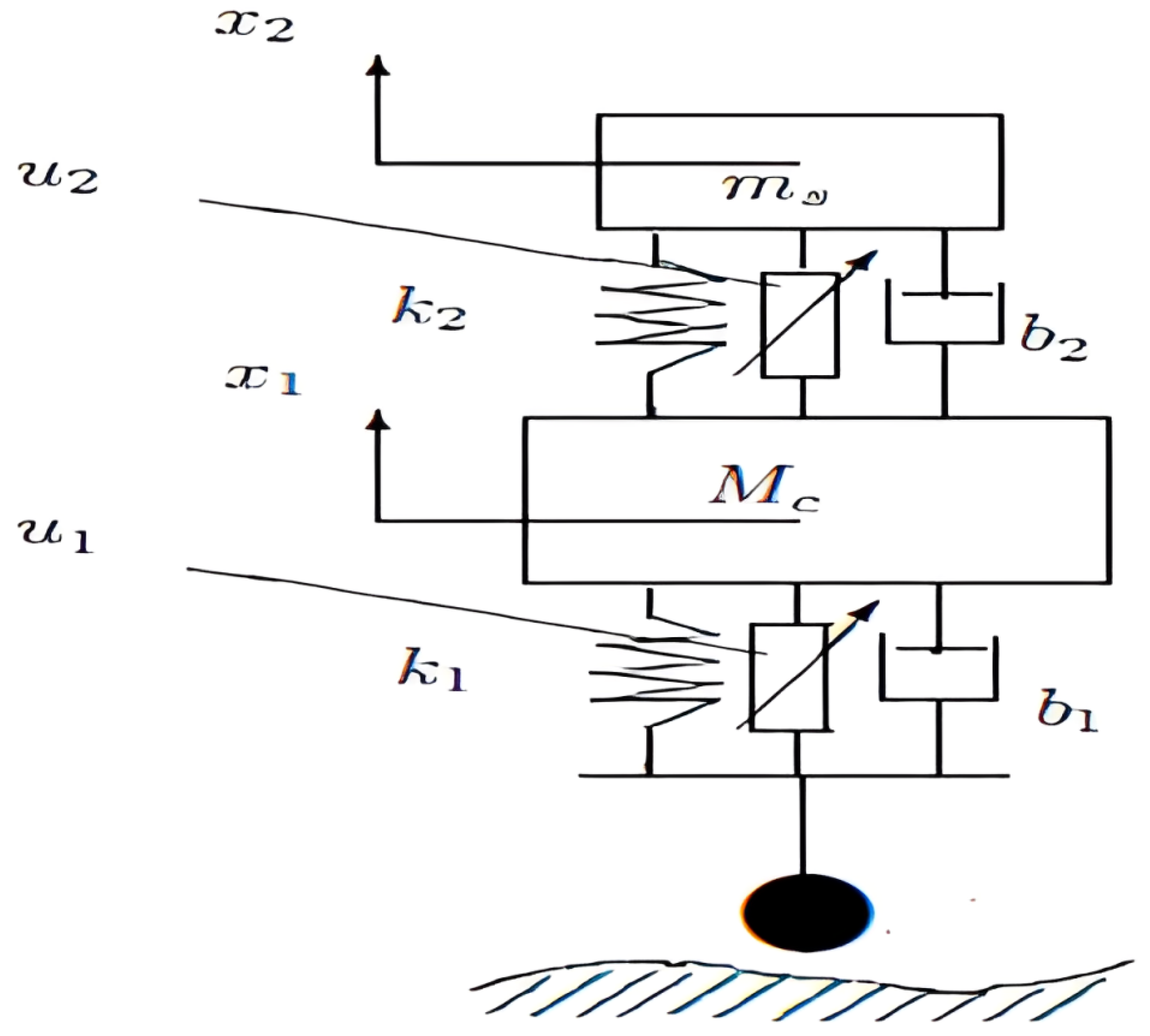
5. Numerical Examples
5.1. Comparison between D-ILC Tracking Control and D-Poly-ILC Tracking Control
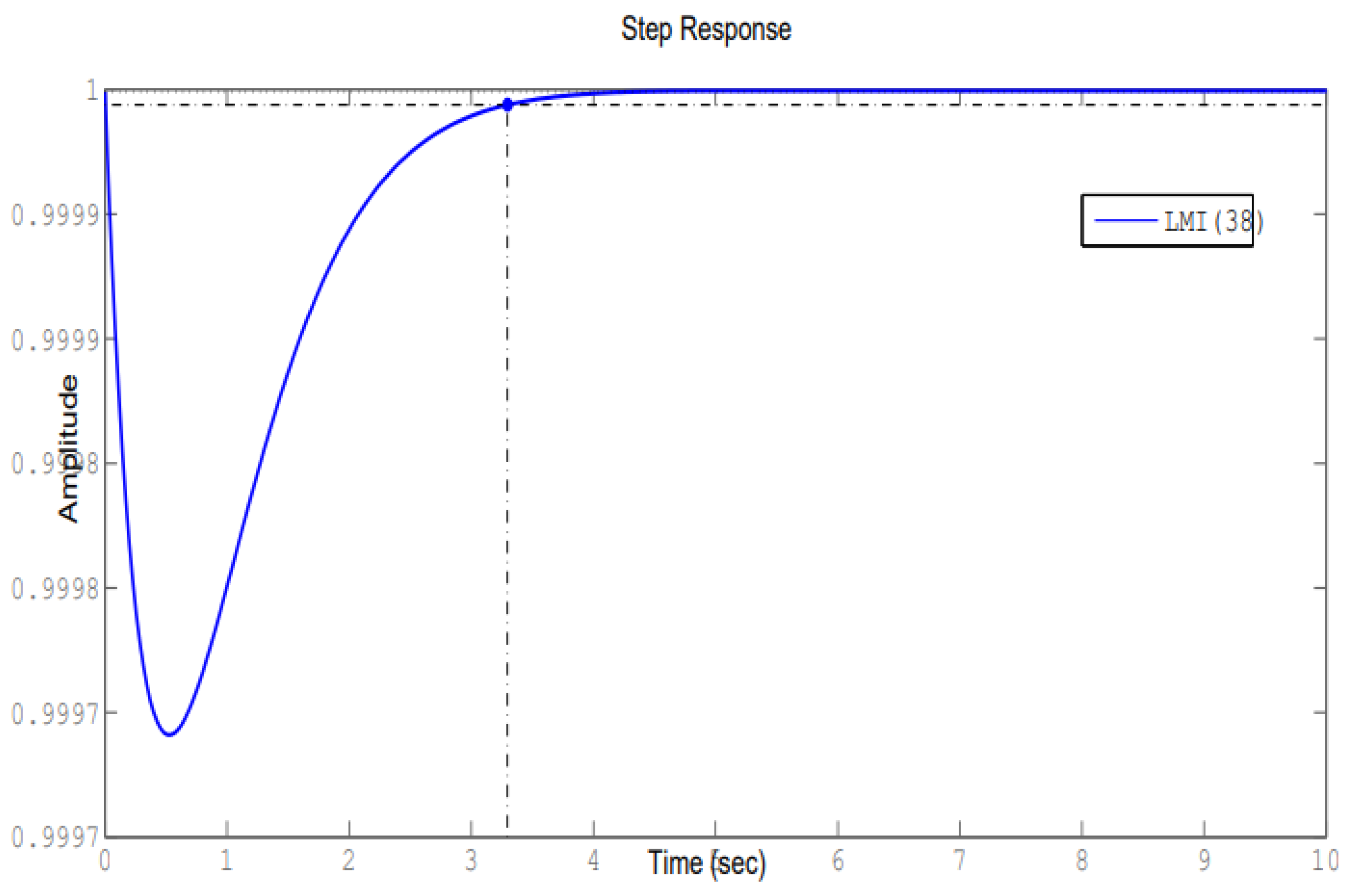
5.1.1. ILC Controller for Desired Performances
- Overshoot .
- Setting time at .
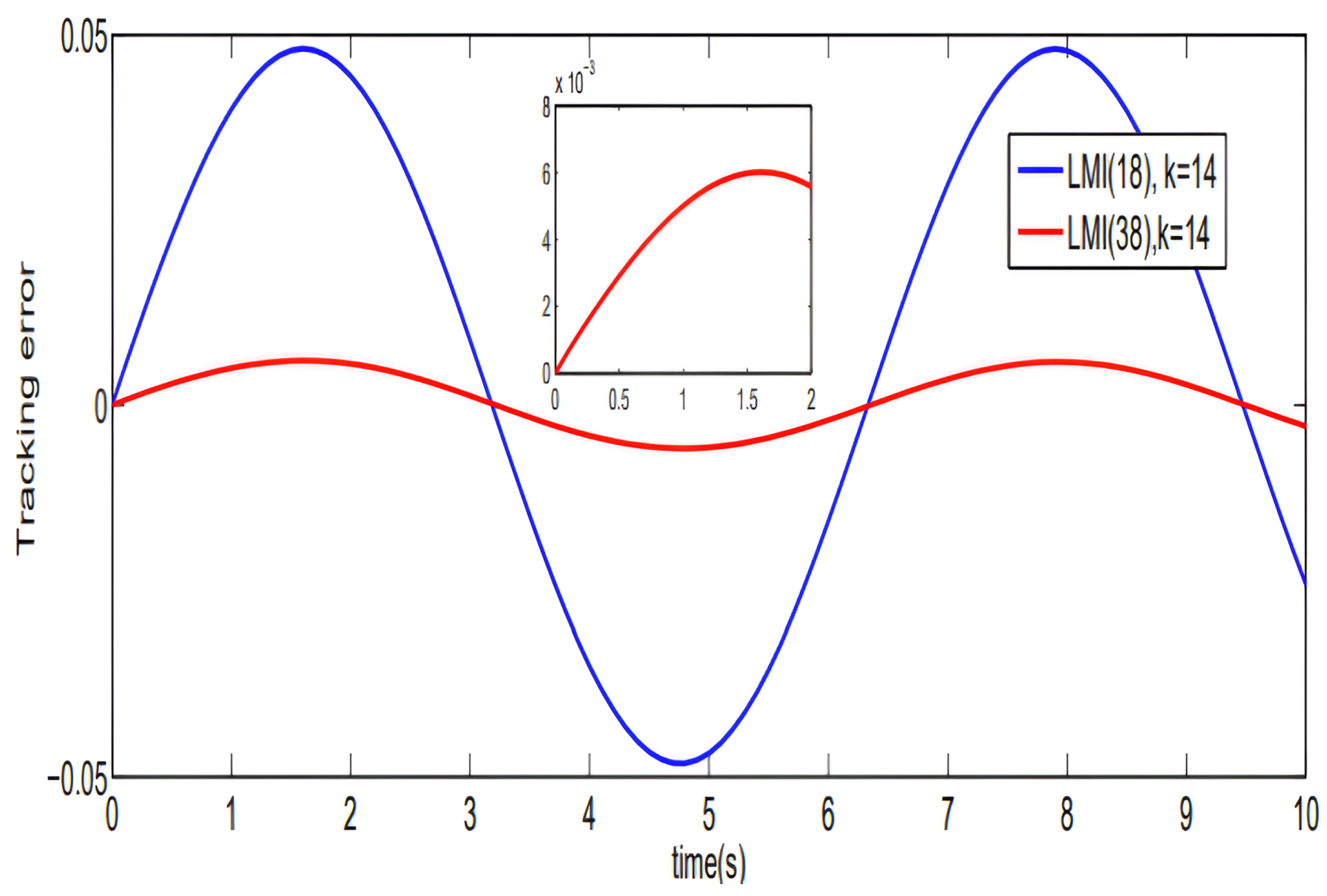
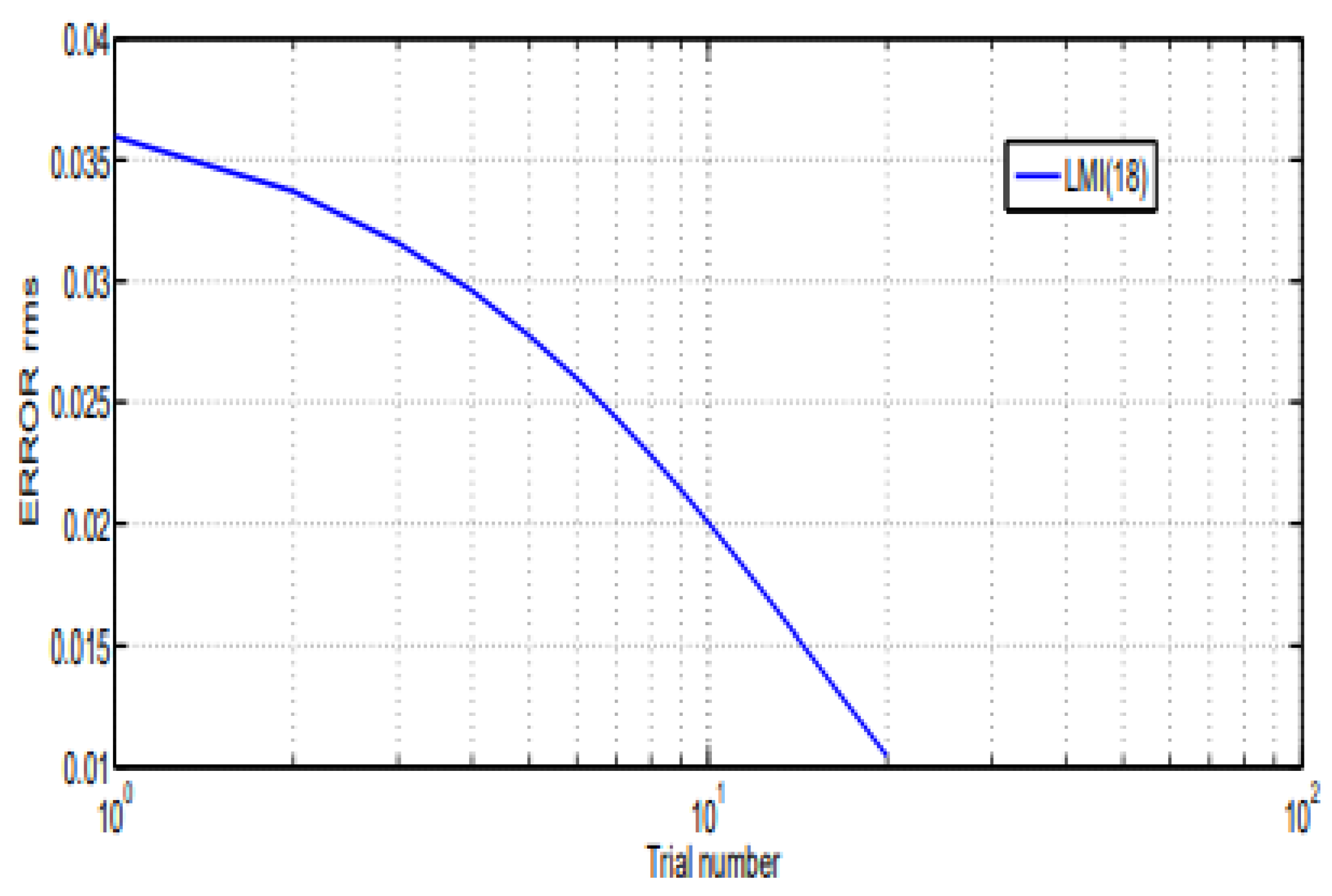
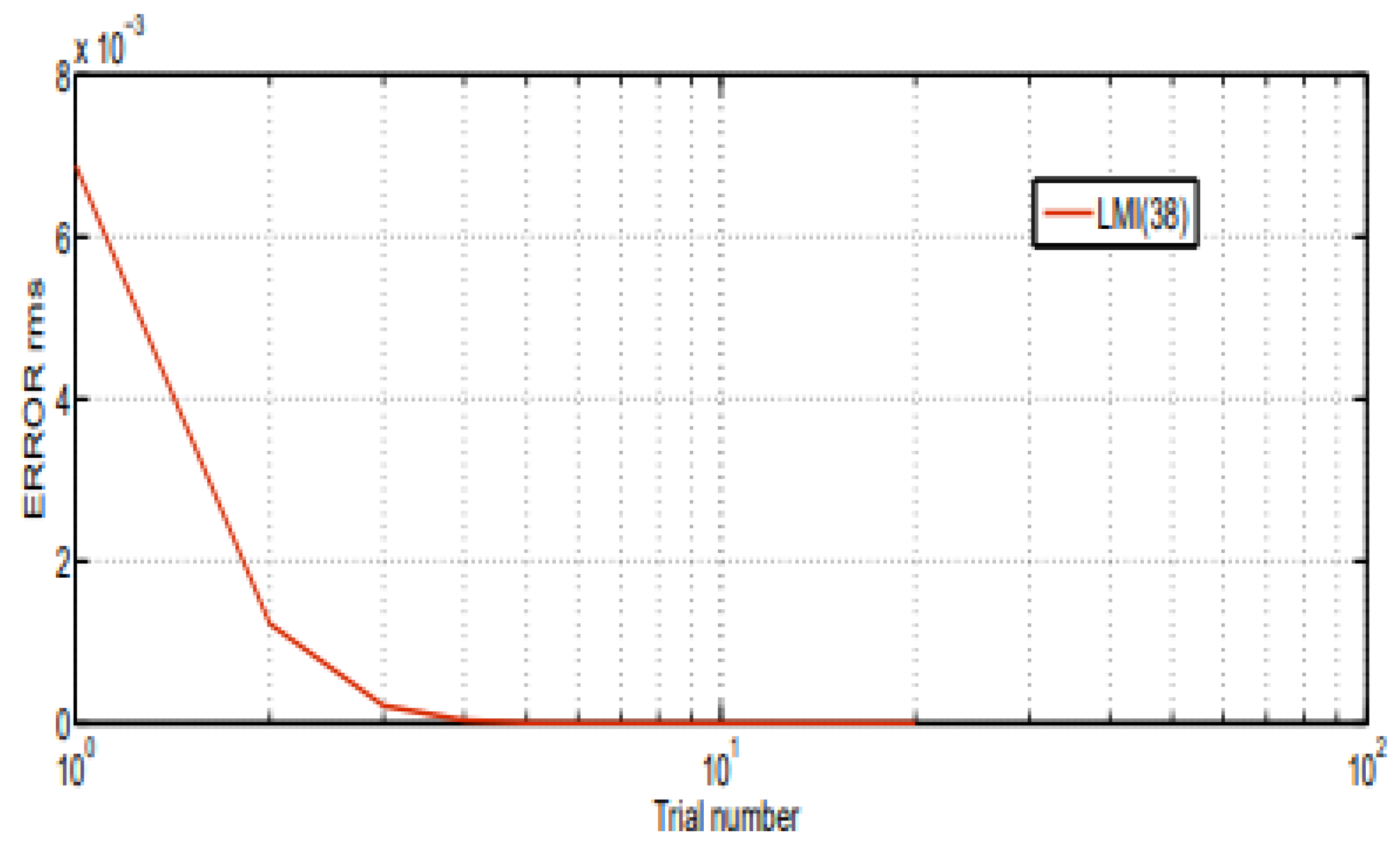
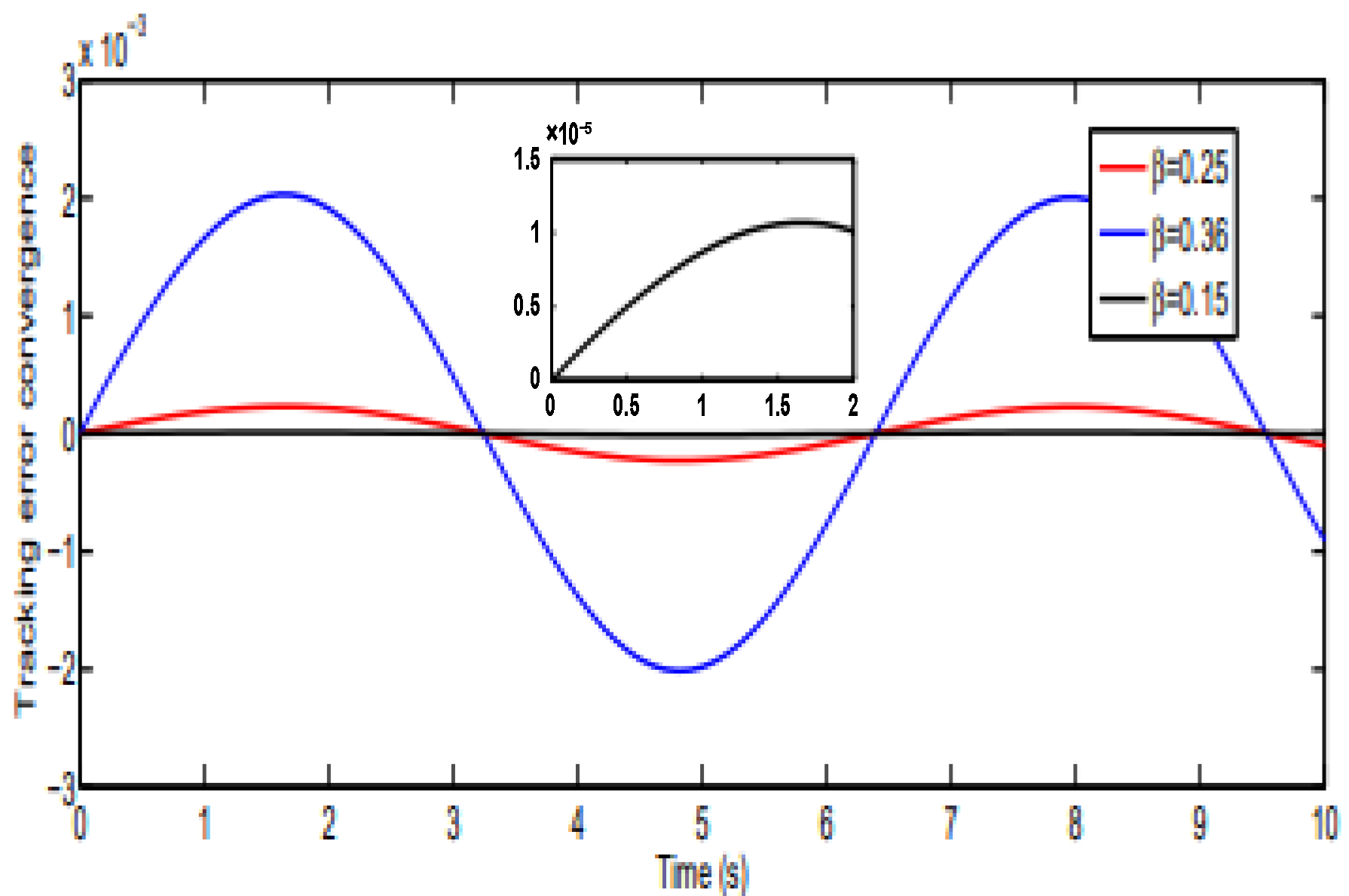
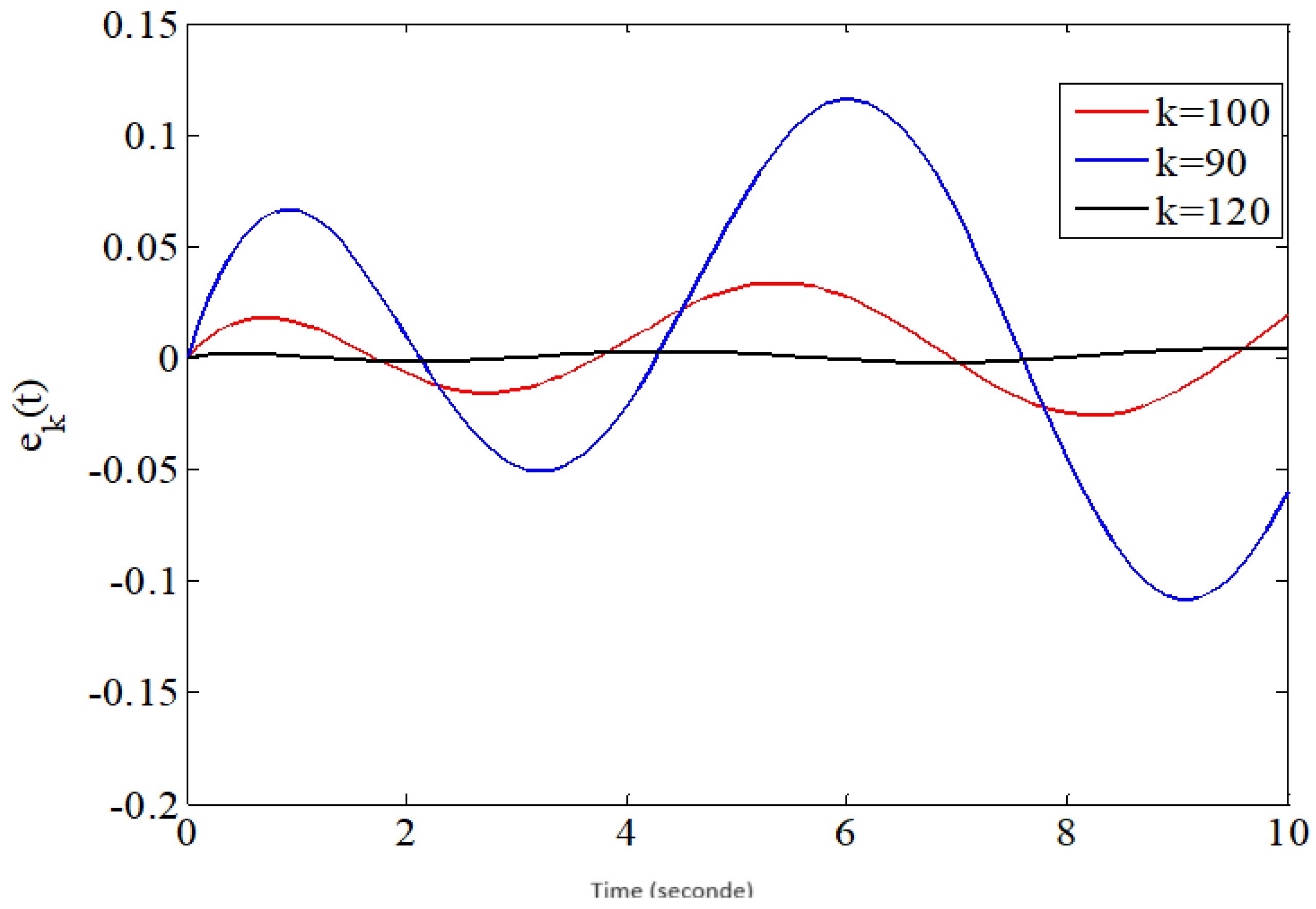
5.1.2. Tracking Error Convergence
5.1.3. Discussion
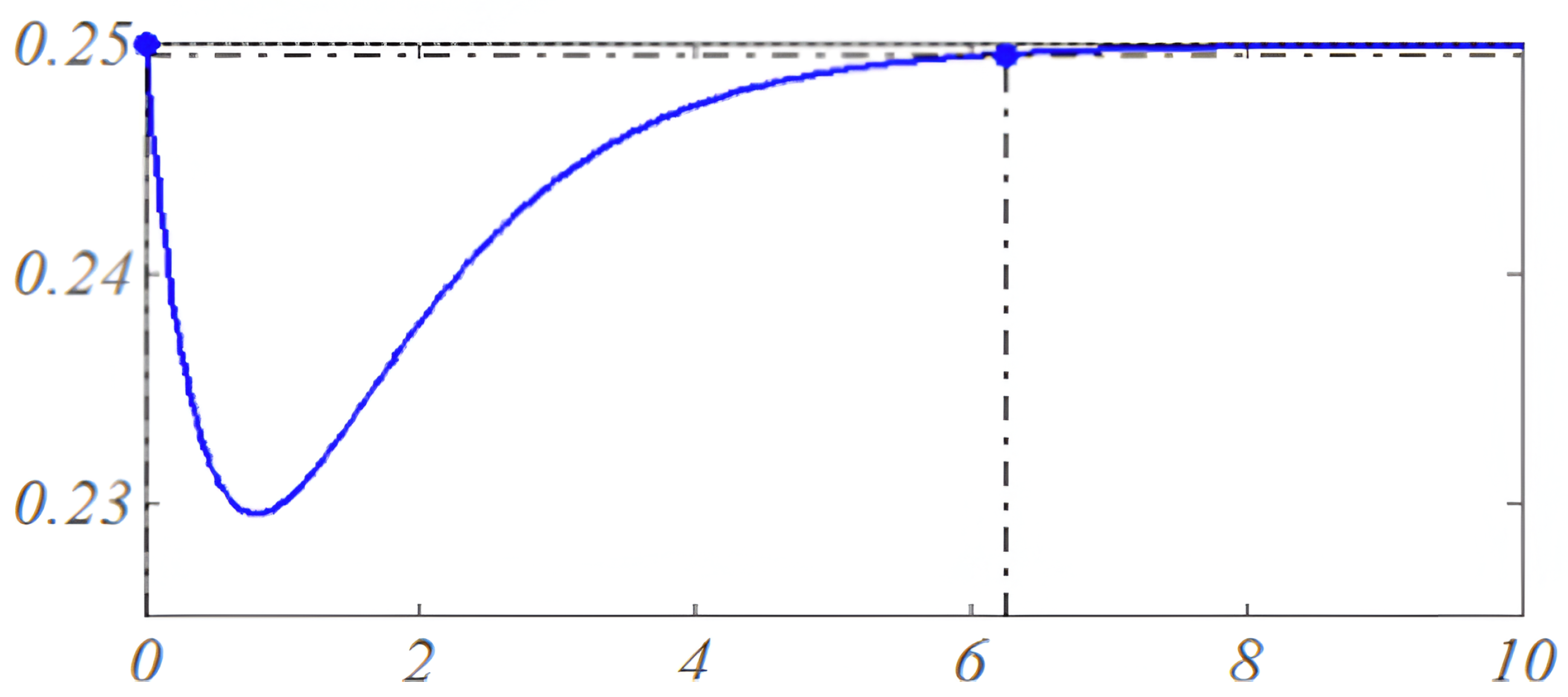
5.2. Uncertain Case
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arimoto, S.; Kawamura, M. Bettering operations of robots by learning. J. Robot. Syst. 1984, 2, 123–140. [Google Scholar] [CrossRef]
- Paszke, W.; Galkowski, K.; Rogers, E. Repetitive process based iterative learning control design using frequency domain analysis. In Proceedings of the IEEE Multi-Conference on Systems and Control, Dubrovnik, Croatia, 3–5 October 2012; pp. 3–6. [Google Scholar]
- Rogers, E.; Galkowski, K.; Owens, D.H. Control Systems Theory and Applications for Linear Repetitive Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; pp. 96–140. [Google Scholar]
- Hmamed, A.; Alfidi, M.; Benzaouia, A.; Tadeo, F. LMI conditions for robust stability of 2D linear discrete-time systems. Math. Probl. Eng. 2008, 2008, 356124. [Google Scholar] [CrossRef]
- Mansouri, B.; Manamanni, N.; Guelton, K.; Kruszewski, A.; Guerra, T.M. Output feedback LMI tracking control conditions with H1 criterion for uncertain and disturbed T-S models. Inf. Sci. 2011, 179, 393–414. [Google Scholar]
- Wu, L.; Su, X.; Shi, P. Mixed H2/H∞ approach to fault detection of discrete linear repetitive processes. J. Frankl. Inst. 2011, 348, 393–414. [Google Scholar] [CrossRef]
- Paszke, W.; Bachelier, O. New Robust stability and stabilization conditions for linear repetitive processes. In Proceedings of the International Workshop on Multidimensional (nD) Systems, Thessaloniki, Greece, 29 June–1 July 2009; pp. 1–6. [Google Scholar]
- Van De Wijdeven, J.J.M.; Donkers, M.C.F.; Bosgra, O.H. Iterative learning control for uncertain systems: Non causal finite time interval robust control design. Int. J. Robust Nonlinear Control. 2011, 21, 1645–1666. [Google Scholar] [CrossRef]
- Paszke, W. Analysis and synthesis of multidimensional system classes using linear matrix inequality methods. In Lecture Notes in Control and Computer Science, Volume 8; Springer: Berlin/Heidelberg, Germany, 2005; pp. 2298–2302. [Google Scholar]
- Chen, Y.; Wen, C.; Sun, M. A robust high-order P-type iterative learning controller using current iteration tracking error. Int. J. Control 1997, 68, 331–342. [Google Scholar] [CrossRef]
- Li, B.; Riaz, S.; Zhao, Y. Experimental Validation of Iterative Learning Control for DC/DC Power Converters. Energies 2023, 16, 6555. [Google Scholar] [CrossRef]
- Jiang, Z.; Chu, B. Norm Optimal Iterative Learning Control: A Data-Driven Approach. IFAC 2022, 55, 482–487. [Google Scholar] [CrossRef]
- Wei, Y.S.; Yang, X.; Shang, W.; Chen, Y.Y. Higher-Order Iterative Learning Control with Optimal Control Gains Based on Evolutionary Algorithm for Nonlinear System. Complexity 2021, 2021, 4281006. [Google Scholar] [CrossRef]
- Paszke, W.; Rapisarda, P.; Rogers, E.; Steinbuch, M. Dissipative stability theory for linear repetitive processes with application in iterative learning control. In Proceedings of the Symposium on Learning Control (CDC), Shanghai, China, 16–18 December 2009; pp. 16–18. [Google Scholar]
- Bristow, D.A.; Tharayil, M.; Alleyne, A.G. A survey of iterative learning control. IEEE Control Syst. Mag. 2006, 26, 96–114. [Google Scholar]
- Ahn, H.S.; Chen, Y.; Moore, K.L. Iterative learning control: Brief survey and categorization. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2007, 37, 456–467. [Google Scholar] [CrossRef]
- Hladowski, L.; Galkowski, K.; Cai, Z.; Rogers, E.; Freeman, C.T.; Lewin, P.L. Output information based iterative learning control law design with experimental verification. ASME J. Dyn. Syst. Meas. Control 2012, 134, 36–42. [Google Scholar] [CrossRef]
- Xu, X.; Xie, H.; Shi, J. Iterative Learning Control (ILC) Guided Reinforcement Learning Control (RLC) Scheme for Batch Processes. In Proceedings of the IEEE 9th Data Driven Control and Learning Systems Conference, Liuzhou, China, 20–22 November 2020. [Google Scholar]
- Spiegel, I.A.; Strijbosch, N.; Oomen, T.; Barton, K. Iterative learning control with discrete-time nonlinear nonminimum phase models via stable inversion. Int. J. Robust Nonlinear Control 2021, 31, 7985–8006. [Google Scholar] [CrossRef]
- Faria, F.A.; Assunção, E.; Teixeira, M.C.M.; Cardim, R.; Da Silva, N.A.P. Robust state derivative pole placement Lmi-based designs for linear systems. Int. J. Control 2009, 82, 1–12. [Google Scholar] [CrossRef]
- Haddad, W.M.; Bernstein, D.S. Controller design with regional pole constraints. IEEE Trans. Automat. Control 1992, 37, 54–69. [Google Scholar] [CrossRef]
- Montagner, V.F.; Leite, V.J.S.; Oliveira, R.; Peres, P.L.D. State feedback control of switched linear systems: An LMI approach. J. Comput. Appl. Math. 2006, 194, 192–206. [Google Scholar] [CrossRef]
- Attia, S.B.; Ouerfelli, H.E.; Salhi, S. ILC-tracking control design for repetitive continuous-time linear system using D-stability along the pass. In Proceedings of the 14th International Multi-Conference on Systems, Signals & Devices (SSD), Marrakech, Morocco, 28–31 March 2017. [Google Scholar]
- Astolfi, D.; Marx, S.; van de Wouw, N. Repetitive control design based on forwarding for nonlinear minimum-phase systems. Int. J. Control 2021, 129, 109671. [Google Scholar] [CrossRef]
- Li, L.; Meng, X.; Liao, Y. Preview Repetitive Control for Linear Continuous-time System. Control Theory Appl. 2023, 129, 508–518. [Google Scholar] [CrossRef]
- Paszke, W.; Rogers, E.; Gałkowski, K. Design of robust iterative learning control schemes in a finite frequency range. In Proceedings of the International Workshop on Multidimensional (nD) Systems, Poitiers, France, 5–7 September 2011; pp. 1–6. [Google Scholar]
- Leila, N.; Noueili, C.; Wassila, K. New Iterative Learning Control Algorithm Using Learning Gain Based on σ Inversion for Nonsquare Multi-InputMulti-Output Systems. Model. Simul. Eng. 2018, 2018, 4195938. [Google Scholar]
- Dridi, J.; Attia, S.B.; Salhi, S. PD-ILC tracking control for discrete-time linear system. Mediterr. J. Meas. Control 2016, 12, 521–528. [Google Scholar]
- Houssem, O.; Selma, B.A.; Salah, S. Robust monotonic Stabilizability for discrete time switched system using D type switching iterative learning control. Mediterr. J. Meas. Control 2016, 12, 598–605. [Google Scholar]





| Parameters | Approaches | Learning Gains |
|---|---|---|
| Theorem 6 | ||
| Theorem 7 | ||
| Parameters | Approach | Learning Gains |
|---|---|---|
| Theorem 7 | ||
| 0.36 | 0.9 | 0.9 | 0.3503 |
| 0.25 | 0.9 | 0.9 | 0.232 |
| 0.15 | 0.9 | 0.9 | 0.148 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attia, S.B.; Alzahrani, S.; Alhuwaimel, S.; Salhi, S.; Ouerfelli, H.E. Polynomial Iterative Learning Control (ILC) Tracking Control Design for Uncertain Repetitive Continuous-Time Linear Systems Applied to an Active Suspension of a Car Seat. Mathematics 2024, 12, 2573. https://doi.org/10.3390/math12162573
Attia SB, Alzahrani S, Alhuwaimel S, Salhi S, Ouerfelli HE. Polynomial Iterative Learning Control (ILC) Tracking Control Design for Uncertain Repetitive Continuous-Time Linear Systems Applied to an Active Suspension of a Car Seat. Mathematics. 2024; 12(16):2573. https://doi.org/10.3390/math12162573
Chicago/Turabian StyleAttia, Selma Ben, Sultan Alzahrani, Saad Alhuwaimel, Salah Salhi, and Houssem Eddine Ouerfelli. 2024. "Polynomial Iterative Learning Control (ILC) Tracking Control Design for Uncertain Repetitive Continuous-Time Linear Systems Applied to an Active Suspension of a Car Seat" Mathematics 12, no. 16: 2573. https://doi.org/10.3390/math12162573
APA StyleAttia, S. B., Alzahrani, S., Alhuwaimel, S., Salhi, S., & Ouerfelli, H. E. (2024). Polynomial Iterative Learning Control (ILC) Tracking Control Design for Uncertain Repetitive Continuous-Time Linear Systems Applied to an Active Suspension of a Car Seat. Mathematics, 12(16), 2573. https://doi.org/10.3390/math12162573







