Quasi-Periodic and Periodic Vibration Responses of an Axially Moving Beam under Multiple-Frequency Excitation
Abstract
:1. Introduction
2. Modeling Equations and Multiple-Scales Method
2.1. Truncation Procedure
2.2. First Multiple-Scales Method
2.3. Secondary Multiple-Scales Method
3. Results and Discussion
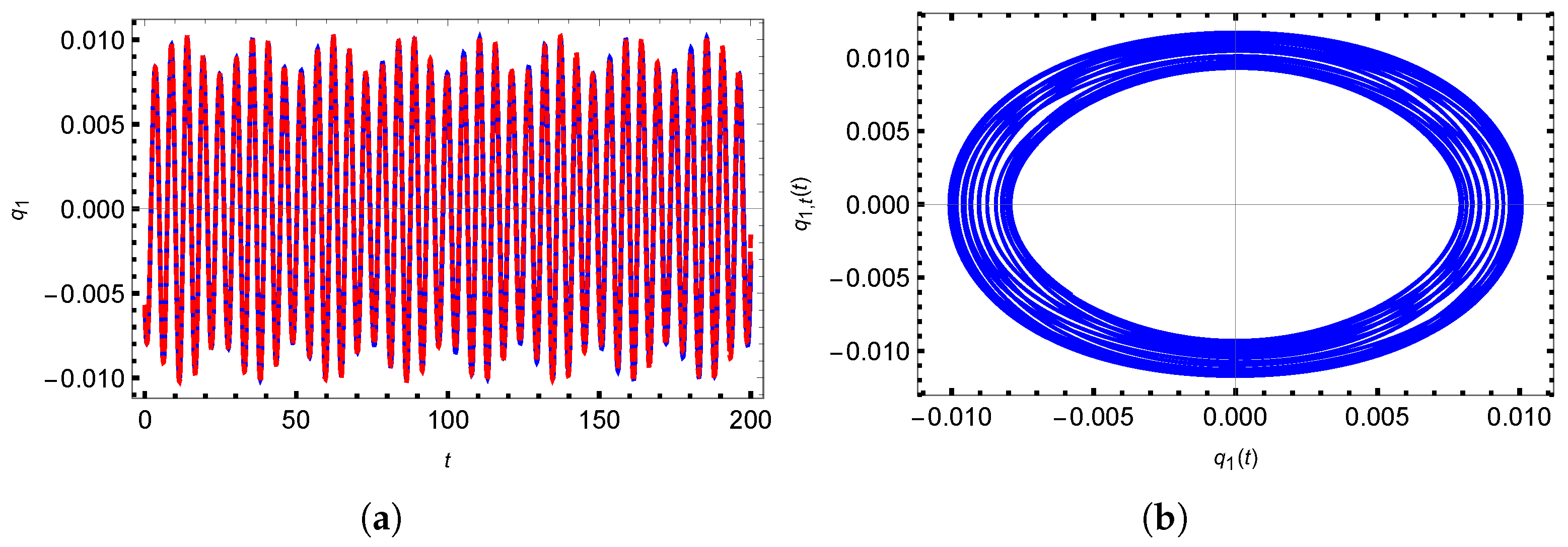
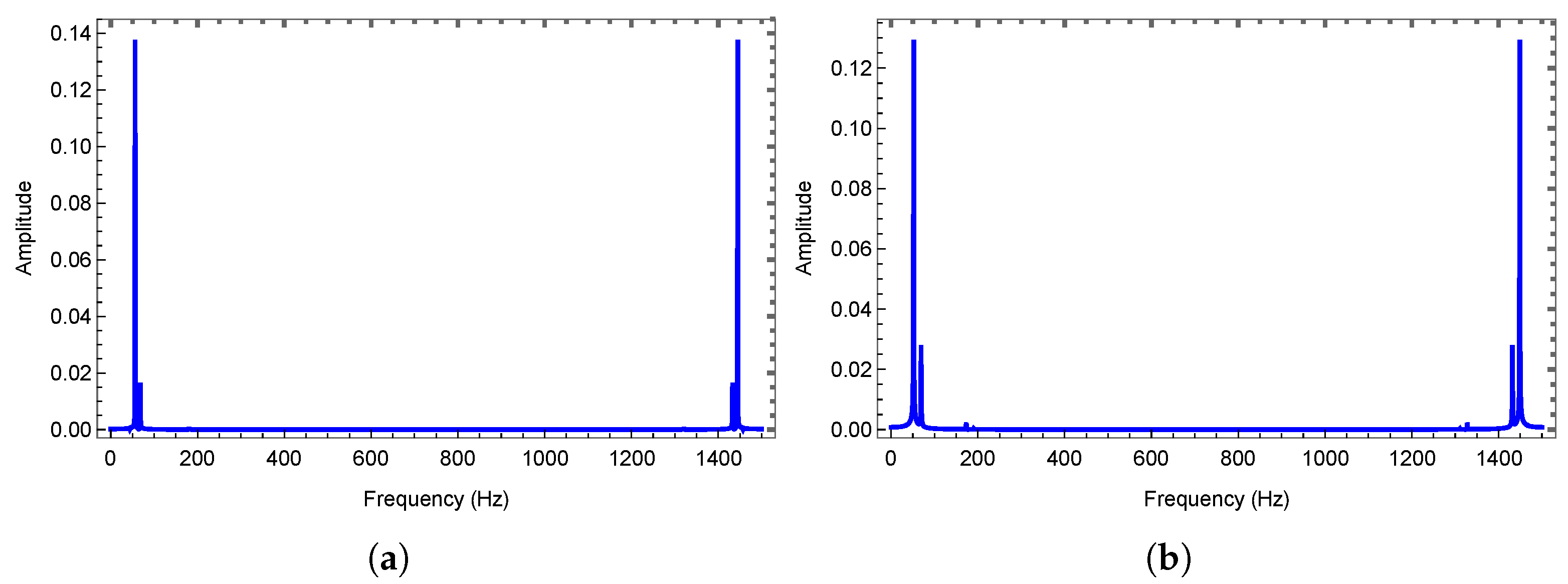
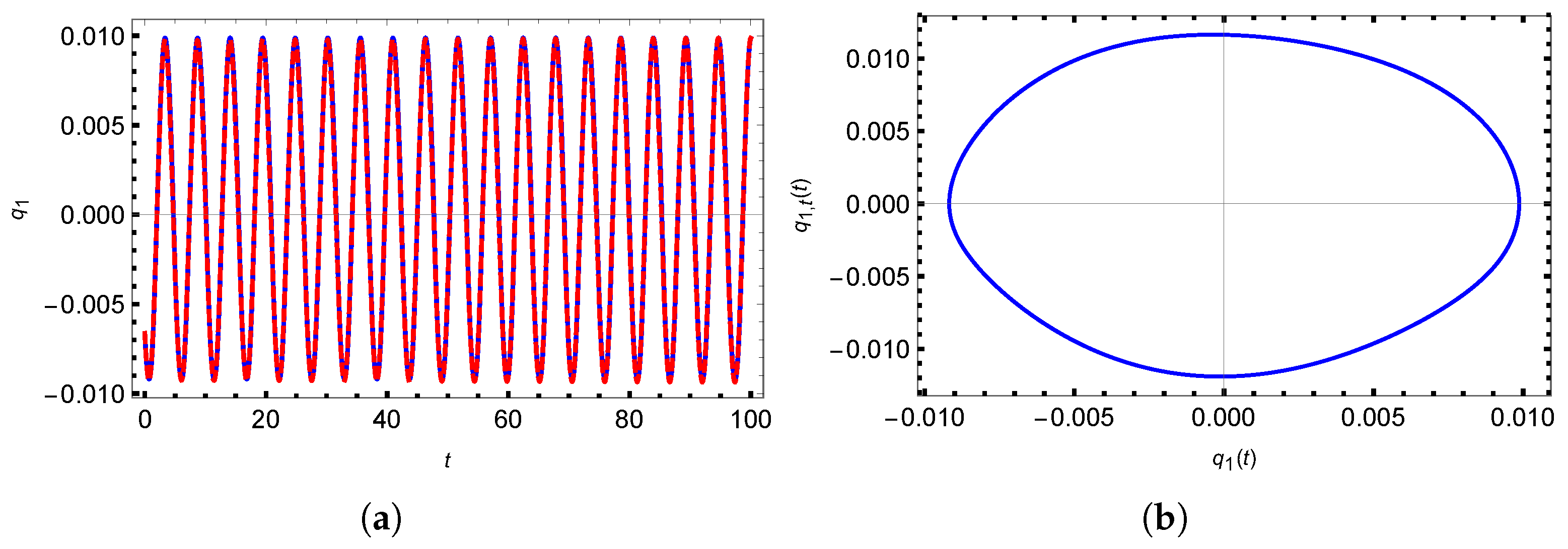
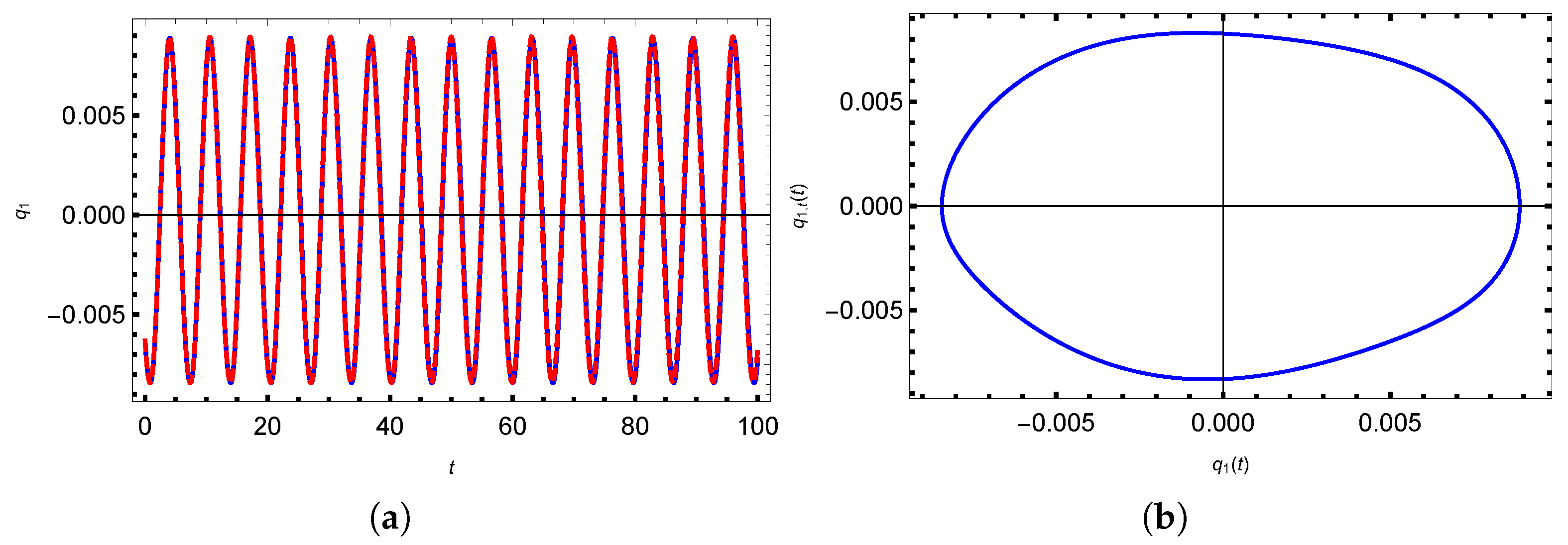
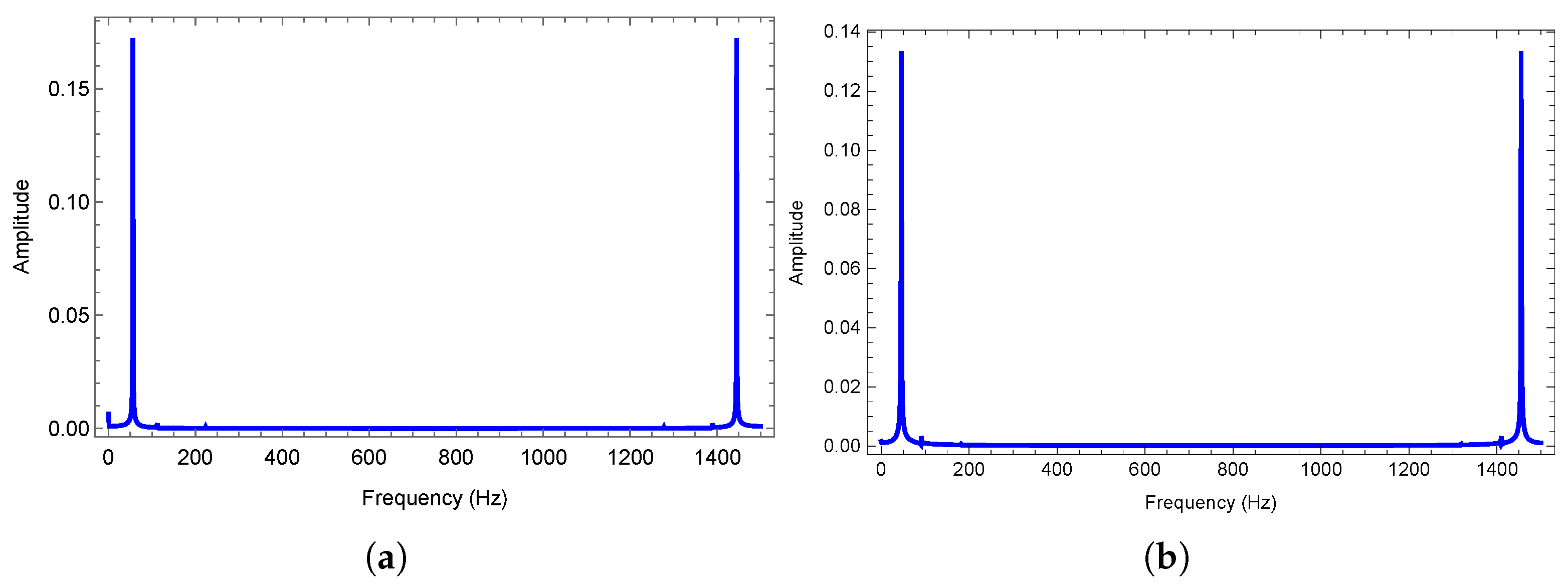
3.1. Quasi-Periodic Vibration
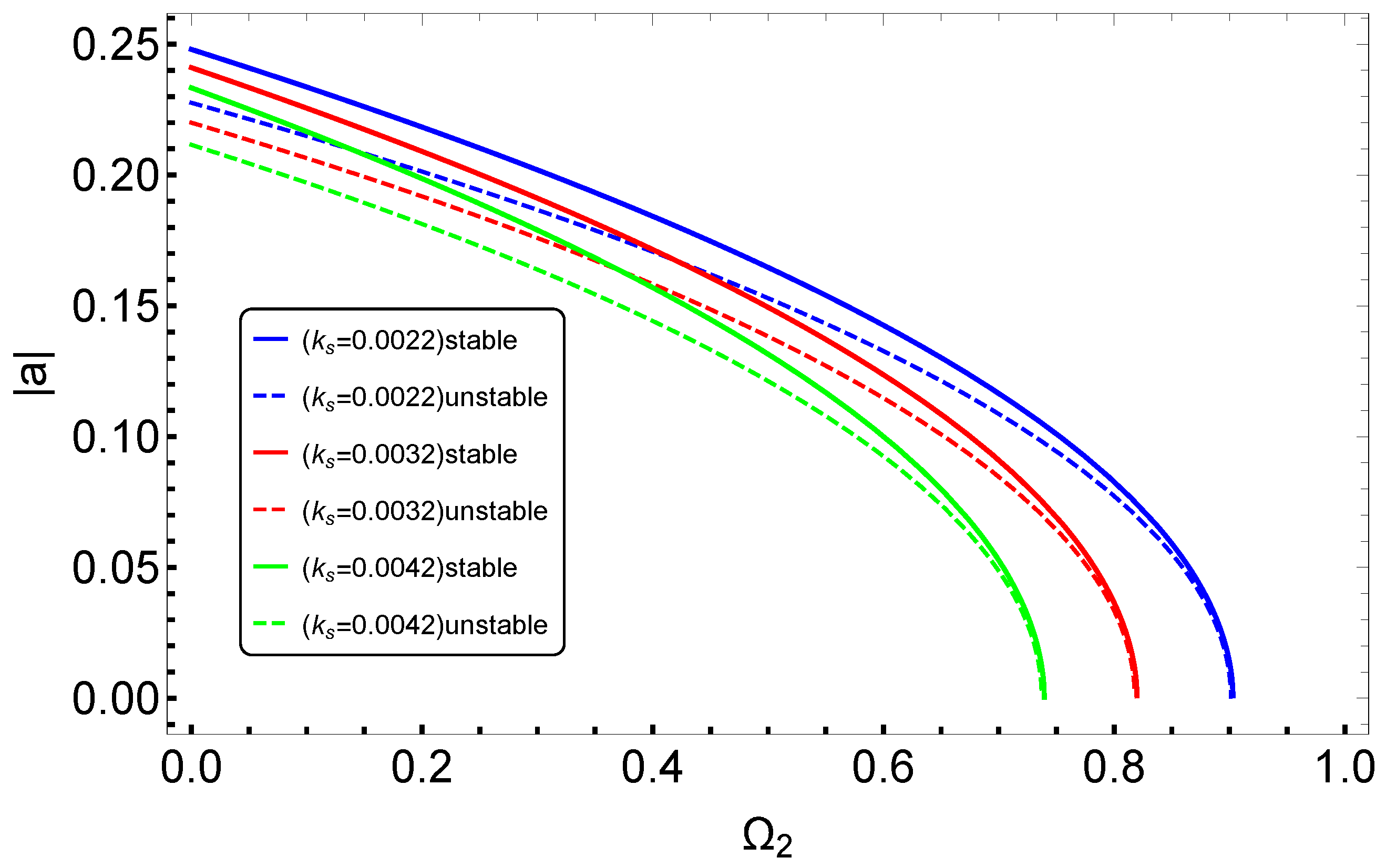
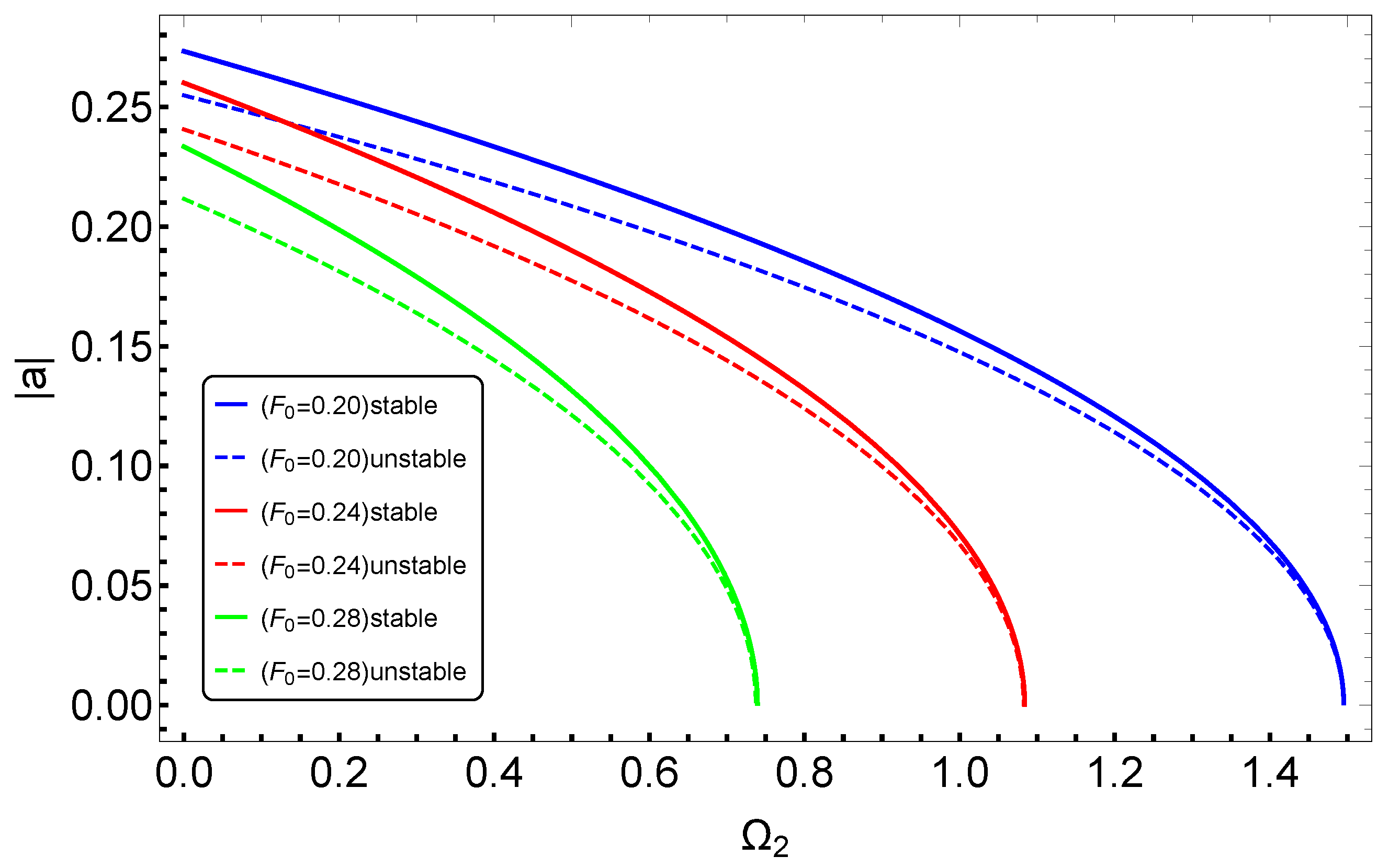
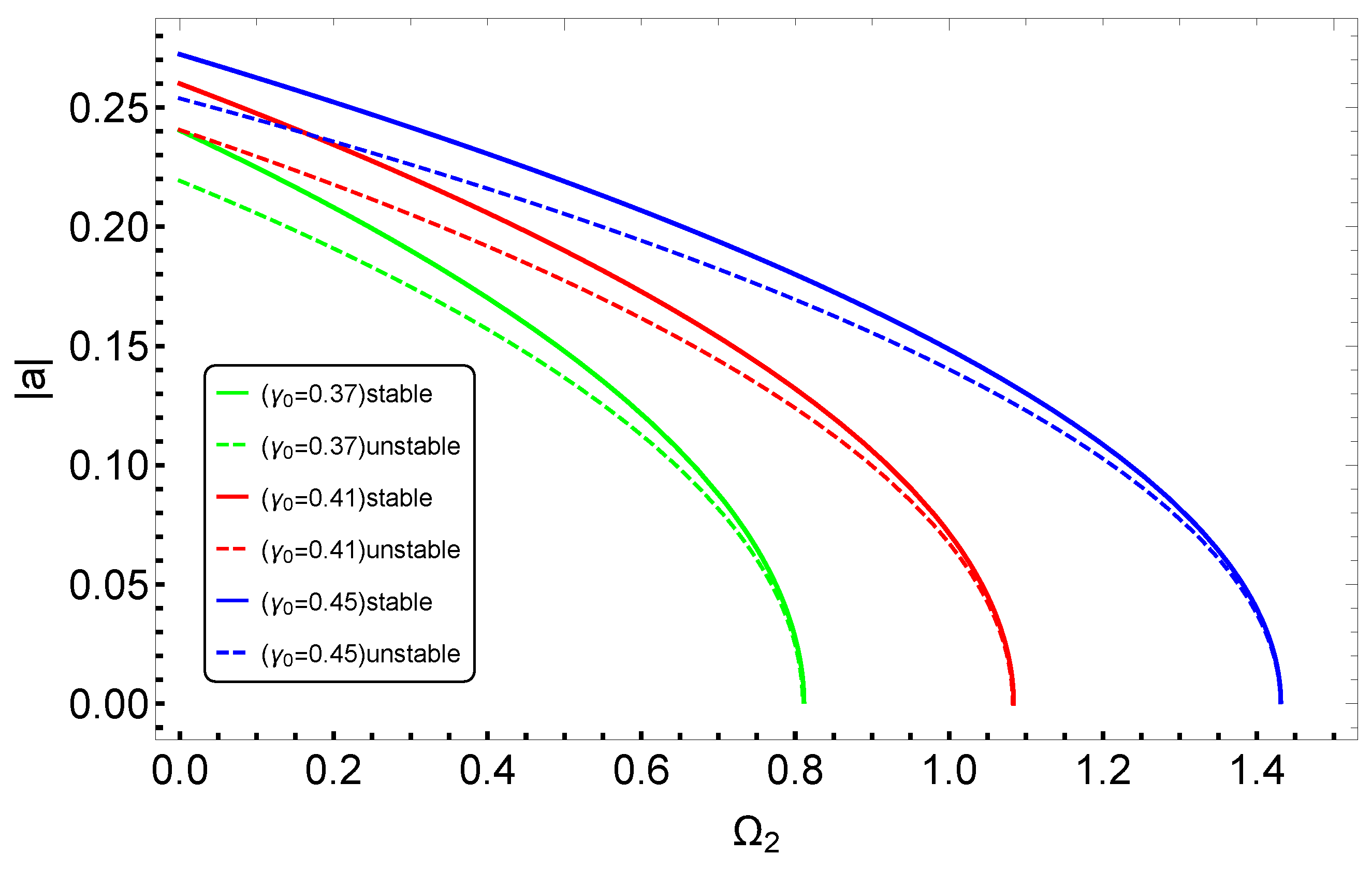
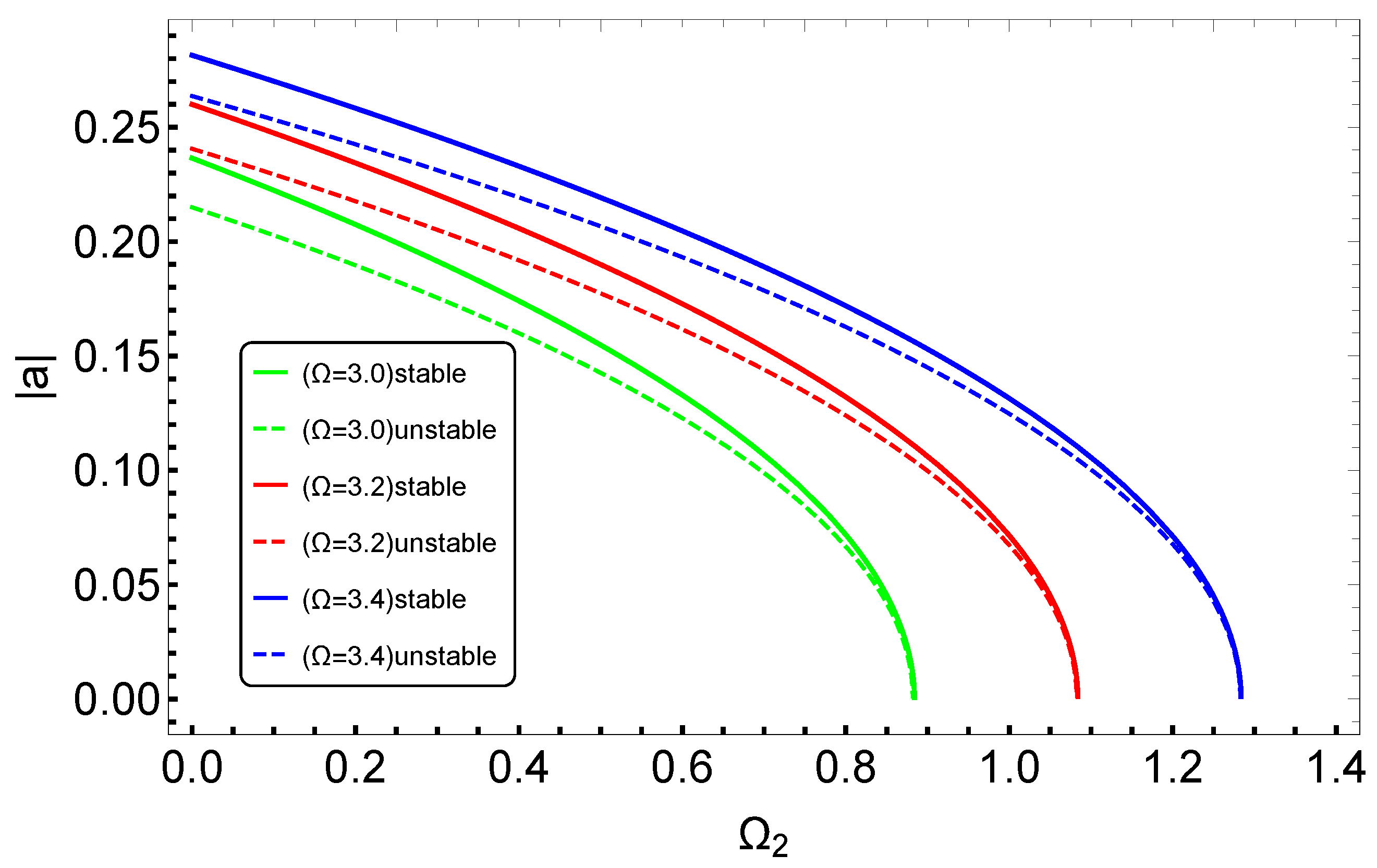
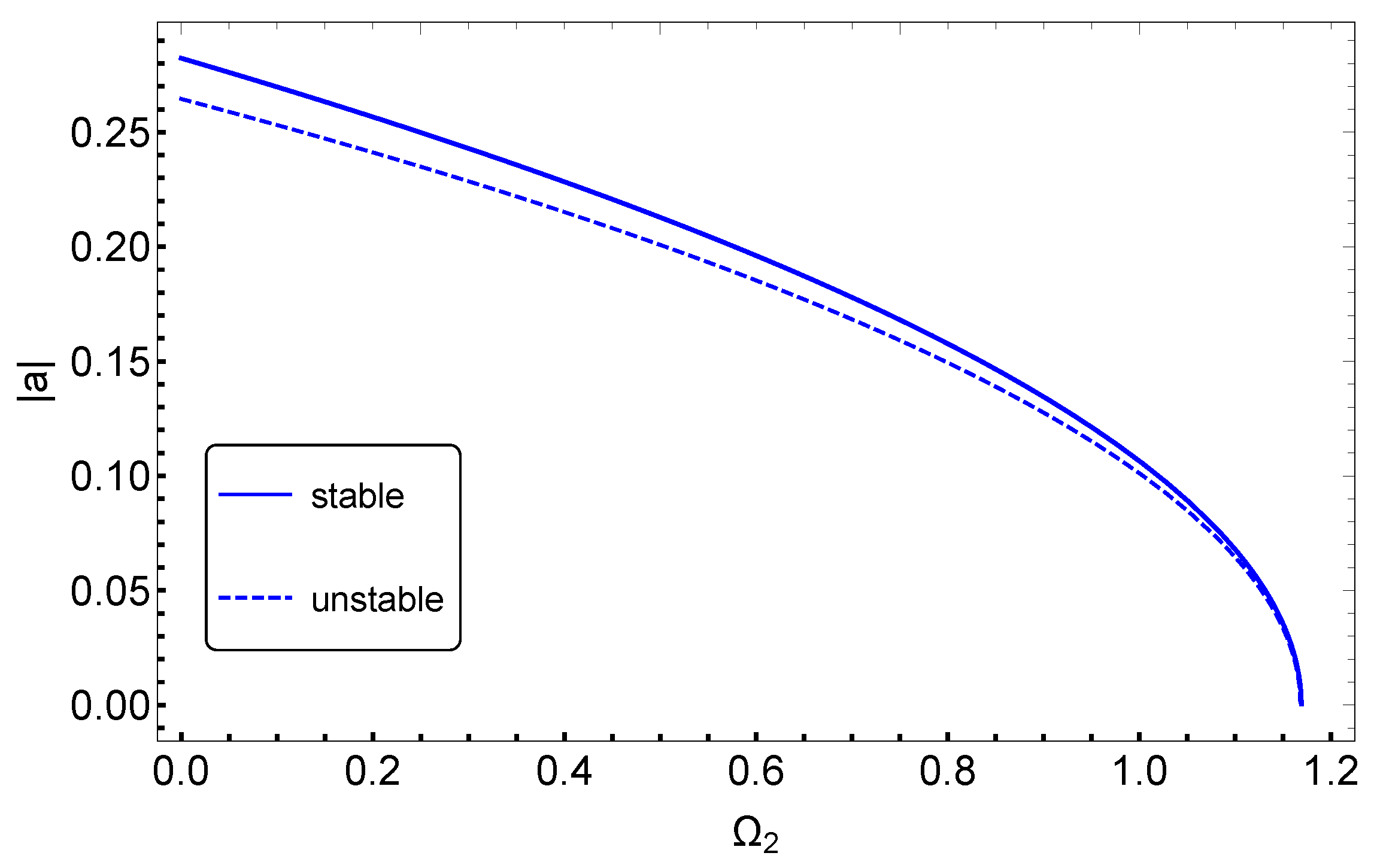
3.2. Effects of System Parameters
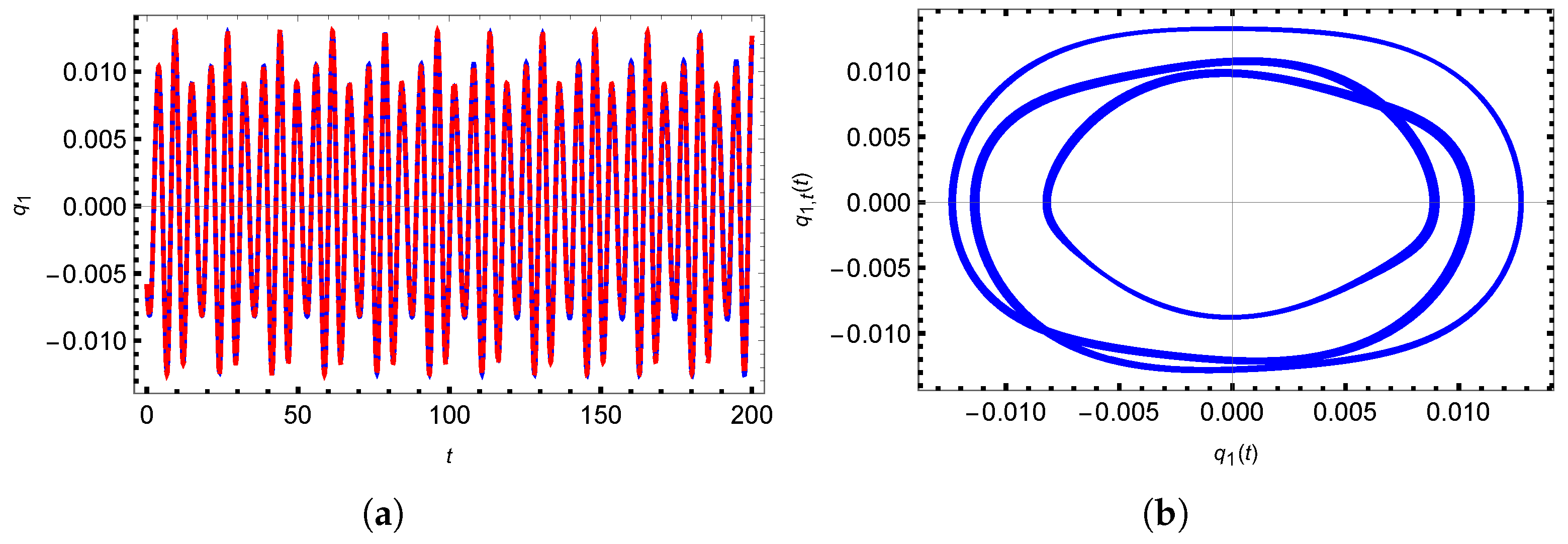
3.3. Periodic Vibration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- He, L.; Li, T. Undamped non-linear vibration mechanism of bolted flange joint under transverse load. J. Asian Archit. Build. Eng. 2022, 22, 1507–1532. [Google Scholar] [CrossRef]
- Zhu, J.; Yuan, W.B.; Li, L.Y. Cross-sectional flattening-induced nonlinear damped vibration of elastic tubes subjected to transverse loads. Chaos Solitons Fractals 2021, 151, 111273. [Google Scholar] [CrossRef]
- Ahmadi, H.; Foroutan, K. Active vibration control of nonlinear stiffened FG cylindrical shell under periodic loads. Smart Struct. Syst. 2020, 25, 643–655. [Google Scholar]
- Jain, V.; Kumar, R.; Patel, S.N.; Dey, T. Geometrically nonlinear dynamic analysis of a damped porous microplate resting on elastic foundations under in-plane nonuniform excitation. Mech. Based Des. Struct. Mach. 2023, 52, 4553–4598. [Google Scholar] [CrossRef]
- Hao, J.; Li, C.; Yang, T.; Yang, J.; Zhang, Y. Dynamic analysis of moving beams featuring time-varying velocity under self-excited force moving along with the end. Meccanica 2022, 57, 2905–2927. [Google Scholar] [CrossRef]
- Alshaqaq, M.; Hawwa, M.A. Nonlinear behavior of a vibrating axially moving small-size beam under an electrostatic force. Zamm-J. Appl. Math. Mech. Angew. Math. Mech. 2020, 100, e201900104. [Google Scholar] [CrossRef]
- Li, Y.; Hu, X.; Peng, L.; Yuan, Y. Simulation and experimental study on transverse nonlinear vibration of axially moving yarn. Text. Res. J. 2024, 00405175231224677. [Google Scholar] [CrossRef]
- Hu, W.; Xi, X.; Song, Z.; Zhang, C.; Deng, Z. Coupling dynamic behaviors of axially moving cracked cantilevered beam subjected to transverse harmonic load. Mech. Syst. Signal Process. 2023, 204, 110757. [Google Scholar] [CrossRef]
- Wu, Q.; Qi, G. Homoclinic bifurcations and chaotic dynamics of non-planar waves in axially moving beam subjected to thermal load. Appl. Math. Model. 2020, 83, 674–682. [Google Scholar]
- Cao, T.; Hu, Y. Magnetoelastic primary resonance and bifurcation of an axially moving ferromagnetic plate under harmonic magnetic force. Commun. Nonlinear Sci. Numer. Simul. 2022, 117, 106974. [Google Scholar] [CrossRef]
- Li, M.; Jiang, W.; Li, Y.; Dai, F. Steady-state response of an axially moving circular cylindrical panel with internal resonance. Eur. J. Mech.-A Solids 2022, 92, 104464. [Google Scholar] [CrossRef]
- Liu, M.; Yao, G. Nonlinear forced vibration and stability of an axially moving beam with a free internal hinge. Nonlinear Dyn. 2024, 112, 6877–6896. [Google Scholar] [CrossRef]
- Cheng, Y.; Wu, Y.; Guo, B.-Z. Boundary Stability Criterion for a Nonlinear Axially Moving Beam. IEEE Trans. Autom. Control 2022, 67, 5714–5729. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Wang, T.; Chu, F.; Peng, Z. Adaptive synchronous demodulation transform with application to analyzing multicomponent signals for machinery fault diagnostics. Mech. Syst. Signal Process. 2023, 191, 110208. [Google Scholar]
- Liu, K.; Zong, S.; Li, Y.; Wang, Z.; Hu, Z.; Wang, Z. Structural response of the U-type corrugated core sandwich panel used in ship structures under the lateral quasi-static compression load. Mar. Struct. 2022, 84, 103198. [Google Scholar] [CrossRef]
- Zhi, S.; Shen, H.; Wang, T. Gearbox localized fault detection based on meshing frequency modulation analysis. Appl. Acoust. 2024, 219, 109943. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X. Friction-induced nonlinear dynamics in a spline-rotor system: Numerical and experimental studies. Int. J. Mech. Sci. 2024, 278, 109427. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, Y.; Liang, R.; Song, Y.; Chen, L. Internal resonance of an axially transporting beam with a two-frequency parametric excitation. Appl. Math. Mech.-Engl. Ed. 2022, 43, 1805–1820. [Google Scholar]
- Zhang, D.; Tang, Y.; Liang, R.; Yang, L.; Chen, L.Q. Dynamic stability of an axially transporting beam with two-frequency parametric excitation and internal resonance. Eur. J. Mech. A-Solids 2021, 85, 104084. [Google Scholar] [CrossRef]
- Raj, S.K.; Sahoo, B.; Nayak, A.R.; Panda, L.N. Nonlinear dynamics of traveling beam with longitudinally varying axial tension and variable velocity under parametric and internal resonances. Nonlinear Dyn. 2023, 111, 3113–3147. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Liu, Y. Vibration suppression and dynamic behavior analysis of an axially loaded beam with NES and nonlinear elastic supports. J. Vib. Control 2023, 29, 844–857. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y. Principal-Internal Joint Resonance of an Axially Moving Beam with Elastic Constraints and Excited by Current-Carrying Wires. Int. J. Struct. Stab. Dyn. 2024, 24, 2450125. [Google Scholar] [CrossRef]
- Ba, Z.; Wu, M.; Liang, J. 3D dynamic responses of a multi-layered transversely isotropic saturated half-space under concentrated forces and pore pressure. Appl. Math. Model. 2020, 80, 859–878. [Google Scholar] [CrossRef]
- Tian, R.; Wang, M.; Zhang, Y.; Jing, X.; Zhang, X. A concave X-shaped structure supported by variable pitch springs for low-frequency vibration isolation. Mech. Syst. Signal Process. 2024, 218, 111587. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, H.; Cui, L. Frequency-chirprate synchrosqueezing-based scaling chirplet transform for wind turbine nonstationary fault feature time—Frequency representation. Mech. Syst. Signal Process. 2024, 209, 111112. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, F.; Zhou, L. Slow-fast motions induced by multi-stability and strong transient effects in an accelerating viscoelastic beam. Nonlinear Dyn. 2021, 106, 45–66. [Google Scholar] [CrossRef]
- Kobayashi, T.K.; Fujisawa, A.; Nagashima, Y.; Moon, C.; Yamasaki, K.; Nishimura, D.; Inagaki, S.; Yamada, T.; Kasuya, N.; Kosuga, Y.; et al. Correlation-estimated conditional average method and its application on solitary oscillation in PANTA. Plasma Phys. Control. Fusion 2021, 63, 032001. [Google Scholar] [CrossRef]
- Villanueva, J. A new averaging-extrapolation method for quasi-periodic frequency refinement. Phys. Nonlinear Phenom. 2022, 438, 133344. [Google Scholar] [CrossRef]
- Liao, H.; Zhao, Q.; Fang, D. The continuation and stability analysis methods for quasi-periodic solutions of nonlinear systems. Nonlinear Dyn. 2020, 100, 1469–1496. [Google Scholar] [CrossRef]
- Liu, G.; Liu, J.; Wang, L.; Lu, Z. A new semi-analytical approach for quasi-periodic vibrations of nonlinear systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 105999. [Google Scholar] [CrossRef]
- Huang, J.L.; Wang, T.; Zhu, W.D. An incremental harmonic balance method with two time-scales for quasi-periodic responses of a Van der Pol-Mathieu equation. Int. J. Non-Linear Mech. 2021, 135, 103767. [Google Scholar] [CrossRef]
- Huang, J.L.; Zhang, B.X.; Zhu, W.D. Quasi-Periodic Solutions of a Damped Nonlinear Quasi-Periodic Mathieu Equation by the Incremental Harmonic Balance Method With Two Time Scales. J. Appl. Mech. Trans. ASME 2022, 89, 091009. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, X.; Ding, H.; Chen, L.Q. Quasi-periodic vibration of an axially moving beam under conveying harmonic varying mass. Appl. Math. Model. 2023, 123, 644–658. [Google Scholar] [CrossRef]
- Nie, X.; Tan, T.; Yan, Z.; Yan, Z.; Wang, L. Revised method of multiple scales for 1:2 internal resonance piezoelectric vibration energy harvester considering the coupled frequency. Commun. Nonlinear Sci. Numer. Simul. 2022, 118, 107018. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Chatterjee, S. Nonlinear dynamics of vortex-induced vibration of a nonlinear beam under high-frequency excitation. Int. J. Non-Linear Mech. 2021, 129, 103656. [Google Scholar] [CrossRef]
- Qian, Y.; Zhou, H. Double Hopf bifurcation analysis of time delay coupled active control system. J. Low Freq. Noise Vib. Act. Control 2024, 14613484241236646. [Google Scholar] [CrossRef]
- Belhaq, M.; Houssni, M. Quasi-Periodic Oscillations, Chaos and Suppression of Chaos in a Nonlinear Oscillator Driven by Parametric and External Excitations. Nonlinear Dyn. 1999, 18, 1–24. [Google Scholar] [CrossRef]
- Bayat, A.; Jalali, A.; Ahmadi, H. Nonlinear dynamic analysis and control of FG cylindrical shell fitted with piezoelectric layers. Int. J. Struct. Stab. Dyn. 2021, 21, 2150083. [Google Scholar] [CrossRef]
- Kirrou, I.; Mokni, L.; Belhaq, M. Quasiperiodic galloping of a wind-excited tower near secondary resonances of order 2. J. Vib. Control 2017, 23, 574–586. [Google Scholar] [CrossRef]
- Mokni, L.; Kirrou, I.; Belhaq, M. Periodic and quasiperiodic galloping of a wind-excited tower under parametric damping. J. Vib. Control 2016, 22, 145–158. [Google Scholar] [CrossRef]
- Guennoun, K.; Houssni, M.; Belhaq, M. Quasi-Periodic Solutions and Stability for a Weakly Damped Nonlinear Quasi-Periodic Mathieu Equation. Nonlinear Dyn. 2002, 27, 211–236. [Google Scholar] [CrossRef]
- Zarastvand, M.R.; Ghassabi, M.; Talebitooti, R. A Review Approach for Sound Propagation Prediction of Plate Constructions. Arch. Comput. Methods Eng. 2021, 28, 2817–2843. [Google Scholar] [CrossRef]
- Pham, P.T.; Hong, K.S. Dynamic models of axially moving systems: A review. Nonlinear Dyn. 2020, 100, 315–349. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Huang, L.; Lou, Z.; Wang, Y. Quasi-Periodic and Periodic Vibration Responses of an Axially Moving Beam under Multiple-Frequency Excitation. Mathematics 2024, 12, 2608. https://doi.org/10.3390/math12172608
Fang X, Huang L, Lou Z, Wang Y. Quasi-Periodic and Periodic Vibration Responses of an Axially Moving Beam under Multiple-Frequency Excitation. Mathematics. 2024; 12(17):2608. https://doi.org/10.3390/math12172608
Chicago/Turabian StyleFang, Xinru, Lingdi Huang, Zhimei Lou, and Yuanbin Wang. 2024. "Quasi-Periodic and Periodic Vibration Responses of an Axially Moving Beam under Multiple-Frequency Excitation" Mathematics 12, no. 17: 2608. https://doi.org/10.3390/math12172608
APA StyleFang, X., Huang, L., Lou, Z., & Wang, Y. (2024). Quasi-Periodic and Periodic Vibration Responses of an Axially Moving Beam under Multiple-Frequency Excitation. Mathematics, 12(17), 2608. https://doi.org/10.3390/math12172608








