Multi-Objective Optimized GPSR Intelligent Routing Protocol for UAV Clusters
Abstract
:1. Introduction
- Mathematical modeling of multi-objective routing optimization problem: combines the multi-objective optimization mechanism of DDQN, transforming the route forwarding process into a Markov decision process (MDP) and modeling the multi-objective routing optimization problem by comprehensively considering multiple routing performance metrics in a mixed-objective way.
- DDQN-based GPSR optimization: uses DDQN to improve the traditional GPSR routing mechanism, constructing a DDQN network model to solve the routing problem.
- NS-3-based implementation and validation: combines the NS-3 network simulator with an AI framework via the NS3-AI interface to integrate and validate the DDQN-MTGPSR intelligent routing protocol, showing superior performance in large-scale, highly dynamic networks compared to other routing protocols.
2. Related Work
2.1. Improved Routing Protocols Based on RL
2.2. Improved Routing Protocols Based on DL
2.3. Improved Routing Protocols Based on DRL
3. Mathematical Modeling of Multi-Objective Routing Optimization Problems
3.1. Deep Double Q-Learning Network
3.2. MDP Modeling of the Routing Forwarding Process
- Signal-to-noise ratio (SNR)
- Residual energy percentage
- Expected total waiting delay within the node
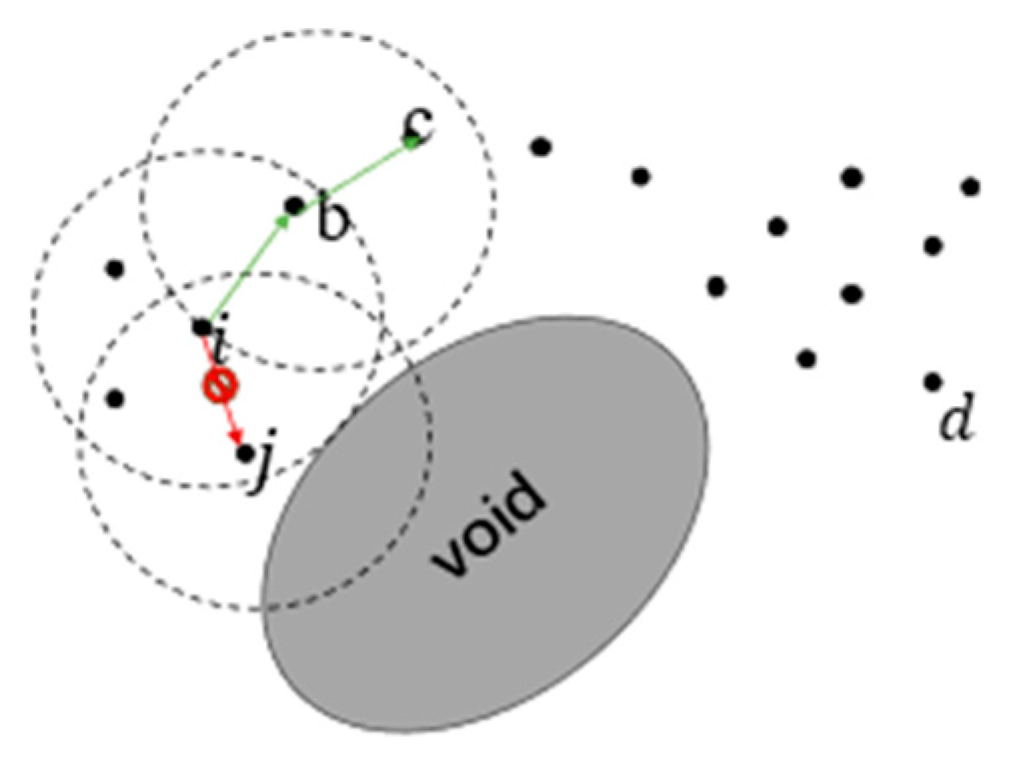
- Routing void possibilities ,
- Relative movement trends .
4. DDQN-MTGPSR Protocol Design
4.1. Broadcast Beacon and Routing Table Optimization
4.2. DDQN Network Construction
4.3. DDQN-MTGPSR Routing Decision
| Algorithm 1: DDQN-MTGPSR Routing Algorithm | |
| 1 | Initialization: Learning rate , discount factor , , experience playback area , ; |
| 2 | Initialization: Evaluation DDQN network parameters ; |
| 3 | Initialization: Target DDQN network parameters ; |
| Phase 1: Routing table creation and maintenance phase: | |
| 4 | if arrive at HELLO beacon send time do |
| 5 | Each node sends a beacon; |
| 6 | Each node extracts the fields based on the received broadcast packets and computes the |
| 7 | The node reacquaints itself with its neighbors and updates ; |
| 8 | end if |
| Phase 2: Route Forwarding Phase: | |
| 9 | if currently need to forward data packets do |
| 10 | Initiate the DDQN-MTGPSR routing algorithm: |
| 11 | Calculate the status information of all neighboring nodes based on : |
| 12 | ; |
| 13 | Construct the state space of this node ; |
| 14 | Enter into the DDQN network to get the corresponding Q values for all neighbors; |
| 15 | if DDQN is in training phase do |
| 16 | Select the next jump according to ; |
| 17 | ; |
| 18 | The status is transferred to ; |
| 19 | Store the experience to ; |
| 20 | Randomizing small batches of experience from ; |
| 21 | Calculate the loss function; |
| 22 | Adam optimizer gradient descent minimizes the loss function to update the parameters of network ; |
| 23 | Update with every ; |
| 24 | else |
| 25 | Select the next hop based on the maximum value; |
| 26 | end if |
| 27 | end if |
5. Experiments and Analysis of Results
5.1. Simulation Architecture
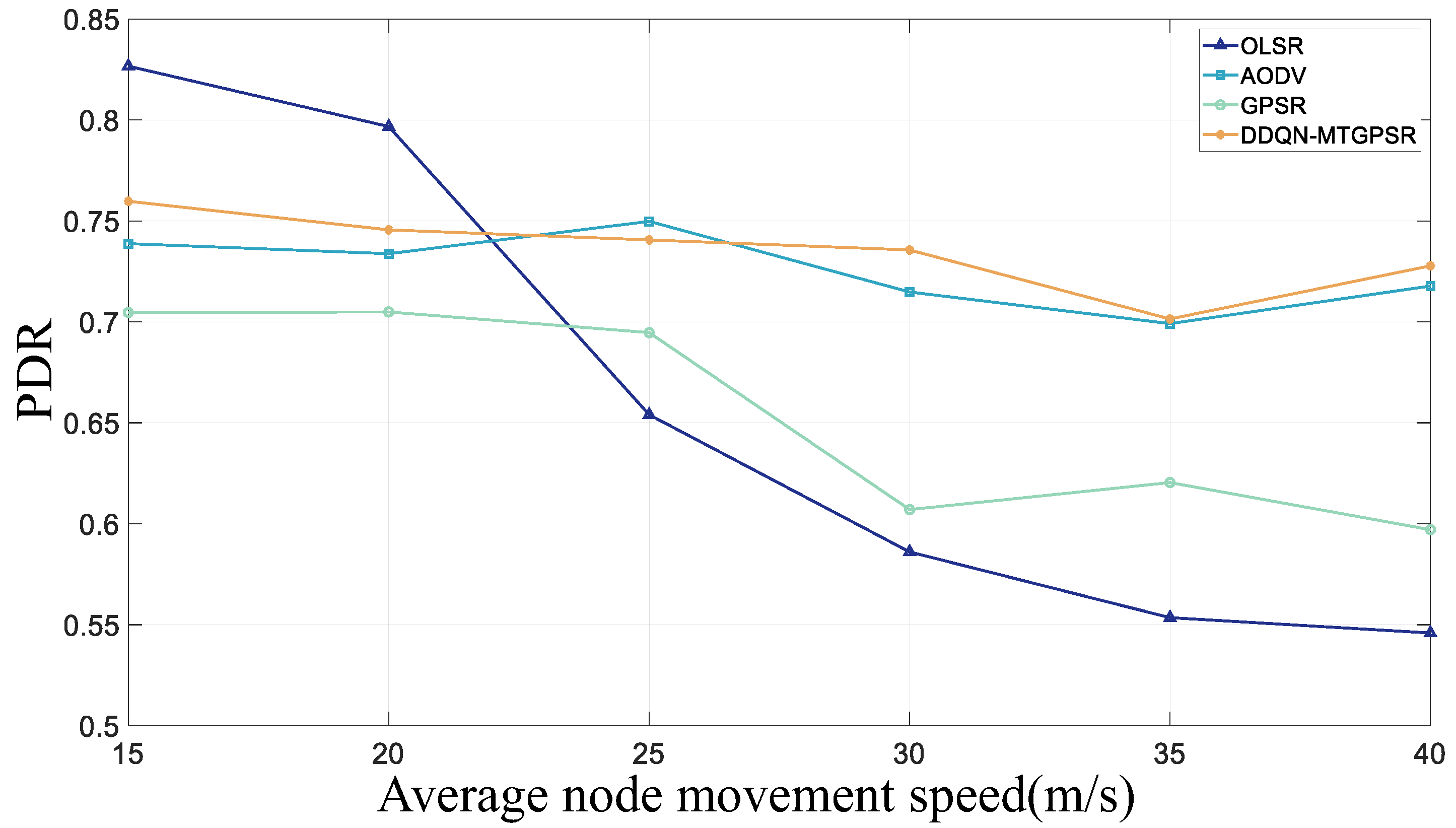
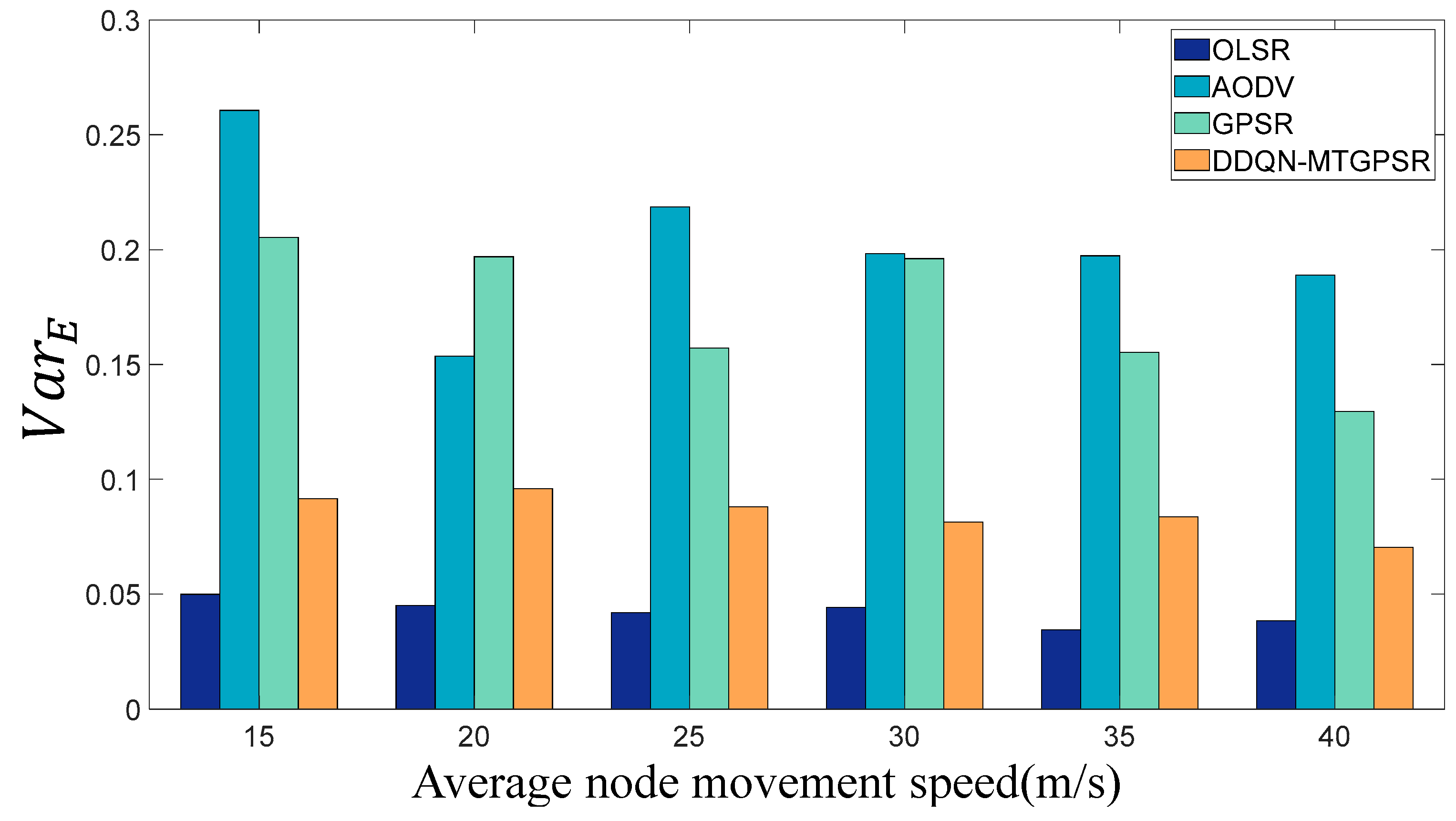
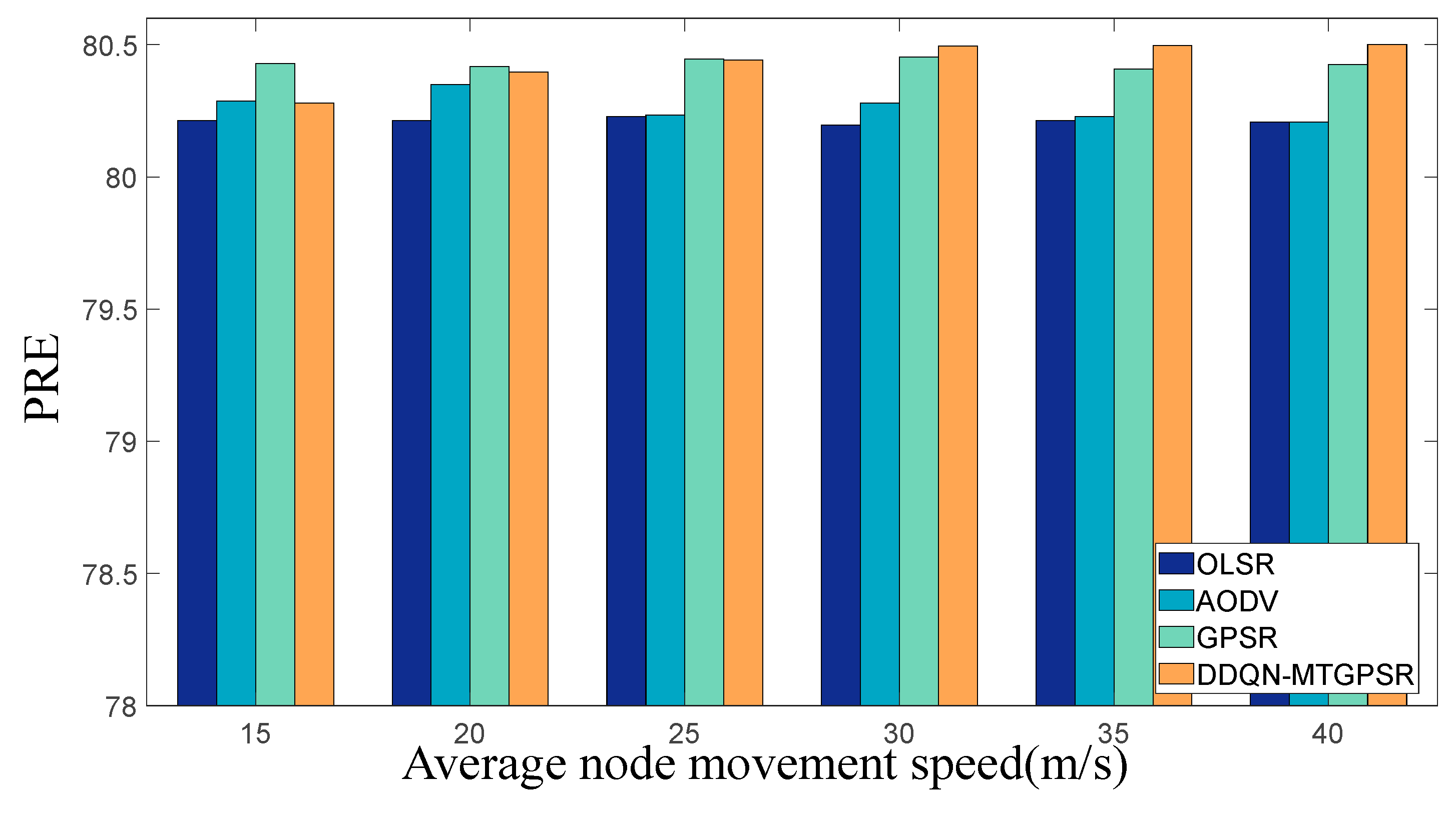
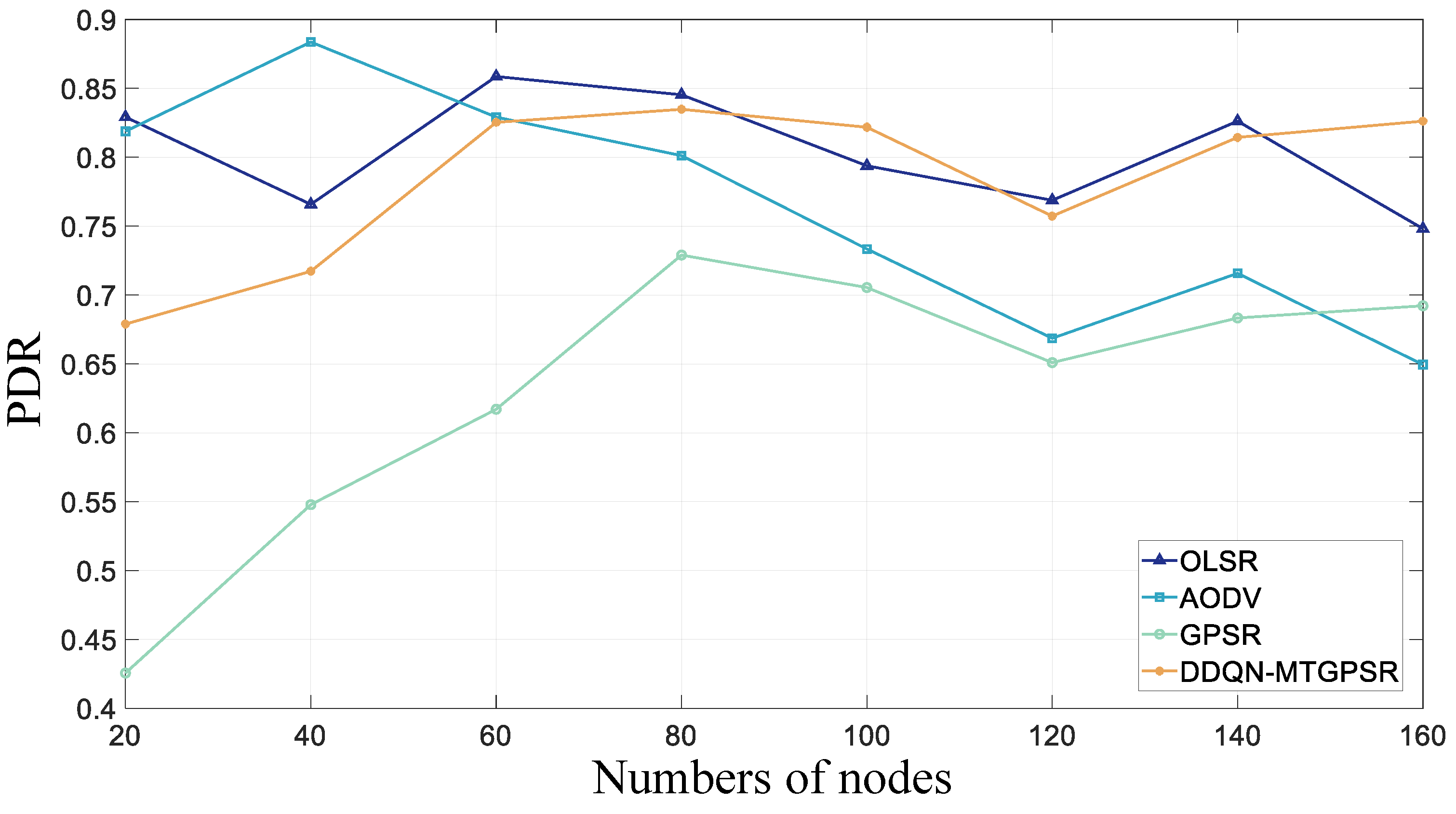
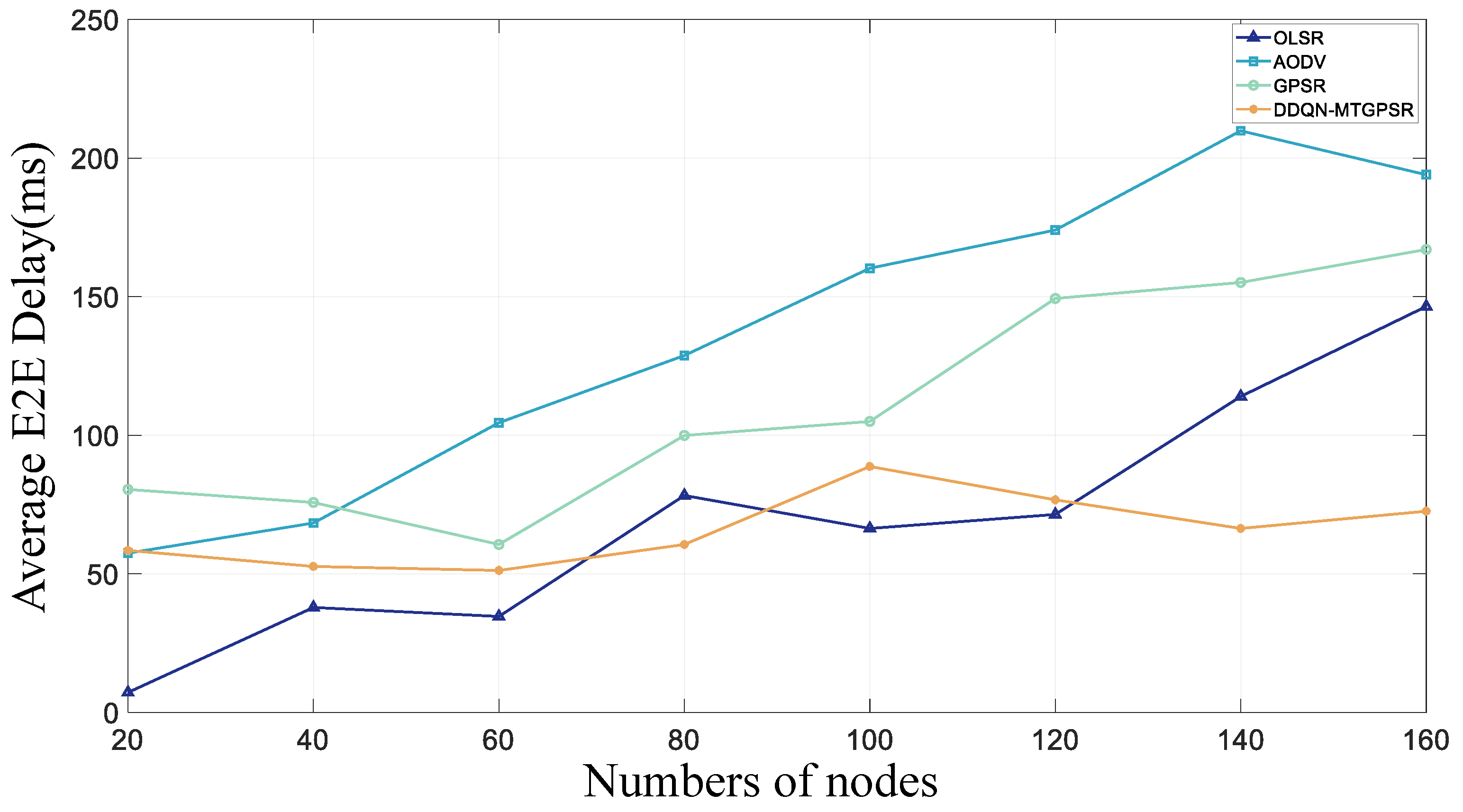
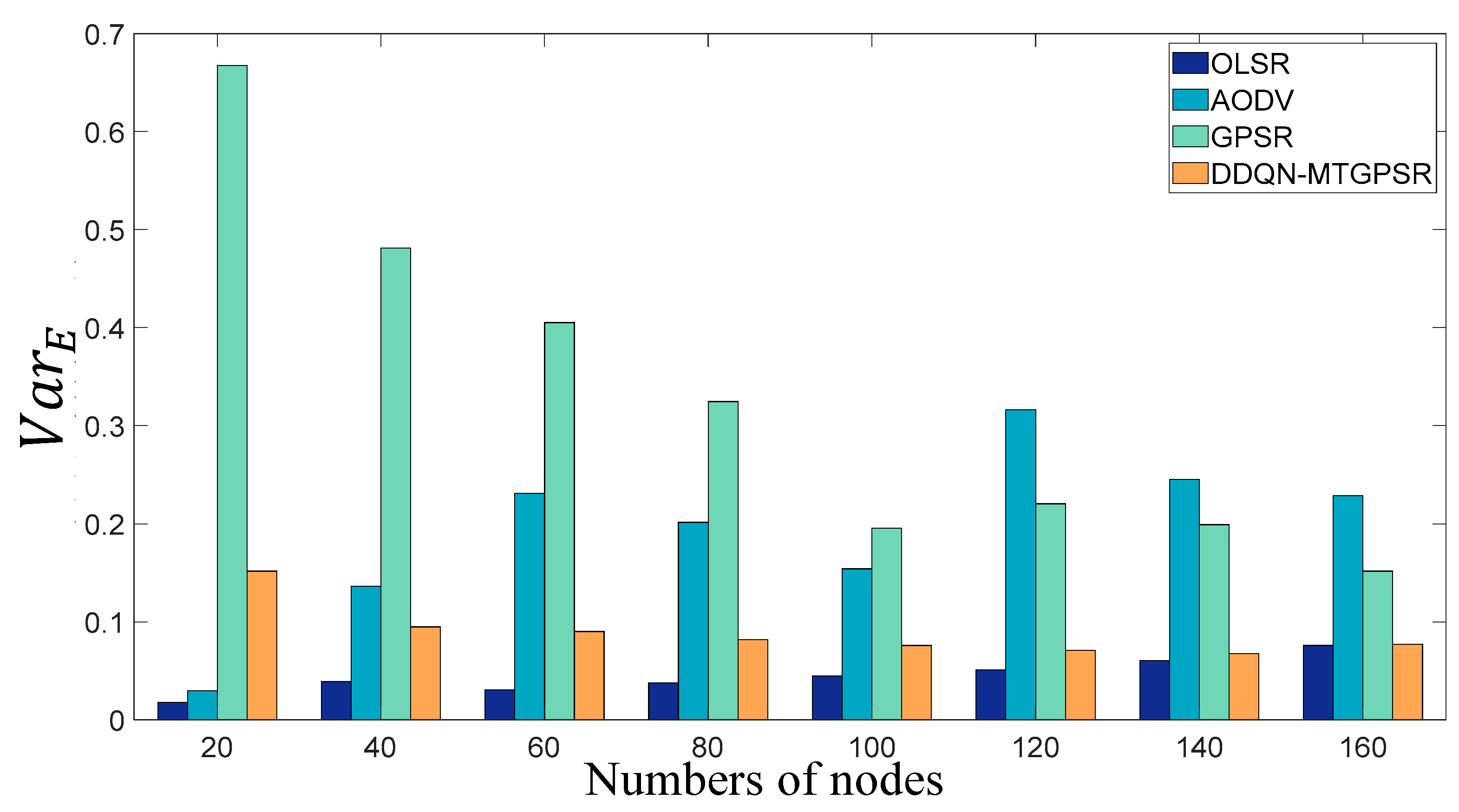
5.2. Experimental Parameters and Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| DDQN | deep double Q-learning network |
| GPSR | greedy perimeter stateless routing |
| DDQN-MTGPSR | multi-objective optimized GPSR routing protocol |
| DSDV | destination-sequenced distance-vector |
| OLSR | optimized link state routing |
| DSR | dynamic source routing |
| AODV | distance vector routing |
| HRP | hybrid routing protocol |
| RL | reinforcement learning |
| DL | deep learning |
| DRL | deep reinforcement learning-based |
| MDP | Markov decision process |
| QL | Q-learning |
| QGeo | geographic routing protocol |
| RFLQGEO | reward function learning for QL-based geographic routing protocol |
| GLAN | geolocation ad hoc network |
| AGLAN | adaptive GLAN |
| DNN | deep neural networks |
| QoS | quality of service |
| DDQN | deep double Q-learning network |
| SA | annealing |
| GA | genetic algorithm |
| PSO | particle swarm optimization |
| ReLU | rectified linear unit |
| RWP | randomized waypoint model |
| PDR | packet delivery rate |
| Average E2E delay | average end-to-end delay |
| node average residual energy variance | |
| PRE | percentage of node average residual energy |
References
- Niyazi, M.; Behnamian, J. Application of Emerging Digital Technologies in Disaster Relief Operations: A Systematic Review. Arch. Comput. Methods Eng. 2023, 30, 1579–1599. [Google Scholar] [CrossRef]
- Flakus, J. Use of Large Unmanned Vehicles in Joint Intelligence, Surveillance, and Reconnaissance. Available online: https://apps.dtic.mil/sti/trecms/pdf/AD1174711.pdf (accessed on 27 June 2024).
- Loukinas, P. Drones for Border Surveillance: Multipurpose Use, Uncertainty and Challenges at EU Borders. Geopolitics 2022, 27, 89–112. [Google Scholar] [CrossRef]
- Xu, G.; Jiang, W.; Wang, Z.; Wang, Y. Autonomous Obstacle Avoidance and Target Tracking of UAV Based on Deep Reinforcement Learning. J. Intell. Robot. Syst. 2022, 104, 60. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Q.; Fu, G. Multi-UAV Collaborative Search and Attack Mission Decision-Making in Unknown Environments. Sensors 2023, 23, 7398. [Google Scholar] [CrossRef] [PubMed]
- Shahzadi, R.; Ali, M.; Naeem, M. UAV Placement and Resource Management in Public Safety Networks: An Overview. In Intelligent Unmanned Air Vehicles Communications for Public Safety Networks; Kaleem, Z., Ahmad, I., Duong, T.Q., Eds.; Unmanned System Technologies; Springer Nature: Singapore, 2022; pp. 19–49. ISBN 978-981-19129-2-4. [Google Scholar]
- AL-Dosari, K.; Hunaiti, Z.; Balachandran, W. Systematic Review on Civilian Drones in Safety and Security Applications. Drones 2023, 7, 210. [Google Scholar] [CrossRef]
- Cheng, L.; Tan, X.; Yao, D.; Xu, W.; Wu, H.; Chen, Y. A Fishery Water Quality Monitoring and Prediction Evaluation System for Floating UAV Based on Time Series. Sensors 2021, 21, 4451. [Google Scholar] [CrossRef] [PubMed]
- Aissaoui, R.; Deneuville, J.-C.; Guerber, C.; Pirovano, A. A Survey on Cryptographic Methods to Secure Communications for UAV Traffic Management. Veh. Commun. 2023, 44, 100661. [Google Scholar] [CrossRef]
- Ding, R.; Chen, J.; Wu, W.; Liu, J.; Gao, F.; Shen, X. Packet Routing in Dynamic Multi-Hop UAV Relay Network: A Multi-Agent Learning Approach. IEEE Trans. Veh. Technol. 2022, 71, 10059–10072. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. Routing Protocols for Unmanned Aerial Vehicle Networks: A Survey. IEEE Access 2019, 7, 99694–99720. [Google Scholar] [CrossRef]
- Peng, J.-X.; Yuan, L.-F.; Liu, S.; Zhang, Q. Review of Unmanned Cluster Routing Protocols Based on Deep Reinforcement Learning. In Proceedings of the International Conference on Signal Processing and Communication Technology (SPCT 2022), Harbin, China, 6 April 2023; Volume 12615, pp. 572–579. [Google Scholar]
- Peng, H.; Razi, A.; Afghah, F.; Ashdown, J. A Unified Framework for Joint Mobility Prediction and Object Profiling of Drones in UAV Networks. J. Commun. Netw. 2018, 20, 434–442. [Google Scholar] [CrossRef]
- Perkins, C.E.; Bhagwat, P. Highly Dynamic Destination-Sequenced Distance-Vector Routing (DSDV) for Mobile Computers. SIGCOMM Comput. Commun. Rev. 1994, 24, 234–244. [Google Scholar] [CrossRef]
- Jacquet, P.; Muhlethaler, P.; Clausen, T.; Laouiti, A.; Qayyum, A.; Viennot, L. Optimized Link State Routing Protocol for Ad Hoc Networks. In Proceedings of the IEEE International Multi Topic Conference, 2001. IEEE INMIC 2001. Technology for the 21st Century, Lahore, Pakistan, 30 December 2001; pp. 62–68. [Google Scholar]
- Arafat, M.Y.; Moh, S. A Q-Learning-Based Topology-Aware Routing Protocol for Flying Ad Hoc Networks. IEEE Internet Things J. 2022, 9, 1985–2000. [Google Scholar] [CrossRef]
- Johnson, D.B.; Maltz, D.A.; Broch, J. DSR: The Dynamic Source Routing Protocol for Multi-Hop Wireless Ad Hoc Networks. Ad. Hoc Netw. 2001, 5, 139–172. [Google Scholar]
- Chakeres, I.D.; Belding-Royer, E.M. AODV Routing Protocol Implementation Design. In Proceedings of the 24th International Conference on Distributed Computing Systems Workshops, Tokyo, Japan, 23–24 March 2004; pp. 698–703. [Google Scholar]
- Rovira-Sugranes, A.; Razi, A.; Afghah, F.; Chakareski, J. A Review of AI-Enabled Routing Protocols for UAV Networks: Trends, Challenges, and Future Outlook. Ad. Hoc Netw. 2022, 130, 102790. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Moh, S. Bio-Inspired Approaches for Energy-Efficient Localization and Clustering in UAV Networks for Monitoring Wildfires in Remote Areas. IEEE Access 2021, 9, 18649–18669. [Google Scholar] [CrossRef]
- Karp, B.; Kung, H.T. GPSR: Greedy Perimeter Stateless Routing for Wireless Networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; Association for Computing Machinery: New York, NY, USA, 1 August, 2000; pp. 243–254. [Google Scholar]
- Boyan, J.; Littman, M. Packet Routing in Dynamically Changing Networks: A Reinforcement Learning Approach. Adv. Neural Inf. Process. Syst. 1993, 6, 671–678. [Google Scholar]
- Jung, W.-S.; Yim, J.; Ko, Y.-B. QGeo: Q-Learning-Based Geographic Ad Hoc Networks. IEEE Commun. Lett. 2017, 21, 2258–2261. [Google Scholar] [CrossRef]
- Jin, W.; Gu, R.; Ji, Y. Reward Function Learning for Q-Learning-Based Geographic Routing Protocol. IEEE Commun. Lett. 2019, 23, 1236–1239. [Google Scholar] [CrossRef]
- Park, C.; Lee, S.; Joo, H.; Kim, H. Empowering Adaptive Geolocation-Based Routing for UAV Networks with Reinforcement Learning. Drones 2023, 7, 387. [Google Scholar] [CrossRef]
- Rao, Z.; Xu, Y.; Pan, S. A Deep Learning-Based Constrained Intelligent Routing Method. Peer-to-Peer Netw. Appl. 2021, 14, 2224–2235. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, J.; Cui, J.; Ng, S.-X.; Maunder, R.G.; Hanzo, L. Deep-Learning-Aided Packet Routing in Aeronautical Ad Hoc Networks Relying on Real Flight Data: From Single-Objective to Near-Pareto Multiobjective Optimization. IEEE Internet Things J. 2022, 9, 4598–4614. [Google Scholar] [CrossRef]
- Gurumekala, T.; Indira Gandhi, S. Toward In-Flight Wi-Fi: A Neuro-Fuzzy Based Routing Approach for Civil Aeronautical Ad Hoc Network. Soft Comput. 2022, 26, 7401–7422. [Google Scholar] [CrossRef]
- Ryu, K.; Kim, W. Multi-Objective Optimization of Energy Saving and Throughput in Heterogeneous Networks Using Deep Reinforcement Learning. Sensors 2021, 21, 7925. [Google Scholar] [CrossRef]
- Moon, S.; Koo, S.; Lim, Y.; Joo, H. Routing Control Optimization for Autonomous Vehicles in Mixed Traffic Flow Based on Deep Reinforcement Learning. Appl. Sci. 2024, 14, 2214. [Google Scholar] [CrossRef]
- Yu, S.; Dingcheng, D. Multi-Objective Mission Planning for UAV Swarm Based on Deep Reinforcement Learning. In Proceedings of the 2023 IEEE International Conference on Unmanned Systems (ICUS), Hefei, China, 13–15 October 2023; pp. 1–10. [Google Scholar]
- Lacage, M.; Henderson, T.R. Yet Another Network Simulator. In Proceedings of the 2006 Workshop on Ns-3, Pisa, Italy, 10 October 2006; Association for Computing Machinery: New York, NY, USA, 2006; p. 12–es. [Google Scholar]
- Lyu, N.; Song, G.; Yang, B.; Cheng, Y. QNGPSR: A Q-Network Enhanced Geographic Ad-Hoc Routing Protocol Based on GPSR. In Proceedings of the 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar]
- Lansky, J.; Rahmani, A.M.; Hosseinzadeh, M. Reinforcement Learning-Based Routing Protocols in Vehicular Ad Hoc Networks for Intelligent Transport System (ITS): A Survey. Mathematics 2022, 10, 4673. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Q.; He, C.; Jaffrès-Runser, K.; Xu, Y.; Li, Z.; Xu, Y. QMR:Q-Learning Based Multi-Objective Optimization Routing Protocol for Flying Ad Hoc Networks. Comput. Commun. 2020, 150, 304–316. [Google Scholar] [CrossRef]
- Yin, H.; Liu, P.; Liu, K.; Cao, L.; Zhang, L.; Gao, Y.; Hei, X. Ns3-Ai: Fostering Artificial Intelligence Algorithms for Networking Research. In Proceedings of the 2020 Workshop on ns-3, Gaithersburg, MD, USA, 17–18 June 2020; pp. 57–64. [Google Scholar] [CrossRef]


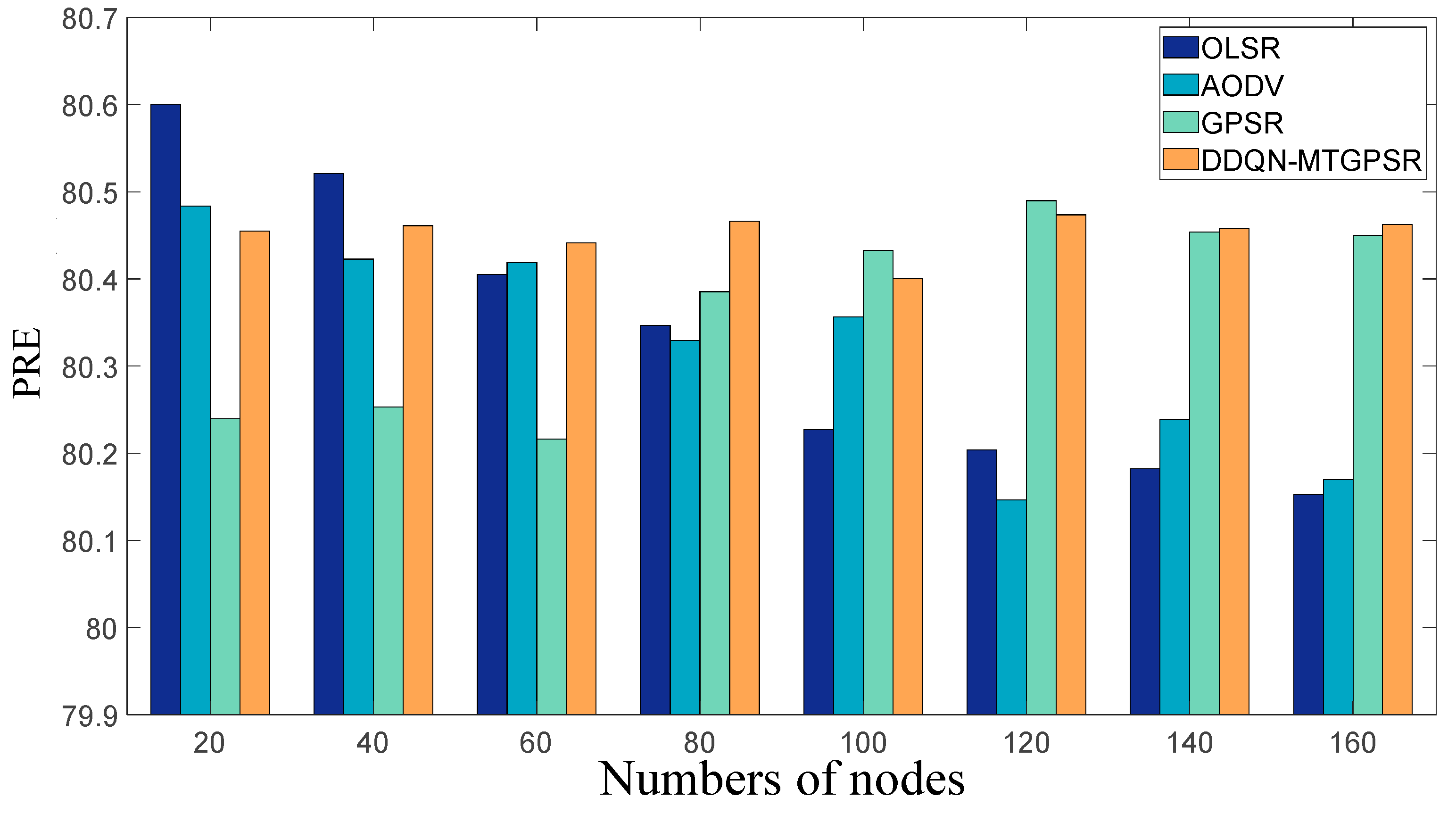
| Routing Protocol | Protocol Type | Geographical Position | Energy Consumption Factor | Routing Hole | Transmission Speed/Delay Factor | Relative Moving Trend |
|---|---|---|---|---|---|---|
| Q-Routing [22] | RL | ✓ | ✗ | ✗ | ✗ | ✗ |
| QGEO [23] | RL | ✓ | ✗ | ✗ | ✓ | ✗ |
| RFLQGEO [24] | RL | ✓ | ✗ | ✗ | ✓ | ✓ |
| GLAN [25] | RL | ✓ | ✗ | ✗ | ✗ | ✗ |
| DL-Aided Routing [27] | DL | ✓ | ✗ | ✗ | ✓ | ✗ |
| NF-Routing [28] | DL | ✓ | ✗ | ✗ | ✓ | ✓ |
| Type | Routing Protocol | Application Scenario | Application Advantage | Application Disadvantage |
|---|---|---|---|---|
| RL-Routing | [22,23,24,25] | Large-scale and highly dynamic unmanned cluster networks | Abstract formulation design, Strong versatility and adaptability, Applications on dynamic or unknown networks. | Not applicable to large-scale networks, Application of multiple objectives in routing problem. |
| DL-Routing | [27,28] | Explore the relationship between environmental characteristics and optimal paths. | Network architecture design training datasets, Overfitting issues. |
| Field 1 | Field 2 | Field 3 | Field 4 | Field 5 | Field 6 | Field 7 | Field 8 |
|---|---|---|---|---|---|---|---|
| coordinate (geometry) | moving model | delay | energy | timestamp | |||
| coordinate (geometry) | moving model | delay | energy | timestamp | |||
| ...... | ...... | ...... | ...... | ...... | …… | …… | ...... |
| coordinate (geometry) | moving model | delay | energy | timestamp |
| Simulation Parameters | Parameter Value |
|---|---|
| operating system | Ubuntu 20.04 |
| software version | NS-3.30.1 |
| transport layer protocol | UDP |
| comparative routing protocols | OLSR, AODV, GPSR, DDQN-MTGPSR |
| MAC/PHY layer protocol | IEEE 802.11b |
| radiant power | 20 dBm |
| transmission rate | 2 Mbps |
| packet transmission rate | 2.048 kb/s |
| packet length | 64 bytes |
| channel fading model | Friis propagation model |
| initial energy | 300 J |
| nodal distribution range | |
| node movement model | randomized waypoint model (RWP) |
| simulation time | 100 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Luo, F.; Zhou, J.; Dong, Y. Multi-Objective Optimized GPSR Intelligent Routing Protocol for UAV Clusters. Mathematics 2024, 12, 2672. https://doi.org/10.3390/math12172672
Chen H, Luo F, Zhou J, Dong Y. Multi-Objective Optimized GPSR Intelligent Routing Protocol for UAV Clusters. Mathematics. 2024; 12(17):2672. https://doi.org/10.3390/math12172672
Chicago/Turabian StyleChen, Hao, Fan Luo, Jianguo Zhou, and Yanming Dong. 2024. "Multi-Objective Optimized GPSR Intelligent Routing Protocol for UAV Clusters" Mathematics 12, no. 17: 2672. https://doi.org/10.3390/math12172672
APA StyleChen, H., Luo, F., Zhou, J., & Dong, Y. (2024). Multi-Objective Optimized GPSR Intelligent Routing Protocol for UAV Clusters. Mathematics, 12(17), 2672. https://doi.org/10.3390/math12172672






