On Blow-Up and Explicit Soliton Solutions for Coupled Variable Coefficient Nonlinear Schrödinger Equations

Abstract

This work is concerned with the study of explicit solutions for a generalized coupled nonlinear Schrödinger equations (NLS) system with variable coefficients. Indeed, by employing similarity transformations, we show the existence of rogue wave and dark–bright soliton-like solutions for such a generalized NLS system, provided the coefficients satisfy a Riccati system. As a result of the multiparameter solution of the Riccati system, the nonlinear dynamics of the solution can be controlled. Finite-time singular solutions in the $L^{\infty }$ norm for the generalized coupled NLS system are presented explicitly. Finally, an n-dimensional transformation between a variable coefficient NLS coupled system and a constant coupled system coefficient is presented. Soliton and rogue wave solutions for this high-dimensional system are presented as well.

1. Introduction

The coupled nonlinear Schrödinger equation models several real phenomena such as the interaction of Bloch-wave packets in a periodic system [1], the evolution of two surface wave packets in deep water [2], and in wavelength-division-multiplexed systems [3]. The starting point of many studies of these kinds of models was the well-known Manakov system introduced in 1974 [4] (see Equations (3) and (4)). The Manakov system is an integrable coupled NLS characterized by equal nonlinear interactions within and between components [5]. A great effort has been made to figure out the dynamics of the soliton-like solutions for coupled NLS. Some of these structures are dark–bright (DB), bright–bright (BB), and dark–dark (DD) solitons. These states have been observed in several experiments in optics [6,7] and in the context of Bose–Einstein condensates [8]. Another important class of solutions is rogue waves. These types of solutions are strong wavelets that can appear in the ocean from nowhere and disappear without a trace. In fact, it is this particular property that makes them candidates for the study of predicting catastrophic phenomena such as tsunamis, thunderstorms, and earthquakes [9].

In order to describe some phenomena dynamics more realistically, the space–time variation of the coefficients must be taken into account in the majority of cases. In this sense, new nonlinear Schrödinger-type coupled systems with variable coefficients have been introduced [10,11,12,13,14,15,16,17,18,19,20]. The difficulty of obtaining non-constant coefficients in the construction of explicit solutions can be overcome by making use of different techniques such as the Hirota bilinear method [21,22], similarity transformations [13,16,20], Darboux transformations [10,11,23] and the Bäcklund transformation [24], to mention a few. These approaches have enabled the study of the existence and construction of non-trivial solutions for NLS models. We can specifically highlight the work [25], which effectively investigated the existence of non-trivial solutions for a superlinear Schrödinger model with sign-changing potential. The existence of singular solutions for NLS models has also been studied and reported in the literature; see for example [26,27].

During recent years and due to their many applications, there has been a growing interest in the study of solitons and rogue wave-type solutions for coupled variable coefficient NLS equations [12,15,17,18,19]. At present, the fields interested in these kinds of solutions and moved by the necessity of data transfer are optical fiber technology and soliton transmission. More precisely, these special solutions can overcome some difficulties related to physical properties of the fiber and the interaction of it and the transmitted soliton. Although some important advances have been made in understanding the dynamics of soliton solutions for generalized coupled NLS systems from the mathematical and physical point of view, it remains a difficult problem. In this context and under the revolution of hardware equipment and software technology, recent studies of these fascinating solutions have been carried out by using a deep learning approach as well [28,29].

In this work, the objective will be to study the Schrödinger-type coupled system with the quadratic Hamiltonian (VCNLS hereafter):

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -a\left(t\right){\psi }_{xx}+\left(b\left(t\right)x^2-id\left(t\right)-xf\left(t\right)\right)\psi +i\left(g\left(t\right)-c\left(t\right)x\right){\psi }_x+h\left(t\right)({\left|\phi \right|}^{2s}+{\left|\psi \right|}^{2s})\psi ,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -a\left(t\right){\phi }_{xx}+\left(b\left(t\right)x^2-id\left(t\right)-xf\left(t\right)\right)\phi +i\left(g\left(t\right)-c\left(t\right)x\right){\phi }_x+h\left(t\right)({\left|\phi \right|}^{2s}+{\left|\psi \right|}^{2s})\phi .\hfill \end{array}$$

(2)

Here $\psi (x,t)$ and $\phi (x,t)$ represent complex wavefunctions, $a\left(t\right)$, $b\left(t\right)$, $c\left(t\right)$, $d\left(t\right)$, $f\left(t\right)$, $g\left(t\right)$, $h\left(t\right)$ are given time-dependent functions, and $s>0$. The coefficient $a\left(t\right)$ is the dispersion management parameter, $b\left(t\right)$ determines the time dependence of the quadratic potential, $d\left(t\right)$ is the gain/loss term, $f\left(t\right)x$ standardizes an arbitrary linear potential, and $h\left(t\right)$ is the nonlinear management. The system (1) and (2) appears to describe the propagation of solitons in birefringence fibers (see for example [13,20]), and also in the framework of solitary waves in multi-component Bose–Einstein condensates [30,31]. We point out that the proposed system (1) and (2) extends many of the models studied in the literature.

The uncoupled case ($\phi \equiv 0$) has been the source of many studies in the recent years [32,33,34,35]. By employing the similarity transformation and imposing the coefficients to satisfy a Riccati system (see Equations (19)–(24) and (58)–(63)), soliton-like solutions (bright, dark, and Peregrine), singular solutions, and the fundamental solution ($h\left(t\right)\equiv 0$) were constructed. Also, the Riccati system allowed the construction and study of explicit solutions for diffusion-type equations [36] and reaction–diffusion equations [37].

This paper’s aim is to establish a relationship between dispersion, potential, damping, and nonlinearity terms by the Riccati system in order to obtain solutions such as dark–bright and rogue wave soliton solutions for the coupled VCNLS (1) and (2). The multiparameters solution of the Riccati system allows the soliton dynamics to be controlled; this is crucial in practice, because one needs to control the soliton transmission of information since standard vector solitons for NLS systems do not have controllable parameters. This relation in the coefficients provides the construction of solutions with blow-up in finite time in the $L^{\infty }$ norm. Finally, an n-dimensional generalization of the VCNLS is studied, and the existence of soliton solutions is shown as well.

This work makes the following contributions:

• It introduces a novel coupled system of Schrödinger equations with variable coefficients. In this regard, our work differs from the models explored in the literature, which typically do not take into account the dynamics of the solutions under the influence of dispersion, potential (linear and quadratic), damping, and nonlinear management all at once.
• It reports on new solitons, rogue waves, and singular solutions to coupled nonlinear Schrödinger systems with variable coefficients. The explicit construction of this important class of solutions demonstrates that coherent structures are possible in the presence of dispersion, potential, damping, and nonlinear management as long as the coefficients fulfill a Riccati system.
• It demonstrates the capacity to control solution dynamics using the Riccati system’s multiparametric solution. To the best of our knowledge, our approach is one of the few capable of analyzing this type of parameter influence. It could be meaningful for manipulating solitons experimentally.

The paper is organized as follows: in Section 2 we introduce the classical coupled Manakov system and its rogue wave and soliton-type solutions. The explicit construction of rogue wave and soliton-type solutions for the generalized coupled NLS system (1) and (2) is presented in Section 3. This objective is obtained by using Theorem 1 and solutions of the Manakov system given in the previous section. In Section 4, we construct explicit $L^{\infty }$ singular solutions for the generalized coupled NLS system, as can be seen in Theorem 2. Section 5 is devoted to the extension of the transformation established in Theorem 1. Such a new transformation allows us to connect an n-dimensional coupled NLS system with an n-dimensional Manakov system; see Theorem 3. Also, soliton and rogue wave solutions are constructed for this model. A Mathematica file has been prepared as Supplementary Materials, verifying the Riccati systems used in the construction of the solutions in all the previous sections. Conclusions and some final remarks are given in Section 6. Appendix A corresponds to the appendix, in which the solution of the Riccati system is presented.

2. Classical Solutions of Coupled NLS

The coupled NLS system, or Manakov system

$$\begin{array}{ccc}\hfill i{\chi }_{\tau }+{\chi }_{\xi \xi }+2({\left|\varphi \right|}^2+{\left|\chi \right|}^2)\chi & =& 0,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill i{\varphi }_{\tau }+{\varphi }_{\xi \xi }+2({\left|\varphi \right|}^2+{\left|\chi \right|}^2)\varphi & =& 0,\hfill \end{array}$$

(4)

is a nonlinear wave system that governs a wide variety of physical phenomena ranging from the dynamics of a two-component Bose–Einstein condensate [8,38], nonlinear optics [6,7], and the dynamics of deep-sea waves under the interaction of two-layer stratification [39]. This system (3) and (4) was shown by Manakov to be integrable [4,5]. It admits soliton-like structures such as dark–bright (DB) solutions. In fact, (3) and (4) possess DB solitons; see for example [6,8,10,20]:

$$\chi (\xi ,\tau )=Ctanh\left[C(\xi -2e\tau )+E\right]exp\left[i(e\xi +(2C^2-e^2)\tau )\right],$$

(5)

$$\varphi (\xi ,\tau )=-4C^2(a_3+i{b}_3)sech\left[C(\xi -2e\tau )+E\right]exp\left[i\left(e\xi +(3C^2-e^2)\tau \right)\right],$$

(6)

where $E={\displaystyle \frac{1}{2}}ln\left({\displaystyle \frac{a_3^2+b_3^2}{2C^2}}\right)$ and $C,e,a_3,b_3$ are arbitrary constants. These kinds of solutions were first experimentally observed in photorefractive crystals [6]. Other interesting solutions with fascinating properties are rogue waves. Indeed, the coupled NLS system (3) and (4) admits the exact rogue wave solution of type I [10,20]:

$$\chi (\xi ,\tau )=Aexp\left(i{\theta }_1\right)\left(-1-i\sqrt{3}+{\displaystyle \frac{-6AB\sqrt{3}-36\tau A^2\sqrt{3}-3+i(36A^2\tau +6AB+5\sqrt{3})}{12A^2{B}^2+8AB\sqrt{3}+144{\tau }^2{A}^4+5}}\right),$$

(7)

$$\varphi (\xi ,\tau )=Aexp\left(i{\theta }_2\right)\left(-1+i\sqrt{3}+{\displaystyle \frac{-6AB\sqrt{3}+36\tau A^2\sqrt{3}-3+i(36A^2\tau -6AB-5\sqrt{3})}{12A^2{B}^2+8AB\sqrt{3}+144{\tau }^2{A}^4+5}}\right),$$

(8)

where $B=\xi +6q\tau ,$ ${\theta }_i=d_i\xi +(2c_1^2+2c_2^2-d_i^2)\tau$ with $i=1,2.$ The parameters $A=d_2+3q,$ $d_1=d_2-2A,$ $c_i=\pm 2A,$ with $i=1,2$ and $d_2,q$, are arbitrary constants. Similarly, the rogue wave solution of type II [10,20] is given by:

$$\chi (\xi ,\tau )=A\left(-1-i\sqrt{3}+{\displaystyle \frac{G_1+i{H}_1}{D}}\right)exp\left(i{\theta }_1\right),$$

(9)

$$\varphi (\xi ,\tau )=A\left(-1+i\sqrt{3}+{\displaystyle \frac{G_2+i{H}_2}{D}}\right)exp\left(i{\theta }_2\right),$$

(10)

where

$$\begin{array}{ccc}\hfill D& =& 1+4\sqrt{3}AB+24A^2{B}^2+16\sqrt{3}{A}^3{B}^3+12A^4{B}^4+48A^4(9+8\sqrt{3}AB+6A^2{B}^2){\tau }^2+1728A^8{\tau }^4,\hfill \\ \hfill G_1& =& -3\left(-1+6A^2{B}^2+4\sqrt{3}{A}^3{B}^3+4A^2(\sqrt{3}+12AB+6\sqrt{3}{A}^2{B}^2)\tau +24A^4(3+2\sqrt{3}AB){\tau }^2+288\sqrt{3}{A}^6{\tau }^3\right),\hfill \\ \hfill G_2& =& 3\left(1-6A^2{B}^2-4\sqrt{3}{A}^3{B}^3+4A^2(\sqrt{3}+12AB+6\sqrt{3}{A}^2{B}^2)\tau -24A^4(3+2\sqrt{3}AB){\tau }^2+288\sqrt{3}{A}^6{\tau }^3\right),\hfill \\ \hfill H_1& =& \sqrt{3}+12AB+18\sqrt{3}{A}^2{B}^2+12A^3{B}^3+12A^2(9+8\sqrt{3}AB+6A^2{B}^2)\tau +24A^4(13\sqrt{3}+6AB){\tau }^2+864A^6{\tau }^3,\hfill \\ \hfill H_2& =& -\sqrt{3}-12AB-18\sqrt{3}{A}^2{B}^2-12A^3{B}^3+12A^2(9+8\sqrt{3}AB+6A^2{B}^2)\tau -24A^4(13\sqrt{3}+6AB){\tau }^2+864A^6{\tau }^3.\hfill \end{array}$$

In the subsequent section, we will use these solutions to construct explicit solutions for the generalized coupled NLS system.

3. Generalized Coupled NLS System

The aim of this section is to establish the existence of soliton-type and rogue wave solutions (by the explicit construction of these solutions) of the generalized coupled NLS system (1) and (2). More precisely, by using similarity transformations and by imposing the coefficients to satisfy the Riccati system, classical solutions of the standard Manakov system (3) and (4) are extended to this general framework. Indeed, the main result of this section is:

Theorem 1. 

Let $l_0=\pm 1.$ Then, the following NLS coupled system (or VCNLS)

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -a\left(t\right){\psi }_{xx}+(b\left(t\right)x^2-id\left(t\right)-xf\left(t\right))\psi +i(g\left(t\right)-c\left(t\right)x){\psi }_x+h\left(t\right)({\left|\phi \right|}^2+{\left|\psi \right|}^2)\psi ,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -a\left(t\right){\phi }_{xx}+(b\left(t\right)x^2-id\left(t\right)-xf\left(t\right))\phi +i(g\left(t\right)-c\left(t\right)x){\phi }_x+h\left(t\right)({\left|\phi \right|}^2+{\left|\psi \right|}^2)\phi ,\hfill \end{array}$$

(12)

admits dark–bright (DB) solitons and rogue wave-type solutions where $h\left(t\right)$ satisfies the integrability condition $h\left(t\right)=\lambda a\left(t\right){\beta }^2\left(t\right)\mu \left(t\right)$ with $\lambda \in \mathbb{R}$.

Proof. 

Assume that $S(x,t)=\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)$. Then, we look for solutions for (11) and (12) of the form

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{\mu \left(t\right)}}}{e}^{iS(x,t)}\chi (\xi ,\tau ),\xi =\beta \left(t\right)x+\epsilon \left(t\right),\tau =\gamma \left(t\right),$$

(13)

and

$$\phi (x,t)={\displaystyle \frac{1}{\sqrt{\mu \left(t\right)}}}{e}^{iS(x,t)}\varphi (\xi ,\tau ).$$

(14)

Computing the first derivatives of the function $\psi$ (derivatives for $\phi$ are obtained by changing $\chi$ by $\varphi$), we have

$${\psi }_x={\mu }^{-1/2}{e}^{iS(x,t)}\left[\beta {\chi }_{\xi }+i(2\alpha x+\delta )\chi \right],$$

(15)

$${\psi }_{xx}={\mu }^{-1/2}{e}^{iS(x,t)}\left[{\beta }^2{\chi }_{\xi \xi }+i\beta (4\alpha x+2\delta ){\chi }_{\xi }+(2\alpha i-4{\alpha }^2{x}^2-4\alpha \delta x-{\delta }^2)\chi \right],$$

(16)

$${\psi }_t={\mu }^{-1/2}{e}^{iS(x,t)}\left[\dot{\gamma }{\chi }_{\tau }+(\dot{\beta }x+\dot{\epsilon }){\chi }_{\xi }+\left(-{\displaystyle \frac{\dot{\mu }}{2\mu }}+i(\dot{\alpha }{x}^2+\dot{\delta }x+\dot{\kappa })\right)\chi \right].$$

(17)

After substituting (15)–(17) in (11) and (12), we obtain

$$\begin{array}{cc}\hfill & x^2\left(\dot{\alpha }+4a{\alpha }^2+b+2\alpha c\right)+x\left(i{\chi }_{\xi }(-\dot{\beta }-4a\alpha \beta -c\beta )+\chi (\dot{\delta }+4a\alpha \delta -f-2\alpha g+c\delta )\right)\hfill \\ & +i{\chi }_{\xi }\left(-\dot{\epsilon }-2a\beta \delta +g\beta \right)+\chi \left(\dot{\kappa }+a{\delta }^2-g\delta +i\left({\displaystyle \frac{\dot{\mu }}{2\mu }}-2a\alpha -d\right)\right)-i\dot{\gamma }{\chi }_{\tau }-a{\beta }^2{\chi }_{\xi \xi }\hfill \\ \hfill & +h{\mu }^{-1}\left({\left|\chi \right|}^2+{\left|\varphi \right|}^2\right)\chi =0.\hfill \end{array}$$

(18)

Therefore, equating each term to zero, and using the conditions $\dot{\gamma }=-l_{0}a{\beta }^2,h\left(t\right)=\lambda a\left(t\right){\beta }^2\left(t\right)\mu \left(t\right)$, we deduce the well-known Riccati system [33,34,35,36]:

$${\displaystyle \frac{d\alpha }{dt}}+b\left(t\right)+2c\left(t\right)\alpha +4a\left(t\right){\alpha }^2=0,$$

(19)

$${\displaystyle \frac{d\beta }{dt}}+(c\left(t\right)+4a\left(t\right)\alpha \left(t\right))\beta =0,$$

(20)

$${\displaystyle \frac{d\gamma }{dt}}+a\left(t\right){\beta }^2\left(t\right)l_0=0,$$

(21)

$${\displaystyle \frac{d\delta }{dt}}+(c\left(t\right)+4a\left(t\right)\alpha \left(t\right))\delta =f\left(t\right)+2\alpha \left(t\right)g\left(t\right),$$

(22)

$${\displaystyle \frac{d\epsilon }{dt}}=(g\left(t\right)-2a\left(t\right)\delta \left(t\right))\beta \left(t\right),$$

(23)

$${\displaystyle \frac{d\kappa }{dt}}=g\left(t\right)\delta \left(t\right)-a\left(t\right){\delta }^2\left(t\right).$$

(24)

Now, considering the standard substitution (also obtained from equalizing to zero)

$$\alpha =\left({\displaystyle \frac{1}{4a\left(t\right)}}{\displaystyle \frac{{\mu }^{\prime }\left(t\right)}{\mu \left(t\right)}}-{\displaystyle \frac{d\left(t\right)}{2a\left(t\right)}}\right),$$

(25)

it follows that the Riccati Equation (19) becomes

$${\mu }^{″}-\eta \left(t\right){\mu }^{\prime }+4\sigma \left(t\right)\mu =0,$$

(26)

with

$$\eta \left(t\right)={\displaystyle \frac{a^{\prime }}{a}}-2c+4d,\sigma \left(t\right)=ab-cd+d^2+{\displaystyle \frac{d}{2}}\left({\displaystyle \frac{a^{\prime }}{a}}-{\displaystyle \frac{d^{\prime }}{d}}\right).$$

(27)

We will refer to (26) as the characteristic equation of the Riccati system. From the last three terms on the left side of the equality (18), the functions $\chi$ and $\varphi$ will satisfy the coupled NLS system in the new variables $\tau$ and $\xi$:

$$\begin{array}{ccc}\hfill i{\chi }_{\tau }-l_0{\chi }_{\xi \xi }+l_0\lambda ({\left|\varphi \right|}^2+{\left|\chi \right|}^2)\chi & =& 0,\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill i{\varphi }_{\tau }-l_0{\varphi }_{\xi \xi }+l_0\lambda ({\left|\varphi \right|}^2+{\left|\chi \right|}^2)\varphi & =& 0,\hfill \end{array}$$

(29)

where $\alpha \left(t\right)$, $\beta \left(t\right)$, $\gamma \left(t\right)$, $\delta \left(t\right)$, $ϵ\left(t\right)$, and $\kappa \left(t\right)$ are given by Equations (A1)–(A13) set out in the Appendix A. Therefore, the existence of these kinds of solutions (DB and rogue wave solutions) are established by letting $\chi$ and $\varphi$ be the solutions discussed in the previous section; see Equations (5)–(10). □

Remark 1. 

It is important to note that Theorem 1 provides a mechanism to establish the existence of soliton and rogue wave solutions for the NLS system (11) and (12). However, the uniqueness of these solutions is not guaranteed due to the use of the Riccati system in the construction of the solutions.

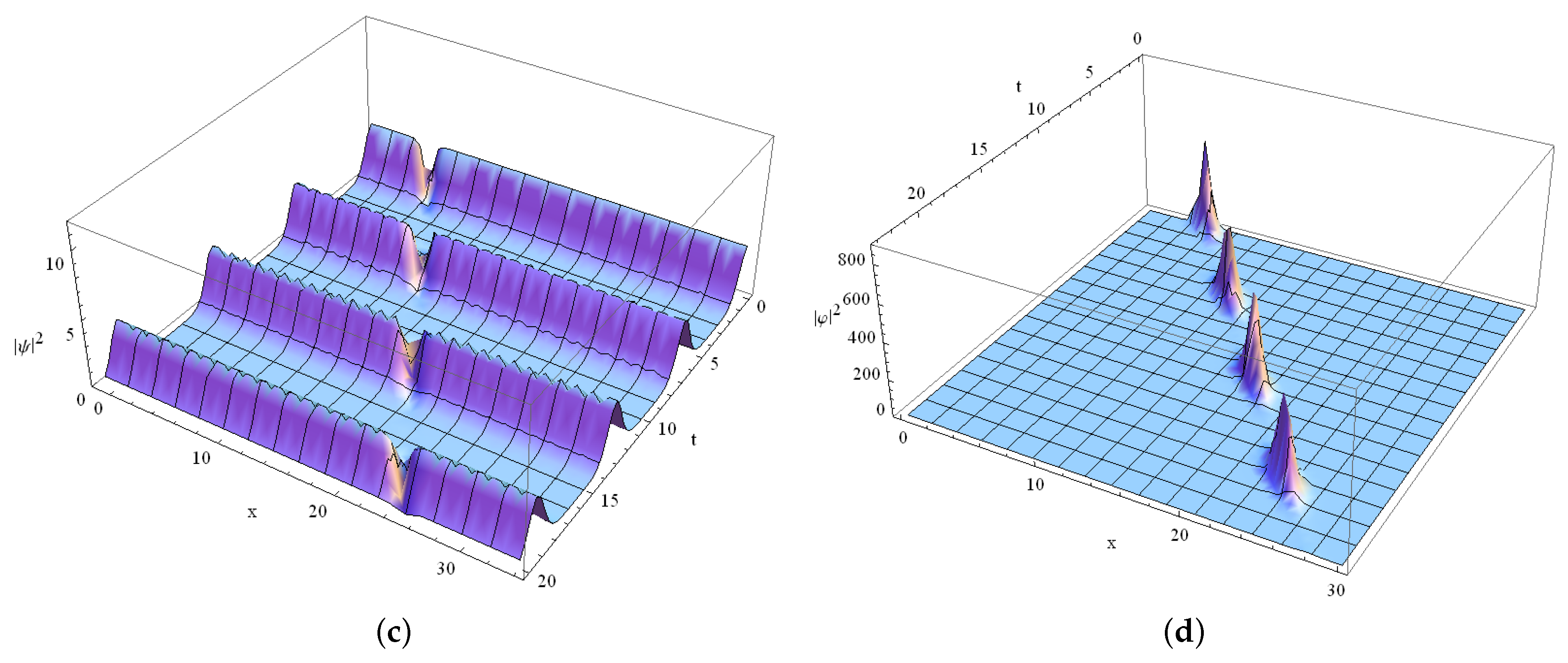
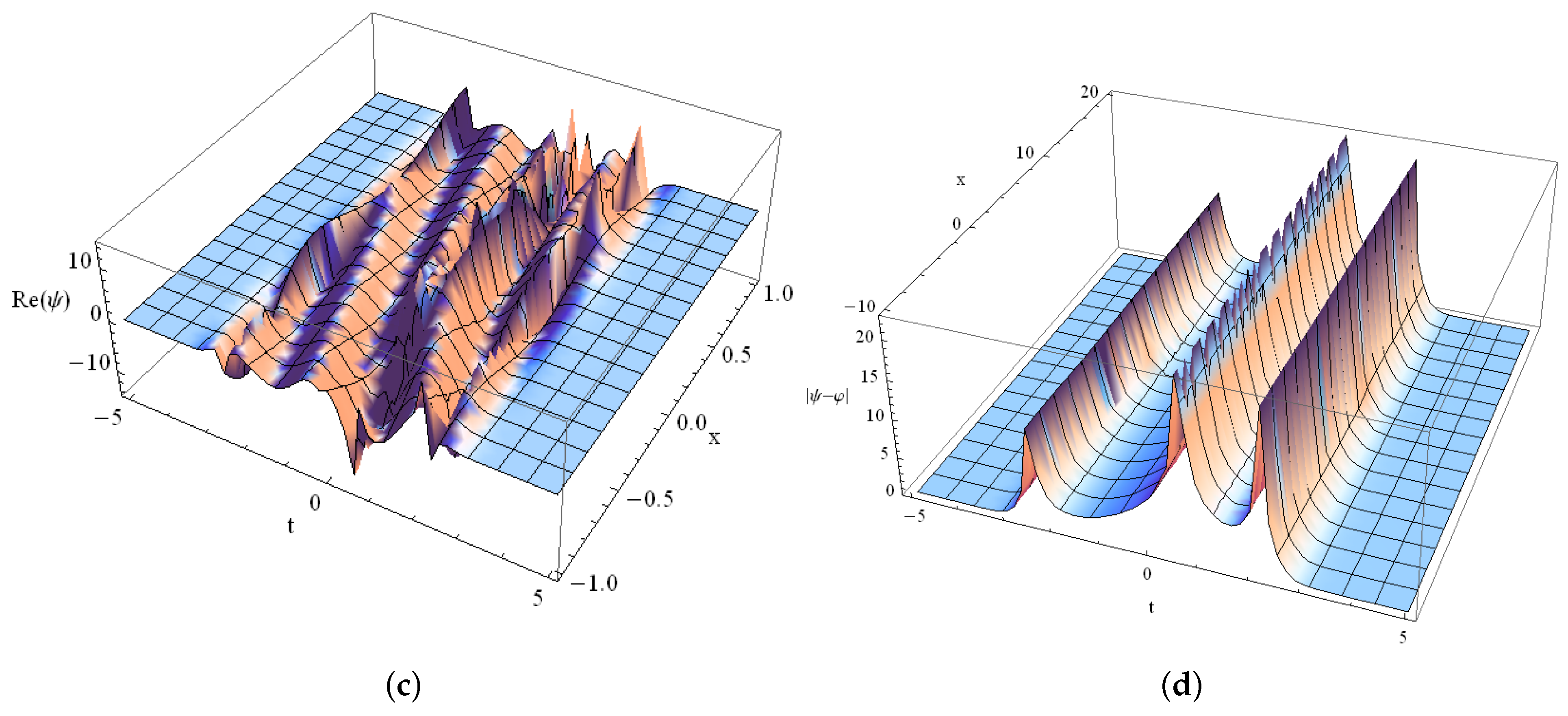
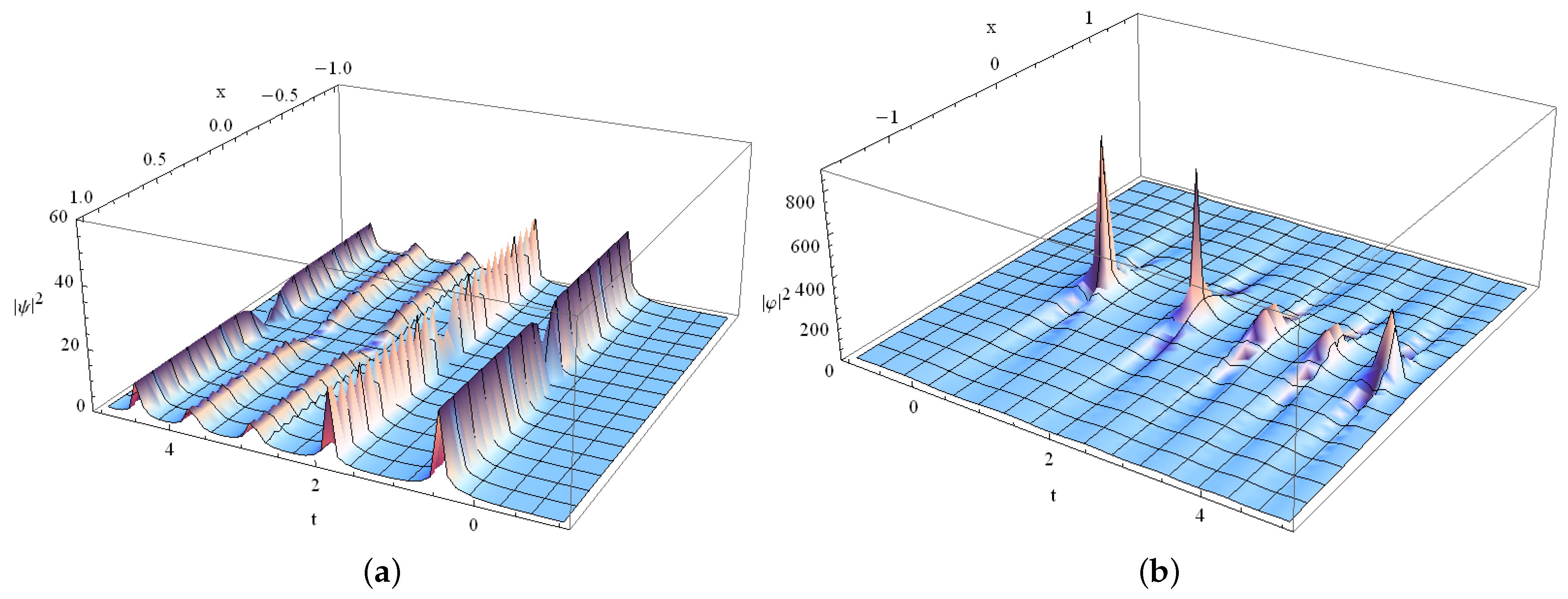
3.1. Rogue Wave Solutions

The generation and behavior of rogue waves is a significant subject in oceanography. In this light, the solutions presented in this section may contribute to a better understanding of how this type of wave emerges as a result of a balance between dispersion, potential (quadratic and linear), damping, and nonlinearity.

The existence of rogue wave solutions for the model (11) and (12) can be guaranteed by the extension of solutions (7)–(10) by the previous Theorem 1, as will be seen in the following examples. Throughout the text, the coefficients are selected in such a way that the formulae corresponding to the solution of the Riccati system (A1)–(A13) provide explicit expressions. We start with the Type I rogue wave solutions.

3.1.1. Case $a=d=1,b=t,c=f=g=0,h={\displaystyle \frac{-2e^{2t}}{{}_{0}F_1\left(2/3,-4t^3/9\right)}}$

In this scenario, we will look at the dynamics of the solutions when they are subjected to constant dispersion and damping, as well as exponential nonlinearities. The model has the form

$$i{\psi }_t=-{\psi }_{xx}+t{x}^2\psi -i\psi -{\displaystyle \frac{2e^{2t}}{{}_{0}F_1\left(2/3,-4t^3/9\right)}}\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\psi ,$$

(30)

$$i{\phi }_t=-{\phi }_{xx}+t{x}^2\phi -i\phi -{\displaystyle \frac{2e^{2t}}{{}_{0}F_1\left(2/3,-4t^3/9\right)}}\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\phi .$$

(31)

Then, according to Theorem 1, we obtain

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{1}{4t}}-{\displaystyle \frac{1+t^3{}_{0}F_1\left(2/3,-4t^3/9\right){}_{0}F_1\left(7/3,-4t^3/9\right)}{4t{}_{0}F_1\left(2/3,-4t^3/9\right){}_{0}F_1\left(4/3,-4t^3/9\right)}},\beta \left(t\right)={\displaystyle \frac{1}{{}_{0}F_1\left(2/3,-4t^3/9\right)}},\\ \\ \hfill \gamma \left(t\right)={\displaystyle \frac{t{}_{0}F_1\left(4/3,-4t^3/9\right)}{{}_{0}F_1\left(2/3,-4t^3/9\right)}},\delta \left(t\right)={\displaystyle \frac{1}{{}_{0}F_1\left(2/3,-4t^3/9\right)}},\epsilon \left(t\right)=-{\displaystyle \frac{2t{}_{0}F_1\left(4/3,-4t^3/9\right)}{{}_{0}F_1\left(2/3,-4t^3/9\right)}},\\ \\ \hfill \kappa \left(t\right)=-{\displaystyle \frac{t{}_{0}F_1\left(4/3,-4t^3/9\right)}{{}_{0}F_1\left(2/3,-4t^3/9\right)}},\mu \left(t\right)=e^{2t}{}_{0}F_1\left(2/3,-4t^3/9\right),\end{array}$$

where ${}_{0}F_1\left(a,z\right)$ is the confluent hypergeometric function given by the series ${}_{0}F_1\left(a,z\right)={\sum }_{k=0}^{\infty }{\displaystyle \frac{z^k}{{\left(a\right)}_{k}k!}}$ with ${\left(a\right)}_k=\Gamma (a+k)/\Gamma \left(a\right)$, and $\Gamma \left(z\right)$ is the gamma function. Here, we have solved the Riccati system with the initial conditions $\alpha \left(0\right)=0$, $\beta \left(0\right)=1$, $\gamma \left(0\right)=0$, $\delta \left(0\right)=1$, $\epsilon \left(0\right)=0,$ $\kappa \left(0\right)=0$, and $\mu \left(0\right)=1.$

Therefore, we can construct a solution in the form:

$$\psi (x,t)={\displaystyle \frac{e^{-t}}{\sqrt{{}_{0}F_1\left(2/3,-4t^3/9\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\chi (\xi ,\tau ),$$

(32)

$$\phi (x,t)={\displaystyle \frac{e^{-t}}{\sqrt{{}_{0}F_1\left(2/3,-4t^3/9\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\varphi (\xi ,\tau ),$$

(33)

where $\chi$ and $\varphi$ are given by Equations (7) and (8). The profiles of these solutions for the parameters $d_2=1$ and $q=0$ are shown in Figure 1a,b. The real part of the function $\psi$ is displayed in Figure 1c. Figure 1d shows the difference between the two solutions to show that they are different.

3.1.2. Case $a=-{\displaystyle \frac{cost}{2}},b=c=f=g=0,d=-1,h=e^{-2t}cost$

This example demonstrates the existence of rogue wave solutions for a system without a quadratic potential but with periodic dispersion, constant damping, and exponential decay nonlinearities. In particular, the corresponding system is given by the equations

$$i{\psi }_t={\displaystyle \frac{cost}{2}}{\psi }_{xx}+i\psi +e^{-2t}cost\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\psi ,$$

(34)

$$i{\phi }_t={\displaystyle \frac{cost}{2}}{\phi }_{xx}+i\phi +e^{-2t}cost\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\phi .$$

(35)

Then,

$$\begin{array}{c}\hfill \alpha \left(t\right)=0,\beta \left(t\right)=1,\gamma \left(t\right)=-{\displaystyle \frac{sint}{2}},\delta \left(t\right)=1,\\ \hfill \epsilon \left(t\right)=sint,\kappa \left(t\right)={\displaystyle \frac{sint}{2}},\mu \left(t\right)=e^{-2t}.\end{array}$$

The initial conditions used to solve the Riccati system are the same as those given in the previous case. In fact, except for the section on bending dynamics, we shall use these initial conditions for the rest of the study. Solutions for the system (34) and (35) are

$$\psi (x,t)=e^{arccos(cos t)}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\chi (\xi ,\tau ),$$

(36)

$$\phi (x,t)=e^{arccos(cos t)}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\varphi (\xi ,\tau ).$$

(37)

Again $\chi$ and $\varphi$ are given by the Equations (7) and (8). Figure 2 shows the time evolution of ${\left|\psi \right|}^2$ and ${\left|\phi \right|}^2$ for the corresponding solutions. The difference between the two solutions are shown in the Figure 2c.

The next two cases correspond to the Type II rogue wave solutions.

3.1.3. Case $a=-secht/2$, $b=-4a$, $c=4a$, $d=2a$, $f=g=0$, $h={\displaystyle \frac{-2secht}{-2cosh\left(\sqrt{8}gdt\right)+\sqrt{2}sinh\left(\sqrt{8}gdt\right)}}$

Assume the system

$$i{\psi }_t=secht\left({\displaystyle \frac{{\psi }_{xx}}{2}}+(i+2x^2)\psi +2ix{\psi }_x-{\displaystyle \frac{2\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\psi }{-2cosh\left(\sqrt{8}gdt\right)+\sqrt{2}sinh\left(\sqrt{8}gdt\right)}}\right),$$

(38)

$$i{\phi }_t=secht\left({\displaystyle \frac{{\phi }_{xx}}{2}}+(i+2x^2)\phi +2ix{\phi }_x-{\displaystyle \frac{2\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\phi }{-2cosh\left(\sqrt{8}gdt\right)+\sqrt{2}sinh\left(\sqrt{8}gdt\right)}}\right),$$

(39)

where $gdt$ is the Gudermannian function given by $gdt=2arctan\left[tanh\left(\frac{1}{2}t\right)\right]$. The expressions for the functions $\alpha \left(t\right)$, $\beta \left(t\right)$, $\gamma \left(t\right)$, $\delta \left(t\right)$, $\epsilon \left(t\right)$, $\kappa \left(t\right)$, and $\mu \left(t\right)$ are

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{1}{1-\sqrt{2}coth\left(\sqrt{8}gdt\right)}},\beta \left(t\right)={\displaystyle \frac{\sqrt{2}}{\sqrt{2}cosh\left(\sqrt{8}gdt\right)-sinh\left(\sqrt{8}gdt\right)}},\\ \\ \hfill \gamma \left(t\right)={\displaystyle \frac{1}{4-4\sqrt{2}coth\left(\sqrt{8}gdt\right)}},\delta \left(t\right)={\displaystyle \frac{\sqrt{2}}{\sqrt{2}cosh\left(\sqrt{8}gdt\right)-sinh\left(\sqrt{8}gdt\right)}},\\ \hfill \epsilon \left(t\right)=-{\displaystyle \frac{1}{2-\sqrt{8}coth\left(\sqrt{8}gdt\right)}},\kappa \left(t\right)=-{\displaystyle \frac{1}{4-4\sqrt{2}coth\left(\sqrt{8}gdt\right)}},\\ \\ \hfill \mu \left(t\right)=cosh\left(\sqrt{8}gdt\right)-{\displaystyle \frac{\sqrt{2}}{2}}sinh\left(\sqrt{8}gdt\right).\end{array}$$

Now, we can give a form for the solutions, that is,

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{cosh\left(\sqrt{8}gdt\right)-\frac{\sqrt{2}}{2}sinh\left(\sqrt{8}gdt\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\chi (\xi ,\tau ),$$

(40)

$$\phi (x,t)={\displaystyle \frac{1}{\sqrt{cosh\left(\sqrt{8}gdt\right)-\frac{\sqrt{2}}{2}sinh\left(\sqrt{8}gdt\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\varphi (\xi ,\tau ),$$

(41)

with $\chi$ and $\varphi$ satisfying the Equations (9) and (10). The dynamics of these solutions are shown in Figure 3.

3.1.4. Case $a=-(1+t^2)cost/2,b=2a,c=4a,d=2a,f=g=0,h={\displaystyle \frac{2a}{cosh\theta -\sqrt{2}sinh\theta }}$

Consider the system of the nonlinear Schrödinger equations

$$i{\psi }_t=(1+t^2)cost\left({\displaystyle \frac{{\psi }_{xx}}{2}}+(i-x^2)\psi +2ix{\psi }_x-{\displaystyle \frac{\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\psi }{cosh\theta -\sqrt{2}sinh\theta }}\right),$$

(42)

$$i{\phi }_t=(1+t^2)cost\left({\displaystyle \frac{{\phi }_{xx}}{2}}+(i-x^2)\phi +2ix{\phi }_x-{\displaystyle \frac{\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\phi }{cosh\theta -\sqrt{2}sinh\theta }}\right),$$

(43)

with $\theta =\sqrt{8}tcost+\sqrt{2}(t^2-1)sint$. In this case, the solution of the Riccati system has the form

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{1}{-2+\sqrt{2}coth\theta }},\beta \left(t\right)={\displaystyle \frac{1}{cosh\theta -\sqrt{2}sinh\theta }},\\ \\ \hfill \gamma \left(t\right)={\displaystyle \frac{1}{4-\sqrt{8}coth\theta }},\delta \left(t\right)={\displaystyle \frac{1}{cosh\theta -\sqrt{2}sinh\theta }},\\ \hfill \epsilon \left(t\right)={\displaystyle \frac{1}{-2+\sqrt{2}coth\theta }},\kappa \left(t\right)={\displaystyle \frac{1}{-4+\sqrt{8}coth\theta }},\\ \\ \hfill \mu \left(t\right)=cosh\theta -\sqrt{2}sinh\theta .\end{array}$$

Then, by the assumption that $\chi$ and $\varphi$ satisfy Equations (9) and (10), Theorem 1 provides the following solutions:

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{cosh\theta -\sqrt{2}sinh\theta }}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\chi (\xi ,\tau ),$$

(44)

$$\phi (x,t)={\displaystyle \frac{1}{\sqrt{cosh\theta -\sqrt{2}sinh\theta }}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\varphi (\xi ,\tau ).$$

(45)

Figure 4 shows the profiles of ${\left|\psi \right|}^2,{\left|\phi \right|}^2$ for these particular solutions.

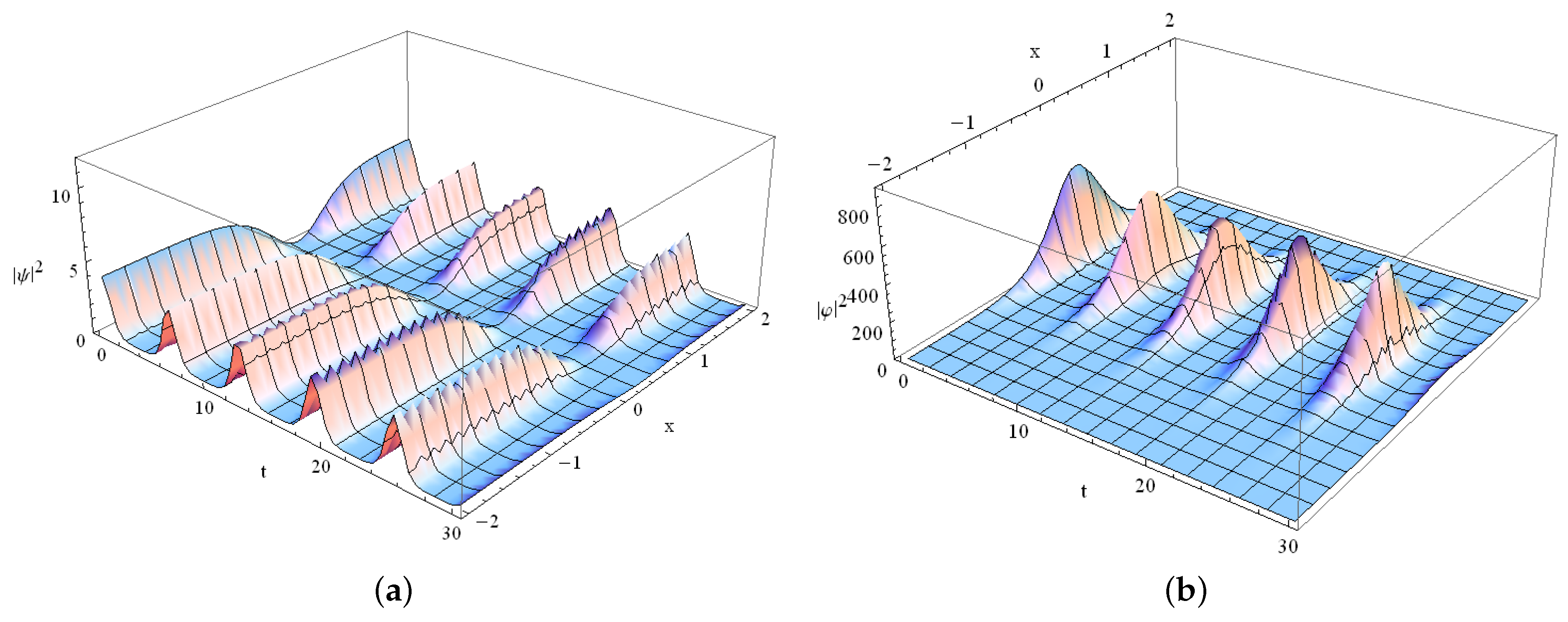
3.2. Dark–Bright Soliton-Type Solutions

This part of the work is concerned with the construction of solutions for the generalized coupled NLS system with soliton-type properties. As we will see, (11) and (12) admits DB-type solitons.

3.2.1. Case $a=2,b={\displaystyle \frac{t+1}{2}},c=-2,d=-1,f=g=0,h={\displaystyle \frac{-4}{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}}$

This example illustrates how the dynamics of the soliton change when subjected to constant dispersion and damping. The associated system

$$i{\psi }_t=-2{\psi }_{xx}+{\displaystyle \frac{t+1}{2}}{x}^2\psi +i\psi +2ix{\psi }_x-{\displaystyle \frac{4\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\psi }{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},$$

(46)

$$i{\phi }_t=-2{\phi }_{xx}+{\displaystyle \frac{t+1}{2}}{x}^2\phi +i\phi +2ix{\phi }_x-{\displaystyle \frac{4\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\phi }{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},$$

(47)

admits the functions

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{1}{4}}+{\displaystyle \frac{1}{8t}}+{\displaystyle \frac{1}{-8t{}_{0}F_1\left(2/3,-4t^3/9\right){}_{0}F_1\left(4/3,-4t^3/9\right)+16t^2{}_{0}F_1^2\left(4/3,-4t^3/9\right)}}-{\displaystyle \frac{t^2{}_{0}F_1\left(7/3,-4t^3/9\right)}{8{}_{0}F_1\left(4/3,-4t^3/9\right)}},\\ \hfill \beta \left(t\right)={\displaystyle \frac{1}{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},\gamma \left(t\right)={\displaystyle \frac{2t{}_{0}F_1\left(4/3,-4t^3/9\right)}{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},\\ \hfill \delta \left(t\right)={\displaystyle \frac{1}{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},\epsilon \left(t\right)={\displaystyle \frac{-4t{}_{0}F_1\left(4/3,-4t^3/9\right)}{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},\end{array}$$

$$\begin{array}{c}\hfill \kappa \left(t\right)={\displaystyle \frac{-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}},\mu \left(t\right)={}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right).\end{array}$$

In these terms, explicit solutions are given by the expressions

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\chi (\xi ,\tau ),$$

(48)

$$\phi (x,t)={\displaystyle \frac{1}{\sqrt{{}_{0}F_1\left(2/3,-4t^3/9\right)-2t{}_{0}F_1\left(4/3,-4t^3/9\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\varphi (\xi ,\tau ),$$

(49)

with $\chi$ and $\varphi$ satisfying Equations (5) and (6).

Figure 5 shows the profiles of ${\left|\psi \right|}^2,{\left|\phi \right|}^2$ for these particular solutions.

3.2.2. Case $a=1,b={\displaystyle \frac{{sin}^{2}t-cost}{4}},c=-sint,d=sint,f=g=0,h=-2e^{3-3cos t}$

Consider the system of nonlinear Schrödinger equations defined for $t>0:$

$$i{\psi }_t=-{\psi }_{xx}+{\displaystyle \frac{{sin}^{2}t-cost}{4}}{x}^2\psi -isint\psi +ixsint{\psi }_x-2e^{3-3cos t}\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\psi ,$$

(50)

$$i{\phi }_t=-{\phi }_{xx}+{\displaystyle \frac{{sin}^{2}t-cost}{4}}{x}^2\phi -isint\phi +ixsint{\phi }_x-2e^{3-3cos t}\left({\left|\phi \right|}^2+{\left|\psi \right|}^2\right)\phi .$$

(51)

It has the explicit soliton-type solutions

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{e^{3-3cos t}}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\chi (\xi ,\tau ),$$

(52)

$$\phi (x,t)={\displaystyle \frac{1}{\sqrt{e^{3-3cos t}}}}exp\left[i\left(\alpha \left(t\right)x^2+\delta \left(t\right)x+\kappa \left(t\right)\right)\right]\varphi (\xi ,\tau ),$$

(53)

where $\chi$ and $\varphi$ satisfy Equations (5) and (6), and

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{sint}{4}},\beta \left(t\right)=1,\gamma \left(t\right)=t,\delta \left(t\right)=1,\\ \hfill \epsilon \left(t\right)=-2t,\kappa \left(t\right)=-t,\mu \left(t\right)=e^{3-3cos t}.\end{array}$$

In Figure 6, we display the profiles of ${\left|\psi \right|}^2, {\left|\phi \right|}^2$ by using the values $e=-1$, $C=2$, $a_3=-1$, and $b_3=1$.

3.3. Bending Dynamics

In practice, many experiments are carried out in controlled surroundings, hence, it is important to have models that accurately replicate these types of conditions. In this sense, the purpose of this section is to demonstrate how the Riccati approach can be used to control the dynamics of solutions. As an example, we consider the system (50) and (51) again, but now, we change the initial conditions for $\delta \left(t\right)$ and $\epsilon \left(t\right)$, i.e., $\delta \left(0\right)=0.8,$ $\epsilon \left(0\right)=-1$; and $\delta \left(0\right)=1.5$, $\epsilon \left(0\right)=-4.5$. The $\delta \left(t\right)$, $\epsilon \left(t\right)$, and $\kappa \left(t\right)$ functions are now:

$$\begin{array}{c}\hfill \delta \left(t\right)=0.8,\epsilon \left(t\right)=-1-1.6t,\kappa \left(t\right)=-0.64t;\\ \hfill \delta \left(t\right)=1.5,\epsilon \left(t\right)=-4.5-3t,\kappa \left(t\right)=-2.25t.\end{array}$$

Figure 7, shows how these new parameters influence the system’s nonlinear dynamics: The propagation axis of the solutions is bended.

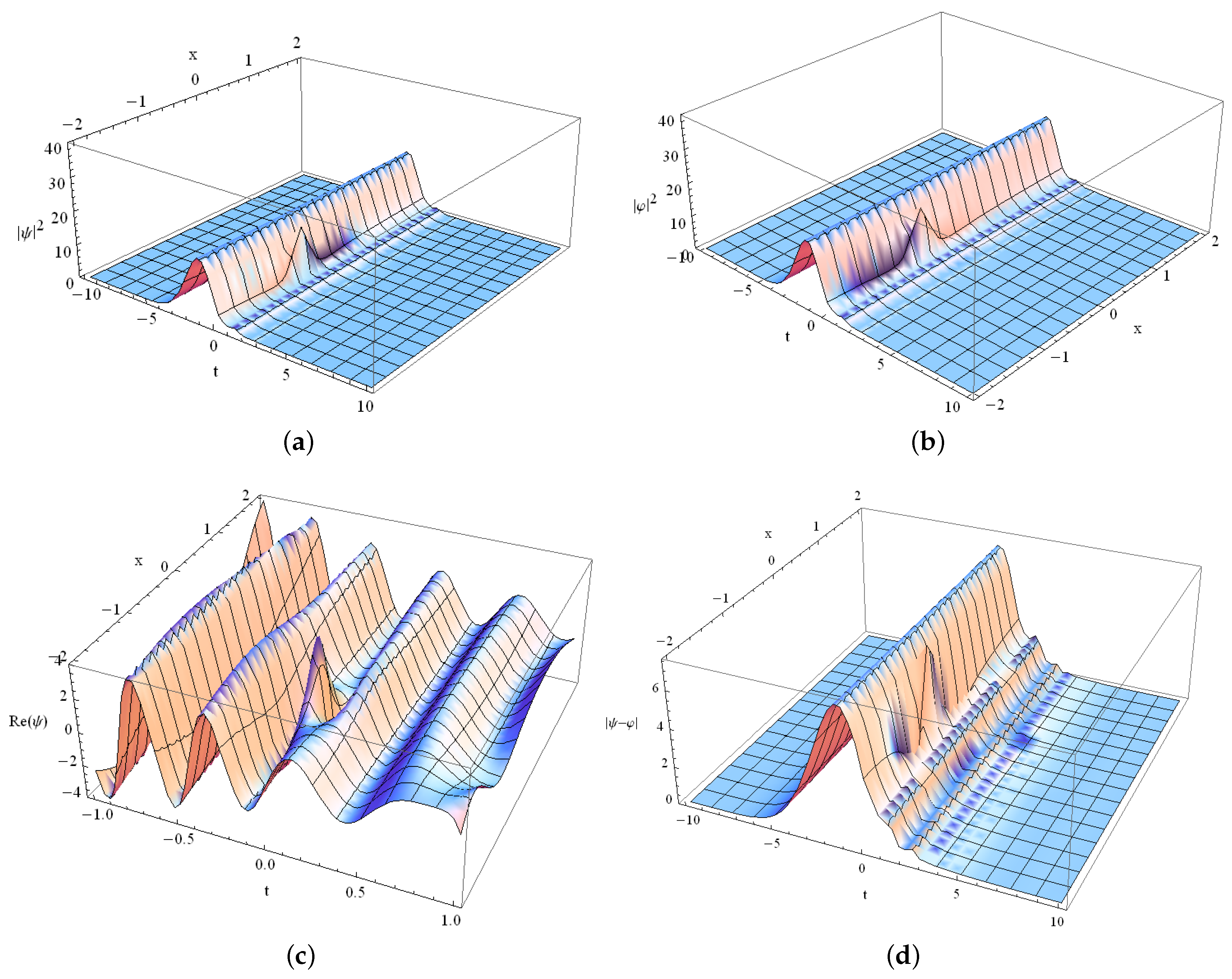
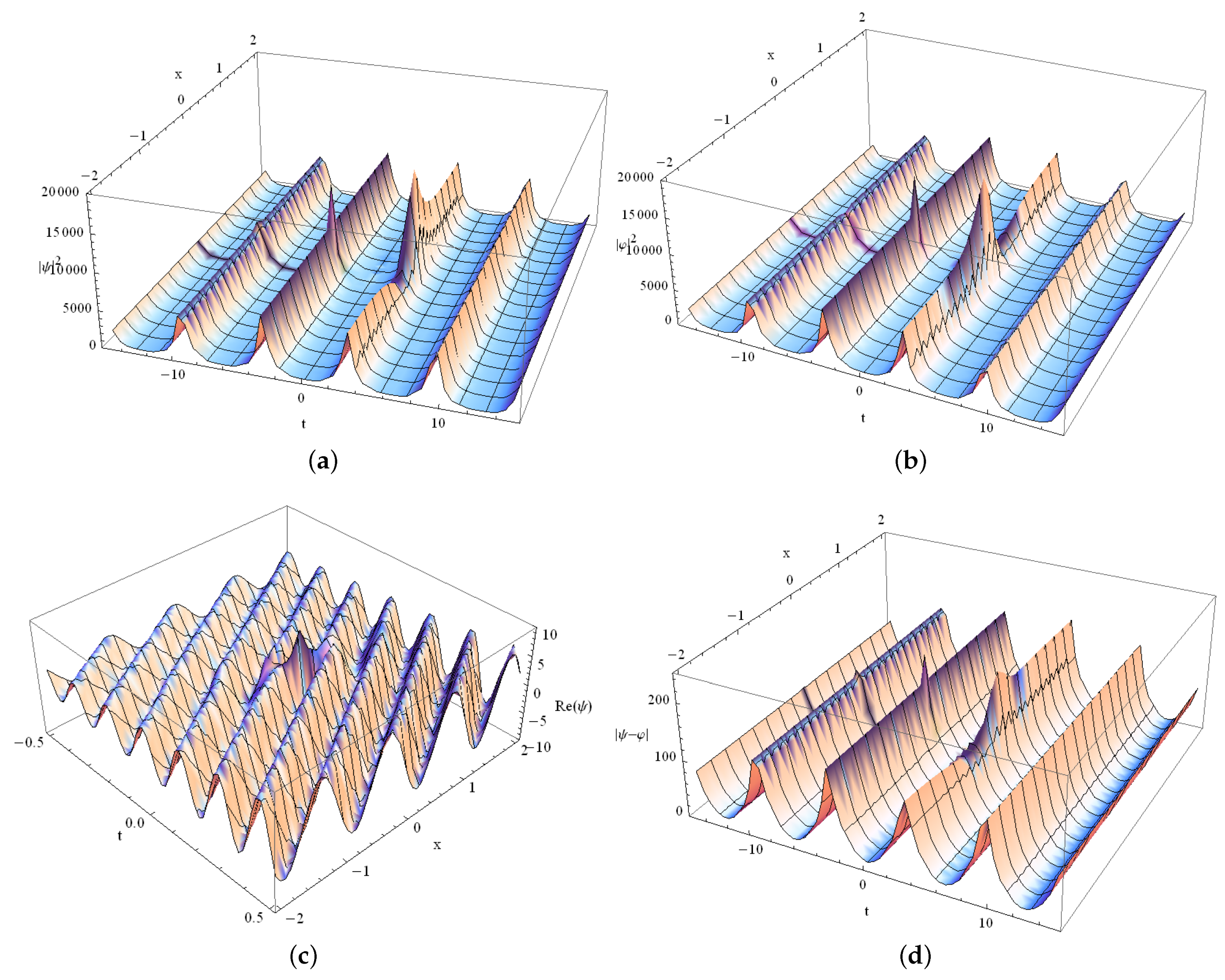
4. Blow-Up Solutions of the Generalized Coupled NLS System

The current section is focused on the study of singular solutions of the coupled VCNLS. More precisely, we demonstrate by explicit construction the existence of finite-time singular solutions in the $L^{\infty }$ norm.

Theorem 2 

(Solutions with singularity in finite time with $L^{\infty }$ norm). Consider the generalized coupled nonlinear Schrödinger system

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -a\left(t\right){\psi }_{xx}+(b\left(t\right)x^2-id\left(t\right)-xf\left(t\right))\psi +i(g\left(t\right)-c\left(t\right)x){\psi }_x+h\left(t\right)({\left|\phi \right|}^{2s}+{\left|\psi \right|}^{2s})\psi ,\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -a\left(t\right){\phi }_{xx}+(b\left(t\right)x^2-id\left(t\right)-xf\left(t\right))\phi +i(g\left(t\right)-c\left(t\right)x){\phi }_x+h\left(t\right)({\left|\phi \right|}^{2s}+{\left|\psi \right|}^{2s})\phi ,\hfill \end{array}$$

(55)

where $a\left(t\right),b\left(t\right),c\left(t\right),d\left(t\right),f\left(t\right),g\left(t\right),h\left(t\right)$ are time-dependent functions and $s>0.$ Then, the system (54) and (55) admits the $L^{\infty }$ singular solutions

$$\psi (x,t)={\displaystyle \frac{1}{\sqrt{\mu \left(t\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\beta \left(t\right)xy+\gamma \left(t\right)y^2+\delta \left(t\right)x+\epsilon \left(t\right)y+\kappa \left(t\right)\right)\right],$$

(56)

$$\phi (x,t)={\displaystyle \frac{1}{\sqrt{\mu \left(t\right)}}}exp\left[i\left(\alpha \left(t\right)x^2+\beta \left(t\right)xz+\gamma \left(t\right)z^2+\delta \left(t\right)x+\epsilon \left(t\right)z+\kappa \left(t\right)\right)\right],$$

(57)

where $y,z$ are real parameters and $\alpha \left(t\right),\beta \left(t\right),\gamma \left(t\right),\delta \left(t\right),\epsilon \left(t\right),\kappa \left(t\right),\mu \left(t\right)$ satisfy the modified Riccati system (58)–(63).

Proof. 

We will proceed as in [33,34]. Substituting (56) and (57) into Equations (54) and (55) we obtain the modified Riccati system:

$${\displaystyle \frac{d\alpha }{dt}}+b\left(t\right)+2c\left(t\right)\alpha +4a\left(t\right){\alpha }^2=0,$$

(58)

$${\displaystyle \frac{d\beta }{dt}}+(c\left(t\right)+4a\left(t\right)\alpha \left(t\right))\beta =0,$$

(59)

$${\displaystyle \frac{d\gamma }{dt}}+a\left(t\right){\beta }^2\left(t\right)=0,$$

(60)

$${\displaystyle \frac{d\delta }{dt}}+(c\left(t\right)+4a\left(t\right)\alpha \left(t\right))\delta =f\left(t\right)+2\alpha \left(t\right)g\left(t\right),$$

(61)

$${\displaystyle \frac{d\epsilon }{dt}}=(g\left(t\right)-2a\left(t\right)\delta \left(t\right))\beta \left(t\right),$$

(62)

$${\displaystyle \frac{d\kappa }{dt}}=g\left(t\right)\delta \left(t\right)-a\left(t\right){\delta }^2\left(t\right)-{\displaystyle \frac{2h\left(t\right)}{{\mu }^s\left(t\right)}}.$$

(63)

Here the previous system (58)–(63) differs from (19)–(24) by the extra term $-2h\left(t\right)/{\mu }^s\left(t\right)$ in Equation (63). Now, considering the substitution

$$\alpha =\left({\displaystyle \frac{1}{4a\left(t\right)}}{\displaystyle \frac{{\mu }^{\prime }\left(t\right)}{\mu \left(t\right)}}-{\displaystyle \frac{d\left(t\right)}{2a\left(t\right)}}\right),$$

(64)

it follows that the Riccati Equation (58) becomes

$${\mu }^{″}-\eta \left(t\right){\mu }^{\prime }+4\sigma \left(t\right)\mu =0,$$

(65)

with

$$\eta \left(t\right)={\displaystyle \frac{a^{\prime }}{a}}-2c+4d,\sigma \left(t\right)=ab-cd+d^2+{\displaystyle \frac{d}{2}}\left({\displaystyle \frac{a^{\prime }}{a}}-{\displaystyle \frac{d^{\prime }}{d}}\right).$$

(66)

Using Equations (A1) and (A12) in the Appendix A with $l_0=1$, (58)–(62) can be solved, but (63) must be solved separately. Let I be an interval such that ${\mu }_0\left(t\right)\ne 0$ for all $t\in I.$ Now, since the functions ${\mu }_0$ and ${\mu }_1$ are linearly independent on an interval $I^{\prime }$, we have

$${\gamma }_0^{\prime }\left(t\right)={\displaystyle \frac{W\left[{\mu }_0\left(t\right),{\mu }_1\left(t\right)\right]}{2{\mu }_0^2\left(t\right)}}\ne 0,t\in I\cap I^{\prime },$$

(67)

and by $\mu \left(t\right)$ given by (A1) (see [40]), functions (56) and (57) will have a finite time blow-up in the $L^{\infty }$ norm at $T_b={\gamma }_0^{\prime }(-\alpha \left(0\right))\in I\cap I^{\prime }$, i.e.,

$$\left|\psi (x,t)\right|,\left|\phi (x,t)\right|\to \infty \mathrm{as}t\to T_b.$$

(68)

□

Remark 2. 

The above theorem shows the possibility of obtaining singular solutions in $L^{\infty }$ for certain choices of the coefficients. In particular, the collapse time of the solutions corresponds to the instant $T_b$ where the function $\mu \left(t\right)$ vanishes (if such time exists).

4.1. Case $a=1/2,b=c=d=f=g=0,$ and Arbitrary h

Consider the coupled VCNLS system

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -{\displaystyle \frac{1}{2}}{\psi }_{xx}+h\left(t\right)({\left|\phi \right|}^{2s}+{\left|\psi \right|}^{2s})\psi ,\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -{\displaystyle \frac{1}{2}}{\phi }_{xx}+h\left(t\right)({\left|\phi \right|}^{2s}+{\left|\psi \right|}^{2s})\phi .\hfill \end{array}$$

(70)

Then, according to Theorem 2, the system admits the explicit solutions given by Equations (56) and (57) with the functions

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{\alpha \left(0\right)}{1+2\alpha \left(0\right)t}},\beta \left(t\right)={\displaystyle \frac{\beta \left(0\right)}{1+2\alpha \left(0\right)t}},\gamma \left(t\right)=\gamma \left(0\right)-{\displaystyle \frac{{\beta }^2\left(0\right)t}{2+4\alpha \left(0\right)t}},\\ \hfill \delta \left(t\right)={\displaystyle \frac{\delta \left(0\right)}{1+2\alpha \left(0\right)t}},\kappa \left(t\right)=\kappa \left(0\right)+{\displaystyle \frac{{\delta }^2\left(0\right)t}{4\alpha \left(0\right)(1+2\alpha (0\left)t\right)}}-{\displaystyle \frac{2}{{\mu }^s\left(0\right)}}{\int }_0^t{\displaystyle \frac{h\left(t^{\prime }\right)}{{(1+2\alpha \left(0\right)t^{\prime })}^s}}d{t}^{\prime },\\ \hfill \epsilon \left(t\right)=\epsilon \left(0\right)-{\displaystyle \frac{\beta \left(0\right)\delta \left(0\right)t}{1+2\alpha \left(0\right)t}},\mu \left(t\right)=\mu \left(0\right)(1+2\alpha \left(0\right)t).\end{array}$$

Therefore,

$${\left|\psi (x,t)\right|}^2={\left|\phi (x,t)\right|}^2={\displaystyle \frac{1}{\mu \left(0\right)(1+2\alpha (0\left)t\right)}},$$

(71)

and these solutions blow up in the $L^{\infty }$ norm at the instant $T_b=-{\displaystyle \frac{1}{2\alpha \left(0\right)}}$, provided $\alpha \left(0\right)<0.$

The next example shows how a different coefficient selection alters the properties of these solutions (no blow-up). The function $\mu \left(t\right)$ does not vanish at any point in time.

4.2. Case $a=1,b={\displaystyle \frac{{sin}^{2}t-cost}{4}},c=-d=-sint,f=g=0,h=-3e^{3-3cos t}$

Consider the coupled VCNLS system

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -{\psi }_{xx}+{\displaystyle \frac{x^2}{4}}\left({sin}^{2}t-cost\right)\psi -isint\psi +ixsint{\psi }_x-3e^{3-3cos t}({\left|\phi \right|}^2+{\left|\psi \right|}^2)\psi ,\hfill \end{array}$$

(72)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -{\phi }_{xx}+{\displaystyle \frac{x^2}{4}}\left({sin}^{2}t-cost\right)\phi -isint\phi +ixsint{\phi }_x-3e^{3-3cos t}({\left|\phi \right|}^2+{\left|\psi \right|}^2)\phi ,\hfill \end{array}$$

(73)

The system admits the explicit solutions given by the Equations (56) and (57) with the functions

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{sint}{4}},\beta \left(t\right)=\beta \left(0\right),\gamma \left(t\right)=\gamma \left(0\right)-{\beta }^2\left(0\right)t,\\ \hfill \delta \left(t\right)=\delta \left(0\right),\kappa \left(t\right)=\kappa \left(0\right)+\left(6-{\delta }^2\left(0\right)\right)t,\\ \hfill \epsilon \left(t\right)=\epsilon \left(0\right)-\beta \left(0\right)\delta \left(0\right)t,\mu \left(t\right)=e^{3-3cos t}.\end{array}$$

In this case, we have

$${\left|\psi (x,t)\right|}^2={\left|\phi (x,t)\right|}^2=e^{-3+3cos t}.$$

(74)

In this context, Theorem 2 allows us to extend the singular solutions established in Theorem 1 in [34] (see also Example 1 in the same reference).

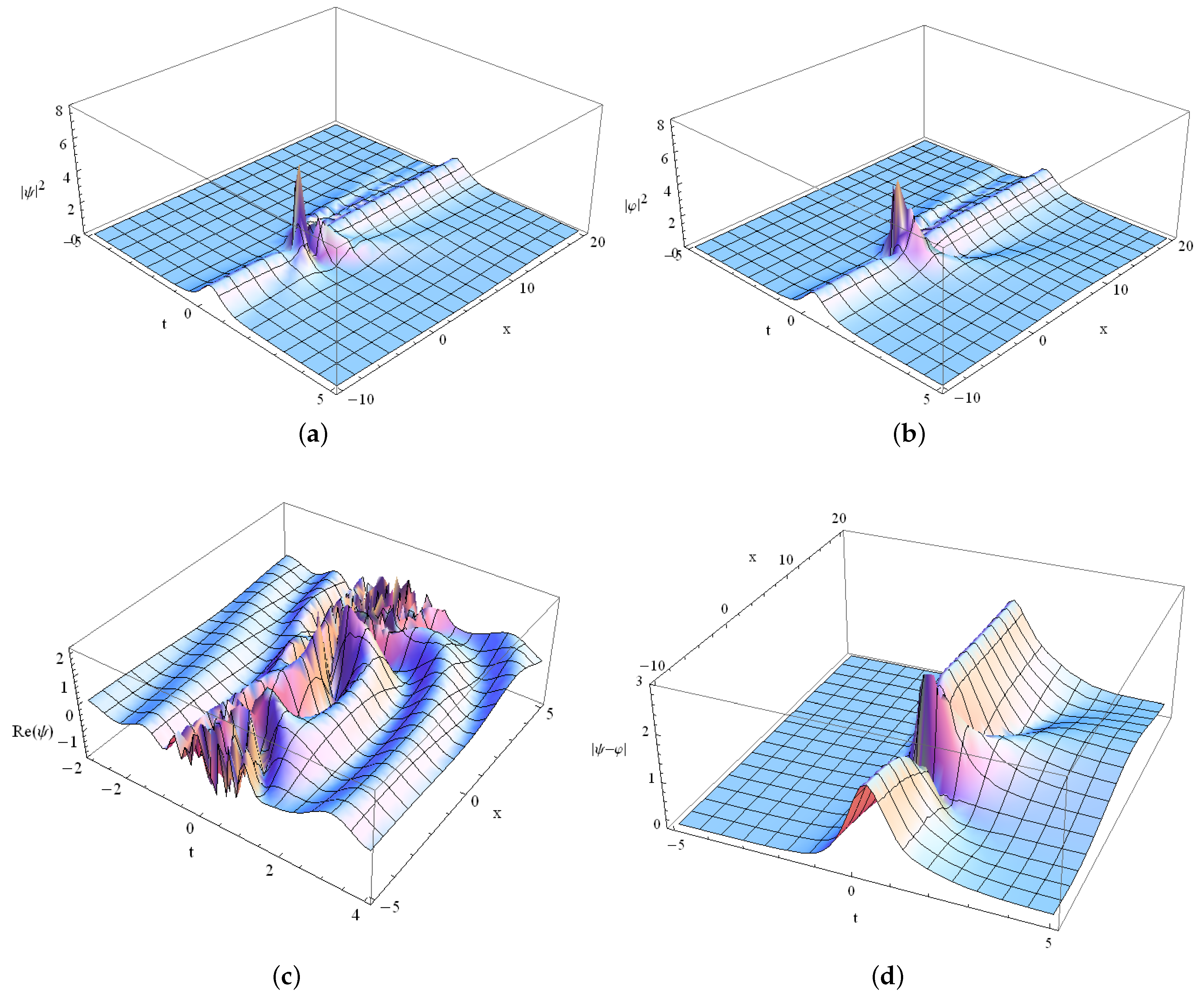
5. An n-Dimensional Generalized Coupled NLS System

In Section 3, we established a relationship between the one-dimensional coupled VCNLS (11) and (12) and the well-known Manakov Equations (3) and (4), provided the coefficients satisfy the Riccati system (19)–(24). In the subsequent Section 4 and by “exploiting” the potential of the Riccati system, the construction of explicit singular solutions for (11) and (12) was shown. In this section, we reveal that a similar Riccati system (see Equations (81)–(86)) allows us to link an n-dimensional coupled NLS system with a generalized Manakov system. It will be useful in constructing soliton solutions for the high-dimensional system.

Theorem 3. 

The nonautonomous coupled NLS n-dimensional

$$i{\psi }_t=-a\left(t\right)\Delta \psi +{b\left(t\right)\left|\mathit{x}\right|}^2\psi +\lambda a\left(t\right){\beta }^2\left(t\right){\mu }^s{\left(t\right)\left(\right|\phi |}^{2s}+{\left|\psi \right|}^{2s})\psi ,$$

(75)

$$i{\phi }_t=-a\left(t\right)\Delta \phi +{b\left(t\right)\left|\mathit{x}\right|}^2\phi +\lambda a\left(t\right){\beta }^2\left(t\right){\mu }^s{\left(t\right)\left(\right|\phi |}^{2s}+{\left|\psi \right|}^{2s})\phi ,$$

(76)

with $t\in \mathbb{R}$ and $\mathit{x}\in {\mathbb{R}}^n$ can be transformed into the standard coupled NLS

$$i{u}_{\tau }={\Delta }_{\xi }u-{\lambda \left(\right|v|}^{2s}+{\left|u\right|}^{2s})u,$$

(77)

$$i{v}_{\tau }={\Delta }_{\xi }v-\lambda ({\left|v\right|}^{2s}+{\left|u\right|}^{2s})v,$$

(78)

by the transformations

$$\psi (\mathit{x},t)={\displaystyle \frac{1}{\sqrt{\mu \left(t\right)}}}{e}^{i({\sum }_{i=1}^n\alpha \left(t\right)x_i^2+{\delta }_i\left(t\right)x_i+{\kappa }_i\left(t\right))}u(\xi ,\tau ),$$

(79)

$$\phi (\mathit{x},t)={\displaystyle \frac{1}{\sqrt{\mu \left(t\right)}}}{e}^{i({\sum }_{i=1}^n\alpha \left(t\right)x_i^2+{\delta }_i\left(t\right)x_i+{\kappa }_i\left(t\right))}v(\xi ,\tau ),$$

(80)

with ${\xi }_i=\beta \left(t\right)x_i+{\epsilon }_i\left(t\right)$ for $i=1,2,\dots ,n$ and $\tau =\gamma \left(t\right).$ Additionally, the following Riccati system is satisfied

$${\displaystyle \frac{d\alpha }{dt}}+b\left(t\right)+4a\left(t\right){\alpha }^2=0,$$

(81)

$${\displaystyle \frac{d\beta }{dt}}+4a\left(t\right)\alpha \left(t\right)\beta =0,$$

(82)

$${\displaystyle \frac{d\gamma }{dt}}+a\left(t\right){\beta }^2\left(t\right)=0,$$

(83)

$${\displaystyle \frac{d{\delta }_i}{dt}}+4a\left(t\right)\alpha \left(t\right){\delta }_i=0,$$

(84)

$${\displaystyle \frac{d{\epsilon }_i}{dt}}+2a\left(t\right)\beta \left(t\right){\delta }_i\left(t\right)=0,$$

(85)

$${\displaystyle \frac{d{\kappa }_i}{dt}}+a\left(t\right){\delta }_i^2\left(t\right)=0,$$

(86)

$i=1,\dots ,n.$ Considering the substitution

$$\alpha ={\displaystyle \frac{{\mu }^{\prime }\left(t\right)}{4na\left(t\right)\mu \left(t\right)}},$$

(87)

it follows that the Riccati Equation (81) becomes

$${\mu }^{″}-{\displaystyle \frac{a^{\prime }}{a}}{\mu }^{\prime }+4nab\mu +\left({\displaystyle \frac{1-n}{n}}\right){\displaystyle \frac{{\left({\mu }^{\prime }\right)}^2}{\mu }}=0.$$

(88)

In general, the study of n-dimensional coupled NLS systems is carried out by degenerating them into the one-dimensional coupled NLS ()see for example [41,42] for the two-dimensional case), or directly dealing with the high-dimensional system, as can be seen in [43] for $n=3$. In contrast, our transformation does not reduce the spatial dimension of the system, and then, to find soliton solutions for (75) and (76) in terms of Theorem 3, we used the ideas given in the works [41,42,43].

5.1. Case $a=2,b=-2,h=-8$

The two-dimensional coupled NLS system

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -2({\psi }_{xx}+{\psi }_{yy})-2(x^2+y^2)\psi -8({\left|\phi \right|}^2+{\left|\psi \right|}^2)\psi ,\hfill \end{array}$$

(89)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -2({\phi }_{xx}+{\phi }_{yy})-2(x^2+y^2)\phi -8({\left|\phi \right|}^2+{\left|\psi \right|}^2)\phi \hfill \end{array}$$

(90)

admits the DB soliton solution given by Equations (79) and (80) with

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{1}{2}}tanh\left(4t\right),\beta \left(t\right)=sech\left(4t\right),\gamma \left(t\right)=-{\displaystyle \frac{1}{2}}tanh\left(4t\right),\\ \hfill {\delta }_i\left(t\right)=sech\left(4t\right),{\kappa }_i\left(t\right)=-{\displaystyle \frac{1}{2}}tanh\left(4t\right),{\epsilon }_i\left(t\right)=-tanh\left(4t\right),\mu \left(t\right)={cosh}^2\left(4t\right),\end{array}$$

and the functions [41,42]:

$$\begin{array}{c}\hfill u({\xi }_1,{\xi }_2,\tau )=\chi ({\xi }_1+{\xi }_2,-2\tau ),\end{array}$$

(91)

$$\begin{array}{c}\hfill v({\xi }_1,{\xi }_2,\tau )=\varphi ({\xi }_1+{\xi }_2,-2\tau ),\end{array}$$

(92)

with $\chi$ and $\varphi$ given by the Equations (5) and (6).

5.2. Case $a=2,b=-{\displaystyle \frac{1+2t^2}{4}},h=-12e^{t^2}$

Consider the three-dimensional coupled NLS system

$$\begin{array}{ccc}\hfill i{\psi }_t& =& -2({\psi }_{xx}+{\psi }_{yy}+{\psi }_{zz})-{\displaystyle \frac{1+2t^2}{4}}(x^2+y^2+z^2)\psi -12e^{t^2}({\left|\phi \right|}^2+{\left|\psi \right|}^2)\psi ,\hfill \end{array}$$

(93)

$$\begin{array}{ccc}\hfill i{\phi }_t& =& -2({\phi }_{xx}+{\phi }_{yy}+{\phi }_{zz})-{\displaystyle \frac{1+2t^2}{4}}(x^2+y^2+z^2)\phi -12e^{t^2}({\left|\phi \right|}^2+{\left|\psi \right|}^2)\phi .\hfill \end{array}$$

(94)

Then, such a system admits the type I rogue wave solution given by Equations (79) and (80) with

$$\begin{array}{c}\hfill \alpha \left(t\right)={\displaystyle \frac{t}{4}},\beta \left(t\right)=e^{-t^2},\gamma \left(t\right)=-\sqrt{{\displaystyle \frac{\pi }{2}}}\mathrm{Erf}\left(\sqrt{2}t\right),\\ \hfill {\delta }_i\left(t\right)=e^{-t^2},{\kappa }_i\left(t\right)=-\sqrt{{\displaystyle \frac{\pi }{2}}}\mathrm{Erf}\left(\sqrt{2}t\right),{\epsilon }_i\left(t\right)=-\sqrt{2\pi }\mathrm{Erf}\left(\sqrt{2}t\right),\mu \left(t\right)=e^{3t^2},\end{array}$$

where $\mathrm{Erf}\left(t\right)={\displaystyle \frac{2}{\sqrt{\pi }}}{\int }_0^t{e}^{-x}dx$ is the Error function and

$$\begin{array}{c}\hfill u({\xi }_1,{\xi }_2,{\xi }_3,\tau )=\chi ({\xi }_1+{\xi }_2+{\xi }_3,-3\tau ),v({\xi }_1,{\xi }_2,{\xi }_3,\tau )=\varphi ({\xi }_1+{\xi }_2+{\xi }_3,-3\tau ),\end{array}$$

(95)

with $\chi$ and $\varphi$ given by Equations (7) and (8).

6. Conclusions and Final Remarks

Through this current work, we proposed and showed the integrability of a generalized coupled VCNLS (containing a dispersion coefficient, potential, damping, and nonlinear coefficient) using the similarity transformation established in Theorems 1 and 3. Here, the Riccati system played a crucial role in the explicit construction of soliton-type solutions, rogue waves, and singular solutions for these kinds of equations. The explicit construction of soliton and rogue wave-type solutions for an n-dimensional coupled NLS system was shown as well. We show solutions with striking characteristics (with the possibility of applications) and the ability to control their propagation dynamics.

On the other hand, even if the solutions reported in this work lacked physical application, they are an important input for the study of the precision and stability of the numerical methods applied to these models. Whatever the case, this work should motivate further analytical and numerical studies looking to clarify the connections between the dynamics of variable-coefficient NLS and the dynamics of Riccati systems. Finally, we hope that this fresh approach to dealing with VCNLS systems will provide new insights into the physics of such models and aid in comprehending real-world applications.