On Polar Jacobi Polynomials

Abstract

In the present work, we investigate certain algebraic and differential properties of the orthogonal polynomials with respect to a discrete–continuous Sobolev-type inner product defined in terms of the Jacobi measure.

1. Introduction

Let us consider a measure $\mu$ supported on the subset of the complex plane $\gamma$.

In the vector space of polynomials with complex coefficients $\mathbb{P}$, let us introduce the following inner product:

$${\langle f,g\rangle }_{\xi }:=Mf\left(\xi \right)g\left(\xi \right)+{\int }_{\gamma }{f}^{\prime }\left(z\right)g^{\prime }\left(z\right)d\mu \left(z\right),M,\xi \in \mathbb{C},$$

(1)

assuming that the integral exists. The inner product Equation (1) is called discrete–continuous Sobolev-type, which is a particular case of the Sobolev-type inner products. Algebraic and analytical properties and the limiting behavior of the families of orthogonal polynomials with respect to Sobolev-type inner products have been thoroughly used for the last 25 years. For an overview of this subject, see  [1], or the introduction of [2] as well as [3].

Discrete–continuous Sobolev inner products were introduced in [4] to study the behavior of the optimal polynomial approximation of absolutely continuous functions in the norm generated by a Sobolev inner product as Equation (1). Later, in [5], R. Koekoek considered the Laguerre case with $d\mu =x^{\alpha }{e}^{-x}dx$, $\alpha >-1$, $\gamma =[0,+\infty )$ and $\xi =0$. The Gegenbauer case was studied by Bavinck and Meijer in [6,7], with $d\mu ={(1-x^2)}^{\lambda -1/2}dx$, $\lambda >-1/2$, $\gamma =[-1,1]$ and ${\xi }_1=-1$ and ${\xi }_2=1$.

The families of orthogonal polynomials with respect to Equation (1) have been studied as an extension of the Bochner–Krall theory (i.e., polynomial sequences which are simultaneously eigenfunctions of a differential operator and orthogonal with respect to an inner product), see for the discrete–continuous case [8,9,10].

The starting point of our work is the orthogonality with respect to the Jacobi case. Let $\left(Q_n\right)$ be the monic orthogonal polynomial sequence with respect to the Sobolev inner product

$$\langle f,g\rangle :=f\left(\xi \right)g\left(\xi \right)+{\int }_{\gamma }{f}^{\prime }\left(z\right)g^{\prime }\left(z\right){(1-z)}^{\alpha }{(1+z)}^{\beta }dz,$$

(2)

where $\alpha ,\beta \in \mathbb{C}$, $\gamma$ is a path encircling the points $+1$ and $-1$ first in a positive sense and then in a negative sense, as shown in Figure 2.1 in [11], $M=1$ and $\xi \in \mathbb{C}$.

Let us consider $\left(P_n^{(\alpha ,\beta )}\left(z\right)\right)$ as the monic Jacobi polynomials, i.e., the monic orthogonal polynomial sequence with respect to the measure $d\mu \left(z\right)={(1-z)}^{\alpha }{(1+z)}^{\beta }dz$. Therefore, for each n$\in \mathbb{N}$, $P_n^{(\alpha ,\beta )}\left(z\right)$ satisfies

$${\int }_{\gamma }{P}_n^{(\alpha ,\beta )}\left(z\right)z^k{(1-z)}^{\alpha }{(1+z)}^{\beta }dz=0,k=0,1,\dots ,n-1,$$

(3)

and let ${\Pi }_{n+1,\xi }$ be the polynomial primitive of $(n+1)P_n^{(\alpha ,\beta )}$ that has a zero at $\xi$, i.e., for all $n\ge 1$, we have

$${\Pi }_{n+1,\xi }\left(\xi \right)=0,{\displaystyle \frac{d}{dz}}{\Pi }_{n+1,\xi }\left(z\right)=(n+1)P_n^{(\alpha ,\beta )}\left(z\right).$$

(4)

Then, by definition of $Q_n$, it is clear that ${\Pi }_{n+1,\xi }\left(z\right)=Q_{n+1}\left(z\right)$ for all $n=0,1,2,\dots$. It is straightforward to prove that the polynomial of degree n which is orthogonal with respect to Equation (2) can be written as follows (one must consider $Q_0\left(z\right)=1$):

$$Q_n\left(z\right)=(z-\xi )P_{n-1}\left(z\right),$$

where $P_n$ is called the polar polynomial associated with $\mu$ (see [12]) and $\xi$ from now on will be called the pole. Let us define the differential operator $L_{\xi }:{\mathcal{H}}^1\left(\gamma \right)\to L^2\left(\gamma \right)$ as

$$L_{\xi }\left[f\left(z\right)\right]=f\left(z\right)+(z-\xi ){\displaystyle \frac{d}{dz}}f\left(z\right),$$

(5)

where ${\mathcal{H}}^1\left(\gamma \right):=\{f\in L^2\left(\gamma \right):f^{\prime }\left(z\right)\in L^2\left(\gamma \right)\}$ is the Sobolev space of index 1. Taking into account that $Q_n$ is orthogonal with respect to the inner product Equation (2), we have

$${\int }_{\gamma }{L}_{\xi }\left[P_n\left(z\right)\right]z^k{(1-z)}^{\alpha }{(1+z)}^{\beta }dz={\int }_{\gamma }\left(P_n\left(z\right)+(z-\xi )P_n^{\prime }\left(z\right)\right)z^k{(1-z)}^{\alpha }{(1+z)}^{\beta }dz=0,$$

for $k=0,1,\dots ,n-1$. Therefore, $P_n$ is the monic orthogonal polynomial of degree n with respect to the differential operator $L_{\xi }$, and the measure $d\mu$ (see [12,13,14,15,16,17]). In such a case, for $n\in {\mathbb{N}}_0$, we have

$$P_n\left(z\right)+(z-\xi )P_n^{\prime }\left(z\right)=(n+1)P_n^{(\alpha ,\beta )}\left(z\right).$$

(6)

The main aim of this work is to study algebraic (zero localization) and differential properties of the polynomial sequences that are orthogonal with respect to the inner product Equation (2) for the Jacobi weight case, which is a natural extension of the Legendre case [12].

In Section 2, we obtain several algebraic relations between the polar Jacobi polynomials and the Jacobi polynomials and some differential and different identities related to the polar Jacobi polynomials. Finally, in Section 3 we study the location of the zeros for the polynomials $P_n$.

2. Algebraic Properties of the Polar Jacobi Polynomials

Let us start by summarizing some basic properties of the Jacobi orthogonal polynomials to be used in the sequel to Chapter 18 in [18]

Proposition 1. 

Let $\left(P_n^{(\alpha ,\beta )}\left(z\right)\right)$ be the classical monic Jacobi orthogonal polynomial sequence. The following statements hold:

1. 

Three-term recurrence relation.

$$P_{n+1}^{(\alpha ,\beta )}\left(z\right)=(z-{\beta }_n)P_n^{(\alpha ,\beta )}\left(z\right)-{\gamma }_n{P}_{n-1}^{(\alpha ,\beta )}\left(z\right),n=0,1,\dots ,$$

(7)

with initial condition $P_0^{(\alpha ,\beta )}\left(z\right)=1$, and recurrence coefficients

$${\beta }_n={\displaystyle \frac{{\beta }^2-{\alpha }^2}{(\alpha +\beta +2n)(\alpha +\beta +2n+2)}},{\gamma }_n={\displaystyle \frac{4n(\alpha +n)(\beta +n)(\alpha +\beta +n)}{(\alpha +\beta +2n-1){(\alpha +\beta +2n)}^2(\alpha +\beta +2n+1)}}.$$

2. 

First structure relation.

$$(1-z^2){\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(z\right)=-n{P}_{n+1}^{(\alpha ,\beta )}\left(z\right)+{\widehat{\beta }}_n{P}_n^{(\alpha ,\beta )}\left(z\right)+{\widehat{\gamma }}_n{P}_{n-1}^{(\alpha ,\beta )}\left(z\right),n=0,1,\dots ,$$

(8)

with coefficients

$${\widehat{\beta }}_n={\displaystyle \frac{2n(\alpha -\beta )(\alpha +\beta +n+1)}{(\alpha +\beta +2n)(\alpha +\beta +2n+2)}},{\widehat{\gamma }}_n={\displaystyle \frac{4n(\alpha +n)(\beta +n)(\alpha +\beta +n)(\alpha +\beta +n+1)}{(\alpha +\beta +2n-1){(\alpha +\beta +2n)}^2(\alpha +\beta +2n+1)}}.$$

3. 

Second structure relation.

$$P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)=P_{n+1}^{(\alpha ,\beta )}\left(z\right)+{\tilde{\beta }}_n{P}_n^{(\alpha ,\beta )}\left(z\right)+{\tilde{\gamma }}_n{P}_{n-1}^{(\alpha ,\beta )}\left(z\right),n=0,1,\dots ,$$

(9)

$${\tilde{\beta }}_n={\displaystyle \frac{(2n+2)(\alpha -\beta )}{(\alpha +\beta +2n)(\alpha +\beta +2n+2)}},{\tilde{\gamma }}_n=-{\displaystyle \frac{4n(n+1)(\alpha +n)(\beta +n)}{(\alpha +\beta +2n-1){(\alpha +\beta +2n)}^2(\alpha +\beta +2n+1)}}.$$

4. 

Squared Norm. For every $n\ge 0$,

$${∥P_n^{(\alpha ,\beta )}\left(z\right)∥}^2={\int }_{\gamma }{\left(P_n^{(\alpha ,\beta )}\left(z\right)\right)}^2\omega (z;\alpha ,\beta )dz={\displaystyle \frac{2^{2n+\alpha +\beta +1}n!\Gamma (\alpha +n+1)\Gamma (\beta +n+1)\Gamma (\alpha +\beta +n+1)}{\Gamma (\alpha +\beta +2n+1)\Gamma (\alpha +\beta +2n+2)}}.$$

(10)

5. 

Second-order difference equation. For every $n\ge 0$,

$$(1-z^2){\displaystyle \frac{d^2}{d{z}^2}}{P}_n^{(\alpha ,\beta )}\left(z\right)+\left(\beta -\alpha -z\left(\alpha +\beta +2\right)\right){\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(z\right)=-n(\alpha +\beta +n+1)P_n^{(\alpha ,\beta )}\left(z\right).$$

(11)

6. 

Forward shift operator.

$${\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(z\right)=n{P}_{n-1}^{(\alpha +1,\beta +1)}\left(z\right),n=0,1,\dots ,$$

(12)

7. 

Asymptotic formula. Let $z\in \mathbb{C}\setminus [-1,1]$. Put $\phi \left(z\right)=z+\sqrt{z^2-1}$ where the branch of the square root is chosen so that $|z+\sqrt{z^2-1}|>1$ for $z\in \mathbb{C}\setminus [-1,1]$. Then,

$$P_n^{(\alpha ,\beta )}\left(z\right)={\displaystyle \frac{{\phi }^n\left(z\right)}{\sqrt{n}}}\left(c(\alpha ,\beta ,z)+\mathcal{O}\left(n^{-1}\right)\right),$$

(13)

where $c(\alpha ,\beta ,z)$ is a function of α and β and x independent of n. The relation holds uniformly on compact sets of $\mathbb{C}\setminus [-1,1]$.

Let us obtain the algebraic relations between the Jacobi polynomials and the polar Jacobi polynomials.

Lemma 1. 

For any $\alpha ,\beta ,\xi \in \mathbb{C}$. The polar Jacobi polynomials can be written in terms of the Jacobi polynomials as follows:

$$\begin{array}{ccc}\hfill P_n\left(z\right)& =& {\displaystyle \frac{P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)-P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right)}{z-\xi }}\hfill \\ \hfill & =& {\displaystyle \frac{1}{\alpha +\beta +n}}\left[(z+\xi ){\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(z\right)+{\displaystyle \frac{{\xi }^2-1}{z-\xi }}\left({\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(z\right)-{\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(\xi \right)\right)\right.\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill & & \left.+(\alpha +\beta )P_n^{(\alpha ,\beta )}\left(z\right)+{\displaystyle \frac{\alpha -\beta +\xi (\alpha +\beta )}{z-\xi }}\left(P_n^{(\alpha ,\beta )}\left(z\right)-P_n^{(\alpha ,\beta )}\left(\xi \right)\right)\right].\hfill \end{array}$$

(15)

Therefore,

$$(z-\xi )P_n\left(z\right)=P_{n+1}^{(\alpha ,\beta )}\left(z\right)+{\tilde{\beta }}_n{P}_n^{(\alpha ,\beta )}\left(z\right)+{\tilde{\gamma }}_n{P}_{n-1}^{(\alpha ,\beta )}\left(z\right)-P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right).$$

(16)

Proof. 

From Equation (6), we have

$$(n+1)P_n^{(\alpha ,\beta )}\left(z\right)={\displaystyle \frac{d}{dz}}\left((z-\xi )P_n\left(z\right)\right).$$

Therefore, by using the forward shift operator Equation (12), we have

$$(z-\xi )P_n\left(z\right)=(n+1){\int }_{\xi }^z{P}_n^{(\alpha ,\beta )}\left(z\right)dz={\int }_{\xi }^z{\displaystyle \frac{d}{dz}}\left(P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)\right)dz.$$

(17)

From Equation (17), the identity (14) follows. Using Equation (14) and the second structure relation (9) the expression (16) follows.

Let us now to prove Equation (15): by using the second-order differential Equation (11) with $n,\alpha ,\beta$ being shifted to $n+1,\alpha -1,\beta -1$, respectively, and the forward shift operator of the Jacobi polynomials, we obtain

$$(1-z^2){\displaystyle \frac{d}{dz}}{P}_n^{(\alpha ,\beta )}\left(z\right)+\left(\beta -\alpha -z(\alpha +\beta )\right)P_n^{(\alpha ,\beta )}\left(z\right)=-(\alpha +\beta +n)P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right).$$

(18)

By using the differential Equation (18) and the identity

$${\displaystyle \frac{f\left(z\right)g\left(z\right)-f\left(\xi \right)g\left(\xi \right)}{z-\xi }}={\displaystyle \frac{f\left(z\right)-f\left(\xi \right)}{z-\xi }}g\left(z\right)+f\left(\xi \right){\displaystyle \frac{g\left(z\right)-g\left(\xi \right)}{z-\xi }},$$

then Equation (15) follows and hence the result holds. □

The following additional property of orthogonality holds.

Theorem 1. 

The polar Jacobi polynomial $P_n$ with pole $\xi \in \mathbb{C}$ fulfills the following property of orthogonality:

$${\int }_{\gamma }\left(P_n\left(z\right)+(z-\xi ){\displaystyle \frac{d}{dz}}{P}_n\left(z\right)\right)P_m^{(\alpha ,\beta )}\left(z\right)\omega (z;\alpha ,\beta )dz=\left\{\begin{array}{cc}0,\hfill & m\ne n,\hfill \\ (n+1){∥P_n^{(\alpha ,\beta )}\left(z\right)∥}^2,\hfill & m=n.\hfill \end{array}\right.$$

(19)

Furthermore, if $n>1$, then

$${\int }_{\gamma }(z-\xi )P_n\left(z\right)P_m^{(\alpha ,\beta )}\left(z\right)\omega (z;\alpha ,\beta )dz=\left\{\begin{array}{cc}-{\displaystyle \frac{2^{\alpha +\beta +1}\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\alpha +\beta +2)}}{P}_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right),\hfill & m=0,\hfill \\ 0,\hfill & 0<m<n-1,\hfill \\ {\tilde{\gamma }}_n{∥P_{n-1}^{(\alpha ,\beta )}\left(z\right)∥}^2,\hfill & n-1=m,\hfill \\ {\tilde{\beta }}_n{∥P_n^{(\alpha ,\beta )}\left(z\right)∥}^2,\hfill & n=m,\hfill \\ {∥P_{n+1}^{(\alpha ,\beta )}\left(z\right)∥}^2,\hfill & n+1=m,\hfill \\ 0,\hfill & n+1<m.\hfill \end{array}\right.$$

(20)

Proof. 

Taking into account Equation (6), we have

$${\int }_{\gamma }\left(P_n\left(z\right)+(z-\xi ){\displaystyle \frac{d}{dz}}{P}_n\left(z\right)\right)P_m^{(\alpha ,\beta )}\left(z\right)\omega (z;\alpha ,\beta )dz=(n+1){\int }_{\gamma }{P}_n^{(\alpha ,\beta )}\left(z\right)P_m^{(\alpha ,\beta )}\left(z\right)\omega (z;\alpha ,\beta )dz.$$

So, the first property of orthogonality follows. By using the relation (16) and considering the property of orthogonality of the Jacobi polynomials, the second property of orthogonality follows. Hence, the result holds. □

Theorem 2. 

The sequence of polar Jacobi polynomials $\left(P_n\right)$ with pole $\xi \in \mathbb{C}$ satisfies the following recurrence relation:

$$P_{n+1}\left(z\right)=z{P}_n\left(z\right)+a_n{P}_n\left(z\right)+b_n{P}_{n-1}\left(z\right)+P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right),n=0,1,\dots ,$$

(21)

with initial conditions $P_{-1}\left(z\right)=0$ and $P_0\left(z\right)=1$, and coefficients

$$a_n={\displaystyle \frac{(\alpha +\beta -2)(\alpha -\beta )}{(\alpha +\beta +2n)(\alpha +\beta +2n+2)}},b_n=-{\displaystyle \frac{4(n+1)(\alpha +n)(\beta +n)(\alpha +\beta +n-1)}{(\alpha +\beta +2n-1){(\alpha +\beta +2n)}^2(\alpha +\beta +2n+1)}}.$$

Proof. 

Let the sequence $\left({\nu }_{n,k}\right)$ be such that

$$(z-\xi )P_n\left(z\right)=\sum _{k=0}^{n+1}{\nu }_{n,k}{P}_k\left(z\right),$$

where ${\nu }_{n,n+1}=1$.

Then, by using Equation (6), we obtain

$$\begin{array}{ccc}\hfill (z-\xi )\left(P_n\left(z\right)+(n+1)P_n^{(\alpha ,\beta )}\left(z\right)\right)& =& (z-\xi )\left(P_n\left(z\right)+{\left((z-\xi )P_n\left(z\right)\right)}^{\prime }\right)\hfill \\ & =& \sum _{k=0}^{n+1}{\nu }_{n,k}\left(P_k\left(z\right)+(z-\xi ){\displaystyle \frac{d}{dz}}{P}_k\left(z\right)\right).\hfill \end{array}$$

(22)

By the property of orthogonality Equation (19), we have

$$\sum _{k=0}^{n+1}{\nu }_{n,k}{\int }_{\gamma }\left(P_k\left(z\right)+(z-\xi ){\displaystyle \frac{d}{dz}}{P}_k\left(z\right)\right)P_m^{(\alpha ,\beta )}\left(z\right)\omega (z;\alpha ,\beta )dz={\nu }_{n,k}(m+1){∥P_m^{(\alpha ,\beta )}\left(z\right)∥}^2,$$

(23)

for $m=0,1,\dots ,n$.

On the other hand, let us denote

$$I_{n,m}={\int }_{\gamma }(z-\xi )P_m^{(\alpha ,\beta )}\left(z\right)\left(P_n\left(z\right)+(n+1)P_n^{(\alpha ,\beta )}\left(z\right)\right)\omega (z;\alpha ,\beta )dz.$$

From the orthogonality of the Jacobi polynomials and the property of orthogonality (20), we obtain

$$I_{n,m}=\left\{\begin{array}{cc}-2^{\alpha +\beta +1}{P}_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right){\displaystyle \frac{\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\alpha +\beta +2)}},\hfill & m=0,\hfill \\ 0,\hfill & 0<m<n-1,\hfill \\ -{\tilde{\gamma }}_n(\alpha +\beta +n-1){∥P_{n-1}^{(\alpha ,\beta )}\left(z\right)∥}^2,\hfill & n-1=m\hfill \\ \left({\displaystyle \frac{2-\alpha -\beta }{2}}{\tilde{\beta }}_n-\xi (n+1)\right){∥P_n^{(\alpha ,\beta )}\left(z\right)∥}^2,\hfill & n=m.\hfill \end{array}\right.$$

(24)

Thus, multiplying Equation (22) by $P_m^{(\alpha ,\beta )}\left(z\right)$, integrating over $\gamma$, and using Equations (23) and (24), we obtain

$${\nu }_{n,m}={\displaystyle \frac{I_{n,m}}{(m+1){∥P_m^{(\alpha ,\beta )}\left(z\right)∥}^2}}=\left\{\begin{array}{cc}-P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right),\hfill & m=0,\hfill \\ 0,\hfill & 0<m<n-1,\hfill \\ -b_n,\hfill & m=n-1,\hfill \\ {\displaystyle \frac{2-\alpha -\beta }{2(n+1)}}{\tilde{\beta }}_n-\xi ,\hfill & m=n.\hfill \end{array}\right.$$

The expression (21) is obtained after a straightforward calculation. □

A direct consequence of this result is the following.

Corollary 1 

(The polar ultraspherical case). The sequence of symmetric polar Jacobi polynomials with pole $\xi \in \mathbb{C}$, i.e., the sequence of polar ultraspherical polynomial with pole $\xi \in \mathbb{C}$, satisfies, namely ${\mathsf{P}}_n$, the following recurrence relation:

$${\mathsf{P}}_{n+1}\left(z\right)=z{\mathsf{P}}_n\left(z\right)-{\displaystyle \frac{(n+1)(2\alpha +n-1)}{(2\alpha +2n-1)(2\alpha +2n+1)}}{\mathsf{P}}_{n-1}\left(z\right)+{\mathsf{P}}_{n+1}^{(\alpha -1,\alpha -1)}\left(\xi \right),n=0,1,\dots ,$$

(25)

with initial conditions ${\mathsf{P}}_{-1}\left(z\right)=0$ and ${\mathsf{P}}_0\left(z\right)=1$.

Another direct consequence is the fact that when one, or both, of the parameters is a negative integer, we can factorize the Jacobi polynomial. In fact (see (1.2) in [11]),

$$\begin{array}{cc}\hfill P_n^{(-k,\beta )}\left(z\right)=& {(z-1)}^k{P}_{n-k}^{(k,\beta )},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill P_n^{(\alpha ,-k)}\left(z\right)=& {(z+1)}^k{P}_{n-k}^{(\alpha ,k)}.\hfill \end{array}$$

(27)

Remark 1. 

Since in some results we will consider the polar Jacobi polynomials with different parameters and poles, to avoid such possible confusion, we will denote by $P_n(z;\alpha ,\beta ;\xi )$ the polar Jacobi polynomial of degree n with parameters α and β, and pole at ξ.

Corollary 2 

(The factorization). For any positive integer k, the following identities hold:

$$\begin{array}{cc}\hfill P_{n+k}(z;-k,\beta ;1)=& {(z-1)}^k{P}_n^{k+1,\beta -1}\left(z\right)\hfill \end{array}$$

(28)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} ={(z-1)}^k\left((z-1)P_{n-1}(z;k+2,\beta ;1)+P_n^{k+1,\beta -1}\left(1\right)\right),$$

(29)

$$\begin{array}{cc}\hfill P_{n+k}(z;\alpha ,-k;-1)=& {(z+1)}^k{P}_n^{\alpha -1,k+1}\left(z\right)\hfill \end{array}$$

(30)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={(z+1)}^k\left((z+1)P_{n-1}(z;\alpha ,k+2;-1)+P_n^{\alpha -1,k+1}(-1)\right).$$

(31)

Moreover, the recurrence coefficients satisfy the following relations:

$$a_{n+k}(-k,\beta ;1)=a_{n-1}(k+2,\beta ;1),b_{n+k}(-k,\beta ;1)=b_{n-1}(k+2,\beta ;1),$$

and

$$a_{n+k}(\alpha ,-k;-1)=a_{n-1}(\alpha ,k+2;-1),b_{n+k}(\alpha ,-k;-1)=b_{n-1}(\alpha ,k+2;-1).$$

Proof. 

The identities (28)–(31) follow by using the factorization of the Jacobi polynomials Equations (26) and (27). In order to obtain the relation between the recurrence coefficients defined in Theorem 2, we must use the former factorization(s), and after a straightforward calculation the identities follow. □

The last result of this section is due the parity relation of the Jacobi polynomials, i.e.,

$$P_n^{(\alpha ,\beta )}\left(z\right)={(-1)}^n{P}_n^{(\beta ,\alpha )}(-z).$$

(32)

Lemma 2. 

For any $\xi \in \mathbb{C}$, the following identity holds:

$$P_n(z;\alpha ,\beta ;\xi )={(-1)}^n{P}_n(-z;\beta ,\alpha ;-\xi ).$$

(33)

Proof. 

Starting from Equation (14) and using Equation (32), we have

$$\begin{array}{cc}\hfill P_n(z;\alpha ,\beta ;\xi )=& {\displaystyle \frac{P_{n+1}^{\alpha -1,\beta -1}\left(z\right)-P_{n+1}^{\alpha -1,\beta -1}\left(\xi \right)}{z-\xi }}={(-1)}^{n+1}{\displaystyle \frac{P_{n+1}^{\beta -1,\alpha -1}(-z)-P_{n+1}^{\beta -1,\alpha -1}(-\xi )}{z-\xi }}\hfill \\ \hfill =& {(-1)}^n{\displaystyle \frac{P_{n+1}^{\beta -1,\alpha -1}(-z)-P_{n+1}^{\beta -1,\alpha -1}(-\xi )}{-z-(-\xi )}}={(-1)}^n{P}_n(-z;\beta ,\alpha ;-\xi ).\hfill \end{array}$$

□

3. Zero Location

Finding the roots of polynomials is a problem of interest in both mathematics and in areas of application such as physical systems, which can be reduced to solving certain equations. There are very interesting geometric relationships between the roots of a polynomial $f_n\left(z\right)$ and those of $f_n^{\prime }\left(z\right)$. The most important result is the following.

Theorem 3 

(The Gauß–Lucas theorem [19]). Let $f_n\left(z\right)\in \mathbb{C}\left[z\right]$ be a polynomial of degree of at least one. All zeros of $f_n^{\prime }\left(z\right)$ lie in the convex hull of the zeros of the zeros of $f_n\left(z\right)$.

In this section, we are going to study the zero distribution for the polar Jacobi polynomials. The next result, which was obtained by G. Szegő, is useful to estimate where such zeros are located.

Theorem 4 

(Szegő’s theorem [20,21]). Let $a\left(z\right)$ and $b\left(z\right)$ be polynomials of the form

$$a\left(z\right)=\sum _{\ell =0}^n{a}_{\ell }\left({\displaystyle \genfrac{}{}{0pt}{}{n}{\ell }}\right)z^{\ell },b\left(z\right)=\sum _{\ell =0}^n{b}_{\ell }\left({\displaystyle \genfrac{}{}{0pt}{}{n}{\ell }}\right)z^{\ell }.$$

If the zeros of $a\left(z\right)$ lie in a closed disk $\overline{D}$ and ${\lambda }_1$, …, ${\lambda }_n$ are the zeros of $b\left(z\right)$, then the zeros of the “composition” of the two

$$c\left(z\right)=\sum _{\ell =0}^n{a}_{\ell }{b}_{\ell }\left({\displaystyle \genfrac{}{}{0pt}{}{n}{\ell }}\right)z^{\ell },$$

have the form ${\lambda }_{\ell }{\gamma }_{\ell }$, where ${\gamma }_{\ell }\in \overline{D}$.

By using this result, we are going to locate the disk within which all the zeros of the polar Jacobi are located.

Theorem 5. 

For any $\Re \alpha ,\Re \beta >-1$ and $\xi \in \mathbb{C}$, the zeros of $P_n(z;\alpha ,\beta ;\xi )$ lie inside the closed disk $\overline{D}(0,2+|\xi \left|\right)$.

Proof. 

Starting from Equation (6) and assuming that

$$a\left(z\right)=P_n^{(\alpha ,\beta )}\left(w\right)=\sum _{k=0}^n{\mu }_k{w}^k,c\left(z\right)=P_n(z;\alpha ,\beta ;w)=\sum _{k=0}^n{\eta }_k{w}^k,$$

where $w:=z-\xi$, then ${\eta }_k=(n+1)/(k+1){\mu }_k$. In order to apply Szegő’s theorem, we consider

$$b\left(z\right)=\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n}{k}}\right){\displaystyle \frac{n+1}{k+1}}{w}^k=\sum _{k=0}^n\left({\displaystyle \genfrac{}{}{0pt}{}{n+1}{k+1}}\right)w^k={\displaystyle \frac{{(w+1)}^{n+1}-1}{w}}.$$

If $b\left(w_1\right)=0$, then $|w_1+1|=1$, so $|z_1|\le 2+|\xi |$. Moreover, if $a\left(z_2\right)=0$, i.e., $z_2$ is a zero of $a\left(z\right)$, then $|z_2|\le 1$. Therefore, combining these inequalities and applying Szegő’s theorem one obtains that if $c\left(z_3\right)=0$, i.e., $z_3$ is a zero of $c\left(z\right)$, then $|z_3|\le 2+|\xi |$ and hence the result follows. □

In Figure 1, we illustrate on the one hand how accurate Theorem 5 is, and on the other hand, we show the behavior of the zeros of the same polar Jacobi polynomial when the pole travels along a specific circle (observe $I=\sqrt{-1}$).

In Figure 2, we illustrate an example of Jacobi polar polynomials where the parameters $\Re \alpha \le -1$ or $\Re \beta \le -1$; therefore, the zeros of the Jacobi polynomial can move away from the interval $[-1,1]$ in a somewhat uncontrolled way. Therefore, Theorem 5 cannot be applied in such a case. However, observe that in the considered example $-2<\Re (\alpha +\beta )=-1.95<-1$.

The next theorem gives the location of the zeros of the polar Jacobi polynomial of degree n and its multiplicity, or equivalently the location of source points and their corresponding strength.

Theorem 6. 

For any $\Re \alpha ,\Re \beta >-1$ and $\xi \in \mathbb{C}$. The following statements hold:

1. 

If $\zeta \in {\mathbb{C}}^{*}$ is a zero of $P_n(z;\alpha ,\beta ;\xi )$, then $z=-\zeta$ is a zero of $P_n(z;\beta ,\alpha ;-\xi )$.

2. 

If $\zeta \in {\mathbb{C}}^{*}$ is a zero of $P_n^{(\alpha ,\beta )}\left(z\right)$, then ζ is a zero of $P_n\left(z\right)$.

3. 

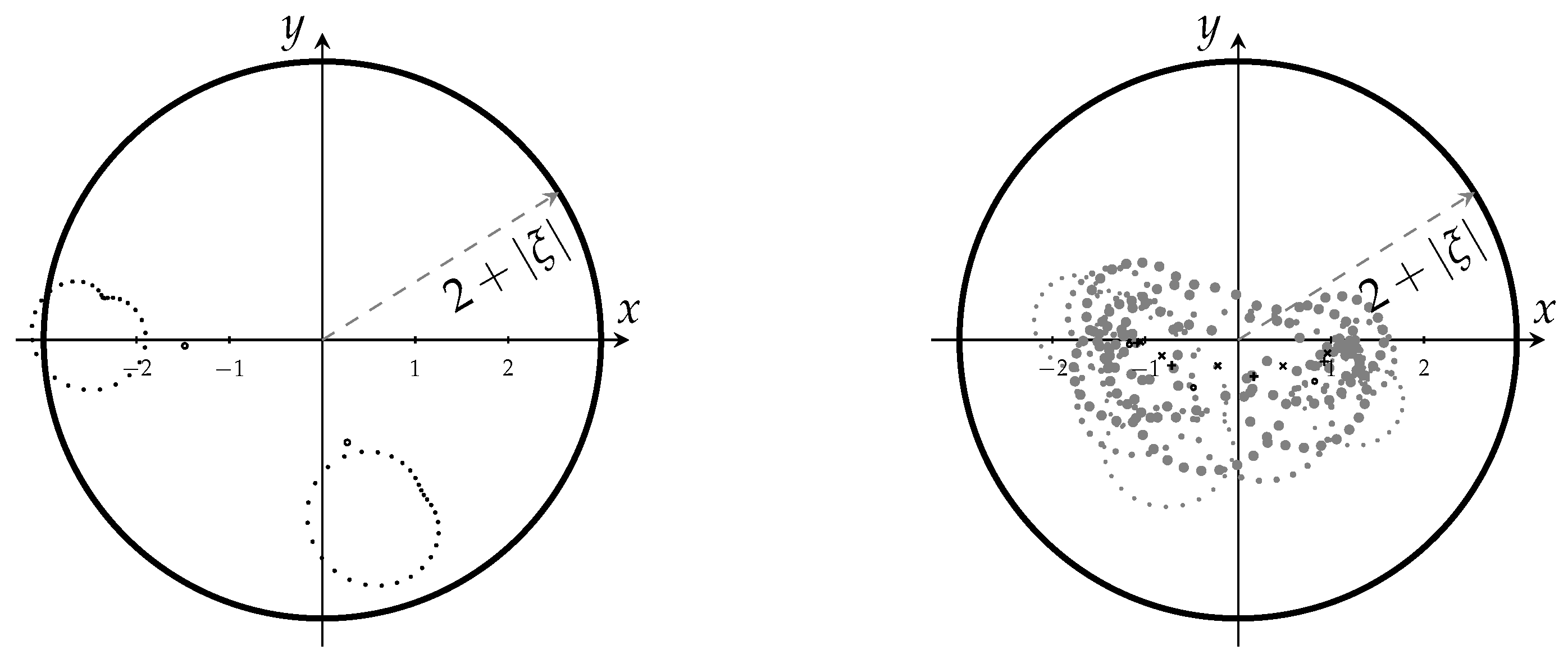
The zeros of $P_n\left(z\right)$ have multiplicity of at most 2 and their multiple zeros are located on $[-1,1]$.

4. 

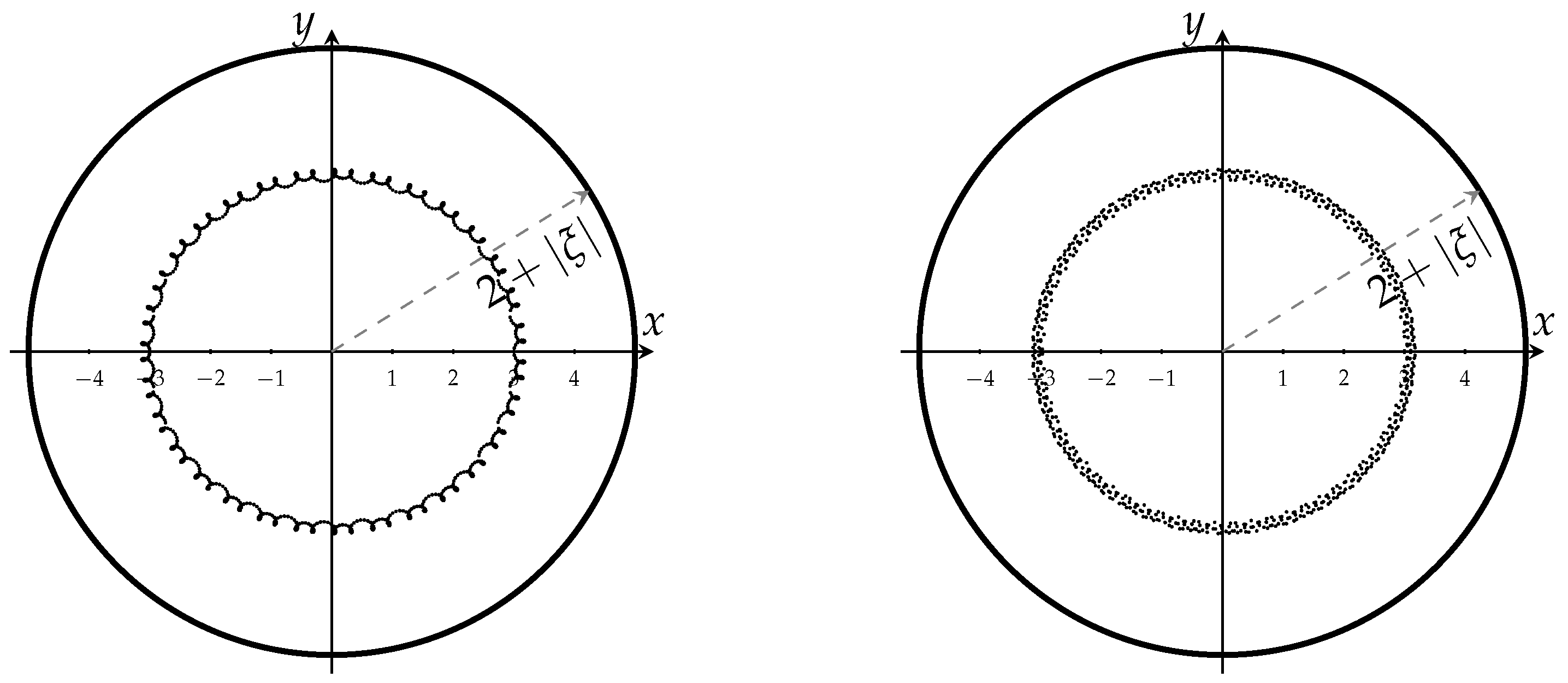
All the zeros of $P_n\left(z\right)$ are located on the curve

$${\mathcal{Z}}_n\left(\xi \right)=\left\{z\in \mathbb{C}:P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)=P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right)\right\}\setminus \left\{\xi \right\}.$$

(34)

Proof. 

The first statement holds true due to Equation (34), the second statement holds true due to Equation (6), and the fourth statement holds true due to Equation (14).

Suppose that $\omega$ is a zero $P_n$ of multiplicity greater than two; then, by (6), $\omega$ is a zero of $P_n^{(\alpha ,\beta )}$ and also a zero of ${\left(P_n^{(\alpha ,\beta )}\right)}^{\prime }$. Thus, $\omega$ is a zero of multiplicity 2 of $P_n^{(\alpha ,\beta )}$. This is a contradiction since the zeros of the Jacobi polynomials are all simple. Therefore, statement 3 holds true. □

Remark 2. 

• Observe that the zeros of $P_n$ do not have to be simple. Let ${\xi }_{+}=(1+2\sqrt{6})/5$ or ${\xi }_{-}=(1-2\sqrt{6})/5$; then, the polar polynomial of degree two $P_2(z;0,1,{\xi }_{+})={\left(z-{\displaystyle \frac{1-\sqrt{6}}{5}}\right)}^2$, or $P_2(z;0,1,{\xi }_{-})={\left(z-{\displaystyle \frac{1+\sqrt{6}}{5}}\right)}^2$.
• When the parameters are not standard, i.e., $\Re \alpha <-1$ or $\Re \beta <-1$ then, by Corollary 2, statement 3 of Theorem 6 is no longer true. For example, if $\alpha =-4$, $\beta =1>0$, and $n=5$, then $P_5(z;-4,1,1)={(z-1)}^4(z-5/7)$.

We can establish the following result concerning the boundedness of the zeros of the polar polynomials.

Lemma 3. 

Given $\xi \in \mathbb{C}$, let us define the two numbers ${\Delta }_{\xi }:=sup\left\{\right|\xi -z|:z\in [-1,1]\}$ and ${\delta }_{\xi }:=inf\left\{\right|\xi -z|:z\in [-1,1]\}$. Then, the following can be stated:

1. 

All zeros of the polar Jacobi polynomials with pole ξ are contained in $\left|z\right|\le {\Delta }_{\xi }+1$.

2. 

If ${\delta }_{\xi }>1$, the zeros of the polar Jacobi polynomials with pole ξ are simple and contained in the exterior of the ellipse $|z+1|+|z-1|=2\alpha$, where $1<\alpha <{\delta }_{\xi }$.

Proof. 

By Equation (14), the zeros of $P_n\left(z\right)$ are located in ${\mathcal{Z}}_n\left(\xi \right)$. Since $\left|P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right)\right|<{\Delta }_{\xi }^{n+1}$, they are contained in the interior of the set $\left|P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)\right|={\Delta }_{\xi }^{n+1}$. It is known that the zeros of $P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)$, namely $x_{n+1,k}$, satisfy $|x_{n+1,k}|\le 1$. Therefore, for any $t\in \mathbb{C}$, such that $\left|t\right|>1+{\Delta }_{\xi }$, we have

$$\left|P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)\right|=\prod _{k=0}^n|z-x_{n+1,k}|\ge \prod _{k=0}^n\left|\right|z|-|x_{n+1,k}\left|\right|>{\Delta }_{\xi }^{n+1}.$$

Hence, the first statement holds.

Concerning the second statement, let z be such that $|z+1|+|z-1|=2\alpha$. From the well-known arithmetic–geometric mean inequality, we have

$$\left|P_{n+1}^{(\alpha -1,\beta -1)}\left(z\right)\right|\le {\left({\displaystyle \frac{1}{n+1}}\sum _{k=0}^n|z-x_{n+1,k}|\right)}^{n+1}<{\alpha }^{n+1}.$$

If $\omega$ is a zero of $P_n$, we obtain, in view of Equation (34),

$$\left|P_{n+1}^{(\alpha -1,\beta -1)}\left(\omega \right)\right|=\left|P_{n+1}^{(\alpha -1,\beta -1)}\left(\xi \right)\right|=\prod _{k=0}^n|\xi -x_{n+1,k}|>{\delta }_{\xi }^{n+1}>{\alpha }^{n+1}.$$

Therefore, the result holds. □

The last result is about the asymptotic behavior of the zeros of the polar Jacobi polynomials.

Theorem 7 

(Theorem 22 in [16]). The accumulation points of zeros of $\left(P_n\right)$ are located on the set $\mathcal{Z}\left(\xi \right)\cup [-1,1]$, where $\mathcal{Z}\left(\xi \right)$ is the ellipse

$$\mathcal{Z}\left(\xi \right)=\{z\in \mathbb{C}:z=cosh(log\left|\phi \left(\xi \right)\right|+i\theta ),0\le \theta <2\pi \}=\left\{z\in \mathbb{C}:\left|z+\sqrt{z^2-1}\right|=\left|\phi \left(\xi \right)\right|\right\},$$

where $\phi \left(z\right)=z+\sqrt{z^2-1}$.