The Discovery of Truncated M-Fractional Exact Solitons and a Qualitative Analysis of the Generalized Bretherton Model
Abstract
:1. Introduction
Truncated M-Fractional Derivative (TMFD)
2. Model Presentation and Its Mathematical Treatment
3. Explanation and Application of the EShGEE Method
3.1. Description
- Stage 1:
- Stage 2:
- Stage 3:
- Stage 4:
3.2. Application to the EShGEE Scheme
- Set 1:
- Set 2:
- Set 3:
- Set 4:
- Set 5:
- Set 6:
4. Explanation of the Modified -Expansion Scheme
- Step 1:
- Step 2:
- Case 1: If , then
- Case 2: If , then
- Case 3: If and , thenHere, and are constants.
- Step 3:
- Step 4:
Application
- Set 1:
- Set 2:
- Set 3:
- Set 4:
- Set 5:
- Set 6:
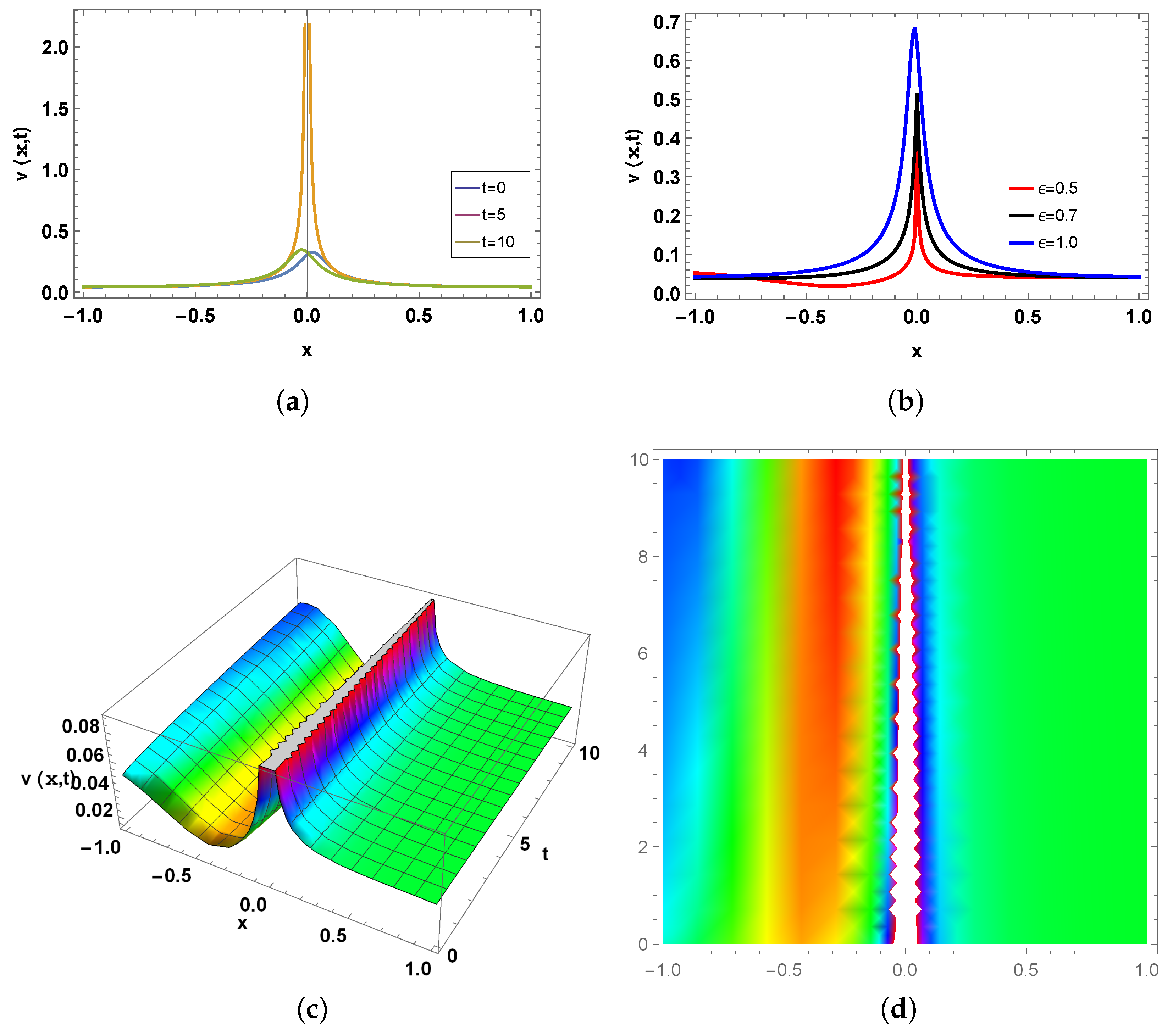
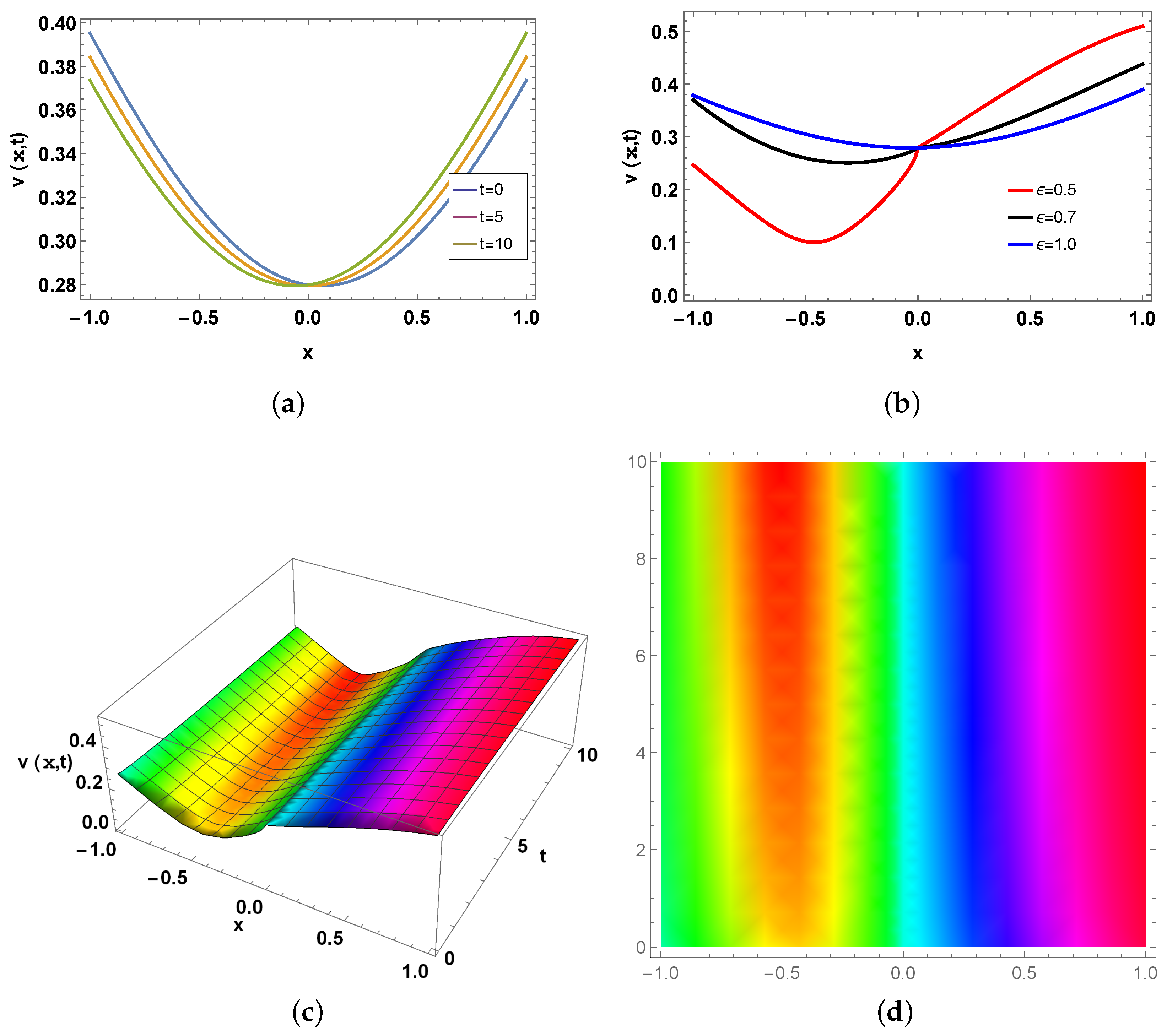
5. Graphical Explanation
6. Physical Interpretation
7. Stability Analysis
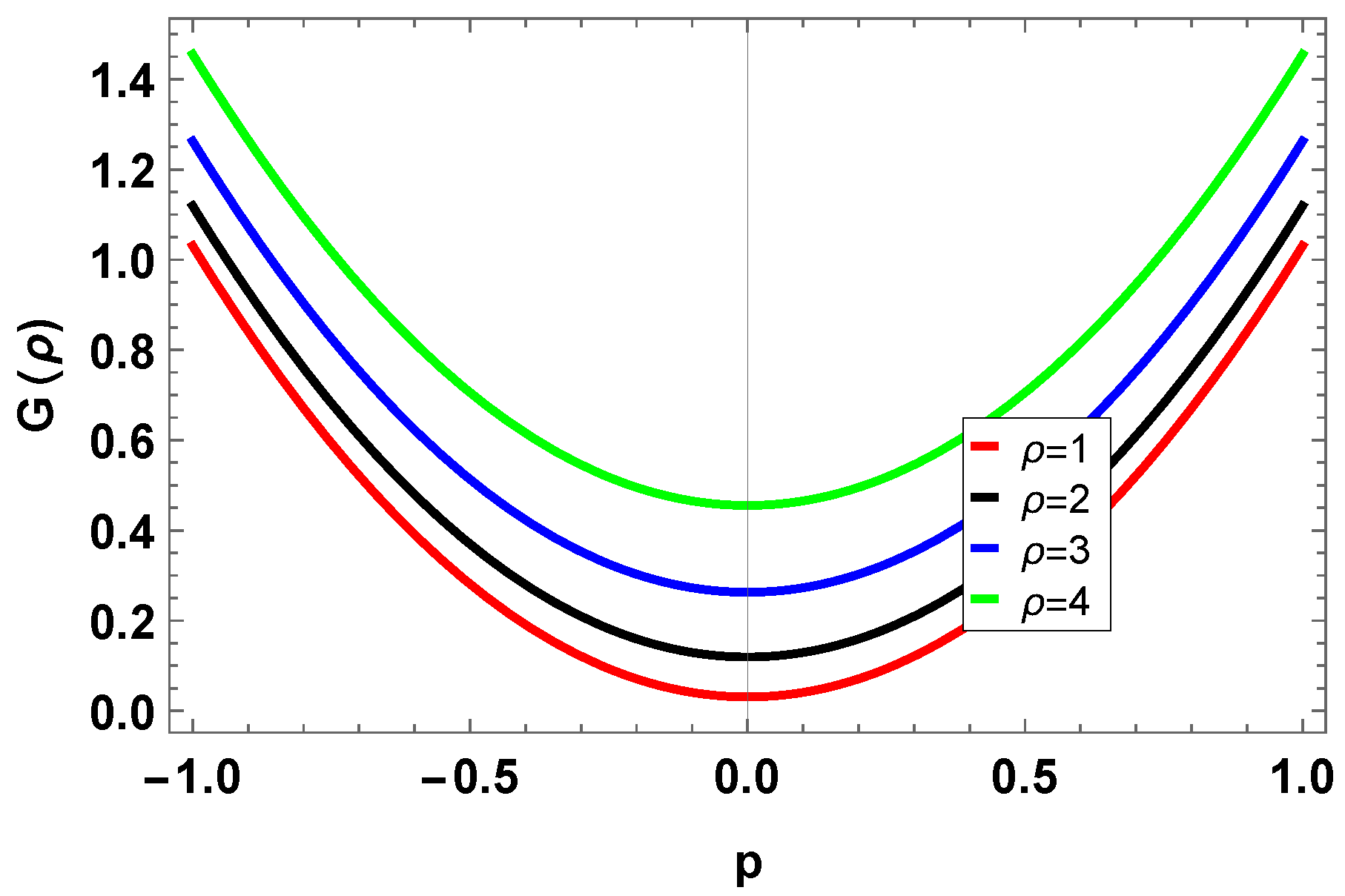
8. Modulation Instability (MI)
9. Results and Discussion
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ripan, R.; Ali, A.M.; Seadawy, A.R.; Baleanu, D. Search for adequate closed form wave solutions to space—Time fractional nonlinear equations. Partial. Differ. Equ. Appl. Math. 2021, 3, 100025. [Google Scholar]
- Bilal, M.; Ren, J. Dynamics of exact solitary wave solutions to the conformable time-space fractional model with reliable analytical approaches. Opt. Quantum Electron. 2022, 54, 40. [Google Scholar] [CrossRef]
- Behera, S.; Mohanty, S.; Virdi, J.P.S. Analytical solutions and mathematical simulation of traveling wave solutions to fractional order nonlinear equations. Partial. Differ. Equ. Appl. Math. 2023, 8, 100535. [Google Scholar] [CrossRef]
- Alsharidi, A.K.; Bekir, A. Discovery of new exact wave solutions to the M-fractional complex three coupled Maccari’s system by Sardar sub-equation scheme. Symmetry 2023, 15, 1567. [Google Scholar] [CrossRef]
- Razzaq, W.; Zafar, A.; Raheel, M. Searching the new exact wave solutions to the beta-fractional Paraxial nonlinear Schrödinger model via three different approaches. Int. J. Mod. Phys. B 2024, 38, 2450132. [Google Scholar] [CrossRef]
- Alijani, Z.; Shiri, B.; Perfilieva, I.; Baleanu, D. Numerical solution of a new mathematical model for intravenous drug administration. Evol. Intell. 2024, 17, 559–575. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Zafar, A.; Raheel, M.; Zaagan, A.A.; Zahran, E.H.M.; Cevikel, A.; Bekir, A. New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques. Opt. Quantum Electron. 2024, 56, 737. [Google Scholar] [CrossRef]
- Batiha, I.M.; Njadat, S.A.; Batyha, R.M.; Zraiqat, A.; Dababneh, A.; Momani, S. Design Fractional-order PID Controllers for Single-Joint Robot Arm Model. Int. J. Adv. Soft Comput. Its Appl. 2022, 14, 96–114. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Alrashedi, Y. Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation. Fractal Fract. 2024, 8, 467. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Manafian, J.; Alharthi, M.; Alrashedi, Y. Stability Analysis, Modulation Instability, and Beta-Time Fractional Exact Soliton Solutions to the Van der Waals Equation. Mathematics 2024, 12, 2257. [Google Scholar] [CrossRef]
- Zafar, A.; Bekir, A.; Raheel, M.; Razzaq, W. Optical soliton solutions to Biswas–Arshed model with truncated M-fractional derivative. Optik 2020, 222, 165355. [Google Scholar] [CrossRef]
- Bezgabadi, A.S.; Bolorizadeh, M.A. Analytic combined bright-dark, bright and dark solitons solutions of generalized nonlinear Schrödinger equation using extended sinh-Gordon equation expansion method. Results Phys. 2021, 30, 104852. [Google Scholar] [CrossRef]
- Kumar, D.; Joardar, A.K.; Hoque, A.; Paul, G.C. Investigation of dynamics of nematicons in liquid crystals by extended sinh-Gordon equation expansion method. Opt. Quantum Electron. 2019, 51, 212. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J. Analytical treatment in optical metamaterials with anti-cubic law of nonlinearity by improved exp (-Ω (η))-expansion method and extended sinh-Gordon equation expansion method. Rev. Mex. Física 2019, 65, 658–677. [Google Scholar] [CrossRef]
- Batool, F.; Rezazadeh, H.; Ali, Z.; Demirbilek, U. Exploring soliton solutions of stochastic Phi-4 equation through extended Sinh-Gordon expansion method. Opt. Quantum Electron. 2024, 56, 785. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Sulaiman, T.A.; Bulut, H. On the new wave behavior to the Klein–Gordon–Zakharov equations in plasma physics. Indian J. Phys. 2019, 93, 393–399. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Opt. Quantum Electron. 2018, 50, 138. [Google Scholar] [CrossRef]
- Razzaq, W.; Alsharidi, A.K.; Zafar, A.; Alomair, M.A. Optical solitons to the beta-fractional density dependent diffusion-reaction model via three different techniques. Int. J. Mod. Phys. B 2023, 37, 2350268. [Google Scholar] [CrossRef]
- Ali, N.H.; Mohammed, S.A.; Manafian, J. New explicit soliton and other solutions of the Van der Waals model through the EShGEEM and the IEEM. J. Modern Tech. Eng. 2023, 8, 5–18. [Google Scholar]
- Mahak, N.; Akram, G. Exact solitary wave solutions of the (1+1)-dimensional Fokas-Lenells equation. Optik 2020, 208, 164459. [Google Scholar] [CrossRef]
- Aljahdaly, N.H. Some applications of the modified (G′/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Behera, S.; Aljahdaly, N.H.; Virdi, J.P.S. On the modified (G′/G2)-expansion method for finding some analytical solutions of the traveling waves. J. Ocean. Eng. Sci. 2022, 7, 313–320. [Google Scholar] [CrossRef]
- Saboor, A.; Shakeel, M.; Liu, X.; Zafar, A.; Ashraf, M. A comparative study of two fractional nonlinear optical model via modified (G′/G2)-expansion method. Opt. Quantum Electron. 2024, 56, 259. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota-Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Altalbe, A.; Taishiyeva, A.; Myrzakulov, R.; Bekir, A.; Zaagan, A.A. Effect of truncated M-fractional derivative on the new exact solitons to the Shynaray-IIA equation and stability analysis. Results Phys. 2024, 57, 107422. [Google Scholar] [CrossRef]
- Yao, S.-W.; Manzoor, R.; Zafar, A.; Mustafa, I.; Abbagari, S.; Houwe, A. Exact soliton solutions to the Cahn–Allen equation and Predator–Prey model with truncated M-fractional derivative. Results Phys. 2022, 37, 105455. [Google Scholar] [CrossRef]
- Bretherton, F.P. Resonant interactions between waves. The case of discrete oscillations. J. Fluidmechanics 1964, 20, 457–479. [Google Scholar] [CrossRef]
- Kudryashov, N.A. On types of nonlinear nonintegrable equations with exact solutions. Phys. Lett. A 1991, 155, 269–275. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Sinelshchikov, D.I.; Demina, M.V. Exact solutions of the generalized Bretherton equation. Phys. Lett. A 2011, 375, 1074–1079. [Google Scholar] [CrossRef]
- Berloff, N.G.; Howard, L.N. Nonlinear wave interactions in nonlinear nonintegrable systems. Stud. Appl. Math. 1998, 100, 195–213. [Google Scholar] [CrossRef]
- Akbar, M.A.; Norhashidah, H.; Mohd, A.; Zayed, E.M.E. Abundant exact traveling wave solutions of generalized Bretherton equation via improved (G′/G)-expansion method. Commun. Theor. Phys. 2012, 57, 173–178. [Google Scholar] [CrossRef]
- Yu, X.; Xu, F.; Zhang, L. Abundant Exact Solition-Like Solutions to the Generalized Bretherton Equation with Arbitrary Constants. Abstr. Appl. Anal. 2013, 7, 284865. [Google Scholar] [CrossRef]
- Yang, X.L.; Tang, J.S. Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion method. Commun. Theor. Phys. 2008, 50, 10471051. [Google Scholar]
- Tariq, K.U.; Wazwaz, A.-M.; Javed, R. Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel’d–Sokolov–Wilson model. Chaos Solitons Fractals 2023, 166, 112903. [Google Scholar] [CrossRef]
- Zulfiqar, H.; Aashiq, A.; Tariq, K.U.; Ahmad, H.; Almohsen, B.; Aslam, M.; Rehman, H.U. On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise. Optik 2023, 289, 171250. [Google Scholar] [CrossRef]
- ur Rehman, S.; Ahmad, J. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qawaqneh, H.; Hakami, K.H.; Altalbe, A.; Bayram, M. The Discovery of Truncated M-Fractional Exact Solitons and a Qualitative Analysis of the Generalized Bretherton Model. Mathematics 2024, 12, 2772. https://doi.org/10.3390/math12172772
Qawaqneh H, Hakami KH, Altalbe A, Bayram M. The Discovery of Truncated M-Fractional Exact Solitons and a Qualitative Analysis of the Generalized Bretherton Model. Mathematics. 2024; 12(17):2772. https://doi.org/10.3390/math12172772
Chicago/Turabian StyleQawaqneh, Haitham, Khalil Hadi Hakami, Ali Altalbe, and Mustafa Bayram. 2024. "The Discovery of Truncated M-Fractional Exact Solitons and a Qualitative Analysis of the Generalized Bretherton Model" Mathematics 12, no. 17: 2772. https://doi.org/10.3390/math12172772





