Data-Driven Modeling and Open-Circuit Voltage Estimation of Lithium-Ion Batteries
Abstract
:1. Introduction
- Develop a data-driven methodology to obtain a state-space model without needing full knowledge of all battery parameters.
- State-space representation model of a battery cell suitable for variable identification, such as battery OCV.
2. Modeling Methods Based on Equivalent (Electric) Circuits
- Internal resistance model (Rint) [2]. This model introduces the voltage drop observed at the battery terminals. Although this model effectively describes the behavior in the linear zone of the battery with relatively low computational complexity, it has limited accuracy in the evaluation of the polarization phenomenon and is highly susceptible to load changes.
- Randles model. This considers the OCV as the state variable of a large capacitor with a resistor connected in parallel. The resistor emulates the intrinsic discharge process of the battery and allows the generation of an accurate SoC curve during charge/discharge cycles [7].
- Partnership for a new generation model (PNGV) is a slightly improved version of the Thevenin model. This model adds equivalent capacitance in series with internal resistance to accurately describe the variations in the OCV when the SoC is within the range of 0–20%. It should be noted that this model is only valid during the discharging process [10,11].
- The fractional order model (FOM) was developed based on Thevenin’s approximation. This model only considers circuits with one or two arrays. It was designed to emulate the double-layer effect and solid-state diffusion, which are associated with the electrodes and the battery electrolyte in LIBs [7,12,13].
3. Recursive Bayesian and Heuristic SoC Estimation Algorithms
3.1. Kalman Filter-Based Methods
3.2. Heuristic Algorithms in SoC Estimation
3.3. Hybrid Methods
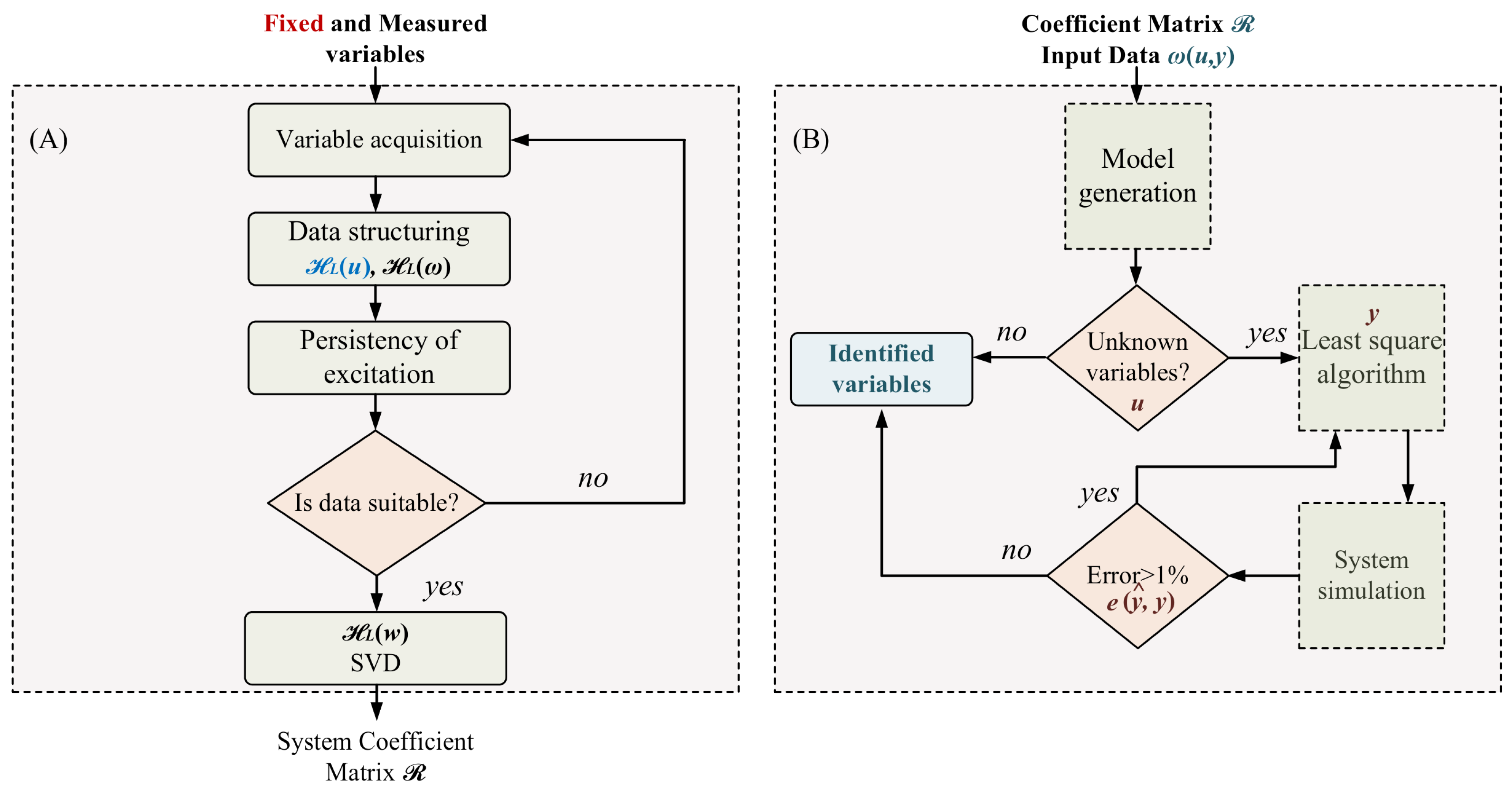
4. Methodology
4.1. Data-Based System Modeling
4.2. Linear Recursive Estimator
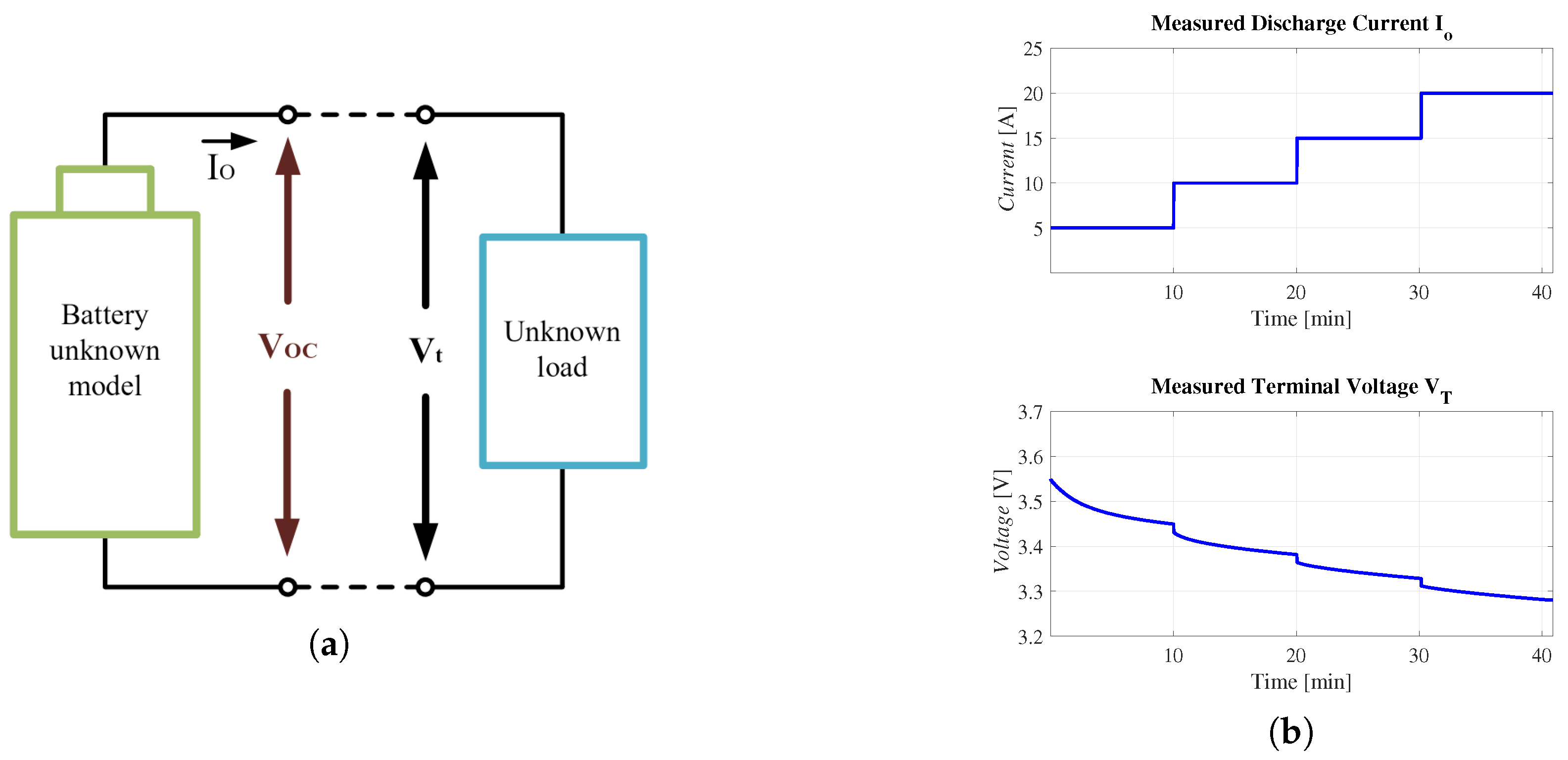
5. Experiments and Results Discussion
5.1. Battery Model Identification
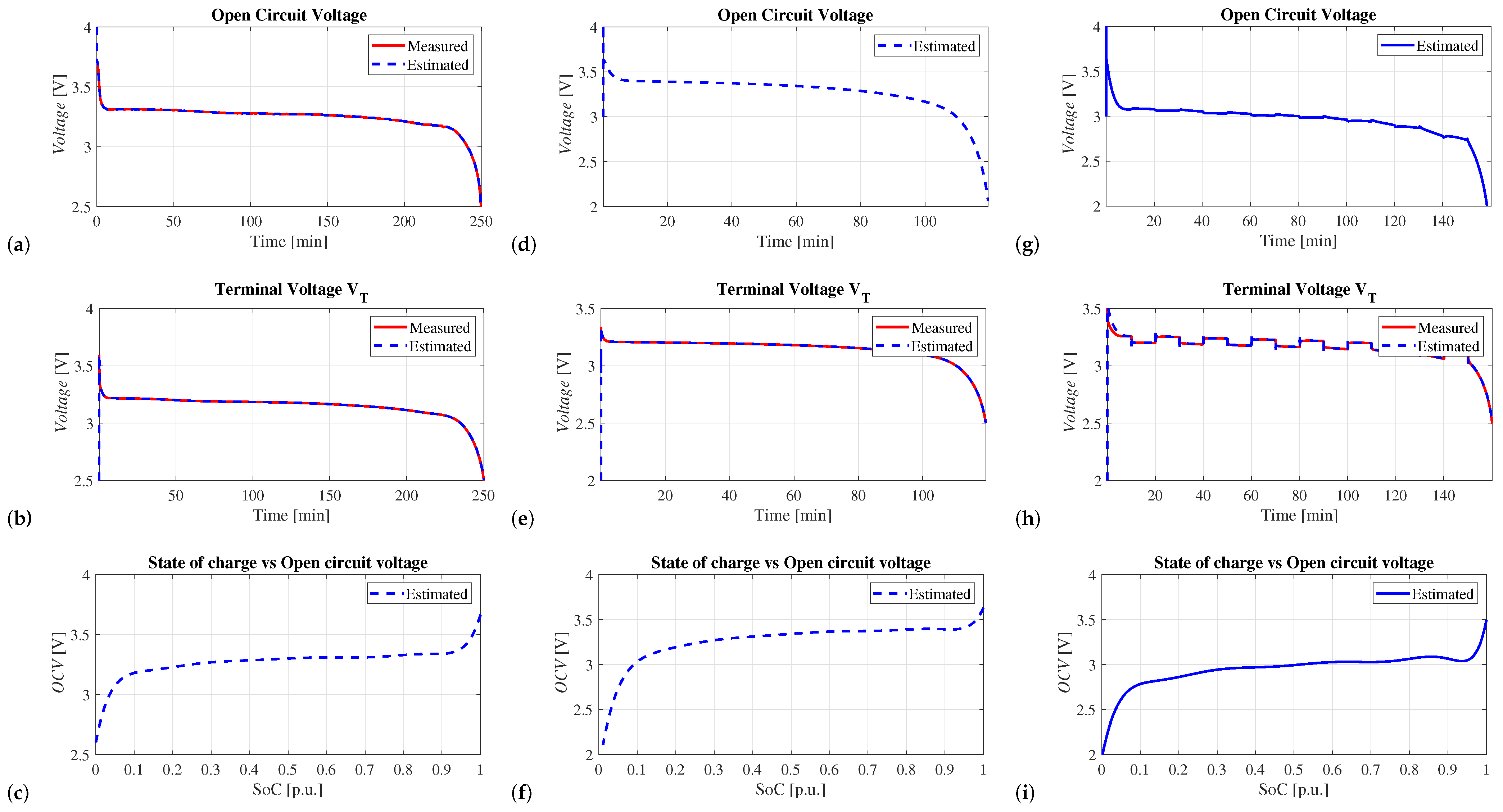
5.2. Experimental Validation
5.2.1. Test 1—Model Validation
5.2.2. Test 2—Constant Current Discharge
5.2.3. Test 3—Step-like Transition Current Discharge
5.2.4. Estimator Error Values
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Y.; Kroeze, R.C.; Krein, P.T. Multi-timescale parametric electrical battery model for use in dynamic electric vehicle simulations. IEEE Trans. Transp. Electrif. 2016, 2, 432–442. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, K.; Che, Y.; Lin, X.; Jin, G.; Liu, B. A practical and comprehensive evaluation method for series-connected battery pack models. IEEE Trans. Transp. Electrif. 2020, 6, 391–416. [Google Scholar] [CrossRef]
- Lee, K.Y.; Vale, Z.A. Applications of Modern Heuristic Optimization Methods in Power and Energy Systems; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Qays, M.O.; Buswig, Y.; Hossain, M.L.; Abu-Siada, A. Recent progress and future trends on the state of charge estimation methods to improve battery-storage efficiency: A review. CSEE J. Power Energy Syst. 2020, 8, 105–114. [Google Scholar]
- Chen, R.; Fan, Y.; Yuan, S.; Hao, Y. Vehicle Collaborative Partial Offloading Strategy in Vehicular Edge Computing. Mathematics 2024, 12, 1466. [Google Scholar] [CrossRef]
- Hussein, A.A.H.; Batarseh, I. An overview of generic battery models. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
- Hasan, R.; Scott, J. Extending randles’s battery model to predict impedance, charge—Voltage, and runtime characteristics. IEEE Access 2020, 8, 85321–85328. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Rimpas, D.; Kaminaris, S.D.; Piromalis, D.D.; Vokas, G. Real-Time Management for an EV Hybrid Storage System Based on Fuzzy Control. Mathematics 2023, 11, 4429. [Google Scholar] [CrossRef]
- Liu, X.; Li, W.; Zhou, A. PNGV equivalent circuit model and SOC estimation algorithm for lithium battery pack adopted in AGV vehicle. IEEE Access 2018, 6, 23639–23647. [Google Scholar] [CrossRef]
- Jung, S.; Tullu, A. Characteristics Evaluation of 14 Battery Equivalent Circuit Models. IEEE Access 2023, 11, 117200–117209. [Google Scholar] [CrossRef]
- Liu, S.; Dong, X.; Zhang, Y. A new state of charge estimation method for lithium-ion battery based on the fractional order model. IEEE Access 2019, 7, 122949–122954. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Mao, J.; Zhou, J.; Xu, D. Fractional order equivalent circuit model and SOC estimation of supercapacitors for use in HESS. IEEE Access 2019, 7, 52565–52572. [Google Scholar] [CrossRef]
- Kim, W.; Lee, P.Y.; Kim, J.; Kim, K.S. A robust state of charge estimation approach based on nonlinear battery cell model for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5638–5647. [Google Scholar] [CrossRef]
- Larijani, M.R.; Kia, S.H.; Zolghadri, M.; El Hajjaji, A.; Taghavipour, A. Linear Parameter-Varying Model Predictive Control for Intelligent Energy Management in Battery/Supercapacitor Electric Vehicles. IEEE Access 2024, 12, 51026–51040. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Combined state of charge and state of energy estimation of lithium-ion battery using dual forgetting factor-based adaptive extended Kalman filter for electric vehicle applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Zhu, Q.; Xu, M.; Liu, W.; Zheng, M. A state of charge estimation method for lithium-ion batteries based on fractional order adaptive extended kalman filter. Energy 2019, 187, 115880. [Google Scholar] [CrossRef]
- Wadi, A.; Abdel-Hafez, M.F.; Hussein, A.A.; Alkhawaja, F. Alleviating dynamic model uncertainty effects for improved battery SOC estimation of EVs in highly dynamic environments. IEEE Trans. Veh. Technol. 2021, 70, 6554–6566. [Google Scholar] [CrossRef]
- Feng, K.; Li, J.; Zhang, D.; Wei, X.; Yin, J. Robust Central Difference Kalman Filter with Mixture Correntropy: A Case Study for Integrated Navigation. IEEE Access 2021, 9, 80772–80786. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control. Syst. Technol. 2014, 23, 357–363. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yang, D.; Chen, Z. An on-line estimation of battery pack parameters and state-of-charge using dual filters based on pack model. Energy 2016, 115, 219–229. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Hurd, T.R. Cubature Kalman filtering for continuous-discrete systems: Theory and simulations. IEEE Trans. Signal Process. 2010, 58, 4977–4993. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Stage of charge estimation of lithium-ion battery packs based on improved cubature Kalman filter with long short-term memory model. IEEE Trans. Transp. Electrif. 2020, 7, 1271–1284. [Google Scholar] [CrossRef]
- Wang, D.; Yang, F.; Tsui, K.L.; Zhou, Q.; Bae, S.J. Remaining useful life prediction of lithium-ion batteries based on spherical cubature particle filter. IEEE Trans. Instrum. Meas. 2016, 65, 1282–1291. [Google Scholar] [CrossRef]
- How, D.N.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.; Ker, P.J.; Muttaqi, K.M. State-of-charge estimation of li-ion battery in electric vehicles: A deep neural network approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
- Li, S.G.; Sharkh, S.M.; Walsh, F.C.; Zhang, C.N. Energy and battery management of a plug-in series hybrid electric vehicle using fuzzy logic. IEEE Trans. Veh. Technol. 2011, 60, 3571–3585. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, D. An Adaptive Cubature Kalman Filter Based on Resampling-Free Sigma-Point Update Framework and Improved Empirical Mode Decomposition for INS/CNS Navigation. Mathematics 2024, 12, 1607. [Google Scholar] [CrossRef]
- Kadem, O.; Kim, J. Real-time state of charge-open circuit voltage curve construction for battery state of charge estimation. IEEE Trans. Veh. Technol. 2023, 72, 8613–8622. [Google Scholar] [CrossRef]
- Su, S.; Li, W.; Mou, J.; Garg, A.; Gao, L.; Liu, J. A hybrid battery equivalent circuit model, deep learning, and transfer learning for battery state monitoring. IEEE Trans. Transp. Electrif. 2022, 9, 1113–1127. [Google Scholar] [CrossRef]
- Guo, R.; Shen, W. A model fusion method for online state of charge and state of power co-estimation of lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2022, 71, 11515–11525. [Google Scholar] [CrossRef]
- How, D.N.; Hannan, M.; Lipu, M.H.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Rapisarda, P.; Willems, J.C. State maps for linear systems. SIAM J. Control. Optim. 1997, 35, 1053–1091. [Google Scholar] [CrossRef]
- Balakrishnan, V. System Identification: Theory for the User: Lennart Ljung; Prentice-Hall: Englewood Cliffs, NJ, USA, 1999; ISBN 0-13-656695-2. [Google Scholar]
- Rivera, D.; Guillen, D.; Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Escobar, G. Power grid dynamic performance enhancement via statcom data-driven control. Mathematics 2021, 9, 2361. [Google Scholar] [CrossRef]
- Willems, J.C.; Rapisarda, P.; Markovsky, I.; De Moor, B.L. A note on persistency of excitation. Syst. Control. Lett. 2005, 54, 325–329. [Google Scholar] [CrossRef]
- Hao, L.; Wang, C.; Shi, Y. Quadratic Tracking Control of Linear Stochastic Systems with Unknown Dynamics Using Average Off-Policy Q-Learning Method. Mathematics 2024, 12, 1533. [Google Scholar] [CrossRef]
- Hänsler, E.; Schmidt, G. Acoustic Echo and Noise Control: A Practical Approach; John Wiley & Sons: Hoboken, NJ, USA, 2005; Chapter 7. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. A robust variable forgetting factor recursive least-squares algorithm for system identification. IEEE Signal Process. Lett. 2008, 15, 597–600. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Young, P.C. Recursive least squares estimation. In Recursive Estimation and Time-Series Analysis: An Introduction for the Student and Practitioner; Springer: Berlin/Heidelberg, Germany, 2011; pp. 29–46. [Google Scholar]
- Amaral, L.F.C.; Lopes, M.V.; Barros, A.K. A nonquadratic algorithm based on the extended recursive least-squares algorithm. IEEE Signal Process. Lett. 2018, 25, 1535–1539. [Google Scholar] [CrossRef]
- IEC. Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles—Part 1: Performance Testing; IEC 62660-1; IEC: Geneva, Switzerland, 2018. [Google Scholar]
- ISO 12405-4; Electrically Propelled Road Vehicles—Test Specification for Lithium-Ion Traction Battery Packs and Systems—Part 4: Performance Testing for High-Power Applications. ISO: Geneva, Switzerland, 2018.




| Estimation Method | Description | Advantages |
|---|---|---|
| Extended Kalman filter (EKF) [16,17,18] | Linearizes systems and observation models; follows a recursive process; covariance matrix presents convergence issues. | Deals with forgetting factor parameter; algorithm for SoC estimation under dynamic conditions. |
| Central difference Kalman filter (CDKF) [19] | High precision; based on Stirling interpolation; high computational cost. | Avoids the linearization error of the battery model; improves the SoC estimation accuracy; used for 1RC model. |
| Unscented Kalman filter (UKF) [20,21] | Attains higher precision in estimating mean and error covariance; however, it is more sensitive to measurement noise. | Battery model to identify nonlinear parameters of the battery model; used for the 2RC model. |
| Cubature Kalman filter (CKF) [22,23] | Employs a cubature rule to address nonlinearities, providing an accurate prediction of the state. | Algorithm to model battery electrical characteristics and to estimate the SoC. |
| Particle filter (PF) [24] | Nonlinear systems and non-Gaussian distributions; Monte Carlo method; high dimensionality; does not require a precise mathematical model. | Pronostic method to estimate the battery life, and to solve the state-space model. |
| Neural network (NN) [25] | Variable layer arrangement that returns the estimated state of charge (SoC). A nonlinear map is obtained that models the relationship between the input and output. | Accuracy in SoC estimation increases with the addition of hidden layers. Predicts SoC values for different profiles. |
| Fuzzy logic (FL) [26] | Introduces the concept of battery working state, which assigns a degree of membership based on both battery terminal voltage and state of charge. | Improves the accuracy of SoC estimation and noise immunity. Superior performance in the face of unknown initial SoC. |
| 20% SoC | 40% SoC | 60% SoC | 80% SoC | 100% SoC | |
|---|---|---|---|---|---|
| 0.7071 | 0.7071 | 0.7071 | 0.7071 | 0.7071 | |
| 0.7071 | 0.7071 | 0.7071 | 0.7071 | 0.7071 | |
| 355.525 | 351.439 | 349.970 | 345.713 | 345.225 | |
| 2.81 ms | 2.84 ms | 2.86 ms | 2.89 ms | 2.89 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva-Vera, E.D.; Valdez-Resendiz, J.E.; Escobar, G.; Guillen, D.; Rosas-Caro, J.C.; Sosa, J.M. Data-Driven Modeling and Open-Circuit Voltage Estimation of Lithium-Ion Batteries. Mathematics 2024, 12, 2880. https://doi.org/10.3390/math12182880
Silva-Vera ED, Valdez-Resendiz JE, Escobar G, Guillen D, Rosas-Caro JC, Sosa JM. Data-Driven Modeling and Open-Circuit Voltage Estimation of Lithium-Ion Batteries. Mathematics. 2024; 12(18):2880. https://doi.org/10.3390/math12182880
Chicago/Turabian StyleSilva-Vera, Edgar D., Jesus E. Valdez-Resendiz, Gerardo Escobar, Daniel Guillen, Julio C. Rosas-Caro, and Jose M. Sosa. 2024. "Data-Driven Modeling and Open-Circuit Voltage Estimation of Lithium-Ion Batteries" Mathematics 12, no. 18: 2880. https://doi.org/10.3390/math12182880
APA StyleSilva-Vera, E. D., Valdez-Resendiz, J. E., Escobar, G., Guillen, D., Rosas-Caro, J. C., & Sosa, J. M. (2024). Data-Driven Modeling and Open-Circuit Voltage Estimation of Lithium-Ion Batteries. Mathematics, 12(18), 2880. https://doi.org/10.3390/math12182880








