On Properties of the Hyperbolic Distribution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hyperbolic Inverse Gaussian Distribution
2.2. Hyperbolic Distribution
2.2.1. Definition and Moments
2.2.2. Probability Density Function
2.2.3. Moment-Generating Function
3. Results
4. Applications
5. Numerical Analysis
5.1. Selection of the Parameters
5.2. Computations
6. Discussion
7. Conclusions
- The hyperbolic distribution is very popular in many applications and the examination of its properties is a direction of research of current interest.
- In comparison with the formulas for other normal mean–variance mixtures, the closed form expressions for the cumulative distribution and partial-moment-generating functions of the hyperbolic law depend also on the values of the Whittaker function.
- The theoretical results can be applied to the problem of option valuation in the hyperbolic model of financial markets. It is shown that the prices of double digital options can differ by more than 12% from the prices of the same options in the normal model.
- Future investigations should relate to the complete analytical specification of the cumulative distribution, partial-moment-generating functions, and partial moments of the hyperbolic law. The research in the area of applications to finance should be continued as well.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Barndorff-Nielsen, O.E. Exponentially decreasing distributions for the logarithm of particle size. Proc. R. Soc. Lond. A 1977, 353, 401–419. [Google Scholar]
- Barndorff-Nielsen, O.E. Models for non-Gaussian variation with applications to turbulence. Proc. R. Soc. Lond. A 1979, 368, 501–520. [Google Scholar]
- Barndorff-Nielsen, O.E. The hyperbolic distribution in statistical physics. Scand. J. Stat. 1982, 9, 43–46. [Google Scholar]
- Barndorff-Nielsen, O.E.; Blaesild, P.; Jensen, J.L.; Sørensen, M. The fascination of sand. In A Celebration of Statistics—The ISI Centenary Volume; Atkinson, A.C., Fienberg, S.E., Eds.; Springer: New York, NY, USA, 1985; pp. 57–87. [Google Scholar]
- Barndorff-Nielsen, O.E.; Christiansen, C. Erosion, deposition and size distribution of sand. Proc. R. Soc. Lond. A 1988, 417, 335–352. [Google Scholar]
- Hartmann, D.; Bowman, D. Efficiency of the log-hyperbolic distribution—A case study: Pattern of sediment sorting in a small tidal-inlet—Het Zwin, The Netherlands. J. Coastal Res. 1993, 9, 1044–1053. [Google Scholar]
- Bhatia, J.C.; Durst, F. Description of sprays using joint hyperbolic distribution in particle size and velocity. Combust. Flame 1990, 81, 203–218. [Google Scholar] [CrossRef]
- Xu, T.H.; Durst, F.; Tropea, C. The three-parameter log-hyperbolic distribution and its application to particle sizing. At. Sprays 1993, 3, 109–124. [Google Scholar] [CrossRef]
- Blaesild, P. On the two-dimensional hyperbolic distribution and some related distributions, with an application to Johannsen’s bean data. Biometrika 1981, 68, 251–263. [Google Scholar] [CrossRef]
- Kristjansson, L.; McDougall, I. Some aspects of the late tertiary geomagnetic field in Iceland. Geophys. J. R. Astronom. Soc. 1982, 68, 273–294. [Google Scholar] [CrossRef]
- Babinsky, E.; Sojka, P.E. Modeling drop size distributions. Prog. Energy Combust. Sci. 2002, 28, 303–329. [Google Scholar] [CrossRef]
- Ghoshal, K.; Mazumder, B.S.; Purkait, B. Grain-size distributions of bed load: Inferences from flume experiments using heterogeneous sediment beds. Sediment. Geol. 2010, 223, 1–14. [Google Scholar] [CrossRef]
- Hajek, E.A.; Huzurbazar, S.V.; Mohrig, D.; Lynds, R.M.; Heller, P.L. Statistical characterization of grain-size distributions in sandy fluvial systems. J. Sediment. Res. 2010, 80, 184–192. [Google Scholar] [CrossRef]
- Eberlein, E.; Keller, U. Hyperbolic distributions in finance. Bernoulli 1995, 1, 281–299. [Google Scholar] [CrossRef]
- Bibby, B.M.; Sørensen, M. A hyperbolic diffusion model for stock prices. Financ. Stoch. 1997, 1, 25–41. [Google Scholar] [CrossRef]
- Eberlein, E.; Keller, U.; Prause, K. New insights into smile, mispricing, and value at risk: The hyperbolic model. J. Bus. 1998, 71, 371–405. [Google Scholar] [CrossRef]
- Küchler, U.; Neumann, K.; Sørensen, M.; Streller, A. Stock returns and hyperbolic distributions. Math. Comput. Model. 1999, 29, 1–15. [Google Scholar] [CrossRef]
- Bauer, C. Value at risk using hyperbolic distributions. J. Econ. Bus. 2000, 52, 455–467. [Google Scholar] [CrossRef]
- Daskalaki, S.; Katris, C. Marginal distribution modeling and value at risk estimation for stock index returns. J. Appl. Oper. Res. 2014, 6, 207–221. [Google Scholar]
- Luciano, E.; Marena, M.; Semeraro, P. Dependence calibration and portfolio fit with factor-based subordinators. Quant. Financ. 2016, 16, 1037–1052. [Google Scholar] [CrossRef]
- Baciu, O.A. Generalized hyperbolic distributions: Empirical evidence on Bucharest stock exchange. Rev. Financ. Bank. 2015, 7, 7–18. [Google Scholar]
- Sheraz, M.H.M.; Dedu, S.A. Bitcoin cash: Stochastic models of fat-tail returns and risk modeling. Econ. Comput. Econ. Cyber. Stud. and Res. 2020, 54, 43–58. [Google Scholar]
- Blaesild, P. Conditioning with conic sections in the two-dimensional normal distribution. Ann. Stat. 1979, 7, 659–670. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Stelzer, R. Absolute moments of generalized hyperbolic distributions and approximate scaling of normal inverse Gaussian Lévy processes. Scand. J. Stat. 2005, 32, 617–637. [Google Scholar] [CrossRef]
- Leobacher, G.; Pillichshammer, F. A method for approximate inversion of the hyperbolic CDF. Computing 2002, 69, 291–303. [Google Scholar] [CrossRef]
- Fonseca, T.; Migon, H.S.; Ferreira, M.A.R. Bayesian analysis based on the Jeffreys prior for the hyperbolic distribution. Braz. J. Probab. Statist. 2012, 26, 327–343. [Google Scholar] [CrossRef]
- Bingham, N.H.; Kiesel, R. Modelling asset returns with hyperbolic distributions. In Return Distributions in Finance; Knight, J., Satchell, S., Eds.; Butterworth-Heinemann: Oxford, UK, 2001; pp. 1–20. [Google Scholar]
- Kabašinskas, A.; Šutiene, K.; Kopa, M.; Lukšys, K.; Bagdonas, K. Dominance-based decision rules for pension fund selection under different distributional assumptions. Mathematics 2020, 8, 719. [Google Scholar] [CrossRef]
- Tan, Y.F.; Ng, K.H.; Koh, Y.B.; Peiris, S. Modelling trade durations using dynamic logarithmic component ACD model with extended generalised inverse Gaussian distribution. Mathematics 2020, 10, 1621. [Google Scholar] [CrossRef]
- Eberlein, E. Fourier-based valuation methods in mathematical finance. In Quantitative Energy Finance; Benth, F., Kholodnyi, V., Laurence, P., Eds.; Springer: New York, NY, USA, 2014; pp. 85–114. [Google Scholar]
- Asmussen, S.; Glynn, P.W. Stochastic Simulation: Algorithms and Analysis; Springer: New York, NY, USA, 2007; pp. 325–349. [Google Scholar]
- Madan, D.; Carr, P.; Chang, E. The variance gamma process and option pricing. Eur. Financ. Rev. 1998, 2, 79–105. [Google Scholar] [CrossRef]
- Ano, K.; Ivanov, R.V. On exact pricing of FX options in multivariate time-changed Lévy models. Rev. Derivat. Res. 2016, 19, 201–216. [Google Scholar]
- Ivanov, R.V. The semi-hyperbolic distribution and its applications. Stats 2023, 6, 1126–1146. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Kent, J.; Sørensen, M. Normal mean-variance mixtures and z distributions. Int. Statist. Rev. 1982, 50, 145–159. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Academic Press: Burlington, VT, USA, 1980; pp. 347–348, 368, 925. [Google Scholar]
- Shiryaev, A.N. Essentials of Stochastic Finance; World Scientific: Singapore, 1999; pp. 189–214, 633–661. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course in Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1927; pp. 337–354. [Google Scholar]
- Srivastava, H.M.; Karlsson, W. Multiple Gaussian Hypergeometric Series; Ellis Horwood Limited: New York, NY, USA, 1985; pp. 22–33. [Google Scholar]
- Bateman, H.; Erdélyi, A. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume I, pp. 239–242. [Google Scholar]
- Musiela, M.; Rutkowski, M. Martingale Methods in Financial Modelling, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 32–34, 193–216. [Google Scholar]
- Carr, P.; Geman, H.; Madan, D.; Yor, M. Self-decomposability and option pricing. Math. Financ. 2007, 17, 31–57. [Google Scholar] [CrossRef]
- Eberlein, E.; Papapantoleon, A.; Shiryaev, A.N. Esscher transform and the duality principle for multidimensional semimartingales. Ann. Appl. Probab. 2009, 19, 1944–1971. [Google Scholar] [CrossRef]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume I, p. 139. [Google Scholar]
- Ivanov, R.V. The risk measurement under the variance-gamma process with drift switching. J. Risk Financ. Manag. 2022, 15, 22. [Google Scholar] [CrossRef]
- Ivanov, R.V.; Temnov, G. Truncated moment-generating functions of the NIG process and their applications. Stochastics Dyn. 2017, 17, 1750039. [Google Scholar] [CrossRef]
- Ivanov, R.V. On the stochastic volatility in the generalized Black-Scholes-Merton model. Risks 2023, 11, 111. [Google Scholar] [CrossRef]
- Cont, R.; Deguest, R.; He, X.D. Loss-based risk measures. Stat. Risk Model. 2013, 30, 133–167. [Google Scholar] [CrossRef]
- Ivanov, R.V. On lower partial moments for the investment portfolio with variance-gamma distributed returns. Lithuan. Math. J. 2022, 62, 10–27. [Google Scholar] [CrossRef]
- Nawrocki, D. A brief history of downside risk measures. J. Investig. 1999, 8, 9–25. [Google Scholar] [CrossRef]
- Schoutens, W.; Simons, E.; Tistaert, J. Model Risk for Exotic and Moment Derivatives. In Exotic Option Pricing and Advanced Lévy Models; Kyprianou, A.E., Schoutens, W., Wilmott, P., Eds.; Wiley: Chichester, UK, 2005; pp. 67–97. [Google Scholar]
- Perreault, L.; Bobée, B.; Rasmussen, P.F. Halphen Distribution System. I: Mathematical and Statistical Properties. J. Hydrol. Eng. 1999, 4, 189–197. [Google Scholar] [CrossRef]
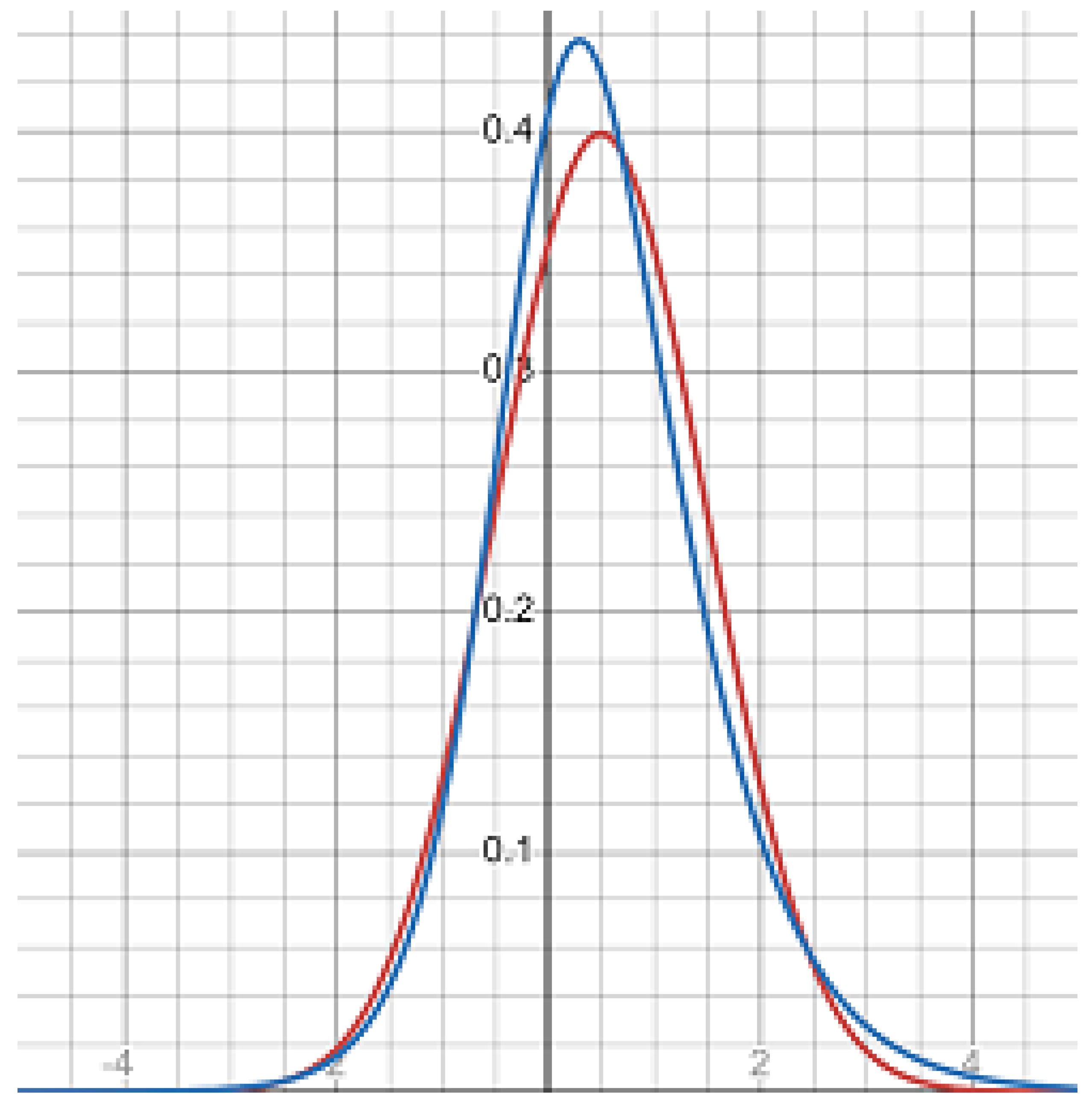
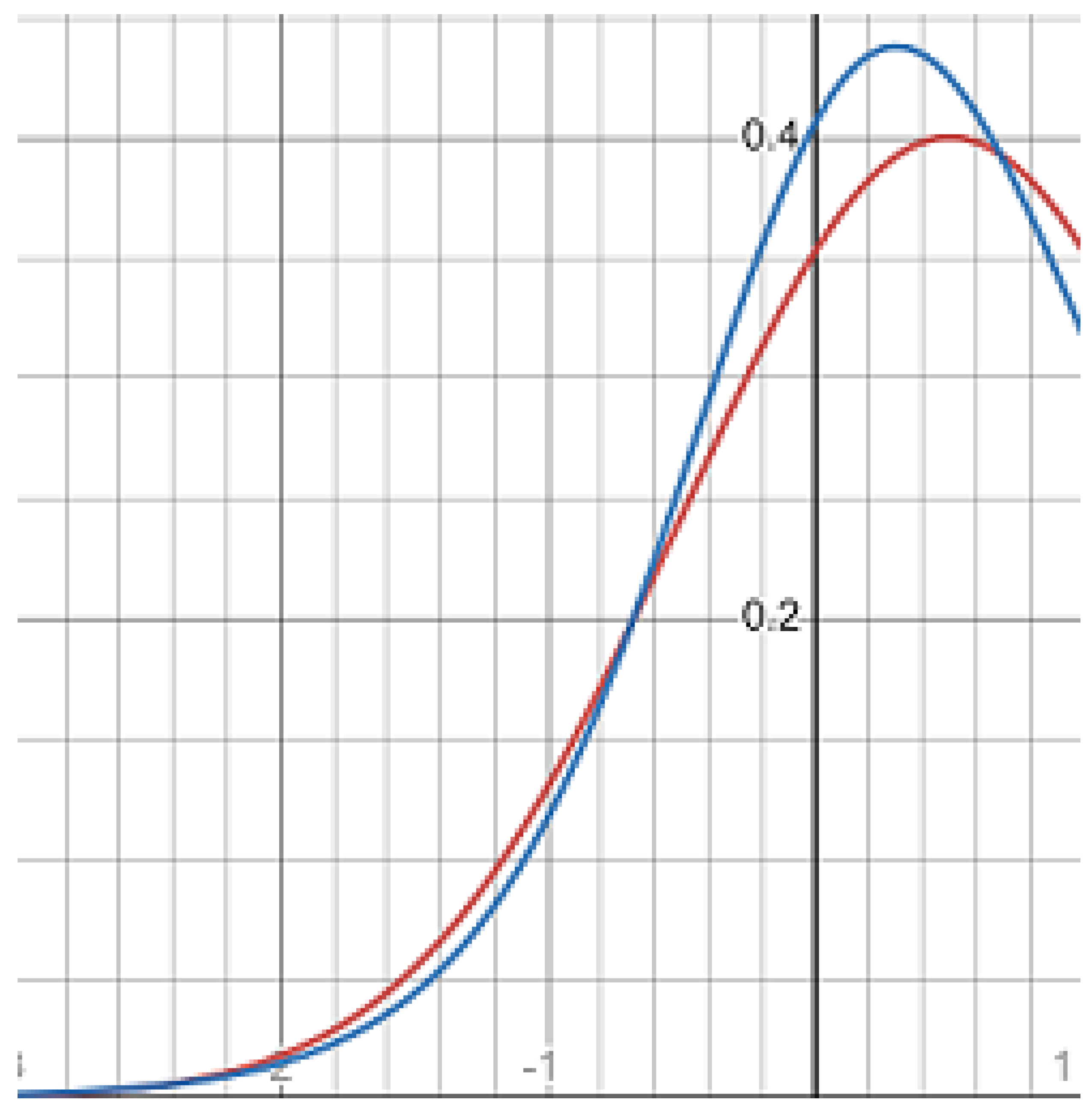
| u | −2 | −1 | −0.5 | −0.2 | 0 |
|---|---|---|---|---|---|
| 0.006 | 0.067 | 0.159 | 0.242 | 0.309 | |
| 0.006 | 0.058 | 0.151 | 0.241 | 0.319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, R.V. On Properties of the Hyperbolic Distribution. Mathematics 2024, 12, 2888. https://doi.org/10.3390/math12182888
Ivanov RV. On Properties of the Hyperbolic Distribution. Mathematics. 2024; 12(18):2888. https://doi.org/10.3390/math12182888
Chicago/Turabian StyleIvanov, Roman V. 2024. "On Properties of the Hyperbolic Distribution" Mathematics 12, no. 18: 2888. https://doi.org/10.3390/math12182888





