Stochastic Differential Games and a Unified Forward–Backward Coupled Stochastic Partial Differential Equation with Lévy Jumps
Abstract
1. Introduction
2. Main Theorem with Examples
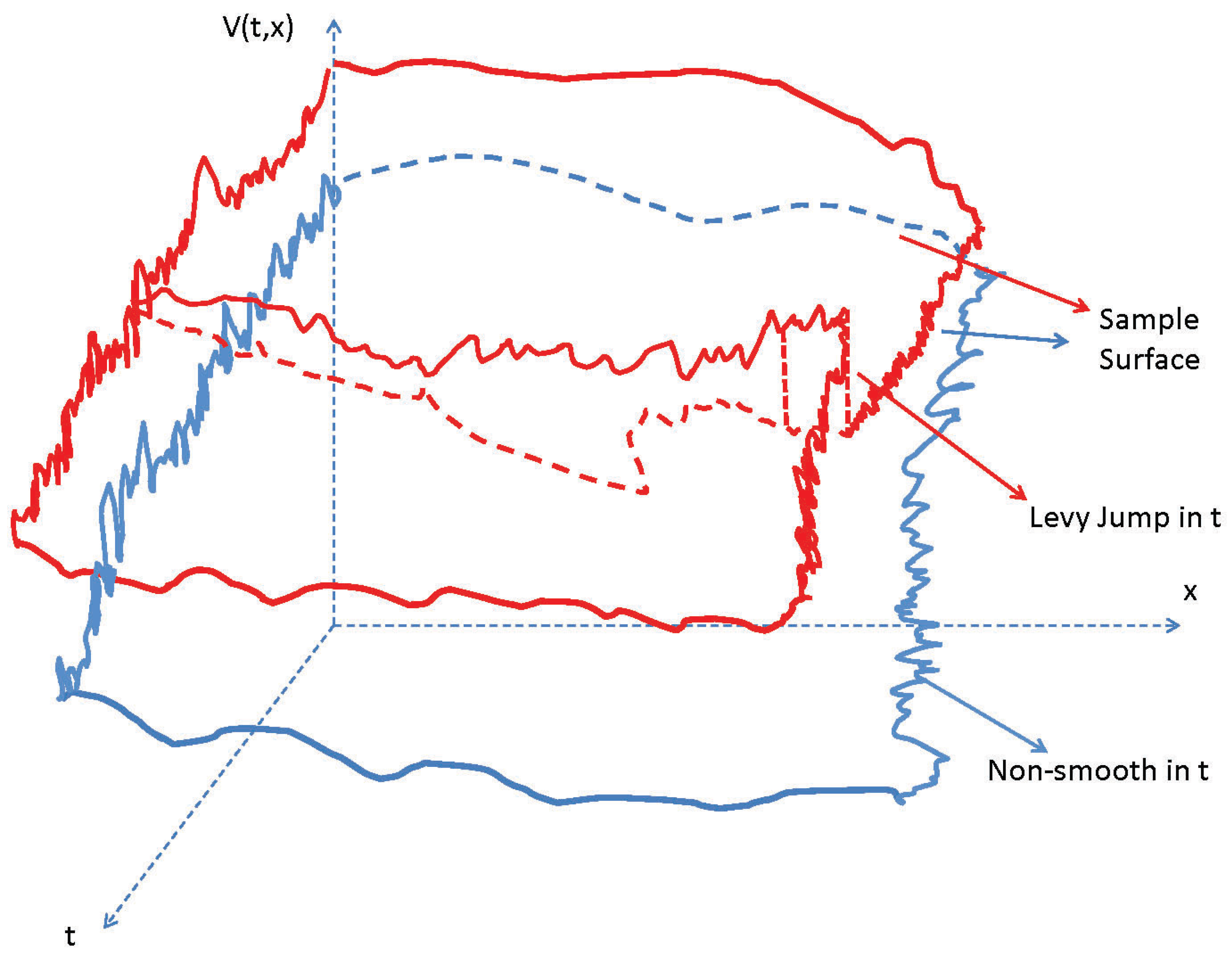
2.1. State and Value Processes
2.2. Main Theorem
2.3. Real-World Examples
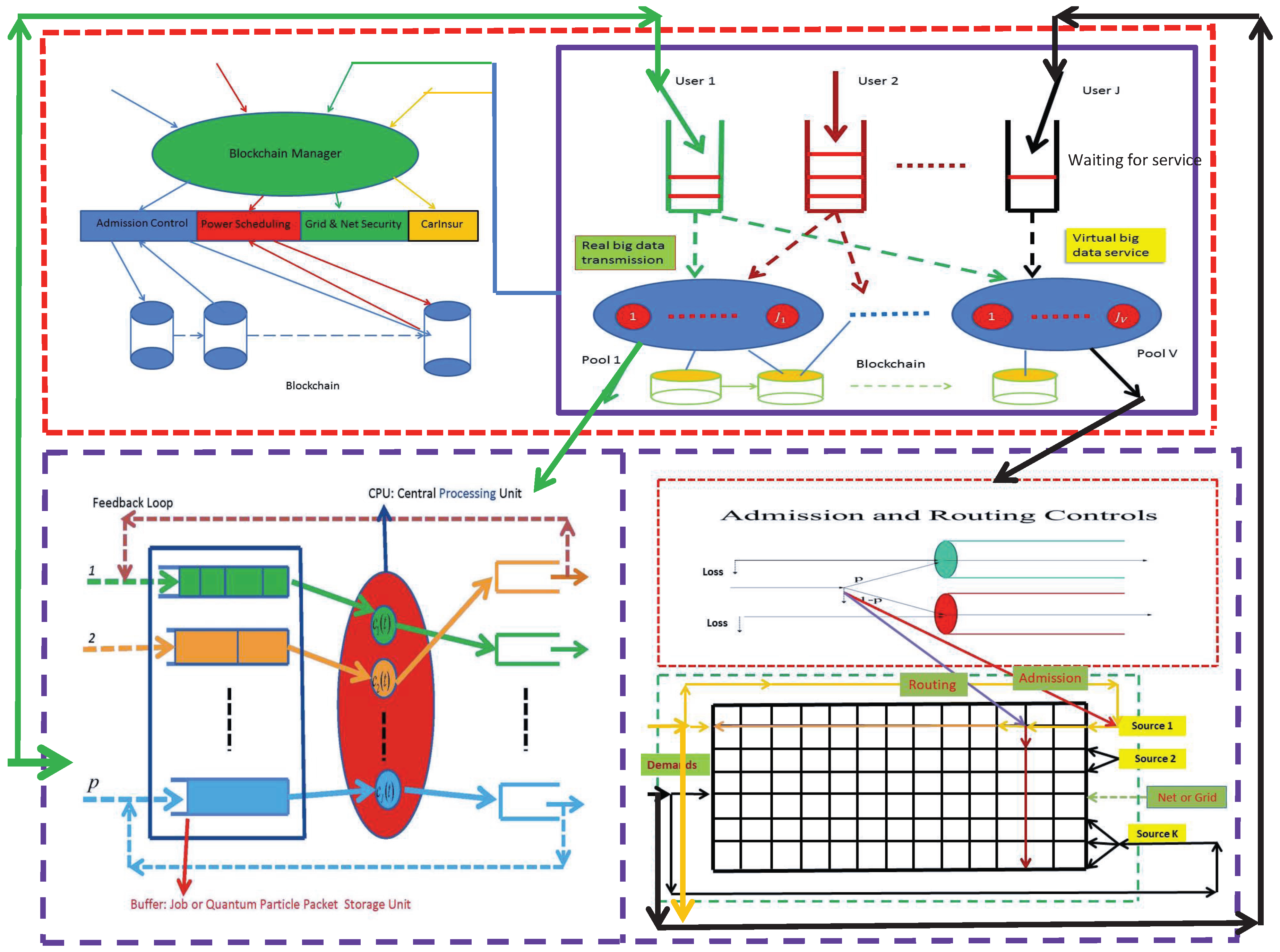
2.3.1. Sharing vs. Competition in Cloud Services and Energy Grids
2.3.2. Mastering the Zero-Sum Game of Go
3. Proof of Main Theorem
3.1. Unique Existence of Solution to the Unified SPDE
3.2. Proof of Theorem 1
3.3. Proof of Proposition 1
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mauro, A.D.; Greco, M.; Grimaldi, M. A formal definition of big data based on its essential features. Libr. Rev. 2016, 65, 122–135. [Google Scholar] [CrossRef]
- Dai, W. A unified system of FB-SDEs with Lévy jumps and double completely-S skew reflections. Commun. Math. Sci. 2018, 16, 659–704. [Google Scholar] [CrossRef]
- Dai, W. Optimal rate scheduling via utility-maximization for J-user MIMO Markov fading wireless channels with cooperation. Oper. Res. 2013, 6, 1450–1462. [Google Scholar] [CrossRef]
- Duncan, T.E. Mutual information for stochastic signals and Lévy processes. IEEE Trans. Inf. Theory 2010, 56, 18–24. [Google Scholar] [CrossRef]
- Dai, W.; Jiang, Q. Stochastic optimal control of ATO systems with batch arrivals via diffusion approximation. Probab. Eng. Inf. Sci. 2007, 21, 477–495. [Google Scholar] [CrossRef][Green Version]
- Mandelbaum, A.; Pats, G. State-dependent stochastic networks. Part I: Approximations and applications with continuous diffusion limits. Ann. Appl. Probab. 1998, 8, 569–646. [Google Scholar] [CrossRef]
- Kong, J.R.; Jiménez-Martínez, R.; Troullinou, C.; Lucivero, V.G.; Tóth, G.; Mitchell, M.W. Measurement-induced, spatially-extended entanglement in a hot, strongly-interacting atomic system. Nat. Commun. 2020, 11, 2415. [Google Scholar] [CrossRef]
- Dai, W. Game-theoretic policy computing and simulation for blockchained buffering system via diffusion approximation. Probab. Eng. Inf. Sci. 2024, 1–36. [Google Scholar] [CrossRef]
- Karatzas, I.; Li, Q. BSDE approach to non-zero-sum stochastic differential games of control and stopping. In Stochastic Processes, Finance and Control; World Scientific Publishers: Singapore, 2012; pp. 105–153. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Driessche, G.V.D.; Schrittwieser, J.; Antonoglu, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglu, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Zidek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Nachum, O.; Yang, M.; Lee, L.; Freeman, D.; Xu, W.; Guadarrama, S.; Fischer, I.; Jang, E.; Michalewski, H. Multi-game decision transformers. arXiv 2022, arXiv:2205.15241v1. [Google Scholar]
- Dai, W. Convolutional neural network based simulation and analysis for backward stochastic partial differential equations. Comput. Math. Appl. 2022, 119, 21–58. [Google Scholar] [CrossRef]
- Dai, W. Simulating a strongly nonlinear backward stochastic partial differential equation via efficient approximation and machine learning. AIMS Math. 2024, 9, 18688–18711. [Google Scholar] [CrossRef]
- Ash, G.R. Dynamic Routing in Telecommunications Network; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Hamidi, V.; Smith, K.S.; Wilson, R.S. Smart grid technology review within the transmission and distribution sector. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe, Gothenburg, Sweden, 1–8 October 2010. [Google Scholar]
- Musiela, M.; Zariphopoulou, T. Stochastic partial differential equations and portfolio choice. In Contemporary Quantitative Finance; Chiarella, C., Novikov, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 195–216. [Google Scholar]
- Peng, S. Stochastic Hamilton-Jacobi-Bellman equations. SIAM J. Control Optim. 1992, 30, 284–304. [Google Scholar] [CrossRef]
- Øksendal, B.; Sulem, A.; Zhang, T. A Stochastic HJB Equation for Optimal Control of Forward-Backward SDEs. In The Fascination of Probability, Statistics and Their Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Applebaum, D. Lévy Processes and Stochastic Calculus; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sato, K.I. Lévy Processes and Infinite Divisibility; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Caselles, V.; Sapiro, G.; Chung, D.H. Vector median filters, morphology, and PDE’s: Theoretical connections. In Proceedings of the International Conference on Image Processing, Kobe, Japan, 24–28 October 1999; Volume 4, pp. 177–184. [Google Scholar]
- Tschumperlé, D.; Deriche, R. Regularization of orthonormal vector sets using coupled PDE’s. In Proceedings of the IEEE Workshop on Variational and Level Set Methods in Computer Vision 2001, Vancouver, BC, Canada, 13 July 2001; pp. 3–10. [Google Scholar]
- Tschumperlé, D.; Deriche, R. Constrained and unconstrained PDE’s for vector image restoration. In Proceedings of the Scandinavian Conference on Image Analysis, Bergen, Norway, 11–14 June 2001. [Google Scholar]
- Tschumperlé, D.; Deriche, R. Anisotropic diffusion partial differential equations for multichannel image regularization: Framework and applications. Adv. Imaging Electron Phys. 2007, 145, 149–209. [Google Scholar]
- Kratsios, A.; Debarnot, V.; Dokmannić, I. Small transformers compute universal metric embeddings. J. Mach. Learn. Res. 2023, 24, 1–48. [Google Scholar]
- Peluchetti, S. Diffusion bridge mixture transports, Schrödinger bridge problems and generative modeling. J. Mach. Learn. Res. 2023, 24, 1–51. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Huang, M.; Malhame, R.P.; Caines, P.E. Large population stochastic dynamic games: Closed-loop Mckean-Vlason systems and the Nash certainty equivalence principle. Commun. Inf. Syst. 2006, 6, 221–252. [Google Scholar]
- Lasry, J.M.; Lions, P.L. Mean field games. Jpn. J. Math. 2007, 2, 229–260. [Google Scholar] [CrossRef]
- Kolokoltsov, V.N. Quantum mean-field games. Ann. Appl. Probab. 2022, 32, 2254–2288. [Google Scholar] [CrossRef]
- Dai, W. Mean-variance hedging based on an incomplete market with external risk factors of non-Gaussian OU processes. Math. Eng. 2015, 2015, 625289. [Google Scholar] [CrossRef]
- Hairer, M. Solving the KPZ equation. Ann. Math. 2013, 178, 559–664. [Google Scholar] [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 1986, 66, 889–892. [Google Scholar] [CrossRef]
- Yong, J.; Zhou, X.Y. Stochastic Controls: Hamiltonian Systems and HJB Equations; Springer: New York, NY, USA, 1999. [Google Scholar]
- de Bouard, A.; Debussche, A. A stochastic nonlinear Schrödinger equation with multiplicative noise. Commun. Math. Phys. 1999, 205, 161–181. [Google Scholar] [CrossRef]
- de Bouard, A.; Debussche, A. The stochastic nonlinear Schrödinger equation in H1. Stoch. Anal. Appl. 2003, 21, 97–126. [Google Scholar] [CrossRef]
- Chai, J.D. Density functional theory with fractional orbit occupations. J. Chem. Phys. 2012, 136, 154104. [Google Scholar] [CrossRef]
- Chai, J.D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. 2014, 140, 18A521. [Google Scholar] [CrossRef]
- Chang, C.Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Li, K.; Ou, Y.; Wei, P.; Wang, L.L.; et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topologic insulator. Science 2013, 340, 167. [Google Scholar] [CrossRef]
- Dai, W. Mean-variance portfolio selection based on a generalized BNS stochastic volatility model. Int. J. Comput. 2011, 88, 3521–3534. [Google Scholar] [CrossRef]
- Hall, E. On a new action of the magnet on electric currents. Am. J. Math. 1879, 2, 287–292. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J.M. Hall effect in ferromagnetics. Phys. Rev. 1954, 95, 1154–1160. [Google Scholar] [CrossRef]
- Lions, P.L.; Souganidis, T. Fully nonlinear stochastic partial differential equations Équations aux dérivés partielles stochastiques compltèement non-linéaires. Comptes Rendus l’Acad. Sci.—Ser. I—Math. 1998, 326, 1085–1092. [Google Scholar]
- Thouless, D.J. The quantum Hall Effect and the Schrödinger equation with competing periods. In Number Theory and Physics: Proceedings of the Winter School, Les Houches, France, 7–16 March 1989; Springer: Berlin/Heidelberg, Germany, 1990; Volume 47, pp. 170–176. [Google Scholar]
- Bertoin, J. Lévy Processes; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Kallenberg, O. Foundations of Modern Probability; Springer: New York, NY, USA, 1997. [Google Scholar]
- Dai, W. Brownian Approximations for Queueing Networks with Finite Buffers: Modeling, Heavy Traffic Analysis and Numerical Implementations. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 1996. [Google Scholar]
- Mandelbaum, A.; Massey, W.A. Strong approximations for time-dependent queues. Math. Oper. Res. 1995, 20, 33–64. [Google Scholar] [CrossRef]
- Konstantopoulos, T.; Last, G.; Lin, S.J. On a class of Lévy stochastic networks. Queueing Syst. 2004, 46, 409–437. [Google Scholar] [CrossRef]
- Dai, W. Optimal control with monotonicity constraints for a parallel-server loss channel serving multi-class jobs. Math. Comput. Model. Dyn. Syst. 2014, 20, 284–315. [Google Scholar] [CrossRef]
- Øksendal, B.; Sulem, A. Applied Stochastic Control of Jump Diffusions; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Øksendal, B.; Zhang, T. The Ito^-Ventzell formula and forward stochastic differential equations driven by Poisson random measures. Osaka J. Math. 2007, 44, 207–230. [Google Scholar]
- Protter, P.E. Stochastic Integration and Differential Equations, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Peskir, G.; Shiryaev, A. Optimal Stopping and Free-Boundary Probelms; Birkhäuser: Basel, Switzerland, 2006. [Google Scholar]
- Situ, R. On solutions of backward stochastic differential equations with jumps and applications. Stoch. Processes Their Appl. 1997, 66, 209–236. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations, 6th ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Ethier, S.N.; Kurtz, T.G. Markov Process: Characterization and Convergence; Wiley: New York, NY, USA, 1986. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, W. Stochastic Differential Games and a Unified Forward–Backward Coupled Stochastic Partial Differential Equation with Lévy Jumps. Mathematics 2024, 12, 2891. https://doi.org/10.3390/math12182891
Dai W. Stochastic Differential Games and a Unified Forward–Backward Coupled Stochastic Partial Differential Equation with Lévy Jumps. Mathematics. 2024; 12(18):2891. https://doi.org/10.3390/math12182891
Chicago/Turabian StyleDai, Wanyang. 2024. "Stochastic Differential Games and a Unified Forward–Backward Coupled Stochastic Partial Differential Equation with Lévy Jumps" Mathematics 12, no. 18: 2891. https://doi.org/10.3390/math12182891
APA StyleDai, W. (2024). Stochastic Differential Games and a Unified Forward–Backward Coupled Stochastic Partial Differential Equation with Lévy Jumps. Mathematics, 12(18), 2891. https://doi.org/10.3390/math12182891





