Design and Implementation of Digital PID Control for Mass-Damper Rectilinear Systems

Abstract

The mechanical systems were modeled using various combinations of mass-damper-spring elements to analyze the system dynamics and improve the system stability. Due to the marginal stability property of the mass-damper rectilinear system, a proper control law is required to control the mass position accurately, improve the relative stability, and enhance the dynamical response. In this paper, a mathematical model of the electromechanical system was first derived and analyzed. Next, a digital PID controller was developed based on the root locus technique, and a systematic design procedure is presented in detail. The proposed digital control system was simulated in MATLAB and compared with other control schemes to check their tracking performance and transient response characteristics. In addition, the digital PID control algorithm of the mass-damper rectilinear system was implemented via dSPACE platform to investigate the real-time control system performance and validate the control design methodology. It has been shown that the digital PID controller yields zero percentage overshoot, fast transient response, adequate stability margins, and zero steady-state error.

1. Introduction

Mass-damper-spring systems have been utilized in various engineering applications, such as robotics, high-rise buildings, and vehicle suspension systems [1,2]. Such mechanical systems are studied to provide reliable design, increase the safety factor, and attenuate the system vibration [3]. For instance, the stability of coupled impedance passive linear time-invariant (LTI) systems is presented in [4], where a tuned mass-damper (TMD) arrangement was utilized to stabilize the system. The electromagnetic regenerative and embedded anti-resonant TMD systems were also introduced in [2] and [5], respectively. Moreover, vibration control of high-rise structures with spring pendulum pounding TMD [6] and lateral displacement control of multistory structures via tuned liquid damper [7] have been discussed. Several passive control methods have been proposed to stabilize the mechanical system dynamics, but they require a large number of construction materials, which increase the implementation cost [8].

Other research works have focused on modeling, analysis, and design of vibration absorber (VA) systems. For instance, the load characteristics of multidimensional force sensors was analyzed in [9], where a spring-mass-damper model was derived. In [10], a model of electrochemical cell was developed using a spring-mass-damper arrangement, in which the mechanical analogy was used to predict the system dynamics. The design and implementation of embedded data acquisition systems of the VA motorcycle model is presented in [11]. Feedback-controlled VA systems have also been discussed in the literature. In [12], the design of a cubic-position negative-velocity (CPNV) feedback controller of VA model was introduced, while the third-order superharmonic resonance analysis of CPNV feedback-controlled VA systems is discussed in [13]. In addition, the balance harmonic method was utilized in [14] to analyze the steady-state response of a nonlinear-controlled mass-damper-spring model. Despite the rigorous analysis given in the previous research, the tracking performance of the closed-loop control schemes has not been investigated.

To enhance the dynamical response and improve the tracking performance of the mechanical systems, several active control approaches have been proposed. For instance, active mass-damper (AMD) control schemes based on adaptive control [3], boundary control [15], and linear quadratic regulator (LQR) with Kalman filter control [16] have been developed to suppress the vibration of high-rise buildings and long-period bridges. On the other hand, modern control techniques have been proposed in the literature to provide robust tracking performance. Such control methods include adaptive fuzzy fault-tolerant control [17,18], optimal adaptive fuzzy fault-tolerant control [19], adaptive fuzzy funnel control [20], decentralized adaptive control [21], adaptive-neural control [22], and switched adaptive control [23]. Other research works have introduced sliding-mode control (SMC) [8], adaptive-fuzzy SMC [1], adaptive SMC [24], and proportional-derivative SMC [25].

It is known that the SMC method has the simplest structure when compared to the other modern control techniques [26]. Moreover, it provides robustness against modeling uncertainties and large disturbances. However, the chattering phenomenon should be considered during the control law derivation to eliminate the noise and other relevant issues [27,28]. In [29,30,31,32], different control approaches have been presented, such as electrostatic force feedback control [29], dynamic event-triggered control [30], neural-network filtering control [31], event-triggered model predictive control (MPC) [32], and mixed sensitivity robust control [33]. The position control of the mass-damper-spring system was also studied in [34] using a servo-controlled linear actuator, in which the system model was derived using the Krylov–Bogoliubov averaging method. Alternatively, proportional-integral-derivative (PID) control schemes have been presented in [35,36,37]. The PID controllers are attractive control methods due to the design simplicity and controller effectiveness against modeling uncertainties.

Table 1. Comparison among various control techniques of dynamical systems.

Control Techniques	Advantages	Drawbacks	References
CPVN feedback control	- Suppress steady-state oscillations - Improve the transient response.	- Tracking performance has not been investigated.	[12,13]
Adaptive control, boundary control, and LQR with Kalman filter control	- Vibration control for AMD.	- Tracking performance has not been investigated.	[3,15,16]
Adaptive fuzzy fault-tolerant control, adaptive fuzzy funnel control, decentralized adaptive control, adaptive-neural control	- Robust tracking performance - Accommodation of faults and modeling uncertainties - Stability enhancement.	- The design is more complicated than the classical control methods. - Systematic design procedure is required.	[17,18,19,20,21,22,23]
SMC, adaptive-fuzzy SMC, adaptive SMC, PD SMC	- Simple control method - Robust tracking performance - Stability enhancement.	- Chattering phenomenon - Systematic design procedure is required.	[1,8,24,25]
PID, PID-R, and feedforward PID control	- Simple control method - Enhancement of stability and transient response.	- Large disturbances issue - Design procedure and experimental validation are required.	[35,36,37]

shows the main features of the relevant active control approaches of dynamical systems.

Although the previous control methods have provided an enhanced control performance with various dynamical systems, the control design for marginal stable mechanical systems, such as the mass-damper rectilinear systems, has not been discussed. The absence of the spring from the dynamical system model results in a slow transient response, high percentage overshoot, and low stability margins. Hence, the modeling, stability analysis, proper control design procedure, and control law implementation are required to characterize the system dynamics and validate the control design methodology. Considering the advancement of the digital control in modern industrial applications, the digital PID controller was proposed to improve the relative stability and tracking performance of such mechanical system. To the best of the authors’ knowledge, detailed design procedure and practical implementation of digitally controlled mass-damper rectilinear systems have not been presented in previous research endeavors.

Hence, this research aimed to design and implement a digital PID controller for a mass-damper (MD) rectilinear system based on the root locus technique. The main contributions of this research are summarized below:

• A mathematical model of an educational control product (ECP) MD rectilinear system was derived and analyzed. The stability and transient response characteristics of the open-loop electromechanical system were studied based on experimental setup integrated with a dSPACE system.
• A detailed design procedure of a digital PID controller was introduced to eliminate the steady-state error, improve the relative stability, and enhance the transient response of the electromechanical system. MATLAB simulations were provided to validate the design methodology.
• The digital PID controller of the electromechanical system was compared to other common control approaches such as the pole-placement technique and digital phase-lead controller to investigate their tracking performance and transient response characteristics.
• The practical implementation of the digital PID-controlled ECP MD rectilinear system using the dSPACE platform is presented to investigate the performance of the proposed digital controller and the dynamical system response in real-time.

The paper is organized as follows. The mathematical model of the ECP MD rectilinear system is given in Section 2. The digital control law is derived in Section 3. The simulation results and experimental validation are presented in Section 4 and Section 5, respectively. The conclusions are summarized in Section 6.

2. Modeling and Analysis of the Electromechanical System

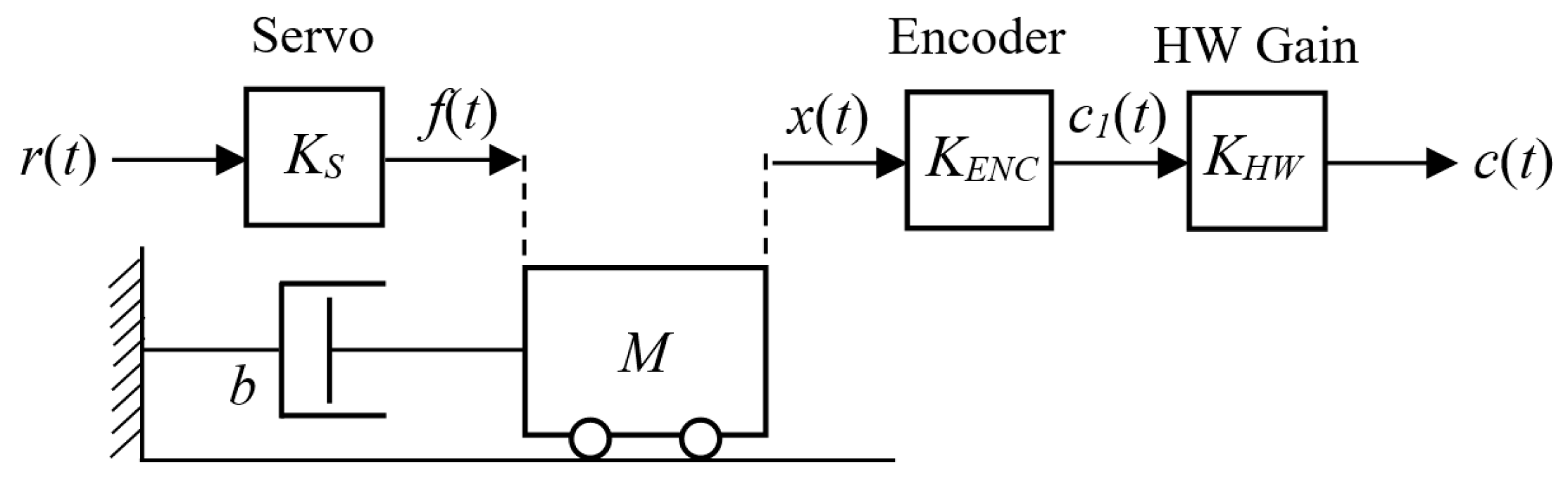
2.1. Mathematical Model of ECP MD Rectilinear System

The block diagram of the ECP MD rectilinear system is shown in Figure 1, which was implemented using the dSPACE platform at Wright State University laboratory. The system model consists of one mass carriage with mass weights connected to a damper. The lumped mass (kg) and the damper viscous friction coefficient (N/m/s) are defined as $M$ and $b$, respectively. The reference and output signals of the open-loop ECP rectilinear system are denoted as $r\left(t\right)$ and $c\left(t\right)$, respectively. The input force is defined as $f\left(t\right)$, while $x\left(t\right)$ is the displacement of the mass $M$.

The linear drive consisted of a gear rack suspended on an antifriction carriage and pinion coupled to a brushless servo shaft. An optical encoder that is defined by the gain $K_{ENC}$, measured the mass carriage position. A servo amplifier represented by the gain $K_s$ was used to drive the actuator. The hardware and software gain of the dSPACE system is defined as $K_{HW}$. The dSPACE system is the platform that is used to control the position of the ECP rectilinear system in real-time.

The relationship between the input force $f\left(t\right)$ and the output displacement $x\left(t\right)$ of the MD rectilinear system is driven by Newton’s second law

$$M\ddot{x}\left(t\right)+b\dot{x}\left(t\right)=f\left(t\right),$$

(1)

where $\ddot{x}\left(t\right)$ and $\dot{x}\left(t\right)$ are the linear acceleration and velocity, respectively. Taking Laplace transform for both sides of (1) gives

$$[M{s}^2+bs]X\left(s\right)=F\left(s\right),$$

(2)

Hence, the transfer function of the mechanical system yields

$${\displaystyle \frac{X\left(s\right)}{F\left(s\right)}}={\displaystyle \frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$M$}\right.}{s\left(s+\raisebox{1ex}{$b$}\!\left/ \!\raisebox{-1ex}{$M$}\right.\right)}}$$

(3)

which represents the relationship between the displacement and the input force.

To obtain the mathematical model of the entire open-loop ECP MD rectilinear system, it is required to combine the equations of both mechanical and electrical subsystems. According to Figure 1, we have

$$F\left(s\right)=K_{s}R\left(s\right)$$

(4)

and

$$X\left(s\right)={\displaystyle \frac{C\left(s\right)}{K_{ENC}{K}_{HW}}}$$

(5)

Substituting (4) and (5) into (3) gives the mathematical model of the ECP MD rectilinear system, which defines the relationship between the output and reference signals

$${\displaystyle \frac{C\left(s\right)}{R\left(s\right)}}={\displaystyle \frac{\raisebox{1ex}{$K_s{K}_{ENC}{K}_{HW}$}\!\left/ \!\raisebox{-1ex}{$M$}\right.}{s\left(s+\raisebox{1ex}{$b$}\!\left/ \!\raisebox{-1ex}{$M$}\right.\right)}}={\displaystyle \frac{K}{s\left(s+\raisebox{1ex}{$b$}\!\left/ \!\raisebox{-1ex}{$M$}\right.\right)}}$$

(6)

where $K$ is the steady-state gain of the system.

The parameters of the ECP rectilinear system were identified experimentally using second-order step response tests and dSPACE system manual.

Table 2. Parameters of ECP rectilinear system.

Description	Parameter	Value
Carriage and brass weights mass	$M$	2.77 kg
Viscous friction coefficient	$b$	15.235 N/m/s
Steady-state gain	$K$	140

shows the key parameters of the practical ECP rectilinear system. Hence, the transfer function in (6) can be evaluated, yielding

$${\displaystyle \frac{C\left(s\right)}{R\left(s\right)}}={\displaystyle \frac{140}{s\left(s+5.5\right)}}$$

(7)

2.2. Analysis of Open-Loop Rectilinear System

In order to design a digital controller for the ECP MD rectilinear system, the open-loop transfer-function should be analyzed in z-domain. Using MATLAB, the continuous transfer function in (7) can be transformed into a discrete transfer function using zero-order hold with a sampling time $T_s=0.01$s, which gives

$$G_p\left(z\right)=0.0068734{\displaystyle \frac{z+0.9818}{(z-1)(z-0.9465)}}$$

(8)

where $G_p\left(z\right)$ is the discrete rectilinear system model. It contains one zero at $z=-0.9818$ and two poles at $z=1$ and $z=0.9465$. It should be noted that the sampling time $T_s$ was selected based on the closed-loop system bandwidth ${\omega }_b$, where $T_s\le {\displaystyle \frac{2\pi }{10{\omega }_b}}$ [38]. For the given dynamical system, the system bandwidth was about 29 rad/s, thus the sampling time was set to 0.01 s.

The step response of the discrete closed-loop transfer function with unity feedback is shown in Figure 2. It can be seen that the transient response exhibited 52.2% maximum percentage overshoot and 1.64 s settling time. Although the steady-state response settled at 1, the transient response characteristics were not desirable due to the high percentage overshoot and long settling time. Hence, the transient response should be enhanced using a proper digital control law.

The Bode plot of the discrete uncompensated loop transfer function of the electromechanical system is given in Figure 3. Although the frequency response shows that the discrete plant model had an 18 dB gain margin at 33 rad/s phase crossover frequency, it also exhibited a low phase margin of 22.9° at the gain crossover frequency of 11.2 rad/s. Therefore, a suitable digital compensator is required to enhance the frequency response and the relative stability of the ECP MD rectilinear system.

The root locus of the discrete plant is also depicted in Figure 4. Obviously, due to the pole located at the unity circle, the dynamical system is considered marginally stable. Nevertheless, the dynamical response and relative stability of the system can be improved by adding a digital PID compensator to the plant, which can shift the root locus to the left, inside the unity circle.

3. Digital PID Control Design

Based on the dynamical system analysis presented in the previous section, it was shown that the discrete uncompensated rectilinear system exhibited high percentage overshoot, long settling time, and low phase margin. Hence, a digital PID controller should be designed to achieve the following specifications:

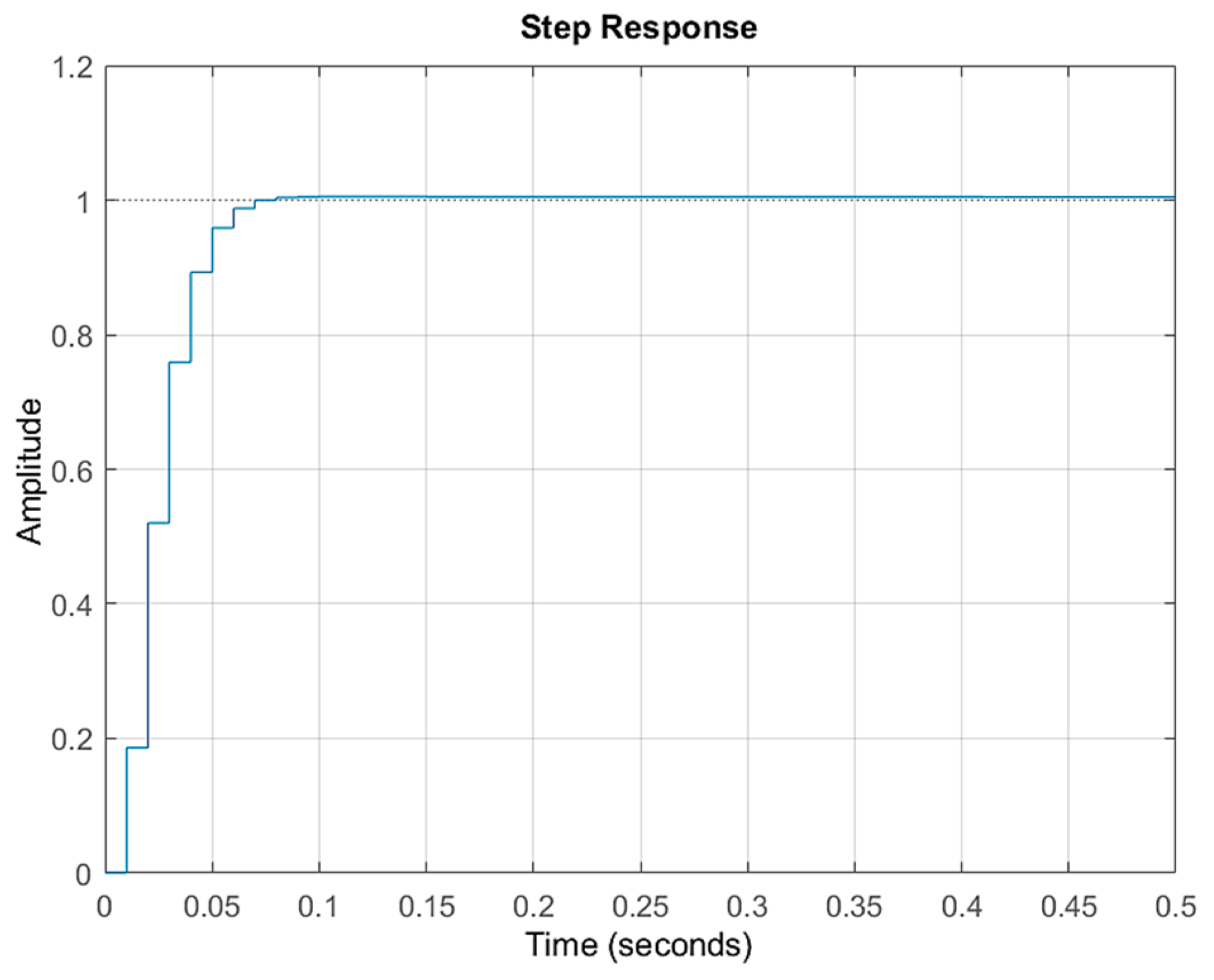
• Percentage overshoot PO ≤ 5%
• Settling time $t_s$ ≤ 1 s
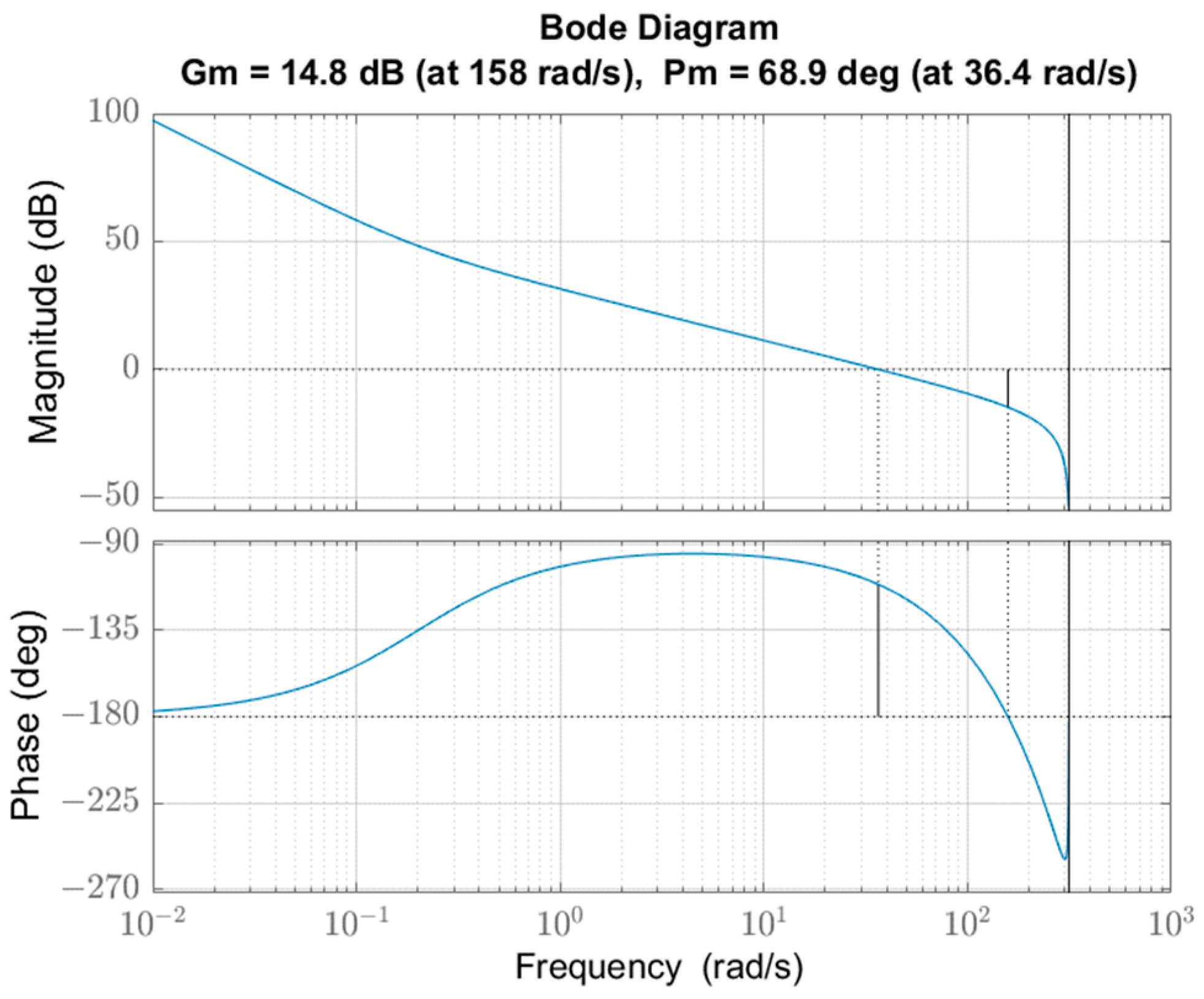
• Phase margin PM ≥ 65$°$.
• Zero steady-state error.

The transfer function of the proposed digital PID controller can be expressed in the following form [38]

$$D(z)={\displaystyle \frac{\left(\frac{K_I{T}_s}{2}+\frac{K_D}{T_s}+K_P\right)z^2+\left(\frac{K_I{T}_s}{2}-\frac{2K_D}{T_s}-K_P\right)z+\frac{K_D}{T_s}}{z\left(z-1\right)}}$$

(9)

where $K_P$, $K_I$, and $K_D$ are the proportional, integral, and derivative gains of the digital PID controller. Figure 5 shows the block diagram of the closed-loop digital PID control system. A/D and D/A blocks refer to the analog-to-digital converter (sampler) and digital-to-analog converter (data hold), respectively. D(z) block is the digital PID controller transfer function defined in (9), while $G_p\left(s\right)$ block represents the continuous plant transfer function given in (7). The position sensor is defined by H(s) block.

The design procedure of the proposed digital controller D(z) can be summarized as follows:

• Set one of the digital PID controller zeros to cancel out the significant pole of the discretized plant, while the other zero is placed close to the unity circle;
• Equate the two digital controller zeros obtained in step 1 with the corresponding controller zeros given in (9);
• Choose the damping ratio $\zeta$ and damped frequency ${\omega }_d$ that satisfy the desired transient response;
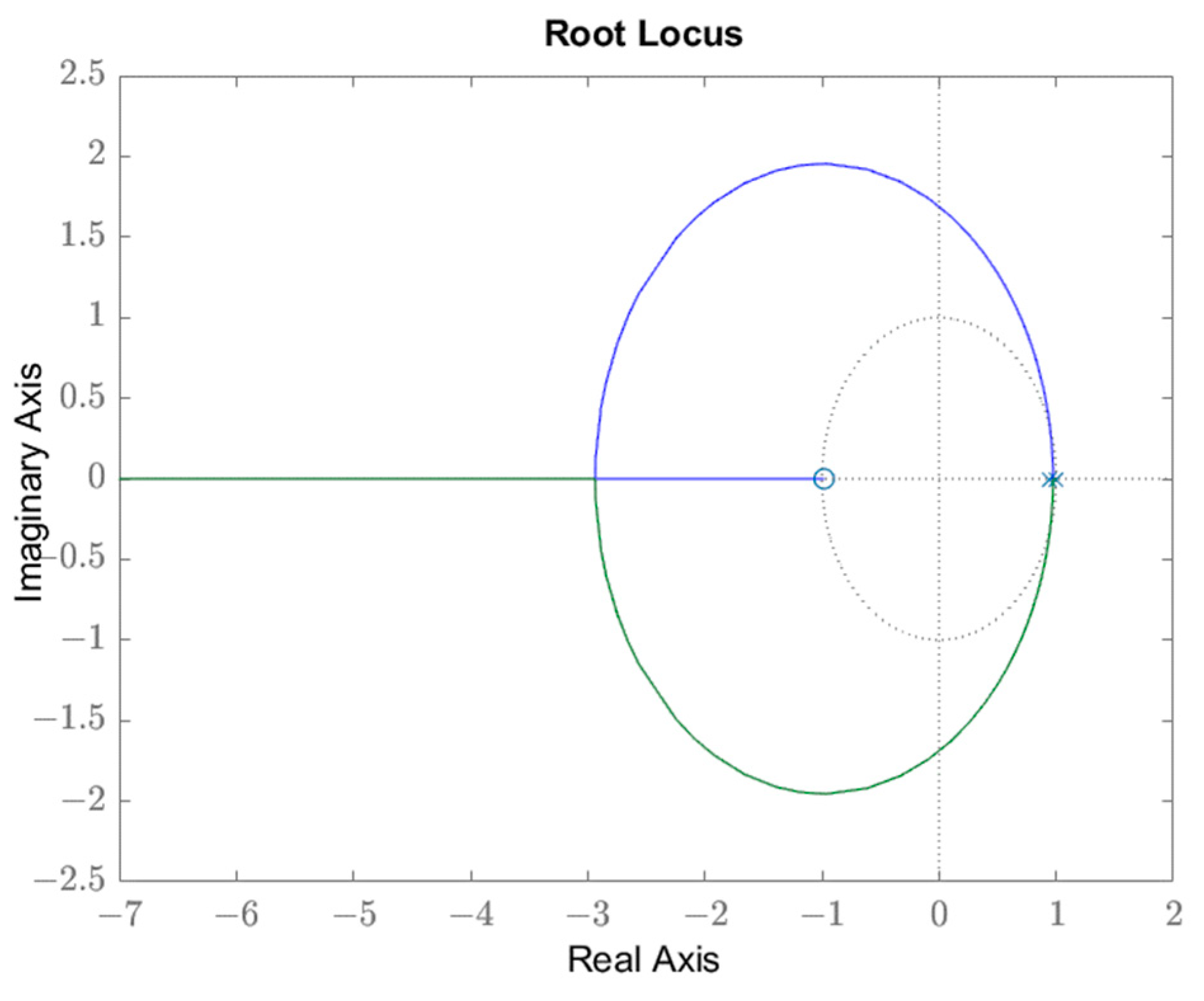
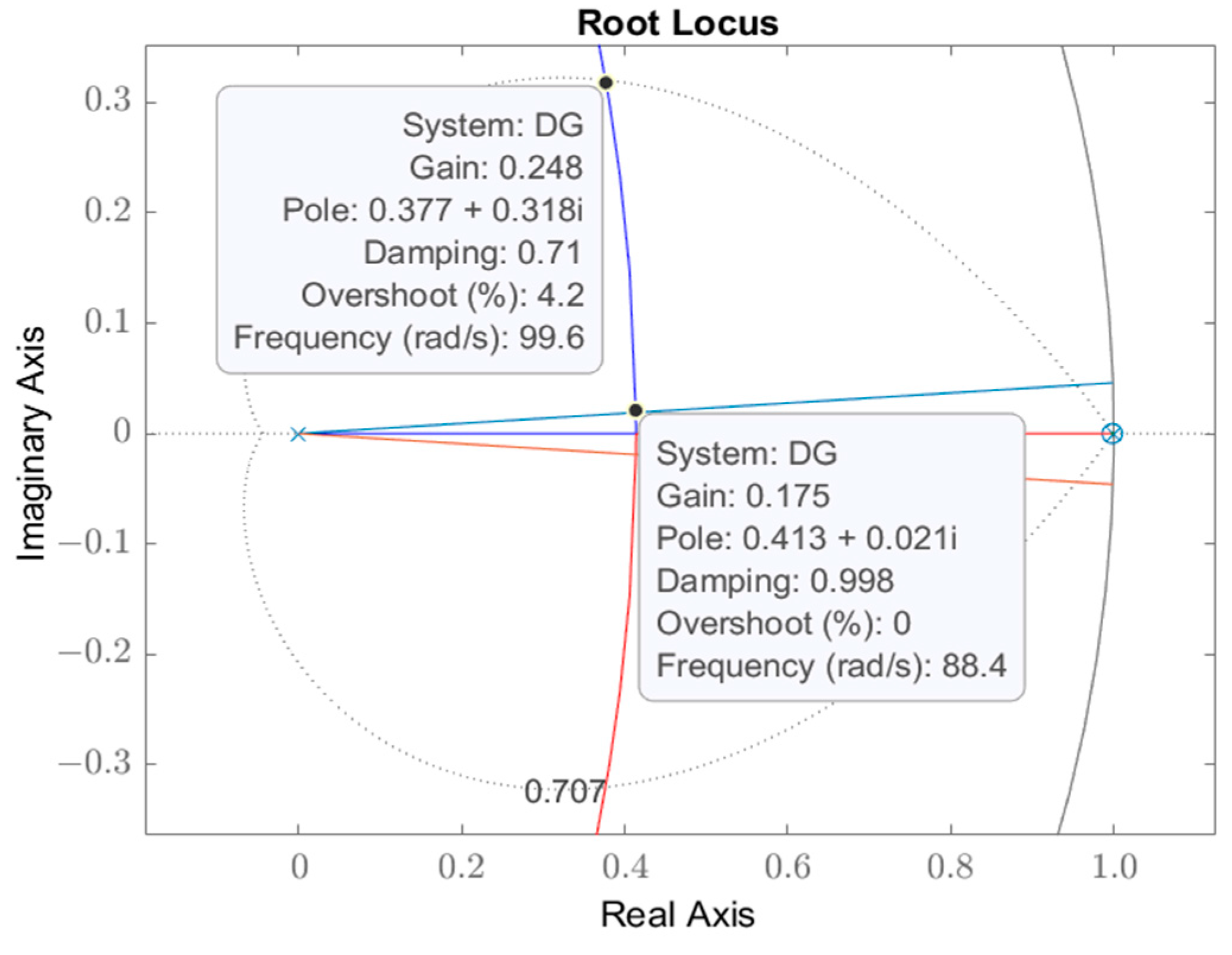
• Plot the root locus of the loop transfer function of the digital compensated system along with $\zeta$ and ${\omega }_d$ lines;
• Determine the range of the controller gain that achieves the desired transient response on the root locus;
• Set the linear system equations to solve for the controller gains $K_P$, $K_I$, and $K_D$;
• Check the time and frequency responses of the digital compensated system to see if the desired specifications are met.

Based on the design procedure given above, the digital PID controller zeros were set to $\left(z-0.9465\right)$ and $\left(z-0.998\right)$, which were equivalent to the digital controller zeros given in (9). In other words,

$$z^2+{\displaystyle \frac{\left(K_I{T}_s^2-2K_P{T}_s-4K_D\right)}{\left(K_I{T}_s^2+2K_P{T}_s+2K_D\right)}}z+{\displaystyle \frac{2K_D}{\left(K_I{T}_s^2+2K_P{T}_s+2K_D\right)}}=z^2-1.9445z+0.9446$$

(10)

where the right-hand side of (10) is the product of the selected zeros of the digital controller. Based on (10), the following set of equations can be obtained

$${\displaystyle \frac{\left(K_I{T}_s^2-2K_P{T}_s-4K_D\right)}{\left(K_I{T}_s^2+2K_P{T}_s+2K_D\right)}}=-1.9445$$

(11)

$${\displaystyle \frac{2K_D}{\left(K_I{T}_s^2+2K_P{T}_s+2K_D\right)}}=0.9446$$

(12)

On the other hand, the loop transfer function of the digital PID-compensated system is expressed as follows

$$D(z)G_p\left(z\right)=\widehat{K}{\displaystyle \frac{\left(z-0.998\right)\left(z+0.9818\right)}{z{\left(z-1\right)}^2}}$$

(13)

where the gain $\widehat{K}$ is defined by

$$\widehat{K}=0.0068734\left({\displaystyle \frac{K_I{T}_s}{2}}+{\displaystyle \frac{K_D}{T_s}}+K_P\right)$$

(14)

Next, $\zeta$ and ${\omega }_d$ should be determined to compute the gain $\widehat{K}$ achieve the desired response. For the damping ratio $\zeta$ ≥ 0.707, the percentage overshoot is about PO ≤ 5%. Additionally, the relationship among the settling time $t_s$, damping ratio $\zeta$, and undamped frequency ${\omega }_n$ can be written as

$$t_s={\displaystyle \frac{4.6}{\zeta {\omega }_n}}$$

(15)

Since the desired $t_s$ ≤ 1 s and $\zeta =$ 0.707, the desired ${\omega }_n$ should be ≥6.5 rad/s. If ${\omega }_n$ is set to 6.5 rad/s, the desired damped frequency ${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}=4.6$ rad/s.

The root locus of the digital compensated system along with $\zeta$ and ${\omega }_d$ lines is depicted in Figure 6. It can be noticed that the root locus is shifted to the left inside the unit circle due to the effect of the poles and zeros of the digital PID controller.

The root locus inside the unity circle yields a stable operation. However, the desirable range of the gain $\widehat{K}$ spans between $\zeta$ and ${\omega }_d$ lines, where $\widehat{K}$ is the gain required to achieve the desired transient response. As shown in the enlarged view of the root locus given in Figure 7, the range of the gain is $0.175\le \widehat{K}\le 0.248$. Thus, to achieve the desired dynamical response, the gain $\widehat{K}$ can be set to 0.186.

Rearranging (11), (12), and (14) with $T_s=0.01$s and $\widehat{K}=0.186$, the following set of linear equations can be written in matrix form

$$\left[\begin{array}{ccc}0.0050& 1.0000& 100.00\\ 0.0003& 0.0189& -0.1110\\ 0.0001& 0.0189& -0.1108\end{array}\right]\left[\begin{array}{c}{K}_I\\ K_P\\ K_D\end{array}\right]=\left[\begin{array}{c}27.06\\ 0\\ 0\end{array}\right]$$

(16)

Based on (16), one can solve for the digital PID controller gains, thus $K_I$, $K_P$, and $K_D$ become 0.2895, 1.4975, and 0.2556, respectively. Therefore, the transfer function of the digital PID controller yields

$$D(z)=27.06{\displaystyle \frac{\left(z-0.998\right)\left(z-0.9465\right)}{z\left(z-1\right)}}$$

(17)

and the loop transfer function of the digital compensated system is

$$D(z)G_p\left(z\right)=0.18599{\displaystyle \frac{\left(z-0.998\right)\left(z+0.9818\right)}{z{\left(z-1\right)}^2}}$$

(18)

Moreover, the closed-loop transfer function of the digital compensated system is defined by

$${\displaystyle \frac{C\left(z\right)}{R\left(z\right)}}={\displaystyle \frac{0.816z^2-0.003013z+0.1822}{z^3-2z^2+z}}$$

(19)

Figure 8 and Figure 9 show the Bode plot and step response of the digital PID-controlled ECP MD rectilinear system, respectively. As shown in Figure 8, the phase margin of the compensated system became 68.9$°$ with a gain crossover frequency of 36.4 rad/s. In contrast, the phase margin and gain crossover frequency of the uncompensated system shown in Figure 3 were 22.9$°$ and 11.2 rad/s, respectively. Hence, it can be noticed that the relative stability of the ECP MD rectilinear system has been improved.

Furthermore, the step response of the digital PID-compensated system given in Figure 9 shows that the percentage overshoot and settling time were about 0.55% and 57 ms, respectively. However, the corresponding transient response characteristics of the uncompensated system presented in Figure 2 were 52.2% and 1.64 s, respectively. Hence, it can be seen that the digital PID controller reduced the percentage overshoot and shortened the settling time of the dynamical system response significantly.

4. Simulation Results and Discussion

In this section, the MATLAB simulation results of the digital PID-controlled ECP MD rectilinear system are presented to analyze the control performance. The tracking performance, the effect of gain $\widehat{K}$ on the transient response, and the comparison of the proposed digital controller with common control methods are discussed.

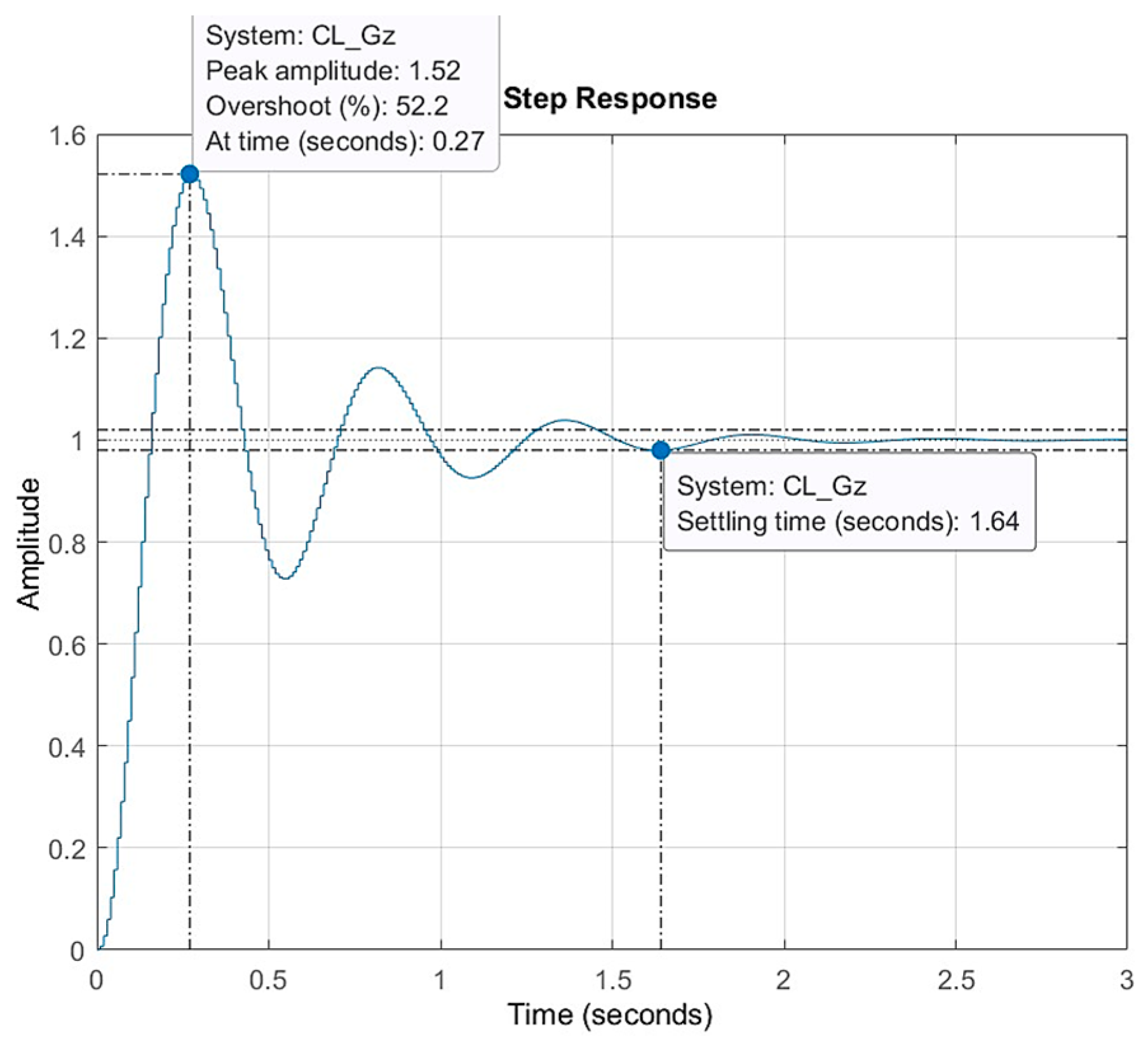
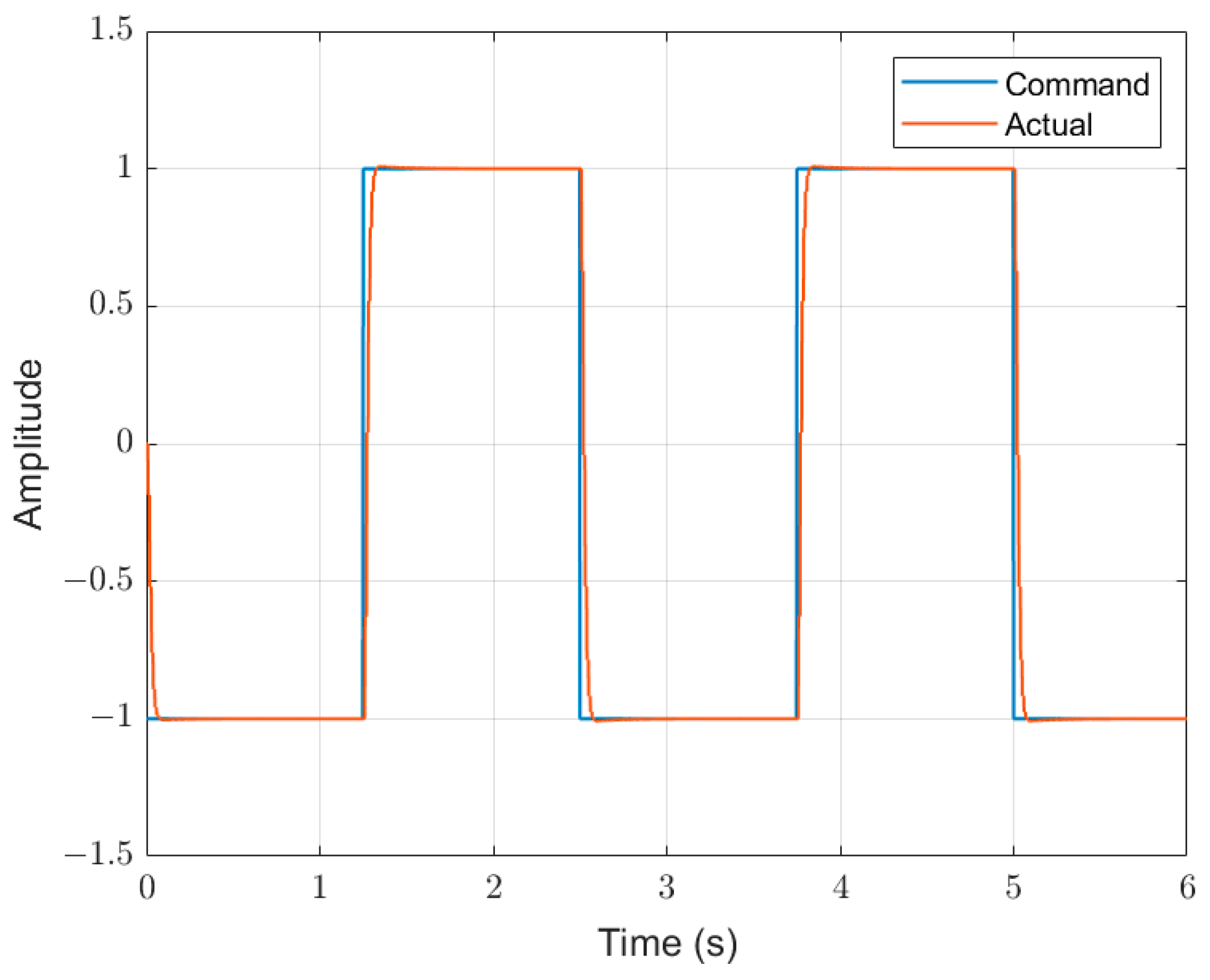
4.1. Tracking Performance

The MATLAB/SIMULINK model of the digital PID-controlled ECP MD rectilinear system is shown in Figure 10. The discrete system model $G_p\left(z\right)$ is described by the position transfer function of the electromechanical system. The digital PID controller is denoted as $D\left(z\right)$.

The tracking performance of the digital PID-controlled system was investigated and a square wave command signal with a 0.4 Hz frequency was applied to the digital closed-loop control system shown in Figure 9. The sampling time was set to 0.01 s, and an automatic solver with a 0.001 fixed step-size was selected. The simulated dynamical system response is shown in Figure 11. It can be observed that the proposed digital control system tracked the command signal and achieved the desired dynamical response specifications, which were 0.55% percentage peak overshoot, 57 ms settling time (1% criterion), and zero steady-state error. The simulation result indicated that the position response of the electromechanical system followed the command signal, which is shown later in the Experimental Validation section.

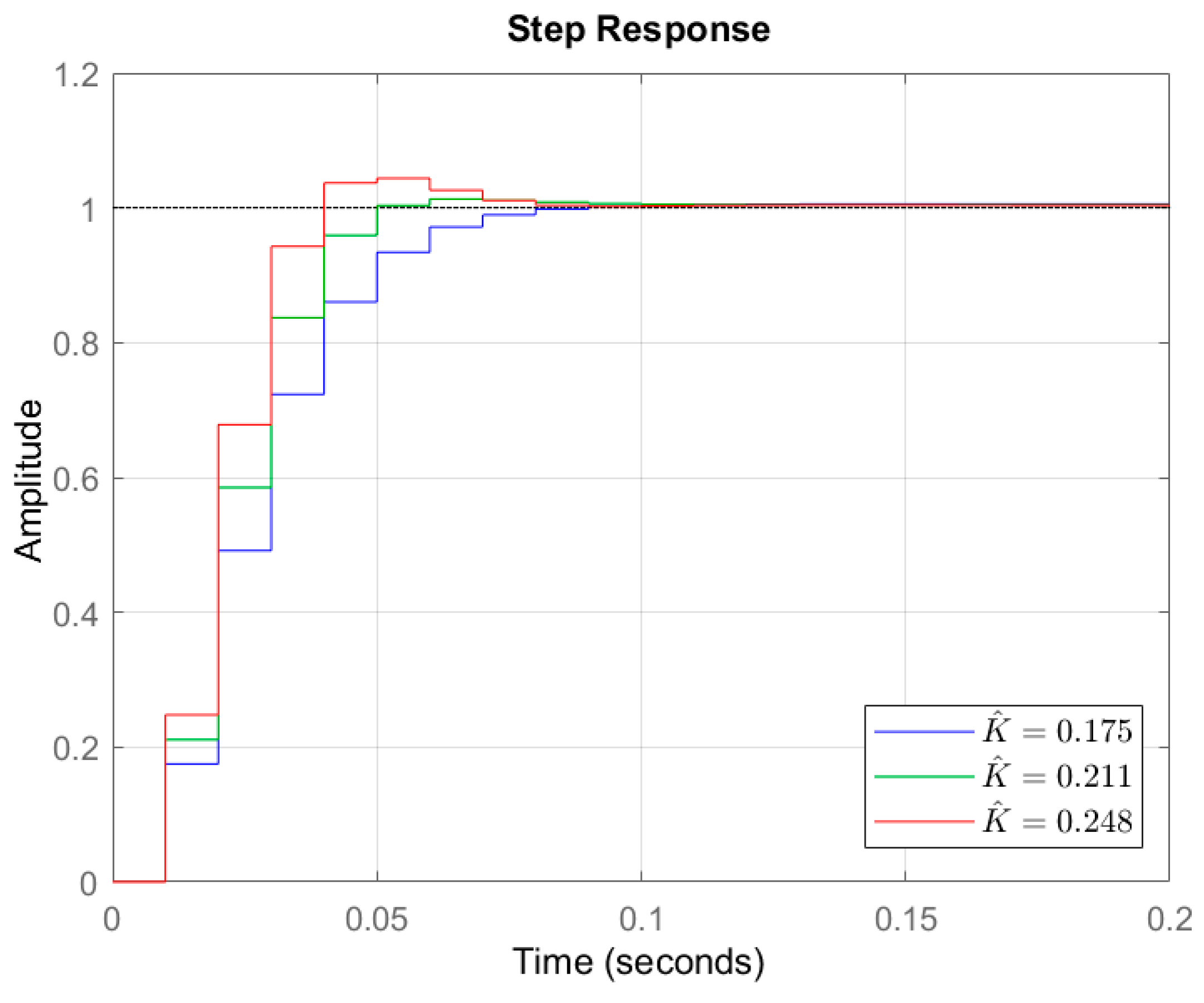
4.2. Effect of Gain Selection on Control Performance

The effect of the controller gain $\widehat{K}$ on the transient response of the digital PID-controlled system was studied. Figure 12 shows the step response of the digital compensated system when the gain values were set to 0.175, 0.211, and 0.248. The summary of the transient response characteristics with respect to $\widehat{K}$ value is given in

Table 3. Transient response characteristics with respect to the gain $\widehat{K}$.

$\mathbf{Gain}\widehat{\mathit{K}}$	Percentage Overshoot (%)	Settling Time (ms)	Rising Time (ms)
0.248	4.39	64	24
0.211	1.31	45	30
0.175	0.56	65	40

. It can be noticed that when $\widehat{K}$ increased, the rising time decreased, while the percentage overshoot increased.

Remarks

• The digital PID controller gains are given in (14), which are represented by $K_P$, $K_I$, and $K_D$. The gain $\widehat{K}$, on the other hand, is defined by the product of the plant dc gain $0.0068734$ and the term $\left({\displaystyle \frac{K_I{T}_s}{2}}+{\displaystyle \frac{K_D}{T_s}}+K_P\right)$. Since the sampling time and the plant dc gain are known, one can easily select the parameter $\widehat{K}$ on the root locus rather than adjusting the PID controller gains to achieve the desired transient response. This feature can simplify the digital control parameter selection.
• A suitable $\widehat{K}$ value can be selected within the range $0.175\le \widehat{K}\le 0.248$, was determined based on the desired dynamical response. As illustrated in Figure 6, the damping ratio $\zeta$ and damped frequency ${\omega }_d$ lines on the root locus define the range of $\widehat{K}$. For the proposed digital PID-controlled electromechanical system, $\widehat{K}$ was set to 0.186 to obtain the minimum percentage overshoot and the shortest settling time.

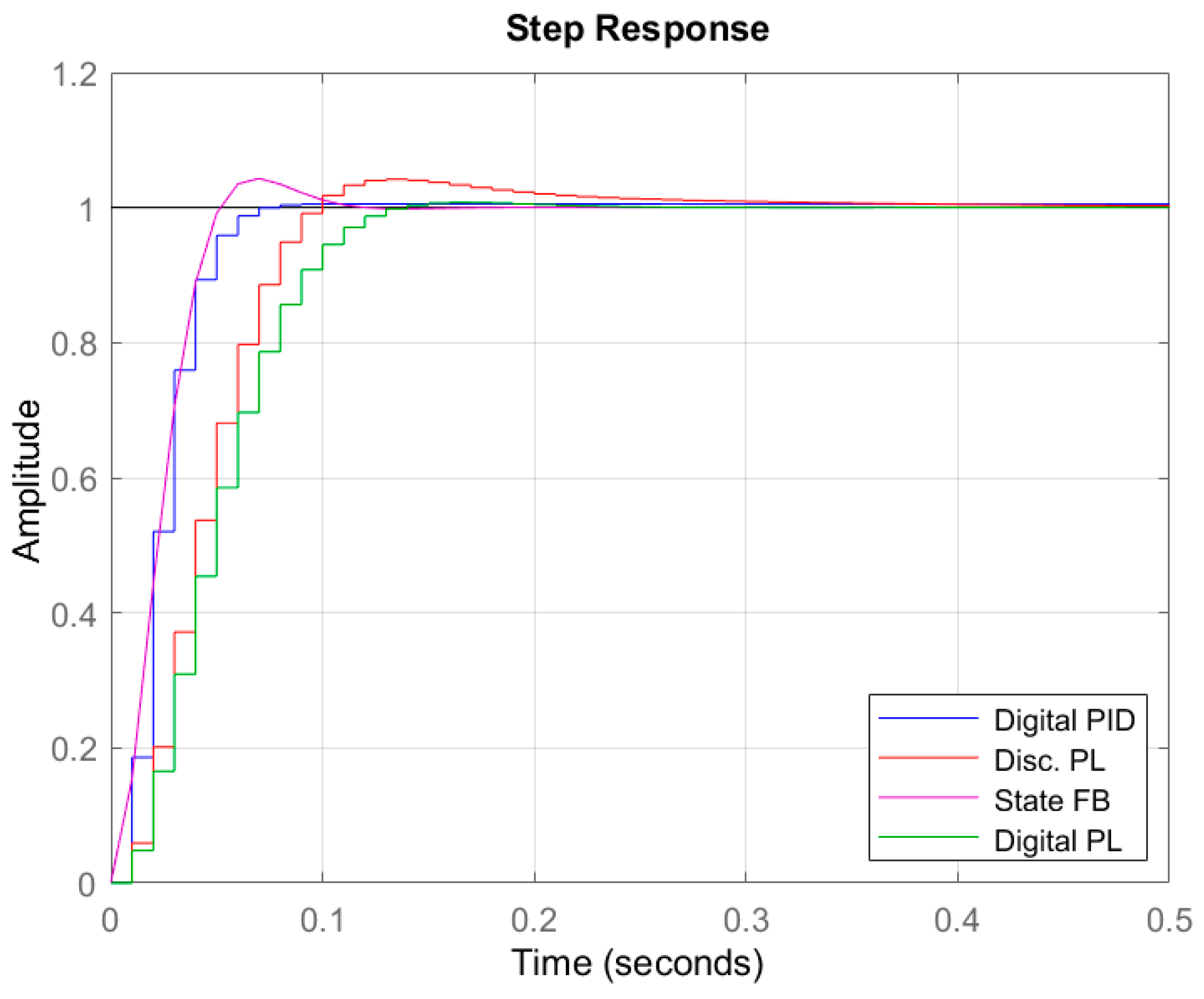
4.3. Comparison with Other Control Schemes

The digital PID controller $D\left(z\right)$ defined in (17) was compared to state-feedback, discretized phase-lead, and digital phase-lead controllers using MATLAB simulations to analyze their control performance. In order to perform a fair comparison, all the controllers were designed to achieve the same desired specifications defined in Section 3.

The state feedback control law was derived based on the design approach in [38]. The state-space model of the ECP MD rectilinear system can be written as

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& -5.5\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ 140\end{array}\right]u$$

(20)

$$\left[\begin{array}{c}{y}_1\\ y_2\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right]u$$

(21)

where $x_1$ and $x_2$ represent the states of the dynamical system. The system outputs $y_1$ and $y_2$ represent the position and velocity measurements, respectively. The state-feedback control input $u$ was designed using the pole-placement technique [38], which places the closed-loop poles ${\lambda }_1$ and ${\lambda }_2$ at the desired location in the s-plane, yielding

$$\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\end{array}\right]=\left[\begin{array}{c}-45.9550+45.9689\mathrm{i}\\ -45.9550-45.9689\mathrm{i}\end{array}\right]$$

(22)

Thus, the state-feedback controller gains $K_1$ and $K_2$ were set to 30.1786 and 0.6172, respectively, and the control law becomes

$$u=-30.1786x_1-0.6172x_2.$$

(23)

The discretized phase-lead controller, on the other hand, was developed in two steps [38]. First, a continuous phase-lead controller $P\left(s\right)$ was designed to achieve a phase margin of $70°$, which yields

$$P\left(s\right)=11.397{\displaystyle \frac{s+6.369}{s+72.58}}$$

(24)

Next, the continuous controller in (24) was converted to a discretized phase-lead controller $P\left(z\right)$ at sampling time $T_s=0.01$s using the Tustin method, thus

$$P\left(z\right)=8.6285{\displaystyle \frac{z-0.9383}{z-0.4674}}$$

(25)

The third control method tested in the comparison was the digital phase-lead controller $Q\left(z\right)$, which was designed based on the root locus technique [38] to achieve the desired specifications. The transfer function of the digital phase-lead controller is

$$Q\left(z\right)=7.0094{\displaystyle \frac{z-0.9465}{z-0.5}}$$

(26)

The step response of the three control schemes of the ECP MD rectilinear system is depicted in Figure 13, while the transient response characteristics are summarized in

Table 4. Comparison of digital PID, discretized phase-lead, state-feedback, and digital phase-lead control methods.

Controller Type	Percentage Overshoot (%)	Settling Time (ms)	Rising Time (ms)
Discretized Phase-Lead	4.18	200	59
State-Feedback	4.30	92	35
Digital Phase-Lead	0.75	116	74
Digital PID	0.55	57	36

. It can be noticed that all the control methods achieved the desired specifications. However, the fastest dynamical response and the lowest percentage overshoot were produced by the proposed digital PID controller, where the settling time and percentage overshoot were 57 ms and 0.55%, respectively. In contrast, the state-feedback controller exhibited the highest percentage overshoot among other control schemes, which was 4.3%. The longest settling time was 200 ms, which was presented by the discretized phase-lead controller response $P\left(z\right)$.

Notably, the proposed digital PID controller exhibited the shortest settling time and the lowest percentage overshoot, which were the optimal transient response characteristics among the others. In addition, the digital PID control method only required the position measurement as a feedback signal. However, the state-feedback control law requires two feedback signals, which are the position and velocity measurements. Adding a velocity sensor to the rectilinear system increased the complexity and implementation cost of the digital controller. Thus, despite the excellent performance of the state-feedback control technique, it was more complicated with a higher cost for the control system when compared to the proposed digital PID controller.

5. Experimental Validation

The dSPACE platform structure, practical implementation, and experimental validation of the proposed digital PID-controlled ECP electromechanical system are presented in this section.

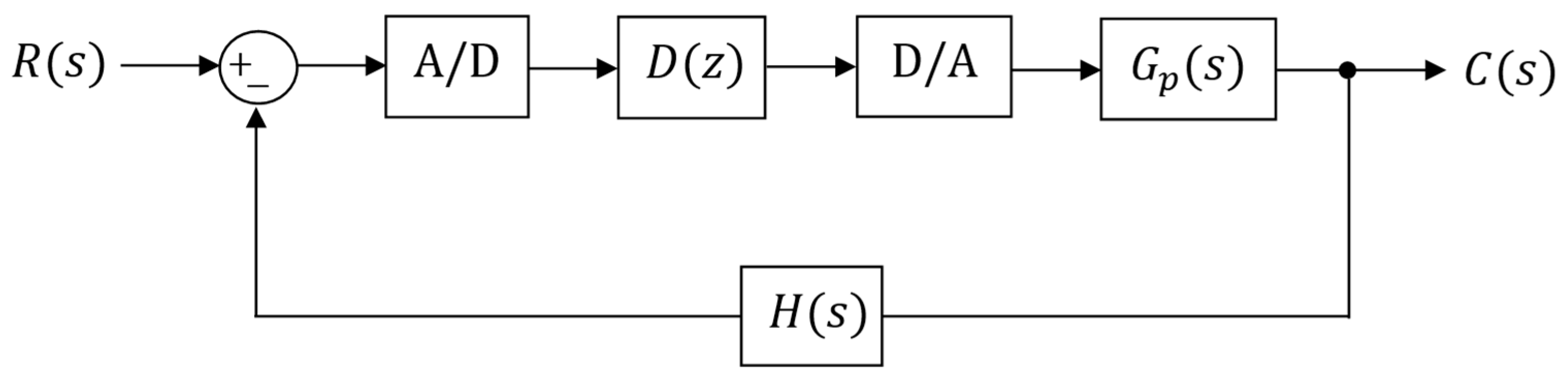
5.1. Structure of the dSPACE Platform

The dSPACE release 2018-A at Wright State University laboratory was utilized to implement the proposed digital PID controller of the ECP MD rectilinear system in real-time. The structure of the dSPACE-based digital control system is depicted in Figure 14. The digital control system included the ECP MD rectilinear system, dSPACE I/O board, dSPACE controller board, and a personal computer.

As shown in Figure 14, the actual ECP MD rectilinear system contained the mass and damper elements. The overall weight of the mass carriage and the brass blocks was 2.77 kg. The mass carriage suspension provided a 3 cm range of bidirectional movement. The linear drive was made up of a gear rack suspended on an antifriction carriage and pinion (pitch diameter of 7.62 cm). The optical encoder measured the mass carriage position via a rack and pinion with a diameter of 3.18 cm. The resolution of the optical encoder was 16,000 count per revolution.

The dSPACE I/O board represents a connector panel that performs analog-to-digital (A/D) and digital-to-analog (D/A) conversions between the ECP MD rectilinear system and the digital controller. The connector panel provides an access to all input and output signals of the dSPACE controller. The dSPACE electronic control unit (ECU), on the other hand, performs the digital control process and provides the required actuating input voltage to the servo motor. The dSPACE controller board receives the feedback signal and transmits the control signal through the dSPACE I/O board. It also contains the necessary power electronics that drive the actuator of the ECP MD rectilinear system.

The personal computer (PC) contains the digital PID control algorithm on MATLAB R2018a to be uploaded to the dSPACE controller board. On this computer, the real-time interface (RTI) platform DS1104 was installed, which included RTI-relevant MATLAB Toolboxes and SIMULINK Blocksets. The ControlDesk 6.3 was also installed on this computer, by which a control panel layout was designed to serve as a graphical user interface.

5.2. Digital Control Algorithm

The digital control algorithm of the ECP rectilinear system was constructed on SIMULINK using dSPACE RTI1104 library as depicted in Figure 15. The ADC and DAC blocks are associated with ADC Channel 5 and DAC Channel 1 of the dSPACE I/O board. ADC Channel 5 was supplied with 10 VDC, while DAC Channel 1 was connected to the dSPACE controller board. The block DS1104ADC_C5 resets the encoder position and sends the command signal through the Encoder Resent gain and On/Off gain, respectively.

The Encoder Position block sends the encoder measurement via hardware adjustment gain (HW Adj Gain) that calibrates the position signal by ${\displaystyle \frac{20}{1604.1\times 7.06}}$. A scaling factor of 0.1 was included at the Output Gain to maintain the desired mass carriage displacement at 1.0 cm. The digital PID controller that was designed in Section 3 was added to the SIMULINK model using the Discrete Transfer Function block. The sampling time of the Zero-Order Hold block was set to 0.01 s.

Since the ECP MD rectilinear system model was an approximation of the actual system dynamics, the ratio of the gain $\widehat{K}$ to the plant dc gain was adjusted to 25.61 to reduce the percentage overshoot. It should be noted that the default value of the Encoder Reset gain and On/Off gain was zero, while the default value of the Closed-Loop gain was 1. In addition, the Model Configuration Parameters in MATLAB were set as follows:

• Start time: 0.0;
• Stop time: inf;
• Type: Fixed Step;
• Solver: ode1 (Euler);
• Periodic sample time constraint: Unconstrained;
• Fixed-step size: 0.01 (Same as the Zero-Order Hold Sample Time).

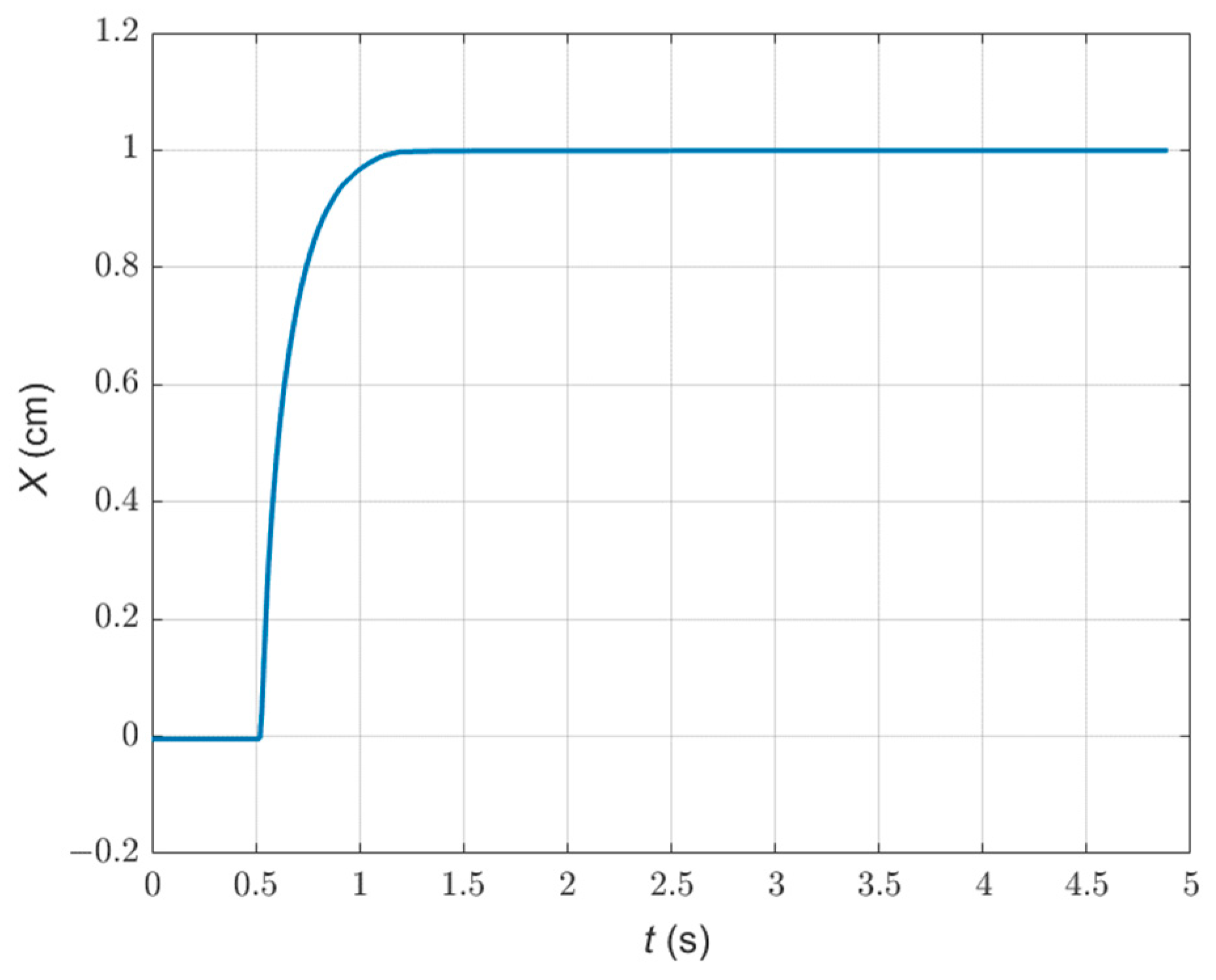
5.3. Experimental Results

The ControlDesk layout was utilized to control the position of the ECP MD rectilinear system and display the control system measurements, such as the mass carriage displacement and control effort. ControlDesk 6.3 was installed on a PC, which facilitated the design of a control panel layout that served as a graphical user interface (GUI). On the ControlDesk layout, virtual instruments that included a plotter, check buttons, a push button, and a numerical input were utilized to allow the user to operate the digital control system and adjust the control parameters in real-time. The virtual instruments were assigned based on the SIMULINK model parameters as shown in

Table 5. Virtual instruments assignment on the ControlDesk layout.

Virtual Instrument	Assigned Variable on SIMULINK
Plotter	HW Adj Gain1
Check Button 1	On/Off Gain
Check Button 2	Closed-Loop Gain
Push Button	Encoder Reset Gain
Numerical Input	Output Gain

.

To run the digital PID-controlled ECP rectilinear system using the ControlDesk layout, the following steps were performed:

• The SIMULINK model parameters were uploaded to the virtual instruments on the ControlDesk layout;
• The mass carriage was set at 0 cm and 10 V of input voltage was applied to the ADC_5 channel on the dSPACE I/O board;
• The dSPACE ECU was connected to the DAC_1 channel on the dSPACE I/O board, and the ECU switch was turned ON;
• The Start Measuring button on the ControlDesk layout was selected to activate the Plotter;
• The On/Off Check button on ControlDesk layout was pressed to apply a unit step command input (i.e., 1 cm) to the ECP rectilinear system.
• The Stop Measuring button was selected once a complete step response was displayed on the Plotter.

The real-time step response of the ECP MD rectilinear system is depicted in Figure 16. It was noticed that the percentage overshoot was approximately 0% and the settling time was about 600 ms. Obviously, a step response with no overshoot indicated that the phase margin of the digital PID-compensated system was greater than $65°$. Hence, the dSPACE-based digital PID-controlled ECP MD rectilinear system satisfied the desired requirements (PO ≤ 5%, $t_s$ ≤ 1 s, and PM ≥ 65°).

The actual position response was plotted in MATLAB as shown in Figure 17. It can be seen that the steady-state value of the actual position response was 1.0 cm. The experimental result indicated that the digital PID control system tracked the command signal precisely and achieved the desired specifications. However, it can be observed that the actual response of the digital closed-loop control system was slower than the simulated response, where the settling time of the actual and simulated response was 600 ms and 57 ms, respectively. The discrepancy between the experimental and simulated settling time was due to the nonlinearities and modeling uncertainties of the electromechanical system, which have not been included in the plant model. Nevertheless, the characteristics of the real-time system response remained within the desired specifications.

6. Conclusions

The digital PID control system design and implementation of the ECP mass-damper rectilinear system based on the root locus technique was introduced. The open-loop electromechanical system model was analyzed, and the digital compensator was developed to achieve the desired specifications. It has been shown that the percentage overshoot, settling time, and phase margin of the digital compensated system were improved significantly as compared to the uncompensated rectilinear system. The effect of the digital PID control parameter $\widehat{K}$ was also studied. It was noticed that the desired transient response can be achieved if the gain $\widehat{K}$ was selected within the allowable range on the root locus, which can be determined based on the desired damped frequency and damping ratio. Furthermore, the proposed digital controller performance was compared with the discretized phase-lead, digital phase-lead, and state-feedback controllers using the MATLAB simulation. It was seen that the proposed digital PID controller exhibited the shortest settling time, minimum percentage overshoot, and enhanced stability margins.

In addition, the real-time performance of the digital PID-controlled ECP MD rectilinear system was investigated using the dSPACE platform. The experimental result showed that the digital PID compensator controlled the position of the mass-damper rectilinear system precisely and enhanced the dynamical system response. It was shown that the experimental position response of the digital PID-controlled ECP MD rectilinear system exhibited zero percentage overshoot, zero steady-state error, and 600 ms settling time. The digital PID compensator had the simplest structure compared to the advanced and modern control methods, which resulted in a cost-effective digital control scheme for electromechanical systems. The research topic will be extended in the future to cover the design aspects, practical implementation, and performance investigation of digital PID-controlled ECP MD rectilinear systems using a low-cost digital signal processor.