On Convergence Rate of MRetrace
Abstract
:1. Introduction
2. Background
2.1. Markov Decision Process
2.2. Learning Algorithms and Their Key Matrices
2.2.1. Off-Policy TD
2.2.2. Retrace(0)
2.2.3. Naive Bellman Residual
2.2.4. GTD
2.2.5. GTD2
2.2.6. TDC
2.2.7. ETD
2.2.8. MRetrace
3. Finite Sample Analysis
3.1. Convergence Rate of General Temporal Difference Learning Algorithm
3.2. Convergence Rate of the MRetrace Algorithm
4. How to Compare?
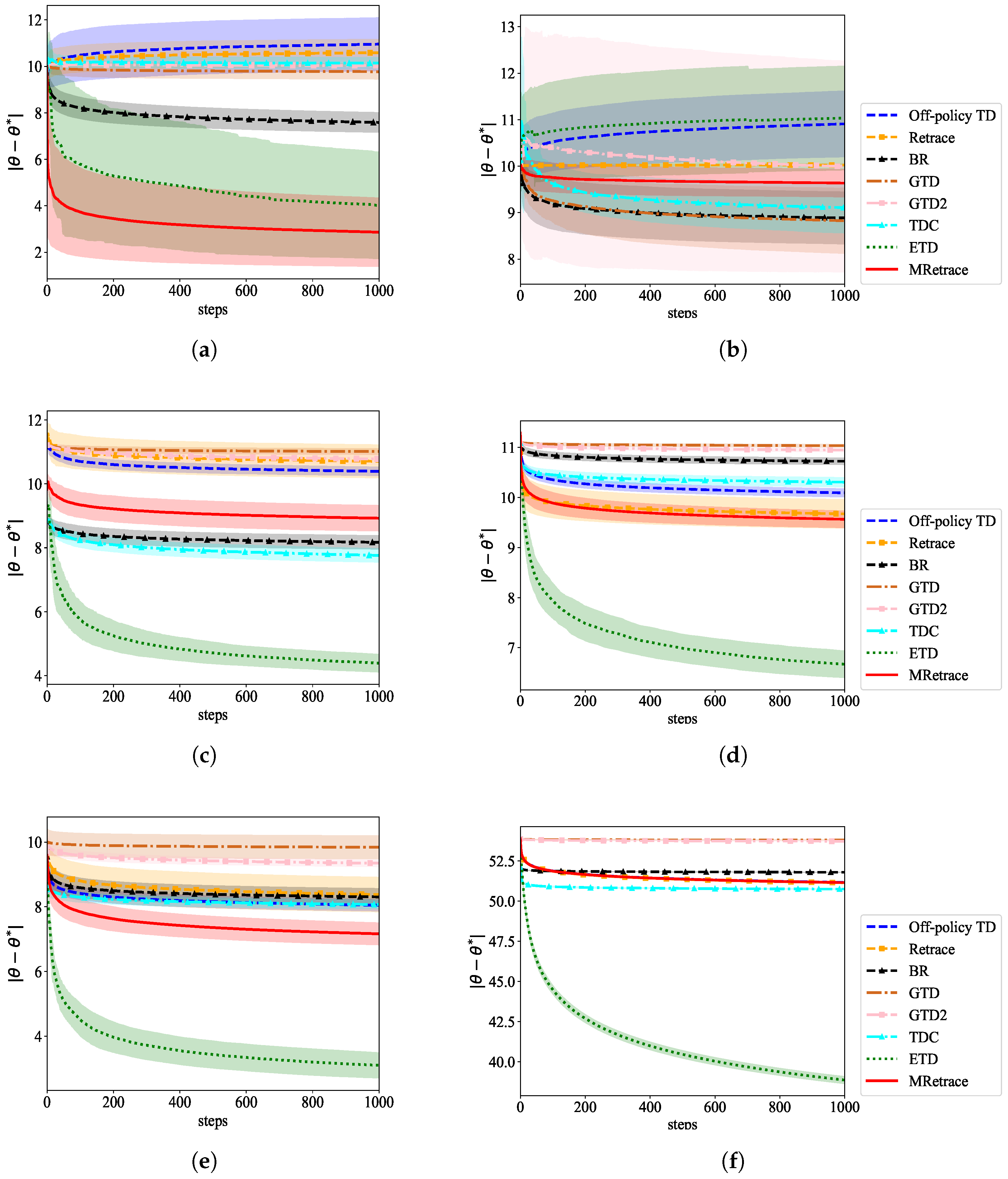
5. Numerical Analysis
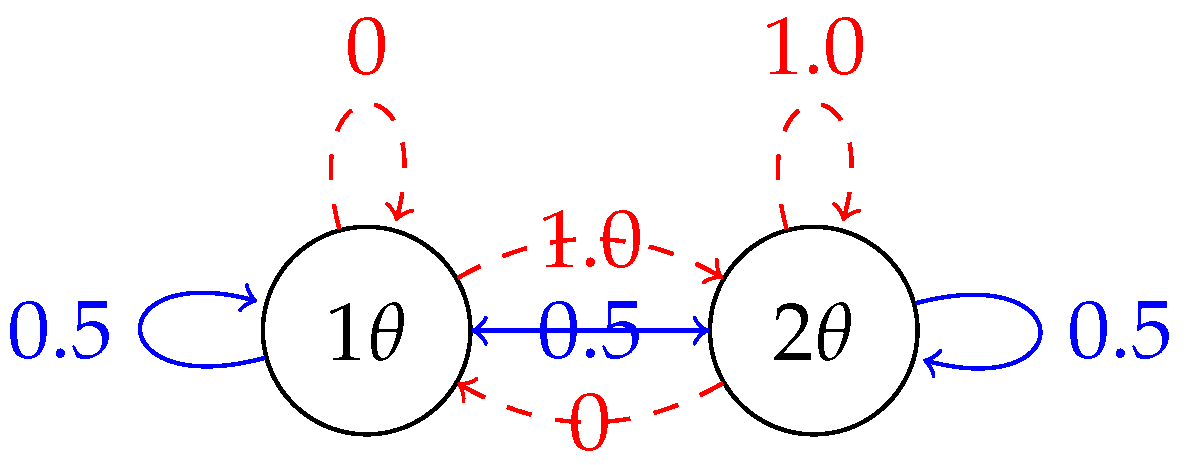
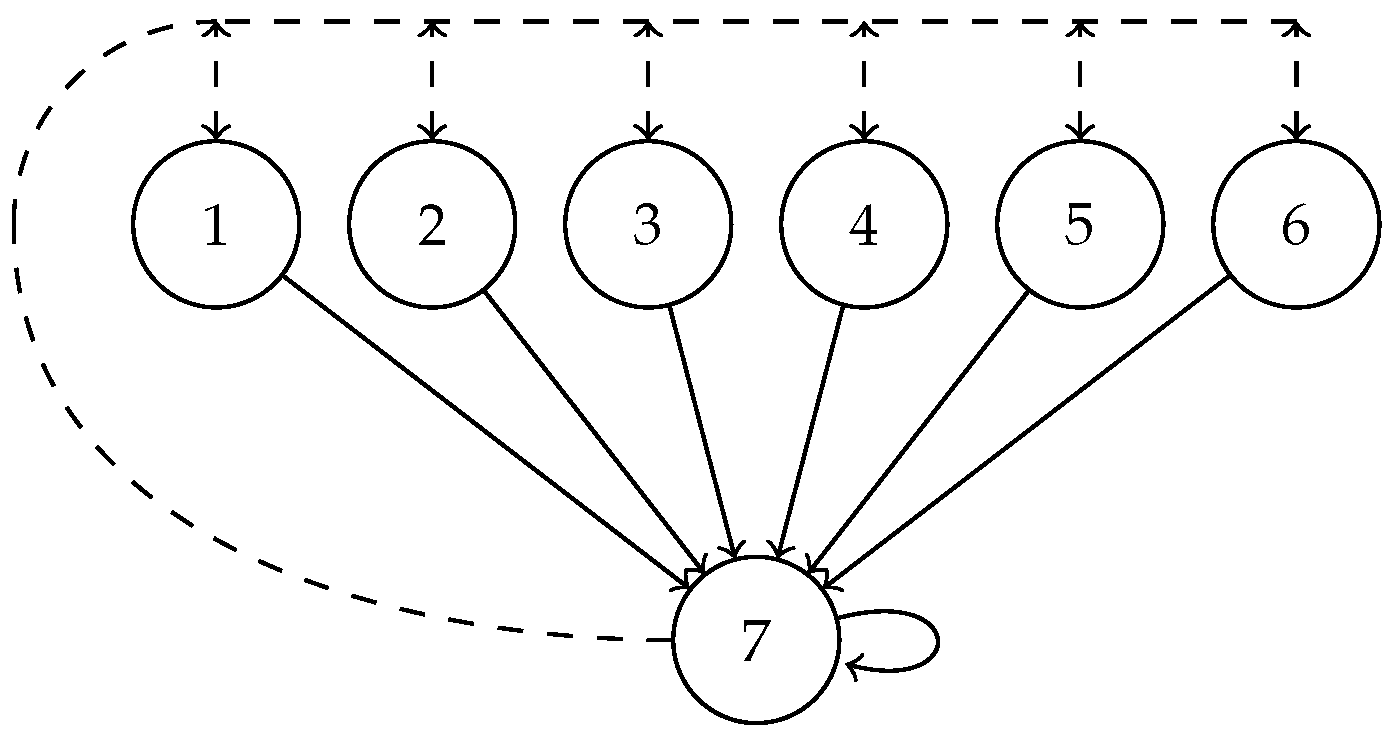
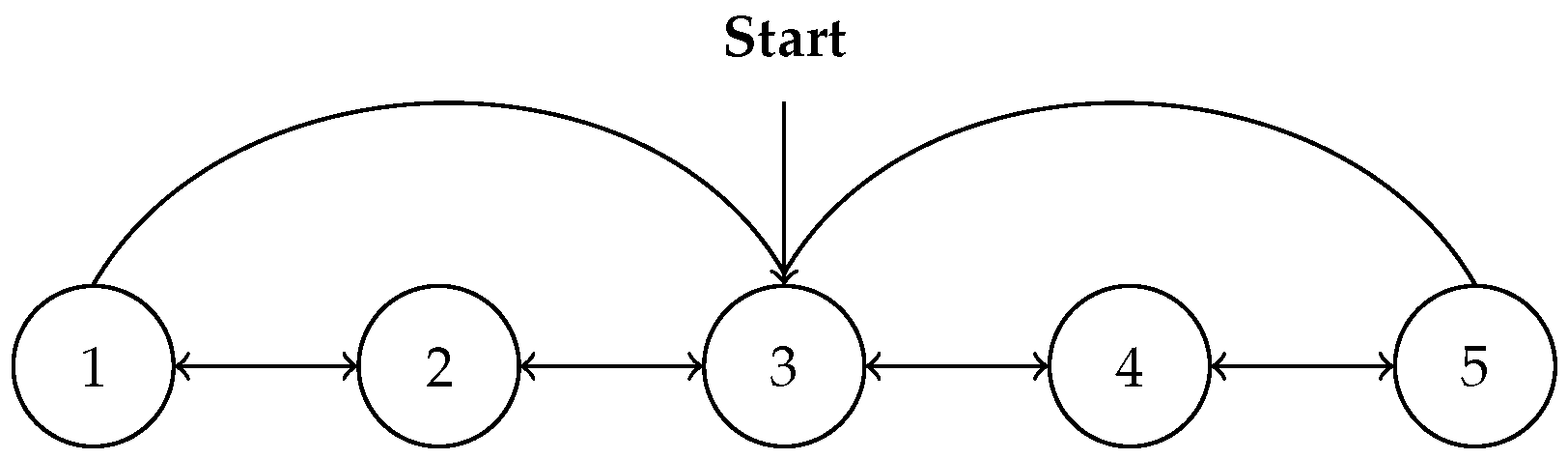
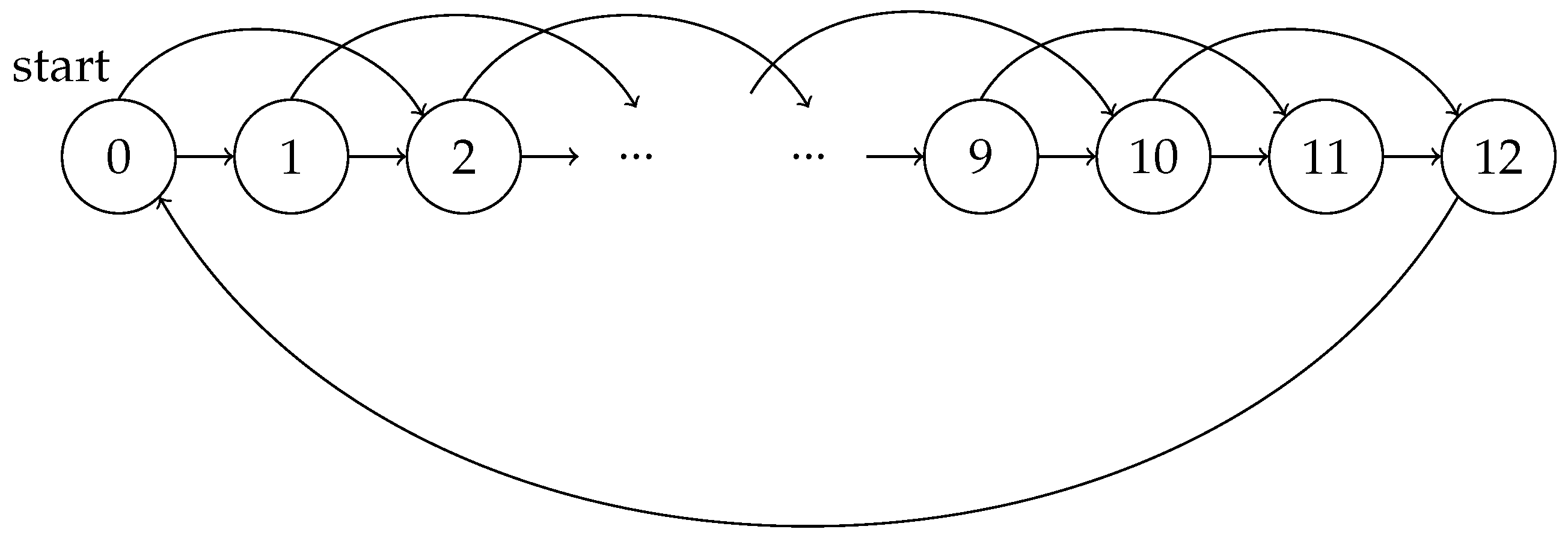
5.1. Example Settings
5.2. Results and Analysis
6. Experimental Studies
7. Conclusions and Future Work
- (1)
- This paper assumes that the learning rates of all algorithms are the same; however, in reality, different algorithms have different ranges of applicable learning rates.
- (2)
- This paper does not consider the scenario of a fixed learning rate.
- (3)
- This paper focuses on learning prediction and does not address learning control.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Sutton, R.S.; Mahmood, A.R.; White, M. An emphatic approach to the problem of off-policy temporal-difference learning. J. Mach. Learn. Res. 2016, 17, 2603–2631. [Google Scholar]
- Baird, L. Residual algorithms: Reinforcement learning with function approximation. In Proceedings of the 12th International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 30–37. [Google Scholar]
- Sutton, R.S.; Maei, H.R.; Szepesvári, C. A Convergent O(n) Temporal-difference Algorithm for Off-policy Learning with Linear Function Approximation. Adv. Neural Inf. Process. Syst. 2008, 21, 1609–1616. [Google Scholar]
- Sutton, R.; Maei, H.; Precup, D.; Bhatnagar, S.; Silver, D.; Szepesvári, C.; Wiewiora, E. Fast gradient-descent methods for temporal-difference learning with linear function approximation. In Proceedings of the 26th International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 993–1000. [Google Scholar]
- Chen, X.; Ma, X.; Li, Y.; Yang, G.; Yang, S.; Gao, Y. Modified retrace for off-policy temporal difference learning. In Proceedings of the Thirty-Ninth Conference on Uncertainty in Artificial Intelligence, Pittsburgh, PA, USA, 31 July–4 August 2023; pp. 303–312. [Google Scholar]
- Dalal, G.; Szörényi, B.; Thoppe, G.; Mannor, S. Finite sample analyses for TD (0) with function approximation. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Dalal, G.; Thoppe, G.; Szörényi, B.; Mannor, S. Finite sample analysis of two-timescale stochastic approximation with applications to reinforcement learning. In Proceedings of the Conference On Learning Theory, PMLR, Stockholm, Sweden, on 5–9 July 2018; pp. 1199–1233. [Google Scholar]
- Gupta, H.; Srikant, R.; Ying, L. Finite-time performance bounds and adaptive learning rate selection for two time-scale reinforcement learning. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 4704–4713. [Google Scholar]
- Xu, T.; Zou, S.; Liang, Y. Two time-scale off-policy TD learning: Non-asymptotic analysis over Markovian samples. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 10634–10644. [Google Scholar]
- Dalal, G.; Szorenyi, B.; Thoppe, G. A tale of two-timescale reinforcement learning with the tightest finite-time bound. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–8 February 2020; Volume 34, pp. 3701–3708. [Google Scholar]
- Durmus, A.; Moulines, E.; Naumov, A.; Samsonov, S.; Scaman, K.; Wai, H.T. Tight high probability bounds for linear stochastic approximation with fixed stepsize. Adv. Neural Inf. Process. Syst. 2021, 34, 30063–30074. [Google Scholar]
- Xu, T.; Liang, Y. Sample complexity bounds for two timescale value-based reinforcement learning algorithms. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 13–15 April 2021; pp. 811–819. [Google Scholar]
- Zhang, S.; Des Combes, R.T.; Laroche, R. On the convergence of SARSA with linear function approximation. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 41613–41646. [Google Scholar]
- Wang, S.; Si, N.; Blanchet, J.; Zhou, Z. A finite sample complexity bound for distributionally robust q-learning. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 3370–3398. [Google Scholar]
- Munos, R.; Stepleton, T.; Harutyunyan, A.; Bellemare, M. Safe and efficient off-policy reinforcement learning. Adv. Neural Inf. Process. Syst. 2016, 29, 1054–1062. [Google Scholar]
- Boyan, J.A. Technical update: Least-squares temporal difference learning. Mach. Learn. 2002, 49, 233–246. [Google Scholar] [CrossRef]
- Ghiassian, S.; Patterson, A.; Garg, S.; Gupta, D.; White, A.; White, M. Gradient temporal-difference learning with regularized corrections. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 3524–3534. [Google Scholar]
- Zhang, S.; Whiteson, S. Truncated emphatic temporal difference methods for prediction and control. J. Mach. Learn. Res. 2022, 23, 6859–6917. [Google Scholar]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
| Algorithm | Key Matrix A | Positive Definite | b |
|---|---|---|---|
| Off-policy TD | × | ||
| Retrace | × | ||
| BR | ✓ | ||
| GTD | ✓ | ||
| GTD2 | ✓ | ||
| TDC | ✓ | ||
| ETD | ✓ | ||
| MRetrace | ✓ |
| Algorithm | Two-State | Baird’s | Random Walk | Boyan Chain | ||
|---|---|---|---|---|---|---|
| Tabular | Inverted | Dependent | ||||
| Off-policy TD | ||||||
| Retrace | ||||||
| BR | 9.673 × 10−17 | |||||
| GTD | 0 | 0 | 0 | 0 | 0 | 0 |
| GTD2 | 0 | −1.077 × 10−17 | 0 | 0 | 0 | 0 |
| TDC | ||||||
| ETD | −2.82 × 10−16 | |||||
| MRetrace | −2.141 × 10−17 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Qin, W.; Gong, Y.; Yang, S.; Wang, W. On Convergence Rate of MRetrace. Mathematics 2024, 12, 2930. https://doi.org/10.3390/math12182930
Chen X, Qin W, Gong Y, Yang S, Wang W. On Convergence Rate of MRetrace. Mathematics. 2024; 12(18):2930. https://doi.org/10.3390/math12182930
Chicago/Turabian StyleChen, Xingguo, Wangrong Qin, Yu Gong, Shangdong Yang, and Wenhao Wang. 2024. "On Convergence Rate of MRetrace" Mathematics 12, no. 18: 2930. https://doi.org/10.3390/math12182930
APA StyleChen, X., Qin, W., Gong, Y., Yang, S., & Wang, W. (2024). On Convergence Rate of MRetrace. Mathematics, 12(18), 2930. https://doi.org/10.3390/math12182930






