Non-Linear Plasma Wave Dynamics: Investigating Chaos in Dynamical Systems
Abstract
:1. Introduction
2. Mathematical Model
2.1. Description of Methods
2.2. The Extended -Expansion Method
2.2.1. Case 1
2.2.2. Case 2
2.2.3. Case 3
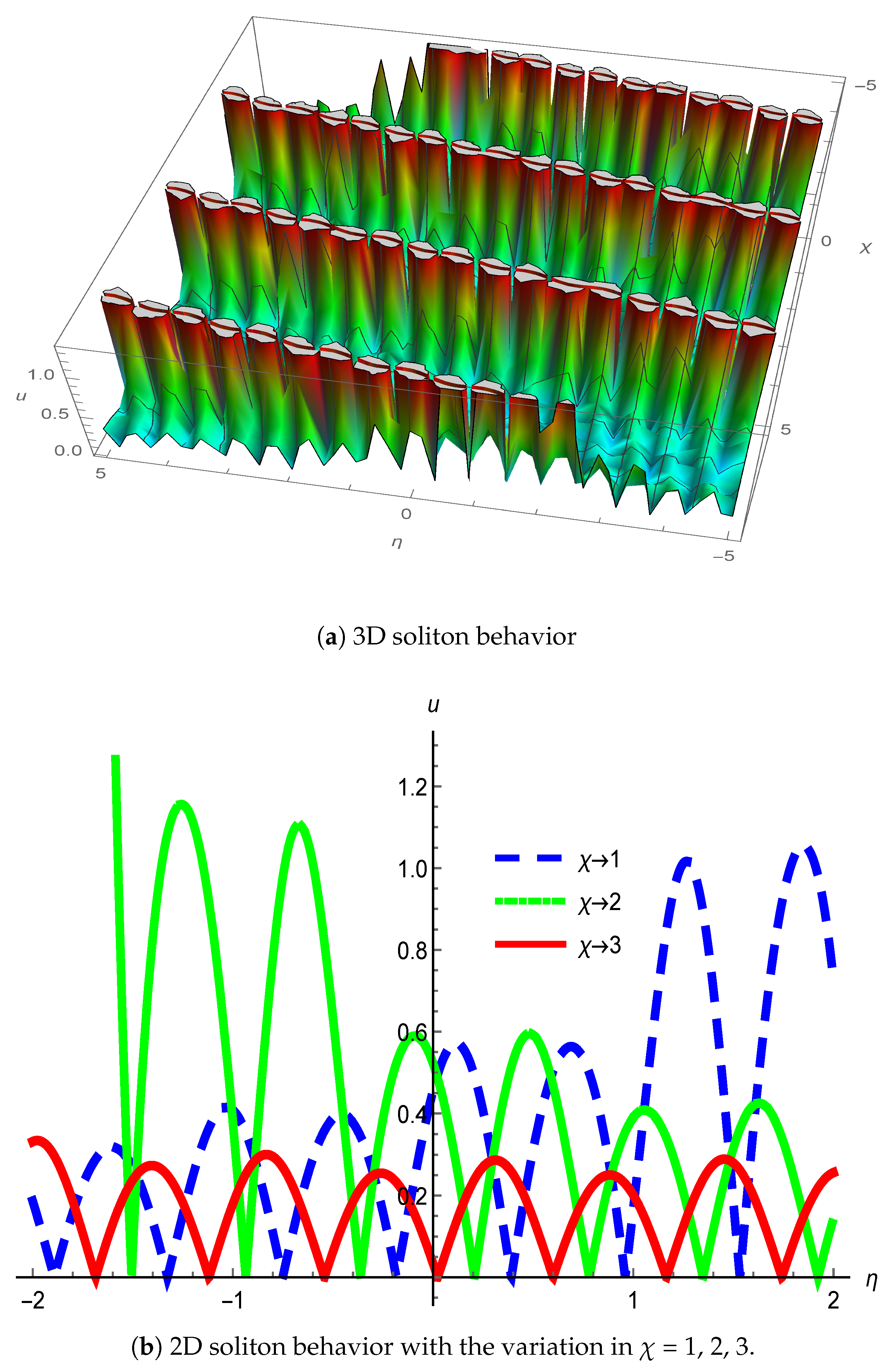
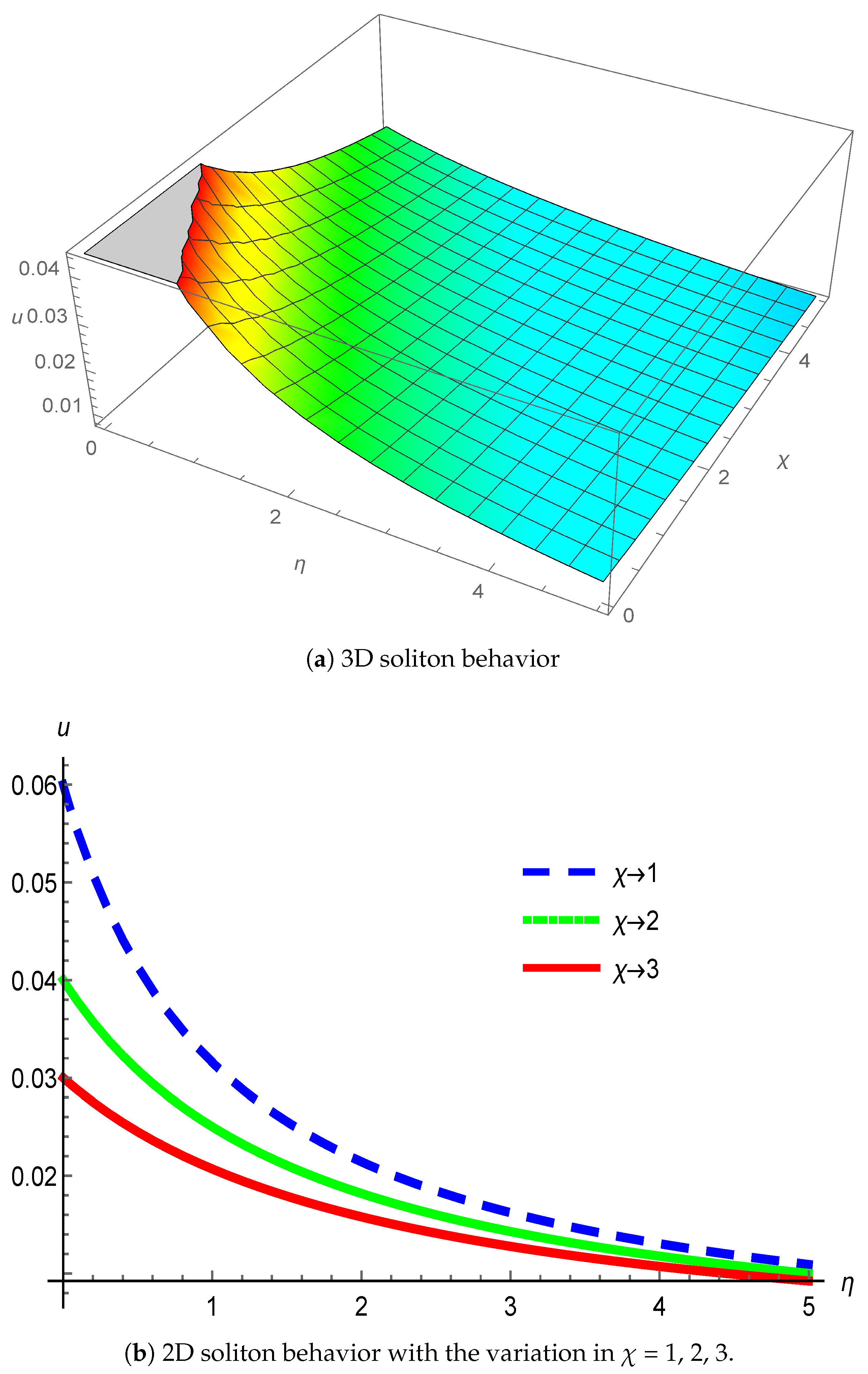
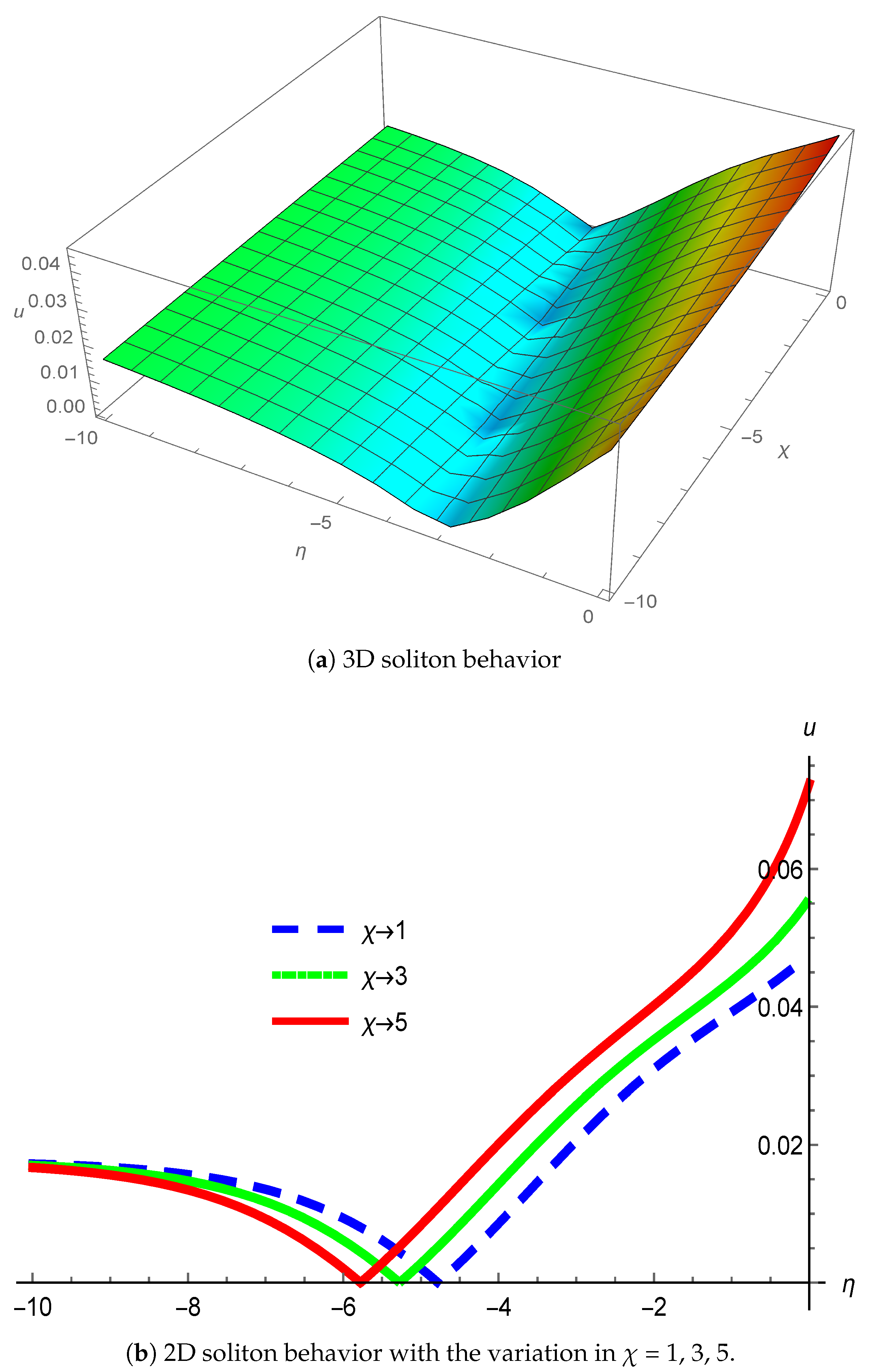
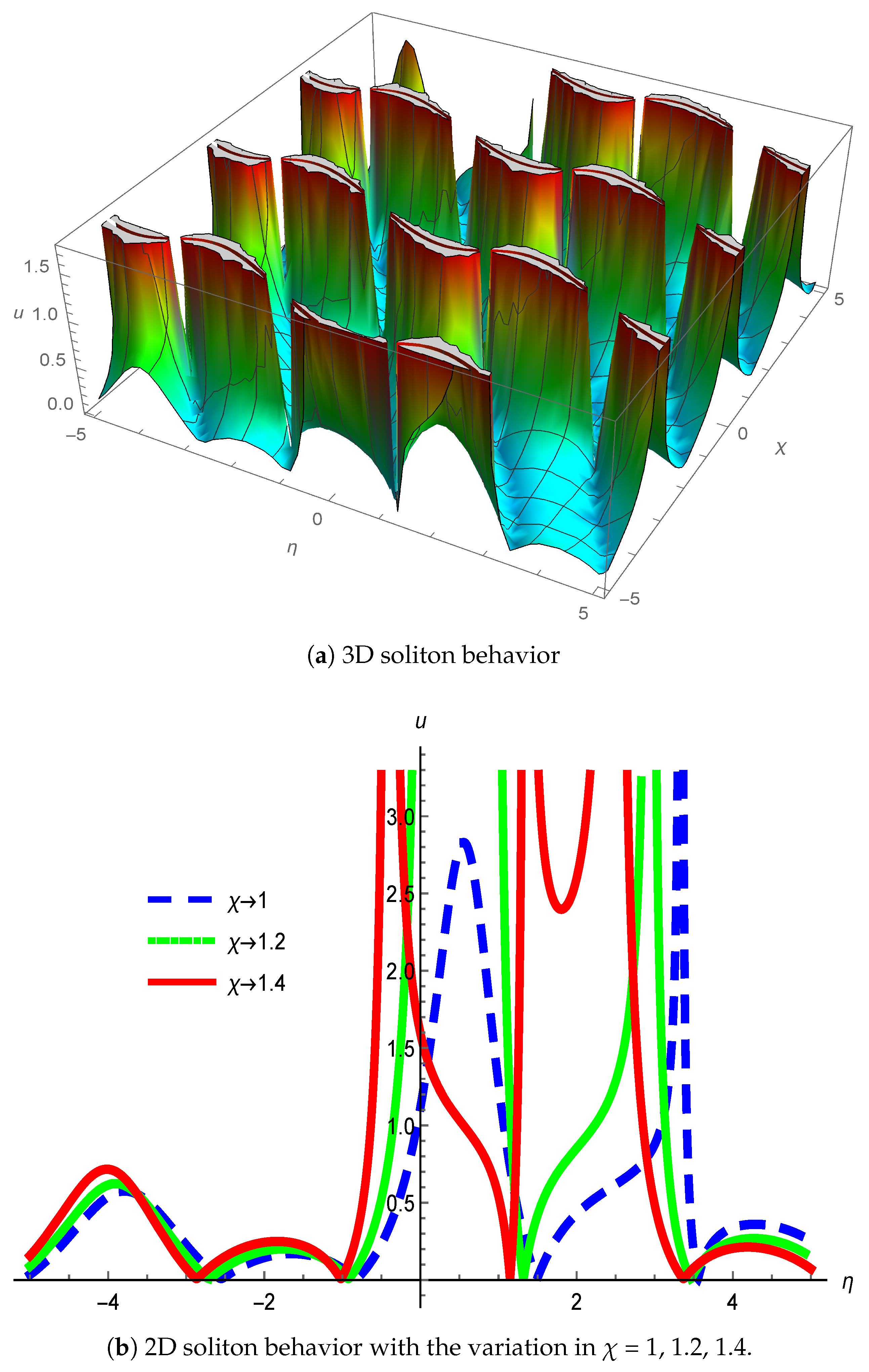
3. Physical Interpretation
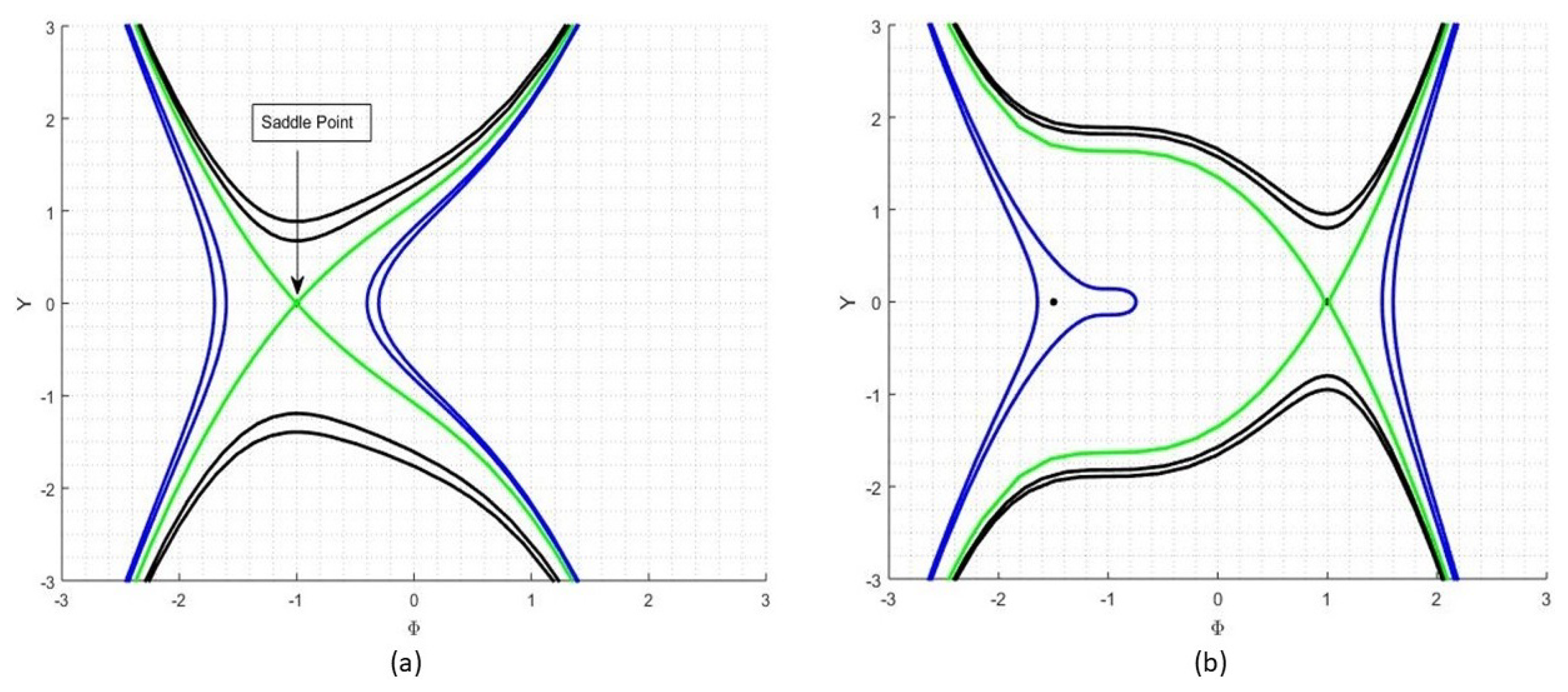
4. Bifurcation Theory
4.1. Case 1
- , ,
- , ,
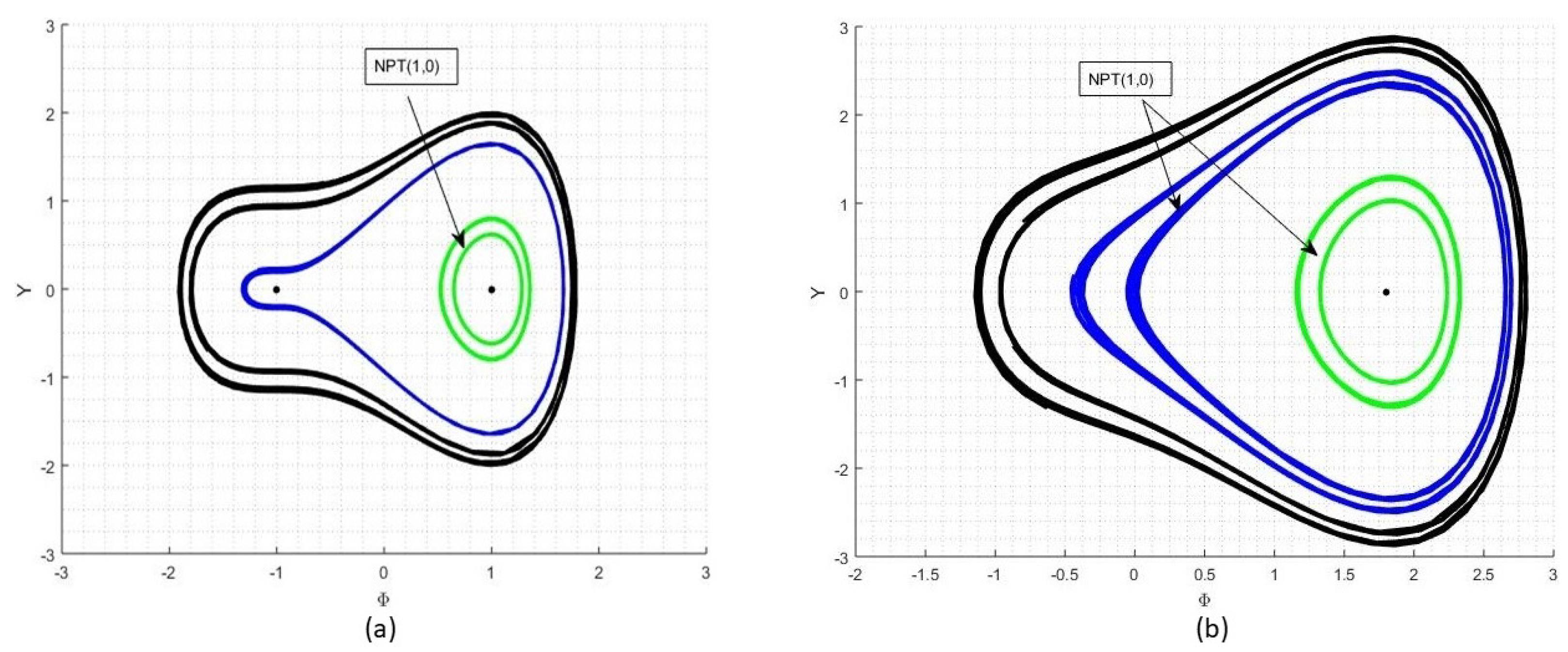
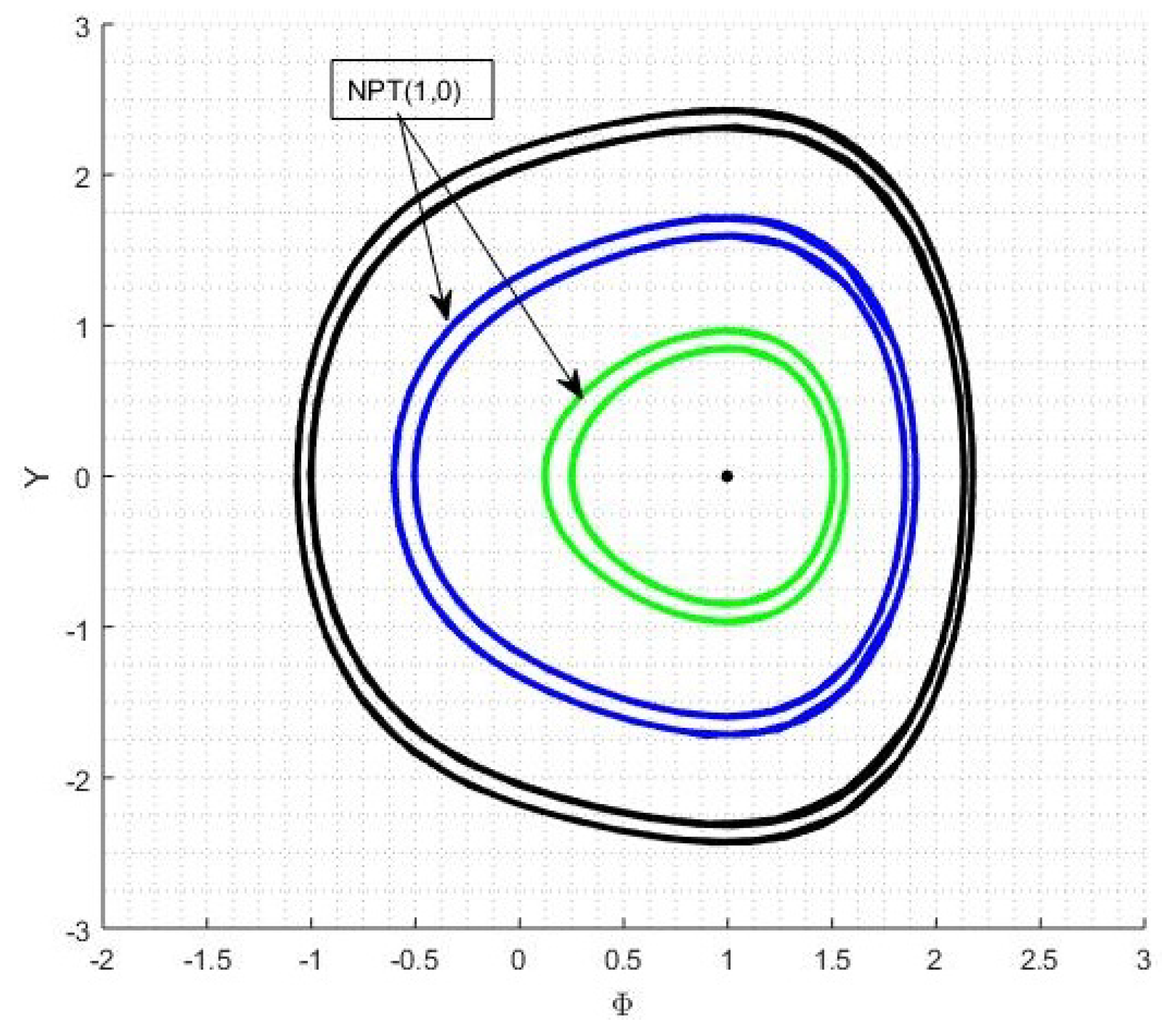
4.2. Case 2
- , ,
- , ,
- , ,
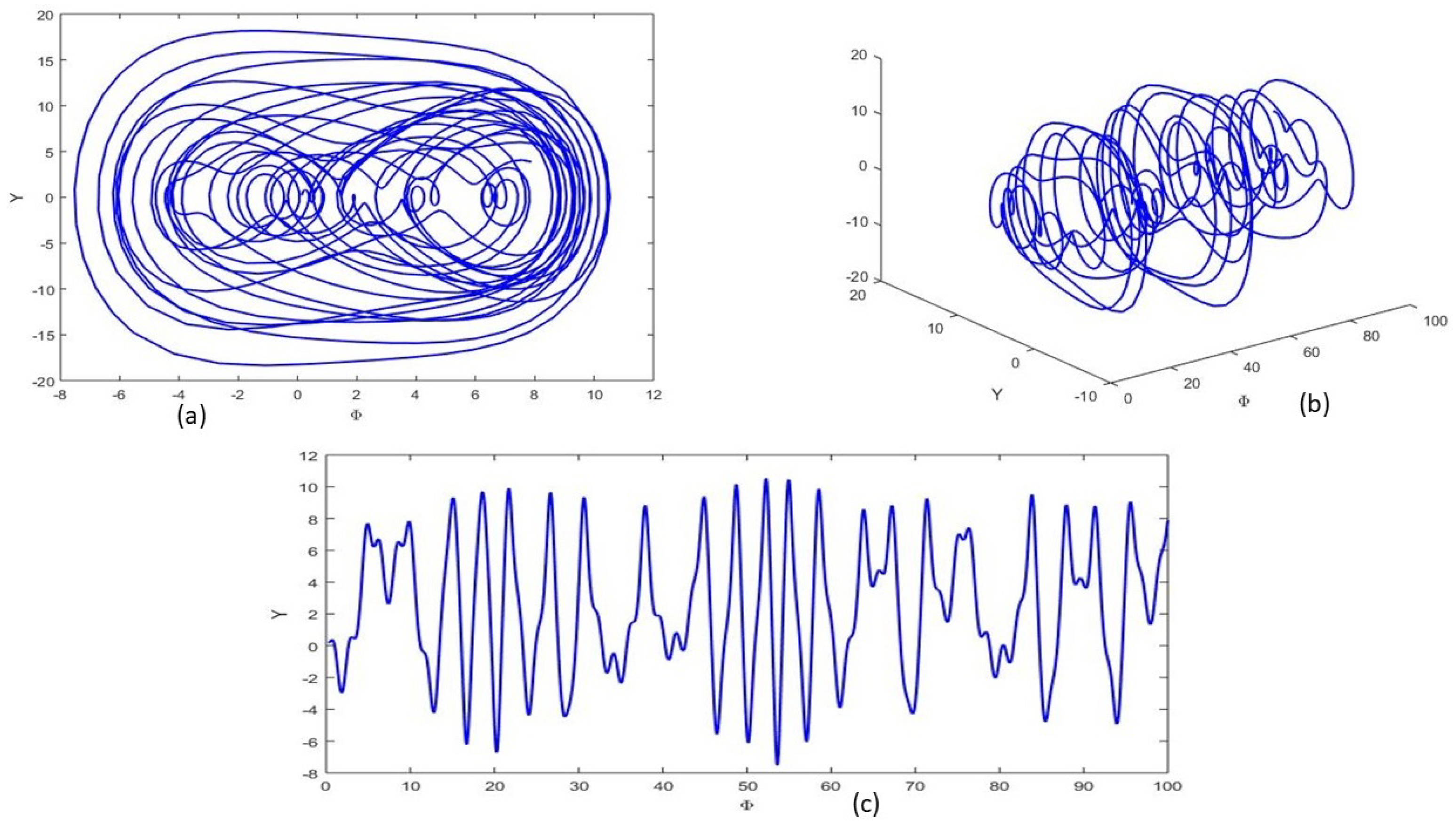
4.3. Chaotic Behavior
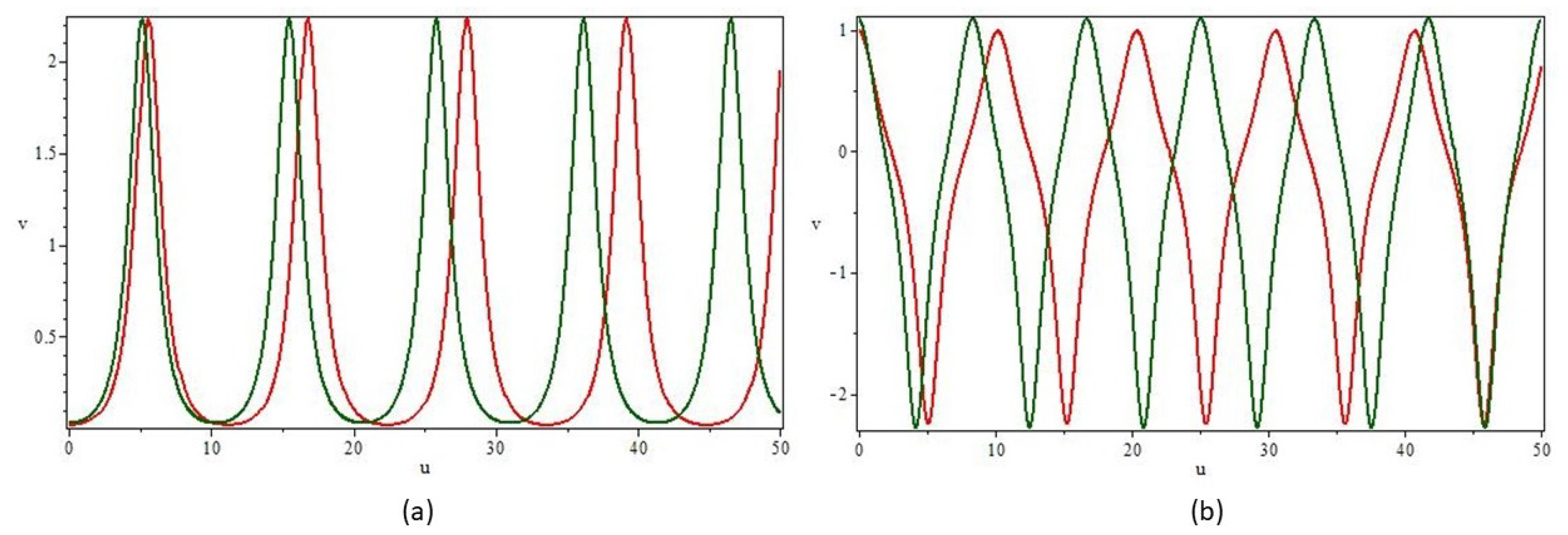
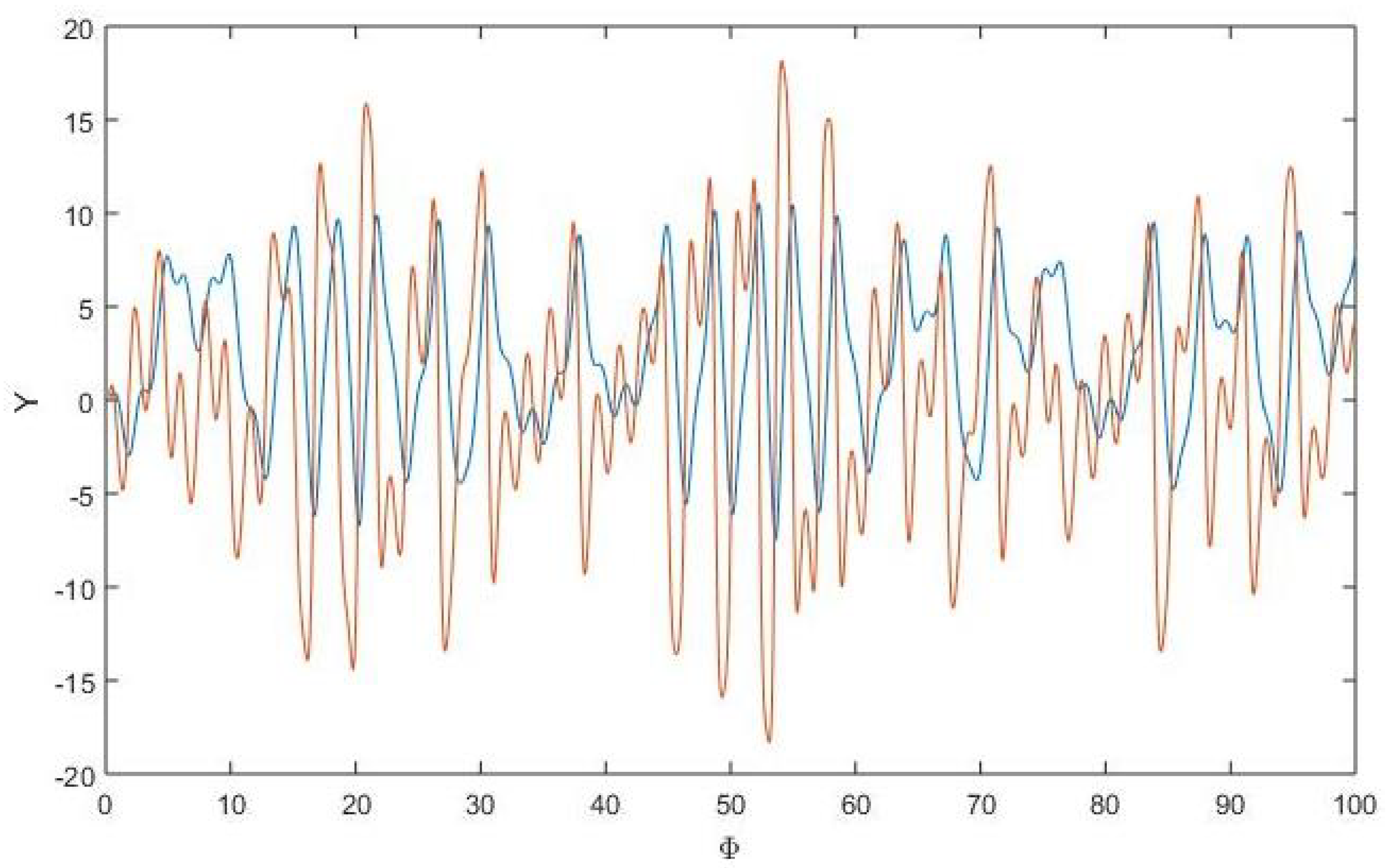
5. Sensitive Behavior
6. Multi-Stable Chaotic System
7. Real-World Case Study: Chaos in Mode-Locked Fiber Lasers
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaufman, A.; Cohen, B. Theoretical plasma physics. J. Plasma Phys. 2019, 85, 205850601. [Google Scholar] [CrossRef]
- Thomas, E.; Eadon, A.; Wallace, E. Suppression of low frequency plasma instabilities in a magnetized plasma column. Phys. Plasmas 2005, 12, 042109. [Google Scholar] [CrossRef]
- Oloniiju, S.D. New sets of soliton solutions for the generalized Whitham–Broer–Kaup–Boussinesq–Kupershmidt system. Results Phys. 2023, 52, 106785. [Google Scholar] [CrossRef]
- Jhangeer, A.; Muddassar, M.; Ur Rehman, Z.; Awrejcewicz, J.; Riaz, M.B. Multistability and dynamic behavior of non-linear wave solutions for analytical kink periodic and quasi-periodic wave structures in plasma physics. Results Phys. 2021, 29, 104735. [Google Scholar] [CrossRef]
- Riaz, M.B.; Atangana, A.; Jhangeer, A.; Junaid-U-Rehman, M. Some exact explicit solutions and conservation laws of Chaffee-Infante equation by Lie symmetry analysis. Phys. Scr. 2021, 96, 084008. [Google Scholar] [CrossRef]
- Houwe, A.; Sabi’u, J.; Hammouch, Z.; Doka, S.Y. Solitary pulses of a conformable nonlinear differential equation governing wave propagation in low-pass electrical transmission line. Phys. Scr. 2020, 95, 045203. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Exact Soliton and Kink Solutions for New (3 + 1)-Dimensional Nonlinear Modified Equations of Wave Propagation. Open Eng. 2017, 7, 169–174. [Google Scholar] [CrossRef]
- Adeyemo, O.D. Applications of cnoidal and snoidal wave solutions via optimal system of subalgebras for a generalized extended (2 + 1)-D quantum Zakharov-Kuznetsov equation with power-law nonlinearity in oceanography and ocean engineering. J. Ocean. Eng. Sci. 2024, 9, 126–153. [Google Scholar] [CrossRef]
- Samina, S.; Jhangeer, A.; Chen, Z. Bifurcation, chaotic and multistability analysis of the (2+1)-dimensional elliptic nonlinear Schrödinger equation with external perturbation. Waves Random Complex Media 2022, 15, 1–25. [Google Scholar] [CrossRef]
- Shukla, P.K.; Mamun, A.A. Introduction to Dusty Plasma Physics. Plasma Phys. Control. Fusion 2002, 44, 395. [Google Scholar] [CrossRef]
- Gu, C. Soliton Theory and Its Applications; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Ramamoorthy, R.; Rajagopal, K.; Leutcho, G.D.; Krejcar, O.; Namazi, H.; Hussain, I. Multistable dynamics and control of a new 4D memristive chaotic Sprott B system. Chaos Solitons Fractals 2022, 156, 111834. [Google Scholar] [CrossRef]
- Lai, Q.; Akgul, A.; Li, C.; Xu, G.; Cavusoglu, U. A New Chaotic System with Multiple Attractors: Dynamic Analysis, Circuit Realization and S-Box Design. Entropy 2018, 20, 12. [Google Scholar] [CrossRef] [PubMed]
- Rehman, Z.U.; Hussain, Z.; Li, Z.; Abbas, T.; Tlili, I. Bifurcation analysis and multi-stability of chirped form optical solitons with phase portrait. Results Eng. 2024, 21, 101861. [Google Scholar] [CrossRef]
- Richardson, M.; Paxton, A.; Kuznetsov, N. Nonlinear methods for understanding complex dynamical phenomena in psychological science. APA Psychol. Sci. Agenda 2017, 31, 1–9. [Google Scholar]
- Bains, A.S.; Misra, A.P.; Saini, N.S.; Gill, T.S. Modulational instability of ion-acoustic wave envelopes in magnetized quantum electron-positron-ion plasmas. Phys. Plasmas 2010, 17, 012103. [Google Scholar] [CrossRef]
- Aljahdaly, N.H. Some applications of the modified (G’/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Guo, Y.; Yao, Z.; Xu, Y.; Ma, J. Control the stability in chaotic circuit coupled by memristor in different branch circuits. AEU-Int. J. Electron. Commun. 2022, 145, 154074. [Google Scholar] [CrossRef]
- Al-Harbi, N.; Basfer, N.; Youssef, A.A.A. Exact solution of arrhenius equation under the square root heating model. Alex. Eng. J. 2023, 65, 475–479. [Google Scholar] [CrossRef]
- Ghosh, U.N.; Chatterjee, P.; Roychoudhury, R. The effect of q-distributed electrons on the head-on collision of ion acoustic solitary waves. Phys. Plasmas 2012, 19, 012113. [Google Scholar] [CrossRef]
- Nadeem, S.; Akhtar, S.; Alharbi, F.M.; Saleem, S.; Issakhov, A. Analysis of heat and mass transfer on the peristaltic flow in a duct with sinusoidal walls: Exact solutions of coupled PDEs. Alex. Eng. J. 2022, 61, 4107–4117. [Google Scholar] [CrossRef]
- Bhowmike, N.; Rehman, Z.U.; Naz, Z.; Zahid, M.; Shoaib, S.; Amin, Y. Non-linear electromagnetic wave dynamics: Investigating periodic and quasi-periodic behavior in complex engineering systems. Chaos Solitons Fractals 2024, 184, 114984. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghandour, R.; Karar, A.S.; Al Barakeh, Z.; Barakat, J.M.H.; Ur Rehman, Z. Non-Linear Plasma Wave Dynamics: Investigating Chaos in Dynamical Systems. Mathematics 2024, 12, 2958. https://doi.org/10.3390/math12182958
Ghandour R, Karar AS, Al Barakeh Z, Barakat JMH, Ur Rehman Z. Non-Linear Plasma Wave Dynamics: Investigating Chaos in Dynamical Systems. Mathematics. 2024; 12(18):2958. https://doi.org/10.3390/math12182958
Chicago/Turabian StyleGhandour, Raymond, Abdullah S. Karar, Zaher Al Barakeh, Julien Moussa H. Barakat, and Zia Ur Rehman. 2024. "Non-Linear Plasma Wave Dynamics: Investigating Chaos in Dynamical Systems" Mathematics 12, no. 18: 2958. https://doi.org/10.3390/math12182958









