The Dynamic Behavior of a Stochastic SEIRM Model of COVID-19 with Standard Incidence Rate
Abstract
1. Introduction
2. Preliminary
3. The Existence of Global Solutions
4. Extinction
5. Stationary Distribution
- (1).
- In the vicinity of the open set U and its surroundings, the smallest eigenvalue of the matrix is bounded.
- (2).
- For any point x outside of U in , the average time t required for a trajectory originating from x to reach the set U is finite. Additionally, the supremum of this time over any compact subset is also finite.
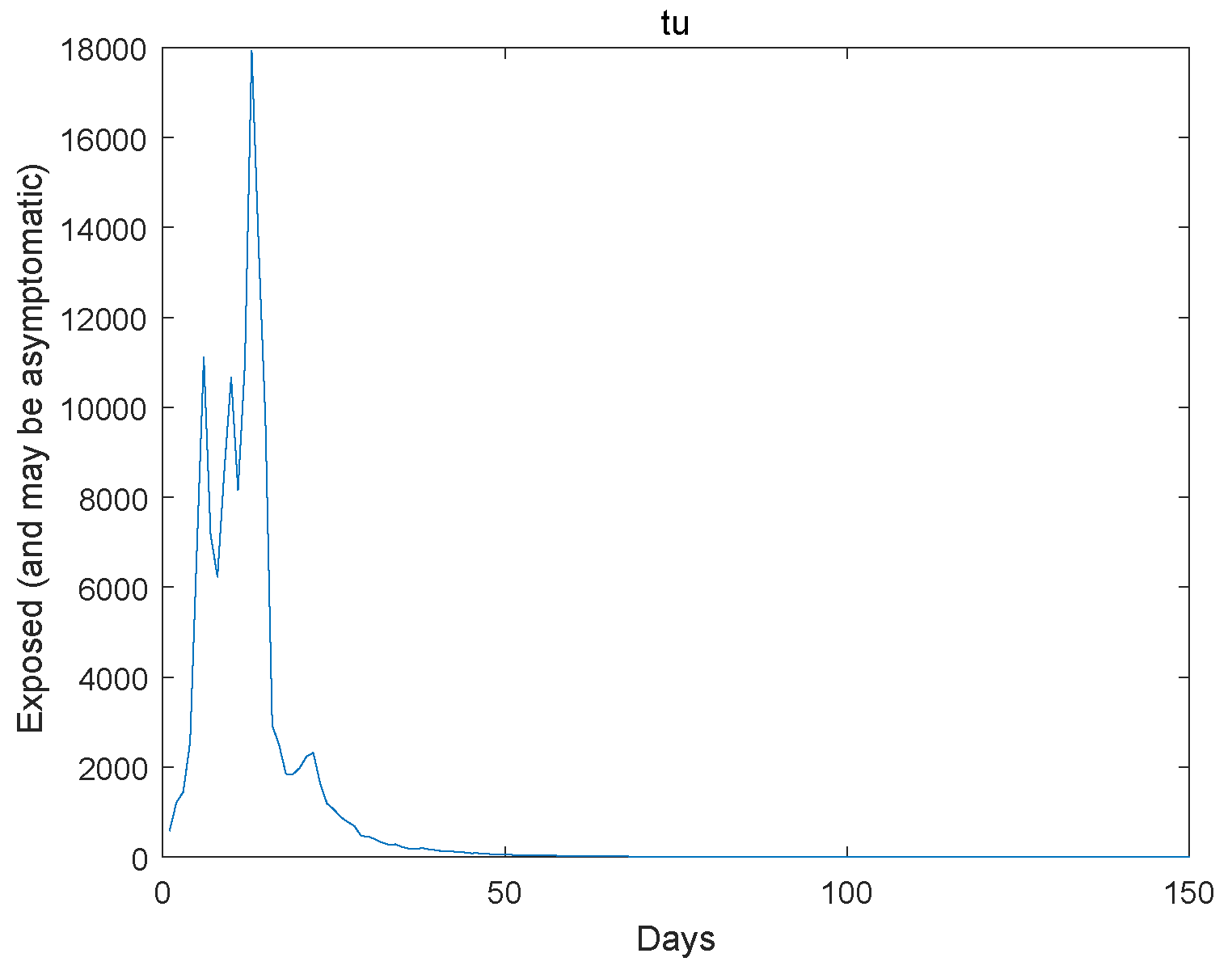
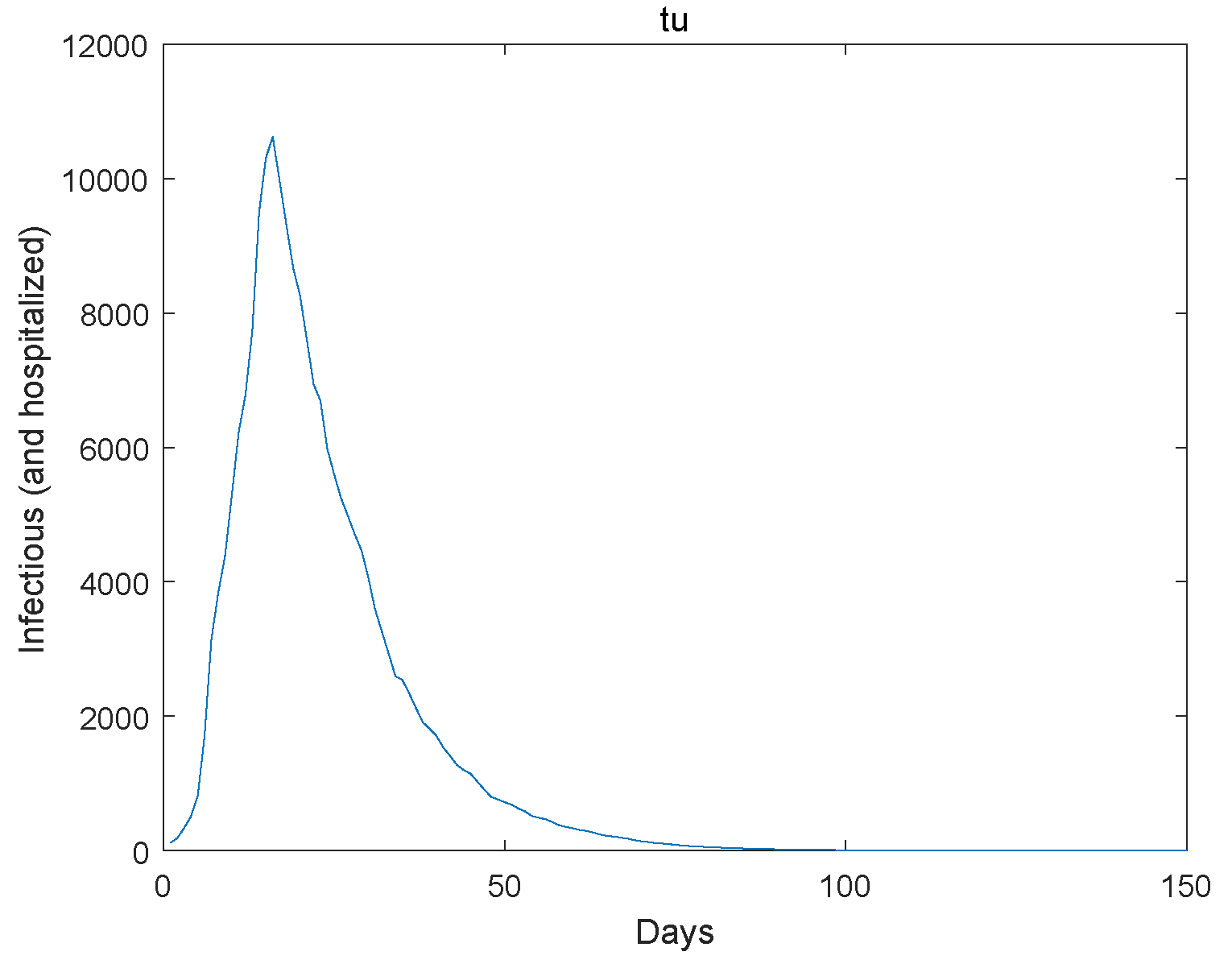
6. An Example
7. Conclusions
- Discuss whether the model assumes a uniform mixing of populations or fails to consider factors such as spatial distribution and varying contact rates among different demographic groups.
- If the model assumes constant parameters, this may be a limitation because real-world scenarios often involve time-varying parameters due to interventions or behavioral changes.
- Evaluate the model’s capacity to predict long-term outcomes in dynamic environments.
- Pandemics can be influenced by external factors such as policy changes, vaccine distribution, or the emergence of new variants.
- Consider unreported cases as potential limitations of the model. Additionally, propose that future research could build on this work by integrating methods to estimate and account for unreported cases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Brauer, F. Compartmental models in epidemiology. Math. Epidemiol. 2008, 19–79. [Google Scholar]
- Aybar, O. Biochemical models of SIR and SIRS: Effects of bilinear incidence rate on infection-free and endemic states. Chaos 2023, 33, 093120. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Jin, Z. Analysis of an SIR model with bilinear incidence rate. Nonlinear Anal. Real World Appl. 2010, 14, 2390–2402. [Google Scholar] [CrossRef]
- Zhang, Q. On small-data solution of the chemotaxis-SIS epidemic system with bilinear incidence rate. Nonlinear Anal. Real World Appl. 2024, 77, 104063. [Google Scholar] [CrossRef]
- Mahmood, P.; Majid, E. Global dynamics of an epidemic model with standard incidence rate and vaccination strategy. Chaos Solitons Fractals 2018, 117, 192–199. [Google Scholar]
- Han, S.; Lei, C.; Zhang, X. Qualitative analysis on a diffusive SIRS epidemic model with standard incidence infection mechanism. Z. Angew. Math. Phys. 2021, 71, 190. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, D. Dynamics and Density Function of a Stochastic SICA Model of a Standard Incidence Rate with Ornstein-Uhlenbeck Process. Qual. Theory Dyn. Syst. 2014, 23, 219. [Google Scholar] [CrossRef]
- Guo, S.; Xue, Y.; Li, X. A novel analysis approach of uniform persistence for a COVID-19 model with quarantine and standard incidence rate. Quant. Biol. 2022. [Google Scholar]
- Guo, S.; He, M.; Cui, J. Global Stability of a Time-delayed Malaria Model with Standard Incidence Rate. Acta Math. Appl.-Sin.-Engl. Ser. 2023, 39, 211–221. [Google Scholar] [CrossRef]
- He, B.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020, 101, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Saroj, K.; Ahmed, N.U. Mathematical modeling and optimal intervention of COVID-19 outbreak. Quatitative Biol. 2021, 9, 84–92. [Google Scholar]
- Shengjie, L. Effects of non-pharmaceutical interventions to contain COVID-19 in China. Nature 2020, 585, 410–413. [Google Scholar]
- Zhao, Y.; Wang, L. Practical exponential stability of impulsive stochastic food chain system with time-varying delays. Mathematics 2023, 11, 147. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H.; Qiao, X. Persistence, extinction and practical exponential stability of impulsive stochastic competition models with varying delays. AIMS Math. 2023, 8, 22643–22661. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Q.; Zheng, W. Exponential stability of stochastic nonlinear delay systems subject to multiple periodic impulses. IEEE Trans. Autom. Control. 2024, 69, 2621–2628. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L. Asymptotic behavior of a stochastic three-species food chain model with time-varying delays. Period. Ocean. Univ. China 2023, 53, 132–136. [Google Scholar]
- Zhao, Y.; Wang, L.; Wang, Y. The Periodic Solutions to a Stochastic Two-Prey One-Predator Population Model with Impulsive Perturbations in a Polluted Environment. Methodol. Comput. Appl. Probab. 2021, 23, 859–872. [Google Scholar] [CrossRef]
- Khan, A.; Ikram, R.; Din, A.; Humphries, U.W.; Akgul, A. Stochastic COVID-19 SEIQ epidemic model with time-delay. Results Phys. 2021, 30, 104775. [Google Scholar] [CrossRef]
- Allen, L. An Introduction to Stochastic Epidemic Models; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Yang, Q.; Zhang, X.; Jiang, D. Dynamical behavior of a stochastic food chain system with ornstein uhlenbeck Process. J. Nonlinear Sci. 2022, 32, 34. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Their Applications; Horwood: Chichester, UK, 1997. [Google Scholar]
- He, S.; Tang, S.; Rong, C. A discrete stochastic model of the COVID-19 outbreak: Forecast and control. Math. Biosci. Eng. 2020, 17, 2792–2804. [Google Scholar] [CrossRef] [PubMed]
- Pei, L.; Zhang, M. Long-Term Predictions of COVID-19 in Some Countries by the SIRD Model. Complexity 2021, 1, 6692678. [Google Scholar] [CrossRef]
- Beghi, E.; Helbok, R.; Ozturk, S.; Karadas, O.; Lisnic, V.; Grosu, O.; Kovács, T.; Dobronyi, L.; Bereczki, D.; Cotelli, M.S.; et al. Short- and long-term outcome and predictors in an international cohort of patients with neuro-COVID-19. Eur. J. Neurol. 2022, 29, 1663–1684. [Google Scholar] [CrossRef] [PubMed]
- El-Shabasy, R. Three waves changes, new variant strains, and vaccination effect against COVID-19 pandemic. Int. J. Biol. Macromol. 2022, 204, 161–168. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z. Predicting the number of reported and unreported cases for the COVID-19 epidemics in China, South Korea, Italy, France, Germany and United Kingdom. J. Theor. Biol. 2021, 509, 110501. [Google Scholar] [CrossRef]
- Hamou, A. Analysis and dynamics of a mathematical model to predict unreported cases of COVID-19 epidemic in Morocco. Comp. Appl. Math. 2021, 41, 289. [Google Scholar] [CrossRef]



| Parameter | Description |
|---|---|
| Recruitment rate of the population | |
| Transmission rate due to social contact | |
| Transmission rate due to frontline contact | |
| Infection rate (Incubation rate) | |
| Recovery rate of infectious individuals (Recovery period) | |
| Immune recovery rate (Natural immune recovery period) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, H.; Wang, D. The Dynamic Behavior of a Stochastic SEIRM Model of COVID-19 with Standard Incidence Rate. Mathematics 2024, 12, 2966. https://doi.org/10.3390/math12192966
Zhao Y, Wang H, Wang D. The Dynamic Behavior of a Stochastic SEIRM Model of COVID-19 with Standard Incidence Rate. Mathematics. 2024; 12(19):2966. https://doi.org/10.3390/math12192966
Chicago/Turabian StyleZhao, Yuxiao, Hui Wang, and Dongxu Wang. 2024. "The Dynamic Behavior of a Stochastic SEIRM Model of COVID-19 with Standard Incidence Rate" Mathematics 12, no. 19: 2966. https://doi.org/10.3390/math12192966
APA StyleZhao, Y., Wang, H., & Wang, D. (2024). The Dynamic Behavior of a Stochastic SEIRM Model of COVID-19 with Standard Incidence Rate. Mathematics, 12(19), 2966. https://doi.org/10.3390/math12192966





