Abstract
By adjusting the propagation environment using reconfigurable reflecting elements, intelligent reflecting surfaces (IRSs) have become potential techniques used to improve the efficiency of wireless communication networks. In IRS-assisted communication systems, accurate channel estimation is crucial for optimizing signal transmission and achieving high spectral efficiency. As mobile data traffic continues to surge and the demand for high-capacity and low-latency wireless connectivity grows, IRSs are becoming pivotal technologies in the development of next-generation communication networks. IRSs offer the potential to revolutionize wireless propagation environments, improving network capacity and coverage, particularly in high-frequency wave scenarios where traditional signals encounter obstacles. Amidst this evolving landscape, machine learning (ML) emerges as a powerful tool to harness the full potential of IRS-assisted communication systems, particularly given the escalating computational complexity associated with deploying and operating IRSs in dynamic environments. This paper presents an overview of preliminary results for IRS-assisted communication using recurrent neural networks (RNNs). We first implement single- and double-layer LSTM, BiLSTM, and GRU techniques for an IRS-based communication system. In the next phase, we explore a hybrid approach, combining different RNN techniques, including LSTM-BiLSTM, LSTM-GRU, and BiLSTM-GRU, as well as their reverse configurations. These RNN algorithms were evaluated with respect to bit error rate (BER) and symbol error rate (SER) for IRS-enhanced communication. According to the experimental results, the BiLSTM double-layer model and the BiLSTM-GRU combination demonstrated the highest BER and SER accuracy compared to other approaches.
MSC:
94A14
1. Introduction
The intelligent reflecting surface (IRS) is evaluated as a novel radio technology for enhancing wireless communication systems. To improve the spectral efficiency of upcoming wireless networks, significant attention has been given to IRS, a planar metasurface composed of multiple reflecting elements [1]. Communication systems can be greatly enhanced because the IRS proactively alters the wireless channel by enabling each reflecting element to adjust the incident signal with a desired phase shift [2]. This allows the IRS to create a virtual line-of-sight (LoS) link between user equipment (UE) and the base station (BS), particularly when obstacles block the direct path between them. This capability increases the degree of freedom (DoF) in terms of flexibility and reduces end-to-end latency for ultra-reliable low-latency communication (URLLC) applications [3]. Smartphones and other web-enabled devices have become essential tools for global communication, information sharing, and entertainment. The wireless communications sector is currently at an exciting juncture: while the fifth-generation (5G) technology has largely been standardized and commercialized, there is a growing focus on the sixth-generation (6G) wireless technology within both academia and industry. The Cisco annual internet report (2018–2023) has stated mobile connectivity is expected to reach over of the world’s population by 2023 [4]. Additionally, the mobile subscriber number is projected to increase from 5.1 billion in 2018 to 5.7 billion by 2023. This signifies a pivotal moment in the wireless sector, with strong momentum toward advancing to the next level of wireless technology to meet the increasing global demand for connectivity [5,6].
Due to increasingly aggressive frequency reuse, cellular networks have grown denser, leading to the development of intercellular synchronization technologies to manage this complexity [7]. However, the unpredictable nature of wireless transmission and the limited available spectrum continue to constrain network capacity. As a result, higher-frequency bands with abundant spectra are gradually gaining popularity. However, in urban areas, electromagnetic (EM) waves at these higher frequencies are more susceptible to blockage by structures such as buildings. To mitigate communication gaps and enhance network coverage, it requires more energy to deploy additional relays and BSs. Consequently, providing wireless service coverage using traditional cellular technologies becomes increasingly challenging. In response to the spectrum shortage faced by communication systems, IRSs have emerged as a key solution, offering the potential to achieve high spectrum and energy efficiency [8].
The utilization of machine learning (ML) techniques in wireless communications, particularly in the context of IRSs [9,10,11,12], has garnered significant attention due to their adaptability and the need to operate across broader search areas. In recent years, numerous researchers have explored diverse ML algorithms tailored to the communication sector in an effort to address challenges within this domain. These efforts aim to enable infrastructure to autonomously overcome various obstacles. Typically, ML methods involve learning parameters and optimization models based on input data to achieve specific objectives. Given the substantial volume of data involved, the efficiency and effectiveness of mathematical optimization procedures are crucial in determining the popularity and application of ML models in the current landscape [13].
By minimizing inter-user interference (IUI), improving non-line-of-sight connections, managing channel blockages, and expanding coverage, Intelligent reflecting surfaces (IRSs) have shown significant potential for enhancing wireless communications. Each IRS component can adjust the phase shifts and amplitude reflection coefficients, modifying the phase and amplitude of incoming signals to enable passive beamforming (BF). Unlike traditional MIMO systems, which focus on beamforming at the base station (BS) and user ends, IRS-assisted communication systems require a joint design of passive BF for IRSs and active BF for BS to effectively harness passive BF gains. Additionally, by employing large-scale passive reflecting components, IRS-assisted systems can enhance both energy efficiency (EE) and spectrum efficiency (SE) while remaining cost-effective and energy-efficient. Recent research has explored various aspects of IRS-supported wireless networks, including channel estimation, modulation and encoding, channel modeling, outage probability, SE analysis, symbol error rate (SER) probability, bit error rate (BER) probability, energy efficiency, weighted sum rate, and performance assessment. The extensive research on these topics reflects the enormous potential benefits offered by IRS-enabled environments.
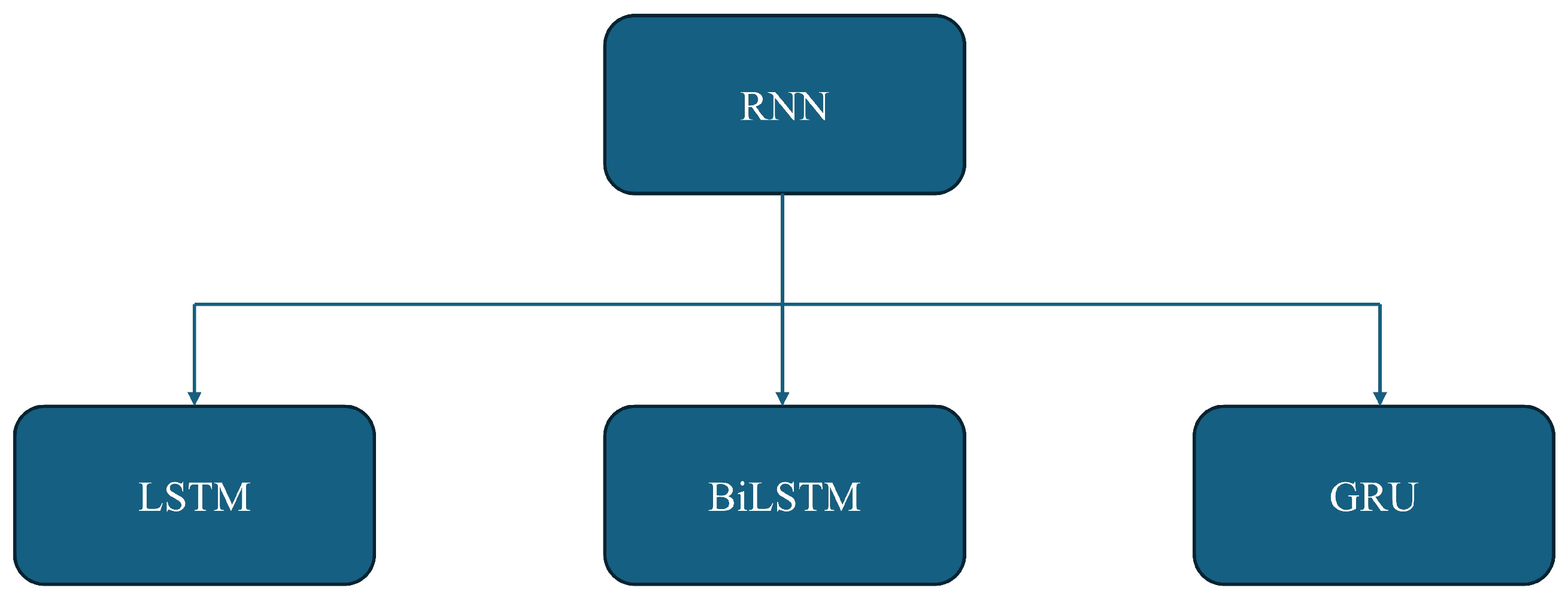
In this paper, we present an overview of the in-depth results of IRS-assisted communication using RNNs. RNN algorithms can efficiently handle temporal dependencies, which can be used for time-varying systems like IRS-based wireless communication systems [14]. In addition, RNN algorithms can help obtain accurate channel state information for the IRS channel. One of the core tasks in IRS-based communication is beamforming, where signals are reflected in specific directions to maximize signal strength and minimize interference. RNNs can help optimize this process by continuously learning the optimal reflection angles and phase shifts over time. RNNs can reduce the computational time required to process data for IRS-based channels. Various RNN algorithms were implemented to evaluate performance in terms of BER and SER probability for IRS-enhanced communication. The types of used RNN algorithms are shown in Figure 1. We examine single-layer and double-layer LSTM, BiLSTM, and gated recurrent units (GRU) models for IRS-based communication. This experiment aims to assess the effectiveness of each RNN model and provide a comparative analysis of the results. In the next phase, we create hybrid models by combining two RNN techniques to observe their performance in IRS-based communication. Specifically, LSTM and BiLSTM are combined to form one hybrid model, and vice versa. Similarly, LSTM and GRU are combined to create another hybrid model, and vice versa. Lastly, we consider a combination of GRU and BiLSTM for IRS-based communication, and vice versa.
Figure 1.
Types of RNN algorithms.
In this paper, the main contributions can be stated as follows:
- The goal of this experiment is to estimate the channel for intelligent reflecting surface-based wireless communication using RNN algorithms. Different combinations of RNN algorithms are considered for channel estimation.
- Rather than using traditional CE techniques like LS and MMSE, the suggested LSTM, BiLSTM, and GRU combined model can jointly estimate and identify the transmitted data from BS to UE.
- Comparative simulation results are presented to evaluate the effectiveness of the suggested system with respect to BER and SER measures.
The rest of the article is organized as follows: Section 3 presents the wireless communication system model with IRS, including the reflecting elements and the training data generation process. Section 4 describes the RNN models, while Section 5 details the proposed model using RNN techniques. Section 6 presents the simulation results, and Section 7 provides the conclusions.
2. Related Works
The utilization of machine learning (ML) techniques in wireless communications, particularly in the context of IRSs [9,10,11,12], has garnered significant attention due to their adaptability and the ability to operate across broader search areas. In recent years, numerous researchers have explored diverse ML algorithms tailored to the communication sector in an effort to address the challenges within this domain. These efforts aim to enable communication infrastructure to autonomously overcome various obstacles. Typically, ML methods involve learning parameters and optimization models from input data to achieve specific objectives. Given the substantial volume of data involved, the efficiency and effectiveness of mathematical optimization procedures play a crucial role in determining the popularity and application of ML models in the current landscape [13]. Today, ML is applied to solve many aspects of IRS-based communication, with key areas of application including channel estimation, beamforming, energy efficiency, resource management, signal detection, and security [15]. Various approaches have been adopted to address different problems, such as supervised learning, unsupervised learning, reinforcement learning, federated learning, graph learning, transfer learning, hierarchical learning, and meta-learning [16]. In supervised learning, models are trained with labeled data using algorithms such as deep neural networks, convolutional neural networks, decision trees, and support vector machines for IRS-based communication [17]. Unsupervised learning, on the other hand, is applied when input data lacks labels, and results are organized into clusters using methods like k-means or unsupervised neural networks. Reinforcement learning has gained particular attention due to its strong problem-solving capabilities. Common reinforcement learning algorithms include Q-learning, actor-critic learning, multi-agent learning, and double-deep Q-learning. Federated learning allows local models to share parameters in order to create a robust global model, which is particularly desirable for user privacy. Graph-based learning, using graph neural networks, has also been studied extensively. Transfer learning, which reuses existing knowledge to speed up the current learning process, is valued for achieving faster training results. Hierarchical learning divides complex tasks into sub-tasks and solves them from the root level. Finally, meta-learning enhances performance by utilizing the experience gained from prior learning tasks. In the literature, various studies have explored recurrent neural network (RNN) techniques for IRS-based communication. A stacked bidirectional LSTM (BiLSTM) architecture for IRS-assisted UAV communication systems was proposed in [12]. A long short-term memory (LSTM)-based neural network for IRS channel tracking and prediction was introduced in [18]. Additionally, Ref. [19] proposed a prediction method that considers the movement of wireless terminals in IRS-based communication as time series data, using LSTM for this purpose. The study in [20] proposed IRS-assisted NOMA network channel estimation using a convolutional neural network (CNN)-LSTM approach. The authors in [21] applied ML techniques to solve complex optimization problems in wireless communication systems. By combining a hybrid approach of ML-driven method and model-free optimization approach, the results show this approach can increase learning efficiency.
3. System Model
3.1. IRS Architecture and Working
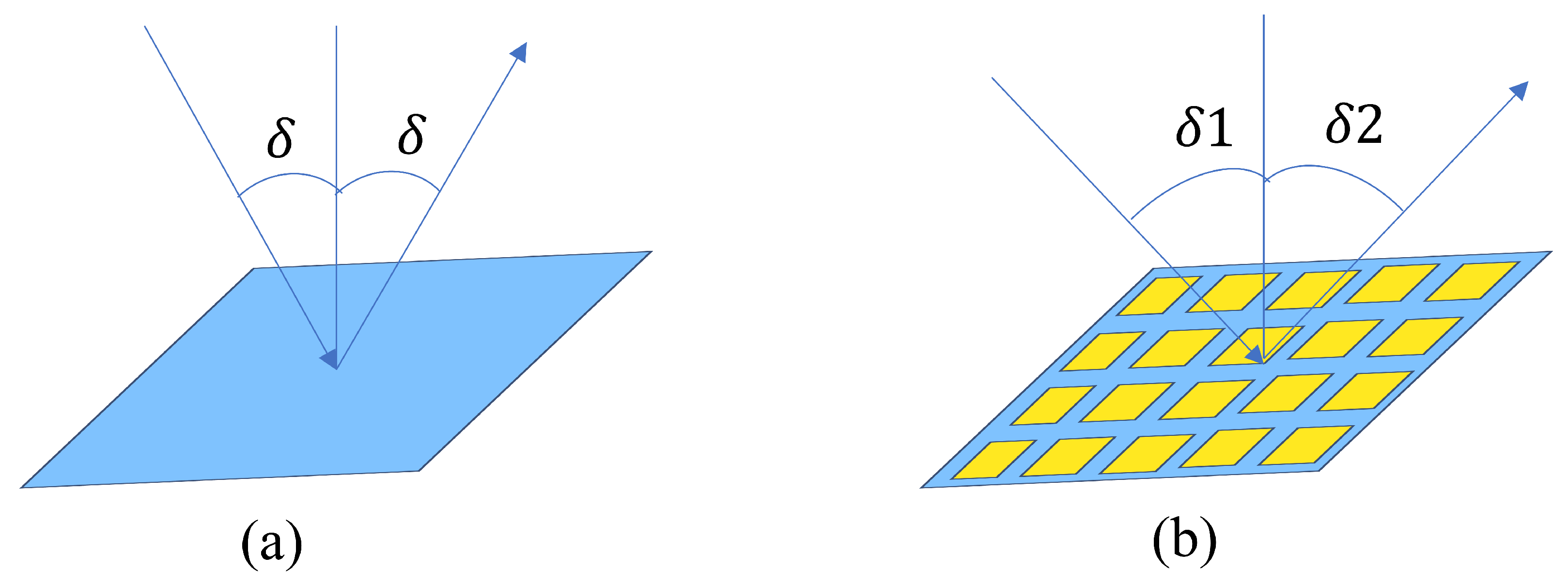
When an electromagnetic (EM) wave encounters the boundary between two isotropic mediums, the relationship between the angles of incidence, reflection, and refraction is described by Snell’s law. In standard cases, the angle of incidence equals the angle of reflection for smooth surfaces, as shown in Figure 2a. However, recent developments in metasurfaces allow modifying surface impedance to induce specific phase shifts between incident and scattered waves. By dividing the surface into many small elements, each programmed with a particular phase shift, the reflected EM wave can be steered to a different angle than predicted by Snell’s law. As shown in Figure 2b, a fully configurable phase shift for each metasurface element can direct the reflected beam to any desired angle. In practice, achieving precise or continuous phase shifts is challenging due to control complexities, making signal processing and machine learning techniques useful for designing IRSs [22].
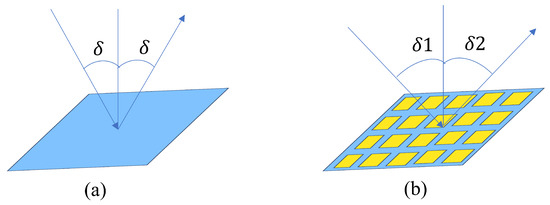
Figure 2.
(a) The regular reflector; (b) IRS reflector.
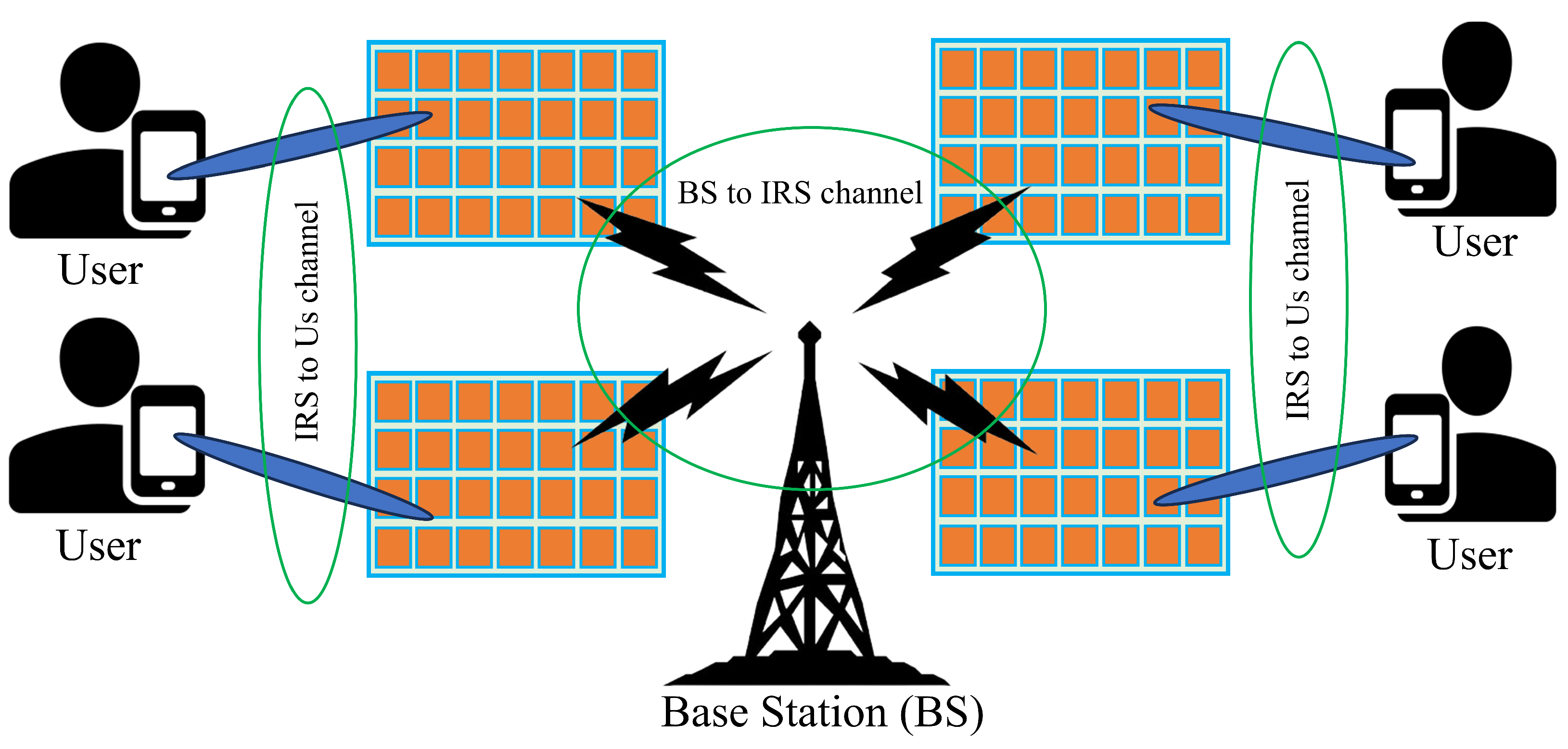
IRSs are made up of a wide range of inexpensive passive reflecting components that are capable of adjusting the incident electromagnetic wave phase, amplitude, and even polarization. The propagation environment of wireless signals may be dynamically adjusted using these programmable surfaces. For a variety of purposes, including boosting signal strength, lowering interference, or covering regions with poor signals, IRSs in wireless communication systems work by reflecting and redirecting signals. An example of an IRS-aided wireless system in action is shown in Figure 3.
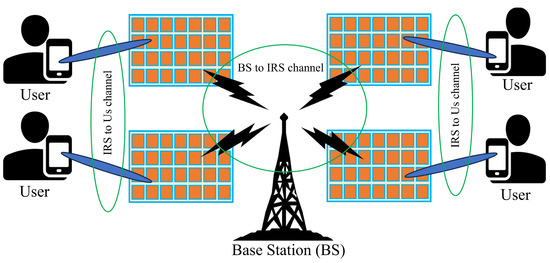
Figure 3.
IRS working principle in wireless mobile communication system.
Here is how IRSs work in a typical wireless communication setup:
Signal Transmission:
A signal is transmitted from a BS or user toward the IRS.
Surface Reflection: The IRS components are adjusted to modify the incoming signal’s phase and/or amplitude in order to direct it toward the intended target, which might be a BS or another user. Signal Reception: The modified signal reaches the receiver with enhanced quality, having avoided obstacles, reduced interference, and optimized the transmission path for improved signal strength and reliability.
In order to provide a smart propagation environment where wireless communication is boosted without the need for active, power-hungry components like amplifiers, IRSs may be managed in real-time to react to changing environmental circumstances, such as user movement or barriers. Key motivations behind using IRSs in wireless communication are listed as follows:
- Improved signal coverage: IRSs may greatly increase the coverage area, especially in areas with many impediments, by reflecting signals around objects like walls or buildings that often impede wireless signals.
- Energy efficiency: IRSs may reflect signals with low energy usage as it is made up of passive components that do not require active, power-hungry transmitters. This lowers the total energy consumption of wireless networks.
- Reduced interference: IRSs may reduce interference by carefully rerouting communications away from places or devices that cause interference. This is especially helpful when there are lots of devices interacting at once in congested areas.
- Enhanced spectral efficiency: IRSs aid in the effective use of the available spectrum by modifying the wireless environment and boosting the data rates and overall capacity of wireless networks.
- Cost-effective deployment: As an IRS is passive, it is less expensive to install and operate than power-hungry relays or new base stations. This makes it a more cost-effective option overall.
- Support for 5G and beyond: By improving communication at high-frequency bands like millimeter waves (mmWave), which are vulnerable to high route loss and limited penetration, IRSs can supplement 5G technology.
The common perception of relays is that they are active components that require a separate power supply to function. The devices are furnished with active electronic components, including mixers, low-noise amplifiers for receiving, power amplifiers for transmission, and digital-to-analog converters (DACs and ADCs). Decoder-and-forward (DF) and amplify-and-forward (AF) relays usually need a number of electrical components. This means that relays to implement multiple-antenna systems in millimeter and submillimeter wave frequency bands may be expensive and energy-intensive [23]. On the other hand, IRSs are composite material layers composed of printed metallic or dielectric patches on a grounded dielectric substrate. Low-power, low-complexity electronic circuits (switches or varactors) guarantee their configurability [24]. Since discrete power amplifiers, mixers, and DACs/ADCs are typically not needed, IRSs are intended to be less complicated than relays, especially when IRSs are implemented in large quantities and with low-cost big-area electronics [25].
The additive noise that exists in relays and degrades the functionality of traditional relaying methods is caused by the active electrical components employed in relays [25]. However, additive noise does not affect IRSs that exhibit aberrant reflector behavior. Nevertheless, phase noises might interfere with them [26]. Furthermore, they are unable to amplify or renew the impulses if they are almost inactive [27].
The spectral efficiency of relay-assisted systems depends on the duplexing method. A half-duplex (HD) reduces the rate by half but can improve the signal-to-noise ratio. A full-duplex (FD) avoids this but introduces interference from simultaneous transmissions. IRSs bypass these issues, as they do not face HD constraints or self-interference and can enhance signal combinations by optimizing their reflection properties [25].
3.2. IRS System Structure
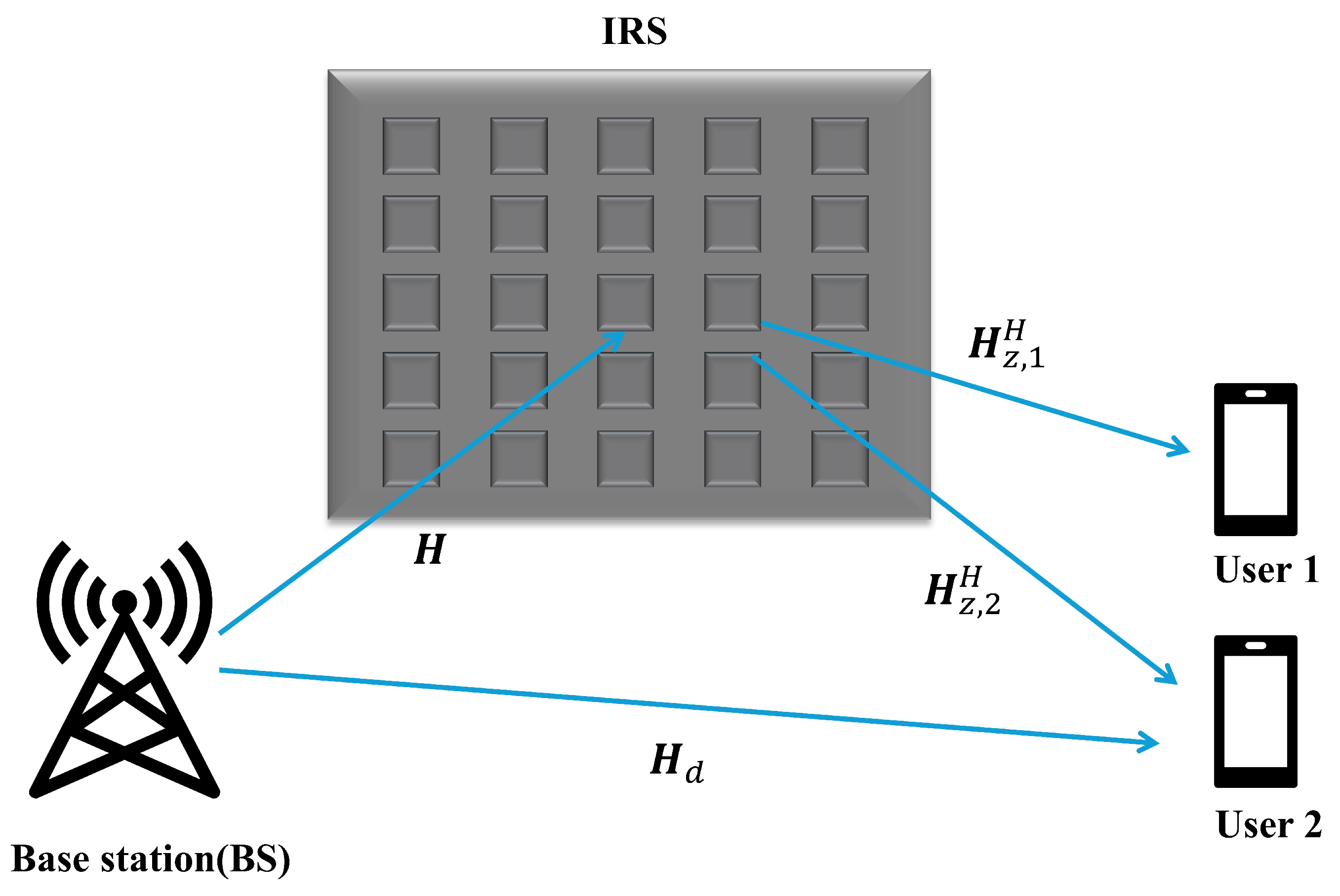
The IRS-assisted communication model consists of a transmitter, a receiver, and IRS-reflecting elements. In this study, we consider IRS-assisted communication as shown in Figure 4. We consider each user, I, to have a single antenna, and the serving base station (BS) has a uniform linear array of L antennas. The number of IRS elements is considered as N. The received signal for the i-th () user from the IRS can be expressed as follows:
where is the received signal at the i-th user, is the transmitted signal, is the channel matrix from the BS to IRS, is the channel from the IRS to the i-th user, and is the additive white Gaussian noise (AWGN) at the i-th user. Again, represents a diagonal matrix that contains phase shift values of reflective elements of the IRS, where , and and denote the phase coefficient and amplitude of the i-th reflective element, respectively. For the experiment in this study, we consider . We also consider that the direct link between BS and the user exists and is expressed as . The is considered as a diagonal matrix, i.e., . The channel from the BS to the user via the IRS can be transformed as follows:
where is the cascaded channel for the i-th user and , which relies on the downlink channel state information. We can write the total channel using both the cascaded channel and direct channel as follows:
where the direct communication link is from the BS to the i-th user.
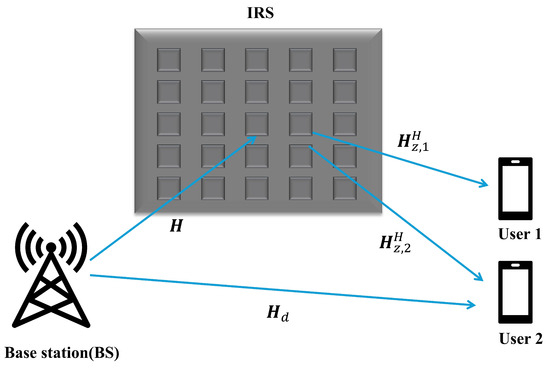
Figure 4.
IRS-based communication system.
Figure 4.
IRS-based communication system.
The three-dimensional (3D) Saleh–Valenzuela channel model is adapted for millimeter-wave (mmWave) propagation [28]. This method is a statistical channel model in a multipath propagation scenario. The channel model for mmWave propagation can be expressed as follows [10]:
where is the channel vector, the t-th path complex gain is represented as , and the total number of paths is T. The elevation angle of departure and azimuth angle of departure for transmission signals are and , respectively. The array response vector is expressed as . We can express the array response vector as follows:
where is the carrier wavelength, d is the antenna spacing, , , and (). For proper communication, the antenna spacing satisfies the condition of . Again, the BS channel to the IRS channel can be expressed as follows:
where represents the number of paths between the BS and IRS, stands for the complex gain of the paths available from the BS to IRS, is the steering vector related to IRS elements, and is the steering vector connected to the BS for the -th path. To define the channel between the IRS and the user, the channel matrix can be described as follows:
where the complex gain of paths is represented as ; is the number of paths between the IRS and the user, is the departure angle in the azimuth direction, and is the elevation angle. The array response vector is represented as . Thus, the total channel can be written as follows:
3.3. Data Generation for Training from the IRS Network
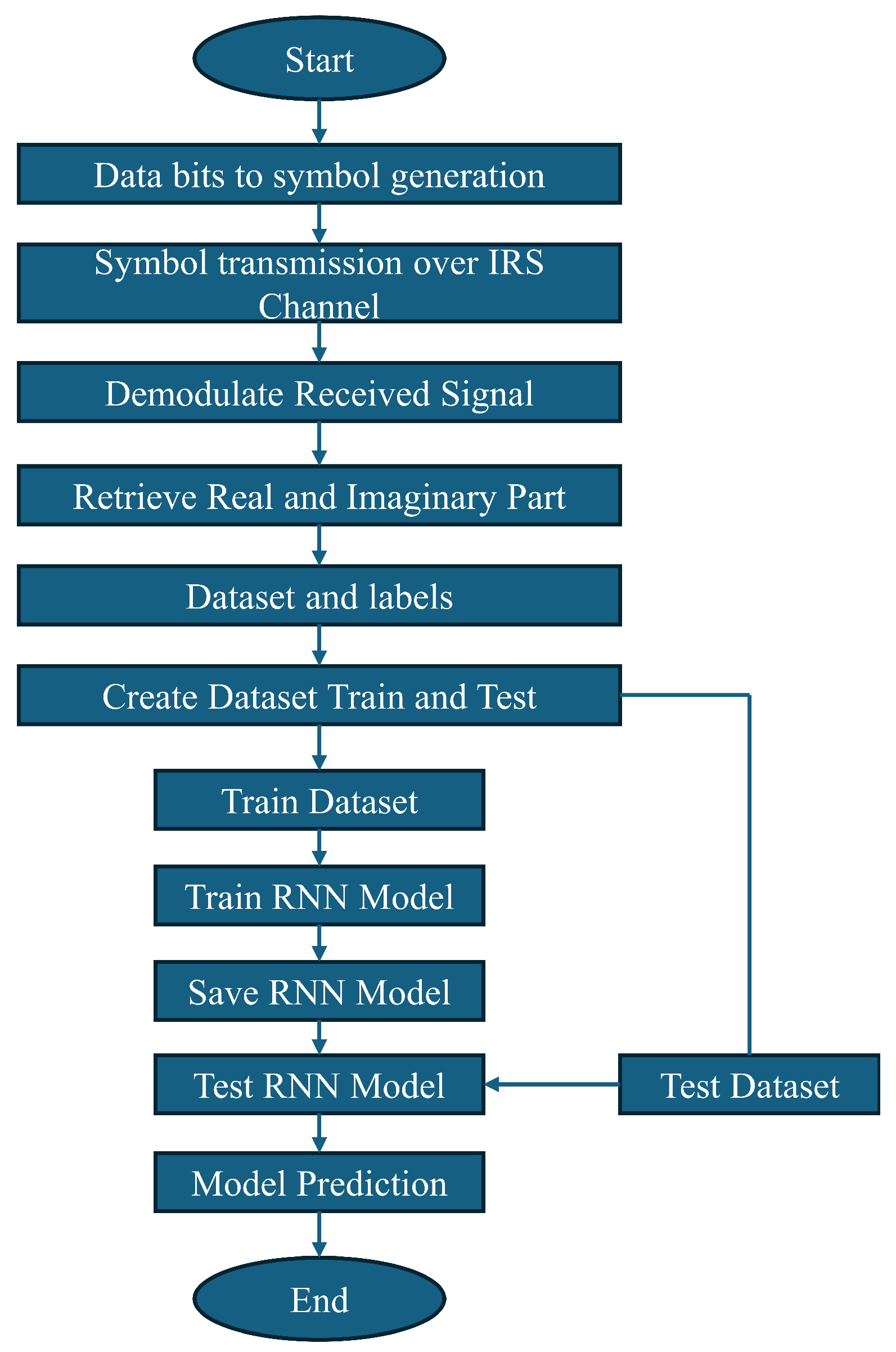
The data generation and model training processes are illustrated in Figure 5. In the first phase, a random binary data sequence is generated for transmission. The generated bits are then transformed into OFDM symbols, using 128 subcarriers with quadrature phase shift keying (QPSK) modulation for symbol generation. The data symbols are transmitted through a simulated transmission channel that considers IRS reflection. The channel state information (CSI) is acquired using the Rayleigh fading model. Pilot signals are transmitted through the IRS channel, and the CSI is estimated based on the received data. Once the CSI is obtained, the training signals are transmitted through the channel and used for model training. The channel simulation parameters are listed in Table 1. The direct link is also considered when the received signal is calculated. Upon reception, the signal is demodulated, and the data symbols are retrieved. Sixteen unique symbols are used, and each symbol is assigned as a label value for classification. The real and imaginary parts of the symbols are separated to generate training data, as complex numbers cannot be directly used in the machine learning training process. A total of 64,000 samples were generated for the training and testing process. Of these, 512,000 data symbols were used for training, and 128,000 symbols were used for testing. Two separate datasets were saved as training and test datasets for model training and evaluation. Each model was then trained using RNN techniques, and the training progress was monitored. Hyperparameters were tuned to optimize performance and improve model accuracy. After training, the test data were used to evaluate each model’s performance on unseen data and were measured as test accuracy. Following this step, the model could be used for IRS-based channel prediction.
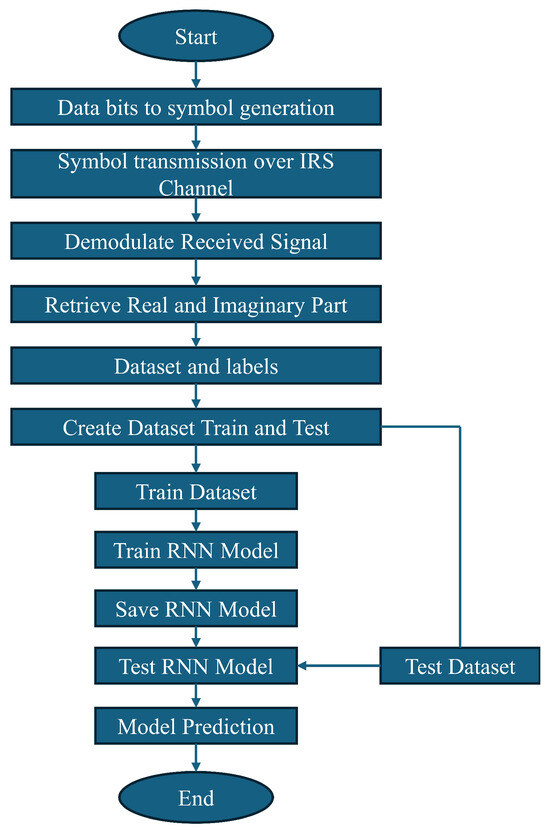
Figure 5.
Training data generation and training process flowchart.

Table 1.
Simulation parameters.
4. Recurrent Neural Network Models
This section briefly describes the fundamentals of LSTM, Bi-LSTM, and GRU approaches. After that, the proposed model descriptions are given.
4.1. LSTM Working Structure
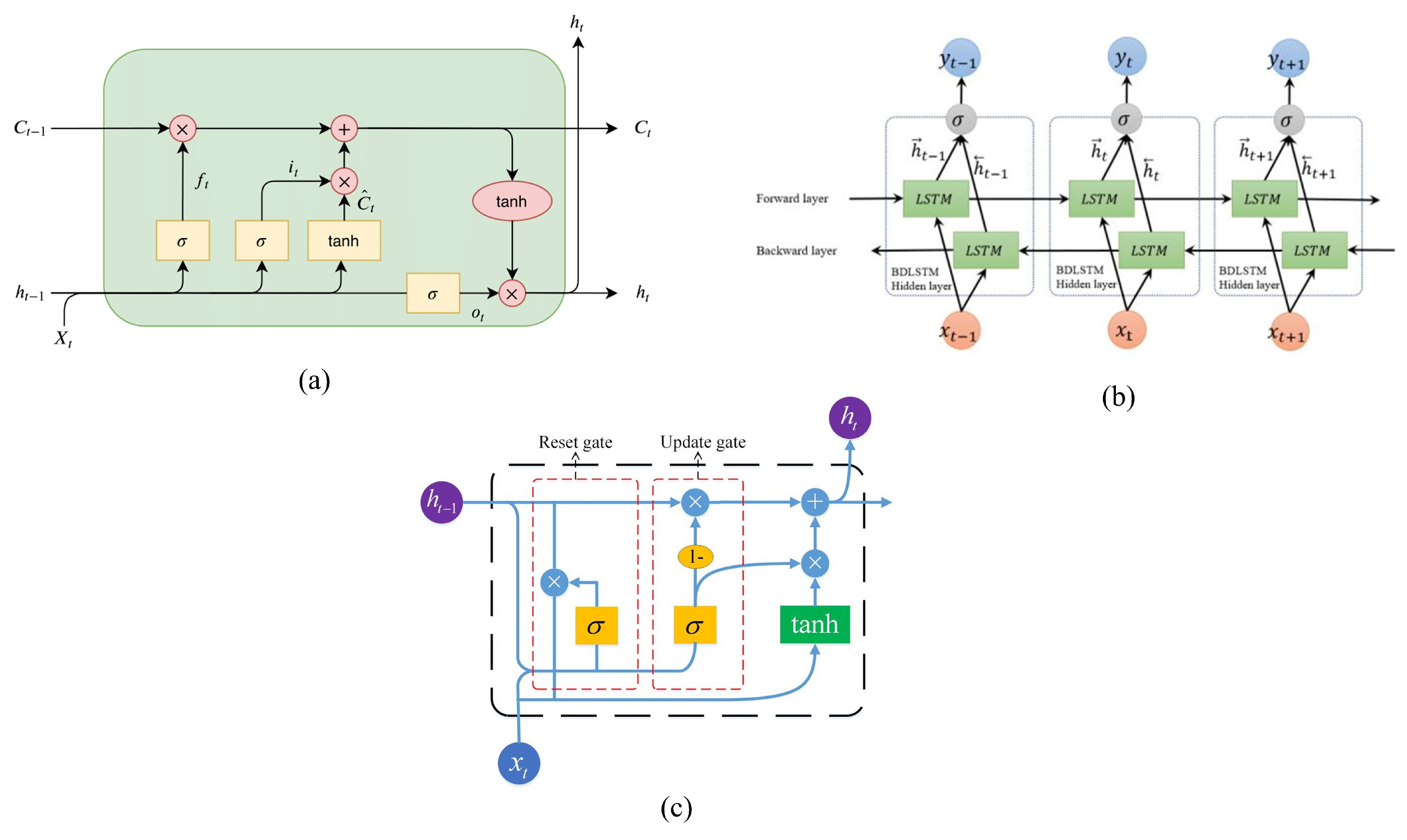
Specialized memory cells with gating mechanisms are incorporated into LSTM networks, enabling them to store, update, and retrieve data selectively over long durations. Because of their distinct architecture, LSTM networks are better able to learn complex temporal patterns and relationships than ordinary RNNs, which helps them overcome some of their limitations. The input gate, forget gate, output gate, and cell state are the main parts of an LSTM unit. They manage information flow and maintain pertinent data throughout several time steps. LSTM networks are powerful tools for jobs requiring long-range temporal modeling and prediction because they can capture complex dependencies and context within sequential data by efficiently controlling the flow of information through the network. Figure 6a shows the internal structure of an LSTM cell. The gates of the LSTM can be mathematically expressed as follows:
where at time step t, the input is , at the time step, the hidden state is expressed as , from the previous time step, is the cell state, the input gate vector is , the forget gate vector is , the update gate vector is , the output gate vector is , is the sigmoid activation function, element-wise multiplication is represented as ⊙, the weight matrix is W, and the bias vector is b. The input layer is connected to the LSTM layer, and the data then move through a fully connected layer and a dropout layer. Lastly, a classification layer is applied to determine the class that the input data belong to. The model can efficiently process sequential data, identify pertinent features, and produce precise predictions due to its architecture.
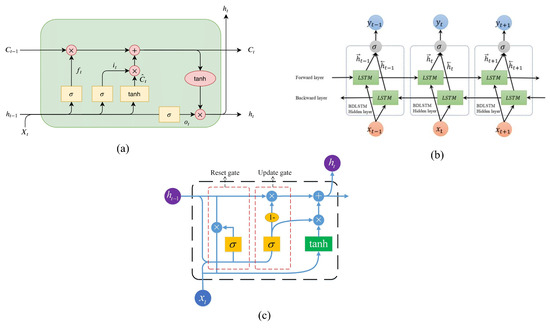
Figure 6.
(a) Internal structure of LSTM [29], (b) internal structure of BiLSTM [30], (c) internal structure of GRU [31].
4.2. BiLSTM Working Structure
BiLSTM networks are extensions of the traditional LSTM architecture designed to store dependencies in sequential data in both directions. BiLSTMs employ two distinct LSTM layers (one for forward-processing input sequences and another for backward-processing) instead of traditional LSTMs, which process input sequences sequentially from the past to the future. The network’s bidirectional processing allows future and past contexts, which facilitates a more full understanding of the input sequence. The internal organization of the BiLSTM is depicted in Figure 6b. For every time step in a BiLSTM, the output of each LSTM layer is merged, combining data from both directions. This concatenated form, which incorporates context from the past and future, represents the input sequence as a whole. Tasks requiring context from both sides, like named entity recognition, sentiment analysis, and part-of-speech tagging, are especially well-suited for BiLSTMs. Because BiLSTMs are bidirectional, they are effective at capturing contextual information and long-range relationships, which improves their performance in a variety of sequence modeling applications. But keep in mind that because BiLSTMs must process input sequences in both ways, they may add to the computational complexity. However, they are a popular option in many sequence prediction and natural language processing applications due to their capacity to take advantage of bidirectional context. BiLSTM can be expressed as follows [32]:
where the activation function is expressed as , the forward and backward time steps are represented as and , the transmitted signal is , the hidden state of the previous step is , the hidden state of next state is , the weights for the forward and reverse direction are and , learnable biases of forward and reverse directions are and , is the forward direction of network output, and is the backward direction of the LSTM network output, respectively. A dropout layer comes after the BiLSTM layer receives the input data. The input data are then classified using a fully connected layer and a classification layer. This architecture improves the model’s capacity to effectively minimize interference by allowing it to capture context information from the past and the future.
4.3. GRU Working Structure
RNN architectures, such as the vanishing gradient problem and the incapacity to accurately capture long-term dependencies, are addressed by the GRU. Because GRUs are made to update and reset their internal state selectively, they can avoid consuming superfluous memory and retain pertinent information across longer sequences. The update gate and the reset gate are two of the main parts of the GRU design. Figure 6c illustrates GRU’s internal organization. At every time step, these gates decide which data to keep and which to delete, controlling the flow of information through the network. At every time step, these gates decide which data to keep and which to delete, controlling the flow of information through the network. In addition, GRUs have a candidate state calculation phase that uses the reset gate and the current input to create a new candidate state. The final concealed state for the current time step is then created by combining the output of the update gate with this candidate state. GRUs have several advantages over conventional RNNs, one of which is their reduced parameter requirements and improved ability to capture long-term dependencies. Because of this, GRUs are especially well suited for sequential data tasks including time series prediction, machine translation, and language modeling. Furthermore, because of their more straightforward architecture, GRUs can be trained more quickly than LSTMs, which makes them a preferred option for many recurrent neural network applications. The GRU calculation procedure is explained using the formulas as follows [33]:
where the biases are expressed as, respectively, , , and . Again, , , , , , and are weight matrices. is used to calculate the gate activation function and expressed as a sigmoid function. The output of the hidden layer at the current instant is denoted as , while the input state and the output of the hidden layer at the preceding instant are combined to yield . The state activation function is computed via the hyperbolic tangent function, . This uniformity makes it possible to assess the effectiveness of various RNN techniques for interference management fairly.
5. Proposed Model Architecture
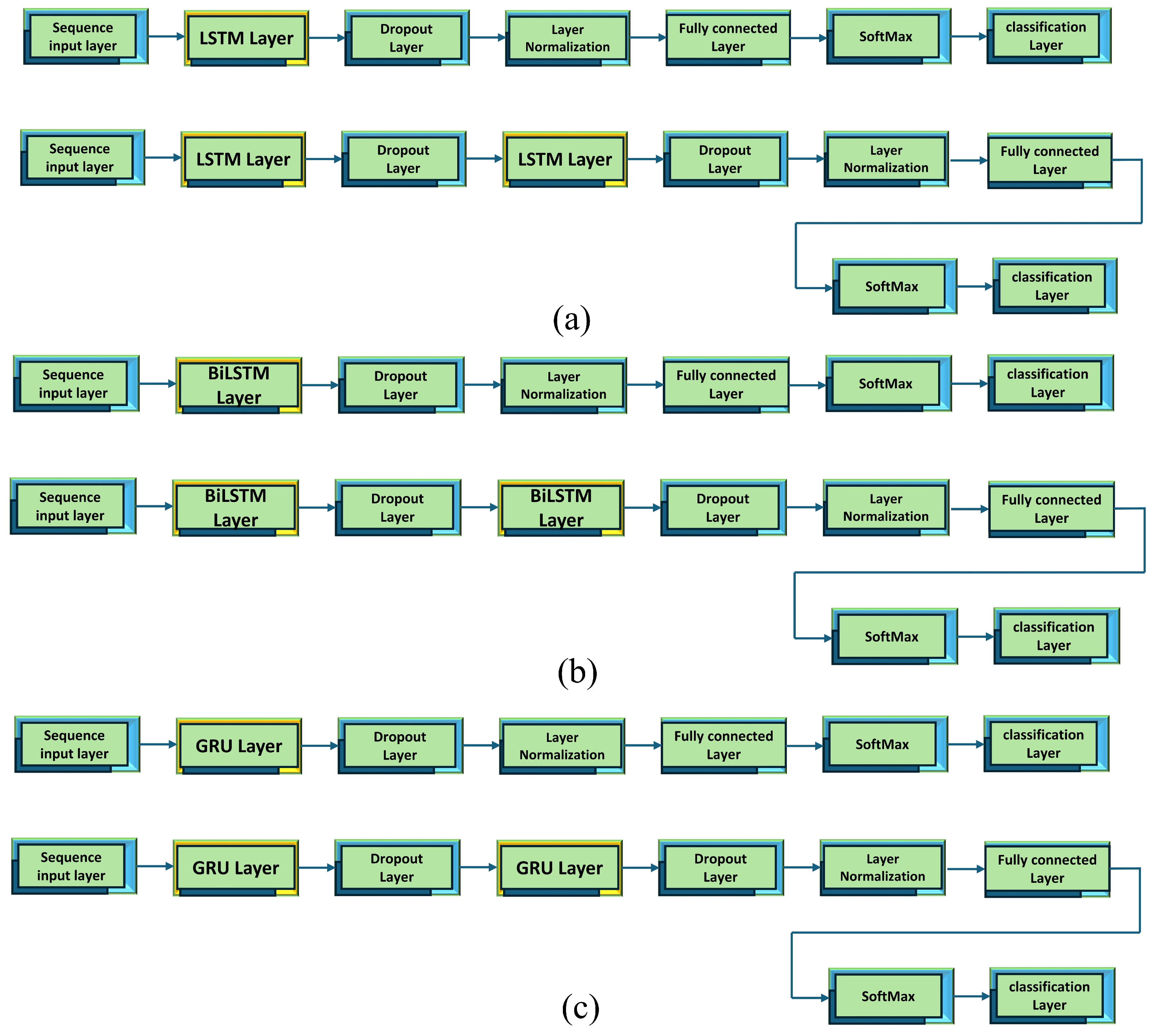
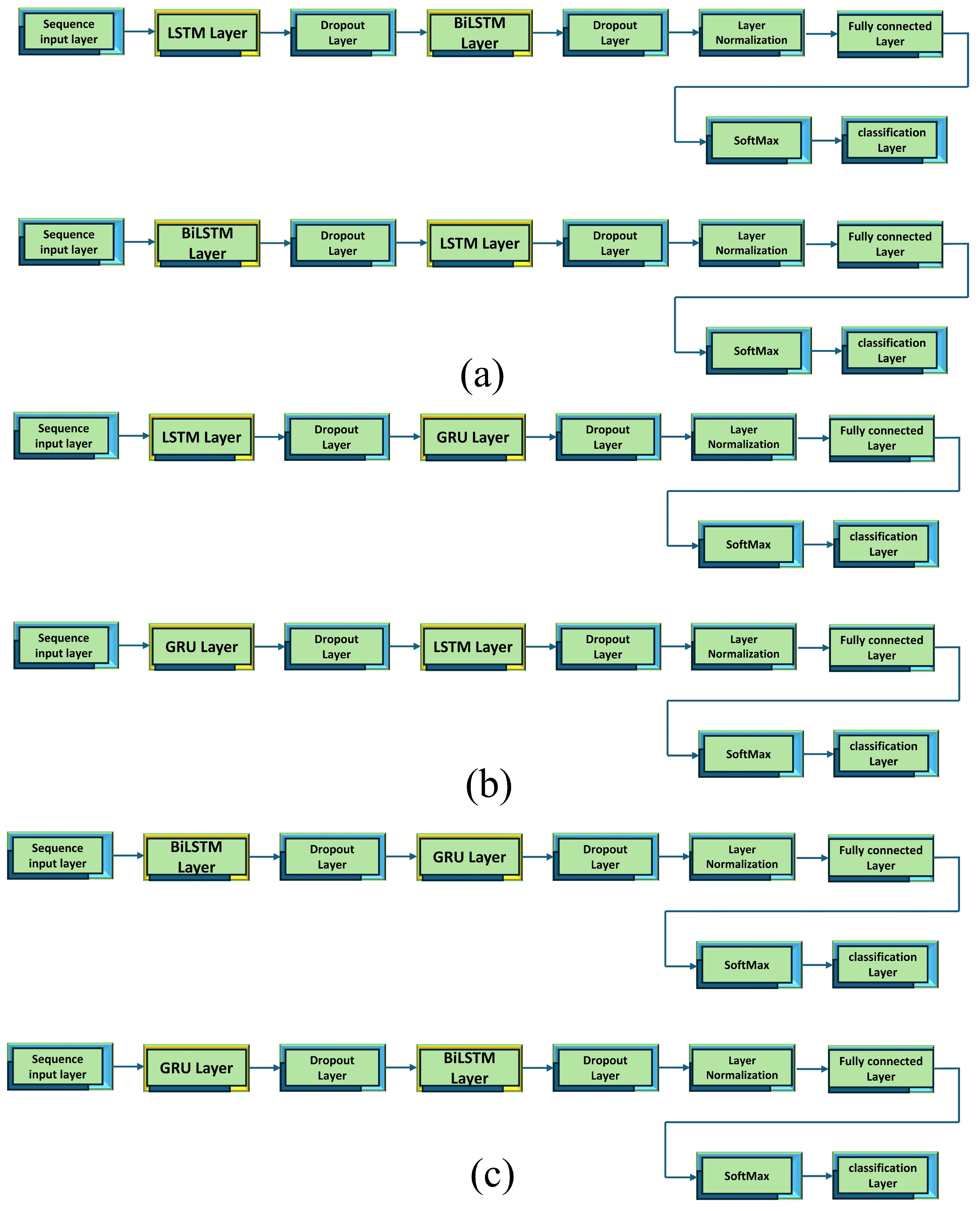
We consider different RNN approaches for this study to estimate the channel performance for IRS-based communication. Two different approaches are considered for the experiment. First, the RNN techniques, namely LSTM, BiLSTM, and GRU, are tested with a single layer and double layer. Figure 7 shows the model architecture for a single RNN approach. To make a fair comparison, we keep the overall architecture similar for each technique. Each layer starts with a sequence input layer followed by an RNN layer and a dropout layer. Another RNN layer and dropout layer are added for the double layer. After that, layer normalization is applied and a fully connected layer is added. Finally, softmax and classification layers are used to classify the input data. LSTM, BiLSTM, and GRU single and double-layer architectures are shown in Figure 7a–c. In the next step, a hybrid approach is applied to see the performance of each combination. We consider combining two approaches, i.e., LSTM-BiLSTM, LSTM-GRU, and BiLSTM-GRU, and vice-versa. The model architectures for the LSTM and BiLSTM layers are shown in Figure 8a. The positions of the LSTM and BiLSTM layers are interchanged to observe the model accuracy effect. Similarly, the LSTM and GRU layer-based model architectures are shown in Figure 8b. The LSTM and GRU layers are switched for model accuracy observations. Lastly, BiLSTM and GRU model architectures are presented in Figure 8c. Here, the positions of the BiLSTM layer and the GRU layer are changed for model accuracy improvements. The other parameter for model training is presented in Table 2.
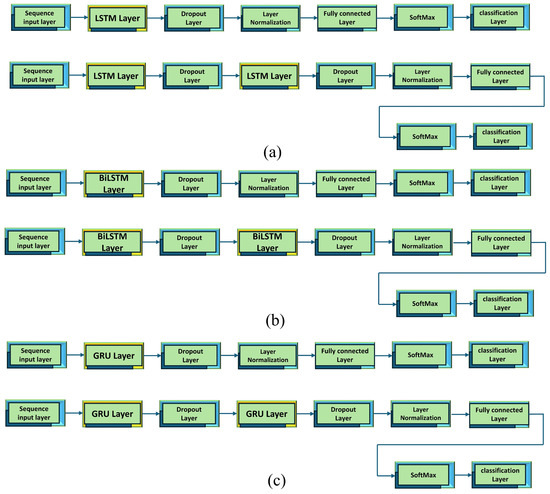
Figure 7.
(a) LSTM model for the single layer and double layer, (b) BiLSTM model for the single layer and double layer, (c) GRU model for the single layer and double layer.
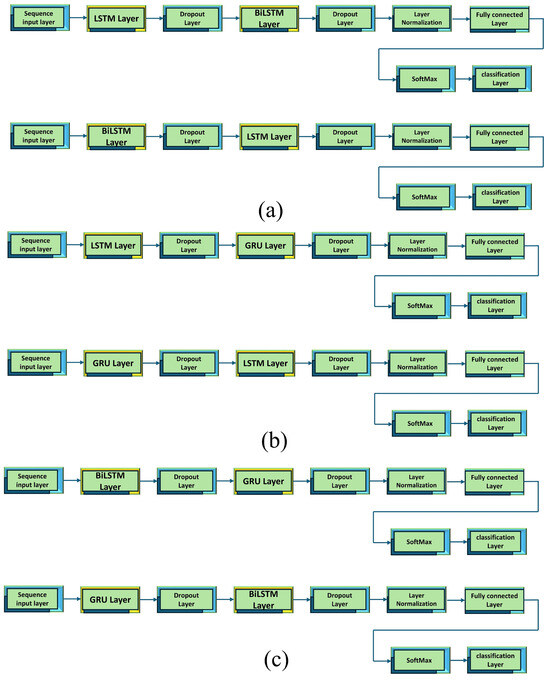
Figure 8.
(a) LSTM and BiLSTM combination model, (b) LSTM and GRU combination model, (c) BiLSTM and GRU combination model.

Table 2.
Machine learning parameters.
6. Results
6.1. Model Training
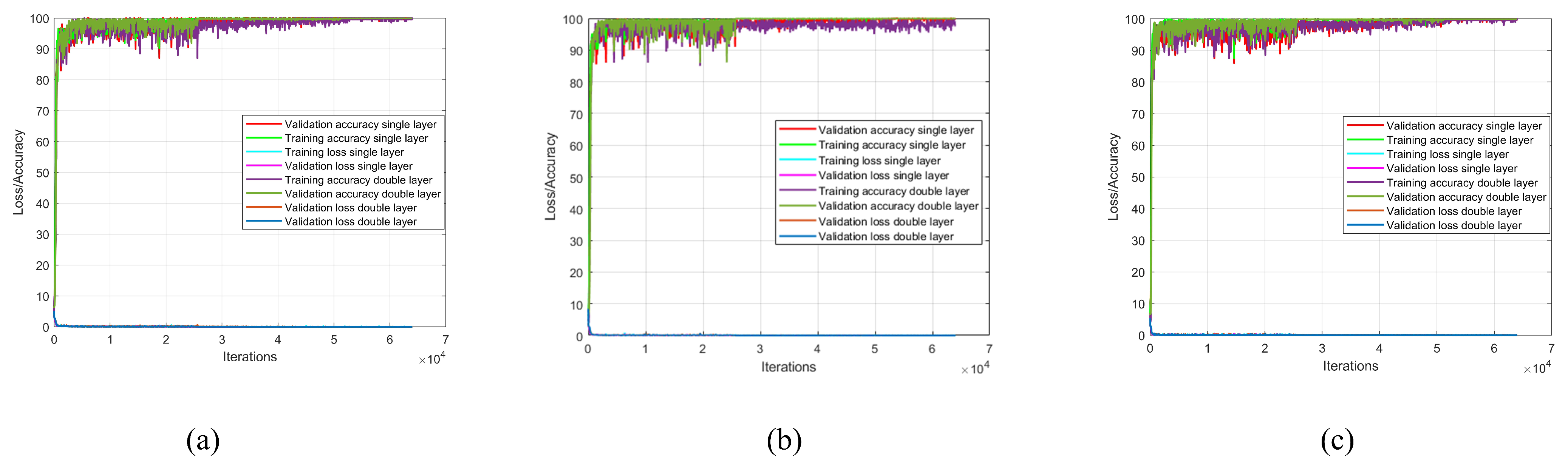
Each model is trained using the generated dataset. First, we examined the LSTM model with the generated dataset under different hyperparameter setups. Table 2 lists the optimal hyperparameters for the best training results. Figure 9a shows the training progress of the LSTM with single and double layers. Both models exhibit a similar trend in reducing loss; however, the single-layer LSTM model reaches stable accuracy sooner than the double-layer model. For the BiLSTM model, the trend of the loss and accuracy curves during the training phase is shown in Figure 9b. As the number of layers increases, the training accuracy remains almost unchanged. The accuracy and loss of GRU-based models are depicted in Figure 9c, where the double-layer GRU achieves slightly higher accuracy than the single-layer GRU model.

Figure 9.
Model training summary; (a) LSTM single and double layer, (b) BiLSTM single and double layer, and (c) single and double layers.
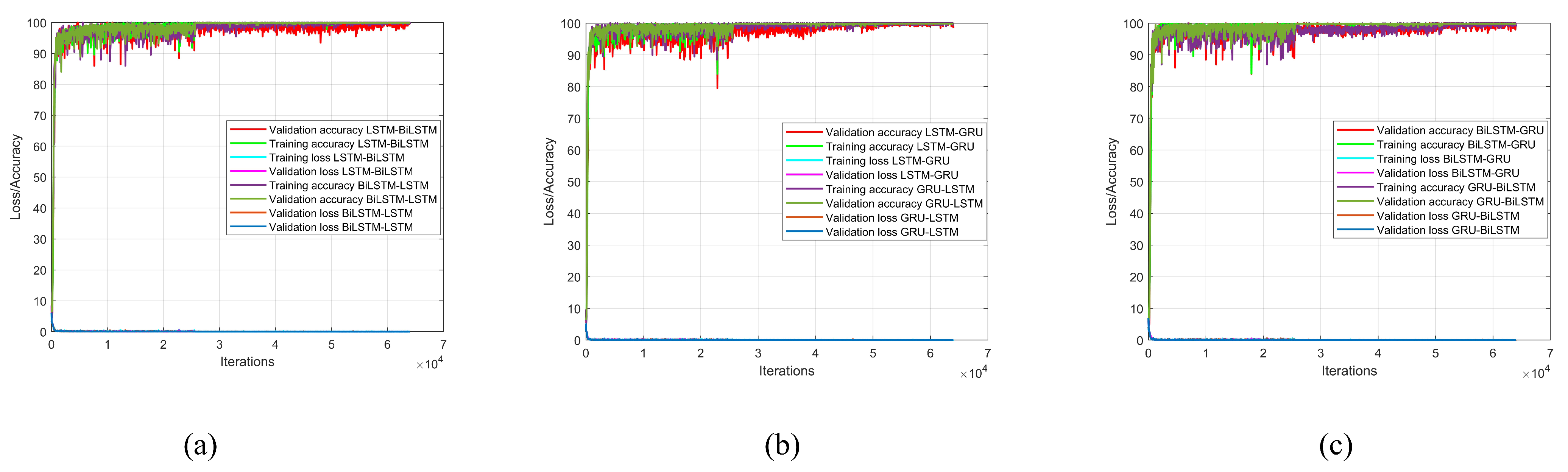
Figure 10 shows the training and loss curves for the hybrid models. The training curves for the LSTM-BiLSTM model are presented in Figure 10a. The validation accuracy for the LSTM-BiLSTM model is lower than that of the BiLSTM-LSTM model, indicating that the BiLSTM-LSTM model can extract more features from the training data and is expected to yield better results compared to the LSTM-BiLSTM model. Figure 10b displays the training curves for the LSTM-GRU and GRU-LSTM models. At the beginning of the training process, the LSTM-GRU model shows instability, but by the end of the training, it becomes more stable and comparable to the GRU-LSTM model. The BiLSTM-GRU and GRU-BiLSTM models are shown in Figure 10c. Both models exhibit similar trends and are expected to have comparable prediction results.
Figure 10.
Model training summary (a) LSTM-BiLSTM model and BiLSTM-LSTM model, (b) LSTM-GRU model and GRU-LSTM model, and (c) BiLSTM-GRU model and GRU-BiLSTM model.
6.2. Results of Individual RNN Techniques
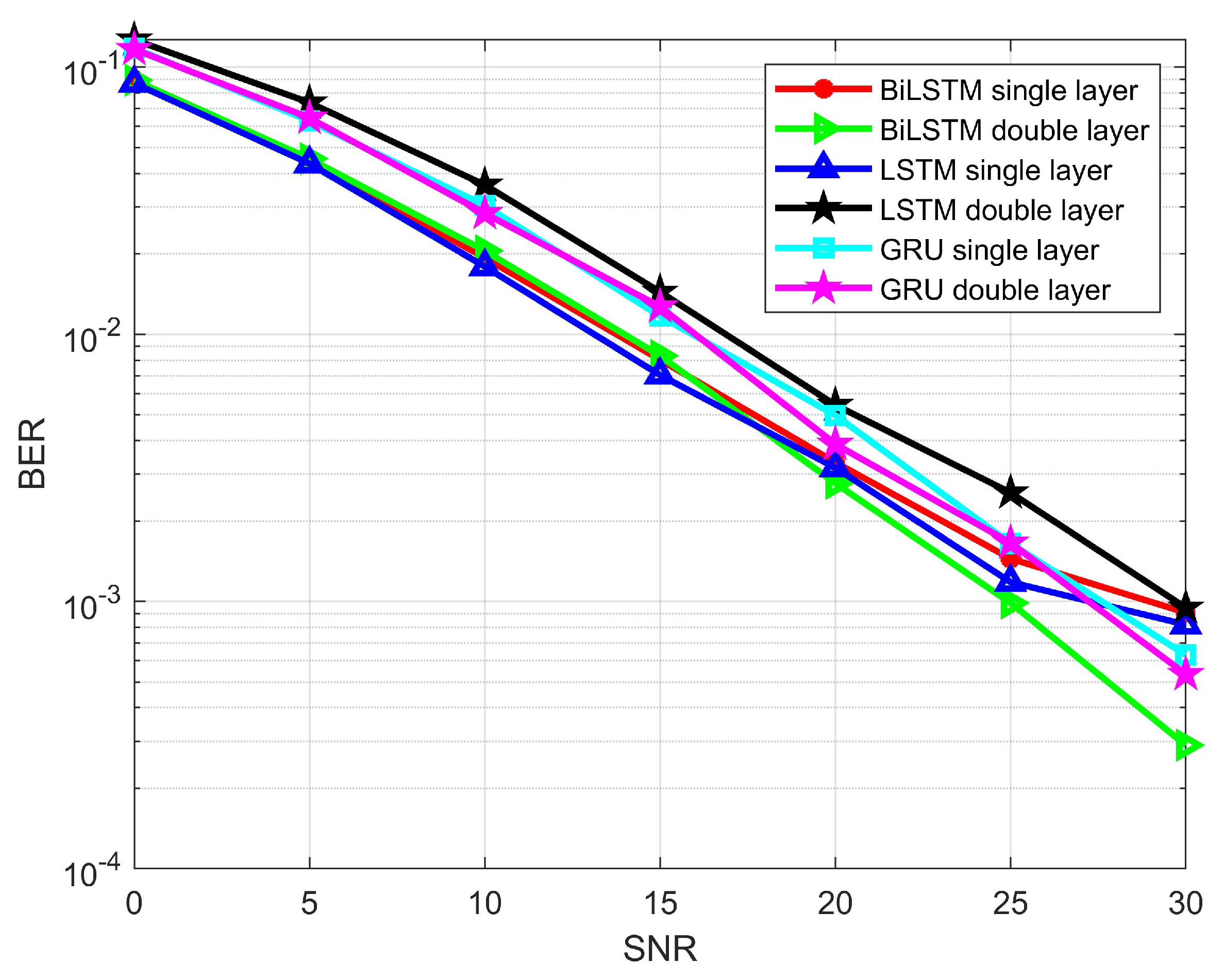
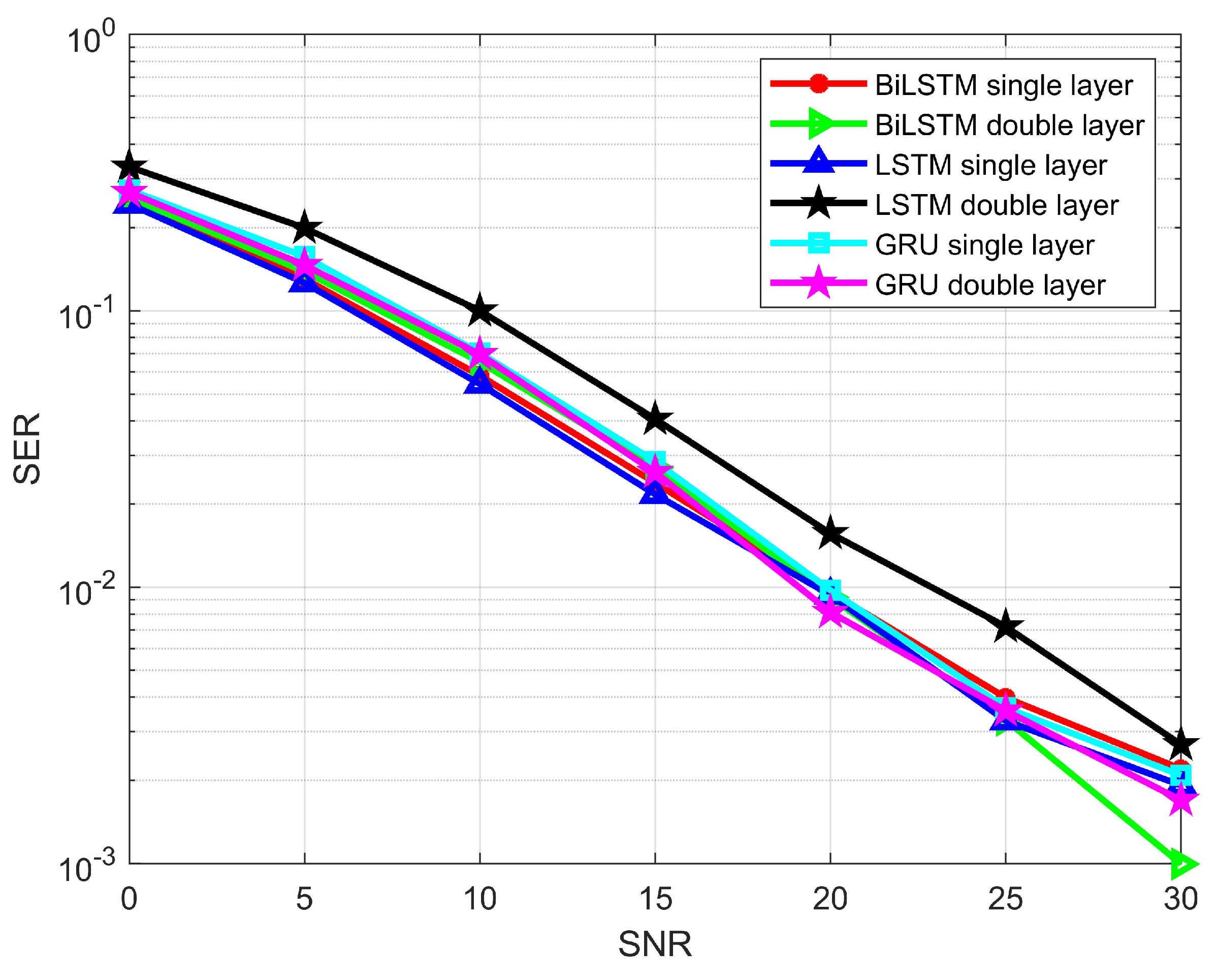
We first describe the results of the RNN techniques with single and double layers. The BER performance of the single-layer LSTM is shown in Figure 11. At an SNR value of 30 dB, the BER reaches . However, when the number of layers is increased, the performance decreases to . This decline is likely due to the feature extraction process being less effective in the double-layer configuration compared to the single-layer setup. A similar trend is observed in Figure 12, which depicts the SER for both the single-layer and double-layer LSTM models. The single-layer BiLSTM, on average, performs better than the LSTM, with the best performance achieved by the double-layer BiLSTM, as shown in Figure 11 and Figure 12. At 30 dB SNR, the BER is , and the SER is . For the single-layer GRU, the BER performance is better than both the LSTM and the single-layer BiLSTM. In contrast, the double-layer GRU shows better performance across all SNR ranges, with the second-highest BER performance, as GRU is effective in feature extraction.
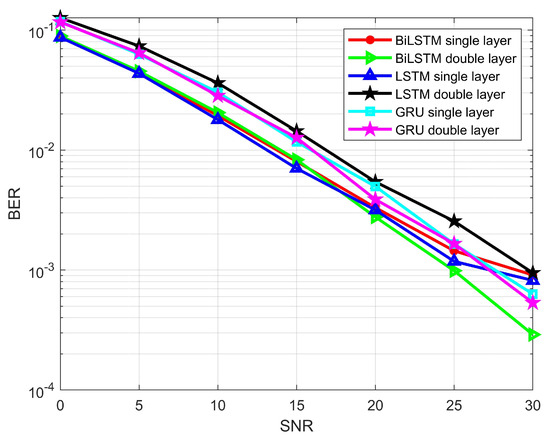
Figure 11.
BER of LSTM, BiLSTM, and the GRU model for single and double layers.
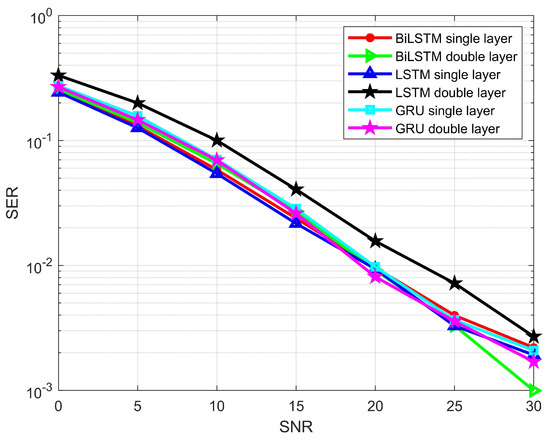
Figure 12.
SER of LSTM, BiLSTM, and the GRU model for single and double layers.
6.3. Hybrid Model Performances
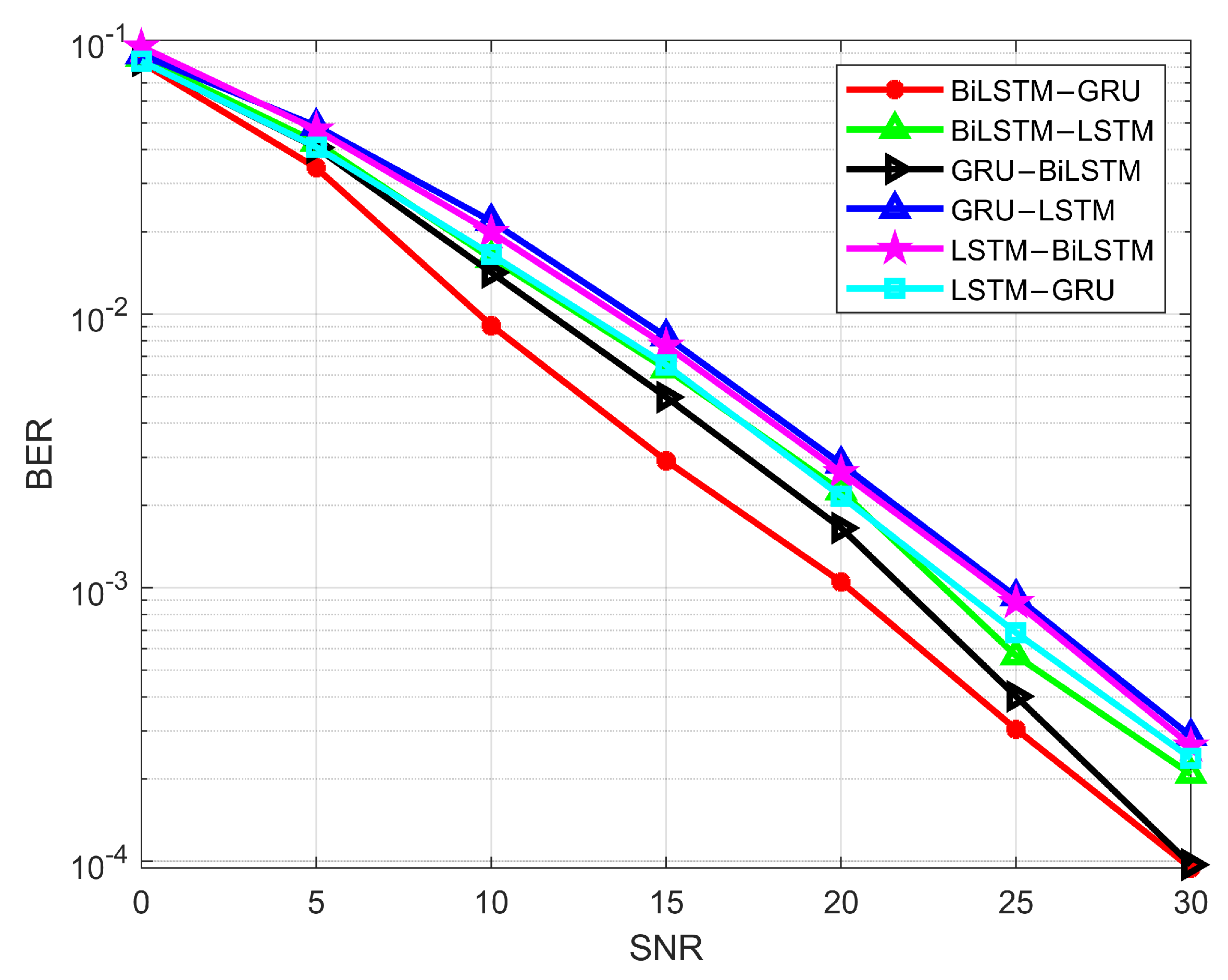
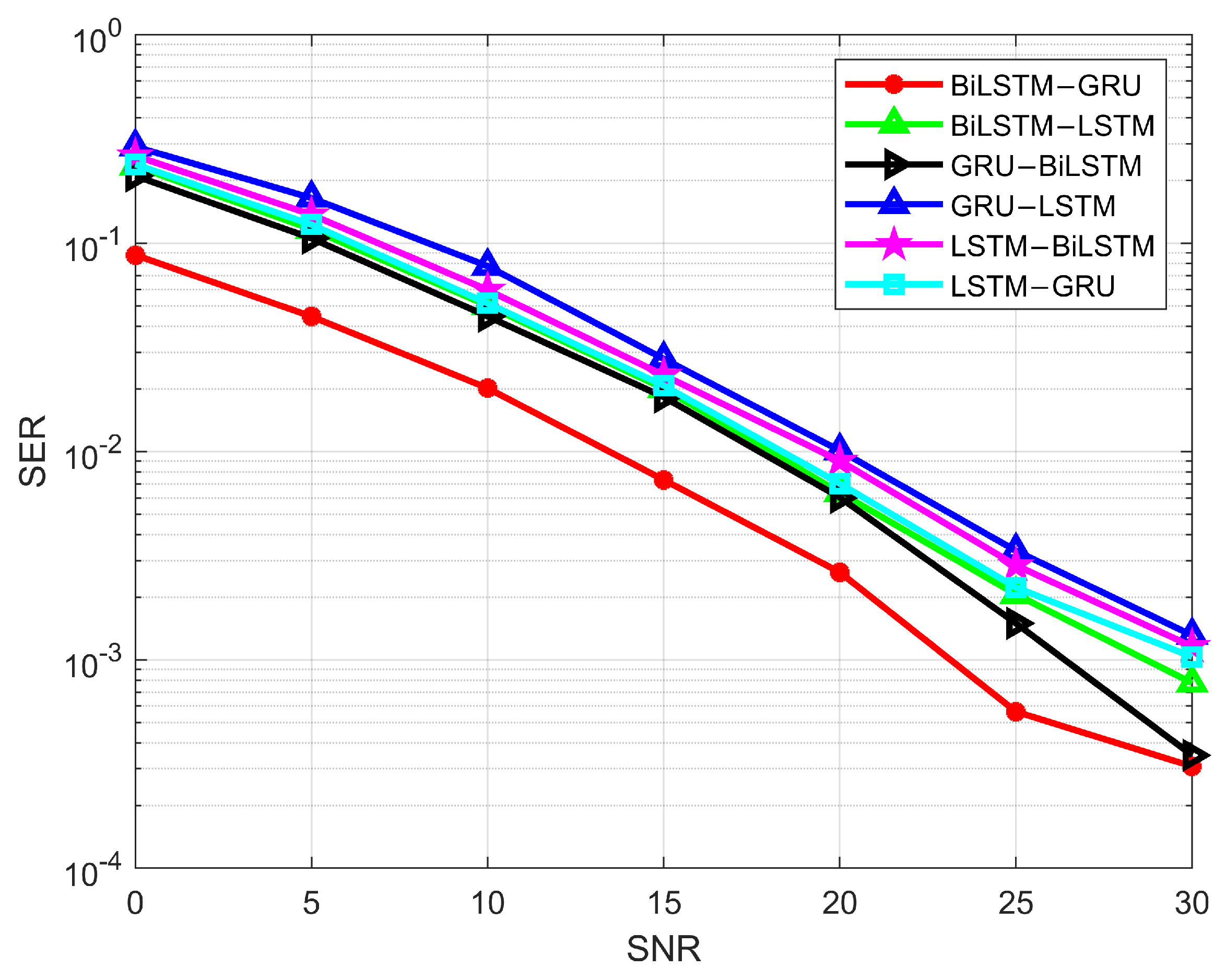
The combination of BiLSTM and LSTM was experimented with in the first step. The input data are first passed through a BiLSTM layer and then through an LSTM layer. The BER results for the BiLSTM-LSTM combination are shown in Figure 13, with a value of at an SNR of 30 dB. However, when the layer order is reversed, the BER increases to . This indicates that IRS channel data demodulation is more accurate with the BiLSTM-LSTM combination. A similar trend is observed in Figure 14, which shows the SER performance for both BiLSTM-LSTM and LSTM-BiLSTM layers. Next, we consider the LSTM-GRU and GRU-LSTM layer combinations for IRS communication. As seen in Figure 13, the LSTM-GRU layer combination achieves BER of , while the GRU-LSTM combination has a BER of at 30 dB SNR. This indicates better performance for the LSTM-GRU combination compared to GRU-LSTM, as LSTM can extract primary features more accurately, and GRU can be applied for classification. This combination demonstrates better accuracy compared to LSTM-BiLSTM. The SER for the LSTM and GRU combination is shown in Figure 14. The final considered combination is between BiLSTM and GRU. Both combinations yield excellent results for BER and SER. At 30 dB SNR, the GRU-BiLSTM combination has a BER of , while the BiLSTM-GRU combination achieves a BER of . Among all the combinations, BiLSTM-GRU demonstrates the best BER performance. Since BiLSTM processes data in both forward and backward directions, its feature extraction capabilities are enhanced. Additionally, the GRU layer helps extract important features, leading to high classification accuracy. Thus, the BiLSTM-GRU-based model achieves more accurate results compared to other combinations.
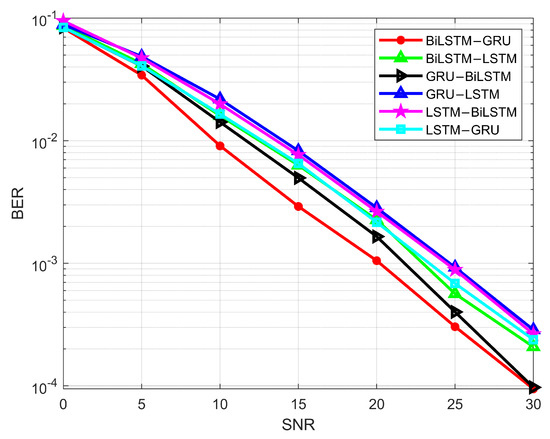
Figure 13.
BER of LSTM, BiLSTM, and GRU hybrid models.
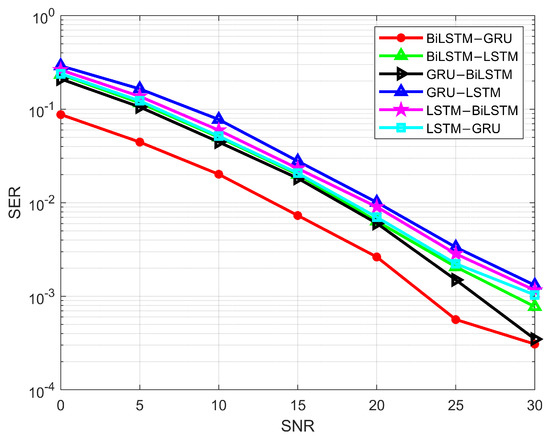
Figure 14.
SER of LSTM, BiLSTM, and GRU hybrid models.
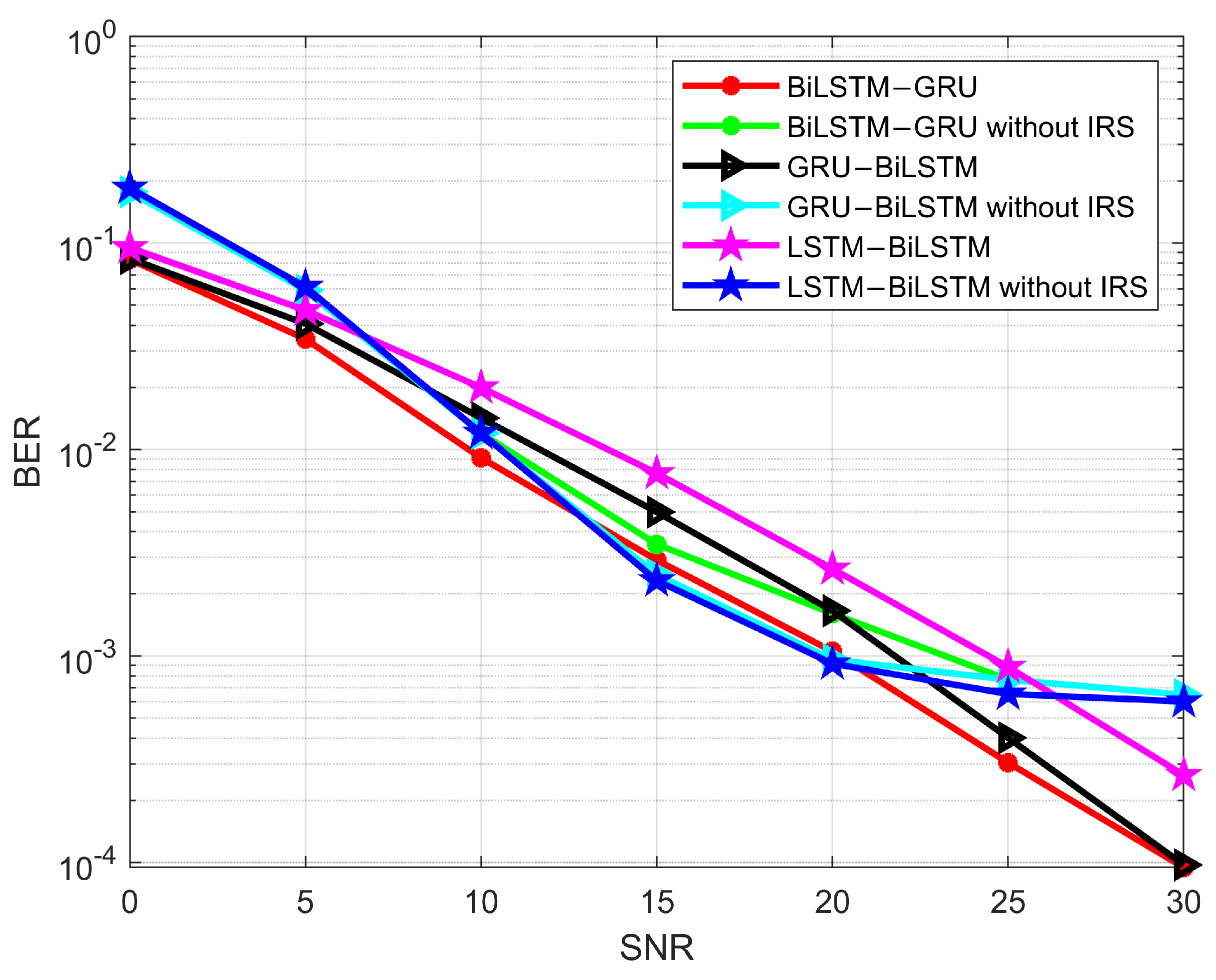
We also compared the performance of the proposed RNN architecture with a traditional wireless communication system without IRS reflection. For this experiment, we adopted three hybrid models, BiLSTM-GRU, GRU-BiLSTM, and LSTM-BiLSTM, as these models perform well in IRS reflection channels. As shown in Figure 15, all models demonstrate good performance at certain SNRs, but the overall performance is not satisfactory. Specifically, in the high SNR range, the system without IRS fails to achieve low BER compared to the IRS-based system. This result highlights the superior BER performance of IRS-based systems.
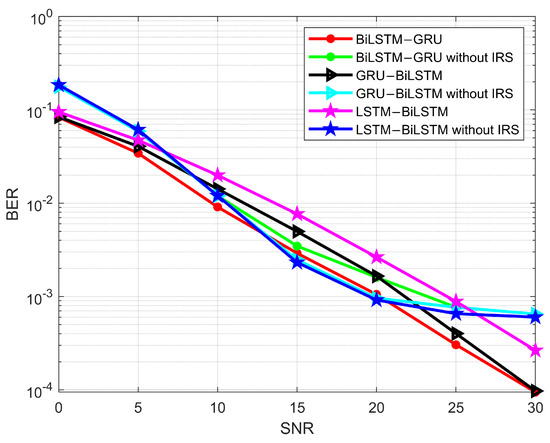
Figure 15.
Comparison of the wireless communication channel performance with and without IRS using RNN hybrid models.
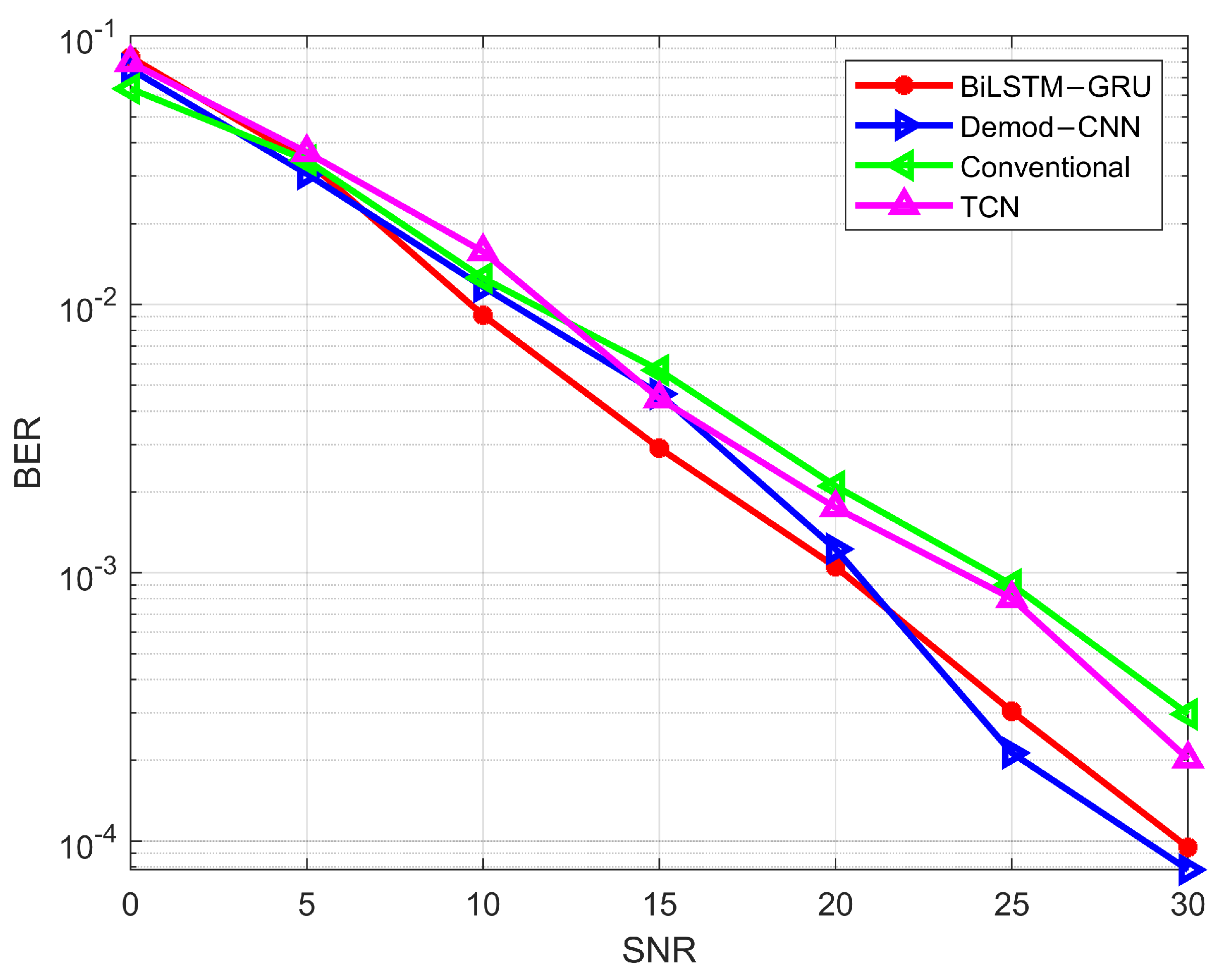
BiLSTM-GRU model’s performance was also evaluated with other studies in the literature. Figure 16 compares the performance with other similar studies. The proposed BiLSTM-GRU model can perform well as compared to TCN [34] and traditional demodulation techniques. However, it has a similar performance to Demod-CNN [35] as CNNs are very powerful in classifying data.
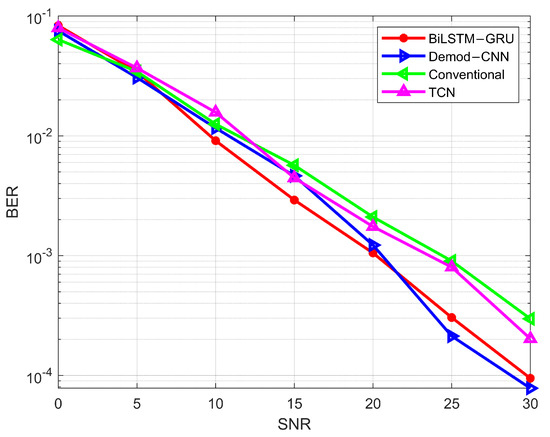
Figure 16.
Comparison with different deep learning models with the proposed BiLSTM-GRU model.
7. Conclusions
In this study, we considered an IRS-based wireless communication system and conducted a performance analysis using RNN approaches. We examined both the IRS-reflected signal and the direct signal for channel estimation. To apply machine learning, we specifically focused on RNN techniques, namely LSTM, BiLSTM, and GRU, for estimating the IRS channel. First, each individual RNN technique was studied with single and double layers. In this setup, the BiLSTM with double layers showed the best BER performance compared to LSTM and GRU. In the next step, a hybrid approach was considered by combining each of the RNN techniques. The experimental results demonstrated that individual RNN techniques are capable of learning data patterns from the training process. Among the RNN techniques, the BiLSTM double-layer model achieved the highest accuracy compared to the LSTM and GRU models. In the hybrid approach, the BiLSTM-GRU combination provided the best performance in terms of BER and SER. We also compared our results with previous algorithms, and the outcomes are comparable to other studies. When the CSI and channel parameters are varied, the model must be adjusted to achieve optimal results. Retraining the model with newly generated data is necessary. Additionally, the model architecture may need to be restructured to reduce the BER. This study can be extended to develop larger models that account for multiple IRS reflection scenarios.
Author Contributions
Conceptualization, R.T. and M.A.S.S.; methodology, R.T., M.A.S.S. and M.A.A.; software, R.T., M.H.R. and M.A.A.; validation, R.T. and M.H.R.; formal analysis, R.T., M.A.S.S., M.H.R. and M.A.A.; investigation, R.T., M.A.S.S. and M.A.A.; resources, H.-K.S.; data curation, R.T. and M.A.S.S.; writing—original draft preparation, R.T.; writing—review and editing, R.T., M.A.S.S., M.H.R., M.A.A. and H.-K.S.; visualization, R.T., M.A.S.S., M.H.R. and M.A.A.; supervision, H.-K.S.; project administration, H.-K.S.; funding acquisition, H.-K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Institute of Information and Communications Technology Planning and Evaluation (IITP) grant funded by the Korean Government [Ministry of Science and ICT (MSIT)], South Korea, under the Metaverse Support Program to Nurture the Best Talents (grant no. IITP-2024-RS-2023-00254529). It was also supported in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (grant no. 2020R1A6A1A03038540); and in part by the IITP (Institute of Information & Communications Technology Planning & Evaluation)–ITRC (Information Technology Research Center) grant, funded by the Korean government (Ministry of Science and ICT), under IITP-2024-RS-2024-00437191.
Data Availability Statement
The data will be made available by the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. 2019, 58, 106–112. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C.; Lerosey, G.; Debbah, M.; Fink, M. Reconfigurable intelligent surfaces and metamaterials: The potential of wave propagation control for 6G wireless communications. arXiv 2020, arXiv:2006.11136. [Google Scholar]
- Mishra, D.; Johansson, H. Channel estimation and low-complexity beamforming design for passive intelligent surface assisted MISO wireless energy transfer. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4659–4663. [Google Scholar]
- Alwazani, H.; Kammoun, A.; Chaaban, A.; Debbah, M.; Alouini, M.S. Intelligent reflecting surface-assisted multi-user MISO communication: Channel estimation and beamforming design. IEEE Open J. Commun. Soc. 2020, 1, 661–680. [Google Scholar]
- Guo, H.; Lau, V.K. Uplink cascaded channel estimation for intelligent reflecting surface assisted multiuser MISO systems. IEEE Trans. Signal Process. 2022, 70, 3964–3977. [Google Scholar] [CrossRef]
- He, Z.Q.; Yuan, X. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO. IEEE Wirel. Commun. Lett. 2019, 9, 210–214. [Google Scholar] [CrossRef]
- Wang, P.; Fang, J.; Duan, H.; Li, H. Compressed channel estimation for intelligent reflecting surface-assisted millimeter wave systems. IEEE Signal Process. Lett. 2020, 27, 905–909. [Google Scholar] [CrossRef]
- Lin, T.; Yu, X.; Zhu, Y.; Schober, R. Channel estimation for intelligent reflecting surface-assisted millimeter wave MIMO systems. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Sejan, M.A.S.; Rahman, M.H.; Shin, B.S.; Oh, J.H.; You, Y.H.; Song, H.K. Machine learning for intelligent-reflecting-surface-based wireless communication towards 6G: A review. Sensors 2022, 22, 5405. [Google Scholar] [CrossRef]
- Wei, X.; Shen, D.; Dai, L. Channel estimation for RIS assisted wireless communications—Part II: An improved solution based on double-structured sparsity. IEEE Commun. Lett. 2021, 25, 1403–1407. [Google Scholar] [CrossRef]
- Shtaiwi, E.; Zhang, H.; Vishwanath, S.; Youssef, M.; Abdelhadi, A.; Han, Z. Channel estimation approach for RIS assisted MIMO systems. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 452–465. [Google Scholar] [CrossRef]
- Yu, J.; Liu, X.; Gao, Y.; Zhang, C.; Zhang, W. Deep learning for channel tracking in IRS-assisted UAV communication systems. IEEE Trans. Wirel. Commun. 2022, 21, 7711–7722. [Google Scholar] [CrossRef]
- Song, H.; Zhang, M.; Gao, J.; Zhong, C. Unsupervised learning-based joint active and passive beamforming design for reconfigurable intelligent surfaces aided wireless networks. IEEE Commun. Lett. 2020, 25, 892–896. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.G.; Giles, C.L. How embedded memory in recurrent neural network architectures helps learning long-term temporal dependencies. Neural Netw. 1998, 11, 861–868. [Google Scholar] [CrossRef] [PubMed]
- Faisal, K.; Choi, W. Machine learning approaches for reconfigurable intelligent surfaces: A survey. IEEE Access 2022, 10, 27343–27367. [Google Scholar] [CrossRef]
- Zhou, H.; Erol-Kantarci, M.; Liu, Y.; Poor, H.V. A Survey on Model-Based, Heuristic, and Machine Learning Optimization Approaches in RIS-Aided Wireless Networks. IEEE Commun. Surv. Tutor. 2024, 26, 781–823. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, X.; Greco, M.S.; Gini, F. CNN based Sparse IRS Design for Channel Estimation in Assisted Uplink Communications. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, Y.; Zhao, M.M.; Liu, A.; Zhao, M.J. Channel Tracking and Prediction for IRS-Aided Wireless Communications. IEEE Trans. Wirel. Commun. 2023, 22, 563–579. [Google Scholar] [CrossRef]
- Tsuchiya, Y.; Suga, N.; Uruma, K.; Fujisawa, M. LSTM-based Spectral Efficiency Prediction by Capturing Wireless Terminal Movement in IRS-Assisted Systems. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Nguyen, C.; Hoang, T.M.; Cheema, A.A. Channel estimation using CNN-LSTM in RIS-NOMA assisted 6G network. IEEE Trans. Mach. Learn. Commun. Netw. 2023, 1, 43–60. [Google Scholar] [CrossRef]
- Gong, S.; Lin, J.; Ding, B.; Niyato, D.; Kim, D.I.; Guizani, M. When optimization meets machine learning: The case of IRS-assisted wireless networks. IEEE Netw. 2022, 36, 190–198. [Google Scholar] [CrossRef]
- Dajer, M.; Ma, Z.; Piazzi, L.; Prasad, N.; Qi, X.F.; Sheen, B.; Yang, J.; Yue, G. Reconfigurable intelligent surface: Design the channel—A new opportunity for future wireless networks. Digit. Commun. Netw. 2022, 8, 87–104. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Di Renzo, M.; Ntontin, K.; Song, J.; Danufane, F.H.; Qian, X.; Lazarakis, F.; De Rosny, J.; Phan-Huy, D.T.; Simeone, O.; Zhang, R.; et al. Reconfigurable intelligent surfaces vs. relaying: Differences, similarities, and performance comparison. IEEE Open J. Commun. Soc. 2020, 1, 798–807. [Google Scholar] [CrossRef]
- Qian, X.; Di Renzo, M.; Liu, J.; Kammoun, A.; Alouini, M.S. Beamforming through reconfigurable intelligent surfaces in single-user MIMO systems: SNR distribution and scaling laws in the presence of channel fading and phase noise. IEEE Wirel. Commun. Lett. 2020, 10, 77–81. [Google Scholar] [CrossRef]
- Basar, E.; Di Renzo, M.; De Rosny, J.; Debbah, M.; Alouini, M.S.; Zhang, R. Wireless communications through reconfigurable intelligent surfaces. IEEE Access 2019, 7, 116753–116773. [Google Scholar] [CrossRef]
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Dai, L.; Rodriguez, J. Millimeter-wave massive MIMO communication for future wireless systems: A survey. IEEE Commun. Surv. Tutor. 2017, 20, 836–869. [Google Scholar] [CrossRef]
- Medium. Long Short-Term Memory (LSTM). Available online: https://medium.com/@saba99/long-short-term-memory-lstm-fffc5eaebfdc (accessed on 29 August 2024).
- Terminology, Z. BiLSTM (Bidirectional Long Short-Term Memory). Available online: https://computer-nerd-zettelkasten.tistory.com/entry/BiLSTM-Bidirectional-Long-Short-Term-Memory (accessed on 29 August 2024).
- Chen, J.; Huang, X.; Jiang, H.; Miao, X. Low-cost and device-free human activity recognition based on hierarchical learning model. Sensors 2021, 21, 2359. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.H.; Sejan, M.A.S.; Aziz, M.A.; You, Y.H.; Song, H.K. HyDNN: A Hybrid Deep Learning Framework Based Multiuser Uplink Channel Estimation and Signal Detection for NOMA-OFDM System. IEEE Access 2023, 11, 66742–66755. [Google Scholar] [CrossRef]
- Rahman, M.H.; Sejan, M.A.S.; Aziz, M.A.; Kim, D.S.; You, Y.H.; Song, H.K. Deep Convolutional and Recurrent Neural-Network-Based Optimal Decoding for RIS-Assisted MIMO Communication. Mathematics 2023, 11, 3397. [Google Scholar] [CrossRef]
- Sejan, M.A.S.; Rahman, M.H.; Aziz, M.A.; You, Y.H.; Song, H.K. Temporal Neural Network Framework Adaptation in Reconfigurable Intelligent Surface-Assisted Wireless Communication. Sensors 2023, 23, 2777. [Google Scholar] [CrossRef]
- Sejan, M.A.S.; Rahman, M.H.; Song, H.K. Demod-CNN: A Robust Deep Learning Approach for Intelligent Reflecting Surface-Assisted Multiuser MIMO Communication. Sensors 2022, 22, 5971. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).