Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems
Abstract
1. Introduction
- The proposed DSRG method optimizes power flow in a fully decentralized manner, eliminating the need for extensive data sharing and centralized control.
- It provides a comprehensive mathematical model for the DSRG method, including detailed formulations of the power flow constraints, tie-line constraints, and recursive gradient descent updates.
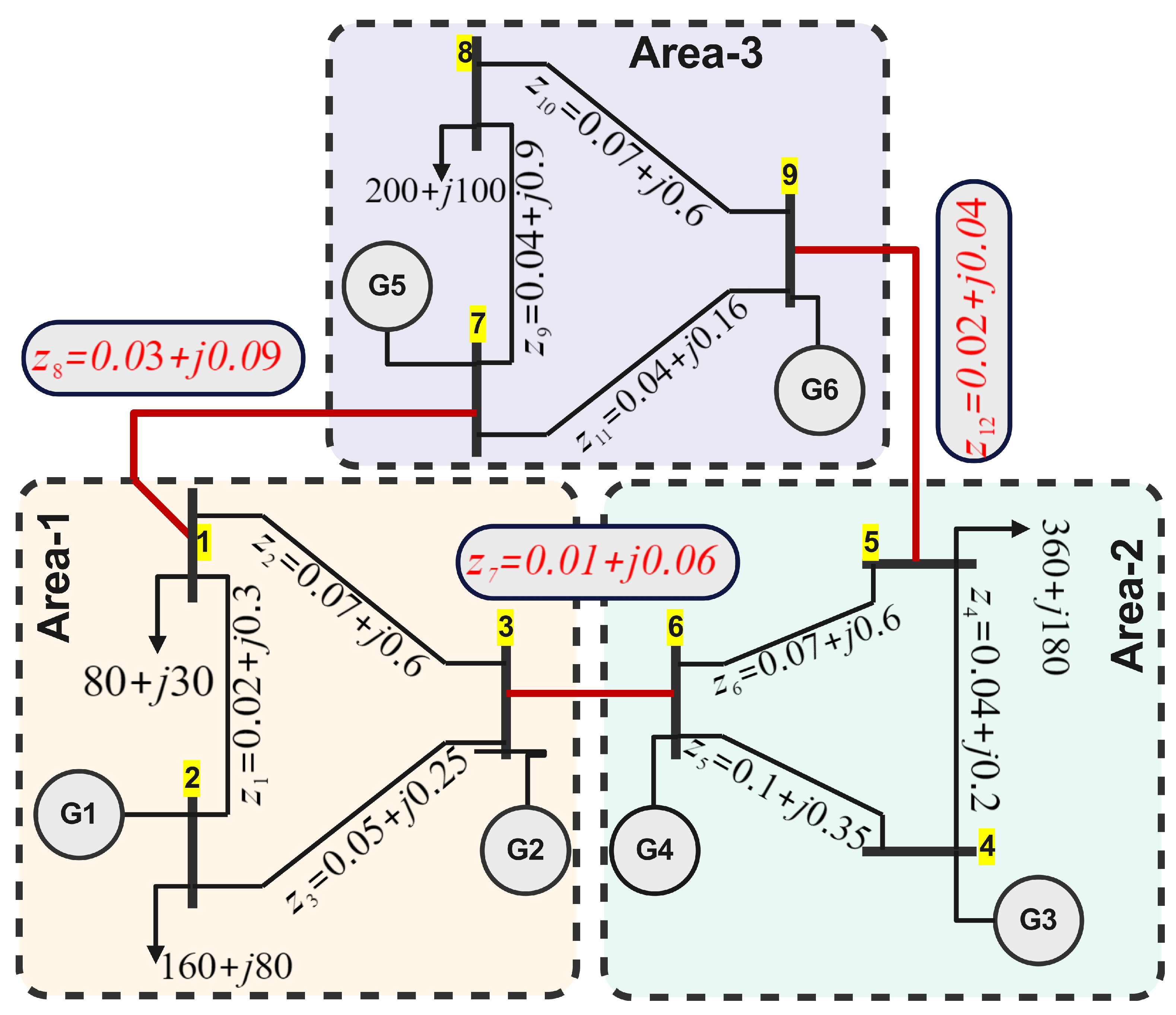
- The DSRG method is rigorously tested on a 3-area, 9-bus system, where it demonstrates superior convergence speed and cost efficiency.
2. Mathematical Model of MAOPF
2.1. Objective Function
2.2. Generation Constraints
2.3. Voltage Magnitude Constraints
2.4. Line Capacity Constraints
2.5. Power Flow Constraints
2.6. Decentralized Tie-Line Constraints
2.7. Decentralized Power Balance Constraints
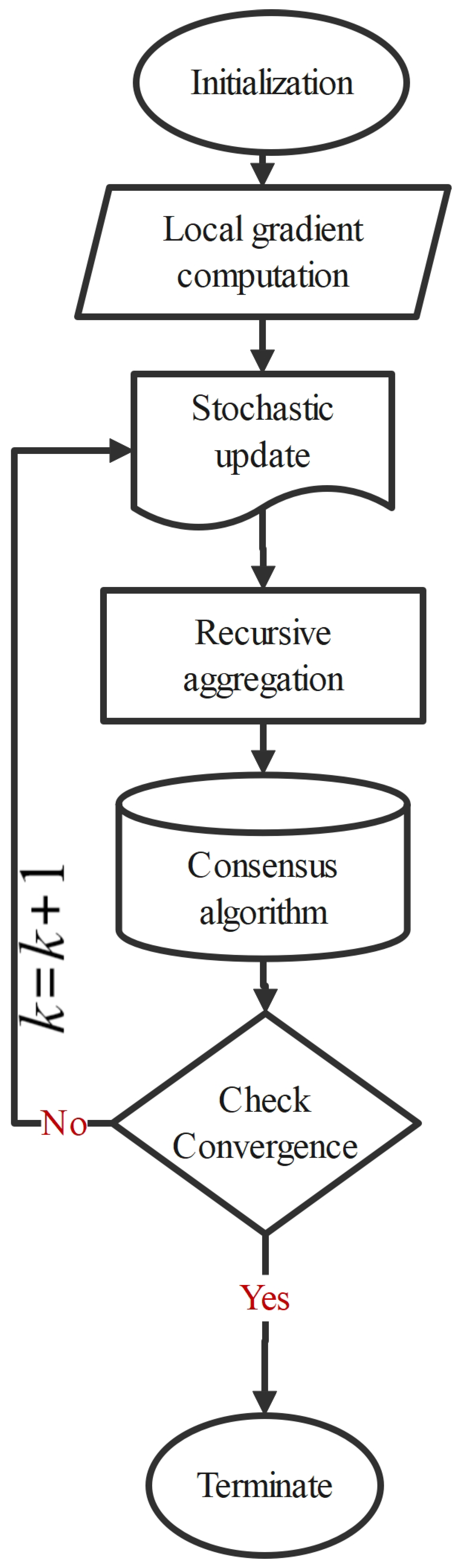
3. Decentralized Stochastic Recursive Gradient Algorithm
| Algorithm 1 DSRG Algorithm for Fully Decentralized OPF in Multi-Area Power Systems |
|
4. Rigorous Convergence Analysis and Theoretical Validation of the DSRG Algorithm
4.1. Convergence Guarantees
- Minimizes generation cost with each iteration;
- Satisfies all constraints at convergence;
- Converges to an equilibrium where no further updates to the decision variables lead to significant improvements, ensuring system-wide feasibility.
4.2. Theoretical Bounds on Convergence
- Linear convergence rate bounds under certain convexity assumptions, where the solution gap reduces proportionally with each iteration. Considering linear convergence with a constant , we demonstrate the rate at which the method approaches the ideal solution .
- Logarithmic convergence rates for more general, non-convex optimization problems like OPF, where diminishing returns are observed as the algorithm proceeds. The mathematical expression for logarithmic convergence rates is:
- Upper bounds on the number of iterations required to reach a near-optimal solution within a predefined tolerance level . If ℘ is the upper bound of a function’s growth rate, the theoretical results can be expressed as:
5. Results and Discussion
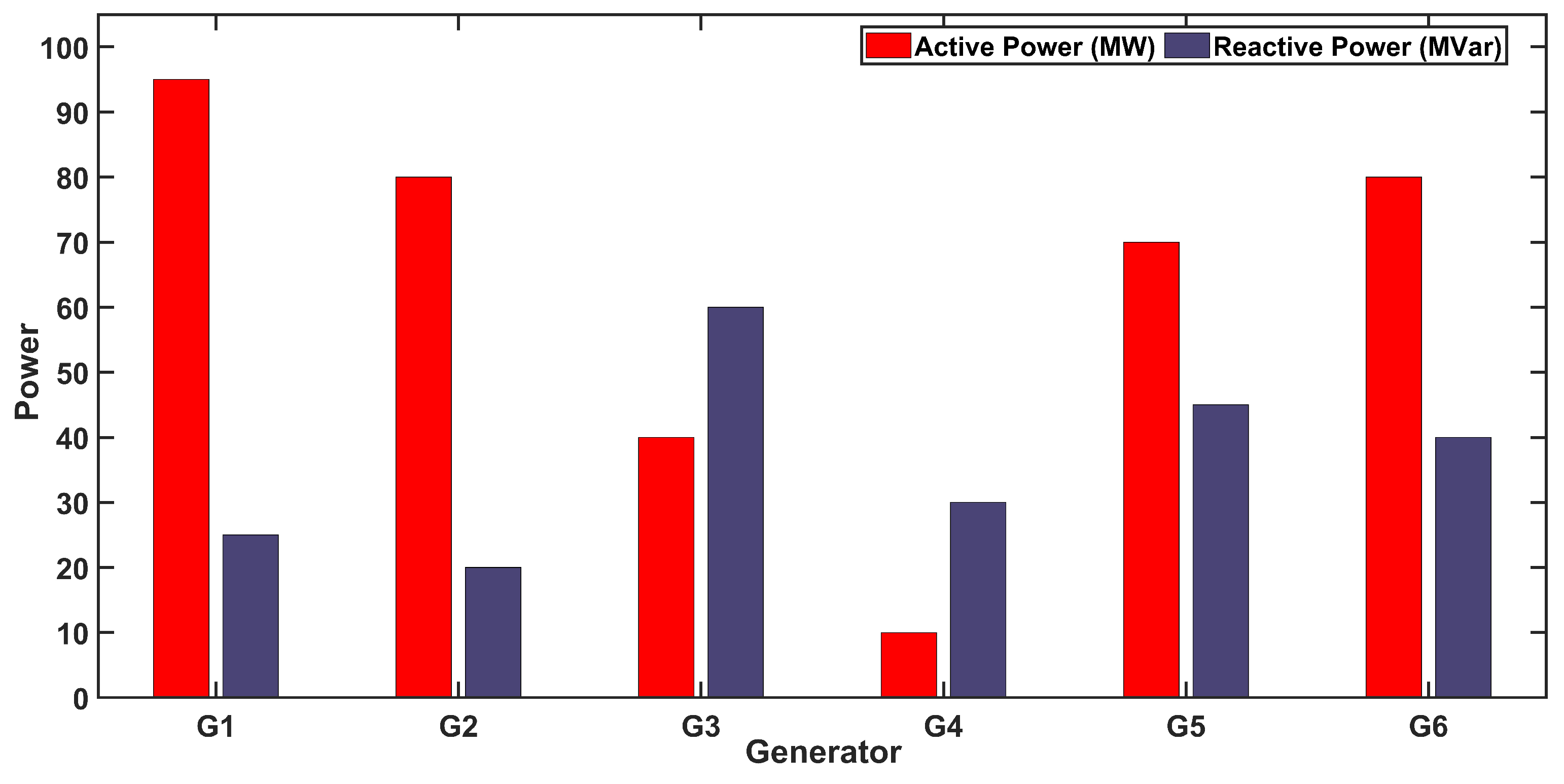
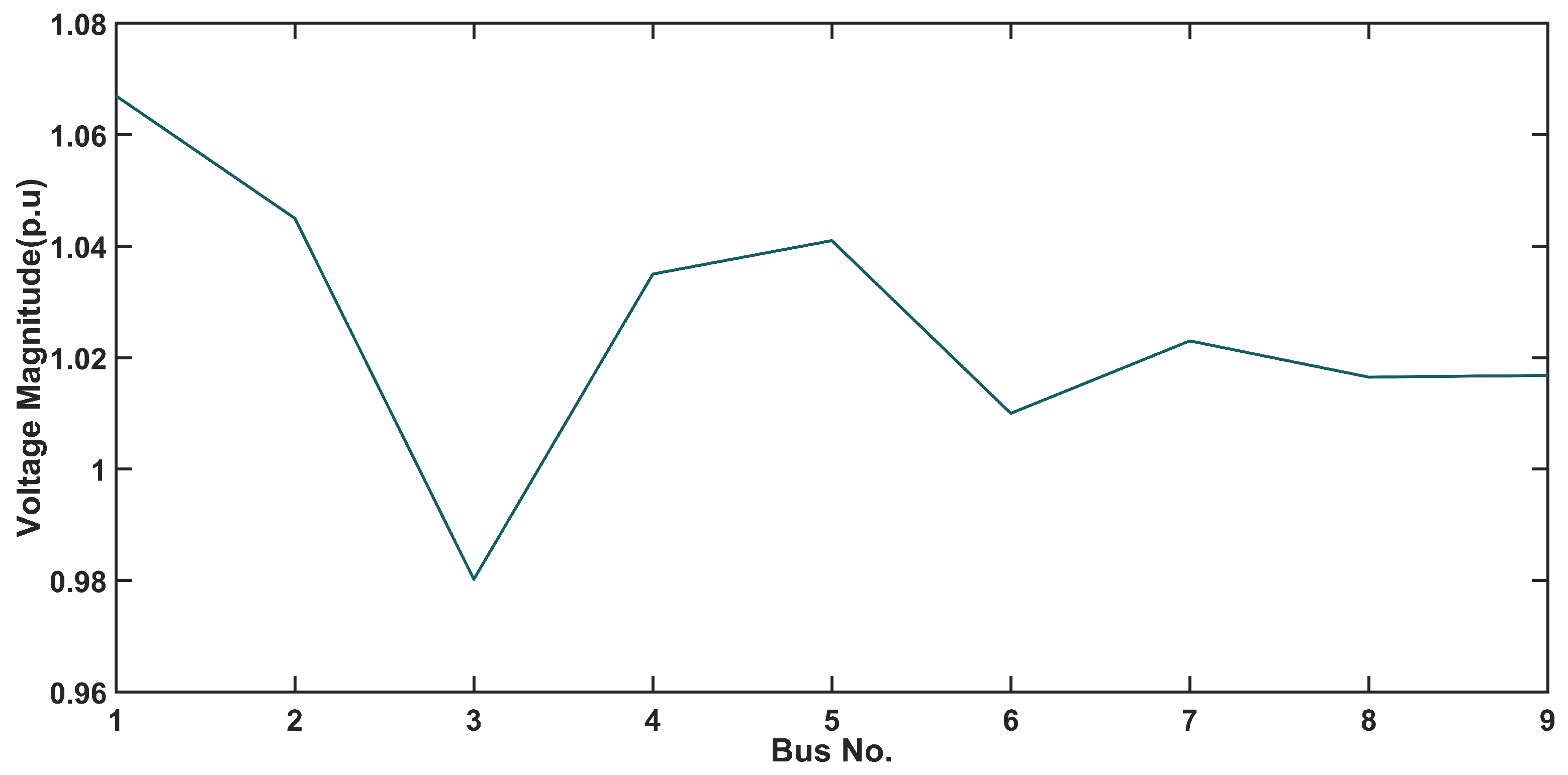
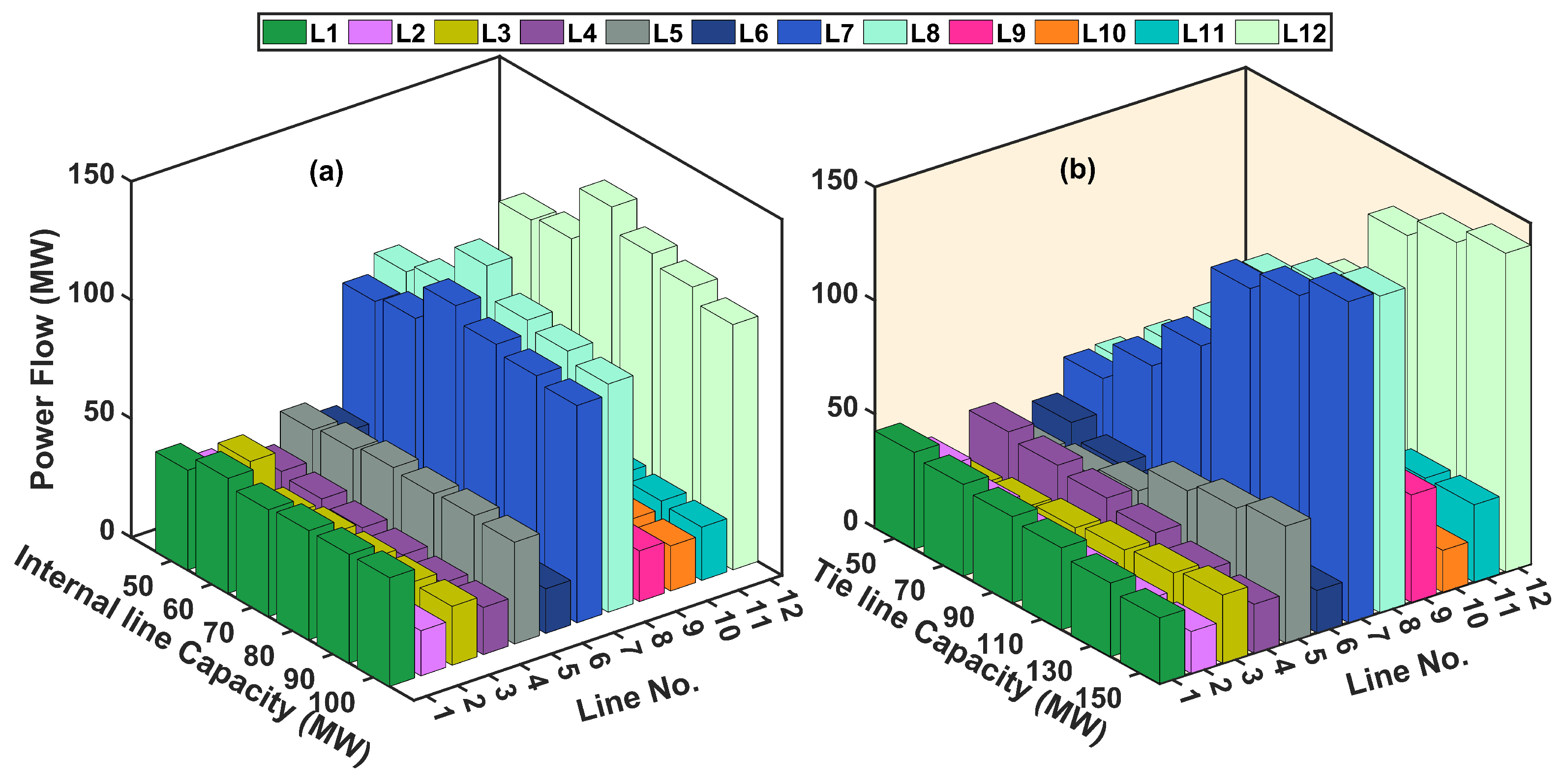
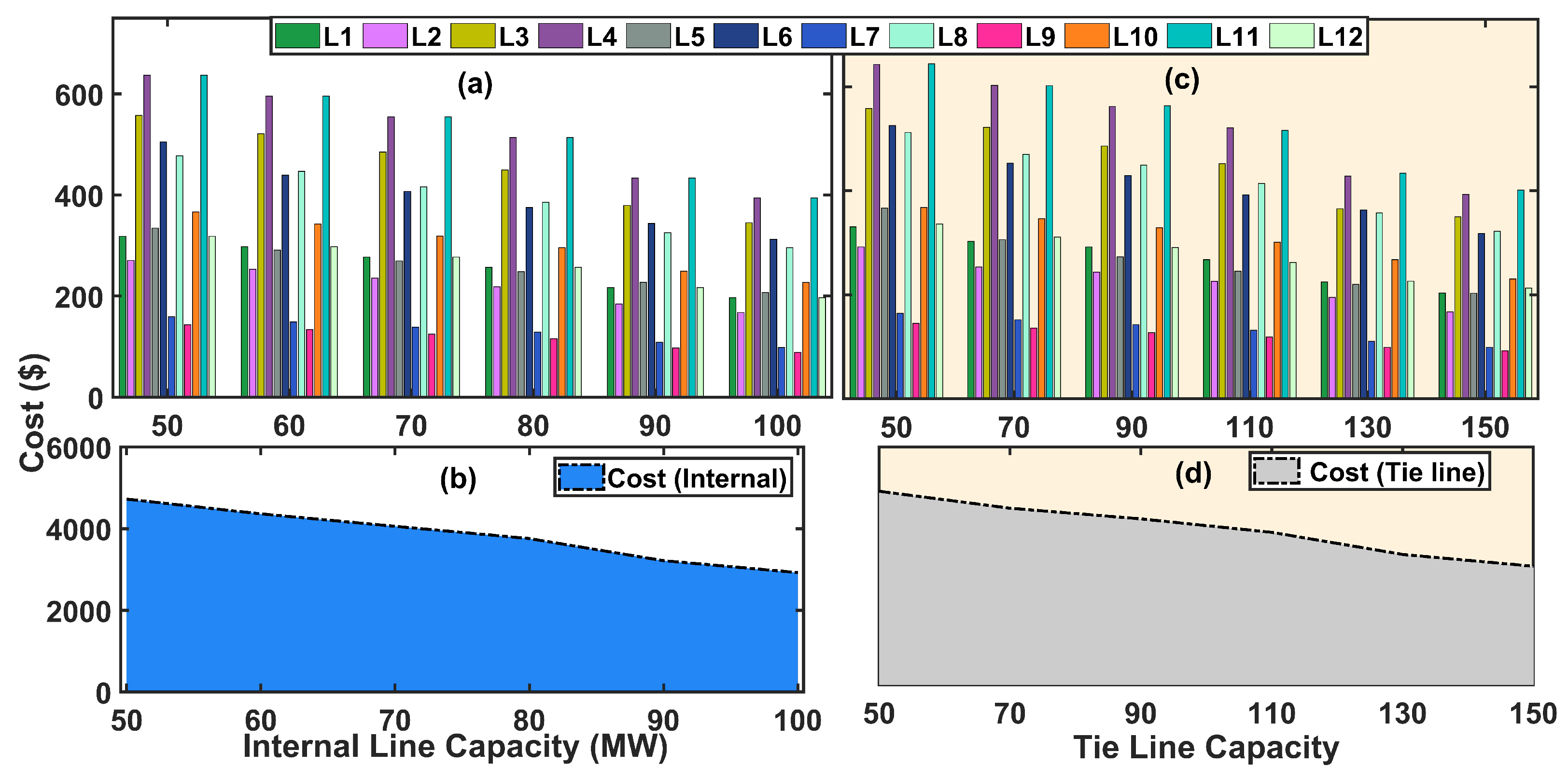
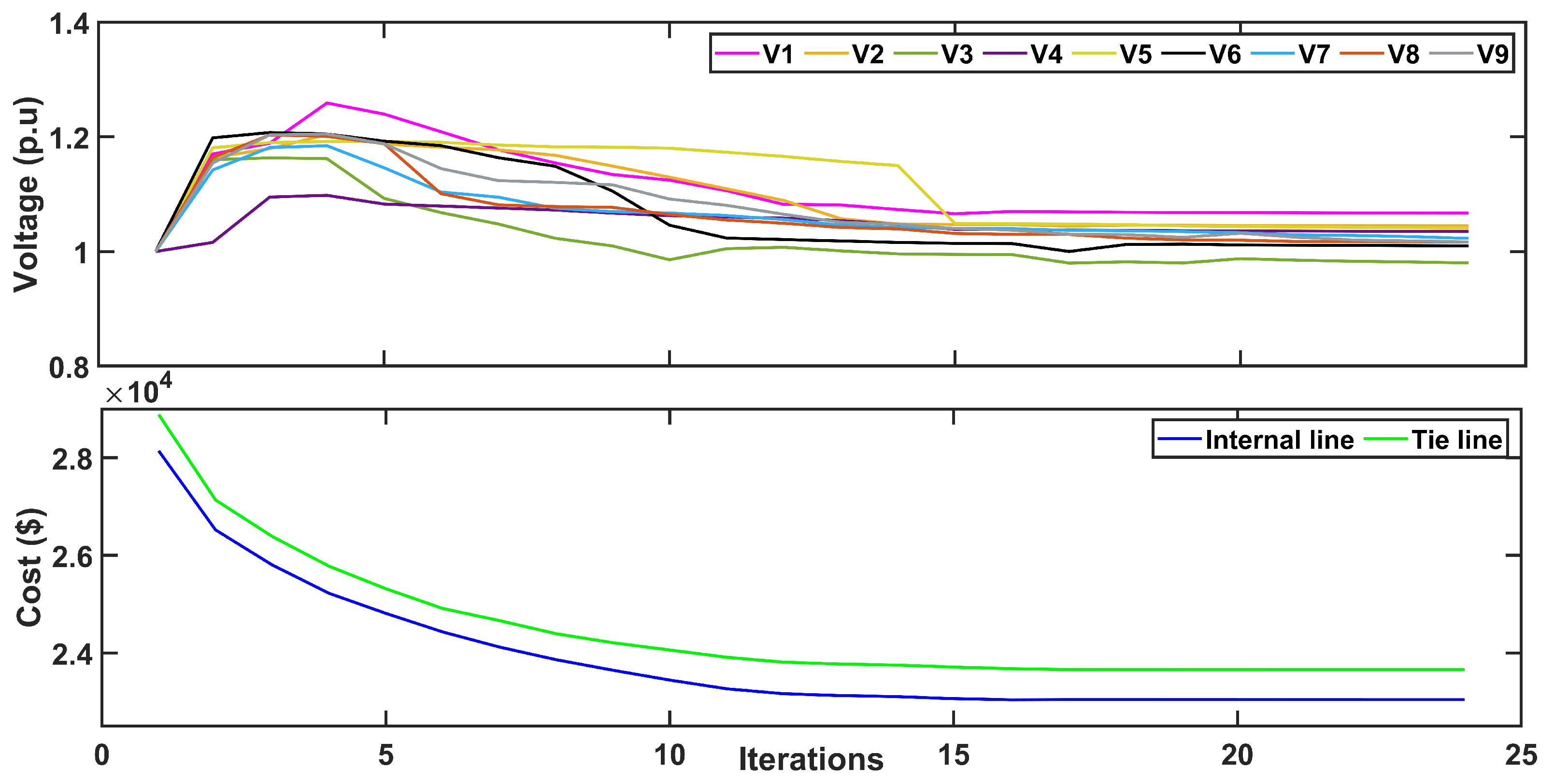
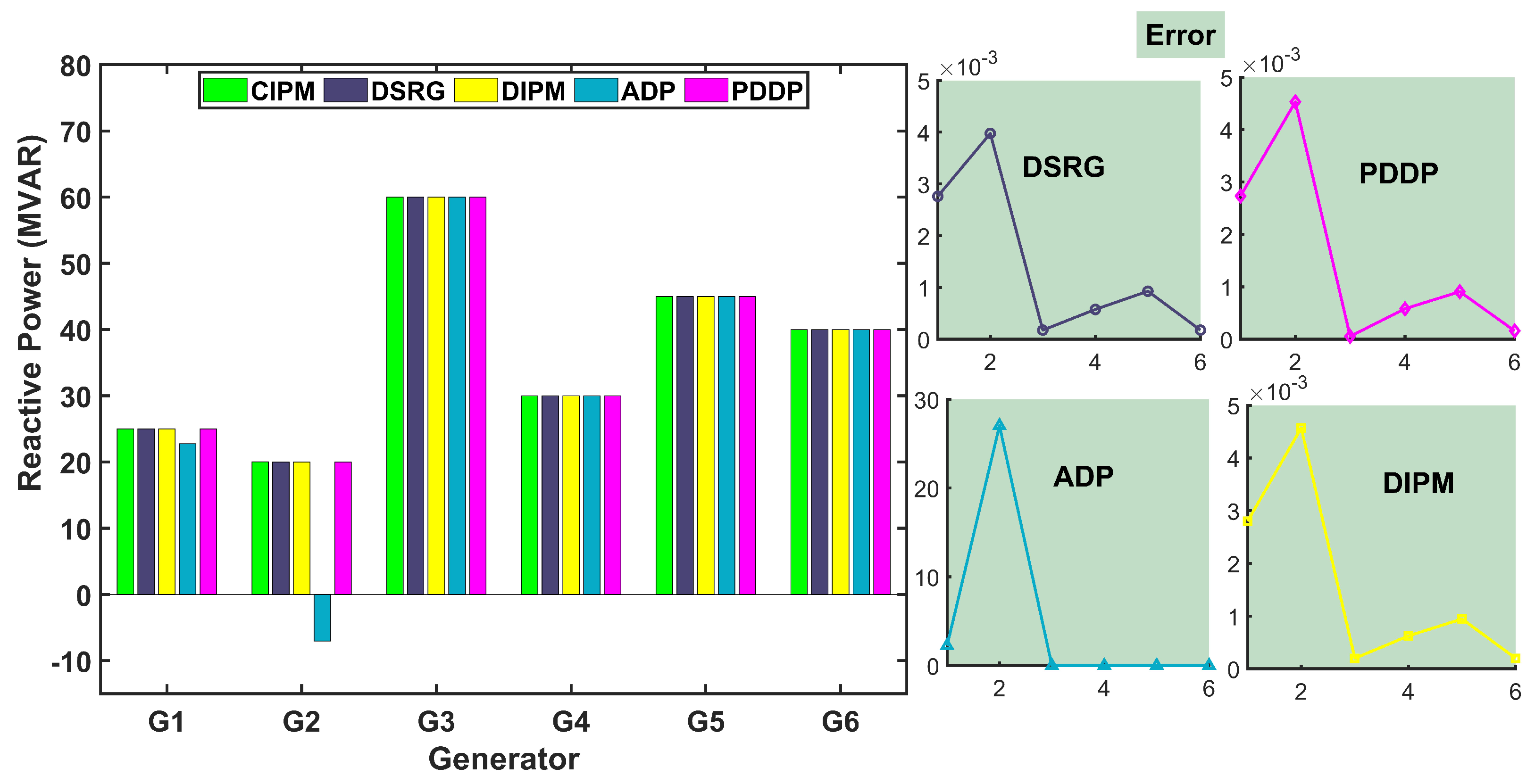
5.1. Numerical Analysis
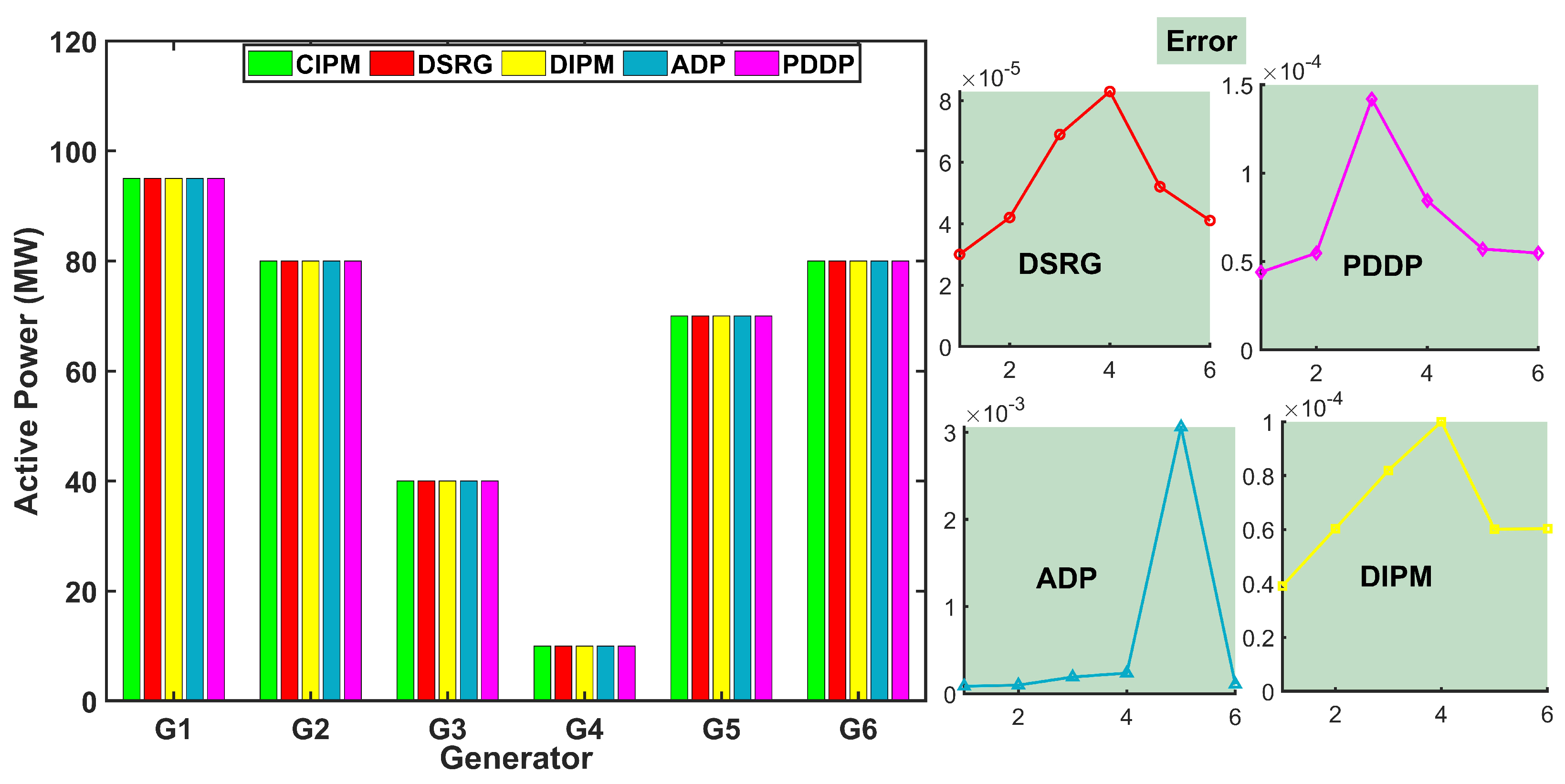
5.2. Comparison Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yi, W.; Lin, Z.; Lin, Y.; Xiong, S.; Yu, Z.; Chen, Y. Solving Optimal Power Flow Problem via Improved Constrained Adaptive Differential Evolution. Mathematics 2023, 11, 1250. [Google Scholar] [CrossRef]
- Li, Q.; Li, B.; Jiang, Q.; Liu, T.; Yue, Y.; Zhang, Y. A Novel Location Method for Interline Power Flow Controllers Based on Entropy Theory. Prot. Control Mod. Power Syst. 2024, 9, 70–81. [Google Scholar] [CrossRef]
- Hmida, J.B.; Chambers, T.; Lee, J. Solving constrained optimal power flow with renewables using hybrid modified imperialist competitive algorithm and sequential quadratic programming. Electr. Power Syst. Res. 2019, 177, 105989. [Google Scholar] [CrossRef]
- Mhanna, S.; Mancarella, P. An exact sequential linear programming algorithm for the optimal power flow problem. IEEE Trans. Power Syst. 2021, 37, 666–679. [Google Scholar] [CrossRef]
- Pourakbari-Kasmaei, M.; Mantovani, J.R.S. Logically constrained optimal power flow: Solver-based mixed-integer nonlinear programming model. Int. J. Electr. Power Energy Syst. 2018, 97, 240–249. [Google Scholar] [CrossRef]
- Raya-Armenta, J.M.; Bazmohammadi, N.; Avina-Cervantes, J.G.; Sáez, D.; Vasquez, J.C.; Guerrero, J.M. Energy management system optimization in islanded microgrids: An overview and future trends. Renew. Sustain. Energy Rev. 2021, 149, 111327. [Google Scholar] [CrossRef]
- Naderi, E.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Lehtonen, M. A novel hybrid self-adaptive heuristic algorithm to handle single-and multi-objective optimal power flow problems. Int. J. Electr. Power Energy Syst. 2021, 125, 106492. [Google Scholar] [CrossRef]
- Huang, S.; Xiong, L.; Zhou, Y.; Gao, F.; Jia, Q.; Li, X.; Li, X.; Wang, Z.; Khan, M.W. Robust Distributed Fixed-Time Fault-Tolerant Control for Shipboard Microgrids with Actuator Fault. IEEE Trans. Transp. Electrif. 2024. [Google Scholar] [CrossRef]
- Tan, S.K.; Peng, J.C.; Wu, M.H.; Jiang, H. A Bus Privacy Preserving Decentralized Power Flow Algorithm Considering Neighbor Partial Derivative Information. IEEE Access 2024, 12, 26295–26307. [Google Scholar] [CrossRef]
- Mo, X.; Zhu, J.; Chen, J.; Guo, Y.; Xia, Y.; Liu, M. A stochastic spatiotemporal decomposition decision-making approach for real-time dynamic energy management of multi-microgrids. IEEE Trans. Sustain. Energy 2020, 12, 821–833. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Chen, J.; Song, Y.D. Hierarchical decentralized optimization architecture for economic dispatch: A new approach for large-scale power system. IEEE Trans. Ind. Inform. 2017, 14, 523–534. [Google Scholar] [CrossRef]
- Lu, W.; Liu, M.; Lin, S.; Li, L. Fully decentralized optimal power flow of multi-area interconnected power systems based on distributed interior point method. IEEE Trans. Power Syst. 2017, 33, 901–910. [Google Scholar] [CrossRef]
- Swief, R.A.; Hassan, N.M.; Hasanien, H.M.; Abdelaziz, A.Y.; Kamh, M.Z. Multi-regional optimal power flow using marine predators algorithm considering load and generation variability. IEEE Access 2021, 9, 74600–74613. [Google Scholar] [CrossRef]
- Zhang, C.; Cheng, H.; Liu, L.; Zhang, H.; Zhang, X.; Li, G. Coordination planning of wind farm, energy storage and transmission network with high-penetration renewable energy. Int. J. Electr. Power Energy Syst. 2020, 120, 105944. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Zhu, H.; Giannakis, G.B. Distributed optimal power flow for smart microgrids. IEEE Trans. Smart Grid 2013, 4, 1464–1475. [Google Scholar] [CrossRef]
- Li, R.; Tang, B.J.; Yu, B.; Liao, H.; Zhang, C.; Wei, Y.M. Cost-optimal operation strategy for integrating large scale of renewable energy in China’s power system: From a multi-regional perspective. Appl. Energy 2022, 325, 119780. [Google Scholar] [CrossRef]
- Kargarian, A.; Mohammadi, J.; Guo, J.; Chakrabarti, S.; Barati, M.; Hug, G.; Kar, S.; Baldick, R. Toward distributed/decentralized DC optimal power flow implementation in future electric power systems. IEEE Trans. Smart Grid 2016, 9, 2574–2594. [Google Scholar] [CrossRef]
- Peng, Q.; Low, S.H. Distributed optimal power flow algorithm for radial networks, I: Balanced single phase case. IEEE Trans. Smart Grid 2016, 9, 111–121. [Google Scholar] [CrossRef]
- Guo, J.; Hug, G.; Tonguz, O.K. Intelligent partitioning in distributed optimization of electric power systems. IEEE Trans. Smart Grid 2015, 7, 1249–1258. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, T.; Liu, M.; Lu, W. Decentralised optimal dispatch of multi-area power systems based on non-linear value-function approximation. IET Gener. Transm. Distrib. 2019, 13, 5083–5090. [Google Scholar] [CrossRef]
- Lin, C.; Wu, W.; Zhang, B.; Sun, Y. Decentralized solution for combined heat and power dispatch through benders decomposition. IEEE Trans. Sustain. Energy 2017, 8, 1361–1372. [Google Scholar] [CrossRef]
- Zhu, J.; Mo, X.; Xia, Y.; Guo, Y.; Chen, J.; Liu, M. Fully-decentralized optimal power flow of multi-area power systems based on parallel dual dynamic programming. IEEE Trans. Power Syst. 2021, 37, 927–941. [Google Scholar] [CrossRef]
- Hao, G.; Han, X.; Luo, S.; Ye, P.; Wen, H. Decentralized DC optimal power flow model based on improved Lagrangian and consensus algorithm. Int. J. Electr. Power Energy Syst. 2024, 155, 109555. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, C.; Li, J.; Zhu, L.; Cao, S.; Huang, W.; Shuai, Z. Multi-Resource Collaborative Service Restoration of a Distribution Network with Decentralized Hierarchical Droop Control. Prot. Control. Mod. Power Syst. 2024, 9, 19–37. [Google Scholar] [CrossRef]
- Ye, H.; Zhu, J.; Chen, J.; Wang, Z.; Zhuo, Y.; Liu, H.; Liu, M. Quadratic Taylor Expansion-Based Approximate Dynamic Programming for Fully Decentralized AC-OPF of Multi-Area Power Systems. IEEE Trans. Power Syst. 2022, 38, 4940–4949. [Google Scholar] [CrossRef]
- Biswas, B.D.; Hasan, M.S.; Kamalasadan, S. Decentralized distributed convex optimal power flow model for power distribution system based on alternating direction method of multipliers. IEEE Trans. Ind. Appl. 2022, 59, 627–640. [Google Scholar] [CrossRef]
- Gu, Y.; Huang, X.; Chen, Z. A data-driven multi-stage stochastic robust optimization model for dynamic optimal power flow problem. Int. J. Electr. Power Energy Syst. 2023, 148, 108955. [Google Scholar] [CrossRef]
- Di Fazio, A.R.; Risi, C.; Russo, M.; De Santis, M. Decentralized voltage optimization based on the auxiliary problem principle in distribution networks with DERs. Appl. Sci. 2021, 11, 4509. [Google Scholar] [CrossRef]
- Hussan, U.; Hassan, M.; Ayub, M.A.; Peng, J.C.; Rasheed, H.; Jiang, H.; Asghar, F. Smooth and Uninterrupted Operation of Standalone DC Microgrid Under High and Low Penetration of RESs. IEEE Access 2024, 12, 48620–48629. [Google Scholar] [CrossRef]
- Yan, B.; Jiang, Z.; Yao, P.; Yang, Q.; Li, W.; Zomaya, A.Y. Game Theory Based Optimal Defensive Resources Allocation with Incomplete Information in Cyber-Physical Power Systems Against False Data Injection Attacks. Prot. Control. Mod. Power Syst. 2024, 9, 115–127. [Google Scholar] [CrossRef]
- Yang, C.; Sun, Y.; Zou, Y.; Zheng, F.; Liu, S.; Zhao, B.; Wu, M.; Cui, H. Optimal power flow in distribution network: A review on problem formulation and optimization methods. Energies 2023, 16, 5974. [Google Scholar] [CrossRef]
- Ayub, M.A.; Hussan, U.; Rasheed, H.; Liu, Y.; Peng, J. Optimal energy management of MG for cost-effective operations and battery scheduling using BWO. Energy Rep. 2024, 12, 294–304. [Google Scholar] [CrossRef]
- Lu, X.; Yin, H.; Xia, S.; Zhang, D.; Shahidehpour, M.; Zhang, X.; Ding, T. A real-time alternating direction method of multipliers algorithm for nonconvex optimal power flow problem. IEEE Trans. Ind. Appl. 2020, 57, 70–82. [Google Scholar] [CrossRef]
- Tu, S.; Wächter, A.; Wei, E. A two-stage decomposition approach for AC optimal power flow. IEEE Trans. Power Syst. 2020, 36, 303–312. [Google Scholar] [CrossRef]
- Pan, X.; Chen, M.; Zhao, T.; Low, S.H. DeepOPF: A feasibility-optimized deep neural network approach for AC optimal power flow problems. IEEE Syst. J. 2022, 17, 673–683. [Google Scholar] [CrossRef]
- Fioretto, F.; Mak, T.W.; Van Hentenryck, P. Predicting ac optimal power flows: Combining deep learning and lagrangian dual methods. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 9–11 February 2020; Volume 34, pp. 630–637. [Google Scholar]
- Shaheen, M.A.; Hasanien, H.M.; Mekhamer, S.F.; Qais, M.H.; Alghuwainem, S.; Ullah, Z.; Tostado-Véliz, M.; Turky, R.A.; Jurado, F.; Elkadeem, M.R. Probabilistic optimal power flow solution using a novel hybrid metaheuristic and machine learning algorithm. Mathematics 2022, 10, 3036. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Kamel, S.; Hassan, M.H.; Mosaad, M.I.; Aljohani, M. Optimal power flow analysis based on hybrid gradient-based optimizer with moth–flame optimization algorithm considering optimal placement and sizing of FACTS/wind power. Mathematics 2022, 10, 361. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Chi, Y. DESTRESS: Computation-optimal and communication-efficient decentralized nonconvex finite-sum optimization. SIAM J. Math. Data Sci. 2022, 4, 1031–1051. [Google Scholar] [CrossRef]

| Technique | Advantages | Disadvantages |
|---|---|---|
| Auxiliary Problem Principle [28] | Simplifies the MAOPF problem by relaxing inter-area constraints | Slow convergence due to the iterative update of Lagrangian multipliers |
| Augmented Lagrangian Relaxation [13] | Enhances convergence by adding penalty terms | Higher computational complexity [29] |
| Analytical Target Cascading [15,16] | Suitable for hierarchical systems and improves convergence via decomposition | Convergence and complexity challenges for highly interconnected systems [30] |
| Auxiliary Problem Principle [18,31] | Converts MAOPF into an unconstrained optimization problem with penalties | Computational burden increases with the size and complexity of the system [32] |
| ADMM [33] | Combines decomposability with superior convergence properties | Still requires significant data exchange between regions |
| Optimality Condition Decomposition [34] | Effective for both linear and nonlinear problems | Performance highly dependent on network partitioning |
| ADP [35] | Decomposes MAOPF into subproblems with Bellman’s equation, improving scalability | High complexity in value function approximation, not suitable for non-linear systems |
| PDDP [23] | Improves performance for nonlinear MAOPF systems | Does not account for renewable energy variability, leading to power fluctuations |
| Improved Lagrangian Consistency Algorithm [36] | Considers line security constraints for decentralized OPF | Convergence issues with non-convex problems |
| Parameters | ||||||
|---|---|---|---|---|---|---|
| (MW) | 100 | 150 | 100 | 100 | 150 | 150 |
| (MW) | 10 | 10 | 10 | 10 | 10 | 50 |
| (MVar) | 60 | 85 | 60 | 80 | 150 | 180 |
| (MVar) | −30 | −40 | −30 | −40 | −75 | −90 |
| (/WM2) | 0.06 | 0.05 | 0.04 | 0.03 | 0.02 | 0.01 |
| (/WM) | 30 | 40 | 50 | 30 | 15 | 25 |
| () | 200 | 80 | 60 | 100 | 80 | 60 |
| Technique | Total Cost | Iterations |
|---|---|---|
| CIPM | USD 46,684.58 | – |
| DSRG | USD 46,685.69 | 24 |
| DIPM | USD 46,689.14 | 45 |
| ADP | USD 46,701.53 | 30 |
| PDDP | USD 46,762.42 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussan, U.; Wang, H.; Ayub, M.A.; Rasheed, H.; Majeed, M.A.; Peng, J.; Jiang, H. Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems. Mathematics 2024, 12, 3064. https://doi.org/10.3390/math12193064
Hussan U, Wang H, Ayub MA, Rasheed H, Majeed MA, Peng J, Jiang H. Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems. Mathematics. 2024; 12(19):3064. https://doi.org/10.3390/math12193064
Chicago/Turabian StyleHussan, Umair, Huaizhi Wang, Muhammad Ahsan Ayub, Hamna Rasheed, Muhammad Asghar Majeed, Jianchun Peng, and Hui Jiang. 2024. "Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems" Mathematics 12, no. 19: 3064. https://doi.org/10.3390/math12193064
APA StyleHussan, U., Wang, H., Ayub, M. A., Rasheed, H., Majeed, M. A., Peng, J., & Jiang, H. (2024). Decentralized Stochastic Recursive Gradient Method for Fully Decentralized OPF in Multi-Area Power Systems. Mathematics, 12(19), 3064. https://doi.org/10.3390/math12193064







