Closed-Form Performance Analysis of the Inverse Power Lomax Fading Channel Model
Abstract
:1. Introduction
- An easy-to-use statistical formulation (in terms of the PDF and CDF) of the inverse power Lomax fading channel model is introduced.
- A specific positioning of the IPL model among the ones most widely used in wireless communications is performed. The results help to identify its capability to handle both severe and light fading, depending on the channel parameters.
- The closed-form expressions are derived for (a) the moment-generating function of the instantaneous SNR; (b) amount of fading (AoF); (c) outage probability (OP); (d) average bit error rate (ABER); and (e) ergodic channel capacity (EC).
- Closed-form high-SNR asymptotic expressions for all the derived channel-performance metrics are derived.
- The closed-form and numerical hyper-Rayleigh analysis of the IPL channel is performed, identifying the boundaries of weak, strong, and full hyper-Rayleigh regimes.
- A thorough joint analysis of the dependence of all the assumed channel-performance metrics on the channel parameters is performed for different fading scenarios—heavy fading and light fading.
- The numerical and statistical simulation results are presented, proving the correctness of the performed theoretical analysis.
- The practical applicability of the proposed model was verified using a variety of datasets, including both synthetic computer-generated data and real-world experimental measurements.
2. IPL Channel Statistical Description
2.1. PDF and CDF of the Instantaneous SNR
2.2. MGF of the Instantaneous SNR
3. IPL Fading Channel Model Application
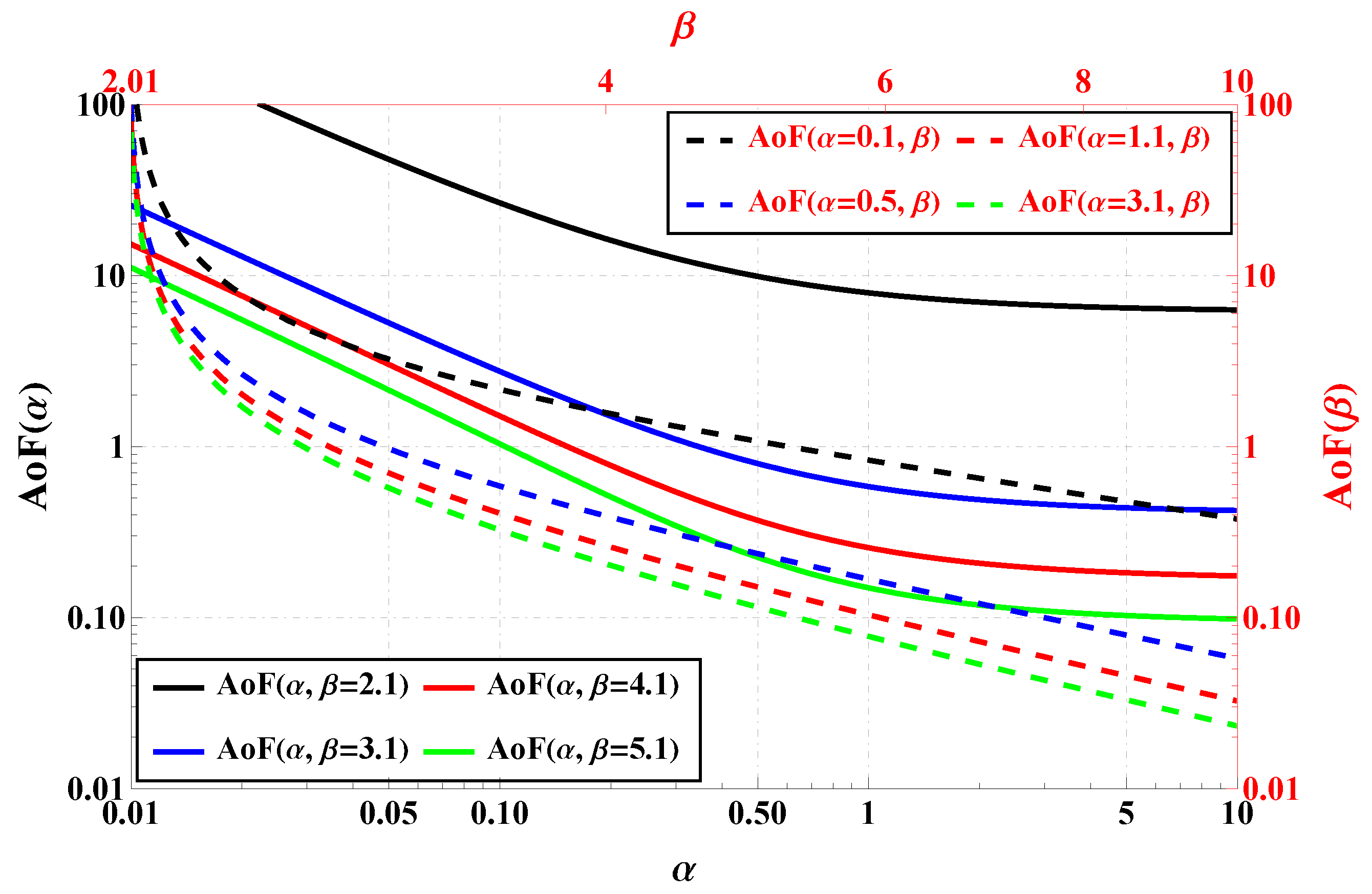
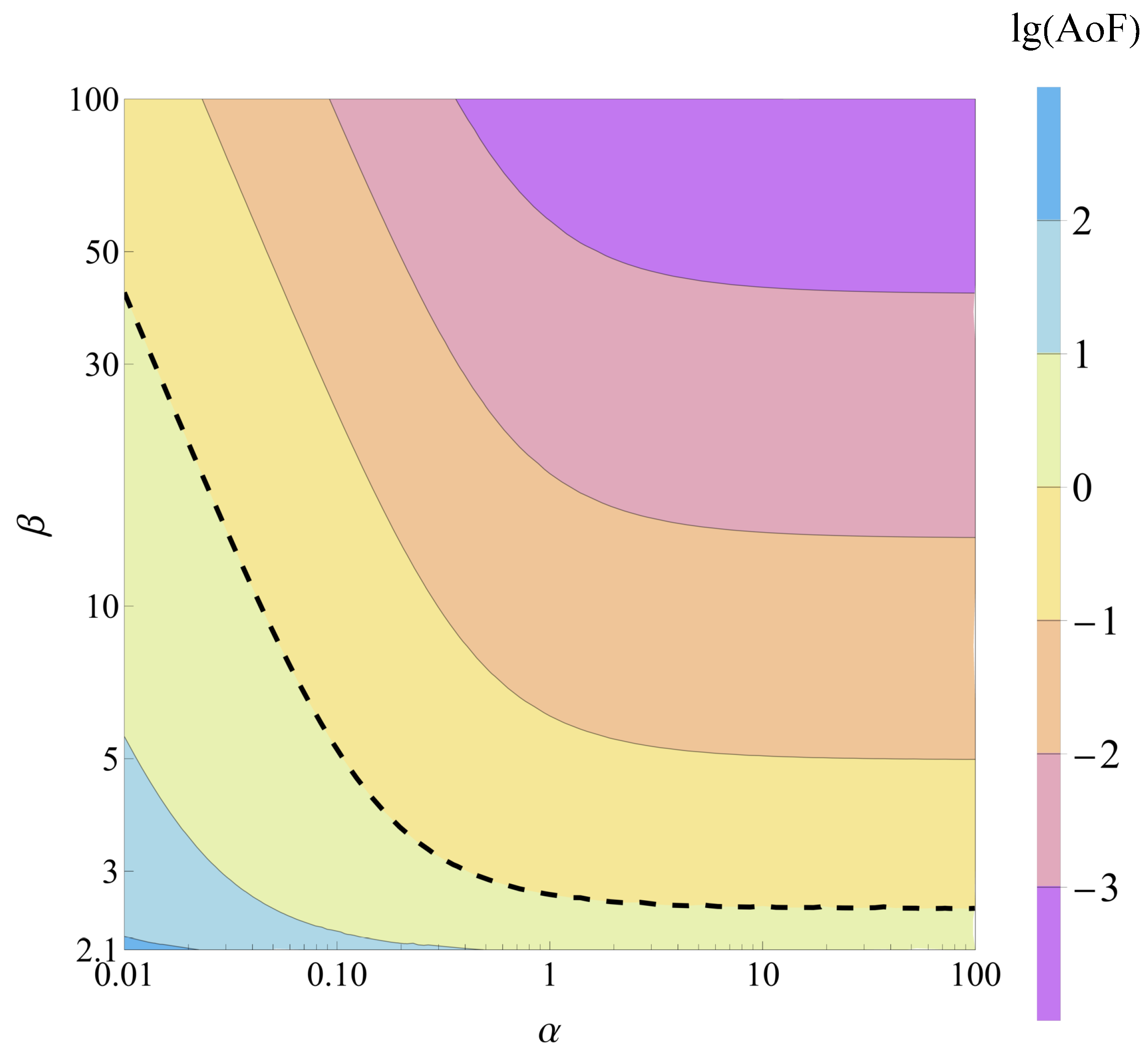
3.1. Amount of Fading
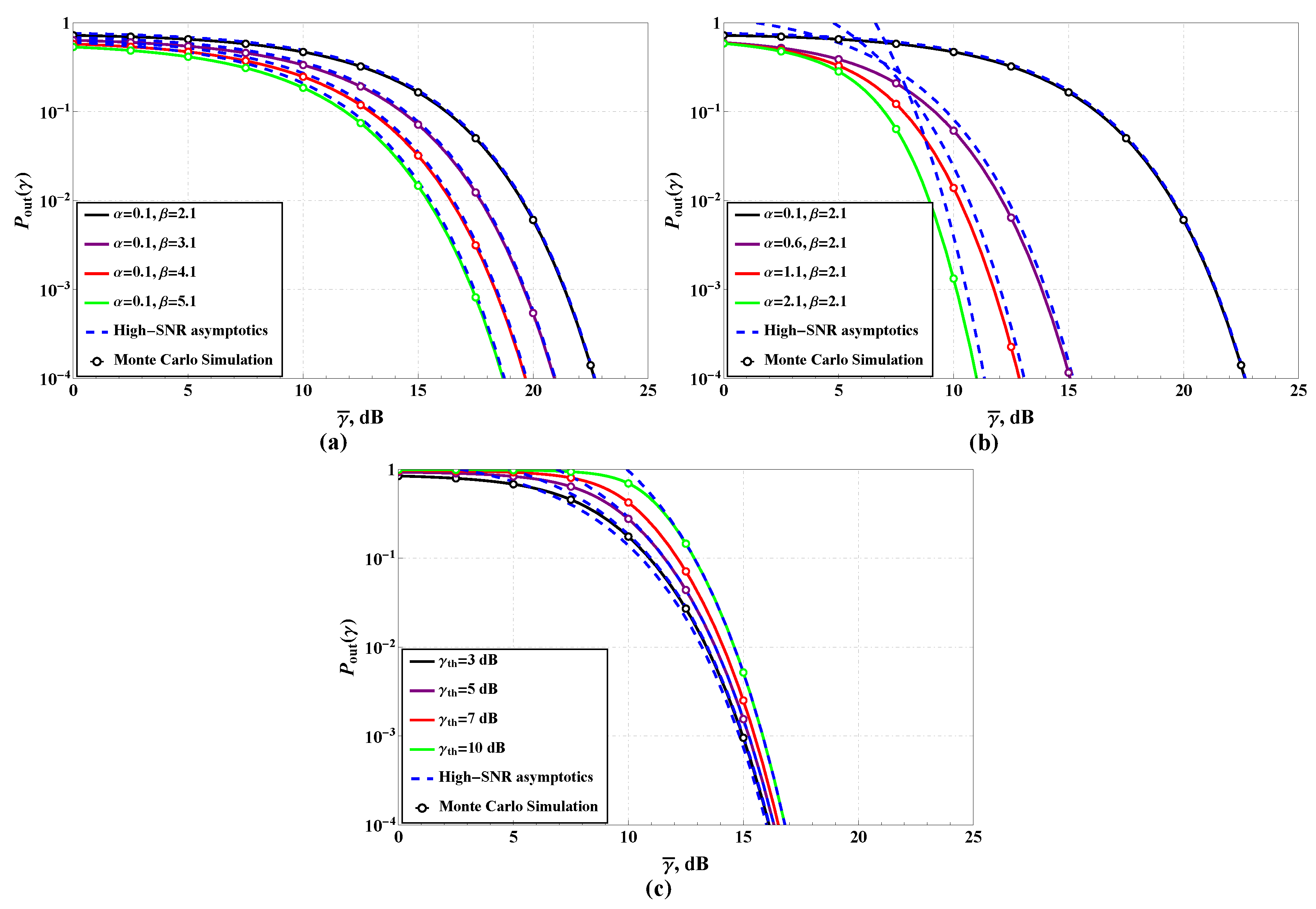
3.2. Outage Probability
3.3. Error Rate Analysis
3.4. Ergodic Channel Capacity Analysis
3.5. Hyper-Rayleigh Analysis
- In the OP sense if or and ;
- In the AoF sense if and ; otherwise, see Section 4.4;
- In the EC sense if and ; otherwise, see Section 4.4.
4. Simulation and Results’ Analysis
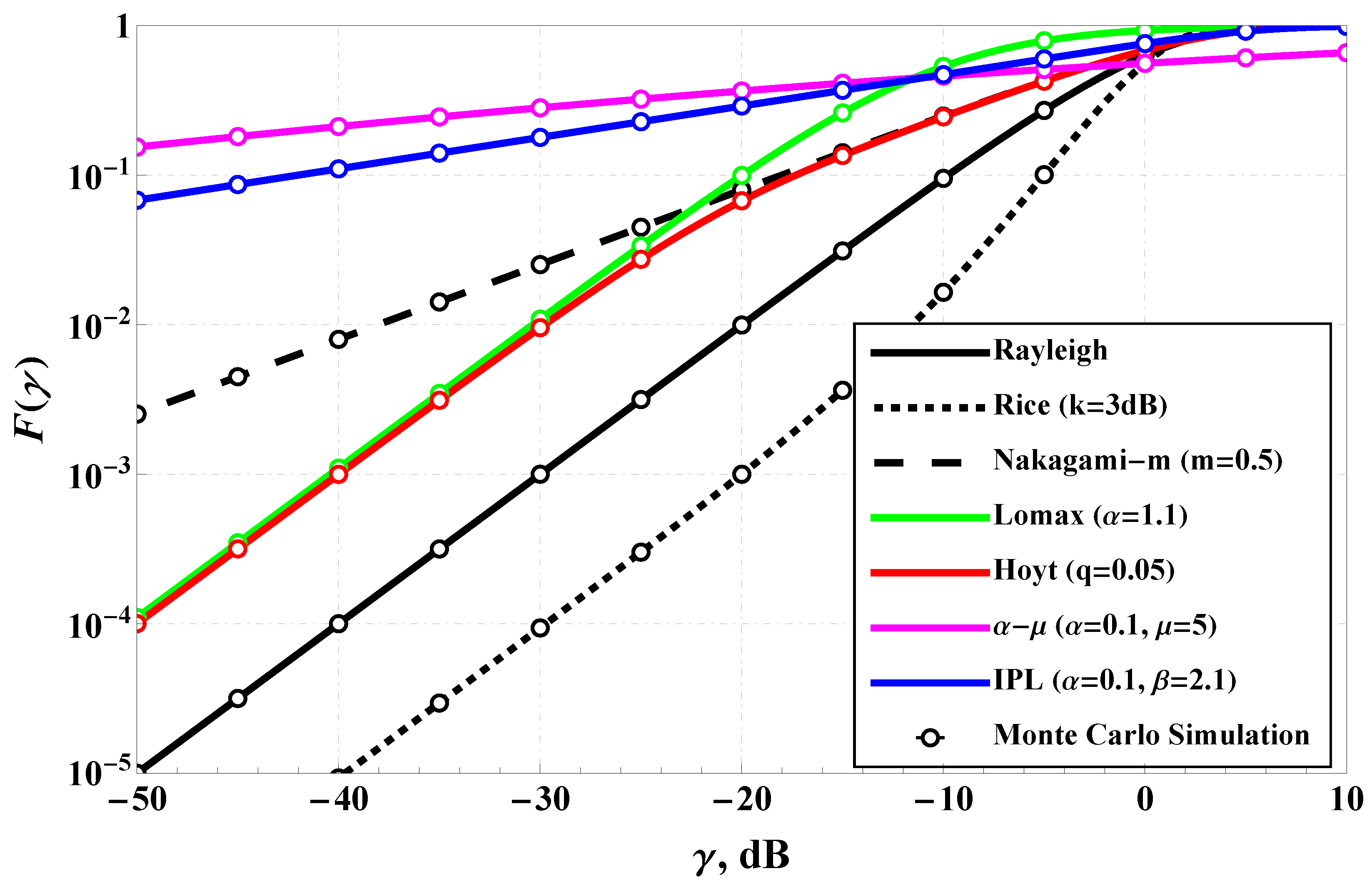
4.1. Model Verification and Positioning
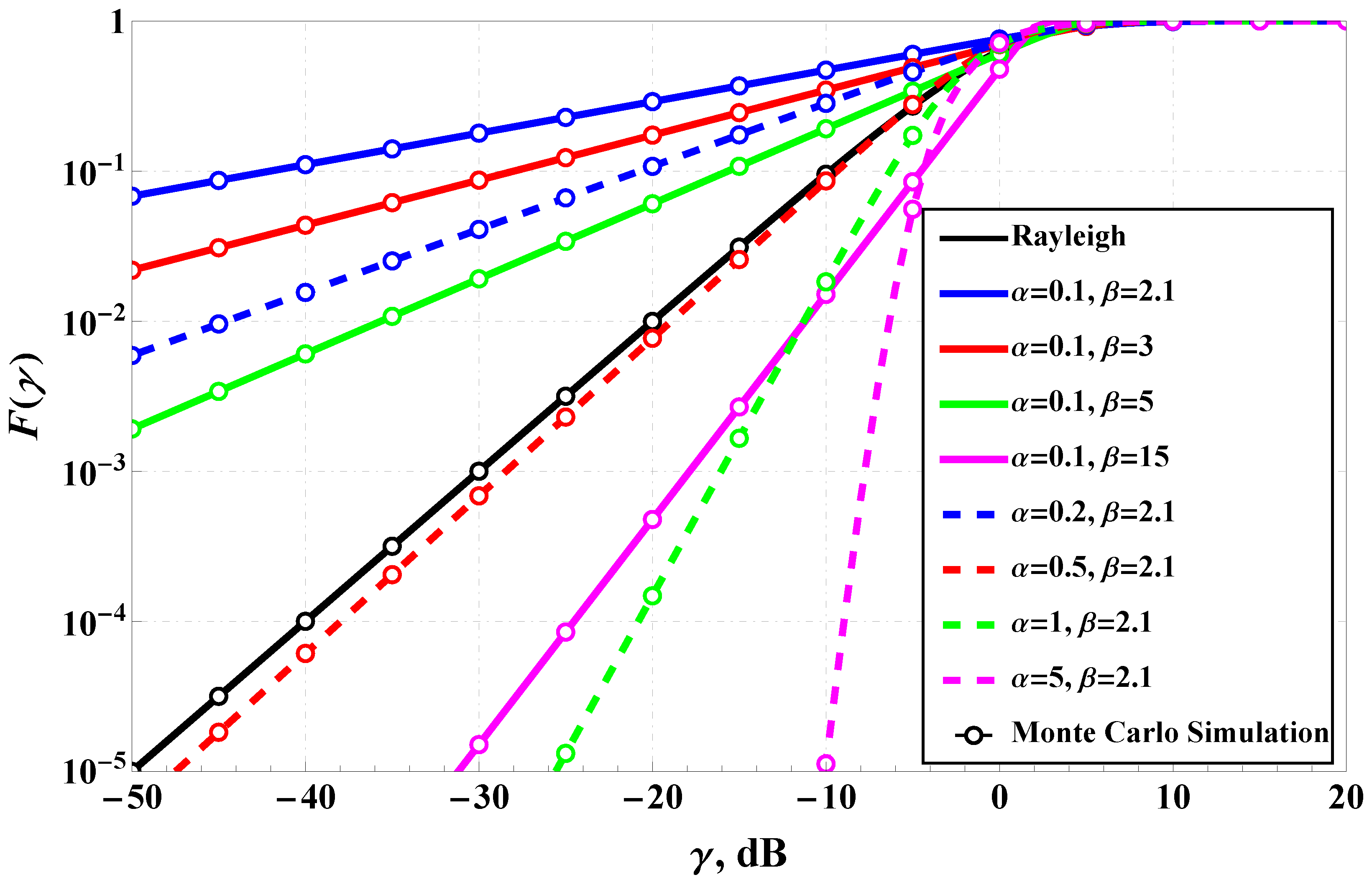
- The increase in the shape parameter for a fixed and small power-transformation parameter (i.e., );
- The increase in the power-transformation parameter for a fixed-shape parameter (i.e., ).
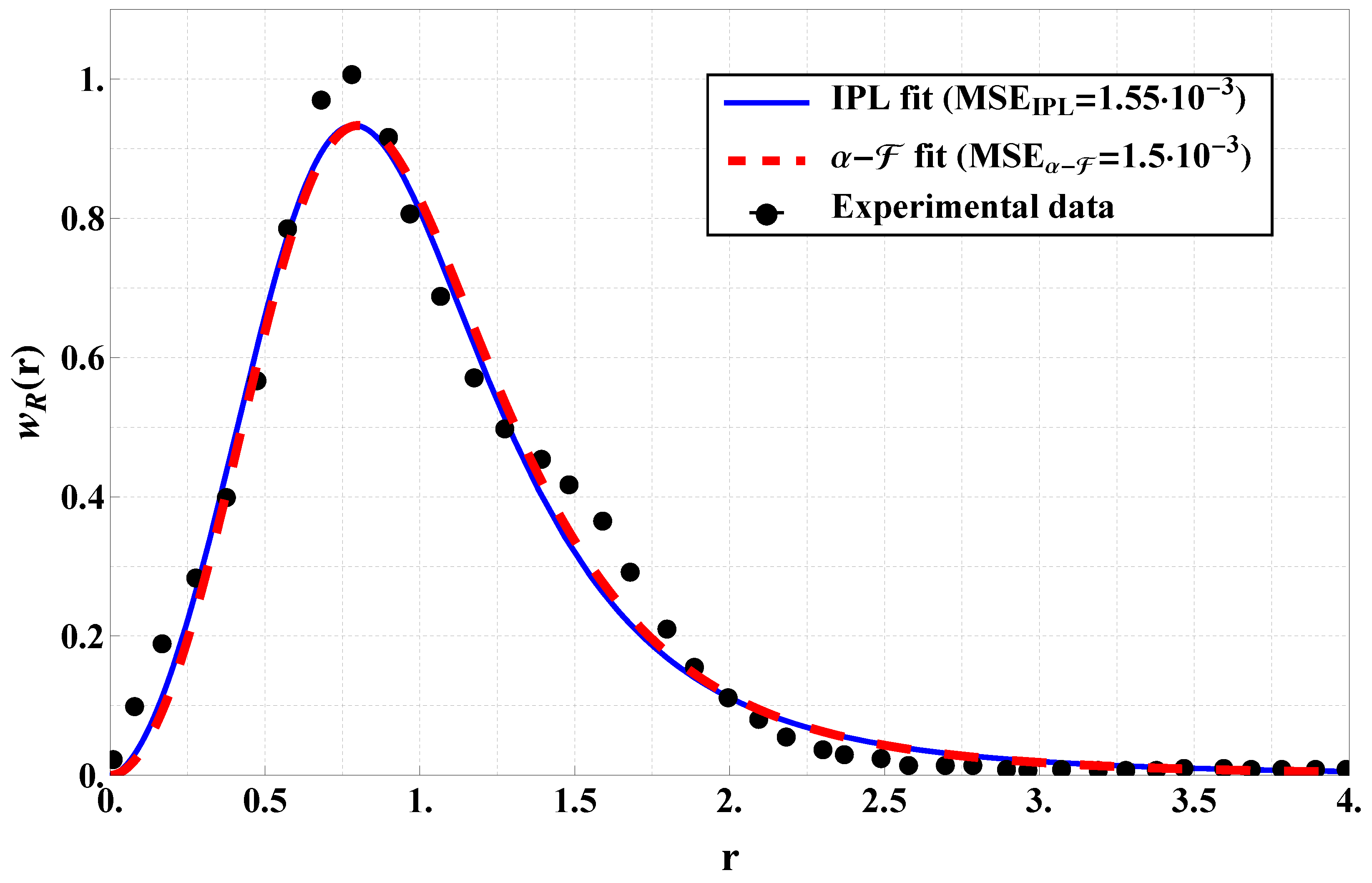
4.2. Experimental Verification
- 1.
- Experimental data from a GHz device-to-device (D2D) communication system with on-body devices forming a body area network (BAN) in indoor and outdoor line-of-sight and non-line-of-sight environments [56].
- 2.
- 3.
- Experimental measurements of a 4G LTE network functioning in a densely populated smart city [58].
- 4.
4.3. IPL Model Performance: AoF, OP, ABER, and EC
4.4. Hyper-Rayleigh Analysis
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paris, J.F. Advances in the Statistical Characterization of Fading: From 2005 to Present. Int. J. Antennas Propag. 2014, 2014, 258308. [Google Scholar] [CrossRef]
- Shankar, P.M. Fading and Shadowing in Wireless Systems; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Khawaja, W.; Guvenc, I.; Matolak, D.W.; Fiebig, U.C.; Schneckenburger, N. A Survey of Air-to-Ground Propagation Channel Modeling for Unmanned Aerial Vehicles. IEEE Commun. Surv. Tutorials 2019, 21, 2361–2391. [Google Scholar] [CrossRef]
- Yadav, P.; Kumar, S.; Kumar, R. A comprehensive survey of physical layer security over fading channels: Classifications, applications, and challenges. Trans. Emerg. Telecommun. Technol. 2021, 32, e4270. [Google Scholar] [CrossRef]
- Liu, S.; Yu, X.; Guo, R.; Tang, Y.; Zhao, Z. THz channel modeling: Consolidating the road to THz communications. China Commun. 2021, 18, 33–49. [Google Scholar] [CrossRef]
- Serghiou, D.; Khalily, M.; Brown, T.W.C.; Tafazolli, R. Terahertz Channel Propagation Phenomena, Measurement Techniques and Modeling for 6G Wireless Communication Applications: A Survey, Open Challenges and Future Research Directions. IEEE Commun. Surv. Tutorials 2022, 24, 1957–1996. [Google Scholar] [CrossRef]
- Launay, F. NG-RAN and 5G-NR: 5G Radio Access Network and Radio Interface, 1st ed.; Wiley-ISTE: Hoboken, NJ, USA, 2021. [Google Scholar]
- Jiang, W.; Luo, F.L. 6G Key Technologies: A Comprehensive Guide; Wiley-IEEE Press: New York, NY, USA, 2022. [Google Scholar]
- Alalewi, A.; Dayoub, I.; Cherkaoui, S. On 5G-V2X Use Cases and Enabling Technologies: A Comprehensive Survey. IEEE Access 2021, 9, 107710–107737. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.; Das, D.; Akhmetov, D.; Cordeiro, C. Overview and Performance Evaluation of Wi-Fi 7. IEEE Commun. Stand. Mag. 2022, 6, 12–18. [Google Scholar] [CrossRef]
- Reshef, E.; Cordeiro, C. Future Directions for Wi-Fi 8 and Beyond. IEEE Commun. Mag. 2022, 60, 50–55. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Qiu, Y.; Liu, X.; Song, M.; Fan, W.; Kokkeler, A.B.J.; Miao, Y. A UAV-Aided Real-Time Channel Sounder for Highly Dynamic Nonstationary A2G Scenarios. IEEE Trans. Instrum. Meas. 2023, 72, 1–15. [Google Scholar] [CrossRef]
- Lyu, Y.; Wang, W.; Sun, Y.; Rashdan, I. Measurement-based fading characteristics analysis and modeling of UAV to vehicles channel. Veh. Commun. 2024, 45, 100707. [Google Scholar] [CrossRef]
- Schmieder, M.; Eichler, T.; Wittig, S.; Peter, M.; Keusgen, W. Measurement and Characterization of an Indoor Industrial Environment at 3.7 and 28 GHz. In Proceedings of the 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Musthafa, A.M.; Luini, L.; Riva, C.; Livieratos, S.N.; Roveda, G. A long-term experimental investigation on the impact of rainfall on short 6G D-band links. Radio Sci. 2023, 58, 1–10. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, J.; Tang, P.; Zhang, Y.; Xu, H.; Gao, T.; Miao, H.; Chai, Z.; Zhou, Z.; Li, Y.; et al. Channel Measurement, Modeling, and Simulation for 6G: A Survey and Tutorial. arXiv 2023, arXiv:2305.16616. [Google Scholar] [CrossRef]
- Qasem, N. Measurement and Simulation for Improving Indoor Wireless Communication System Performance at 2.4 GHz by Modifying the Environment. IEEE Access 2024, 12, 96660–96671. [Google Scholar] [CrossRef]
- Huang, Y.; Xin, W.; Wang, X.; Wang, T.; Shi, Y.; Jiang, Z. A Comparative Study on Urban Micro-Cell Channel Measurements at 4.9 and 28 GHz. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Ju, S.; Shakya, D.; Poddar, H.; Xing, Y.; Kanhere, O.; Rappaport, T.S. 142 GHz Sub-Terahertz Radio Propagation Measurements and Channel Characterization in Factory Buildings. IEEE Trans. Wirel. Commun. 2024, 23, 7127–7143. [Google Scholar] [CrossRef]
- Fraidenraich, G.; Yacoub, M.D. The α-η-μ and α-κ-μ Fading Distributions. In Proceedings of the 2006 IEEE Ninth International Symposium on Spread Spectrum Techniques and Applications, Manaus, Brazil, 28–31 August 2006; pp. 16–20. [Google Scholar] [CrossRef]
- Yacoub, M.D. The κ-μ distribution and the η-μ distribution. IEEE Antennas Propag. Mag. 2007, 49, 68–81. [Google Scholar] [CrossRef]
- Yacoub, M.D. The α-μ Distribution: A Physical Fading Model for the Stacy Distribution. IEEE Trans. Veh. Technol. 2007, 56, 27–34. [Google Scholar] [CrossRef]
- Rabelo, G.S.; Yacoub, M.D. The κ-μ Extreme Distribution. IEEE Trans. Commun. 2011, 59, 2776–2785. [Google Scholar] [CrossRef]
- Paris, J.F. Statistical Characterization of κ-μ Shadowed Fading. IEEE Trans. Veh. Technol. 2014, 63, 518–526. [Google Scholar] [CrossRef]
- Yacoub, M.D. The α-η-κ-μ Fading Model. IEEE Trans. Antennas Propag. 2016, 64, 3597–3610. [Google Scholar] [CrossRef]
- Sánchez, I.; López-Martínez, F.J. The Lomax Distribution for Wireless Channel Modeling: Theory and Applications. IEEE Open J. Veh. Technol. 2024, 5, 162–171. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Costa, D.B.d. Fluctuating Nakagami-m Fading Distribution. IEEE Wirel. Commun. Lett. 2024, 13, 959–963. [Google Scholar] [CrossRef]
- Hassan, A.S.; Abd-Allah, M. On the Inverse Power Lomax Distribution. Ann. Data Sci. 2018, 6, 259–278. [Google Scholar] [CrossRef]
- El-Sherpieny, E.S.A.; Almetwally, E.M.; Muhammed, H.Z. Progressive Type-II hybrid censored schemes based on maximum product spacing with application to Power Lomax distribution. Phys. Stat. Mech. Its Appl. 2020, 553, 124251. [Google Scholar] [CrossRef]
- Shi, X.; Shi, Y. Inference for Inverse Power Lomax Distribution with Progressive First-Failure Censoring. Entropy 2021, 23, 1099. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.S.; Al-Omar, A.I.; Ismail, D.M.; Al-Anzi, A. A new generalization of the inverse Lomax distribution with statistical properties and applications. Int. J. Adv. Appl. Sci. 2021, 8, 89–97. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Giri, R.L.; Szymkowiak, M. Some results on characterization of distributions in reliability analysis. Commun.-Stat.-Theory Methods, 2024; 1–12. [Google Scholar] [CrossRef]
- Akueson, G.A.H.; Bogninou, M.J.; Akossou, A.Y.J. Modified Alpha Power Transformed Inverse Power Lomax Distribution with appllications. Res. Sq. 2024; preprint. [Google Scholar] [CrossRef]
- ZeinEldin, R.A.; ul Haq, M.A.; Hashmi, S.; Elsehety, M. Alpha Power Transformed Inverse Lomax Distribution with Different Methods of Estimation and Applications. Complexity 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Ogunde, A.A.; Oseghale, I.O.; Nwanyibuife, O.B. The Type II Topp-Leone Inverse Power Lomax distribution with Simulation and Applications. J. Mod. Appl. Stat. Methods 2023, 23, 1–28. [Google Scholar] [CrossRef]
- Lomax, K.S. Business Failures: Another Example of the Analysis of Failure Data. J. Am. Stat. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Lopez-Martinez, F.J.; Morales-Jimenez, D.; Martos-Naya, E.; Paris, J.F. On the Bivariate Nakagami-m Cumulative Distribution Function: Closed-Form Expression and Applications. IEEE Trans. Commun. 2013, 61, 1404–1414. [Google Scholar] [CrossRef]
- Gvozdarev, A.S.; Artemova, T.K.; Manahov, R.; Mozzhukhin, S.; Veselkov, A. Energy-Based Spectrum Sensing Over the Severe Fading Channels. In Proceedings of the 2024 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russian, 12–14 March 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Gvozdarev, A.S.; Artemova, T.K. Closed-form energy-based signal detection analysis in presence of a Lomax fading channel in full hyper-Rayleigh regime. Phys. Commun. 2024, 66, 102473. [Google Scholar] [CrossRef]
- Ramírez-Espinosa, P.; López-Martínez, F.J. Composite Fading Models Based on Inverse Gamma Shadowing: Theory and Validation. IEEE Trans. Wirel. Commun. 2021, 20, 5034–5045. [Google Scholar] [CrossRef]
- Agrawal, R.; Karmeshu; Sehgal, A. Composite Channel Model for Wireless Propagation with Wide-Range Signal Variation Using Rayleigh–Generalized Inverse Gaussian Distribution. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 46, 213–223. [Google Scholar] [CrossRef]
- Badarneh, O.S. The α-F Composite Fading Distribution: Statistical Characterization and Applications. IEEE Trans. Veh. Technol. 2020, 69, 8097–8106. [Google Scholar] [CrossRef]
- Badarneh, O.S. The α-η-F and α-κ-F Composite Fading Distributions. IEEE Commun. Lett. 2020, 24, 1924–1928. [Google Scholar] [CrossRef]
- Badarneh, O.S.; Muhaidat, S.; da Costa, D.B. The α-η-κ-F Composite Fading Distribution. IEEE Wirel. Commun. Lett. 2020, 9, 2182–2186. [Google Scholar] [CrossRef]
- Gvozdarev, A.S. Closed-Form Analysis of the α-Beaulieu-Xie Shadowed Fading Channel. IEEE Wirel. Commun. Lett. 2023, 12, 1623–1627. [Google Scholar] [CrossRef]
- Olver, F.W.J. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Simon, M.K.; Alouini, M.S. Digital Communication over Fading Channels; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Atapattu, S.; Tellambura, C.; Jiang, H. MGF Based Analysis of Area under the ROC Curve in Energy Detection. IEEE Commun. Lett. 2011, 15, 1301–1303. [Google Scholar] [CrossRef]
- Gvozdarev, A.S. The Generalized MGF Approach to Closed-Form Average Symbol Error Rate Calculation. IEEE Commun. Lett. 2021, 25, 1124–1128. [Google Scholar] [CrossRef]
- Gvozdarev, A.S. A novel unified framework for energy-based spectrum sensing analysis in the presence of fading. Sensors 2022, 22, 1742. [Google Scholar] [CrossRef]
- Mathai, A.; Saxena, R.; Haubold, H. The H-Function: Theory and Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series: More Special Functions; Gordon and Breach Science Publishers: New York, NY, USA, 1990; Volume 3, p. 800. [Google Scholar]
- Chauhan, P.S.; Kumar, S.; Jain, A.; Hanzo, L. An Asymptotic Framework for Fox’s H-Fading Channel With Application to Diversity-Combining Receivers. IEEE Open J. Veh. Technol. 2023, 4, 404–416. [Google Scholar] [CrossRef]
- Garcia-Corrales, C.; Fernandez-Plazaola, U.; Canete, F.J.; Paris, J.F.; Lopez-Martinez, F.J. Unveiling the Hyper-Rayleigh Regime of the Fluctuating Two-Ray Fading Model. IEEE Access 2019, 7, 75367–75377. [Google Scholar] [CrossRef]
- Wang, Z.; Giannakis, G. A simple and general parameterization quantifying performance in fading channels. IEEE Trans. Commun. 2003, 51, 1389–1398. [Google Scholar] [CrossRef]
- Bhargav, N.; da Silva, C.R.N.; Chun, Y.J.; Leonardo, E.J.; Cotton, S.L.; Yacoub, M.D. On the Product of Two κ – μ Random Variables and its Application to Double and Composite Fading Channels. IEEE Trans. Wirel. Commun. 2018, 17, 2457–2470. [Google Scholar] [CrossRef]
- Cotton, S.L. Human Body Shadowing in Cellular Device-to-Device Communications: Channel Modeling Using the Shadowed κ-μ Fading Model. IEEE J. Sel. Areas Commun. 2015, 33, 111–119. [Google Scholar] [CrossRef]
- Imoize, A.L.; Orolu, K.; Atayero, A.A.A. Analysis of key performance indicators of a 4G LTE network based on experimental data obtained from a densely populated smart city. Data Brief 2020, 29, 105304. [Google Scholar] [CrossRef]
- Gvozdarev, A.; Artemova, T.; Morkovkin, A. The impact of modulation constellation type on the finite signal-to-noise ratio diversity gain in the presence of a multipath fading channel. Probl. Inf. Transm. 2024, 60, 71–93. [Google Scholar]
- Blanza, J.; Teologo, A.J.; Materum, L. Datasets for Multipath Clustering at 285 MHz and 5.3 GHz Bands Based on COST 2100 MIMO Channel Model. In Proceedings of the 2019 International Symposium on Multimedia and Communication Technology (ISMAC), Quezon City, Philippines, 19–21 August 2019. [Google Scholar] [CrossRef]
- Blanza, J.F.; Teologo, A.T.; Materum, L. Datasets for Multipath Clustering at 285 MHz and 5.3 GHz Bands Based on COST 2100 MIMO Channel Model. In Proceedings of the 2019 International Symposium on Multimedia and Communication Technology (ISMAC), Quezon City, Philippines, 19–21 August 2019; pp. 1–5. [Google Scholar] [CrossRef]



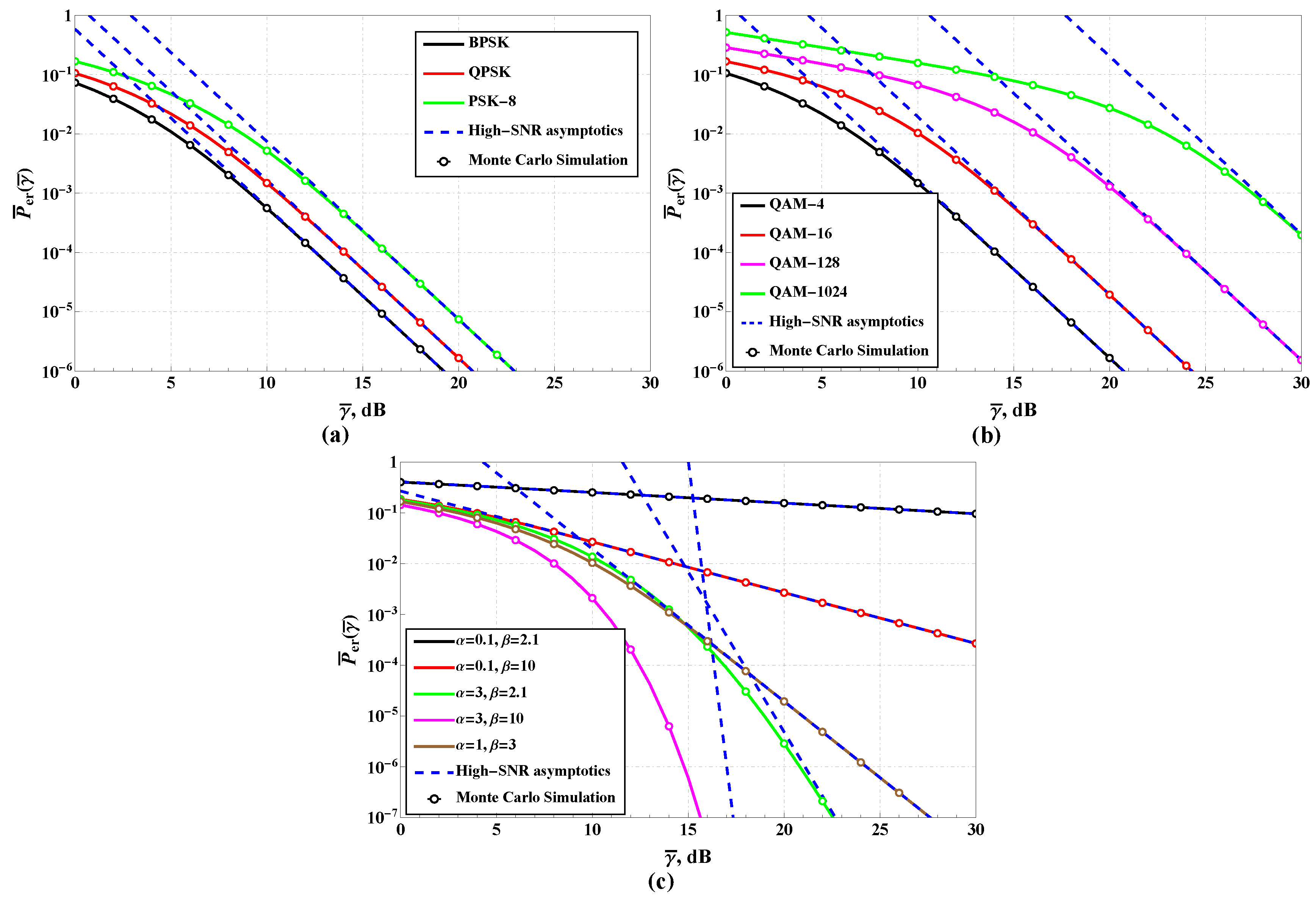


| M-QAM | |||
| M-PSK |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gvozdarev, A.S. Closed-Form Performance Analysis of the Inverse Power Lomax Fading Channel Model. Mathematics 2024, 12, 3103. https://doi.org/10.3390/math12193103
Gvozdarev AS. Closed-Form Performance Analysis of the Inverse Power Lomax Fading Channel Model. Mathematics. 2024; 12(19):3103. https://doi.org/10.3390/math12193103
Chicago/Turabian StyleGvozdarev, Aleksey S. 2024. "Closed-Form Performance Analysis of the Inverse Power Lomax Fading Channel Model" Mathematics 12, no. 19: 3103. https://doi.org/10.3390/math12193103








