Abstract
Parallel Concatenated Block (PCB) codes are conventionally represented as high-rate codes with low error correcting capability. To form a reliable and outstanding code, this paper presents a modification on the structure of PCB codes, which is accomplished by encoding some parity bits of one of their component codes. For the newly proposed code, named as the braided code, non-stuff bit-based convolutional interleavers are applied, aiming to minimize the design complexity while ensuring the proper permutations of the original message and selected parity bits. To precisely determine the error correcting capability, a tight bound for the minimum weight of braided code is presented. Additionally, further analyses are provided, which verify iterative decoding performance and the complexity of the constructed code. It is concluded that an outstanding braided code is formed by utilizing a reasonable number of iterations applied at its decoding processes, while maintaining its design complexity at a level similar to other well-known codes. The significant performance of short and long-length-based braided codes is evident in both waterfall and error floor regions.
MSC:
94B05; 94B15; 94B99
1. Introduction
Advanced Forward Error Correcting (FEC) codes are fundamentally constructed using the combination of two or more basic codes in the serial, parallel, or hybrid form. Amongst concatenated codes, the Parallel Concatenated Block (PCB) code has less interest as it does not provide an error-correcting capability at a level similar to its counterparts. This is due to the non-recursive structure of its constituent codes as well as the lack of parity-on-parity bits, which conclude a low minimum weight for the code obtained from messages with weight one [1]. This means that conventional interleavers do not significantly impact the performance of the PCB code.
As a solution, stuff bit-based interleavers were proposed, which add some redundant bits (with the value of zero) to the permuted data aiming to mitigate the multiplicity of the minimum weight of the component code and provide the proper permuted data for the component code [2]. Although these interleavers improve the performance of PCB codes, their block (frame) error-correcting capability is not at the same level as outstanding codes.
PCB code designed using the abovementioned structure applied either Euclidean Geometry (EG) or Projective Geometry (PG) cyclic Low-Density Parity Check (LDPC) codes in its structure [3]. These codes, classified as Finite Geometry (FG) codes, do not have harmful trapping sets in their Tanner graphs [4]. This means that the performance of the PCB code constituted by FG LDPC codes is relevant to the minimum weight parameter.
As a result, to overcome the existing issue of such PCB code, it is essential to increase its minimum weight significantly. This is achievable by utilizing braided block codes, in which codewords obtained from a constituent code of the PCB code are interleaved and then encoded using the alternative constituent code [5]. Due to the encoding of parity bits of the codeword, braided block codes are considered as a class of product codes. The structure of these codes can also be modified by encoding rotated parity bits or through removing a number of them placed at a two-dimensionally formed codeword in a specific manner to construct the staircase or half braided codes [6,7], respectively. They mainly utilize Bose–Chaudhuri–Hocquenghem (BCH) codes as their component codes, which allow them to apply an efficient hard decision-based decoding technique [8,9]. Recently, a new scheme of these codes, i.e., zipper code, represented as a Spatially-Coupled (SC) product-type code, was introduced, which provides high performance and throughput for high-speed transmission systems. The combining of this code with other codes, particularly with the LDPC code, was also investigated in [10,11].
There exist several SC codes, which are fundamentally formed by turbo-like component codes [12,13,14]. These codes are represented as capacity-approaching codes for different channels when a long-length and relatively low rate (codes with a rate of 1/3 or lower) together with a pipeline decoding algorithm are applied to their structure. Similarly, serially SC codes are represented, where an inner convolutional code encodes parity bits of the outer convolutional code [15,16].
Alternatively, partial SC-LDPC code is designed using the coping fractions of a LDPC protograph in an efficient way to mitigate the gap between the proposed and original codes [17]. Partial-product LDPC block codes can also be formed by free riding codes, which transmit a few numbers of bits compared to the original code allocated for the column-wise encoding [18,19,20]. As partial columns check bits are transmitted, codes with higher rates are constructed. These codes mainly apply a soft decision decoding algorithm for one of the constituent codes, while a hard decision-based decoding algorithm is implemented for another constituent code.
Despite the above braided block coding or SC coding techniques, which apply a combination of soft and hard decision decoding techniques, some services for satellite communications, broadcasting systems, and similar ones require an outstanding code with a medium to low rate. This feature motivates us to implement a reliable soft decision-based decoding technique for the braided block code, whose performance and design complexity maintain it as the competitive code to other well-known ones.
Contributions:
- To achieve the abovementioned goal, a new scheme of the braided block code is accomplished, whose component codes (FG and EG LDPC codes) are decoded using the Min-Sum Algorithm (MSA).
- Instead of re-encoding all codeword bits, the first encoder concentrates on the most important parity bits; those contribute to the generation of low-weight codewords. This is achievable by determining the low weight distribution of the constituent code when messages with weights 1 and 2 are encoded. Then, some parity bits contributed to those weights of codewords are interleaved and encoded by the second constituent encoder.
- The paper applies a non-stuff bit-based convolutional interleaver. Similar to the messages, the permutation of the selected parity bits is conducted by the convolutional interleaver. As a convolutional interleaver is flexible to permute data with different lengths, one interleaver for the permutation of both messages and selected parity bits is applied. Despite the method proposed in [2], the convolutional interleaver used for the braided code does not add any stuff bits to the interleaved data. However, it still guarantees that only one bit of a message block is placed in an interleaved data block.
- Based on the interleaver specifications, the minimum weight of braided code is presented. It is proven that the obtained minimum weight is much greater than the minimum weight of PCB code.
- A comprehensive analysis is provided to extract the advantage of the braided code. It is shown that codes have outstanding performance, while they require similar or lower computation on their iterative decoding compared to other well-known codes.
The paper is organized as follows: Section 2 gives non-stuff bits-based convolutional interleavers for the PCB code. The structure of the braided code is explained in Section 3. Section 4 and Section 5 discuss the convergence behavior of the iterative decoding and latency of the proposed code, respectively. Section 6 compares the performance of braided codes with PCB codes through their upper bounds of probability of bit and block errors. Section 7 gives simulation results and finally Section 8 concludes the paper. To read this article better, we summarize the abbreviations in Table A1.
2. Non-Stuff-Based Convolutional Interleaver for PCB Codes
Figure 1 shows the encoder structure of PCB codes, whose constituent codes (codes 1 and 2) are identical [21]. The code accepts messages with the length of bits, where k is a positive integer. Every message with the length L is changed to k blocks with the length of k bits and considered as the input of constituent encoders. These blocks are named message blocks. A codeword with the length of n obtained from the first encoder (code 1) is added to the parity bits of the second encoder (code 2) to make a new codeword with the length of . Finally, k codewords with the length of are multiplexed to make a codeword with the length of . Hence, its code rate is .

Figure 1.
Structure of the PCB encoder [21].
In [2], a new technique for the interleaving of messages was presented, which adds some stuff bits to the permuted data to obtain the minimum weight of the PCB code from messages with weight one and reduce the multiplicity of the minimum weight. This is accomplished by the convolutional interleaver, which consists of T parallel lines represented as its period. Conventionally, each line has M memory units more than the previous line, which defines the space value. The interleaver accepts data with an arbitrary length of , where . Hence, depending on the data distribution to each line, the interleaved data will appear in different time slots. Figure 2 shows the general structure of interleaver [22]. Based on , such interleaved data with the length of together with stuff bits are represented as matrix. Two submatrices can define this matrix. The first one includes the matrix’s first rows, while the last rows form the second submatrix. The first and second submatrices have and stuff bits, respectively.
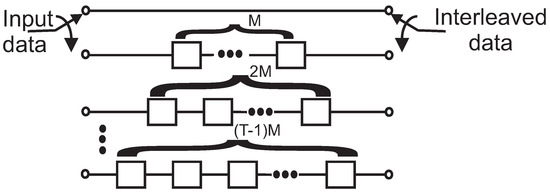
Figure 2.
Convolutional interleaver with period T and space M [22].
Despite the above structure, it is possible to obtain interleaved data without any stuff bits when the convolutional interleaver with the period of T and length of is applied. In this case, non-stuff bits of the second submatrix are used to replace stuff bits of the first submatrix. Indeed, non-stuff bits positioned at a column of the second submatrix are placed in the same column of the first submatrix.
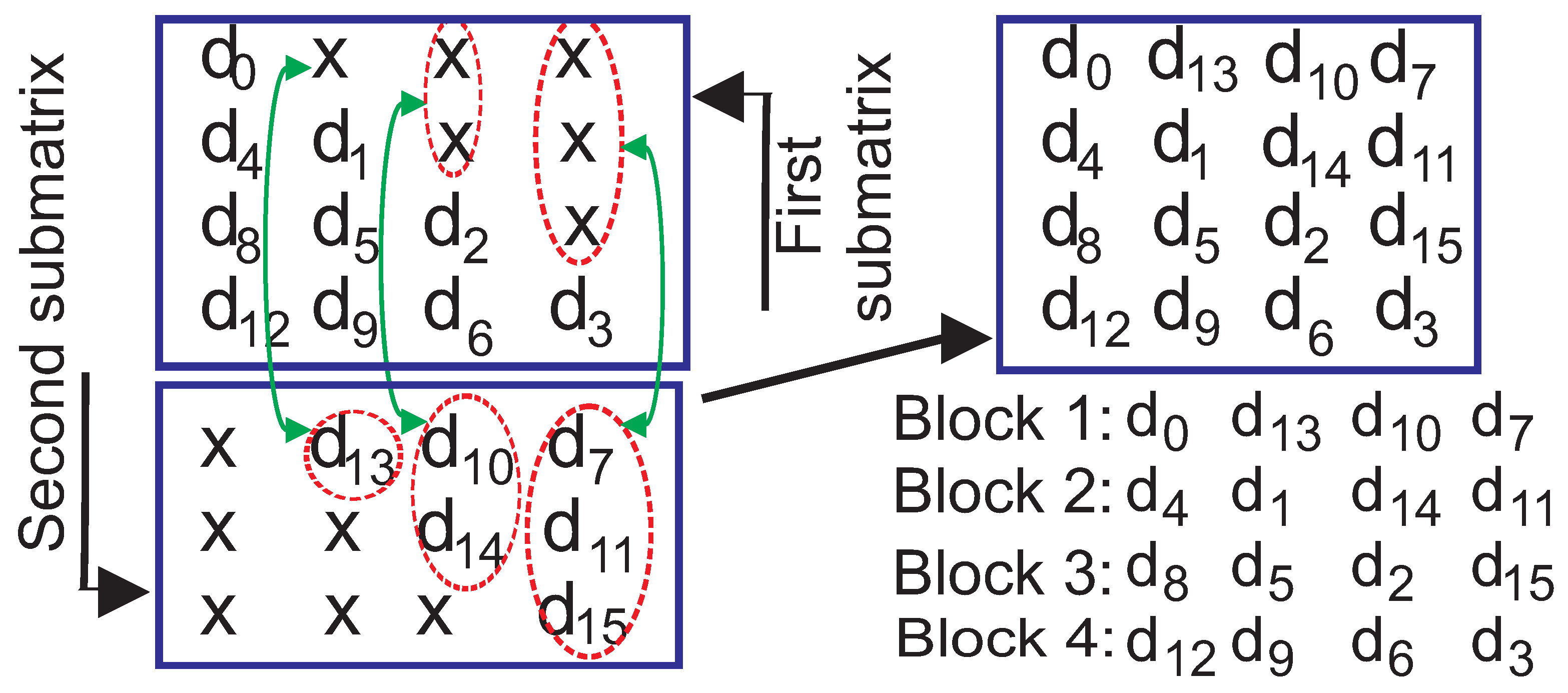
Figure 3 shows the application of (4,16,1) convolutional interleaver for the construction of four blocks of the permuted data. Here, s, , and “x”s represent sixteen bits of a message and twelve stuff bits, respectively. Considering this structure, for PCB codes with , interleaver is used to permute the messages properly.
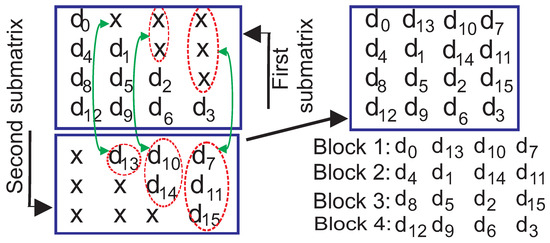
Figure 3.
Interleaved data formed by interleaver.
Lemma 1.
The minimum weight of the PCB code constructed by interleaver is , where is the minimum weight of codes.
Proof.
To gain the minimum weight of , it is required to place only one bit from each message block in a block of interleaved data [2]. At the jth row of the first submatrix, , non-stuff bits are indexed by , where . In one row of the first submatrix, these bits originated from th message block. It is evident that for a certain value of j, each value of i returns a unique number. This concludes that all non-stuff bits placed at a row of the first submatrix are from different message blocks.
Moreover, at the second submatrix of the interleaved data, non-stuff bits of the th row are specified by , where and . For all s, . Hence, these bits are originated from th message block. Again, this means that bits of the th row of the second submatrix originated from different message blocks.
The lowest bit index in each row of the second submatrix is . This is obtained when . Non-stuff bits of the th row of this submatrix are placed at the th row of the first submatrix. In each of rows of the first submatrix, the greatest bit index of non-shifted bits is . The difference between the lowest index of shifted bits from the second submatrix to the first one and the greatest index of those bits placed at the first submatrix is . For all s, the above difference will be greater than the value of T. Therefore, in one row of the updated first submatrix, bits are also originated from different message blocks. Based on the structure of bits placed at the first submatrix and those shifted from the second submatrix, it is concluded that all bits of an interleaved data block are from different message blocks. As a result, the minimum weight of the PCB code is , which is obtained from messages with weight one. □
3. A New Scheme of PCB Codes
EG and PG cyclic LDPC codes are free of cyclic four and do not have any harmful trapping sets in their structure [4]. Hence, the error-correcting capability of the PCB code proposed in Section 2 and formed by the mentioned cyclic codes is limited due to its low (or relatively low) minimum weight.
It is possible to form a PCB code with a high minimum weight by encoding of the codewords of codes. Such a technique is basically represented as braided coding [5]. However, the encoding of all codeword bits will significantly reduce the overall code rate and increase the design complexity. To minimize the complexity and maintain the performance of the braided block code at a high level, only a number of parity bits of one cyclic code, which contribute to the minimum and other low weights of the constituent cyclic codes are encoded. This requires determining the suitable cyclic code, which has more influence on the performance of PCB code. For this purpose, an analysis is conducted by considering messages with weights 1 and 2 that generate the minimum weight for component codes.
Table 1 gives the minimum weights of PCB codes from messages with weights 1 and 2. Here, is the number of messages and interleaved data blocks, which simultaneously generate the minimum weight for the first and second cyclic codes. and are also weights of the message and interleaved data blocks applied for cyclic codes, respectively. Moreover, and are multiplicities of of the cyclic code obtained from the message and interleaved data blocks with weights and , respectively.

Table 1.
Minimum weight specifications of cyclic codes.
Example 1.
For (3293,1369) PCB code constructed by two (63,37) EG cyclic codes of 37 blocks with length 37 originating from a message with weight two and length 1369, it is possible to have two blocks with weight one and length 37. Considering all messages with weight two, 26,640 blocks with weight one generate the minimum weight for the first cyclic code. These message blocks applied for the first code form 7030 blocks of the interleaved data with weight two for the second cyclic code. However, none of these 7030 blocks generate the minimum weight for the second code. On the other hand, 888 message blocks with weight two generate the minimum weight for the first code. Each of these blocks will conclude two blocks of the interleaved data with weight one. Hence, 888 cases exist to obtain two blocks of interleaved data with weight one. Again, none of these blocks generate a codeword with the minimum weight for the second code.
From the above example, it is evident that for the input data with weight two, due to the proper interleaving, the multiplicity of the minimum weight relevant to the first cyclic code is greater than that obtained from the second cyclic code. This means that parity bits of the first cyclic code have more influence on the performance of the PCB code. As a result, the encoding of the most important parity bits of the first cyclic code is followed to construct a braided block code.
3.1. Selection of Important Parity Bits of the Cyclic Code
Let , , be a set, whose elements, i.e., s, , are codewords’ weights of code obtained from messages with weight i. In this case, represents the number of elements of . Obviously, each of s have different multiplicities in the construction of the weight distribution of code based on messages with weight i. Define the set , whose elements express indices of the parity bits of codewords for code.
For , select some parity bits having the highest contribution to the defined codewords’ weights. Such a selection from the remaining elements of S is continued to obtain the contribution of at least two elements on all codewords. In the second step, ignore the codewords of if the position of one of their parity bits (or more than one parity bit) is among the elements selected from the first step. Then, select some parity bits (elements of S that are not selected at the first step), which are highly contributed to the weights of the remaining codewords of . The contribution of at least one parity bit to the weight of each codeword of is required.
Example 2.

The weight distribution of (15,7) cyclic LDPC code obtained from messages with weights 1 and 2 are given in Table 2, where and are weights of messages and codewords, respectively. Based on messages with weight 1, , where and having 5 and 2 multiplicites, respectively. In this case, bits 10, 8, and 9 have the highest contributions on weights of . The selection of these bits together with the 12th bit of the codewords guarantees that at least two of the selected bits are contributed on all weights of . At least one of these selected bits is also in weights of , .

Table 2.
Some weights of (15,7) cyclic code.
3.2. Structure of the Braided Code
Figure 4 shows the encoding process of the selected parity bits of the first constituent code of the PCB code, which is highlighted by four grey blocks. Encoding of these bits and conventional PCB encoding will form the encoder of the braided code. Let , , be the number of parity bits selected for the encoding. Based on k message blocks applied for the first code, parity bits are considered for the encoding. These bits are interleaved by the (,,1) interleaver proposed in Section 2. The interleaved data can be viewed as two-dimensional data having k rows and columns. In this case, column-wise reading of such data provides blocks of data with the length of k, which can be encoded by the second code.
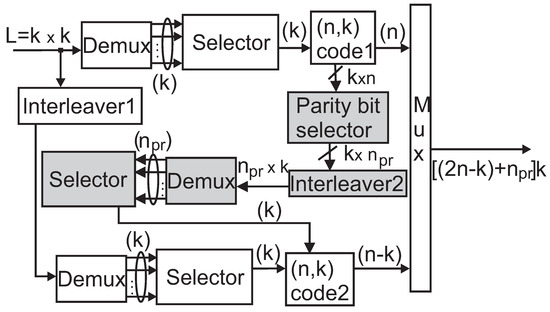
Figure 4.
Structure of the braided encoder.
Lemma 2.
Every block of interleaved data formed by the above interleaving has one parity bit of a codeword.
Proof.
There exist blocks of interleaved data, , with k bits. Bits are given by , where and is the remainder of . For all s, . Hence, and th bit of the th block of interleaved data is from th codeword block. Thus, a block of the permuted data has one parity bit of a codeword. □
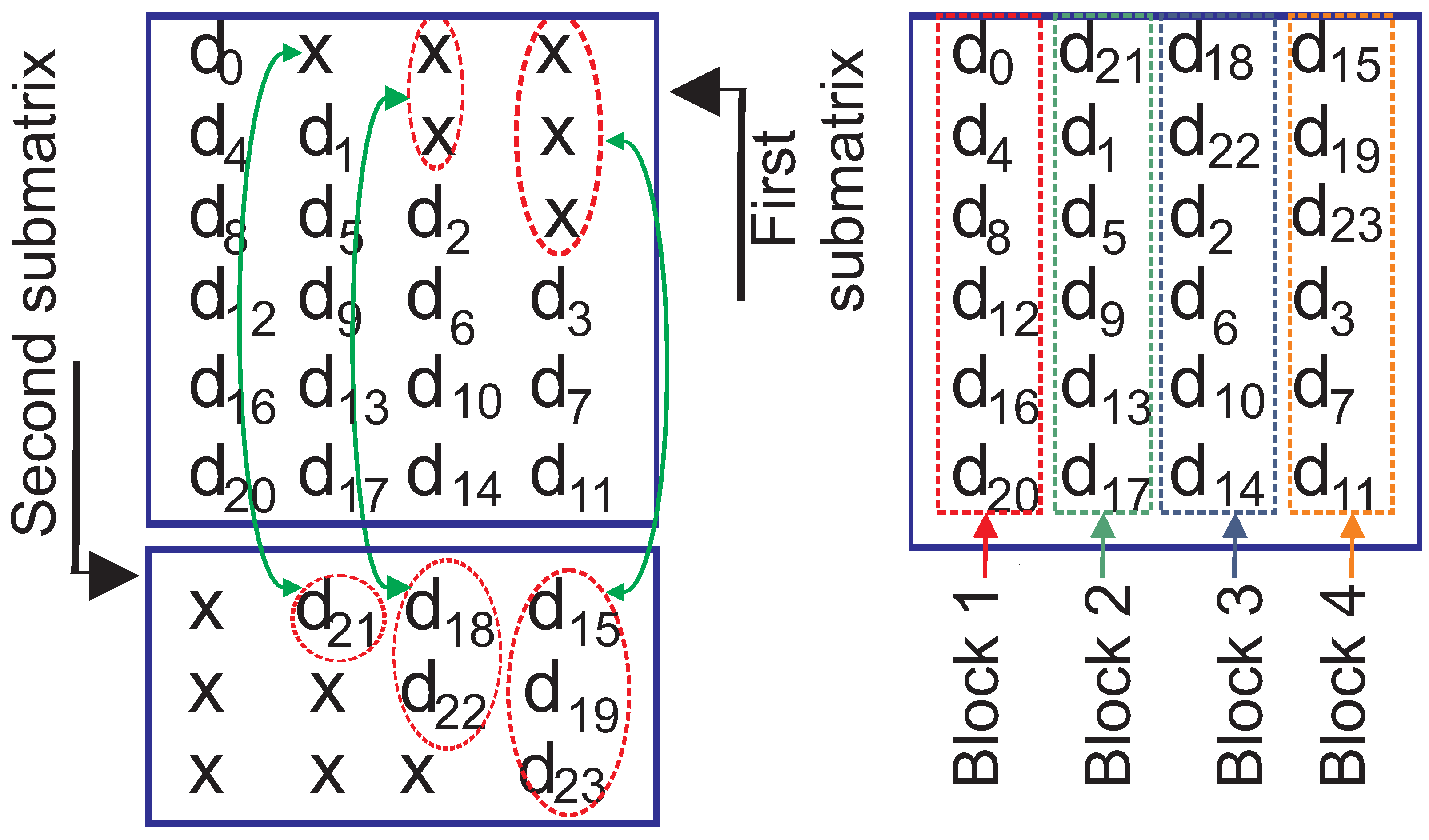
Figure 5 shows data obtained from (4,24,1) convolutional interleaver. The interleaver accepts data in the shape of six blocks with a length of four. In each of the four blocks of interleaved data, only one bit from the originally constructed six blocks exists. Such a property is guaranteed by the column-wise reading of two-dimensional interleaved data.

Figure 5.
Interleaved data obtained from (4,24,1) convolutional interleaver.
Theorem 1.
The minimum weight of the constructed braided block code is at least , where .
Proof.

The weight of the braided code can be expressed as the sum of the weight of the PCB code and the parity weight of the second constituted code obtained from the encoding of selected parity bits of the first codeword. In the proposed algorithm, at least two parity bits are selected from the encoding of the messages with weight one. As parity bits of a codeword block are placed in different blocks of interleaved data, the minimum parity weight obtained from the encoding of these bits is . The minimum weight of conventional PCB code based on messages with weight one is . Therefore, the minimum weight of the braided code from messages with weight one will be .
Similarly, the minimum weight of selected parity bits obtained from the encoding of messages with weight two is 1. This means encoding of these selected bits will form a codeword whose parity weight is at least . On the other hand, the minimum weight of PCB code formed from messages with weight two is [2]. As a result, the minimum weight of the braided code obtained from messages with weight two will be .
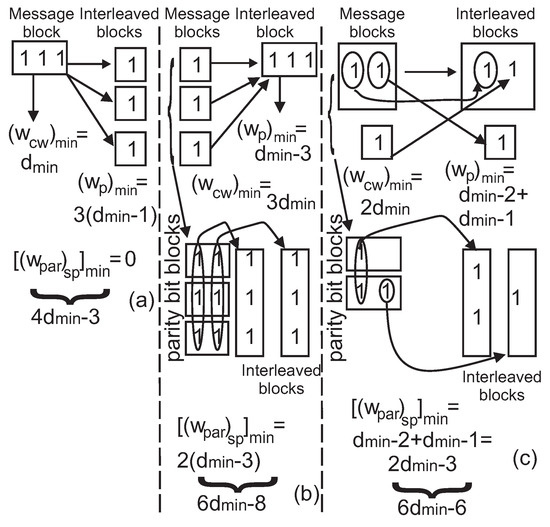
Figure 6 shows all possibilities of the message and interleaved data blocks with weight three, which generate the minimum weight for both component codes. In case (a), only one non-zero-weight message block exists. As the weight of this message block is three, the lowest possible parity weight obtained from the encoding of the selected parity bits is zero. The minimum weight of codewords from the first encoder is . As each of bits 1 of a message block are placed in different interleaved blocks, the minimum parity weight obtained from encoding of three interleaved blocks with weight one will be . Hence, the minimum weight of the braided code is . In cases (b) and (c), message blocks applied for the first encoder have weights of one or two. Considering this and the interleaving process of the selected parity bits, the lowest possible parity weights obtained from the encoding of these interleaved blocks are and , respectively. Therefore, the minimum weights of the braided code obtained from these two cases will be and . The minimum weights of utilized EG and PG codes are greater than three [3]. Based on this and the minimum weights of the three cases, is represented as the minimum weight of the braided code.

Figure 6.
Minimum weight of braided codes obtained from messages with weight 3.
Table 3 gives minimum weights of the braided code relevant to the encoding of messages with weight four, where represents the multiplicity of . In this table, and are the minimum weight of interleaved parity bits per block and its multiplicity, respectively. Moreover, represents the minimum parity weight generated by the encoding of the interleaved parity bits.

Table 3.
Possible minimum weights of braided code obtained from messages with weight 4.
Again, the effect of the parity bits encoding is observed for messages whose weights are placed in more than one message block. As shown, without the encoding of the parity bits, the minimum weight of the PCB code will be . This is possible when each of the two message blocks and two interleaved blocks with weight two generate the minimum weight for both codes. However, the weight of the selected parity bits of each codeword will be one since each non-zero weight message block has weight of two. As these two 1s are placed at two blocks of selected parity bits (they originate from two separate codewords), the interleaving of parity bits can form one non-zero-weight block with the weight of two. Hence, the parity weight obtained from encoding of the interleaved parity bits will be , which consequently concludes the minimum weight of for the braided code. The above analysis can be followed for other cases given in table. From the last column, the minimum weight of is achieved for the braided code. This means the given minimum weight of the braided code is greater than obtained from encoding of messages with weights 1, 2 and 3. Similar analysis can be applied for messages with weight of five and above. The lowest possible minimum weight is from messages with even weights when 1s are equally placed at two messaged blocks. Let be the message weight, which is equal to the sum of weights of the message blocks . For a message with even weights, the minimum weight of PCB code is (For messages with odd weights, is added to the mentioned weight). If none of the selected parity bits are involved in the encoding process, and will remain as . For , this weight and that obtained from messages with odd weigths are greater than . Hence, . □
As the of cyclic LDPC codes is increased by their lengths [3], the given bound grows with the length of cyclic codes.
4. Convergence Behavior of the Iterative Decoding of the Braided Code
Figure 7 shows the structure of iterative decoding applied for the braided code. The fundamental operation is the conventional interactive decoding applied for the PCB code. Furthermore, the decoder for decoding the first cyclic code accepts two pieces of a-priori information from another decoder. This information is obtained from the deinterleaving of the interleaved messages and selected parity bits. (in Figure, two (n,k) cyclic codes that accept and blocks of information can be represented as one decoder for decoding of blocks of information).
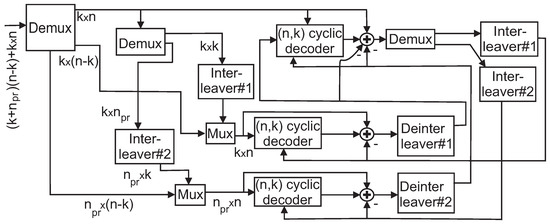
Figure 7.
Iterative decoding of the braided code.
Let , , and be the soft output extrinsic information relevant to the ith original and interleaved messages, respectively. At th iteration, , the interactive decoding applied between two MSA-based decoders of cyclic codes is terminated if the polarities of soft-output extrinsic information obtained from both decoders are not changed at two consecutive iterations and the difference between magnitudes of the information of a decoder input and output is small [23]. Figure 8 shows the average number of iterations applied for the iterative decoding of braided codes constructed using (73,45) and (21,11) PG cyclic LDPC codes. Codes are modulated using Binary Phase Shift Keying (BPSK) and verified for Additive White Gaussian Noise (AWGN) channel. Maximum 10 iterations are applied for the MSA-based decoder and . It is evident that increasing the decreases the number of iterations. This concludes the proper error-correcting capability of the braided code at the waterfall region, which is confirmed by simulations presented in Section 7.
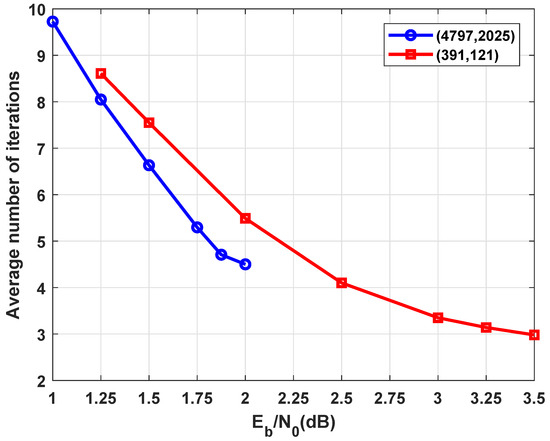
Figure 8.
Average number of iterations for braided codes.
5. Latency of the Designed Braided Code
The latency of encoding and the interleaving of data is proportional to the number of utilized registers. For the cyclic code, registers are applied. For the PCB code, as k message blocks are encoded, overall, registers are involved in the encoding of one code. On the other hand, the interleaving delay for interleaver is [22]. This latency is added to the latency required for transferring non-stuff bits of the second submatrix to the first one. Hence, the overall latency of the interleaving will be . For the braided code, the period of the interleaver applied for the permutation of messages is equal to the value of k. Hence, the overall interleaving latency will be .
For cyclic codes applied in the PCB code, . This means that the latency generated by the interleaver is greater than that obtained from one encoder. As the message interleaving and first cyclic encoding are processed in parallel with each other after the completion of the message interleaving, the latency of the PCB encoding is only related to the second encoder. On the other hand, the latency required for the convolutional interleaving of parity bits will be . The factor of 2 appeared because of the column-wise reading of the interleaved data. As and , the abovementioned latency is less than the latency of the second cyclic encoding. Therefore, during the second encoding, the interleaver constructed for the message interleaving also has enough time to permute selected parity bits of the first cyclic code. This is achievable due to the flexibility of the convolutional interleaver in permuting data with an arbitrary length. Hence, the complexities of the braided and original PCB encodings remain at the same level.
6. Upper Bound of Probability of Error for Braided Codes Constructed by the Proposed Interleaver
For a linear block code, the input-redundancy weight enumerating function (IRWEF) is defined as follows [21]:
In this equation, is the number of codewords with weight , whose message and parity weights are and j, respectively. Based on this definition, the conditional weight enumerating function (CWEF) of the parity check bits is given by
For codes implemented by a maximum likelihood soft decision decoding algorithm, the probability of error under AWGN is upper bounded by
where and are the code rate and energy per bit per noise ratio, respectively.
Based on the finite number of terms, the above bound is approximated by
where . Simarly, the probability of block error, represented as blcok error rate , is bounded by
Table 4 gives partial IRWEF of braided codes constructed by different EG and PG cyclic codes. Weights are obtained from messages whose weights are not greater than three and placed in one block.

Table 4.
Partial IRWEF of braided codes.
It is concluded that (4797,2025) and (401,121) codes have the minimum weight from messages with weights 1, 2, and 3. By contrast, the minimum weight of (193,49) is obtained from messages with weights 1 and 3, while for (3579,1369) code, it is only generated from messages with weight 1.
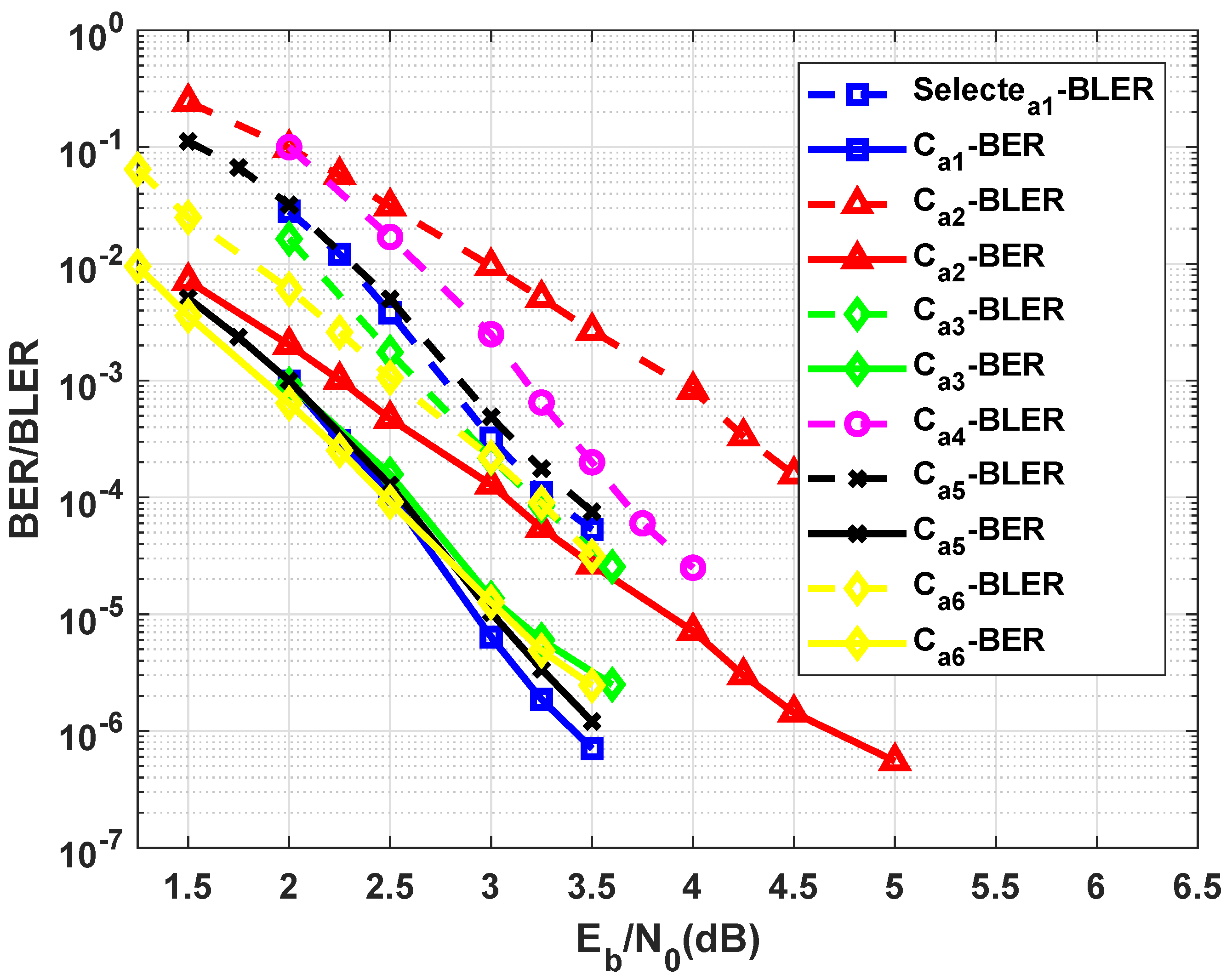
Figure 9 shows the upper bounds of the probability of bit and block errors for (193,49) and (401,121) braided codes and their performance obtained from simulations. It also shows bounds for (161,49) and (341,121) PCB codes. For braided codes, the three lowest weights are applied, while for PCB code, only the minimum weight is considered (minimum weight of (161,49) is 9 with 35 multiplicities, while (341,121) PCB code has a minimum weight of 11 with 110 multiplicities). Constituent (21,11) and (15,7) cyclic codes implemented for the encoding of messages with lengths 49 and 121 are decoded by the MSA with no more than ten iterations, respectively. Moreover, twenty iterations are used for the iterative decoding of MSA-based decoders. It is confirmed that at the medium to high signal-to-noise ratios, BER and BLER performances of braided codes modulated by BPSK are compatible with their relevant upper bounds. For (193,49) code, this is evident at dB, while for code, it occurs at dB. As expected, the given bounds demonstrate that braided codes have better error-correcting capability compared to their PCB codes.
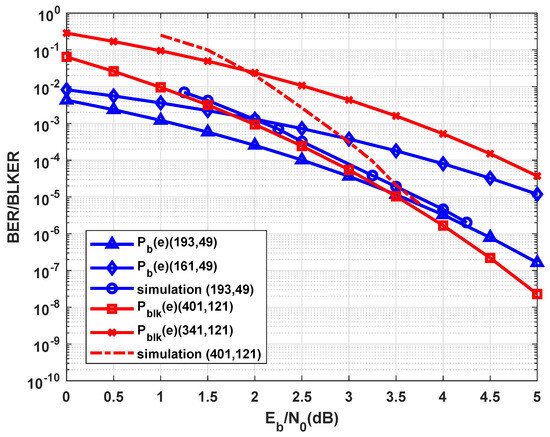
Figure 9.
Upper bounds of error and performance of (193,49) and (401,121) braided codes.
To verify the effectiveness of the correct selection of parity bits, Figure 10 shows the performance of the (193,49) braided code formed by three different sets of parity bits. The braided code constructed by the 8th, 9th, 10th, and 12 parity bits outperforms two other codes. This is an expected result because, in two other codes, two parity bits of all codewords obtained from messages with weight one are not encoded. In the iterative decoding of codes, 20 iterations are applied. In this case, for the decoding of cyclic codes, maximum 10 iterations are considered.
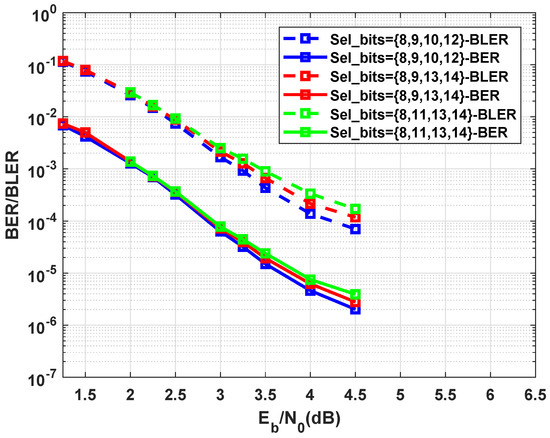
Figure 10.
Performance of (193,49) braided codes formed by different selected parity bits.
7. Simulation Results
Table 5 represents codes applied in simulations. In simulations, the codewords of the braided block codes are also modulated by BPSK and verified for the AWGN channel. Constituent EG and PG cyclic LDPC codes are decoded by the MSA with no more than ten iterations . Maximum ten iterations are also applied for the interactive decoding of MSA-based decoders . The performance of braided codes is compared with the punctured polar codes, which are decoded by the Successive Cancellation List (SCL) algorithm (polar codes are constructed by the Gaussian approximation method). These codes are also assisted by the Cyclic Redundancy Check (CRC) codes. Puncturing on their lengths is accomplished based on the Worst Quality Puncturing (WQP) algorithm [24].

Table 5.
Codes applied in simulations.
Figure 11 shows the Bit Error Rate (BER) and Block Error Rate (BLER) performances of (391,121) braided code constructed by the two (21,11) PG cyclic LDPC codes with . The result is based on . With a reduction in the coding rate and without a visible error floor, for , the braided code outperforms (361,121) PCB code by dB. In addition, for dBs, it outperforms (401,121) polar code constructed by the 4-bit CRC code and the list size of , while their BLER performances are the same. Such results are also observed between the braided code and (391,121) polar code constructed by the list size and 4-bit CRC. Indeed, by utilizing a greater list size and shorter length, the performance of polar code and braided become similar. The (401,121) braided code has a better BLER performance than the girth-8-based (500,125) QC-LDPC code proposed in [25], where the reference code can provide coding gain over the 5G NR LDPC codes. Moreover, it slightly shows a better performance than the same braided code implemented by two row-column interleavers formed by and matrices, which are applied in permuting messages and selected parity bits, respectively . (In row-column interleavers, data are written in rows of the matrix and then read column-by-column). Figure 12 shows the performances of (3579,1369) braided code , which is constructed by two (63,37) EG cyclic LDPC codes with . With the similar rate and , the code provides a better block error correcting capability compared to the (3345,1369) PCB code presented in [1]. The error floor of the braided code decoded based on expects at and , which are lower than those obtained from (3579,1369) polar codes and concatenated by 4-bit CRC code and decoded by and , respectively. Figure 13 shows the results of (4797,2025) braided code formed by two (73,45) PG cyclic LDPC codes with . Based on , this code outperforms PCB [2] and (4608,2304) QC-LDPC codes with the girth of 8 given in [26]. The result is obtained when the braided code utilizes a lower rate than the QC-LDPC code. This code also outperforms (4601,2025) polar code implemented by the 8-bit CRC and . At , it is 1.83 dB away from the Shannon limit.

Figure 11.
Performance of (391,121) braided and other codes.
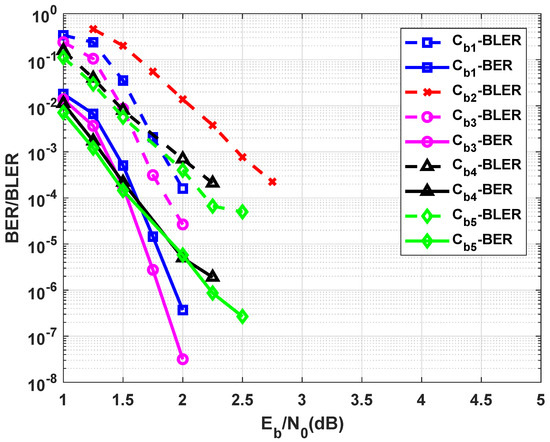
Figure 12.
Performance of (3579,1369) braided and other codes.
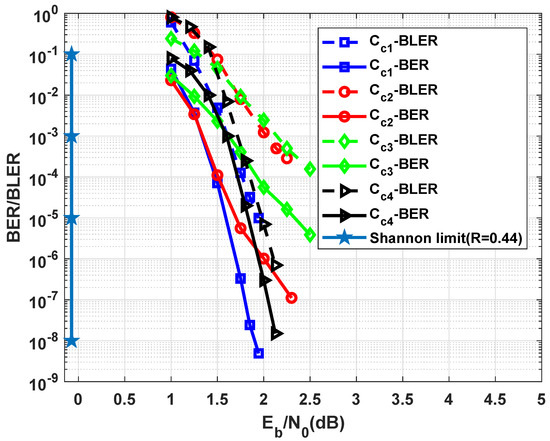
Figure 13.
Performance of (4797,2025) braided and other codes.
Decoding Complexity of Braided Codes
The overall number of sums (or products) required for the braided decoding is , which is proportional to the density of the utilized cyclic codes [27]. For SCL-based decoding of polar codes, this is given by , where is the original length of the polar code. For dB, where the MSA decoding of (21,11) PG cyclic codes is conducted by few iterations, the decoding complexity of (391,121) PCB code is higher than that of formed by the (401,121) polar code. However, the maximum number of operations required for decoding blocks with length n (maximum number of operations applied for the decoding unit) will be similar to the one used for the SCL decoding of the polar code. Based on and , which occurs for dB, the number of operations required for the decoding of (3579,1369) braided code is slightly lower than that used for the decoding of (3579,1369) polar code with . With the maximum of 50 iterations, the MSA-based decoding of (3,6) regular (4608,2304) QC-LDPC code demands sums, which is a bit lower than the number of operations required for (4797,2025) braided code based on the average of 4 iterations for the MSA algorithm. However, the encoder of the QC code is more complex than the cyclic PG code. Hence, the overall complexity of codes is at the same level.
It is also worth mentioning that increasing the length of constituent cyclic code increases the complexity of selecting parity bits. However, most selected parity bits are from codewords formed by messages with weight 1. By choosing two parity bits from those codewords, the number of codewords obtained from messages with weight 2, which are not amongst those selected parity bits, will be significantly reduced.
8. Conclusions and Future Work
A scheme of an outstanding braided block codes constructed by the encoding of some parity bits of the PCB codeword was presented. To achieve this goal and minimize the design complexity, a non-stuff-based convolutional interleaver was applied for permuting the original message and selected parity bits. Conducted analysis proved braided codes with high minimum weights, while a reasonable number of iterations is applied in its iterative decoding process. Moreover, simulations confirmed that the code has an outstanding error-correcting capability. This is achievable for both short and long-length codes. In future work, the algorithm applied for selecting parity bits will be presented to minimize the number of parity bits involved in the encoding. This will consequently optimize the rate and complexity of the designed code.
Funding
This research received no external funding.
Data Availability Statement
The data in this study are available from the corresponding author upon request.
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Table A1 gives list of the notations used in the paper.

Table A1.
Description of the utilizied symbols.
Table A1.
Description of the utilizied symbols.
| Symbol | Description |
|---|---|
| L | Message length |
| k | Message length of cyclic codes |
| n | Codeword length of cyclic codes |
| T | Period of convolutional interleavers |
| Interleaver length | |
| M | Space value of the convolutional interleavers |
| Minimum weight of cyclic codes | |
| Number of message and interleaved blocks | |
| Multiplicity of from encoding of messages | |
| Multiplicity of from encoding of interleaved messages | |
| Weight of the message block | |
| Codeword weight of code obatined from encoding of k message blocks | |
| Weight of parity bits of code obtained from encoding of k interleaved message blocks | |
| Number of selected parity bits | |
| Multiplicity of | |
| Minimum weight of selected parity bits per block | |
| Multiplicity of | |
| Minimum weight of parity bits obtained from encoding of the selected parity bits | |
| Minimum weight of the braided code | |
| Weight of the message | |
| Number of iterations applied for the interactive iterative decoding | |
| soft output extrinsic information relevant to the ith message | |
| soft output extrinsic information relevant to the ith interleaved message | |
| Successive cancellation list size |
References
- Vafi, S. Parallel concatenated block codes constructed by convolutional interleavers. IEEE Access 2021, 9, 41218–41226. [Google Scholar] [CrossRef]
- Vafi, S. Modified convolutional interleavers for parallel concatenated block codes. IEEE Commun. Lett. 2022, 6, 1469–1473. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D. Error Control Coding: Fundamentals and Applications, 2nd ed.; Printice Hall: Upper Saddle River, NJ, USA, 2004; Chapter 17; pp. 858–870. [Google Scholar]
- Diao, Q.; Tai, Y.T.; Lin, S.; Abdel-Ghaffar, K. Trapping set structure of LDPC codes on finite geometries. In Proceedings of the Information Theory and Applications Workshop, San Diego, CA, USA, 10–15 February 2013; pp. 3088–3092. [Google Scholar]
- Feltstrom, A.J.; Truhachev, D.; Lentmaier, M.; Zigangirov, K.S. Braided block codes. IEEE Trans. Inf. Theory 2009, 55, 2640–2658. [Google Scholar] [CrossRef]
- Justesen, J. Performance of product codes and related structures with iterated decoding. IEEE Trans. Commun. 2011, 59, 407–415. [Google Scholar] [CrossRef]
- Smith, B.P.; Farhood, A.; Hunt, A.; Kschischang, F.R.; Lodge, J. Staircase codes: FEC for 100 Gb/s OTN. IEEE J. Light. Technol. 2012, 30, 110–117. [Google Scholar] [CrossRef]
- Jian, Y.Y.; Pfister, H.D.; Narayan, K.; Rao, R.; Mazahreh, R. Iterative hard decision decoding of braided BCH codes for high speed optical communication. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013; pp. 2376–2381. [Google Scholar]
- Galligan, K.; Solomon, A.; Riaz, A.; MÃľdard, M.; Yazicigil, R.; Duffy, K. IGRAND: Decode any product code. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Sukmadji, A.; M-PeÌČnas, U.; Kschischang, F.R. Zipper codes. J. Light. Technol. 2022, 40, 6397–6407. [Google Scholar] [CrossRef]
- Barakatain, M.; Kschischang, F.R. Low-complexity rate- and channel configurable concatenated codes. J. Light. Technol. 2021, 37, 1976–1983. [Google Scholar] [CrossRef]
- Moloudi, S.; Lentmaier, M.; Amat, A.G.I. Spatially coupled turbo like codes. IEEE Trans. Inf. Theory 2017, 63, 6199–6215. [Google Scholar] [CrossRef]
- Wang, Q.; Cai, S.; Lin, W.; Zhao, S.; Chen, L.; Ma, X. Spatially coupled LDPC codes via partial superposition and their application to HARQ. IEEE Trans. Veh. Technol. 2021, 70, 3493–3504. [Google Scholar] [CrossRef]
- Yang, C.; Zhao, S. Spatially Coupled Serially Concatenated Codes: Analysis and Extension; Elsevier: Amsterdam, The Netherlands, 2022; Volume 126, pp. 1–9. [Google Scholar]
- Mahdavi, M.; Weithoffer, S.; Herrmann, M.; Liu, L.; Edfors, O.; Wehn, N.; Lentmaier, M. Spatially coupled serially concatenated codes: Performance evaluation and VLSI design tradeoffs. IEEE Trans. Circ. Syst. Regul. Pap. 2022, 69, 1962–1975. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, C.; Wen, J. Spatially coupled serially concatenated codes via parity re-encoding. IET Electron. Lett. 2021, 57, 129–131. [Google Scholar] [CrossRef]
- Ali, I.; Ha, J. Partial spatial coupling of LDPC codes: Reducing the gap to capacity by improving the rate. IEEE Trans. Commun. 2023, 71, 6898–6912. [Google Scholar] [CrossRef]
- Wang, Q.; Cai, S.; Ma, X. Free-Ride coding for constructions of coupled LDPC codes. IEEE Trans. Commun. 2023, 71, 1259–1270. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Q.; Cai, S.; Xie, X. Implicit partial product-LDPC codes using free-ride coding. In Proceedings of the ICC 2022—IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 2471–2476. [Google Scholar]
- Wang, Y.; Wang, Q.; Ma, X. Design of implicit partial product-LDPC codes and low complexity decoding algorithm. IEEE Commun. Lett. 2023, 27, 419–423. [Google Scholar] [CrossRef]
- Benedetto, S.; Montorsi, G. Unveiling turbo codes:some results on parallel concatenated coding schemes. IEEE Trans. Inf. Theory 1996, 42, 409–428. [Google Scholar] [CrossRef]
- Clark, G.; Cain, J. Error-Correction Coding for Digital Communications; Plunum Press: Jundiaí, Brasil, 1981. [Google Scholar]
- Shao, R.Y.; Lin, S.; Fossorier, M.P.C. Two simple stopping criteria for turbo decoding. IEEE Trans. Commun. 1999, 47, 1117–1120. [Google Scholar] [CrossRef]
- Niu, K.; Chen, K.; Lin, J.; Zhang, Q.T. Polar codes: Primary concepts and practical decoding algorithms. IEEE Commun. Mag. 2014, 52, 192–203. [Google Scholar] [CrossRef]
- Kim, I.; Kojima, G.T.; Song, H.Y. Some short-length girth-8 QC-LDPC codes from primes of the form t2 + 1. IEEE Commun. Lett. 2022, 26, 1211–1215. [Google Scholar] [CrossRef]
- Li, J.; Liu, K.; Lin, S.; Abdel-Ghaffar, K. Algebraic Quasi-Cyclic LDPC codes: Construction, low error-floor, large girth and a reduced-complexity decoding scheme. IEEE Trans. Commun. 2014, 62, 2626–2637. [Google Scholar] [CrossRef]
- Abu-Surra, S.; Liva, G.; Ryan, W.E. Low-floor Tanner codes via Hamming node or RSCC-node doping. In Proceedings of the 16th International Symposium on Applied Algebra, Algebraic Algorithms and Error, Las Vegas, NV, USA, 20–24 February 2006; pp. 245–254. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).