On the Construction of 3D Fibonacci Spirals
Abstract
:1. Introduction and Motivation
2. Two 2D Spirals
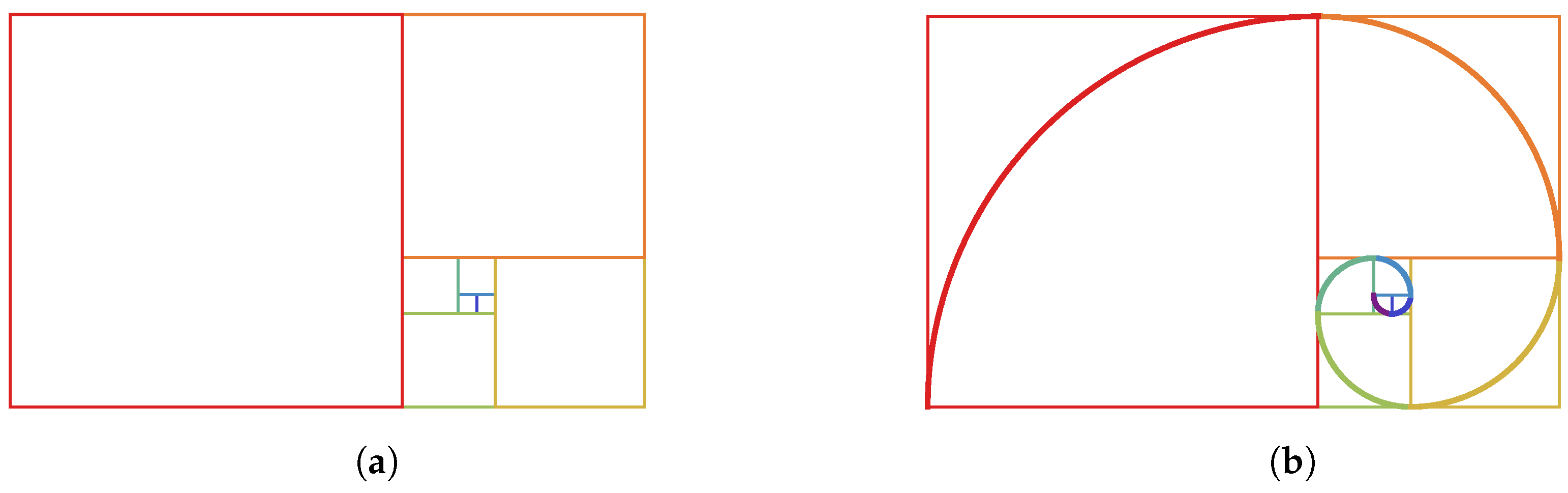
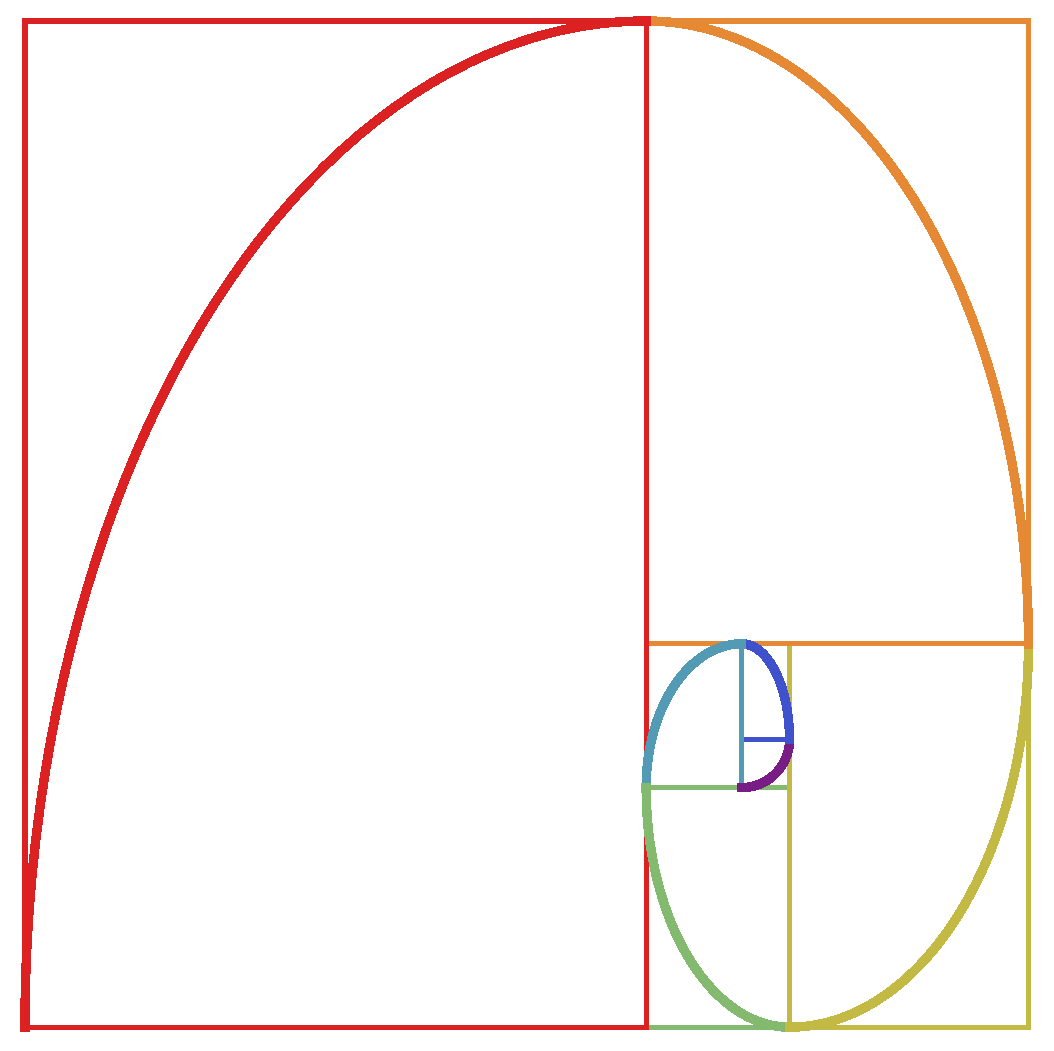
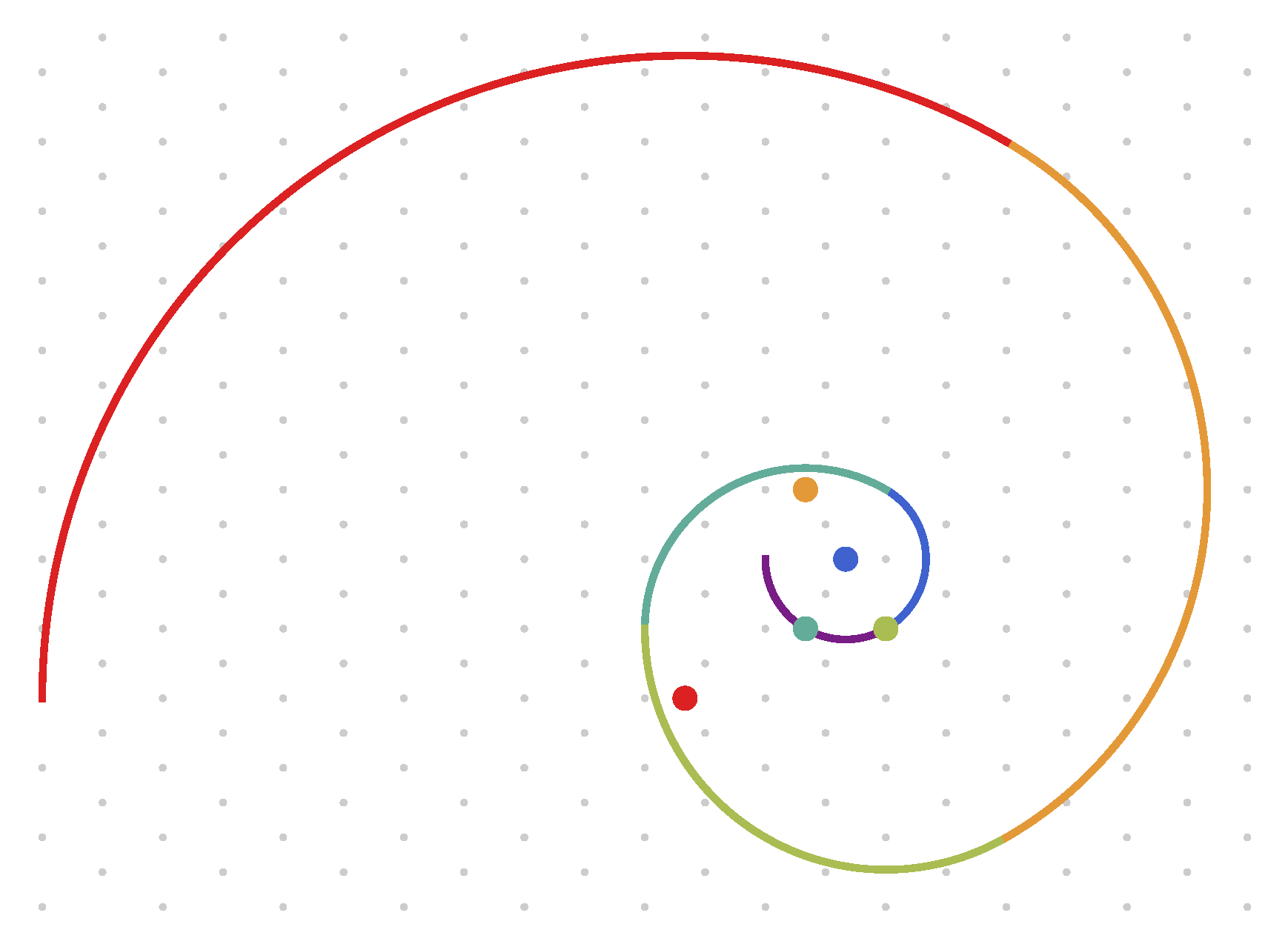
2.1. The Classical 2D Fibonacci Spiral
- Rely only on 2D tiles having Fibonacci number sides (squares, rectangles, etc.);
- i = Identify a (particular) quadratic Fibonacci identity that reveals a covering of the 2D space (there are plenty of quadratic Fibonacci identities including squares and/or rectangles );
- Select a favorable way of tiling the space, i.e., a particular ordering and placement of the square and rectangular tiles (corresponding to the quadratic Fibonacci identity selected);
- Use a smooth curve to connect through (and/or around) these tiles.
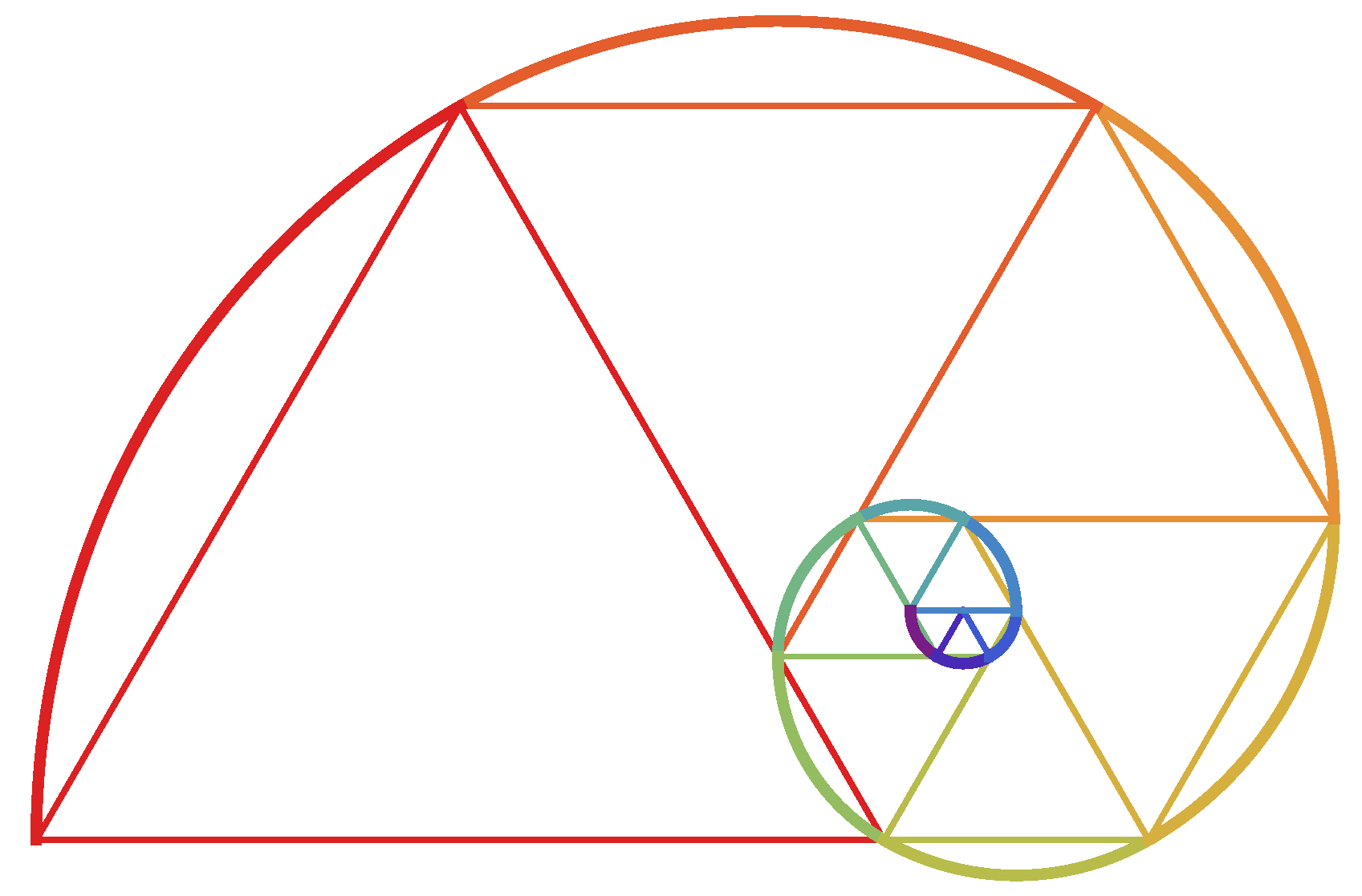
2.2. The Classical 2D Padovan Spiral
3. State of the Art of 3D Fibonacci Spirals
3.1. Artistic Views on 3D Fibonacci Spirals
3.2. Mathematical Generalizations towards 3D Fibonacci Spirals
4. 3D Spirals
4.1. A Planar Padovan-like Spiral Embedded in 3D
4.2. A Scaled Planar Fibonacci Spiral Embedded in 3D
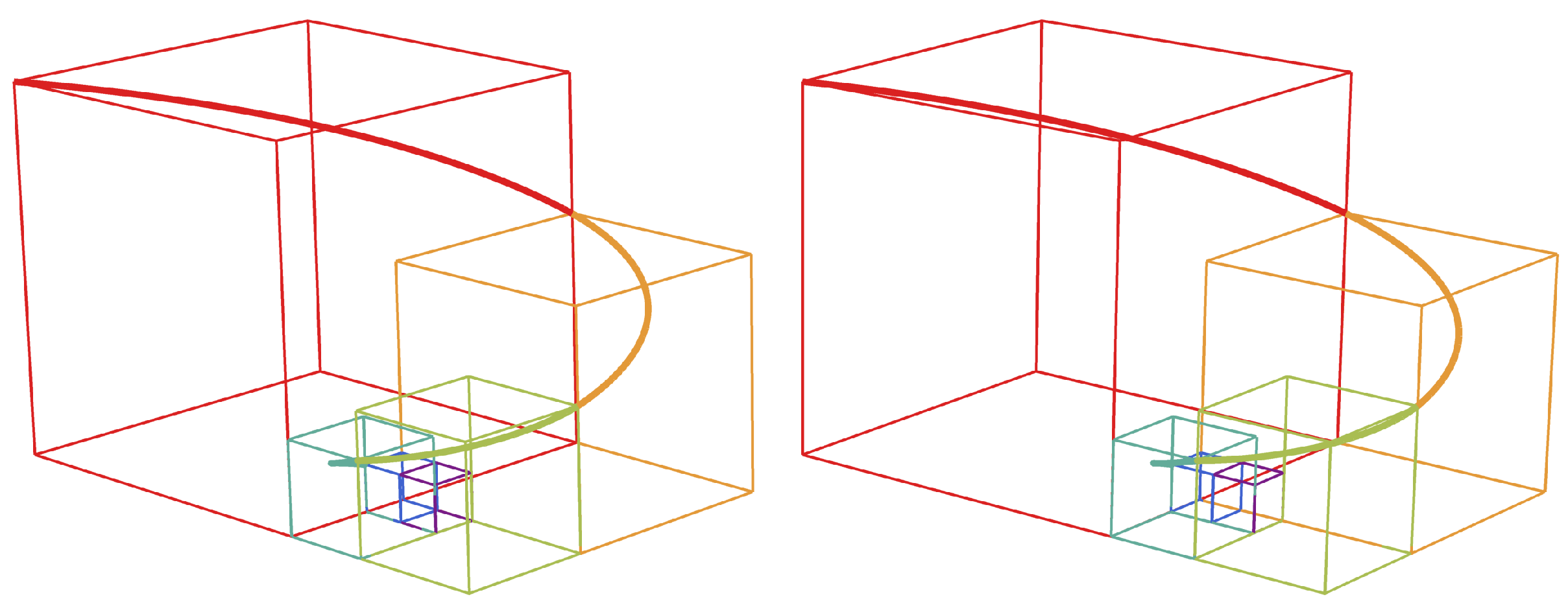
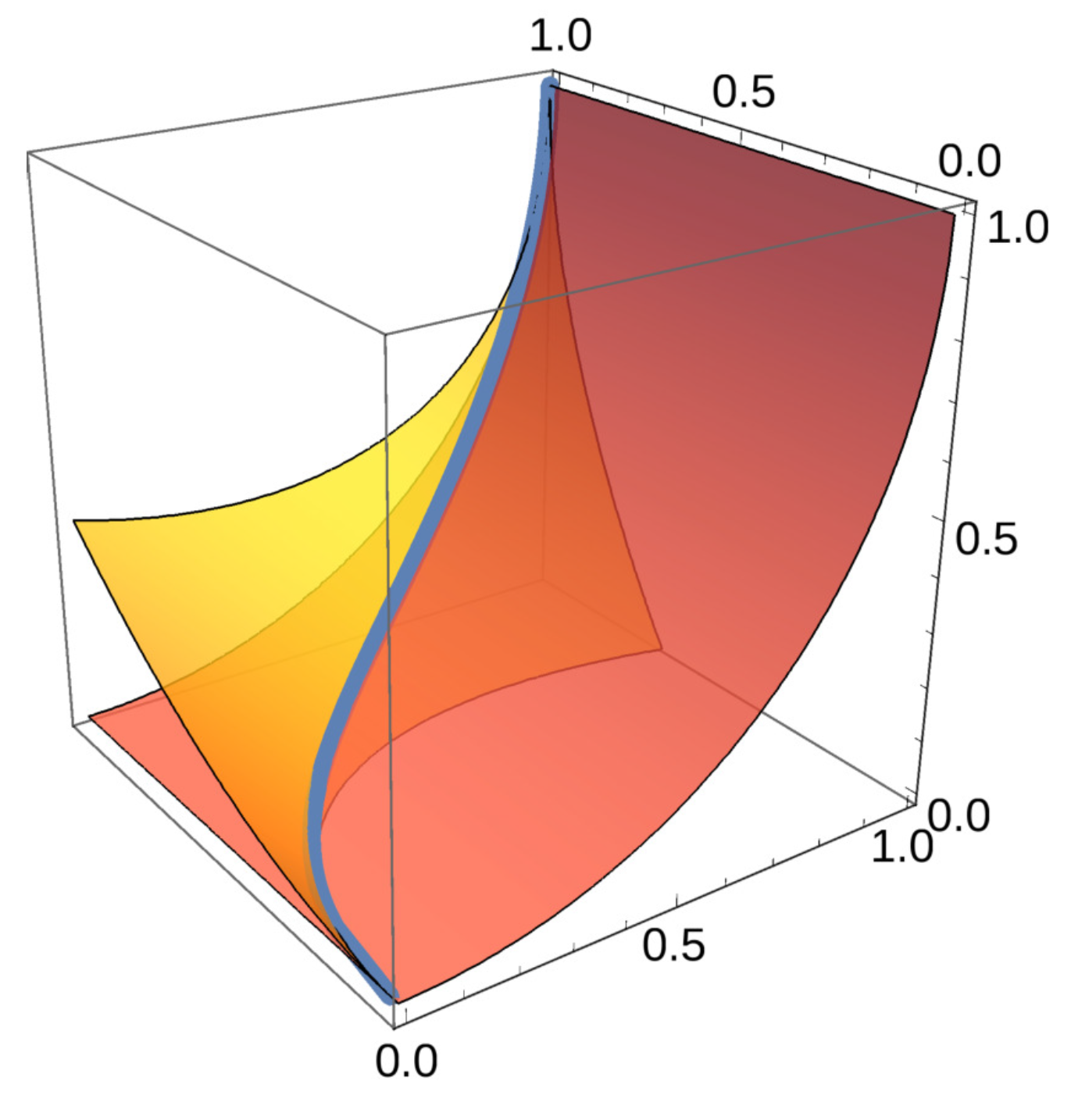
4.3. A Non-Planar 3D Fibonacci Spiral
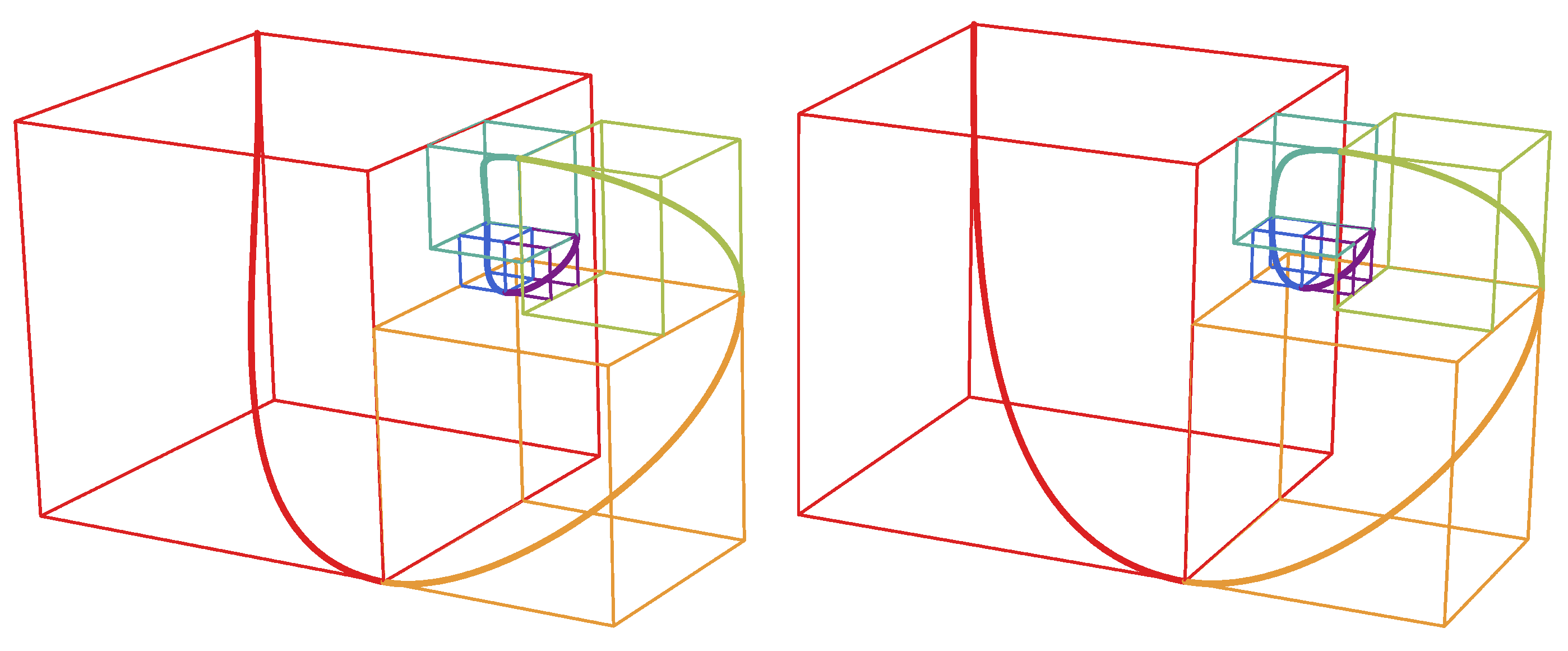
4.4. A Padovan-Style 3D Fibonacci Spiral
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Netz, R. The Works of Archimedes: Translation and Commentary (Volume 2: On Spirals); Cambridge Univ. Press: Cambridge, UK, 2017. [Google Scholar]
- Tsuji, K.; Müller, S.C. Spirals and Vortices; Springer: Cham, Switzerland, 2019. [Google Scholar]
- OEIS Foundation Inc. The On-Line Encyclopedia of Integer Sequences. Available online: http://oeis.org/A000045 (accessed on 19 November 2023).
- Nagy, M.; Cowell, S.R.; Beiu, V. Are 3D Fibonacci spirals for real?—From science to arts and back to sciences. In Proceedings of the International Conference on Computers Communications and Control (ICCCC), Oradea, Romania, 8–12 May 2018; pp. 91–96. [Google Scholar]
- Lucas, F.É.A. Note Sur le Triangle Arithmétique de Pascal et Sur la série de Lamé [Note on the Arithmetic Triangle of Pascal and on the Series of Lamé]. Nouv. Corresp. Math. 1876, 2, 70–75. Available online: https://archive.org/details/nouvellecorresp01mansgoog (accessed on 19 November 2023).
- Lucas, F.É.A. Recherches Sur Plusieurs Ouvrages de Léonard de Pise et Sur Diverses Questions d’Arithmétique Supérieure [Research on Several Publications of Leonardo of Pisa and on Various Questions of Advanced Arithmetic]. Bull. Di Bibliogr. E Di Stor. Delle Sci. Mat. E Fis. 1877, 10, 129–193, 239–293. Available online: http://gallica.bnf.fr/ark:/12148/bpt6k99634z (accessed on 28 December 2023).
- Dickson, L.E. History of the Theory of Numbers (Vol. I: Divisibility and Primality); Carnegie Inst. Washington: Washington, DC, USA, 1919; Available online: https://archive.org/details/historyoftheoryo01dick (accessed on 19 November 2023).
- Block, D. Curiosum #330: Fibonacci summations. Scripta Math. 1953, 19, 191. [Google Scholar]
- Ginsburg, J. Curiosum #343: A relationship between cubes of Fibonacci numbers. Scripta Math. 1953, 19, 242. [Google Scholar]
- Subba Rao, K. Some properties of Fibonacci numbers. Amer. Math. Month. 1953, 60, 680–684. [Google Scholar]
- Brousseau, A. A sequence of power formulas. Fib. Quart. 1968, 6, 81–83. Available online: https://www.fq.math.ca/Scanned/6-1/brousseau3.pdf (accessed on 19 November 2023).
- Benjamin, A.T.; Carnes, T.A.; Cloitre, B. Recounting the Sums of Cubes of Fibonacci Numbers. In Applications of Fibonacci Numbers, Proceedings of the Eleventh International Conference on Fibonacci Numbers and Their Applications, Braunschweig, Germany, 5–9 July 2004; Webb, W.A., Ed.; Utilitas Mathematica Publ.: Winnipeg, MB, Canada, 2009; pp. 45–51. Available online: https://math.hmc.edu/benjamin/wp-content/uploads/sites/5/2019/06/Recounting-the-Sums-of-Cubes-of-Fibonacci-Numbers.pdf (accessed on 19 November 2023).
- Clary, S.; Hemenway, P.D. On Sums of Cubes of Fibonacci Numbers. In Applications of Fibonacci Numbers, Proceedings of the Fifth International Conference on Fibonacci Numbers and Their Applications, St. Andrews, Scotland, 20–24 July 1992; Bergum, G.E., Philippou, A.N., Horadam, A.F., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993; pp. 123–136. [Google Scholar]
- Melham, R.S. A three-variable identity involving cubes of Fibonacci numbers. Fib. Quart. 2003, 41, 220–223. Available online: https://www.mathstat.dal.ca/FQ/Scanned/41-3/melham.pdf (accessed on 19 November 2023).
- Nagy, M.; Cowell, S.R.; Beiu, V. Survey of cubic Fibonacci identities—When cuboids carry weight. Intl. J. Comp. Comm. Ctrl. 2022, 17, 4616. [Google Scholar] [CrossRef]
- Streltsov, V.A.; Luang, S.; Peisley, A.; Varghese, J.N.; Ketudat Cairns, J.R.; Fort, S.; Hijnen, M.; Tvaroška, I.; Ardá, A.; Jiménez-Barbero, J.; et al. Discovery of processive catalysis by an exo-hydrolase with a pocket-shaped active site. Nat. Comm. 2019, 10, 2222. [Google Scholar] [CrossRef]
- Fibonacci, L. Liber Abaci [Book of Calculations]. Biblioteca Nazionale Centrale di Firenze. Conventi Sopressi C.1.2616, 1202 (Revised Manuscript, 1228). Available online: https://catalog.lindahall.org/discovery/delivery/01LINDAHALL_INST:LHL/1286504470005961 (accessed on 19 November 2023).
- Sigler, L.E. Fibonacci’s Liber Abaci—A Translation into Modern English of Leonardo Pisano’s Book of Calculation; Springer: New York, NY, USA, 2002. [Google Scholar]
- Brousseau, A. Fibonacci and Related Number Theoretic Tables; Fibonacci Assoc.: Santa Clara, CA, USA, 1972; Available online: http://www.fq.math.ca/fibonacci-tables.html (accessed on 19 November 2023).
- Vorob’ev, N.N. Chisla Fibonachchi; Gostekhteoretizdat: Moscow-Leningrad, Russia, 1951; Translated as: Fibonacci Numbers; Pergamon Press: London, UK, 1961. [Google Scholar]
- Benjamin, A.T.; Quinn, J.J. Proofs that Really Count—The Art of Combinatorial Proof; Mathematical Association of America: Washington, DC, USA, 2003. [Google Scholar]
- Koshy, T. Fibonacci and Lucas Numbers with Applications; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Caldarola, F.; d’Atri, G.; Maiolo, M.; Pirillo, G. New algebraic and geometric constructs arising from Fibonacci numbers. Soft Comput. 2020, 24, 17497–17508. [Google Scholar] [CrossRef]
- Eğecioğlu, Ö.; Klavžar, S.; Mollard, M. Fibonacci Cubes with Applications and Variations; World Scientific: Singapore, 2023. [Google Scholar]
- Cassini, J.D. Mathematique [Mathematics]. Hist. Acad. Royale Sci. 1680, I, 201. Available online: http://gallica.bnf.fr/ark:/12148/bpt6k56063967/f219.image (accessed on 28 December 2023).
- Bicknell, M.; Hoggatt, V.E., Jr. Golden Triangles, Rectangles, and Cuboids. Fib. Quart. 1969, 7, 73–91, 98. Available online: https://www.fq.math.ca/Scanned/7-1/bicknell-a.pdf (accessed on 19 November 2023).
- Brousseau, A. Fibonacci Numbers and Geometry. Fib. Quart. 1972, 10, 303–318, 323. Available online: https://www.fq.math.ca/Scanned/10-3/brousseau2-a.pdf (accessed on 19 November 2023).
- Hoggatt, V.E., Jr.; Alladi, K. Generalized Fibonacci Tiling. Fib. Quart. 1975, 13, 137–145. Available online: https://www.fq.math.ca/Scanned/13-2/hoggatt1.pdf (accessed on 19 November 2023).
- Hoggatt, V.E., Jr.; Alladi, K. In-Winding Spirals. Fib. Quart. 1976, 14, 144–146. Available online: https://www.fq.math.ca/Scanned/14-2/hoggatt3.pdf (accessed on 19 November 2023).
- Holden, H.L. Fibonacci Tiles. Fib. Quart. 1975, 13, 45–49. Available online: https://www.fq.math.ca/Scanned/13-1/holden.pdf (accessed on 19 November 2023).
- Bicknell-Johnson, M.; DeTemple, D.W. Visualizing Golden Ratio Sums with Tiling Patterns. Fib. Quart. 1995, 33, 298–303. Available online: https://www.fq.math.ca/Scanned/33-4/bicknell.pdf (accessed on 19 November 2023).
- Turner, J.C.; Shannon, A.G. Introduction to a Fibonacci geometry. In Applications of Fibonacci Numbers, Proceedings of the International Conference on Fibonacci Numbers and their Applications, Graz, Austria, 14–19 July 1996; Bergum, G.E., Philippou, A.N., Horadam, A.F., Eds.; Springer: Dordrecht, The Netherlands, 1998; Volume 7, pp. 435–448. [Google Scholar]
- Arkin, J.; Arney, D.C.; Bergum, G.E.; Burr, S.A.; Porter, B.J. Recurring-Sequence Tiling. Fib. Quart. 1989, 27, 323–332. Available online: https://www.fq.math.ca/Scanned/27-4/arkin2.pdf (accessed on 19 November 2023).
- Arkin, J.; Arney, D.C.; Bergum, G.E.; Burr, S.A.; Porter, B.J. Tiling the kth Power of a Power Series. Fib. Quart. 1990, 28, 266–272. Available online: https://www.fq.math.ca/Scanned/28-3/arkin.pdf (accessed on 19 November 2023).
- Livio, M. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number; Broadway Books: New York, NY, USA, 2002. [Google Scholar]
- OEIS Foundation Inc. The On-Line Encyclopedia of Integer Sequences. Available online: http://oeis.org/A000931 (accessed on 19 November 2023).
- Padovan, R. Dom Hans van der Laan: Modern Primitive; Architectura & Natura Press: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Padovan, R. Dom Hans van der Laan and the Plastic Number. In Nexus IV: Architecture and Mathematics; Williams, K., Rodrigues, J.F., Eds.; Kim Williams Books: Fucecchio, Italy, 2002; pp. 181–193. Available online: https://www.nexusjournal.com/the-nexus-conferences/nexus-2002/148-n2002-padovan.html (accessed on 19 November 2023).
- Wilson, E.M. The Scales of Mountain Meru. Personal Notes. 1993, pp. 3–4. Available online: http://www.anaphoria.com/meruone.pdf (accessed on 19 November 2023).
- OEIS Foundation Inc. The On-Line Encyclopedia of Integer Sequences. Available online: http://oeis.org/A134816 (accessed on 26 December 2023).
- Stewart, I. Mathematical recreations—Tales of a neglected number. Sci. Amer. 1996, 274, 102–103. [Google Scholar]
- Tyng, A.G. Geometric Extensions of Consciousness. Zodiac 1969, 19, 130–162. Available online: http://www.radicalsoftware.org/volume2nr1/pdf/VOLUME2NR1_art08.pdf (accessed on 19 November 2023).
- Sharp, J. Beyond the Golden Section—The Golden Tip of the Iceberg; Bridges: Winfield, KS, USA, 2000; pp. 87–98. Available online: http://archive.bridgesmathart.org/2000/bridges2000-87.html (accessed on 19 November 2023).
- Stakhov, A.; Rozin, B. The golden shofar. Chaos Solit. Frac. 2005, 26, 677–684. [Google Scholar] [CrossRef]
- Özvatan, M.; Pashaev, O.K. Generalized Fibonacci sequences and Binet-Fibonacci curves. arXiv 2017, arXiv:1707.09151. [Google Scholar]
- Falcón, S.; Plaza, Á. The k-Fibonacci hyperbolic functions. Chaos Solit. Fract. 2008, 38, 409–420. [Google Scholar] [CrossRef]
- Falcón, S.; Plaza, Á. On 3-dimensional k-Fibonacci spirals. Chaos Solit. Fract. 2008, 38, 993–1003. [Google Scholar] [CrossRef]
- Harary, G.; Tal, A. The natural 3D spiral. Comput. Graph. Forum 2011, 30, 237–246. [Google Scholar] [CrossRef]
- Parodi, B.R. A generalized Fibonacci spiral. arXiv 2020, arXiv:2004.08902. [Google Scholar]
- Ollerton, R.L. Fibonacci cubes. Intl. J. Math. Edu. Sci. Tech. 2006, 37, 754–756. [Google Scholar] [CrossRef]
- Pond, J.C. Generalized Fibonacci Summations. Fib. Quart. 1968, 6, 97–108. Available online: https://www.fq.math.ca/Scanned/6-2/pond.pdf (accessed on 19 November 2023).
- Lang, W. A215037: Applications of the Partial Summation Formula to Some Sums over Cubes of Fibonacci Numbers; Tech. Notes for A215037; Karlsruhe Institute of Technology (KIT): Karlsruhe, Germany, 9 August 2012; Available online: https://www.itp.kit.edu/~wl/EISpub/A215037.pdf (accessed on 19 November 2023).
- Weisstein, E.W. Steinmetz Curve. MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/SteinmetzCurve.html (accessed on 19 November 2023).
- Kepler, J. De Nive Sexangula; Godfrey Tampach: Frankfurt am Main, Germany, 1611; Available online: http://www.thelatinlibrary.com/kepler/strena.html (accessed on 28 December 2023)Translated by Hardie, C. The Six-Cornered Snowflake; Clarendon Press: Oxford, UK, 1966.
- Morton, A.A. The Fibonacci Series and the Periodic Table of Elements. Fib. Quart. 2010, 15, 173–175. Available online: https://www.fq.math.ca/Scanned/15-2/morton.pdf (accessed on 28 December 2023).
- Wlodarski, J. The “Golden-Ratio” and the Fibonacci Numbers in the World of Atoms. Fib. Quart. 1963, 1, 61–63. Available online: https://www.fq.math.ca/Scanned/1-4/wlodarski.pdf (accessed on 28 December 2023).
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman & Co.: New York, NY, USA, 1982. [Google Scholar]
- Sadegh, S.; Higgins, J.L.; Mannion, P.C.; Tamkun, M.M.; Krapf, D. Plasma membrane is compartmentalized by a self-similar cortical actin meshwork. Phys. Rev. X 2017, 7, 011031. [Google Scholar] [CrossRef] [PubMed]
- Enright, M.B.; Leitner, D.M. Mass fractal dimension and the compactness of proteins. Phys. Rev. E 2005, 71, 011912. [Google Scholar] [CrossRef] [PubMed]
- Castro, T.G.; Munteanu, F.-D.; Cavaco-Paulo, A. Electrostatics of tau protein by molecular dynamics. Biomolecules 2019, 9, 116. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
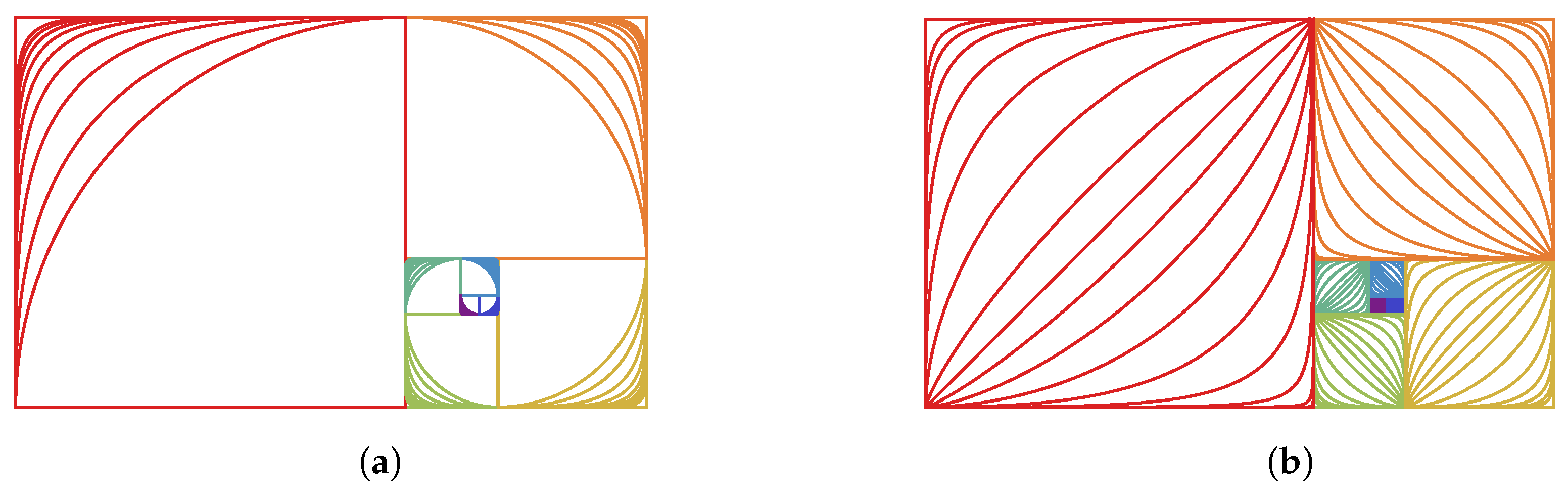




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, M.; Cowell, S.R.; Beiu, V. On the Construction of 3D Fibonacci Spirals. Mathematics 2024, 12, 201. https://doi.org/10.3390/math12020201
Nagy M, Cowell SR, Beiu V. On the Construction of 3D Fibonacci Spirals. Mathematics. 2024; 12(2):201. https://doi.org/10.3390/math12020201
Chicago/Turabian StyleNagy, Mariana, Simon R. Cowell, and Valeriu Beiu. 2024. "On the Construction of 3D Fibonacci Spirals" Mathematics 12, no. 2: 201. https://doi.org/10.3390/math12020201
APA StyleNagy, M., Cowell, S. R., & Beiu, V. (2024). On the Construction of 3D Fibonacci Spirals. Mathematics, 12(2), 201. https://doi.org/10.3390/math12020201






