Mathematical Modeling of Two Interacting Populations’ Dynamics of Onchocerciasis Disease Spread with Nonlinear Incidence Functions
Abstract
1. Introduction
2. Model Description
- Every member of the human population is initially vulnerable to the illness, which means they could get it.
- Infected sensitive individuals in the human population go into the exposed state, where they are not contagious.
- After being exposed, the affected persons develop into infectious individuals, who can spread the illness to other people.
- Infected people can die naturally or from the disease, but if not, they return to be cured of their human illness through treatment.
- After individuals recover from the infection, they become susceptible to the disease once more, implying that they can potentially contract it in future.
- Since all black flies are initially prone to the sickness, it follows that they have the potential to contract the infection.
- When susceptible black flies become infected, they transition into the exposed state, where they are still not able to infect humans with the disease.
- The black flies in the exposed state subsequently progress to becoming infectious, where they can transmit the disease to humans.
- There is no distinct recovered class for the population of black flies since the infected black flies stay infectious for the whole of their lives.
Existence and Positivity of the Model Solutions
3. Analysis of DFE and Endemic Equilibrium
3.1. Disease-Free Equilibrium (DFE)
3.2. Global Stability Analysis
3.3. Global Stability of Disease-Free Equilibrium
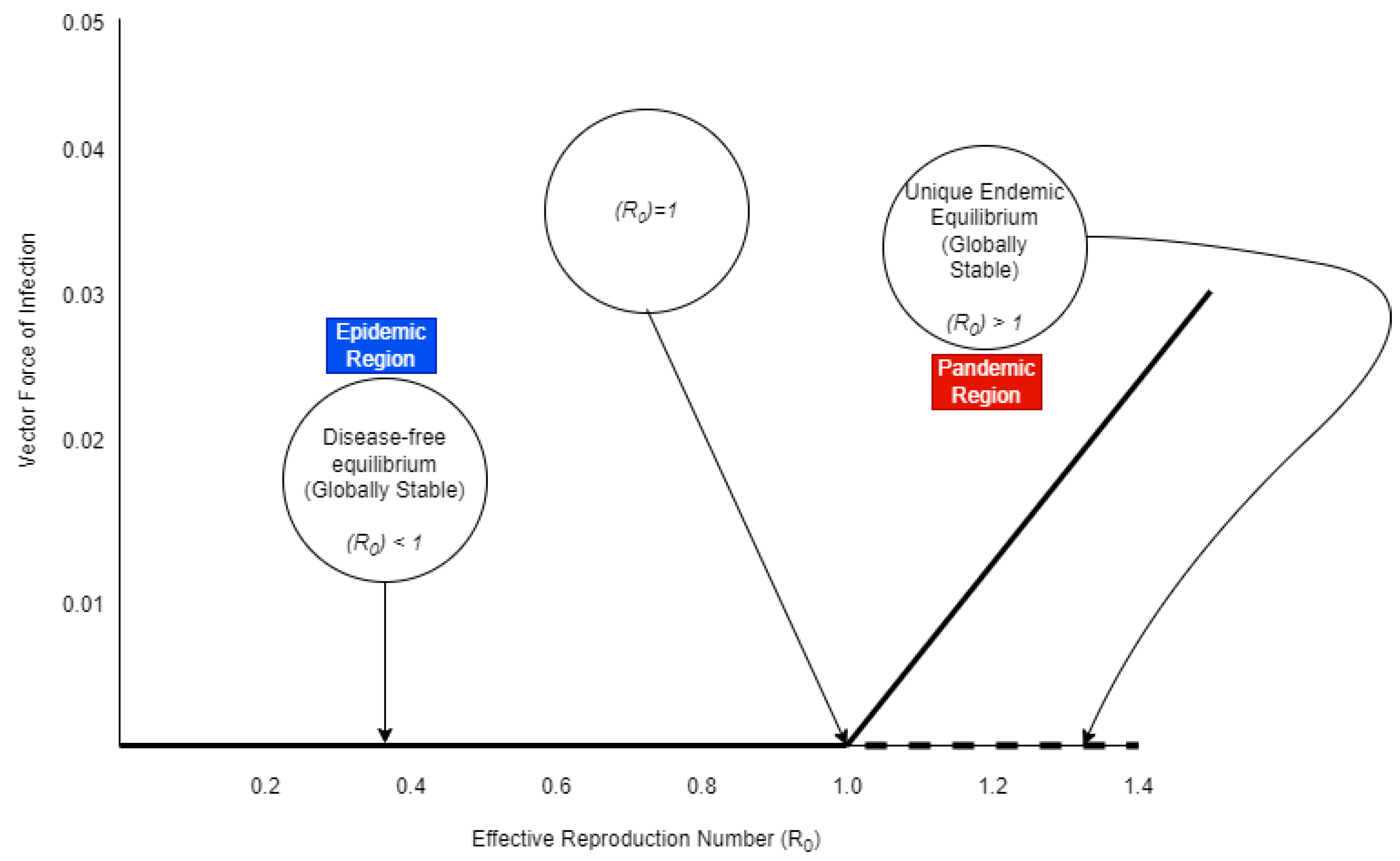
4. Bifurcation Analysis
- is the linearization matrix of the system in Theorem 5 around the equilibrium 0 where φ evaluated at 0. A’s simple eigenvalue is zero, while its other eigenvalues have real components that are negative;
- The right eigenvector κ of Matrix A is non-negative, while the left eigenvector η corresponds to the zero eigenvalue.
- , . When with , 0 is locally stable asymptotically and ∃ an unstable equilibrium that is positive; when , 0 is unstable and ∃ a negative, locally stable asymptotically equilibrium;
- , . When with , 0 is unstable; when 1, 0 is locally stable asymptotically, and ∃ an unstable equilibrium that is positive;
- , . When with , 0 is unstable, and ∃ a locally asymptotically stable equilibrium that is negative; when , 0 is stable, and a unstable equilibrium appears that is positive;
- 0 transforms ’s stability from stable to unstable when it goes from negative to positive. As a result, a negatively unstable equilibrium turns positive and asymptotically stable locally. In particular, if and , then there exists a backward bifurcation.
5. Quantitative Analysis
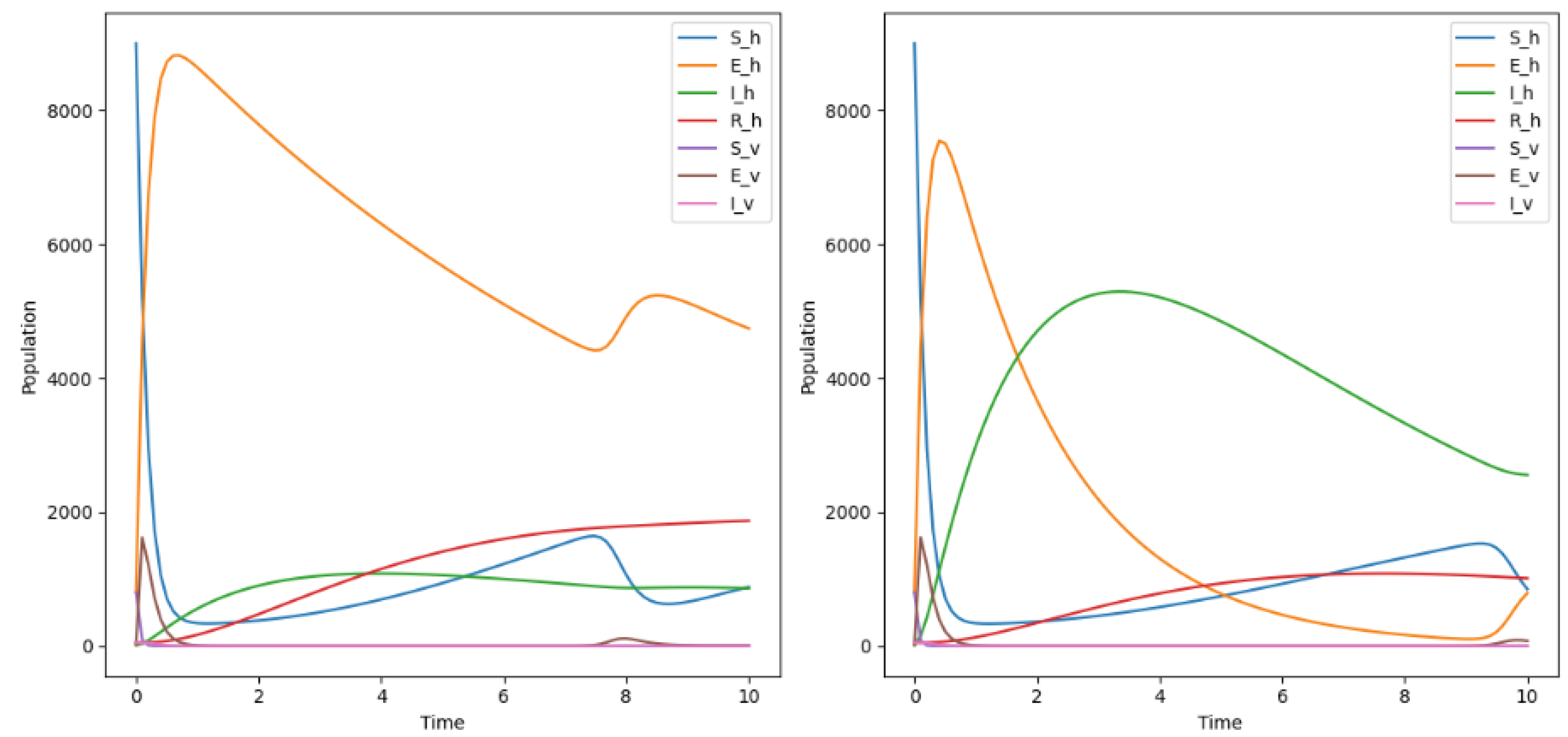
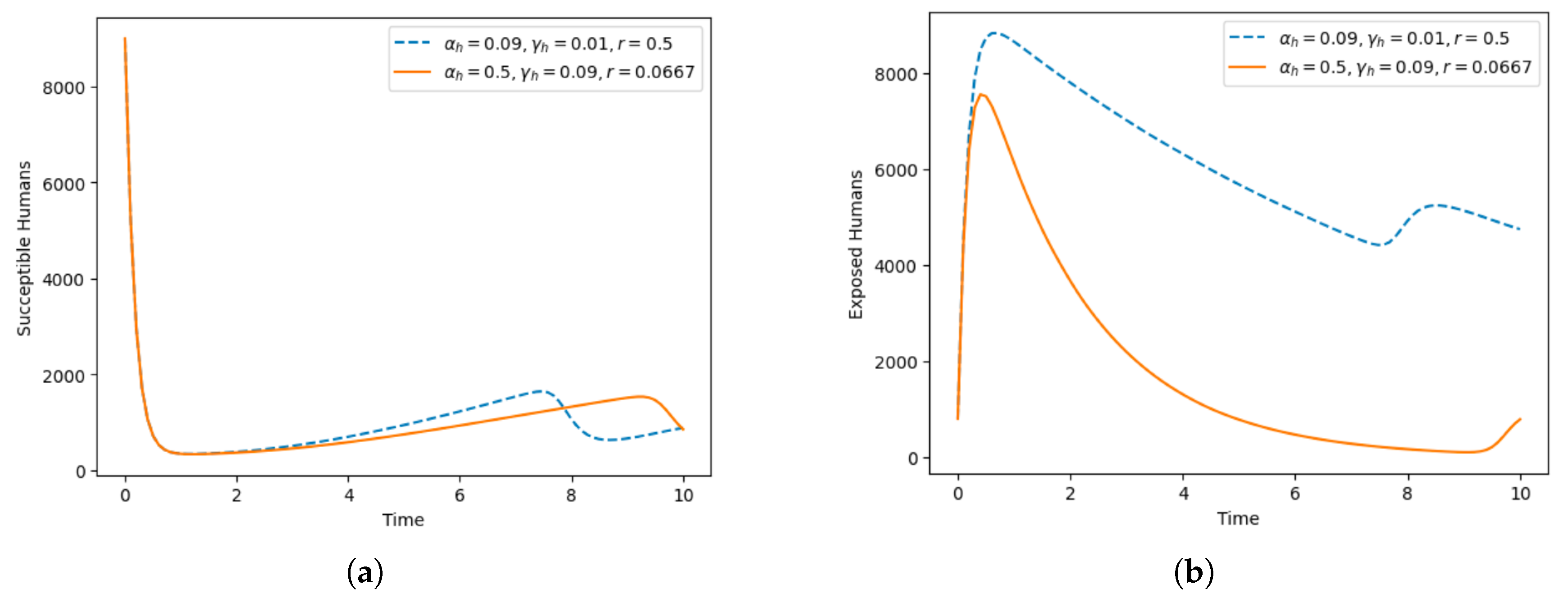
5.1. Simulation of Numerical Analysis
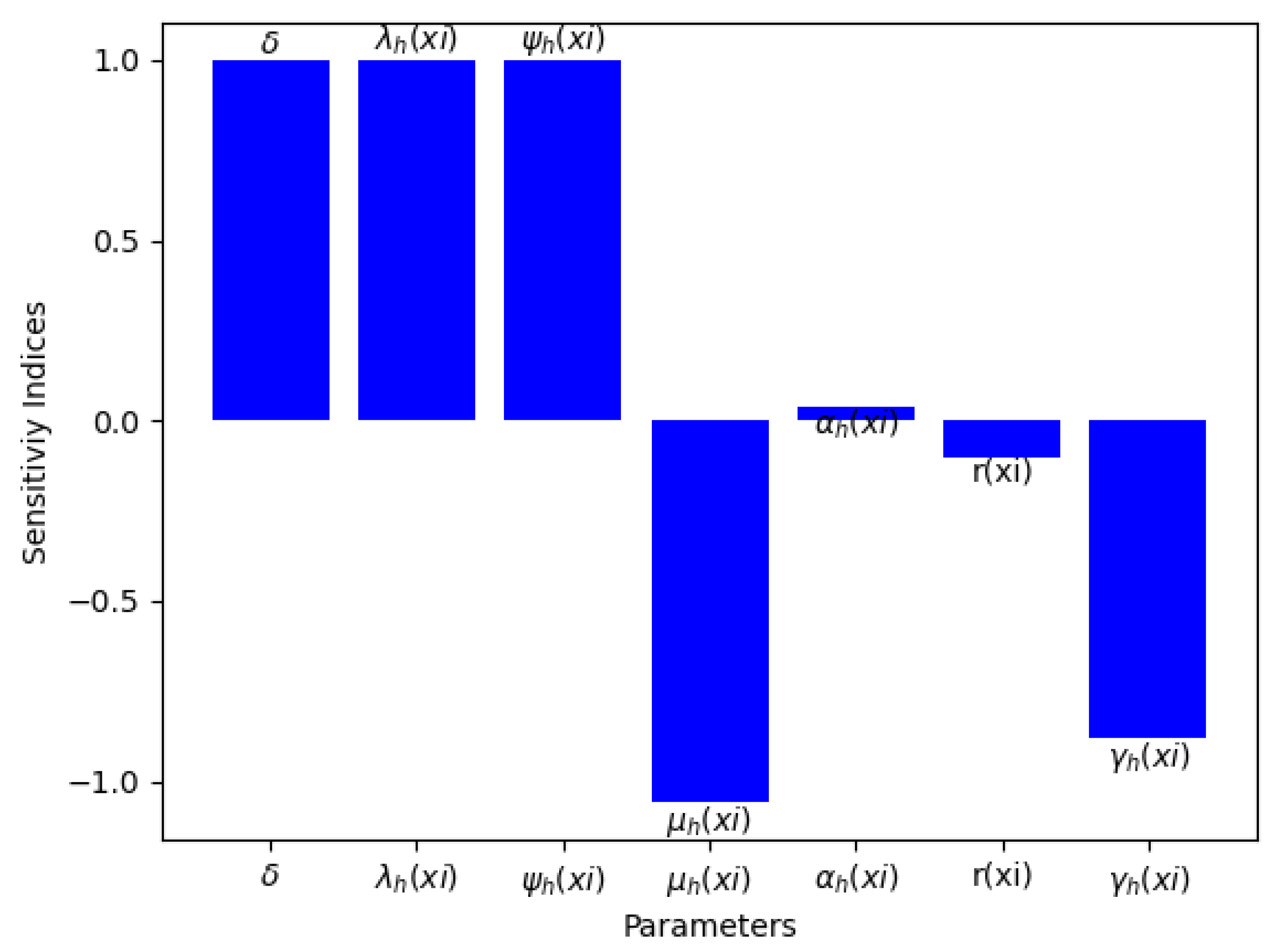
5.2. Sensitivity Analysis
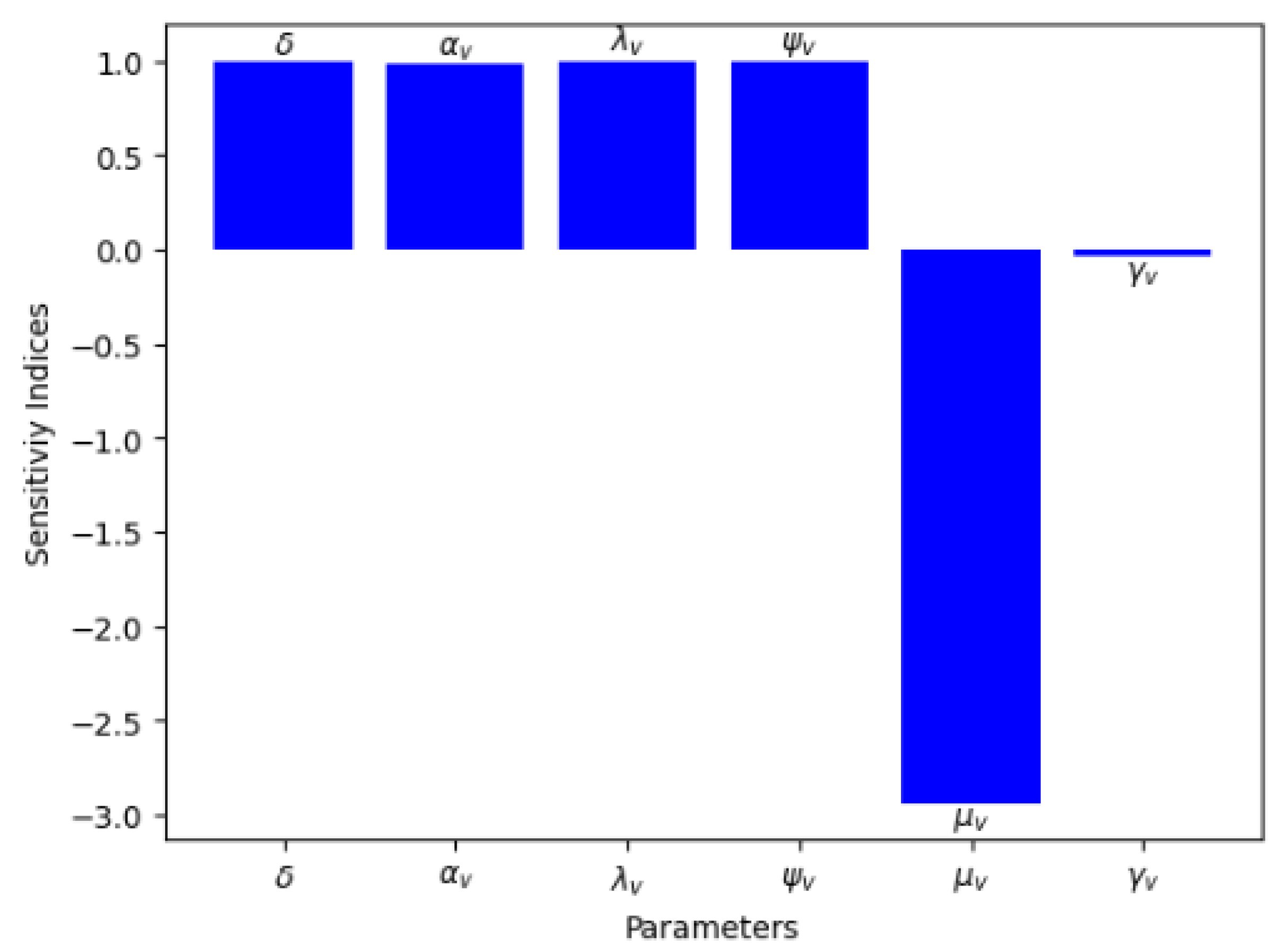
5.2.1. Sensitivity Analysis of Basic Reproduction Number,
5.2.2. Sensitivity Analysis of Basic Reproduction Number,
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Babasola, O.; Kayode, O.; Peter, O.J.; Onwuegbuche, F.C.; Oguntolu, F.A. Time-delayed modelling of the COVID-19 dynamics with a convex incidence rate. Inform. Med. Unlocked 2022, 35, 101124. [Google Scholar] [CrossRef] [PubMed]
- Amazigo, U.; Noma, M.; Bump, J.; Benton, B.; Liese, B.; Yaméogo, L.; Zouré, H.; Seketeli, A. Chapter 15: Onchocerciasis. In Disease and Mortality in Sub-Saharan Africa, 2nd ed.; The International Bank for Reconstruction and Development/The World Bank: Washington, DC, USA, 2006. [Google Scholar]
- Mopecha, J.P.; Thieme, H.R. Competitive dynamics in a model for Onchocerciasis with cross-immunity. Can. Appl. Math. Q. 2003, 11, 339–376. [Google Scholar]
- World Health Organization. African Programme for Onchocerciasis Control: Meeting of national onchocerciasis task forces, September 2012. Wkly. Epidemiol. Rec. Relev. Épid. Hebd. 2012, 87, 494–502. [Google Scholar]
- Holt, R.D.; Pickering, J. Infectious disease and species coexistence: A model of Lotka-Volterra form. Am. Nat. 1985, 126, 196–211. [Google Scholar] [CrossRef]
- Venturino, E. The influence of diseases on Lotka-Volterra systems. Rocky Mt. J. Math. 1994, 24, 381–402. [Google Scholar] [CrossRef]
- Latipah, K.; Putri, A.; Syafwan, M. Stability analysis of prey predator model Holling type II with infected prey. J. Phys. Conf. Ser. 2020, 1554, 012038. [Google Scholar] [CrossRef]
- Hassan, A.; Shaban, N. Onchocerciasis dynamics: Modelling the effects of treatment, education and vector control. J. Biol. Dyn. 2020, 14, 245–268. [Google Scholar] [CrossRef]
- Hamley, J.I.; Walker, M.; Coffeng, L.E.; Milton, P.; de Vlas, S.J.; Stolk, W.A.; Basáñez, M.G. Structural uncertainty in onchocerciasis transmission models influences the estimation of elimination thresholds and selection of age groups for seromonitoring. J. Infect. Dis. 2020, 221, S510–S518. [Google Scholar] [CrossRef]
- Ogunmiloro, O.M.; Idowu, A.S. Bifurcation, sensitivity, and optimal control analysis of onchocerciasis disease transmission model with two groups of infectives and saturated treatment function. Math. Methods Appl. Sci. 2022, 6, 12–29. [Google Scholar] [CrossRef]
- Idowu, A.S.; Ogunmiloro, O.M. Transmission dynamics of onchocerciasis with two classes of infection and saturated treatment function. Int. J. Model. Simul. Sci. Comput. 2020, 11, 2050047. [Google Scholar] [CrossRef]
- Hamley, J.I.; Blok, D.J.; Walker, M.; Milton, P.; Hopkins, A.D.; Hamill, L.C.; Downs, P.; De Vlas, S.J.; Stolk, W.A.; Basáñez, M.G. What does the COVID-19 pandemic mean for the next decade of onchocerciasis control and elimination? Trans. R. Soc. Trop. Med. Hyg. 2021, 115, 269–280. [Google Scholar] [CrossRef] [PubMed]
- Melchers, N.V.; Coffeng, L.E.; Boussinesq, M.; Pedrique, B.; Pion, S.D.; Tekle, A.H.; Zouré, H.G.; Wanji, S.; Remme, J.H.; Stolk, W.A. Projected Number of People With Onchocerciasis-Loiasis Coinfection in Africa, 1995 to 2025. Clin. Infect. Dis. 2020, 70, 2281–2289. [Google Scholar] [CrossRef] [PubMed]
- Remme, J.; De Sole, G.; Van Oortmarssen, G. The predicted and observed decline in onchocerciasis infection during 14 years of successful control of Simulium spp. in west Africa. Bull. World Health Organ. 1990, 68, 331. [Google Scholar] [PubMed]
- Plaisier, A.; Alley, E.; Van Oortmarssen, G.; Boatin, B.; Habbema, J. Required duration of combined annual ivermectin treatment and vector control in the Onchocerciasis Control Programme in west Africa. Bull. World Health Organ. 1997, 75, 237. [Google Scholar] [PubMed]
- Poolman, E.M.; Galvani, A.P. Modeling targeted ivermectin treatment for controlling river blindness. Am. J. Trop. Med. Hyg. 2006, 75, 921. [Google Scholar] [CrossRef] [PubMed]
- Alley, W.S.; van Oortmarssen, G.J.; Boatin, B.A.; Nagelkerke, N.J.; Plaisier, A.P.; Remme, J.H.; Lazdins, J.; Borsboom, G.J.; Habbema, J.D.F. Macrofilaricides and onchocerciasis control, mathematical modelling of the prospects for elimination. BMC Public Health 2001, 1, 12. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Basanez, M.G.; Boussinesq, M. Population biology of human onchocerciasis. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 1999, 354, 809–826. [Google Scholar] [CrossRef] [PubMed]
- Basáñez, M.G.; Ricárdez-Esquinca, J. Models for the population biology and control of human onchocerciasis. Trends Parasitol. 2001, 17, 430–438. [Google Scholar] [CrossRef]
- Adeyemo, K.M. Local Stability Analysis of Onchocerciasis Transmission Dynamics With Nonlinear IncidenceFunctions in Two Interacting Populations. Eur. J. Math. Anal. 2023, 3, 22. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef]
- Kennedy, C.A.; Carpenter, M.H. Higher-order additive Runge–Kutta schemes for ordinary differential equations. Appl. Numer. Math. 2019, 136, 183–205. [Google Scholar] [CrossRef]

| Symbols | Definitions |
|---|---|
| Term of recruitment for susceptible individuals at a discrete age | |
| Term of recruitment for the susceptible vectors | |
| Vector’s rate of biting | |
| Probability that a human will contract a disease at a specific age as a result of being bitten by an infectious vector | |
| Probability that a bite will cause a parasite to spread to a susceptible vector | |
| Human mortality rate per capita at a discrete age | |
| Per capita vector death rate | |
| Human disease-related mortality rate at a given age . | |
| Rate of disease-induced vector mortality | |
| Per capita rate at discrete age of human progression from the exposed state to the infectious state | |
| The rate at which vectors move from an exposed state to an infectious state per person | |
| Percentage of individuals who, after treatment, go from an infectious state to a recovered state at a discrete age | |
| At each discrete age , the per capita transition rate from the recovered human condition to the susceptible state | |
| Factors that prevent sickness in humans at specific ages . | |
| Factors that suppress illness in vectors |
| Symbols | Value | Source |
|---|---|---|
| 0.459 | Estimated | |
| 0.4 | Estimated | |
| 0.758 | [10] | |
| 0.8354 | [11] | |
| 0.5 | [12] | |
| 0.6 | [13] | |
| 0.09 | [10] | |
| 0.085 | [10] | |
| 0.08 | [10] | |
| 17.3809 | [11] | |
| 0.01567 | [11] | |
| 0.05 | [12] | |
| 0.01 | [12] | |
| 0.013 | [13] | |
| 0.0667 | [13] |
| Parameters | Sensitivity Index |
|---|---|
| 1 | |
| 1 | |
| 1 | |
| Parameters | Sensitivity Index |
|---|---|
| 1 | |
| 1 | |
| 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeyemo, K.M.; Adam, U.M.; Adeniji, A.; Oshinubi, K. Mathematical Modeling of Two Interacting Populations’ Dynamics of Onchocerciasis Disease Spread with Nonlinear Incidence Functions. Mathematics 2024, 12, 222. https://doi.org/10.3390/math12020222
Adeyemo KM, Adam UM, Adeniji A, Oshinubi K. Mathematical Modeling of Two Interacting Populations’ Dynamics of Onchocerciasis Disease Spread with Nonlinear Incidence Functions. Mathematics. 2024; 12(2):222. https://doi.org/10.3390/math12020222
Chicago/Turabian StyleAdeyemo, Kabiru Michael, Umar Muhammad Adam, Adejimi Adeniji, and Kayode Oshinubi. 2024. "Mathematical Modeling of Two Interacting Populations’ Dynamics of Onchocerciasis Disease Spread with Nonlinear Incidence Functions" Mathematics 12, no. 2: 222. https://doi.org/10.3390/math12020222
APA StyleAdeyemo, K. M., Adam, U. M., Adeniji, A., & Oshinubi, K. (2024). Mathematical Modeling of Two Interacting Populations’ Dynamics of Onchocerciasis Disease Spread with Nonlinear Incidence Functions. Mathematics, 12(2), 222. https://doi.org/10.3390/math12020222







