From the DeGroot Model to the DeGroot-Non-Consensus Model: The Jump States and the Frozen Fragment States
Abstract
:1. Introduction
2. Model and Some Theoretical Analysis
2.1. Dynamics Description: From Intra-Personal Information Process to the Inter-Personal Information Process
2.2. A Detailed Analysis: Dynamics on the Nearest Neighbor Network
3. Results and Analysis
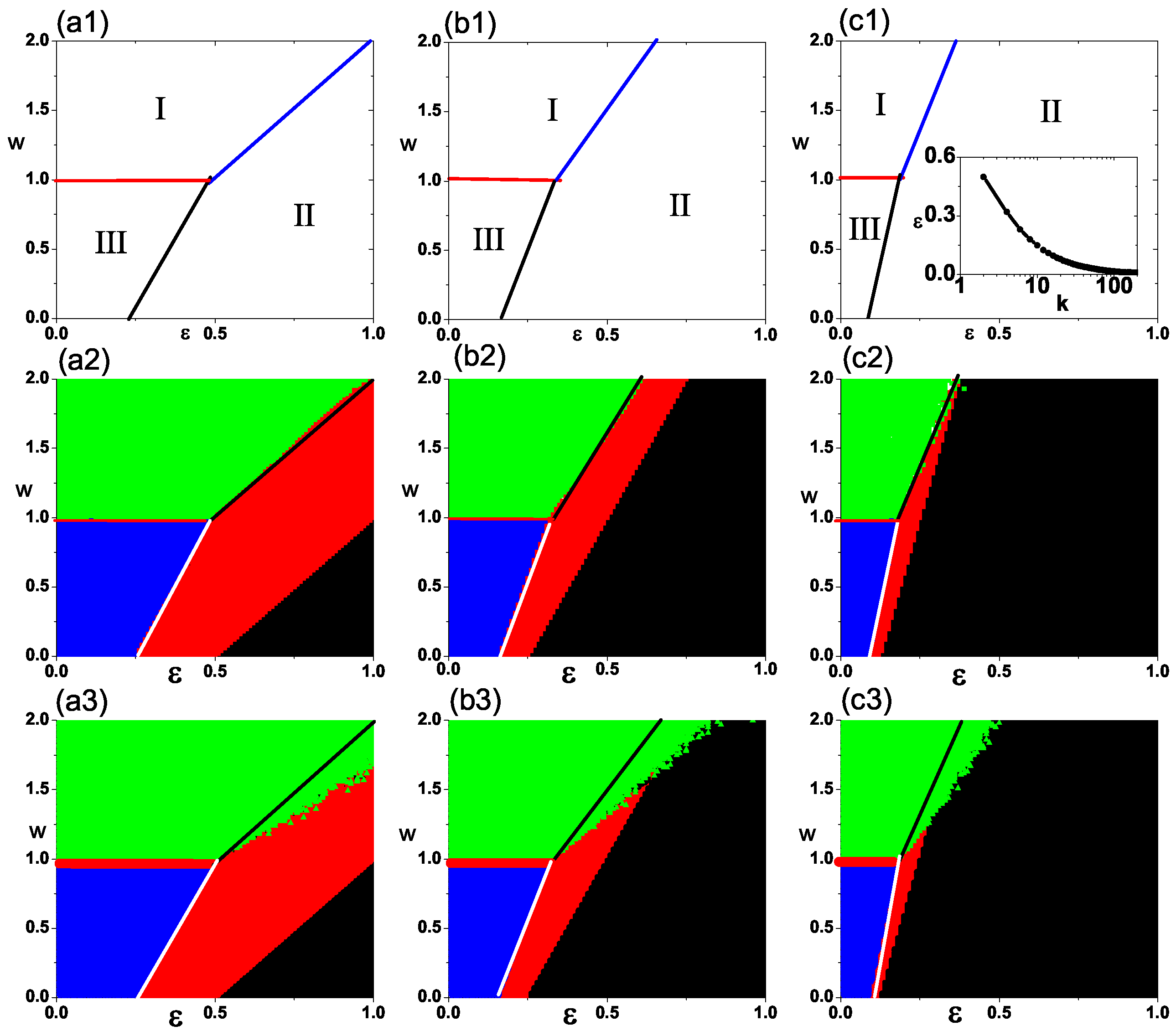
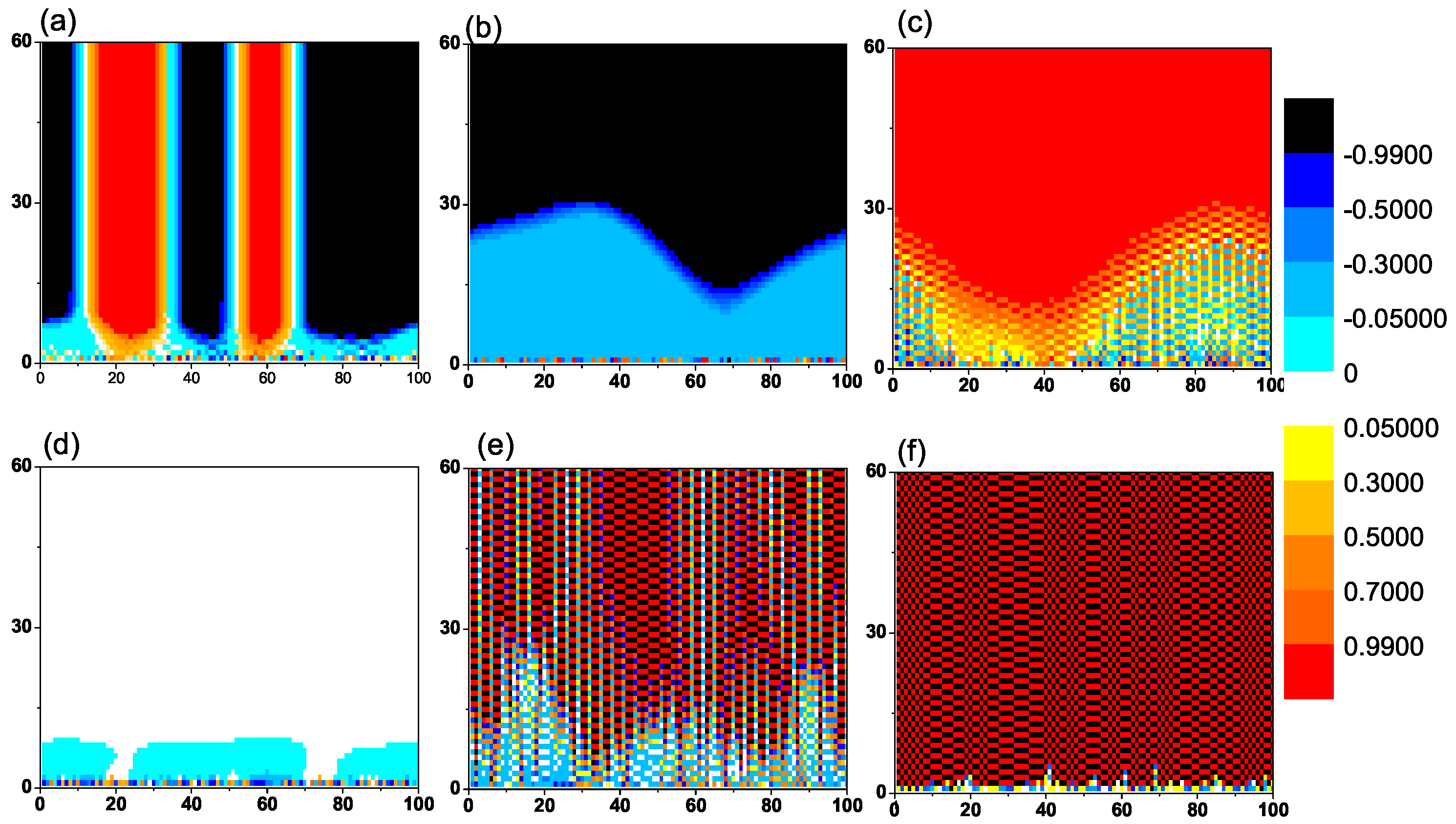
3.1. Phase Diagrams and Opinion Dynamical States
3.2. Finite Size Effects
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- French, J.R.P. A formal theory of social power. Psychol. Rev. 1956, 63, 181–194. [Google Scholar] [CrossRef] [PubMed]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Saber, R.O.; Fan, J.A.; Murray, R.M. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Ding, Z.G.; Chen, X.; Dong, Y.C.; Herrera, F. Consensus reaching in social network DeGroot Model: The roles of the Self-confidence and node degree. Inf. Sci. 2019, 486, 62–72. [Google Scholar] [CrossRef]
- Sznajd-Weron, K.; Sznajd, J. Opinion evolution in closed community. Int. J. Mod. Phys. C 2000, 11, 1157–1165. [Google Scholar] [CrossRef]
- Galam, S. Minority opinion spreading in random geometry. Eur. Phys. J. B 2002, 25, 403–406. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Johnsen, E.C. Social influence networks and opinion change. Adv. Group Process 1999, 16, 1–29. [Google Scholar]
- Friedkin, N.E.; Proskurnikov, A.V.; Tempo, R.; Parsegov, S.E. Network science on belief system dynamics under logic constraints. Science 2016, 354, 321–326. [Google Scholar] [CrossRef]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Compl. Sys. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics and bounded confidence models, analysis, and simulation. J. Artif. Soc. Soc. Simul. 2002, 5, 1–33. [Google Scholar]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591. [Google Scholar] [CrossRef]
- Shao, J.; Havlin, S.; Stanley, H.E. Dynamic opinion model and invasion percolation. Phys. Rev. Lett. 2009, 103, 018701.1–018701.4. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Du, Y.J.; Chen, X.L.; Li, X.Y. Newly exposed conflicting news based network opinion reversal. Acta Phys. Sin. 2016, 65, 030502. [Google Scholar] [CrossRef]
- Hou, Z.; Bin, H. Impact of information on public opinion reversal-An agent based model. Phys. A 2018, 512, 578–587. [Google Scholar]
- Telba, Z.I.; Pereira, c.A.d.B.; Ram, C.T. Analysis of opinion swing: Comparison of two correlated proportions. Am. Stat. 2000, 54, 57–62. [Google Scholar]
- Pearson, P.T.; Cooper, C.I. Using self organizing maps to analyze demographics and swing state voting in the 2008 U.S. Presidential Election. In Proceedings of the Artificial Neural Networks in Pattern Recognition (ANNPR) 2012, Trento, Italy, 17–19 September 2020. [Google Scholar]
- Akgiray, V.; Booth, G.G. Mixed diffusion-jump process modeling of exchange rate movements. Rev. Econ. Stat. 1988, 70, 631–637. [Google Scholar] [CrossRef]
- Fu, G.; Zhang, W.; Li, Z. Opinion dynamics of modified Hegselmann-Krause model in a group-based population with heterogenenous bounded confidence. Phys. A 2015, 419, 558–565. [Google Scholar] [CrossRef]
- Ghaderi, J.; Srikant, R. Opinion dynamics in social networks with stubborn agents: Equilibrium and convergence rate. Automatica 2014, 50, 3209–3215. [Google Scholar] [CrossRef]
- Olshevsky, A.; Tsitsiklis, J.N. Convergence speed in distributed consensus and averaging. SIAM J. Control Optim. 2009, 48, 33–55. [Google Scholar] [CrossRef]
- Han, W.; Huang, C.; Yang, J.Z. Opinion clusters in a modified Hegselmann-Krause model with heterogeneous bounded confidences and stubbornness. Phys. A 2019, 531, 121791. [Google Scholar] [CrossRef]
- Bearden, W.O.; Hardesty, D.M.; Rose, R.L. Consumer self-confidence: Refinements in conceptualization and measurement. J. Consum. Res. 2001, 28, 121–134. [Google Scholar] [CrossRef]
- Koehler, D.J. Explanation, imagination, and confidence in judgment. Am. Psychol. Assoc. 1991, 110, 499–519. [Google Scholar] [CrossRef] [PubMed]
- Bandura, A.; Wood, R. Effect of perceived controllability and performance standards on selfregulation of complex decision making. J. Personal. Soc. Psychol. 1989, 56, 805–814. [Google Scholar] [CrossRef]
- Ghosh, D.; Ray, M. Risk, ambiguity, and decision choice: Some additional evidence. Decis. Sci. 1997, 28, 81–104. [Google Scholar] [CrossRef]
- Adams, J.K.; Adams, P.A. Realism of confidence judgments. Psychol. Rev. 1961, 68, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, C.; Pettitt, J.; Woollard, A.; Rutherford, A.; Bickmore, W.; Ferguson-Smith, A.; Hurst, L.D. People with more extreme attitudes towards science have self-confidence in their understanding of science, even if this is not justified. PLoS Biol. 2023, 21, e3001915. [Google Scholar] [CrossRef]
- Van Prooijen, J.W.; Krouwel, A.P.M. Psychological Features of Extreme Political Ideologies. Curr. Dir. Psychol. Sci. 2019, 28, 159–163. [Google Scholar] [CrossRef]
- Chuang, S.C.; Cheng, Y.H.; Chang, C.J.; Chiang, Y.T. The impact of self-confidence on the compromise effect. Int. J. Psychol. 2013, 48, 660–675. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, X.; Han, W.; Yang, J. From the DeGroot Model to the DeGroot-Non-Consensus Model: The Jump States and the Frozen Fragment States. Mathematics 2024, 12, 228. https://doi.org/10.3390/math12020228
Qian X, Han W, Yang J. From the DeGroot Model to the DeGroot-Non-Consensus Model: The Jump States and the Frozen Fragment States. Mathematics. 2024; 12(2):228. https://doi.org/10.3390/math12020228
Chicago/Turabian StyleQian, Xiaolan, Wenchen Han, and Junzhong Yang. 2024. "From the DeGroot Model to the DeGroot-Non-Consensus Model: The Jump States and the Frozen Fragment States" Mathematics 12, no. 2: 228. https://doi.org/10.3390/math12020228
APA StyleQian, X., Han, W., & Yang, J. (2024). From the DeGroot Model to the DeGroot-Non-Consensus Model: The Jump States and the Frozen Fragment States. Mathematics, 12(2), 228. https://doi.org/10.3390/math12020228




